Patterns of steady axisymmetric supersonic compression flows with a Mach disk

Abstract

Results of a numerical simulation of steady axisymmetric supersonic flows in convergent conical ducts and in overexpanded jets are presented. The characteristic feature of these compression flows is the formation of an initial longitudinally curved shock wave with intensity increasing downstream and toward the flow axis, which is finalized by the generation of a central Mach disk. Computations have demonstrated patterns of an irregular interaction of these shocks followed by the formation of a triple-shock configuration, including a reflected shock and a shear layer with entropy varying across the layer. The formation of triple-shock configurations is analogous to the configurations known for the steady inviscid two-dimensional flows where the irregular reflection of a wedge-generated shock from a wall with Mach stem formation occurs. Either a single triple-shock Mach configuration occurs or a triple-shock configuration corresponding to the von Neumann paradox condition is formed at the considered flow Mach numbers and initial angles of deflection to the axis of the flow behind the longitudinally curved shock wave.

1 Introduction

The topic of the present paper is steady axisymmetric supersonic flows in convergent conical ducts. Let us briefly consider the state of research on this subject.

Early studies of these flows related to the first-time development of turbojet-powered supersonic aircraft designed for flight Mach numbers up to M $=$ 1.5–2. Ferri and Nucci [1] analyzed the capabilities of the simplest internal-compression inlets in the form of a conical funnel as applied to such aircraft. Ferri presented an example of calculating an axisymmetric flow in such an inlet at $M=1.6$ using the method of characteristics [2, 3].

An initially conical internal shock wave (the flow velocity behind which converges to the axis) forms immediately at the circular leading edge of this inlet. The shock develops further downstream into a shock in the form of a longitudinally curved surface of revolution. This shock is incident onto the duct axis; its slope and intensity continuously increase as the shock approaches the axis; the flow velocity behind the shock decreases appropriately. The axisymmetric flow downstream of the longitudinally curved shock was calculated by Ferri [2, 3] up to a point where the velocity behind the shock became sonic. According to the problem statement, a reflected shock arose here with its development continuing up to the conical funnel wall. The supersonic compression flow of interest was calculated from the initial incident shock up to the reflected shock. According to Ferri [2, 3], another hypothetical strong shock wave, the flow behind which is subsonic, has to form in the direction from the sonic point to the axis with its gradual transformation into a normal shock at this axis. Instead of this, a central transverse shock close to the normal one, i.e., a Mach disk, arises in the steady axisymmetric supersonic flows. This is explained, for example, in the work of Courant and Friedrichs [4] by showing that a conical shock wave with the flow behind it converging to the axis cannot reflect from this axis in a regular manner.

A large size of a Mach disk at $M<2$ results in a low pressure recovery factor of the internal-compression inlets in the form of a funnel duct and worsening of the performance of such inlets as compared to external-compression inlets with a nose cone body [5]. The problems associated with inlet starting are complicated for internal-compression inlets. These and other problems were apparently responsible for the lack of substantial progress in the development of the mentioned internal-compression inlets, and for a long time there was little interest in studying axisymmetric supersonic compression flows with a Mach disk. Some investigations on this subject were carried out due to the development of hypersonic flying vehicles powered by ramjets or scramjets. The flows in inlets in the form of a conical funnel in the range M $=$ 1.6–12 were computed by Gutov and Zatoloka [6] analogously to Ferri [3]; it was shown that the possible transversal size of the central flow core determined by Ferri’s hypothetical shock essentially decreases with increasing free-stream Mach numbers at $M>4.$ The experiments by Antonov et al. [7] demonstrated a high compression performance of the simplest internal-compression inlets in the form of a conical funnel at a hypersonic Mach number $M=11.5.$ There are recent considerations of funnel-shaped inlets of fully internal compression as applied to hypersonic scramjet-powered vehicles flying at Mach numbers $M>4,$ for example, Tirtey et al. [8]. A numerical computation of a laminar flow in the simplest inlet with a funnel-shaped compression section at $M=4$ presented by Bashkin and Egorov [9] is worth mentioning. There are reconsiderations of the problem on the irregular reflection of a conical shock wave compressing the flow to an axis and conditions of forming a Mach disk in this case [10]. Nevertheless, knowledge of the features of the formation of axisymmetric supersonic converging flows with a Mach disk remains scarce. Note that such flows occur also in the initial section of overexpanded jets exhausting into still air or into an external co-current air stream.

A numerical simulation of the axisymmetric flows with a Mach disk was performed in the present work. The peculiarities of the formation of these flows were studied depending on the free-stream Mach number and the conical funnel angle or the initial angle of flow deflection to the axis for the overexpansion jet. The representative flow patterns are discussed below.

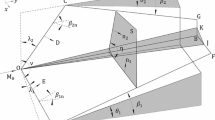
A general structure of the axisymmetric flow in a convergent conical duct is schematically pictured in Fig. 1, where x is the coordinate along the duct axis and y is the radial coordinate. The free-stream flow is assumed to be directed from left to right along the duct axis; further, in the figures showing flow patterns, this direction is denoted by an arrow. The conical wall 1 of the duct with an inclination angle $\theta _{\mathrm{c}}$ forms a longitudinally curved shock 2 incident onto the axis. A local deflection angle $\updelta$ of the perturbed flow is assumed to be positive if the flow velocity is inclined to the duct axis. Due to the irregular reflection of the incident shock 2 from the axis, a Mach disk 3 and a reflected shock 4 arise, and so the triple-shock configuration 5 originates. Occurrence of a contact discontinuity—the slipline 6 emanating from the triple-shock intersection point in a longitudinal plane (x, y)—is also allowed. Note here, since the flow is axisymmetric, all the shocks can be visualized as surfaces of revolution and the slipline 6 is a generatrix of a slip surface of revolution.

Let us discuss the types of triple-shock configurations possible in the axisymmetric flows under consideration using the shock polars and triple-shock theory developed by von Neumann and based on the Rankine–Hugoniot jump relations, see e.g., [4]. Note that this theory is valid for two-dimensional (2D) flows of an ideal gas. The theory yields the solution for the triple-shock configuration forming at the irregular reflection of an oblique shock wave incident onto a flat wall and including a reflected shock, a shock known as the Mach stem, and the slip line. The solution implies these shocks and slip line to be of negligible thickness and curvature.

Fig. 1

Schematic of supersonic flow in a convergent conical duct

In the present work, the known triple-shock solution is assumed to be valid for the considered axisymmetric flows with respect to a local area of the triple-shock interaction (marked by a circle in Fig. 1). The 2D analysis of the shock polars in the given case is based upon known considerations of discontinuities, particularly the shock waves, in gas dynamic theory. If a three-dimensional (3D) shock surface is smooth, the conservation equations at an arbitrary point of this surface can be reduced to an equivalent form in terms of the 2D Rankine–Hugoniot jump relations. These 2D equations describe the plane shock tangent to the 3D shock surface and have to be considered in the longitudinal plane passing through the point and defined by the flow velocity vectors in front of the shock and behind it; it is the plane of symmetry for the axisymmetric flow. This proposition can be exemplified by a conical shock wave, the parameters of which equal to those of the plane oblique shock with the same inclination angle to the flow velocity ahead of the shock.

Fig. 2

Shock polars at $M = 1.6$

2 On possible patterns of interaction of the incident longitudinally curved shock and the Mach disk

Let us first analyze the conditions of possible interactions of the incident longitudinally curved shock and the Mach disk with the use of shock polars in an example of the flow with a free-stream Mach number $M=1.6$. Figure 2 presents the pertinent shock polars in the pressure ratio–flow deflection angle plane; here the pressure $p_{\mathrm{s}}$ behind the shock is normalized to the free-stream flow pressure $p_{\infty }$, $\bar{p}_{\mathrm{s}}=p_{\mathrm{s}}/p_{\infty }$. Polar 1 in Fig. 2 is a locus of all shocks forming at $M=1.6;$ particularly, it is pertinent to the incident longitudinally curved shock. It is evident that the point ${\delta }=0$ on the ordinate axis at which $\bar{p}_{\mathrm{s}}=1$ corresponds to a degenerate shock; it is the Mach line in a two-dimensional flow or the Mach cone in an axisymmetric flow. The point ${\delta }=0$ at which $\bar{p}_{\mathrm{s}}=2.82$ corresponds to the normal shock arising in the free-stream flow; it gives the pressure jump behind the Mach disk on the axis. Point 7 of polar 1 at ${\delta }={\delta }_{{M=1}}=14.24{^{\circ }}$ where $\bar{p}_{\mathrm{s}}=2.15$ corresponds to the sonic flow velocity $M_{\mathrm{s}}=1$ behind the incident shock. This point separates polar 1 into two branches: a “weak” branch for which the flow velocity behind the shock is supersonic and a “strong” branch for which the flow velocity behind the shock is subsonic. Let us assume that a secondary shock wave forms in the flow behind the initial shock wave in a point corresponding to the weak branch of polar 1 at ${ \delta }={\delta }_{\mathrm{i}}$. Let $M_{\mathrm{s}}$ be the Mach number of the flow behind this initial shock and ${\delta }_{\mathrm{r}}$ the angle of flow deflection behind the secondary shock to the direction of the flow with $M_{\mathrm{s}}$. A set of polars of such secondary shocks corresponding to different angles ${\delta }_{\mathrm{i}}$ is presented in Fig 2. The secondary shock with a flow deflection angle ${ \delta }_{\mathrm{r}}>0$ will be of the same family as the initial one; the secondary shock will be of the opposite family at ${\delta }_{\mathrm{r}}<0$. For the inviscid two-dimensional flow, the secondary shock with ${\delta }_{\mathrm{r}}<0, { \delta }={ \delta }_{\mathrm{i}}+{\delta }_{\mathrm{r}}=0$ can be treated as a reflected shock arising at the regular reflection of a wedge-generated oblique shock from a flat wall. In accordance with the considered problem, secondary shocks with ${\delta }_{\mathrm{r}}<~0$ and intersections of their polars with the strong branch of the initial shock polar 1 are of interest, and the above-mentioned triple-shock theory can be applied in these cases.

The secondary shock polar 2 corresponding to ${\delta }_{\mathrm{i}}=3{^{\circ }}$ intersects the initial shock polar 1 at a point with ${\delta }_{\mathrm{t}}={ \delta }_{\mathrm{i}}+{\delta }_{\mathrm{r}}<0$; therewith, the flow along the slip line behind the triple-shock configuration corresponding to this point has to deflect from the axis. The secondary shock polar 3 corresponding to ${\delta }_{\mathrm{i}}=5{^{\circ }}$ intersects the initial shock polar 1 at a point with ${\delta }_{\mathrm{t}}={ \delta }_{\mathrm{i}}+{\delta }_{\mathrm{r}}>0;$ in this case, the flow along the slip line has to deflect to the axis. The triple-shock solutions in these cases are known, respectively, as the inverse (or inverted) and direct Mach reflections, respectively [4, 11, 12]. The inverse Mach triple-shock configuration does not occur in ordinary steady two-dimensional flows. The direct Mach triple-shock configuration is typical of these flows; in the case of the irregular reflection problem, it is also defined as the single triple-shock Mach reflection [4, 12]. The inverse and direct Mach triple-shock configurations are separated by the configuration where the second shock polar 2 intersects the strong branch of the initial shock polar 1 at ${\delta }_{\mathrm{t}}={\delta }_{\mathrm{i}}+{\delta }_{\mathrm{r}}=0$ (here, ${ \delta }_{\mathrm{i}}={\delta }_{\mathrm{i}0}=3.975{^{\circ }}$ for the presented example at $M=1.6).$ The Mach stem in the latter case has to be straight linear; such a Mach triple-shock configuration in an unsteady two-dimensional flow is known as the stationary Mach configuration. This configuration does not seem to contradict the conditions of steady two-dimensional flows.

As for the steady axisymmetric supersonic flows, the Mach disk in the case of the inverse Mach triple-shock configuration has to be convex toward the free-stream flow direction; the flow behind the disk has to be diverging and decelerating, so that this solution disagrees with the known patterns of the steady axisymmetric supersonic converging flows. The direct Mach triple-shock configuration is quite pertinent in these flows, because the Mach disk has to be convex away from the free-stream flow direction; the flow behind the disk has to be converging and accelerating. The triple-shock configuration with a flat Mach disk in the steady axisymmetric supersonic flows in a convergent conical duct must form at the intersection of the reflected shock polar and the initial shock polar 1 at the axis of the latter where ${\delta }_{\mathrm{t}}={\delta }_{\mathrm{i}}+{\delta }_{\mathrm{r}}=0,$ as it is for the straight-linear Mach stem in the 2D flows. This condition for the considered axisymmetric flows seems to take place at a small angle ${\theta }_{\mathrm{c0}}$ of the conical wall; particularly, it should be ${\theta }_{\mathrm{c0}}<{\delta }_{\mathrm{i0}}=3.975{^{\circ }}$ for the presented example at $M=1.6.$ Here, the angle ${ \delta }_{\mathrm{i0}}$ is analytically determined for the 2D flow as indicated above; the angle ${\theta }_{\mathrm{c0}}$ for the axisymmetric flow is unknown in advance. Note, a virtually flat Mach disk was obtained in a numerical computation of the axisymmetric flow at $M=4$ and ${\theta }_{\mathrm{c}}=3.5{^{\circ }}$ [10]. Altogether, numerical computations aimed at examining the axisymmetric flows with a flat Mach disk at a certain angle $0<{\theta }_{\mathrm{c0}}<{\delta }_{\mathrm{i0}}$ would be complicated because the Mach disc size has to decrease essentially with decreasing ${\theta }_{\mathrm{c}}$. The latter was shown analytically [10]. Small Mach disks are not resolved in numerical computations of axisymmetric supersonic flows and in experiments, so that, as noted in [10], “an illusory regular reflection” with a quasi-conical reflected shock wave is observed near the axis. Generally, the problem as to the determination of the exact conditions at which the flat Mach disk forms in the steady axisymmetric supersonic converging flows needs further investigation.

The secondary shock polar 6 corresponding to ${ \delta }_{\mathrm{i}}=12{^{\circ }}$ is presented in Fig. 2 for which there is no intersection with the initial shock polar 1, i.e., there is no Mach triple-shock solution. An irregular triple-shock configuration does form experimentally in this case. This situation is known as the von Neumann paradox, and the associated reflection is called the von Neumann reflection. The secondary shock polar 4 intersects the initial shock polar 1 at a point with ${\delta }_{\mathrm{t}}={\delta }_{\mathrm{i}}$, where the slope of the secondary shock to the velocity ahead of it equals ${\beta }={\pi }/2,$ i.e., this shock is normal. The secondary shock polar 5 corresponding to ${\delta }_{\mathrm{i}}=10{^{\circ }}$ intersects the initial shock polar 1 at a point with ${\delta }_{\mathrm{t}}={\delta }_{\mathrm{i}}+~{\delta }_{\mathrm{r}}>{\delta }_{\mathrm{i}}$ on the right of the point corresponding to ${\delta }_{\mathrm{t}}={\delta }_{\mathrm{i}}$. It is also known that the interaction of shocks in the latter case has to correspond to an irregular triple-shock configuration of the same type that occurs under the conditions of the von Neumann paradox (see [12, 13]). The case ${\delta }_{\mathrm{t}}={\delta }_{\mathrm{i}}$ is transitional between the Mach and von Neumann reflections.

There are a considerable number of publications on experimental and theoretical studies of the von Neumann paradox in the 2D flows; a detailed review is presented in [13]. Numerical simulations were made to refine theoretical views of this subject in the framework of the ideal gas dynamic model. One of the approaches used to resolve the von Neumann paradox was the accounting of viscous effects, which was based on experimentally observed flow patterns. Sternberg gave an adequate semi-quantitative solution [14]. The von Neumann irregular reflection was computed in [15] with the Navier–Stokes code.

The limiting case should be noted with regard to secondary shocks, and it corresponds to the angle ${\delta }_{\mathrm{i}}={\delta }_{M=1}$ at the sonic point 7 of the initial shock polar 1. There is no proper secondary shock polar in this case; however theoretically, the secondary shock could be initiated as a normal shock in the flow with the sonic velocity $M_{\mathrm{s}}=1$ and $\bar{p}_{\mathrm{s}}=2.15$ behind the initial shock. The Mach disk in this case also has to begin from the same sonic point where its slope and the relative pressure behind it have to correspond to the incident longitudinally curved shock at ${\delta }={\delta }_{{M=1}}$. This Mach disk has to continue in a direction to the axis with its transformation into the normal shock at this axis; particularly, the pressure behind it has to increase up to $\bar{p}_{\mathrm{s}}=2.82.$ The resulting Mach disk has to be highly convex away from the oncoming flow. The described limiting case virtually corresponds to Ferri’s assumptions for the above-mentioned axisymmetric supersonic flow in the funnel-shaped inlet [2, 3].

Thus, the flow example considered for the analysis of the irregular interaction of the initial incident longitudinally curved shock wave and the Mach disk in steady axisymmetric supersonic converging flows demonstrates two possible types of these interactions. One type fits the single triple-shock Mach reflection; another meets the von Neumann paradox conditions. A particular interaction occurring in such a flow at a preset free-stream Mach number is determined by the angle ${\delta }_{\mathrm{i}}$ of flow deflection behind the incident shock just near the triple-shock intersection, but this angle depends on the development of the incident longitudinally curved shock generated at the initial flow deflection angle ${\theta }_{\mathrm{c}}$. The range of the indicated interactions depending on the angle ${\theta }_{\mathrm{c}}$ is bounded by the following theoretically possible limiting irregular configurations. On the one hand, it is the configuration with a flat Mach disk which can form at a small angle ${\theta }_{\mathrm{c}}$; it should be of a very small transverse size. On the other hand, it is the above-mentioned Ferri’s limiting triple-shock configuration when the reflected shock polar is degenerate.

As for the steady reflections of wedge-generated shock waves in two-dimensional supersonic flows, the following problem is significant, being highlighted by a number of investigators. Only either regular or irregular reflection is possible at $M<2.2;$ however, at higher Mach numbers $M>2.2,$ a domain of dual solution exists where both regular and irregular reflection is possible. There is no such problem for steady axisymmetric flows due to the mentioned impossibility of regular reflection of a conical shock wave incident onto the axis in such flows.

The following dissimilarity between the wave structure in axisymmetric flows with a Mach disk and in two-dimensional flows with a Mach stem should be noted. The incident wedge-generated shock in the two-dimensional flow is straight linear, and its parameters do not vary downstream so that the type of its irregular reflection is uniquely determined and does not depend on the Mach stem position. The parameters of the initial incident longitudinally curved shock in the axisymmetric flow vary downstream; that is why a continuous family of particular irregular triple-shock solutions is possible according to the Mach disk position which is previously unknown. The numerical solution of the problem by the pseudo-unsteady method yields a particular irregular triple-shock configuration and its parameters, including a Mach disk position. The configurations obtained in the computed examples of flows will be illustrated below.

3 Numerical technique and flow conditions

The numerical simulation and investigation of the considered flows in the present work was performed with the use of codes provided by ANSYS Fluent software. The Navier–Stokes codes for turbulent flows and the Euler code for inviscid flows were applied. The problem was solved by the pseudo-unsteady method, in the form implemented in ANSYS Fluent, with initialization of the free stream parameters. Adiabatic flows of an ideal gas (air) with the ratio of specific heats ${\gamma }=7/5$ and with the stagnation temperature constant everywhere were considered.

A general approach to a problem is based on works [15, 16] where the problems of the three-shock interaction in the cases of irregular reflections of strong and weak shock waves in the 2D flows were solved numerically with the use of Navier–Stokes equations in comparison to the direct simulation Monte Carlo method. Convergence of the numerical solution of the Navier–Stokes equations was analyzed as the Reynolds number increased from ${\mathrm{Re}}_{L}\sim 10^{3}$ to ${\mathrm{Re}}_{L}\sim 10^{9}$ where the reference length L pertains to the wedge generating the incident shock. There were no significant differences in the triple-shock configurations and in the behavior of the numerical solutions in the pressure ratio-flow deflection angle plane at high Reynolds numbers.

Density-based, time-explicit codes and ${k\hbox {-}\omega }$ SST turbulence model provided by ANSYS Fluent software were used in the present work. Grids with uniform spacing were used; the overall number of grid cells was up to $5\times 10^{6}$. A set of computations was performed with increasing a reference step in the radial direction from $D_{0}/1000$ to $D_{0}/2000$; here, $D_{0}$ is the duct entrance diameter or the initial overexpanded jet diameter. The shock interaction type for a given input data did not change with the increase in reference step; there was no significant quantitative difference in the computation results. The step $D_{0}/2000$ was used in further computations.

The diameter of the entrance cross section equal to 1 m was taken as a reference size in computations of the flows in convergent conical ducts. Examples of the computed flows are presented below for the following free-stream Mach numbers and angles of the conical funnel: $M=1.6,$ ${\theta }_{\mathrm{c}}=5{^{\circ }}$ and $M=2.0,$ ${\theta }_{\mathrm{c}}=10{^{\circ }}$. The static free-stream pressure and temperature were equal to $p_{\infty }=10^{4}$ Pa and $T_{\infty }=300\, \mathrm{K};$ the unit Reynolds numbers had the values from $35\times 10^{6}$ up to $50\times 10^{6}\;1/\mathrm{m}.$ The flows in overexpanded jets were computed for the case of these flows exhausting into still air, the initial jet diameter was equal to 1 m, and the air pressure was $p_{\mathrm{a}}=10^{4}$ Pa. The jets were considered to have the parameters ${M}_{\mathrm{j}}=1.6, p_{\mathrm{j}}/p_{\mathrm{a}}=0.7$ and $M_{\mathrm{j}}=2,$ $p_{\mathrm{j}}/p_{\mathrm{a}}=0.6.$ The static temperature of the jets was equal to $T_{\mathrm{j}}=300~\mathrm{K},$ and the unit Reynolds number values were $24\times 10^{6}$ and $26\times 10^{6}1/{\mathrm{m}}.$

Fig. 3

Flow pattern (field of Mach number isolines) in a funnel-shaped duct at $M~=~2$ and ${\theta }_{\mathrm{c}}=10{^{\circ }}$

Fig. 4

Shock polars for the flow in a funnel-shaped duct at $M=2$ and ${\theta }_{\mathrm{c}}=10{^{\circ }}$

4 Computed flow patterns in convergent conical ducts

The figures of the computed flow patterns are presented hereafter over the coordinates (x, y) where the x-coordinate along the duct axis and the y-coordinate in the radial direction are equivalent to the normalized $\bar{x}=x/D_{0}$ and $\bar{y}=y/D_{0}$ taking into account $D_{0}=1\,{\mathrm{m}}.$ That is why they can be treated either as dimensionless or as having dimensionality of meters; the latter may be of any meaning in terms of viscous flows.

The first computed example of a flow pattern in a conical funnel duct is shown in Fig. 3 for $M=2$ and ${\theta }_{\mathrm{c}}=10{^{\circ }}$, a field of the Mach number isolines is pictured, and the Mach number values are also marked at individual points of the flow field. The Mach disk of diameter $\bar{D}_{\mathrm{M}}=D_{\mathrm{M}}/D_{0}\approx 0.315\pm 0.05$ is located at a distance $\bar{x}_{\mathrm{M}}=x_{\mathrm{M}}/D_{0}\approx ~0.395$ from the entrance cross section. The shock polars corresponding to this case are presented in Fig. 4. First, polar 1 is plotted, which presents shocks forming in the free-stream flow with $M=2.$ The parameters of the initial incident longitudinally curved shock and the Mach disk correspond to this polar. Polar 2 corresponds to a reflected shock just near the triple intersection of the shocks.

Regarding the polars of the reflected shocks, namely polar 2 in Fig. 4 and the analogous polars in other figures below, the following should be noted: the initial incident longitudinally curved shock in the considered axisymmetric flows has no analytical solution at present. Since this shock is computed numerically, it has a certain thickness across which the flow parameters vary. As the shock is longitudinally curved, flow parameters behind it vary also in a direction tangent to the shock. That is why there is no point behind this shock exactly corresponding to the point of the incident shocks polar 1 where the reflected shock should theoretically form if the shocks have negligible thickness. Polar 2 in Fig. 4 was determined for flow parameters ${\delta }_{\mathrm{i}}=16.2{^{\circ }}$, $M_{\mathrm{s}}=1.4,$ and $\bar{p}_{\mathrm{s}}=2.34$ just behind the initial incident longitudinally curved shock along a streamline defined by the coordinate $y_{\mathrm{t}}=0.162$ (Fig. 3). The above-mentioned streamline was selected as close as possible to a “smeared” zone of the triple-shock interaction. Transversal sizes of this zone as well as the reflected shock also are not determined rigorously by the numerical computation data. That is why the flow parameters along the mentioned streamline behind the incident shock and ahead of the reflected shock, particularly the values of ${\delta }_{\mathrm{i}}$ and $M_{\mathrm{s}}$, initial point for calculating the reflected shock polar, could be determined only approximately. As a result, the initial point of the presented reflected shock polar 2 with ${\delta }_{\mathrm{i}}=16.2{^{\circ }}$ and $\bar{p}_{\mathrm{s}}=2.34$ is somewhat shifted as compared to a position on the incident shock, which could be determined theoretically in the case with shocks of negligible thickness. The shift is rather small and is not discernible due to the scale of the figures.

The point ${\delta }=0{^{\circ }}$, $\bar{p}_{\mathrm{s}}=4.5$ of shock polar 1 corresponds to a pressure jump through the Mach disk directly along the axis; points of polar’s arc from ${\delta }={\theta }_{\mathrm{c}}$ to ${\delta }={\delta }_{\mathrm{i}}=16.2{^{\circ }}$ correspond to the incident longitudinally curved shock parameters. The angle ${\delta }={\delta }_{\mathrm{t}}=7.7{^{\circ }}$ defines the point of intersection of the reflected shock polar 2 with the strong branch of the incident shock polars 1. This point is on the left of the axis of polar 2 and on the right of the axis of polar 1, i.e., $0<{\delta }_{\mathrm{t}}<{\delta }_{\mathrm{r}}$. Thereby, the reflected shock deflects the flow in the direction opposite to the flow deflection behind the incident shock. According to these considerations, the analytical solution for interaction of shocks at this point corresponds to the single triple-shock Mach configuration.

Fig. 5

Flow pattern (field of Mach number isolines) in a funnel-shaped duct at $M=1.6$ and ${\theta }_{\mathrm{c}}=5{^{\circ }}$

Fig. 6

Shock polars for the flow in a funnel-shaped duct at $M=1.6$ and ${\theta }_{\mathrm{c}}=5{^{\circ }}$

The diamond-shaped symbols 3 in Fig. 4 show variation of the relative pressure just behind the Mach disk and the reflected shock in the numerically computed flow pattern when the radial coordinate varies from $y=0,$ where $\delta \approx 0{^{\circ }}$ and $\bar{p}_{\mathrm{s}}\approx 4.5,$ up to $y=0.24,$ in which ${\delta }\approx 2.45{^{\circ }}$ and $\bar{p}_{\mathrm{s}}\approx 3.83.$ One can see that the transition from the flow parameters behind the Mach disk to those behind the reflected shock at ${\delta }\approx {\delta }_{\mathrm{t}}=7.7{^{\circ }}$ occurs with a deviation from the strong branch of the incident shock.

Another computed example of the flow pattern in the conical funnel is presented in Fig. 5 for $M=1.6$ and ${\theta }_{\mathrm{c}}=5{^{\circ }}$. The Mach disk of diameter $\bar{D}_{\mathrm{M}}\approx 0.195\pm 0.005$ is located at a distance $\bar{x}_{\mathrm{M}}\approx 0.38$ from the entrance cross section. Polar 1 of shocks forming in the free-stream flow with $M=1.6$ and polar 2 of the reflected shock forming just near the triple intersection of the shocks for this case are presented in Fig. 6. Polar 2 in Fig. 6 was determined for the flow parameters ${\delta }_{\mathrm{i}}=10.2{^{\circ }}$, $M_{\mathrm{s}}=1.22,$ and $\bar{p}_{\mathrm{s}}=1.66$ just behind the initial incident longitudinally curved shock along a streamline defined by a coordinate $y_{\mathrm{t}}=0.104.$ Polar 2 of the reflected shock intersects the strong branch of the incident shock polar 1 on the right of its own axis at a point with ${\delta }_{\mathrm{t}}=13.4{^{\circ }}> {\delta }_{\mathrm{i}}=10.2{^{\circ }}$. The irregular interaction of shocks in this case has to correspond, as it was analyzed above, to the triple-shock configuration of the same type that occurs under the conditions of the von Neumann paradox.

Let us consider another secondary shock with a polar for which positions of its axis at ${\delta }_{\mathrm{r}}=8.4{^{\circ }}$ and the point ${\delta }_{\mathrm{t}}=8.4{^{\circ }}$ of its intersection with shock polar 1 are coincident. Polar 3 of this shock is also plotted in Fig. 6. This shock has an inclination angle ${\beta }={{\pi /2}}$ with respect to the flow direction immediately in front of it, i.e., this shock is normal in the flow behind the initial shock wave.

The diamond-shaped symbols 4 in Fig. 6 show variation of the relative pressure just behind the Mach disk and the reflected shock in the numerically computed flow pattern when the radial coordinate varies from $y=0,$ where ${\delta }\approx 0{^{\circ }}$ and $\bar{p}_{\mathrm{s}}\approx 2.82,$ up to $y=0.27,$ where ${\delta }\approx 0.4{^{\circ }}$ and $\bar{p}_{\mathrm{s}}\approx 2.14.$ In this case, as in the previous one, the transition from the flow parameters behind the Mach disk to those behind the reflected shock occurs with a deviation from the strong branch of the incident shock beginning from a point at ${\delta }\approx 8.4{^{\circ }}$, just near the position of to the axis of polar 3 for the reflected shock with the inclination angle ${\beta }={\pi /2}.$ Subsequently, this transition culminates on the reflected shock polar 2. That is why one can assume that the reflected shock with polar 2 is incipient immediately at the triple-shock interaction as a normal shock; after that, its slope decreases as it emerges from the zone of immediate interaction. Note that the reflected shock with polar 2 remains strong; the flow velocity behind this shock is subsonic.

For the above computed flow patterns, it is worth noting the formation of a shear layer with entropy varying across it; the layer develops downstream immediately from the local zone of the irregular triple-shock interaction. The formation of this specific layer at the triple-shock interaction conforms to the concept of Sternberg [14] explaining the triple-shock interaction under the conditions of the von Neumann paradox. The shocks in the viscous flow have a finite thickness, so that the zone of triple-shock interaction has a transverse size of the same order. That is why the transition of flow parameters in the transverse direction just downstream of this interaction from the state behind the Mach disk to the state behind the reflected shock wave occurs continuously rather than in a jump described by the Rankine–Hugoniot relations. The mentioned shear layer, in the case of the single triple-shock Mach configuration, develops instead of the slip surface of the theoretically zero thickness. In the case of the irregular triple-shock configuration of the von Neumann paradox type, this layer develops as a zone of transition from the state behind the Mach disk described by the Rankine–Hugoniot jump relations to the state behind the reflected shock also described by the same relations.

The types of the irregular triple-shock configurations obtained in computations of steady axisymmetric flows with a Mach disk in the present work are the same as those investigated by Ivanov et al. [15] and Khotyanovsky et al. [16], who studied the reflection of wedge-generated shock waves with the formation of the Mach stem in steady two-dimensional supersonic flows. The reflection problems were solved numerically with the Navier–Stokes solver and compared with the results computed by the direct simulation Monte Carlo method. In [16], irregular reflection of strong shock waves was considered at $M=4, \upgamma =5/3,$ and ${\theta }_{\mathrm{w}}=25{^{\circ }}$ in the case where the single triple-shock Mach configuration occurred. It was found that the transition of flow parameters from the state behind the Mach disk to the state behind the reflected shock wave, with increase in the transverse coordinate, does not occur in a jump described by the Rankine–Hugoniot relations; instead, it occurs continuously with deviation from the strong branch of the incident shock. The results gained in [16] testify to the convergence of the numerical solution predicted by the Navier–Stokes code to the theoretical triple-shock Mach configuration. In [15], irregular reflection of the oblique shock wave was considered under the conditions of the von Neumann paradox at $M=1.7,\upgamma =5/3,{\theta }_{\mathrm{w}}=12{^{\circ }}$ and 13.5${^{\circ }}$. Here, the triple-shock interaction at ${\theta }_{\mathrm{w}}=12{^{\circ }}$ has to occur at the crossing of the polars of the incident and reflected shock waves on the right of the reflection shock axis; at ${\theta }_{\mathrm{w}}=13.5{^{\circ }}$, the polars of the incident and reflected shock waves do not intersect. As noted in [15], the presumptions of Sternberg [14] about a transitional zone of triple-shock interaction between the flow domains where the Rankine–Hugoniot relations are valid were confirmed by computations.

Thus, the irregular triple-shock configurations in the present computations of steady axisymmetric flows with a Mach disk correspond in general to those forming in reflection of the wedge-generated shock wave with Mach stem in steady two-dimensional supersonic flows.

5 Flow patterns in overexpanded jets

It is evident that the flows in axisymmetric supersonic overexpanded jets exhausting into still air or into an external air stream are analogous to the above-considered supersonic axisymmetric flows in converging conical ducts.

The flow patterns with a Mach disk are generally typical of supersonic axisymmetric non-isobaric jets as reviewed in [17]. A Mach disk trails either an initial barrel-shaped shock wave in underexpanded jets or an initial longitudinally curved shock wave in overexpanded jets. The irregular triple-shock solutions known for two-dimensional flows seem to be possible for the interaction of the initial shock and a Mach disk in axisymmetric jets. These are the above-mentioned direct, inverse, and stationary irregular Mach configurations with formation of a Mach stem, as defined by Courant and Friedrichs [4]. The inverse Mach reflection occurs in underexpanded jets if the angle of flow deflection in the triple-shock solution is ${\delta }_{\mathrm{t}}<0$ (the flow geometry definitions are given above in the present paper); in this case, the slip line slopes away from the flow axis, and the Mach disk is convex toward the flow ahead of it. The direct Mach reflection occurs in overexpanded jets at ${\delta }_{\mathrm{t}}>0;$ in this case, the slip line slopes toward the flow axis, and the Mach disk is convex away from the flow ahead of it. The stationary Mach reflection separates these Mach reflection types; it corresponds to the case of intersection of the reflected shock polar with the strong branch of the incident shock polar at ${\delta }_{\mathrm{t}}=0;$ the Mach disk is flat in this case. The plane structure of a Mach disk is assumed in many works aimed at investigating axisymmetric jets to determine the Mach disk position. It seems there are no publications with a detailed analysis as to when and which an irregular triple-shock configuration occurs in such flows.

Examples of axisymmetric supersonic turbulent overexpanded jets exhausting into still air with a pressure $p_{\mathrm{a}}$ were computed in the present work. The jet with an initial Mach number $M_{\mathrm{j}}=1.6$ at a level of overexpansion $p_{\mathrm{j}}/p_{\mathrm{a}}=0.7$ and the jet with $M_{\mathrm{j}}=2$ at $p_\mathrm{j}/p_{\mathrm{a}}=0.6$ were considered. The overexpansion levels were preset so that the initial intensity $p_{\mathrm{s}}/p_{\mathrm{j}}$ of the longitudinally curved shock corresponded to the initial angles of flow deflection ${\theta }_{\mathrm{c}}\approx 5{^{\circ }}$ and ${\theta }_{\mathrm{c}}\approx 10{^{\circ }}$, respectively, which were considered above for the flows in the funnel-shaped ducts.

Fig. 7

Flow pattern (field of Mach number isolines) in an exhausting jet at $M_{\mathrm{j}}=1.6$ and $p_{\mathrm{j}}/p_{\mathrm{a}}=0.7$

Fig. 8

Shock polars for the flow in an exhausting jet at $M_{\mathrm{j}}=1.6$ and $p_{\mathrm{j}}/p_{\mathrm{a}}=0.7$

Fig. 9

Flow pattern (field of Mach number isolines) in an exhausting jet at $M_{\mathrm{j}}=2$ and $p_{\mathrm{j}}/p_{\mathrm{a}}=0.6$

Fig. 10

Shock polars for the flow in an exhausting jet at $M_{\mathrm{j}}=2$ and $p_{\mathrm{j}}/p_{\mathrm{a}}=0.6$

The flow patterns and shock polars are depicted in Figs. 7 and 8 for the jet with $M_{\mathrm{j}}=1.6$ and in Figs. 9 and 10 for the jet with $M_{\mathrm{j}}=2;$ the data are similar to those for the flows in the funnel-shaped duct. In Fig. 8 (the jet with $M_{\mathrm{j}}=1.6),$ polar 1 of the initial incident longitudinally curved shock and polar 2 of the reflected shock just near the triple intersection of the shocks are presented as before. Polar 3 of another reflected shock is shown in addition; the positions of its axis and the point of intersection with polar 1 are coincident, and the inclination angle of the reflected shock at ${\delta }={\delta }_{\mathrm{t}}$ is ${\beta }={{\pi /2}}$ with respect to the velocity ahead of it, i.e., this shock is normal. The obtained results demonstrate firstly that the triple-shock solution for $M_{\mathrm{j}}=1.6$ and $p_{\mathrm{j}}/p_{\mathrm{a}}=0.7$ corresponds to an irregular triple-shock configuration of the same type that occurs under the conditions of the von Neumann paradox. Secondly, the solution for $M_{\mathrm{j}}=2$ and $p_{\mathrm{j}}/p_{\mathrm{a}}=0.6$ corresponds to the single triple-shock Mach configuration. The diamond-shaped symbols 4 in Figs. 8 and 10 show how the relative pressure just behind the Mach disk and the reflected shock in the numerically computed flow patterns varies when the radial coordinate varies from the axis $y=0$ to a certain point behind the reflected shock. This variation occurs in both cases with a deviation from the strong branch of incident shock polar 1 to the reflected shock polar 2, which is the same as discussed above for the examples of the flow in the funnel-shaped duct at $M=1.6,$ ${\theta }_{\mathrm{c}}=5{^{\circ }}$ and $M=2,$ ${\theta }_{\mathrm{c}}=10{^{\circ }}$, respectively. Similarly, the shear layer with varying entropy develops downstream of the local zones of the irregular triple-shock interaction.

6 Determining the Mach disk position

The subject of determining the position and size of the Mach stem at the irregular reflection of wedge-generated shock waves in steady two-dimensional supersonic flows or the position and size of the Mach disk in steady axisymmetric supersonic jets is of long-standing interest. For the reflection of the wedge-generated shock wave in two-dimensional flows, a hypothesis based on one-dimensional treatment of the virtual stream forming downstream of the Mach stem was commonly used [12, 18]. This stream is primarily subsonic; the flow in it accelerates to form a virtual throat where the flow velocity becomes sonic; the stream becomes supersonic further downstream. The flow domain under consideration usually includes an expansion wave emanating from the rear edge of the wedge and impinging onto the virtual stream near its sonic throat. Similar assumptions were used to determine the Mach disk in axisymmetric non-isobaric jets [19] and the Mach stem in two-dimensional overexpanded inviscid jets [20]. The mentioned approach to determine the Mach stem parameters through the sonic throat of the virtual stream led to a hypothesis that the Mach stem position and, hence, its height depend on the flow conditions downstream of it, which was investigated analytically in Ref. [21]. Experiments proved convincingly, however, that the Mach stem height at the irregular reflection of wedge-generated shock waves in the two-dimensional flows is not affected by the downstream flow conditions [22]. In addition, it was shown analytically [10] that the origin of the Mach disk and its size can be accounted for properly by the amplification of the incident longitudinally curved shock as it approaches the axis.

Let us consider an example that illustrates the conditions determining the position and size of the Mach disk in a steady axisymmetric flow in more detail. This is an inviscid flow at $M=1.6$ in a duct with an initial convergent conical funnel of an angle ${\theta }_{\mathrm{c}}=5{^{\circ }}$ and a following cylindrical part of a constant cross-sectional area—a “throat” of the duct. This flow was computed in a domain extending up to the exit cross section at $x_{\mathrm{f}}=1.0;$ a set of values of the coordinate $x_{\mathrm{c}}$ of the initial cross section of the throat was considered. According to the value $x_{\mathrm{c}}$, the relative cross-sectional area of the duct throat varied, and an influence zone of the focused expansion wave emanating from the break point $x_{\mathrm{c}}$ on the virtual stream downstream of the Mach disk shifted depending on $x_{\mathrm{c}}$. An example of the inviscid flow pattern computed at $x_{\mathrm{c}}=0.5$ is presented in Fig. 11, where the Mach number isolines are visualized and the Mach number values are marked at individual points in the flow field.

A Mach disk of diameter $\bar{D}_{\mathrm{M}}=0.173\,\pm \,0.012$ is located at a distance $\bar{x}_{\mathrm{M}}\approx 0.396\,\pm \,0.002.$ Downstream of the Mach disk, a virtual subsonic stream forms; it is initially converging, further downstream, at $x\approx 0.65,$ a virtual throat forms after which the stream becomes supersonic. Note that the flow behind the reflected shock is subsonic near the Mach disk (at $y=0.09 {\ldots } 0.2$), and this local subsonic sub-area extends downstream along the virtual stream up to $x\approx 0.54.$ Above, at $y>0.2,$ the flow behind the reflected shock is supersonic. The expansion wave emanating from the break point $x_{\mathrm{c}}=0.5$ passes through the supersonic flow field sub-area and acts on the virtual stream beginning from $x\approx ~0.6.$ The data computed with varying $x_{\mathrm{c}}$ reveal that this situation remains unchanged in the range $x_{\mathrm{c}}=0.3 {\ldots } 0.55$, but the position and size of the Mach disk do not vary. Note that the parameters of the Mach disk obtained in this case just somewhat differ from $\bar{D}_{\mathrm{M}}~\approx 0.195\pm \,0.005$ and $\bar{x}_{\mathrm{M}}\approx 0.38\,\pm \,0.002$ presented above for the viscous flow and computed in the shortened domain with $x_{\mathrm{f}}=0.55$ (Fig. 5) when there was no influence of the expansion wave emanating from the wall end point $x_{\mathrm{f}}$ on the virtual stream. The difference is explained by the displacement effect of the boundary layer developed on the duct wall in the viscous flow case.

Fig. 11

Pattern of an inviscid flow (field of Mach number isolines) in a duct with funnel-shaped and cylindrical sections at $M=1.6,$ ${\theta }_{\mathrm{c}}=5{^{\circ }}$, and $x_{\mathrm{c}}=0.5$

Fig. 12

Pattern of an inviscid flow (field of arcsin (1 / M) isolines) in a duct with funnel-shaped and cylindrical sections at $M=1.6,$ ${\theta }_{\mathrm{c}}=5{^{\circ }}$, and $x_{\mathrm{c}}=0.15$

The flow field pattern for $x_{\mathrm{c}}=0.15$ is given in Fig. 12, a field of the arcsin (1 / M) isolines is drawn, and the Mach number values are marked at individual points of the flow field. The expansion wave emanating from the break point $x_{\mathrm{c}}=0.15$ is incident onto the reflected shock at $y=0.09 {\ldots } 0.2$ near the Mach disk. A local subsonic flow sub-area, where the isolines of arcsin (1 / M) are absent, takes place behind and somewhat above the Mach disk. In the considered flow case, a Mach disk with a diminished diameter $\bar{D}_{\mathrm{M}}=0.123\,\pm \,0.005$ at a distance $\bar{x}_{\mathrm{M}}\approx 0.412\,\pm \,0.001$ forms. This is explained by the influence of the expansion wave on the subsonic part of the virtual stream forming immediately behind the Mach disk.

The Mach disk in the flow in the computation at $x_{\mathrm{c}}=0.6$ did not reach the steady position in the duct. The transformation of the flow field patterns in the iteration process is illustrated in Fig. 13. At iteration numbers $I<15{,}000,$ an irregular triple-shock configuration with a Mach disk formed, being of the same type as that considered above and presented in Fig 11. The coordinate $y_{\mathrm{s}}$ of the reflected shock in the cross section $x=x_{\mathrm{c}}=0.6$ is $y_{\mathrm{s}}<y_{\mathrm{c}}$ (see Fig. 13 for $I=10{,}000)$. At $I\approx ~15{,}000,$ the reflected shock drifts upstream and reaches the break point so that $y_{\mathrm{s}}\approx y_{\mathrm{c}}$; further, it begins to impinge onto the wall of the initial conical funnel where it irregularly reflects with the formation of the secondary triple-shock configuration, as presented in Fig. 13 for $I~=~25{,}000$. The flow over the entire cross section $x_{\mathrm{c}}=0.6$ is subsonic in this case. The formed secondary triple-shock configuration moves upstream, up to the instant when it merges with the primary one, as shown in Fig. 13 for $I=40{,}000.$

Fig. 13

Patterns of an inviscid flow (field of Mach number isolines) at flow steadying in a duct with funnel-shaped and cylindrical sections at $M=1.6,$ ${\delta }_{\mathrm{c}}=5{^{\circ }}$, and $x_{\mathrm{c}}=0.6$

It should be noted that, already from $I\approx 17{,}000$ and up to $I\approx 37{,}000,$ the parameters of the primary triple-shock configuration with the Mach disk of diameter $\bar{D}_{\mathrm{M}}=0.174\,\pm \,0.006$ located at the distance $\bar{x}_{\mathrm{M}}\approx 0.396\,\pm \,0.002$ correspond to those for the steady-state flows computed at $x_{\mathrm{c}}=0.3{\ldots }0.55.$ At $I>37{,}000,$ the Mach disk begins to move upstream with increase in its diameter up to the instant when it goes out upstream from the duct and the flow pattern with a bow shock in front of the duct entrance forms. Thus, the supersonic compression inflow initially forming in the duct with the initial convergent funnel breaks down—flow choking occurs.

The simplest limiting condition of the supersonic flow existence in a convergent duct without its choking, under the one-dimensional consideration, is the decreasing of the flow velocity to the critical one $(M=1)$ in a duct cross section of the minimal cross-sectional area (in the throat). The flow in the considered duct is substantially nonuniform. It is supersonic along the duct wall and has local subsonic zones along the axis. That is why the one-dimensional critical condition of flow choking is not applicable.

Let us consider such a condition for a nonuniform flow assumed by the author and presented in Ref. [23]. It is based on the following reasoning. The mass flow rate for the adiabatic flow in a duct with the total temperature constant everywhere can be determined in the form:

$$\begin{aligned} {\dot{m}}=\;\int \limits _A {\rho V\cos } \;\delta \, \mathrm{d}A\;=\frac{k_{{\mathrm{m}}} }{\sqrt{R_{{\mathrm{u}}} T_0 }}\int \limits _A {p_0 q(M)\cos } \;\delta \mathrm{d}A. \end{aligned}$$

Here, ${\rho }$, V, M, $p_{0}$, and $T_{0}$ are the local values of density, velocity, Mach number, total pressure, and total temperature of the flow, ${\delta }$ is the angle of inclination of the velocity vector to the duct axis, A is the cross-sectional area, $R_{\mathrm{u}}$ is the specific gas constant, $k_{\mathrm{m}} =\;\sqrt{\gamma \left( {2/\hbox {(}\gamma +1\hbox {)}} \right) ^{\hbox {(}\gamma +\;1\hbox {)}/2/\hbox {(}\gamma -\;1\hbox {)}}}$ is a coefficient depending on the ratio of specific heats ${\gamma }$, and $q(M)=\;M\left[ {\frac{2}{\gamma +1}\left( {1+\frac{\gamma -1}{2}M^{2}} \right) } \right] ^{-\frac{\gamma +1}{2(\gamma -1)}}$ is the known gas dynamic function of the reduced flow rate.

Determining the mass-averaged total pressure and the flow rate in the form

$$\begin{aligned} \tilde{p}_0 =\;\frac{\int \nolimits _A {p_0 \rho V\cos \delta ~ \mathrm{d}A} }{\dot{m}}=\;\frac{\int \nolimits _A {p_0^2 q(M)\cos } \;\delta ~ \mathrm{d}A}{\int \nolimits _A {p_0 q(M)\cos } \;\delta ~\mathrm{d}A}, \end{aligned}$$

$$\begin{aligned} \dot{m}=\;\frac{k_\mathrm{m} }{\sqrt{R_\mathrm{u} T_0 }}\tilde{p}_0 \tilde{q}({M})A, \end{aligned}$$

one can obtain the following integral function of the reduced flow rate for the nonuniform flow

$$\begin{aligned} \tilde{q}({M})=\frac{1}{A}\frac{\left( {\int \nolimits _A {p_0 q(M)\cos } \;\delta ~ \mathrm{d}A} \right) ^{2}}{\int \nolimits _A {p_0^2 q(M)\cos } \;\delta ~\mathrm{d}A}. \end{aligned}$$

It would be expected that the nonuniform flow choking occurs as $\tilde{q}(M)\rightarrow \;1$ in the duct throat, which is equivalent to the critical condition of the one-dimensional flow choking $q(M)=1$ at $M=1.$ Note that two values of the flow Mach number $\tilde{M}_{{\text{ sub }}} < 1$ and $\tilde{M}_{{{\text{ sup }}}} >1$ corresponding to a value $\tilde{q}(M)<1$ can be determined in a cross section of the duct ahead of the critical one; the correct value has to be chosen on the basis of the flow development history.

The above-mentioned results of the computation of the flow reaching the steady state at $x_{\mathrm{c}}=0.6$ demonstrate that, at the beginning of the iteration process, the value of $\tilde{q}(M)$ in the exit cross section at $x_{\mathrm{f}}=1$ increases (in particular, $\tilde{q}(M) =0.9691$ at $I=10{,}000$ and $\tilde{q}(M)=0.9955$ at $I=15{,}000),$ then the value of $\tilde{q}(M)$ remains virtually unvaried. The difference from $\tilde{q}(M)=1$ does not exceed fractions of a percent up to the instant when the flow pattern with a bow shock in front of the duct entrance becomes steady. Note that the relative cross-sectional throat area at $x_{\mathrm{c}}=0.6$ is $\bar{A}_{\mathrm{th}}=A_{\mathrm{th}}/A_{0}=0.801,$ which can be compared with the data for the steady-state flow without choking at $x_{\mathrm{c}}=0.55$ when $\bar{A}_{\mathrm{th}}=0.817$ and $\tilde{q}(M)=0.987.$ The presented data demonstrate that the flow choking takes place when $x_{\mathrm{c}}=0.6.$

Considering the example of the inviscid axisymmetric flow in the duct with the initial convergent conical funnel and the following cylindrical part of a constant cross-sectional area, i.e., the throat, demonstrates the following. There exists a certain range of the break point coordinate $x_{\mathrm{c}}$ determining the longitudinal position of the initial cross section of the throat at which the Mach disk position and size do not depend on the focused expansion wave emanating from the break point on the virtual stream downstream of the Mach disk. It can be associated with a particular geometry of the duct. However, from the presented examples of the flow, one can derive a conclusion on the above-considered problem of overexpanded jets exhausting into still air, namely, the non-focused expansion wave forming in such flows should not affect the position and size of a Mach disk.

Specific conditions determining the Mach disk position in axisymmetric supersonic converging flows, considered with their numerical simulation, are not revealed. The numerical solution of the problem by the pseudo-unsteady method gives a particular irregular triple-shock configuration, which corresponds to the integral equations of the conservation laws (flow rate, energy, and momentum) for the steady flow. The flow geometry, including the Mach disk position, is determined by the preset boundary and initial flow data.

7 Conclusions

Steady axisymmetric supersonic converging flows with irregular interaction of the initial incident longitudinally curved shock wave and a Mach disk with formation of the reflected shock were investigated. Numerical computations of viscous and inviscid flows were performed by the pseudo-unsteady method for different conditions for the free-stream Mach numbers and initial angles of deflection to the axis of the flow behind the longitudinally curved shock wave. The interaction of shocks leads to irregular triple-shock configurations similar to the ones in steady two-dimensional flows where irregular reflection of the wedge-generated shock from the wall occurs with the formation of a Mach stem. Either the single triple-shock Mach configuration occurred or the triple-shock configuration corresponding to the von Neumann paradox conditions formed, depending on the governing parameters. The shear layer with entropy varying across the layer developed downstream of a local zone of irregular triple-shock interaction.

Conditions determining the position and size of a Mach disk were considered with a computed example of an inviscid axisymmetric flow in the duct with an initial convergent conical section and a following cylindrical section of a constant cross-sectional area, i.e., the throat. It was demonstrated that in a certain range of the coordinate $x_{\mathrm{c}}$, determining the longitudinal position of the initial cross section of the throat, the Mach disk parameters are independent of the expansion wave emanating from the break point $x_{\mathrm{c}}$ and incident onto the virtual stream forming downstream of the Mach disk.