Spherical gravitational curvature boundary-value problem

Abstract

Values of scalar, vector and second-order tensor parameters of the Earth’s gravitational field have been collected by various sensors in geodesy and geophysics. Such observables have been widely exploited in different parametrization methods for the gravitational field modelling. Moreover, theoretical aspects of these quantities have extensively been studied and well understood. On the other hand, new sensors for observing gravitational curvatures, i.e., components of the third-order gravitational tensor, are currently under development. As the gravitational curvatures represent new types of observables, their exploitation for modelling of the Earth’s gravitational field is a subject of this study. Firstly, the gravitational curvature tensor is decomposed into six parts which are expanded in terms of third-order tensor spherical harmonics. Secondly, gravitational curvature boundary-value problems defined for four combinations of the gravitational curvatures are formulated and solved in spectral and spatial domains. Thirdly, properties of the corresponding sub-integral kernels are investigated. The presented mathematical formulations reveal some important properties of the gravitational curvatures and extend the so-called Meissl scheme, i.e., an important theoretical framework that relates various parameters of the Earth’s gravitational field.

Appendices

Appendix 1: Differential operators for the gravitational curvatures

To obtain the gravitational curvatures from the gravitational potential, some differential operators are necessary. The ten differential operators in terms of the spherical geocentric coordinates $(r,\Omega )$ read as follows (Tóth 2005):

$$\begin{aligned} \mathcal{{D}}^{xxx}= & {} - \frac{1}{r^2} \left( \frac{2}{r} \frac{\partial }{\partial \varphi } - 3 \frac{\partial ^2}{\partial r \partial \varphi } - \frac{1}{r} \frac{\partial ^3}{\partial \varphi ^3}\right) ,\end{aligned}$$

(62)

$$\begin{aligned} \mathcal{{D}}^{xxy}= & {} - \frac{1}{r^2 \cos \varphi } \left( \frac{2 \tan ^2 \varphi }{r} \frac{\partial }{\partial \lambda } + \frac{\partial ^2}{\partial r \partial \lambda } + \frac{2 \tan \varphi }{r} \frac{\partial ^2}{\partial \varphi \partial \lambda } \right. \nonumber \\&\left. + \frac{1}{r} \frac{\partial ^3}{\partial \varphi ^2 \partial \lambda }\right) ,\end{aligned}$$

(63)

$$\begin{aligned} \mathcal{{D}}^{xxz}= & {} - \frac{1}{r} \left( \frac{1}{r} \frac{\partial }{\partial r} - \frac{\partial ^2}{\partial r^2} + \frac{2}{r^2} \frac{\partial ^2}{\partial \varphi ^2} - \frac{1}{r} \frac{\partial ^3}{\partial r \partial \varphi ^2}\right) ,\end{aligned}$$

(64)

$$\begin{aligned} \mathcal{{D}}^{xyy}= & {} - \frac{1}{r^2} \left( \frac{1}{r \cos ^2 \varphi } \frac{\partial }{\partial \varphi } - \frac{\partial ^2}{\partial r \partial \varphi } + \frac{\tan \varphi }{r} \frac{\partial ^2}{\partial \varphi ^2} \right. \nonumber \\&\left. -\, \frac{2 \tan \varphi }{r \cos ^2 \varphi } \frac{\partial ^2}{\partial \lambda ^2} - \frac{1}{r \cos ^2 \varphi } \frac{\partial ^3}{\partial \varphi \partial \lambda ^2}\right) ,\end{aligned}$$

(65)

$$\begin{aligned} \mathcal{{D}}^{xyz}= & {} \frac{1}{r^2 \cos \varphi } \Big (\frac{2 \tan \varphi }{r} \frac{\partial }{\partial \lambda } - \tan \varphi \frac{\partial ^2}{\partial r \partial \lambda }\nonumber \\&\quad \quad + \frac{2}{r} \frac{\partial ^2}{\partial \varphi \partial \lambda } - \frac{\partial ^3}{\partial r \partial \varphi \partial \lambda } \Big ),\end{aligned}$$

(66)

$$\begin{aligned} \mathcal{{D}}^{xzz}= & {} \frac{1}{r} \left( \frac{2}{r^2} \frac{\partial }{\partial \varphi } - \frac{2}{r} \frac{\partial ^2}{\partial r \partial \varphi } + \frac{\partial ^3}{\partial r^2 \partial \varphi } \right) ,\end{aligned}$$

(67)

$$\begin{aligned} \mathcal{{D}}^{yyy}= & {} \frac{1}{r^2 \cos \varphi } \left( \frac{2}{r \cos ^2 \varphi } \frac{\partial }{\partial \lambda } - 3 \frac{\partial ^2}{\partial r \partial \lambda } + \frac{3 \tan \varphi }{r} \frac{\partial ^2}{\partial \varphi \partial \lambda } \right. \nonumber \\&\left. - \frac{1}{r \cos ^2 \varphi } \frac{\partial ^3}{\partial \lambda ^3}\right) , \end{aligned}$$

(68)

$$\begin{aligned} \mathcal{{D}}^{yyz}= & {} - \frac{1}{r} \bigg (\frac{1}{r} \frac{\partial }{\partial r} - \frac{2 \tan \varphi }{r^2} \frac{\partial }{\partial \varphi } - \frac{\partial ^2}{\partial r^2} + \frac{\tan \varphi }{r} \frac{\partial ^2}{\partial r \partial \varphi } \nonumber \\&+\, \frac{2}{r^2 \cos ^2 \varphi } \frac{\partial ^2}{\partial \lambda ^2}-\ \frac{1}{r \cos ^2 \varphi } \frac{\partial ^3}{\partial r \partial \lambda ^2} \bigg ),\end{aligned}$$

(69)

$$\begin{aligned} \mathcal{{D}}^{yzz}= & {} - \frac{1}{r \cos \varphi } \left( \frac{2}{r^2} \frac{\partial }{\partial \lambda } - \frac{2}{r} \frac{\partial ^2}{\partial r \partial \lambda } + \frac{\partial ^3}{\partial r^2 \partial \lambda } \right) ,\end{aligned}$$

(70)

$$\begin{aligned} \mathcal{{D}}^{zzz}= & {} \frac{\partial ^3}{\partial r^3}. \end{aligned}$$

(71)

The superscripts on the left-hand sides of Eqs. (62)–(71) indicate the corresponding gravitational curvatures which are obtained by applying the differential operators.

Appendix 2: Formulas for the variable u and the backward azimuth $\alpha '$

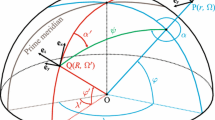
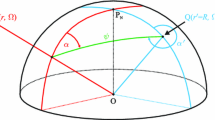
We summarize now equations for numerical evaluation of cosine of the spherical distance u and of the backward azimuth $\alpha '$ given the spherical coordinates of the computational point and the integration element are known. The formulas read as follows:

$$\begin{aligned}&u = \cos \psi \ = \sin \varphi \sin \varphi '\ +\ \cos \varphi \cos \varphi ' \cos (\ \lambda ' - \lambda \ ),\nonumber \\ \end{aligned}$$

(72)

$$\begin{aligned}&\cos \alpha ' = \frac{\sin \varphi \cos \varphi ' - \cos \varphi \sin \varphi ' \cos (\ \lambda ' - \lambda \ )}{\sqrt{1 - u^2}},\end{aligned}$$

(73)

$$\begin{aligned}&\sin \alpha ' = -\ \frac{\cos \varphi \sin (\ \lambda ' - \lambda \ )}{\sqrt{1 - u^2}},\end{aligned}$$

(74)

$$\begin{aligned}&\cos 2 \alpha ' = 2\ \cos ^2 \alpha '\ -\ 1,\end{aligned}$$

(75)

$$\begin{aligned}&\sin 2 \alpha ' = 2\ \cos \alpha ' \sin \alpha ',\end{aligned}$$

(76)

$$\begin{aligned}&\cos 3 \alpha ' = \cos \alpha '\ (\ \cos ^2 \alpha ' - 3 \sin ^2 \alpha '\ ),\end{aligned}$$

(77)

$$\begin{aligned}&\sin 3 \alpha ' = - \sin \alpha '\ (\ \sin ^2 \alpha ' - 3 \cos ^2 \alpha '\ ). \end{aligned}$$

(78)

Equations (72)–(74) can be derived from the cosine, sine-cosine and sine rules of spherical trigonometry (see, e.g., Chauvenet 1875, pp. 151–154). Equations (75)–(78) follow from the multiple-angle formulas for trigonometric functions (see, e.g., Abramowitz and Stegun 1972, p. 72). A detailed derivation for cosine and sine of the backward azimuth $\alpha '$ was provided in Grafarend (2001, Appendix A). However, his resulting expressions, see (ibid., Eqs. A24 and A25), differ by the sign from those of Eqs. (73) and (74). Both versions of expressions for cosine and sine of the backward azimuth $\alpha '$ were empirically tested. The numerical testing proved correctness of Eqs. (73) and (74) given in this article.