A fast and accurate algorithm for high-frequency trans-ionospheric path length determination

Abstract

This paper presents a fast and accurate algorithm for high-frequency trans-ionospheric path length determination. The algorithm is merely based on the solution of the Eikonal equation that is solved using the conformal theory of refraction. The main advantages of the algorithm are summarized as follows. First, the algorithm can determine the optical path length without iteratively adjusting both elevation and azimuth angles and, hence, the computational time can be reduced. Second, for the same elevation and azimuth angles, the algorithm can simultaneously determine the phase and group of both ordinary and extra-ordinary optical path lengths for different frequencies. Results from numerical simulations show that the computational time required by the proposed algorithm to accurately determine 8 different optical path lengths is almost 17 times faster than that required by a 3D ionospheric ray-tracing algorithm. It is found that the computational time to determine multiple optical path lengths is the same with that for determining a single optical path length. It is also found that the proposed algorithm is capable of determining the optical path lengths with millimeter level of accuracies, if the magnitude of the squared ratio of the plasma frequency to the transmitted frequency is less than $1.33\times 10^{-3}$, and hence the proposed algorithm is applicable for geodetic applications.

Appendices

Appendix A: Reformulation and approximation of the OPL equation as derived by Moritz (1967)

By applying the conformal theory of refraction to the Eikonal equation as presented in Eq. (1), Moritz (1967) derived the OPL equation $L_i$, for the $i^{th}$ frequency, that is expressed as:

$$\begin{aligned} L_i= & {} S+\frac{\zeta }{2}\int \limits _{p_{c}}\eta (f_i,\mathbf {r}_c)\,\mathrm{d}s-\frac{\zeta ^2}{8}\int \limits _{p_{c}}\eta (f_i,\mathbf {r}_c)^2\mathrm{d}s \nonumber \\&-\frac{\zeta ^2}{8}\int \limits _{p_{c}}\frac{1}{X^2}\left( \int \limits _0^\xi \frac{\partial \eta (f_i,\mathbf {r}_c)}{\partial Y}\text {}\xi \mathrm{d}\xi \right) ^2\,\mathrm{d}s \nonumber \\&-\frac{\zeta ^2}{8}\int \limits _{p_{c}}\frac{1}{X^2}\left( \int \limits _0^\xi \frac{\partial \eta (f_i,\mathbf {r}_c)}{\partial Z}\text {}\xi \mathrm{d}\xi \right) ^2\,\mathrm{d}s\;, \end{aligned}$$

(A1)

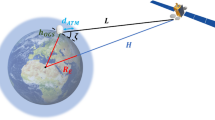
where $\zeta$ is a small constant parameter and $\eta$ is a parameter that depends on frequency $f_i$ and position $\mathbf {r}_c$ along the known chord path $p_c$ (the straight line path on which the wave would travel from the transmitter to the receiver through a vacuum medium). The terms X, Y and Z, respectively, represent the components of the cartesian coordinate system for any point along the path $p_i$ and $p_c$ (see Fig. 1). Here, the term X denotes the propagation direction, while the terms Y and Z represent the lateral and vertical directions, respectively. The term $\xi$ is the integration variable in the X directions that increases as the wave travels toward the receiver.

Moritz (1967) used a linear relation between the terms $\zeta \eta (f_i,\mathbf {r}_c)$ and $n (f_i,\mathbf {r}_c)^2$ that is expressed as

$$\begin{aligned} \zeta \eta (f_i,\mathbf {r}_c) = n (f_i,\mathbf {r}_c)^2 -1, \end{aligned}$$

(A2)

where $n (f_i,\mathbf {r}_c)$ denotes the phase refractive index. Introducing the refractivity term, which is defined as:

$$\begin{aligned} N (f_i,\mathbf {r}_c)\ \equiv \left( n (f_i,\mathbf {r}_c)-1\right) \times 10^6, \end{aligned}$$

(A3)

and introducing Eq. (A3) into Eq. (A2) yields:

$$\begin{aligned} \zeta \eta (f_i,\mathbf {r}_c) = 10^{-12}N (f_i,\mathbf {r}_c)^2 + 2\times 10^{-6}N (f_i,\mathbf {r}_c). \end{aligned}$$

(A4)

Furthermore, by making use of Eq. (A4), the square of Eq. (A2) can be approximated as (Brunner and Leppan 1976):

$$\begin{aligned} \left\{ \zeta \eta (f_i,\mathbf {r}_c)\right\} ^2= & {} 10^{-24}N (f_i,\mathbf {r}_c)^4+4\times 10^{-18}N (f_i,\mathbf {r}_c)^3 \nonumber \\&+\,4\times 10^{-12}N (f,\mathbf {r}_c)^2 \nonumber \\\approx & {} 4\times 10^{-12}N (f_i,\mathbf {r}_c)^2. \end{aligned}$$

(A5)

Finally, by substituting Eqs. (A4) and (A5) into Eq. (A1), the OPL equation can be expressed in the form:

$$\begin{aligned} L_i=S+\mathcal {I}-\,\mathcal {K}_{ic}, \end{aligned}$$

(A6)

where the terms $\mathcal {I}$ and $\mathcal {K}_{ic}$ represent the ionospheric group delay (or phase advance) and the arc-to-chord propagation correction, respectively, which are expressed as:

$$\begin{aligned} \mathcal {I}=10^{-6}\int \limits _{p_{c}}N (f_i,\mathbf {r}_c)\,\mathrm{d}s, \end{aligned}$$

(A7)

$$\begin{aligned} \mathcal {K}_{ic}= & {} \frac{10^{-12}}{2}\int \limits _{p_c}\frac{1}{X^2}\left( \int \limits _0^\xi \frac{\partial N (f_i,\mathbf {r}_c)}{\partial Y}\text {}\xi \mathrm{d}\xi \right) ^2\mathrm{d}s \nonumber \\&+\frac{10^{-12}}{2}\int \limits _{p_c}\frac{1}{X^2}\left( \int \limits _0^\xi \frac{\partial N (f_i,\mathbf {r}_c)}{\partial Z}\text {}\xi \mathrm{d}\xi \right) ^2\mathrm{d}s. \end{aligned}$$

(A8)

The term $\mathcal {K}_{ic}$ represents the arc-to-chord corrections that account for the following effects: (i) propagation corrections from the unknown ray path $p_i$ to the known chord path $p_c$, and (ii) correction for the curvature effects (the geometric bending effects). According to Moritz (1967), the lateral gradient $\frac{\partial N (f_i,\mathbf {r}_c)}{\partial Y}$ may safely be ignored and hence the term $\mathcal {K}_{ic}$ can be written into a simple form as:

$$\begin{aligned} \mathcal {K}_{ic} =\frac{10^{-12}}{2}\int \limits _{p_c}\frac{1}{X^2}\left( \int \limits _0^\xi \frac{\partial N (f_i,\mathbf {r}_c)}{\partial Z}\text {}\xi \mathrm{d}\xi \right) ^2\mathrm{d}s. \end{aligned}$$

(A9)

The next step is to provide an expression for the terms $\mathcal {I}$ and $\mathcal {K}_{ic}$. By combining Eqs.(A7), (A3), and (B7), the ionospheric delay $\mathcal {I}$ can then be expressed in the form:

$$\begin{aligned} \mathcal {I}= & {} c_1\frac{C_x}{2f_i^2}\int \limits _{p_{c}}N_e(\mathbf {r}_c)\;\mathrm{d}s \nonumber \\&+k\,c_2\frac{C_xC_y}{f_i^3}\int \limits _{p_{c}}N_e(\mathbf {r}_c)\;H_o(\mathbf {r})\cos \Theta \;\mathrm{d}s\,,\nonumber \\&+c_3\frac{C_x^2}{8f_i^4}\int \limits _{p_{c}}N_e(\mathbf {r}_c)^2\;\mathrm{d}s, \end{aligned}$$

(A10)

where the first, second and last terms in Eq. (A10) represent the first, second and third-order ionospheric effects, respectively (Gu and Brunner 1990; Bassiri and Hajj 1993). The term k refers to the ordinary ($k=+1$) and extra-ordinary ($k=-1$) waves, while $c_i$ is the constant for defining the phase or group refractive index (see Appendix B).

To further simplify Eq. (A10), the last integral can accurately be approximated as (Hartmann and Leitinger 1984):

$$\begin{aligned} \int \limits _{p_c}Ne(\mathbf {r}_c)^2\,\mathrm{d}s\approx N_m\,\nu \,\int \limits _{p_c}Ne(\mathbf {r}_c)\,\mathrm{d}s, \end{aligned}$$

(A11)

where $N_m$ is the maximum electron density and $\nu$ is a nearly constant parameter whose average value is about 0.66 (Brunner and Gu 1991; Hoque and Jakowski 2008). Finally, by combining Eqs. (A10) and (A11), the ionospheric delay $\mathcal {I}$ can then be further expressed in the form:

$$\begin{aligned} \mathcal {I}=\left[ \Omega _1(f_i)+\Omega _3(f_i)\right] \mathcal {I}_1+\Omega _2(f_i)\;\mathcal {I}_2, \end{aligned}$$

(A12)

where

$$\begin{aligned} \mathcal {I}_1=\int \limits _{p_{c}}N_e(\mathbf {r}_c)\;\mathrm{d}s, \end{aligned}$$

(A13)

$$\begin{aligned} \mathcal {I}_2=\int \limits _{p_{c}}N_e(\mathbf {r}_c)\;H_o(\mathbf {r}_c)\cos \Theta \;\mathrm{d}s, \end{aligned}$$

(A14)

$$\begin{aligned} \Omega _1(f_i)=c_1\frac{C_x}{2f_i^2}, \end{aligned}$$

(A15)

$$\begin{aligned} \Omega _2(f_i)=k\,c_2\frac{C_xC_y}{f_i^3}, \end{aligned}$$

(A16)

$$\begin{aligned} \Omega _3(f_i)=c_3\frac{C_x^2}{8f_i^4}\,N_m\,\nu . \end{aligned}$$

(A17)

The terms $\Omega _1(f_i)$, $\Omega _2(f_i)$ and $\Omega _3(f_i)$ represent the dispersion factors. It is important to emphasize here that the term $\mathcal {I}_2$ in Eq. (A14) is evaluated by considering the geomagnetic field effect $H_o(\mathbf {r})\cos \Theta$ at any point along the chord path $p_c$.

Now, by substituting only the first-order expansion term of Eq. (B7) into Eq. (A9), the arc-to-chord correction $\mathcal {K}_{ic}$ can be expressed as:

$$\begin{aligned} \mathcal {K}_{ic}=\frac{\Omega _1(f_i)^2}{2}\int \limits _{p_c}\frac{1}{X^2}\left( \int \limits _0^\xi \frac{\partial N_e(f_i,\mathbf {r}_c)}{\partial Z}\text {}\xi \mathrm{d}\xi \right) ^2\mathrm{d}s. \end{aligned}$$

(A18)

Appendix B: Accurate approximation for the ionospheric refractive index

If the collision effects are neglected, the ionospheric phase refractive index $n(f,\mathbf {r})$ can be given by the Appleton–Hartree formula as follows (Budden 1985):

$$\begin{aligned} n(f,\mathbf {r})^2=1-\frac{2\mathcal {X} \left( 1-\mathcal {X}\right) }{2\left( 1-\mathcal {X}\right) -\mathcal {Y}_T^2+k\sqrt{\mathcal {Y}_T^4+4\left( 1-\mathcal {X}\right) ^2\mathcal {Y}_L^2}}, \end{aligned}$$

(B1)

where k refers to the ordinary ($k=+1$) and extra-ordinary ($k=-1$) waves. The terms $\mathcal {X}$ and $\mathcal {Y}$ are expressed as:

$$\begin{aligned} \mathcal {X}\left( f,\mathbf {r}\right) =\frac{C_x}{f^2}N_e(\mathbf {r}),\quad \text {where}\quad C_x\equiv \frac{e^2}{4\pi ^2\varepsilon _o m}\;, \end{aligned}$$

(B2)

$$\begin{aligned} \mathcal {Y}_T=\mathcal {Y}\left( f,\mathbf {r}\right) \sin \Theta ; \quad \mathcal {Y}_L=\mathcal {Y}\left( f,\mathbf {r}\right) \cos \Theta \;, \end{aligned}$$

(B3)

$$\begin{aligned} \mathcal {Y}\left( f,\mathbf {r}\right) =\frac{C_y}{f}H_o(\mathbf {r}),\quad \text {where} \quad C_y\equiv \frac{|e|}{2\pi m}\;. \end{aligned}$$

(B4)

The term $N_e(\mathbf {r})$ denotes the electron density, e and m are the electron charge and mass, respectively, $\varepsilon _o$ is the permittivity of the free space, $\Theta$ is the angle between the Earth’s magnetic vector $\mathbf {H_o}$ and the propagation direction of the ray path, $H_o$ represents the amplitude of the vector $\mathbf {H_o}$, and $\mathbf {r}$ is the position vector.

According to Bassiri and Hajj (1993), Eq. (B1) can accurately be expanded up to the fourth inverse powers of frequency:

$$\begin{aligned} n(f,\mathbf {r})\approx & {} 1-\frac{C_x}{2f^2}\;Ne(\mathbf {r}) \nonumber \\&+\,k\frac{C_xC_y}{2f^3}\;Ne(\mathbf {r})\;H_o(\mathbf {r})\cos \Theta -\frac{C_x^2}{8f^4}\;Ne(\mathbf {r})^2 \nonumber \\&-\,\frac{C_xC_y^2}{4f^4}\;Ne(\mathbf {r})H_o(\mathbf {r})^2(1+\cos ^2\Theta )\;. \end{aligned}$$

(B5)

It should be noticed from Eq. (B5) that the phase refractive index $n(f,\mathbf {r})$ is smaller than unity, which corresponds to a phase velocity greater than the speed of light in a vacuum medium. On the other hand, the group refractive index, which is defined as $n_g(f,\mathbf {r})=n(f,\mathbf {r})+f\,\frac{\partial n(f,\mathbf {r})}{\partial f}$, can be approximated as (Bassiri and Hajj 1993):

$$\begin{aligned} n_g(f,\mathbf {r})\approx & {} 1+\frac{C_x}{2f^2}\;Ne(\mathbf {r}) \nonumber \\&+\,k\frac{C_xC_y}{f^3}\;Ne(\mathbf {r})\;H_o(\mathbf {r})\cos \Theta +\frac{3C_x^2}{8f^4}\;Ne(\mathbf {r})^2 \nonumber \\&+\,\frac{3C_xC_y^2}{4f^4}\;Ne(\mathbf {r})H_o(\mathbf {r})^2(1+\cos ^2\Theta )\;. \end{aligned}$$

(B6)

It has been found that the last term of Eqs. (B5) and (B6) may safely be ignored (Brunner and Gu 1991; Bassiri and Hajj 1993; Hoque and Jakowski 2008).

Formulation of the algorithm as outlined in Sect. 2 shall automatically use both the phase and group refractive indices. Therefore, it would be beneficial to express both refractive indices by a single equation as follows (after neglecting the last term in Eqs. (B5) and (B6):

$$\begin{aligned} n_{pg}(f,\mathbf {r})\approx & {} 1+c_1\frac{C_x}{2f^2}\;Ne(\mathbf {r}) \nonumber \\&+k\;c_2\frac{C_xC_y}{f^3}\;Ne(\mathbf {r})\;H_o(\mathbf {r})\cos \Theta \nonumber \\&+c_3\frac{C_x^2}{8f^4}\;Ne(\mathbf {r})^2\;. \end{aligned}$$

(B7)

The term $n_{pg}(f,\mathbf {r})$ will represent the phase refractive index if the constants $c_i$ are chosen as follows: $c_1=-1, c_2=\frac{1}{2},c_3=-1$. On the other hand, the group refractive index can be expressed by selecting the constants $c_i$ as follows: $c_1=1, c_2=-1,c_3=3\,q$, where q is the propagation correction factor from the group path onto the phase path. This correction factor should be applied since the OPL equation in Eq. (4) can only be used to calculate the phase OPL (Moritz 1967). Therefore, the propagation correction factor is necessary if one attempts to use Eq. (4) to calculate the group OPL. Neglecting such correction factor will implicitly assume that the phase and group propagation paths are different. This assumption is not valid since the group wave propagates along the phase path (Born and Wolf 1999; Budden 1985). Numerical simulations (not shown here) indicate that the propagation correction can be compensated by multiplying the third-order term with the term q. Furthermore, it is found that the accuracy requirement for q is not too stringent and a constant value of approximately $-$3.026 is accurate enough to correct this possible invalid assumption.

Appendix C: Hamiltonian formalism for the Eikonal equation

In general, the Eikonal equation in Eq. (1) can be expressed in the Hamiltonian canonical formalism as follows (Červenỳ 2005):

$$\begin{aligned} \mathcal {H}\left( \mathbf {r},\nabla L_i\right) \equiv \frac{1}{\alpha }\left( \left( \nabla L_i\cdot \nabla L_i\right) ^{\frac{\alpha }{2}}-n\left( \mathbf {r}\right) ^{\alpha }\right) =0, \end{aligned}$$

(C1)

$$\begin{aligned} \frac{\mathrm{d}\mathbf {r}}{\mathrm{d}u}=\frac{\partial \mathcal {H}}{\partial \nabla L_i}, \end{aligned}$$

(C2)

$$\begin{aligned} \frac{\nabla L_i}{\mathrm{d}u}=-\frac{\partial \mathcal {H}}{\partial \mathrm{d}\mathbf {r}}, \end{aligned}$$

(C3)

$$\begin{aligned} \frac{\mathrm{d}L}{\mathrm{d}u}=-\nabla L_\tau \frac{\partial \mathcal {H}}{\partial \nabla L_\tau }, \end{aligned}$$

(C4)

where $n\left( \mathbf {r}\right)$ is the phase refractive index along the ray path and $\alpha$ is a scalar value that determines the parameter of interest u. The subscript $\tau$ denotes the $\tau$th element of the ray directions.

According to Červenỳ (2005), $\alpha$ may be set to 1, so that the parameter of interest u will represent the arc length dl along the ray path. Furthermore, by representing the function $\mathcal {H}$ in a spherical coordinate system, the following Hamiltonian formalism for the Eikonal equation can be derived (Červenỳ 2005):

$$\begin{aligned} \mathcal {H}\left( f,r,\theta ,\lambda ,L_r,L_{\theta },L_{\lambda }\right) \equiv \mathcal {H}_L-n\left( f,r,\theta ,\lambda ,\right) =0, \end{aligned}$$

(C5)

where $\mathcal {H}_L$ is defined as:

$$\begin{aligned} \mathcal {H}_L\equiv \left( L_r^2+\frac{L_{\theta }^2}{r^2}+\frac{L_{\lambda }^2}{r^2\sin ^2 \theta }\right) ^{\frac{1}{2}}. \end{aligned}$$

(C6)

The terms $L_r$, $L_{\theta }$ and $L_{\lambda }$ are the element of the ray directions, which are expressed as:

$$\begin{aligned} L_r=\frac{\partial L}{\partial r}, \end{aligned}$$

(C7)

$$\begin{aligned} L_{\theta }=\frac{\partial L}{\partial \theta }, \end{aligned}$$

(C8)

$$\begin{aligned} L_{\lambda }=\frac{\partial L}{\partial \lambda }, \end{aligned}$$

(C9)

where r denotes the radial distance, $\theta$ is the co-latitude and $\lambda$ is the longitude.

By substituting Eq. (C5) into Eqs.(C2) and (C3), the following first-order differential equations are obtained:

$$\begin{aligned} \frac{\mathrm{d}r}{\mathrm{d}l}=\frac{1}{\mathcal {H}_L}L_r, \end{aligned}$$

(C10)

$$\begin{aligned} \frac{\mathrm{d}\theta }{\mathrm{d}l}=\frac{1}{\mathcal {H}_L}\frac{L_{\theta }}{r^2}, \end{aligned}$$

(C11)

$$\begin{aligned} \frac{\mathrm{d}\lambda }{\mathrm{d}l}=\frac{1}{\mathcal {H}_L}\frac{L_{\lambda }}{r^2\sin ^2 \theta }, \end{aligned}$$

(C12)

$$\begin{aligned} \frac{\mathrm{d}L_r}{\mathrm{d}l}=\frac{\partial n\left( f,r,\theta ,\lambda ,\right) }{\partial r}+\frac{1}{\mathcal {H}_L\,r}\left( \frac{L_{\theta }^2}{r^2}+\frac{L_{\lambda }^2}{r^2\sin ^2 \theta }\right) , \end{aligned}$$

(C13)

$$\begin{aligned} \frac{\mathrm{d}L_{\theta }}{\mathrm{d}l}=\frac{\partial n\left( f,r,\theta ,\lambda ,\right) }{\partial {\theta }}+\frac{\cot \theta }{\sin ^2 \theta }\frac{L_{\lambda }^2}{\mathcal {H}_L\,r^2}, \end{aligned}$$

(C14)

$$\begin{aligned} \frac{\mathrm{d}L_{\lambda }}{\mathrm{d}l}=\frac{\partial n\left( f,r,\theta ,\lambda ,\right) }{\partial {\lambda }}. \end{aligned}$$

(C15)

Furthermore, by substituting Eq. (C5) into Eq. (C4), additional first-order differential equations can be derived:

$$\begin{aligned} \frac{\mathrm{d}L}{\mathrm{d}l}=n\left( f,r,\theta ,\lambda ,\right) , \end{aligned}$$

(C16)

$$\begin{aligned} \frac{\mathrm{d}P}{\mathrm{d}l}=n\left( f,r,\theta ,\lambda ,\right) +f\frac{\partial n\left( f,r,\theta ,\lambda ,\right) }{\partial f}, \end{aligned}$$

(C17)

$$\begin{aligned} \frac{\mathrm{d}G}{\mathrm{d}l}=1. \end{aligned}$$

(C18)

The terms L, P and G denote the phase OPL, the group OPL and the geometric path length, respectively. The values of L, P and G along the ray path can be determined by simultaneously integrating Eqs. (C10)–(C18) using any numerical integration method such as the Rungge–Kutta method. Analytical expressions for the partial derivatives of the phase refractive index $n\left( f,r,\theta ,\lambda ,\right)$ with respect to r, $\theta$ and $\lambda$ can be found in Jones and Stephenson (1975).

Initial conditions for the ray directions, which are needed to solve the first-order differential equations, can be written as:

$$\begin{aligned} L_{r_o}=n_o\,\cos z_o, \end{aligned}$$

(C19)

$$\begin{aligned} L_{\theta _o}=-n_o\,r_o\,\sin z_o\,\cos a_o, \end{aligned}$$

(C20)

$$\begin{aligned} L_{\lambda _o}=n_o\,r_o\,\sin z_o\,\sin a_o\,\sin \theta _o, \end{aligned}$$

(C21)

where $n_o$ is the phase refractive index at the transmitter position $r_o$, $\theta _o$ and $\lambda _o$. The terms $z_o$ and $a_o$ denote the geodetic zenith and azimuth angles, respectively, from the transmitter to receiver.