Abstract
This paper shows that monetary policy has uneven impacts on local housing markets, and that the magnitude of the impacts are correlated with housing supply regulations. We apply the linearized present value model, which allows the log rent–price ratio to be decomposed into the expected present values of all future real interests rates, real housing premia, and real rent growth, to the housing markets in 23 US metropolitan statistical areas. Based on the indirect inference bias-corrected VAR estimates, we find that MSAs that are more regulated have (i) a higher variance in the log rent–price ratio, (ii) a larger share of the variance explained by real interest rate, and (iii) a stronger impulse response of house price to the real interest rate shock.


Similar content being viewed by others
Notes
Engsted et al. (2012) argue that a properly specified VAR for return decomposition should include the log rent–price ratio, \(rp_t\), as one of the state variables together with either real housing return or real rent growth, since log real house price \(p_t\), hence \(rp_t\), is in the time t information set. Given the approximate identity of Eq. (2), a VAR that contains \(\phi _t\), \(rp_t\), and a set of other state variables is equivalent to a VAR that contains \(\Delta r_t\), \(rp_t\), and the same set of other variables. As a result, one of the expectations at the right-hand side of Eq. (2) can be directly derived and the other expectation is backed out residually through the approximate identity. Moreover, as long as the VAR is properly specified, i.e., the log rent–price ratio is included as a state variable, the return variance decompositions are independent of which component is treated as a residual. However, if all three variables, \(rp_t\), \(\phi _t\), and \(\Delta r_t\), are included in the VAR system, the model becomes redundant and there would be a problem of multicollinearity, since knowing any two of the three equations for \(rp_{t+1}\), \(\phi _{t+1}\), and \(\Delta r_{t+1}\), one can infer the third, apart from the approximation error. Then, the VAR estimates would be meaningless. Here, in the present work we exclude \(rp_t\) from the VAR but include both \(\phi _t\) and \(\Delta r_t\) (of course, real housing return \(\phi _t\) has been split into real interest rate \(i_t\) and real housing premium \(\pi _t\)). This exercise does not violate the argument of Engsted et al. (2012) that \(p_t\) is in the information set of time t and should be included in some form for the VAR to be legitimate, since the information in \(p_t\) has been included in \(\phi _t\). However, our method is fundamentally different from that of Engsted et al. (2012) in the sense that we are directly estimating the two expectations on the right-hand side of Eq. (2) without arbitrarily assuming that the first-order Taylor approximation-based linearized present value model holds exactly. Over our sample period, the US housing markets experienced large fluctuations both in 1980s and in the recent financial crisis. Ignoring the pricing error that comes from omitting the second- and higher-order moments is problematic. Indeed, as we show in Sects. 3 and 4, the pricing error is sizeable and it accounts for a large fraction of overall volatility of log rent–price ratio.
Campbell et al. (2009) follow the finance literature and treat the present value of future real rent growth as a residual. They attribute most of the variation in log rent–price ratio to changes in expected future real rent growth over the period 1997–2007. However, this phenomenon is mostly driven by the behavior of the forecast discrepancy. Fairchild et al. (2015) treat the residual as part of the future real housing premia instead, and they find that the housing premia account for most variation in the rent–price ratio. Attributing the pricing error either to rent growth or housing premium is arbitrary. Based on our discussion in “Appendix 3”, this discrepancy should exist and a significant part of it is caused by the existence and the time variation of the second moment of the log rent–price ratio.
Recent work by Ambrose et al. (2015) argues that the BLS rent index fails to adequately capture changes in housing service flow prices and suggests to use a weighted repeat rent index instead. Unfortunately, since the construction of the repeat rent index requires detailed information on rent contracts, available data only cover 11 large MSAs and range from 2003 to 2009 for most of these MSAs.
Campbell et al. (2009) include a set of macroeconomic conditions, including population growth, employment growth, and real personal income growth, in the VAR model. However, macroeconomic variables at MSA-level are only observed at annual frequency and they have to be converted into semi-annual frequency by assuming that their growth rates are constant throughout a given year. To avoid such an arbitrary assumption, we do not include macroeconomic conditions in this paper. In fact, in earlier attempts we find that macroeconomic conditions have little additional explanatory power to the housing variables, once the lags of the housing variables are included.
In stock markets, Campbell and Shiller (1988) reject the null hypothesis that the fitted log dividend–price ratio statistically equals the actual counterpart. Instead, they observe substantial unexplained variation in the log dividend–price ratio.
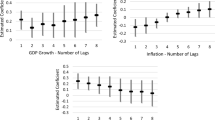
The result of Cholesky decomposition depends on the ordering of the variables. In our framework, \(\widehat{\mathcal {I}}_t\) is the estimate of a national-level variable \(\mathcal {I}_t\) which does not depend on any local conditions, and \(\widehat{e}_t\) is a pricing error which is supposed to depend on all other three components. As a result, we fix \(\widehat{\mathcal {I}}_t\) as the first variable and \(\widehat{e}_t\) as the last one, and change the ordering of \(\widehat{\varPi }_t\) and \(\widehat{\mathcal {G}}_t\).
Such standard error estimates do not incorporate full estimation of uncertainty of the impulse responses of VAR-computed variables. In order to capture full estimation uncertainty, one should estimate the VAR and the orthogonal impulse responses separately for each simulated realization.
Dallas (TX) and Houston (TX) are the only two housing markets that experienced a large price fall in 1980s and have not fully recovered. It is reasonable that the linearized present value model fails to capture the sharp fluctuation in these markets, since the model depends on a first-order approximation. If the data for the 1980s are discarded, we are able to obtain more sensible results.
A major difference between the BLS rent index and the repeat rent index suggested by Ambrose et al. (2015) is that the later shows a substantial decrease in rents following the onset of the housing crisis in 2007 while the former does not. The robustness of our result over the non-crisis subsample period 1978H2:2006H2 indicates that the discrepancy between these two rent indexes is not likely to affect the findings of this paper.
References
Ambrose BW, Coulson NE, Yoshida J (2015) The repeat rent index. Rev Econ Stat 97:939–950
Ambrose BW, Eichholtz P, Lindenthal T (2013) House prices and fundamentals: 355 years of evidence. J Money Credit Bank 45:477–491
Bauer MD, Rudebusch GD, Wu JC (2012) Correcting estimation bias in dynamic term structure models. J Bus Econ Stat 30:454–467
Campbell JY, Shiller RJ (1987) Cointegration and tests of present value models. J Polit Econ 95:1062–1088
Campbell JY, Shiller RJ (1988) The dividend-price ratio and expectations of future dividends and discount factors. Rev Financ Stud 1:195–228
Campbell JY, Vuolteenaho T (2004) Bad beta, good beta. Am Econ Rev 94:1249–1275
Campbell SD, Davis MA, Gallin J, Martin RF (2009) What moves housing markets: a variance decomposition of the rent-price ratio. J Urban Econ 66:90–102
Davis MA, Lehnert A, Martin RF (2008) The rent-price ratio for the aggregate stock of owner-occupied housing. Rev Income Wealth 54:279–284
Engsted T, Pedersen TQ, Tanggaard C (2012) Pitfalls in VAR based return decompositions: a clarification. J Bank Financ 36:1255–1265
Engsted T, Tanggaard C (2001) The Danish stock and bond markets: comovement, return predictability and variance decomposition. J Empir Financ 8:243–271
Fairchild J, Ma J, Wu S (2015) Understanding housing market volatility. J Money Credit Bank 47:1309–1337
Fratantoni M, Schuh S (2003) Monetary policy, housing, and heterogeneous regional markets. J Money Credit Bank 35:557–589
Glaeser EL, Gyourko J, Saks RE (2005) Why have housing prices gone up? Am Econ Rev 95:329–333
Gourieroux C, Monfort A, Renault E (1993) Indirect inference. J Appl Econom 8:S85–S118
Gourieroux C, Renault E, Touzi N (2000) Calibration by simulation for small sample bias correction. In: Mariano R, Schuermann T, Weeks MJ (eds) Simulation-based inference in econometrics: methods and applications. Cambridge University Press, Cambridge, pp 328–358
Gyourko J, Saiz A, Summers A (2008) A new measure of the local regulatory environment for housing markets: the Wharton residential land use regulatory index. Urban Stud 45:693–729
Himmelberg C, Mayer C, Sinai T (2005) Assessing high house prices: bubbles, fundamentals and misperceptions. J Econ Perspect 19:67–92
Leung CKY, Teo WL (2011) Should the optimal portfolio be region-specific? A multi-region model with monetary policy and asset price co-movements. Reg Sci Urban Econ 41:293–304
Mayer CJ, Somerville CT (2000) Land use regulation and new construction. Reg Sci Urban Econ 30:639–662
Paciorek A (2013) Supply constraints and housing market dynamics. J Urban Econ 77:11–26
Saiz A (2010) The geographic determinants of housing supply. Q J Econ 125:1253–1296
Saks RE (2008) Job creation and housing construction: constraints on metropolitan area employment growth. J Urban Econ 64:178–195
Smith AA (1993) Estimating nonlinear time-series models using simulated vector autoregressions. J Appl Econom 8:S63–S84
Acknowledgements
We would like to thank editor Robert Kunst and two anonymous referees for their suggestions. We also thank Charles Leung and Jun Ma for useful comments.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Campbell–Shiller decomposition
Starting from the realized log gross return to housing defined in Eq. (1) and using lowercase letters for logs, we have
Applying a Taylor approximation to the function \(f(x)=\ln (1+\exp (x))\) around \(x=\overline{r-p}\) yields
or equivalently,
where \(\rho =(1+\exp (\overline{r-p}))^{-1}\in (0,1)\). The last term \(O((r_{t+1}-p_{t+1})^2)\) is positive, since its sign is determined by the second-order derivative of f(x),
Substituting Eqs. (23) into (21) yields:
and
Iterating Eq.(25) forward yields:
and
which gives Eq. (2) with a negative approximation bias under rational expectations.
Appendix 2: Estimation without bias correction
See Table 7 and Figs. 3 and 4.
Appendix 3: Sources of the pricing error
There are two potential sources of error in \(\widehat{e}_t\): (1) The VAR-computed \(\widehat{\mathcal {I}}_t\), \(\widehat{\varPi }_t\), and \(\widehat{\mathcal {G}}_t\) might not be good estimates of \(\mathcal {I}_t\), \(\varPi _t\), and \(\mathcal {G}_t\) under rational expectations and (2) the linearized present value model ignores the second- and higher-order moments. We deal with the first source of error by utilizing the indirect inference estimator, and it turns out that the bias correction procedure considerably reduces the pricing error; see a comparison between Figs. 1 and 3 and between Figs. 2 and 4. In order to investigate the pricing error that comes from the second source, we conduct a Monte Carlo experiment for the US national market by repeating the following steps 1000 times:
-
1.
We keep \(i_t\) and \(\Delta r_t\) as in the original sample and construct a new series of log rent–price ratio with small fluctuations around its sample mean, \(rp_t'=\overline{rp}+\nu _t\), where \(\nu _t\sim \mathcal {N}(0,\sigma _\nu ^2)\). Then, using \(rp_t'\) we back out the relevant housing premium \(\pi _t'\).
-
2.
We estimate the VAR with \(\mathbf {Z}_t=(i_t,\pi _t',\Delta r_t)\) and compute the pricing error, \(\widehat{e_t'}=rp_t'-\widehat{rp_t'}\).
Figure 5 compares the average absolute value of the pricing error over 1000 repetitions when \(\sigma _\nu \) takes on different values. The black line shows that, when \(\sigma _\nu \) equals one tenth of the standard error of the actually observed log rent–price ratio, the pricing error is small and relatively stable. When we increase \(\sigma _\nu \) to one half of the observed standard error (the purple line), the pricing error becomes larger in magnitude and the series starts to vary over time. As the log rent–price ratio becomes as volatile as the observed series (the blue line), both the first and the second moments of the pricing error increase dramatically.
However, the constant standard error can hardly replicate the model-implied pricing error. Therefore, we assign different standard errors to the simulated log rent–price ratio for the earlier period 1978H2:1999H2 and the later period 2000H1:2014H2. As the red line shows, the pricing error shoots up once the simulated log rent–price ratio becomes more volatile.
This simulation exercise suggests that both the presence and the time variation of the second moment in the log rent–price ratio contribute to a sizeable pricing error. A necessary condition for the Campbell–Shiller decomposition, which utilizes a first-order Taylor approximation around the steady-state log rent–price ratio, to fit the data well, is that the log rent–price ratio is relatively stable over time. In the data, however, the log rent–price ratio experienced large fluctuations between 2000 and 2012, during which period the fitted log rent–price ratio largely deviates from the actual counterpart; see Fig. 1.
Appendix 4: Orthogonal impulse response functions
Given the response functions of state variables to an orthogonal impulse in real interest rate, those for VAR-computed \(\widehat{\mathcal {I}}_t\), \(\widehat{\varPi }_t\), and \(\widehat{\mathcal {G}}_t\) are readily available via a linear combination. According to Eqs. (8)–(10), the responses of \(\widehat{\mathcal {I}}_t\), \(\widehat{\varPi }_t\), and \(\widehat{\mathcal {G}}_t\) to an orthogonal impulse in real interest rate are:
with \(\mathfrak {z}_1=\mathcal {I}\), \(\mathfrak {z}_2=\varPi \), and \(\mathfrak {z}_3=\mathcal {G}\), which infer the response of the VAR-computed log rent–price ratio to an orthogonal impulse in real interest rate as,
Given the log real rent at time \(t-1\), \(r_{t-1}\), the \(\tau \)-period ahead prediction of log real rent with \(\tau \ge 0\) can be expressed as:
and \(\tau \)-period prediction of log real price takes the following form:
Then, we are able to obtain the \(\tau \)-period ahead responses of the predicted log real rent and the predicted log real price to an orthogonal interest rate shock at time t,
Rights and permissions
About this article
Cite this article
Sun, X., Tsang, K.P. The impact of monetary policy on local housing markets: Do regulations matter?. Empir Econ 54, 989–1015 (2018). https://doi.org/10.1007/s00181-017-1255-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-017-1255-0