1 Introduction

Consumers make many decisions every day. They decide which products to buy and where to buy them. In a real purchasing setting, consumers are confronted with dozens and sometimes even hundreds of choices among similar competing products. In order to replicate the consumer decision process, researchers often use primary data to analyze consumer choices relying on surveys to elicit preferences. Many surveys elicit individual preferences by asking respondents to rank several competing alternatives. Given a set of alternatives, respondents may be asked to provide a rank-order of their preferred brands of sodas, or their preferred football teams or their preferred transportation mode to work. The traditional full ranking procedure involves the selection of the most preferred option in a choice set with J alternatives \(C=\{ {1,2,3,4,\ldots ,J} \}\), eliminating it from the choice set, and then selecting the most preferred option out of the remaining alternatives and rank it second; this process is repeated again with the remaining choices until all the alternatives are ranked. Statistical procedures are then used to analyze the ranking choices based on the random utility theory (McFadden 1974).

In order to estimate preferences on the most preferred alternative, a traditional multinomial logit (MNL) or conditional logit (CL) model can be used. The MNL produces estimates for individual specific characteristics for each alternative minus one which can lead to over-parameterization in models with large number of choice probabilities. The CL refers to choice-specific attributes. Other than that both models are mathematically equivalent (Greene 2012). Both the MNL and CL models provide preferences for the most preferred option only, and no additional information is obtained even if other preference rankings are available. However, in many cases, researchers use elicitation procedures to obtain full or partial rankings. Beggs et al. (1981) introduced the rank-order logit (ROL) model for the analysis of preference rankings with an application to the potential demand for electric cars. The ROL model allows for the analysis of individual preferences for all (or partial) rankings when ranked-ordered data are available. This model has become the ranking model of choice in the literature and has been applied to many fields, including socioeconomics and politics (Koop and Poirier 1994), music (Ophem et al. 1999) and marketing (Bronnenberg and Vanhonacker 1996) to name a few.

The ROL is useful as a data augmentation tool for small sample sizes by allowing the data to include more observations. However, there are several reasons why one could argue that using the full set of rankings in the choice set C may not be appropriate. For example, if the available alternatives for transportation mode to work are car, bus, bicycle and train, one or more alternatives, such as train, may not be available to all respondents in some cities or in his/her particular route to work. Relevant alternatives may not always be so obvious; in the case of the preferred brands of sodas, some respondents may not know all the brands in the choice set, making the ranking of the unknown or unfamiliar alternatives problematic. Furthermore, when ranking preferred football teams some alternatives may be viewed positively, while others may be viewed with indifference or even negatively. Relevant alternatives for the purpose of this article are defined as those alternatives in the consideration set that an individual is capable of ranking. Note that in this context, the number of relevant alternatives in the consideration set may differ for each respondent. That is, for one respondent maybe only the top-ranked alternative is relevant, while other respondents may have two or more relevant alternatives in the consideration set. Hausman and Ruud (1987) developed specification tests to compare the consistency of top (best) ranked choices with the lower (worst) ranked choices. They found that respondents tend to rank more carefully the top-ranked choices and suggested using a subset of the choice set which includes only a few of the top rankings. Because their results depended on the particular products being studied and the total number of alternatives being ranked, they concluded there were no general rules a priori on survey design to address the appropriate number of ranks to be used in the analysis. Fok et al. (2012) argue that respondents may not perform the ranking task according to their true preference. They point out that even if respondents know their true preferences, they may find the task too tedious or complicated.

Chapman and Staelin (1982) found that as the number of rankings used in the analysis increases, and hence the number of independent choice observations increases, there is a reduction in the sampling variance. They also noted that using more rankings means using more observations with ‘lower ranks,’ which according to them are more likely to be characterized as random or noisy. They concluded a trade-off exists between the number of rankings used and the associated reduction in variance with the reliability of the parameter estimates. In order to solve this problem Chapman and Staelin (1982) suggested using only the first few top-ranked alternatives following a set of rules based on a pooling test for equality of the parameter estimates for different ranks. In doing so, they test the stability of the parameters across ranking stages. Hausman and Ruud (1987) analyzed a set of eight choices to rank preferences for cell phones using full and partial ROL models. They found that as the number of rankings is increased, the absolute value of the estimated coefficients falls. These results are in agreement with the findings of Chapman and Staelin (1982). Hausman and Ruud (1987) proposed a heteroscedastic ROL model that allows the variance in the lower rankings to differ from the variance in the higher rankings by introducing a scale parameter. Recently the scale parameter approach has been used in several applications to account for potential asymmetry of preferences across different ranking stages (Scarpa et al. 2011; Auger et al. 2007; Flynn et al. 2007; Cohen et al. 2009).

Obtaining and using more ranking information is becoming more important, particularly given the rise of individual heterogeneity applications in the literature (Hess and Rose 2009). The elicitation of full (or partial) rankings is designed with the purpose of improving the precision of the parameters and the prediction of the models (Vermeulen et al. 2011). If a partial number of rankings are used, the problem is identifying the optimal number of rankings to use given a set of J available alternatives. Several studies have estimated partial ranked-ordered logit (PROL) models. In general, the procedure involves a multi-step cognitive choice process in which respondents first identify a subset of products within all the alternatives and then evaluate those choices. In their study of brand preferences, Bronnenberg and Vanhonacker (1996) suggest a two-stage process involving a choice set formation of relevant brands, and then a selection process from the alternatives in the choice formation stage. Chiang et al. (1998) proposed an integrated consideration set-choice model that accounts for heterogeneity in the first stage of the consideration set and the second step of the choice formation model using a nonparametric Markov chain Monte Carlo (MCMC) sampling procedure applied to scanner panel data. Ophem et al. (1999) suggest a three-step process for selecting the number of relevant rankings. The first step is to choose the 0.5J most preferred choices from J alternatives. The second step is to select 0.25J most preferred alternatives from step one. The third step is to rank the alternatives in the choice set from step two. Hensher and Ho (2014) evaluated the behavioral effects of choice set formation of relevant alternatives and whether adding certain alternatives improves the prediction of the most preferred alternative. They find differences in preferences depending on which alternatives are included in the relevant choice set. In terms of evaluating the attractiveness or acceptability of different alternatives in the consideration set, Hensher and Rose (2012) found improvements in prediction when accounting for the acceptability of each alternative.

An alternative method for partial rankings consists of eliciting the best and worst (BW) alternatives in a choice set (Finn and Louviere 1992). The BW method rose as a way to facilitate the cognitive process of ranking competing alternatives. The general idea is that asking respondents to select extreme options and moving away from middle ranked alternatives results in more consistent and stable preferences (Flynn et al. 2007; Giergiczny et al. 2013). There are three relevant BW cases (Louviere et al. 2013; Rose 2014). The object case (case 1) consists of participants being asked to select the best and worst objects, and no information is provided about the attributes of each object (Finn and Louviere 1992). In the profile case (case 2), participants are asked to evaluate combinations of attributes, and select the best and worst attribute levels for each alternative (Rose 2014). In the choice alternative case (case 3), participants choose the best and worst designed profiles from several choice sets derived from an experimental design (Marley and Pihlens 2012; Giergiczny et al. 2013).

All of the partial ranking methods described above rely on adding the same number of choices per respondent, thus assuming that all respondents know their utility and are able to rank the same number of alternatives. In reality, this assumption may be too restrictive, as some participants may only care about the best available alternative, while others may be interested in more than one alternative. The objectives of this article are: (1) to introduce a simple survey elicitation method for relaxing the homogeneity in the number of rankings assumption and allowing each respondent to have a different number of rankings; (2) to empirically compare the results of full and partial ranked-ordered logit models with and without individual heterogeneity in the number of rankings; (3) to estimate (case 1) BW models of the exploded data; (4) to evaluate the predictive power of the partial ranking methods, including exploded BW, with constant and heteroscedastic error variances; and (5) to test the stability of preferences across ranking stages. The paper is organized as follows. First, the general rank-ordered logit model is presented. Second, a simple survey elicitation mechanism to allow for heterogeneity in the number of relevant rankings is introduced. Third, estimation methods for an empirical application are presented. The results are followed by a summary and conclusions section.

2 The rank-ordered logit model

Following (Chapman and Staelin 1982), a consumer n (\(n=1,2,3,\ldots ,N\)) has a choice set C consisting of J alternatives (\(1<J<\infty )\). The alternatives in the choice set are described in terms of their attributes X. Each participant chooses an alternative i in the choice set to maximize utility. The utility function U, which measures the unobserved desirability or attractiveness of an alternative, can be described as \(U_{{nit}} =V_{{nit}} +\varepsilon _{{nit}} \), where \(U_{{nit}} \) is assumed to have a deterministic component \(V_{{nit}} \) and an error term \(\varepsilon _{{nit}} \), which is assumed to follow some distribution function. Let the deterministic portion of the utility function for participant n, alternative i in ranking situation t be explained by:

$$\begin{aligned} V_{{nit}} =\beta _{{nt}} x_{{nit}} \end{aligned}$$
(1)

where \(X_{{nit}}\) is a vector of product attributes describing alternative i faced by respondent n in ranking situation t, where t is a baseline ranking round and a tasting treatment round.

An individual n would choose alternative i at time t from the choice set \(C \Leftrightarrow U_{{nit}} >U_{{njt}} \) for \(\forall j\ne i\). Let \(y_{nit} =1\) represent that for respondent n the most preferred alternative is i, which implies that \(U_{nit} >\max \{ {U_{n1t} ,\ldots U_{njt} } \}\forall j\ne i\). Then for an observed ordinal ranking of the choices the probability of being selected is given by:

$$\begin{aligned} \Pr \left( {U_{n1t}\!>\!U_{n2t} \!>\!\cdots \!>\!U_{njt} } \right) =\mathop \int \nolimits _{-\infty }^\infty \mathop \int \nolimits _{-\infty }^{U_{n1t} } \mathop \smallint \nolimits _{-\infty }^{U_{n2t} } \cdots \mathop \int \nolimits _{-\infty }^{U_{njt} } \hbox {d}G\left( {U_{n1t} ,U_{n2t} ,\ldots U_{njt} } \!\right) \end{aligned}$$
(2)

where \(\hbox {d}G({U_{n1t} ,U_{n2t} ,\ldots U_{njt} })\) is the joint distribution of the \(U_{nit}\)’s induced by the error term. Note that throughout this article the most preferred option is assigned a rank of 1, the second preferred option a rank of 2, and so on. Therefore, a preferred (higher) ranked alternative implies a lower numerical value. Theoretically, any joint distribution function can be assumed in Eq. (2). If the error term is assumed to be identically and independently distributed (iid) extreme value over respondents and alternatives, then the probability of alternative i being selected is:

$$\begin{aligned} \hbox {Pr}_{nit} =\frac{\hbox {e}^{\left( {V_{nit} } \right) }}{\mathop \sum \nolimits _{j=1}^J \hbox {e}^{\left( {V_{njt} } \right) }} \end{aligned}$$
(3)

where J refers to the total number of alternatives in the choice set for respondent n at time period t. Data on the most preferred option are enough to estimate the model; however, an efficiency gain can be obtained by asking respondents to rank more alternatives in the choice set. Then the probability of observing the rank ordering for person n and alternative i at period t is:

$$\begin{aligned} \Pr \left[ {U_{nit1}>U_{nit2}>\cdots >U_{njt} } \right] =\hbox {Pr}_{nit} =\prod \limits _{j=1}^{J-1} \frac{\hbox {e}^{\left( {V_{nit} } \right) }}{\sum \nolimits _{j=1}^J \hbox {e}^{\left( {V_{njt} } \right) }} \end{aligned}$$
(4)

The rank-order data is ‘exploded’ to become a series of independent choice decisions where the most preferred alternative (best) is selected first and removed from the choice set; next, the second most preferred alternative (second-best) out of the remaining alternatives is selected, and so on, until all products are ranked. In reality, respondents do not have to make the decision process in that order, but this provides a practical way of visualizing the concept of Eq. (4).Footnote 1 Suppose that participant n faces the choice set \(C=\{a,b,c,d\}\) and selects the full ranking ordering \(b\succ a\succ c\succ d\). This would imply that for that individual, \(U_n ( b )>U_n ( a )>U_n ( c )>U_n (d)\). The data is exploded to three choice decisions where the selected alternatives are removed from the choice set at each step and the probability of the exploded rank-order is:

$$\begin{aligned} \Pr ( {b>a>c>d} )=\frac{\hbox {e}^{\left( {V_{ntb} } \right) }}{\mathop \sum \nolimits _{j=a,b,c,d} \hbox {e}^{\left( {V_{ntj} } \right) }}\cdot \frac{\hbox {e}^{\left( {V_{nta} } \right) }}{\mathop \sum \nolimits _{j=a,c,d} \hbox {e}^{\left( {V_{ntj} } \right) }}\cdot \frac{\hbox {e}^{\left( {V_{ntc} } \right) }}{\mathop \sum \nolimits _{j=c,d} \hbox {e}^{\left( {V_{ntj} } \right) }} \end{aligned}$$
(5)

The conditional distribution of the ordering is independent of the ranking because of the independence of irrelevant alternatives property (IIA) of the multinomial logit model, which is also assumed by the ROL model (Beggs et al. 1981).

2.1 A ROL model with partial rankings

The full ranked-ordered logit model assumes that respondents know their utility for each alternative and are able to rank each alternative according to the framework. However, as Fok et al. (2012) point out this assumption may not always hold. Respondents may not be familiar with all the available alternatives in the choice set or may consider some alternatives less important and commit less time or effort. Even though including more alternatives would reduce the variance, it would also bias the parameter estimates toward zero (Chapman and Staelin 1982). Current application methods for partial ranked-ordered logit models consist of estimating separate models for the top j alternatives and merging the data sets based on pooling tests. In the example above, if only the best option is selected, then the probability would be defined as:

$$\begin{aligned} \Pr \left( {b>a>c>d} \right) =\frac{e^{\left( {V_{ntb} } \right) }}{\mathop \sum \nolimits _{j=a,b,c,d} e^{\left( {V_{ntj} } \right) }} \end{aligned}$$
(6)

If the top two options are selected then the probability becomes:

$$\begin{aligned} \Pr \left( {b>a>c>d} \right) =\frac{\hbox {e}^{\left( {V_{ntb} } \right) }}{\mathop \sum \nolimits _{j=a,b,c,d} \hbox {e}^{\left( {V_{ntj} } \right) }}\cdot \frac{\hbox {e}^{\left( {V_{nta} } \right) }}{\mathop \sum \nolimits _{j=a,c,d} \hbox {e}^{\left( {V_{ntj} } \right) }} \end{aligned}$$
(7)

In this example, selecting the top three alternatives will result in a full ranking ordering as described in Eq. (5) since choosing an alternative in the third step identifies the last ranked alternative.

For the exploded BW ranking procedure, respondents make a sequence of choices by selecting the best alternative first and then out of the remaining choices they select the worst alternative. Depending on the experimental design, this process may be repeated several times. The utility function associated with the worst alternative is then multiplied by −1, assuming that worst is the direct opposite of best (Giergiczny et al. 2013; Rose 2014). That is the characteristics that make the best alternative attractive, make the worst alternative unattractive. The BW partial ranking procedure in the example above would change the outcome probability to:

$$\begin{aligned} \Pr ({b>a>c>d})=\frac{\hbox {e}^{\left( {V_{ntb} } \right) }}{\mathop \sum \nolimits _{j=a,b,c,d} \hbox {e}^{\left( {V_{ntj} } \right) }}\cdot \frac{\hbox {e}^{\left( {-V_{ntd} } \right) }}{\mathop \sum \nolimits _{j=a,c,d} \hbox {e}^{\left( {V_{ntj} } \right) }} \end{aligned}$$
(8)

Note that all partial ranking methods discussed so far assume the same number of choices for each participant. If the best two alternatives are used, then they are used for every respondent. If the exploded BW procedure is used, the ranking stages are the same for every respondent.

2.2 The proposed ranking mechanism

The proposed ranking elicitation mechanism consists of two phases. In phase one, participants choose the alternatives they consider relevant to be included in their consideration set. During the second phase, each participant ranks the alternatives in the consideration set. Hence, each participant would have a different consideration set that may include none, a subset, or all of the alternatives. In order to test and compare the proposed model with traditional full and partial ranking models, an additional alternative was included in the choice set \(C=(J+1)\) to be used as a natural self-selected break point to establish a threshold of relevant alternatives in the choice consideration set. The \((J+1)\) alternative is an ‘opt-out’ option for ‘no-product,’ which implies a respondent preferred none of the available alternatives over the option of choosing any of the remaining alternatives in the choice set. By ranking the alternatives respondents would purchase, the elicitation mechanism provides a closer representation of the process a consumer faces in a real purchasing setting. In the context of the example above, in addition to the four alternatives, a, b, c,  and d, each participant would evaluate the choice set C \(=\) {a, b, c, d, ‘no-product’}. A ranking of {b, a,  no-product, c, d} for individual n would imply that \(b\succ a\succ ( {np} )\succ c\succ d\). The probability of the rank-order for that particular ordering will be that represented on Eq. (7). The ‘opt-out’ option is not directly used in the analysis, but it is only used to classify the relevant alternatives (i.e., those ranked higher than no-product) and restrict the consideration set to only those relevant alternatives. The opt-out option acts as a natural self-selected endogenous breakpoint in the choice set allowing each respondent to choose the number of alternatives in their consideration set, thus relaxing the assumption that every respondent has the same number of alternatives in the consideration set. Behaviorally, this modeling framework implies that the consideration and ability of subjects to rank a set of alternatives is not the same.Footnote 2 The survey implementation procedure proposed would generally only ask participants to rank the alternatives in the relevant consideration set (i.e., alternatives b and a in the example above). Rankings of alternatives below the opt-out option were only elicited in the survey for testing whether the utility preference parameters are symmetric and stable across the ranking stages. If the utility parameters are not stable across the ranking stages, then it can be concluded that a mismatch between the ranking response format and the true preference exists. This framework can be tested by evaluating error variance scale differences and the structural stability of the parameters across the two ranking stages (alternatives ranked below and above the no-product option). The generalized probability of any observed outcome is the expression in Eq. (4) \(\forall j\ne i, \hbox {s.t.}\,\hbox {rank}( j )\succ \hbox {rank}({\hbox {no}\,\hbox {product}})\).

2.3 Testing symmetry and stability of parameters across ranking stages

Differences in error variances can be tested by estimating heteroscedastic error variance models through a scale parameter across ranking stages. A statistically significant scale parameter implies asymmetry in variance across the ranking stages. While differences in the variance across ranking stages can be easily accommodated by the scale parameter, a more important test is whether the different ranking stages represent the same utility preferences. If structural differences of the parameters across ranking stages are found, it would provide evidence of non-stable preferences across the two stages (i.e., preferences from choosing alternatives ranked below the opt-out option are different than preferences from alternatives ranked above the opt-out option). The stability of particular ranking stages can also be tested; that is a test of stability of preferences across the best and second-best rankings or best and worst rankings or any other partial rankings. If structural changes in the parameters are found across rankings then the common practice of pooling ranking data sets without properly testing would be inappropriate. This would imply that the set of decision rules to define preferences are not the same across ranking stages. Structural breakpoints are tested by estimating separate models across ranking stages and conducting a test of the pooling hypothesis (Greene 2012). An alternative test conducted for robustness consists of adding to the pooled model the original parameters multiplied by a stage specific indicator variable (Allison and Christakis 1994; Giergiczny et al. 2013).

2.4 Predicting ranking choices

Comparing the results across the estimated models with different number of rankings presents a problem because the models are non-nested and have different number of observations. Since the pseudo-\(R^{2}\) is a likelihood-based test, comparison across non-nested models is meaningless. The models are compared based on their predictive power. The basic notion used is that a good model is one that predicts choices well. In that context, Tjur (2009) recently proposed a measure of fitness for logistic regression models called the coefficient of discrimination. The coefficient of discrimination is defined as: \(D=E[\hat{\pi } _1] - E[\hat{\pi }_0 ]\). It measures the difference of the means of the predicted values for successes and failures, and hence the name, since it measures the model’s ability to discriminate between successes and failures. Tjur’s statistic was developed for binomial responses, and it compares the mean of the predictions for \(y=1\) (success) with the mean of the predictions for \(y=0\) (failures). The general idea is that a good model (one that predicts well) will have high predicted values for observations when the alternative was chosen and low predicted values when the alternatives were not chosen. With multiple alternatives in the exploded data, the Tjur \(R^{2}\) was calculated as the difference between the mean of the predicted probabilities when \(y=1,\) and the mean of all other alternatives not chosen \((y=0)\). The test is asymptotically equivalent to several \(R^{2}\) measures used for linear models (Tjur 2009). Since Tjur’s \(R^{2}\) is not based on the likelihood function of the models, it can be used to compare the explanatory power for non-nested models with different number of observations. However, Tjur’s \(R^{2}\) was developed for binary logit regressions and has not been applied no multinomial analysis. For robustness, a compliance test for the predicted probabilities is included (Hensher and Ho 2014). The compliance statistic is the percentage of cases where the chosen alternative had the highest predicted probability. While the compliance test indicates the accuracy of prediction of the chosen alternative, the Tjur’s \(R^{2}\) provides an indication of the distance of the mean predicted values for the chosen and not chosen alternatives.

2.5 The random parameters rank-ordered logit

The availability of multiple observations from the same individual provides rich data to model respondents preference heterogeneity using a random parameter rank-ordered logit (RPROL) model (Train 2009; Hess and Rose 2009). In the RPROL, the stochastic terms are used to represent deviations from the mean coefficients; then the errors can be allowed to be correlated across ranking alternatives. Within the same framework, \(U_{nit} =V_{nit} +\varepsilon _{nit} \), for participant n and product alternative i, at time period t,  each \(\varepsilon _{nit}\) is assumed to be iid extreme value over time, respondents, and alternatives. Let j correspond to each of the product options to be ranked, with \(J - 1\) choice decisions to be made and t treatment rounds, the model can now be specified as: \(U_{nit} =\beta _n x_{nit} +\varepsilon _{nit} \), where \(V_{nit} =\beta _{nt} x_{nit} \). In order to allow correlation across multiple ranking individuals, the utility function can be modified with further specification of \(\beta _{n}\). The \(\beta _{n}\) is the unobserved vector of coefficients for each individual n that is randomly distributed with a conditional probability density function given by \(f( {\beta _n | {\theta ^{*}}})\) where \(\theta ^{*}\) represents the true parameters of the distribution (Calfee et al. 2001); The stochastic source of error \(\varepsilon _{nit} \) remains uncorrelated with \(\beta _n \), and \(x_{nit} \) is iid extreme value. The \(\beta \) coefficient vector takes on the form: \(\beta =b+\eta _n \) where b is the population mean and \(\eta _{n}\) are individual deviations from the average population (Calfee et al. 2001). Utility is specified as \(U_{nit} =bx_{nit} +\eta _n x_{nit} +\varepsilon _{nit}\), where the stochastic portion of utility is now correlated across alternatives through the attributes in the model. The conditional probability that individual n will choose alternative j at time period t is given by:

$$\begin{aligned} F_{nit} ({\beta _n })=\frac{\hbox {e}^{\left( {\beta _n x_{nit} }\right) }}{\mathop \sum \nolimits _{j=1}^J \hbox {e}^{\left( {\beta _n x_{njt} } \right) }} \end{aligned}$$
(9)

The conditional probability of assigning a ranking for the full choice set of alternatives \(j^{1},j^{2},j^{3},\ldots ,j^{J-1}\) can be calculated as the product of the conditional probability for all choice decisions of the exploded data:

$$\begin{aligned} \hbox {Pr}_{nt} \left( {j^{1},j^{2},j^{3},\ldots ,j^{J-1}\left| {\theta ^{*}} \right. } \right) =\prod \limits _{j=1}^{J-1} \frac{\hbox {e}^{\left( {\beta _n x_{nit} } \right) }}{\sum \nolimits _{j=1}^J \hbox {e}^{\left( {\beta _n x_{njt} } \right) }} \end{aligned}$$
(10)

Integration of the conditional probability over all possible values of \(\beta _{n}\) where the parameters \(\theta ^{*}\) define the distribution of \(\beta _{n}\) gives the unconditional probability that a given alternative j is chosen yields:

$$\begin{aligned} \hbox {Pr}_{nt} \left( {j_1 ,j_2 ,j_3 ,\ldots ,j_{J-1} \left| {\theta ^{*}} \right. } \right) =int \mathop \prod \limits _{j=1}^{J-1} \frac{\hbox {e}^{\left( {\beta _n x_{nit} } \right) }}{\sum \nolimits _{j=1}^J \hbox {e}^{\left( {\beta _{njt} } \right) }}f\left( {\beta _n \left| {\theta ^{*}} \right. } \right) \hbox {d}\beta _n \end{aligned}$$
(11)

Thus, for estimating \(\theta ^{*}\), which are the parameters defining the distribution of coefficients \(\beta _{n}\), the log-likelihood function to be maximized is:

$$\begin{aligned} \hbox {LL}(\theta )=\mathop \sum \limits _{n=1}^N \hbox {ln}int \mathop \prod \limits _{j=1}^{J-1} \frac{\hbox {e}^{\left( {\beta _n x_{nit} } \right) }}{\mathop \sum \nolimits _{j=1}^J \hbox {e}^{\left( {\beta _{njt} } \right) }}f\left( {\beta _n \left| {\theta ^{*}} \right. } \right) \hbox {d}\beta _n \end{aligned}$$
(12)

The integral to be maximized in (12) has no closed-form solution; therefore, a numerical approximation is done using simulated maximum likelihood estimation (Train 2009; Greene 2012).

2.5.1 Experimental procedures and data

A total of 202 individuals (nonstudents) were recruited for the experiment using newspapers and internet ads. Participants were assigned to one of eight sessions based on schedule availability and according to their age and gender to reflect demographic characteristics of US shoppers (Carpenter and Moore 2006). Table 1 shows demographic summary statistics of participants. The experiment consisted of two parts: a ranking procedure and an auction bid. In the first part, participants were asked to rank the relative desirability of seven fruit products plus an ‘opt-out’ alternative for ‘no-purchase’ as described in the proposed ranking procedure section. The fruit products included in the experiment were: (1) California wonderful fresh pomegranate (the predominant variety in the market), (2) Texas red fresh pomegranate, (3) Texas Salavatski fresh pomegranate, (4) ready-to-eat California pomegranate arils, (5) ready-to-eat Texas pomegranate arils, (6) pomegranate juice, and (7) a pineapple as a control fruit. Pomegranates were selected because they are relatively new in the market and also based on funding availability. None of the Texas products were available in retail markets.

Table 1 Demographic Characteristics of participants
Full size table

The use of an unfamiliar product allows for testing how familiarity with the products affects choices by having a treatment where participants taste each product. Each session ranged from 20 to 30 participants. Subjects received a $35 compensation fee for their participation paid in cash, minus any purchases they made during the experiment. A combination of an 11th price sealed bid (Vickrey 1961) nonhypothetical auction and a nonhypothetical ranking procedure were used to elicit consumer preferences. The objective of the auction was to determine a market price for the products. In an 11th price auction, the 11th highest price is the market price. Hence the market price was close to the median bid for each session. Based on the ranking procedure, some participants would have to buy a product at the market price. This was done to incentivize participants to provide their true rankings. The nonhypothetical ranking mechanism was modeled following Lusk et al. (2008). The probability that a product j with ranking r was randomly selected as binding is given by: \(\hbox {Pr}_{lr}= \frac{J+1-r_1 }{\sum \nolimits _{j=1}^J j}\times 100\). The probability for a product being selected is higher for the most preferred alternatives and lower for the least preferred alternatives, with at least one product being selected. If product j is selected, then participants would pay the market price based on the auction procedure, making the mechanism nonhypothetical.

Prior to eliciting ranking and bidding preferences, participants received extensive instructions about the mechanism and were explained that they would have to pay for any purchases they made. In addition, there were two practice rounds with soft drinks and snacks to train participants with the procedures. For the practice rounds, market prices were posted to ensure participants understood the procedures, but prices were not posted after each treatment to avoid bid affiliation (Corrigan and Rousu 2006). Subjects participated in four rounds of rankings and auctions for all the fruit products. The first round was a baseline round and no information was provided about the products. Following the baseline, participants were provided with three treatment rounds and were asked to submit their rankings and bids after each treatment. The treatments included two information treatments for nutritional information and anti-cancer properties of the fruit and a tasting treatment. For the tasting treatment, participants had the opportunity to taste a small sample (about two oz.) of each product. The tasting was voluntary, but none of the participants refused to taste any of the products. The tasting treatment is used to evaluate the effect of familiarity and preferences after purchase in a real life setting, where a consumer goes to a store, evaluates competing products, decides to purchase some of the products, and updates his/her preferences after tasting the purchased products. After conducting the treatments, the market price and buyers were announced. Only one round and one product were randomly selected as binding.

3 Results and discussion

The parameter estimates for the ROL model of the exploded data for the full choice set including all available rankings, and for the restricted choice consideration set with alternatives ranked above the opt-out choice are presented in Table 2. The results show the parameter estimates with different number of rankings, including the best alternative (rank \(=\) 1), partial rankings (rank \(=\) 2–rank \(=\) 5), and the full ranking (rank \(=\) 6). As the number of rankings increases, the number of independent observations also increases. For the full choice set ROL model the number of observations increased from 2782 (with rank \(=\) 1) to 10,650 (with rank \(=\) 6). The model with the restricted choice set, hereafter the heterogeneous ROL (hROL) had less observations since the choice set is restricted to those alternatives ranked higher than the opt-out alternative (2552 for rank \(=\) 1–8401 for rank \(=\) 6). The utility parameters include product attributes and the tasting information treatment. The tasting treatment captures changes in the choice variable as participants became more familiar with the products. Price is usually included in hypothetical discrete choice experiments; it was not included as an explanatory variable because the market price in the nonhypothetical mechanism was determined in the auction procedure, and it is highly correlated with the ranking.

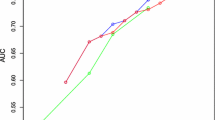
Table 2 Rank-ordered logit parameter estimates of the exploded data for the full and restricted choice set
Full size table

Using more rankings increases the sample size leading to a reduction in the variance of the parameters. This is observed in Table 2 with a reduction of the standard errors of all parameters as the number of rankings increases. When examining the predictive power of the models, the proposed mechanism improves the prediction of the models over the conventional ranking method. The models which include only the best ranked alternative (rank \(=\) 1) have the highest predictive power. A small increase in the prediction of the best alternative is observed from the conventional ranking method to the proposed mechanism with Tjur’s \(R^{2}\) going from 0.297 to 0.309 and compliance from 0.600 to 0.611. The predictive power of the models decreases as the number of rankings increases with one important exception. Notably, including the worst ranked alternative increases the explanatory power of both ranking methods compared to models using middle ranks (ranks 4–5).

This issue is further explored by estimating (case 1) best–worst models of the exploded data as described in Eq. (8). The BW models use the same number of observations as the best two ranking model. The Tjur’s \(R^{2}\) (0.137) are lower for the BW ranking than for the models with the best two alternatives. The compliance test of the proportion of cases in which the chosen alternative had the highest predicted choice probabilities shows similar results. The model with the highest overall correct prediction of the most preferred alternative is the partial ranking of the top (best) alternative only (rank \(=\) 1) for the restricted choice set (0.611). If two rankings are used, then using the best and second-best alternatives yields higher correct predictions compared to using exploded BW rankings. These results were robust across all logit specifications estimated for the data set. This provides evidence that using exploded BW rankings as a data augmentation tool leads to inferior predictive power compared to using the best and second-best alternatives. The results are in agreement with those of Hensher and Ho (2014) and as they point out raise some concerns about the behavioral validity of exploded BW models when used as a data augmentation tool.

The models in Table 2 assume constant error variances across the two ranking stages. Table 3 presents the results for the exploded rankings allowing for scale differences in the error variance. The scale parameter for alternatives ranked below and above the opt-out choice was not statistically significant for rank \(=\) 1–rank \(=\) 5, suggesting preferences are symmetrical for alternatives ranked above and below the opt-out choice for ranks \(=\) 1–5. Scale differences were found for the full ranking model (rank \(=\) 6). The scale was higher for alternatives ranked higher than no-product (lower variance) in the full ranking model.

Table 3 Heteroscedastic error variance models of the exploded data for different rankings
Full size table

A scale parameter of the rankings as a function of age and household size was also estimated. Results suggest that when middle rankings are used (rank \(=\) 2–rank \(=\) 5) older respondents have a larger scale (lower variance) for products ranked below no-product. Larger households had a smaller scale (larger variance) for the models which include the less preferred alternatives (rank \(=\) 4–rank \(=\) 6). The scale parameter of the BW model was statistically significant and lower (higher variance) for the worst alternative. When scale was made a function of age and household size, the BW model had a lower scale (higher variance) for larger households.

A structural change in the parameters to test for stability across choices above and below the defined consideration set was conducted by estimating separate models of the pooled data, and above and below the opt-out choice. A likelihood ratio test was calculated as \(\hbox {LR}=-2[ {L_{r1+r2} -( {L_{r1} +L_{r2} } )}]\) where r1 is the data from the ranking stage 1, r2 is the data from the ranking stage 2, and \(r1+r2\) is the pooled data from the two ranking stages. As the number of rankings increases, the number of alternatives preferred to the opt-out choice increases (230 for rank \(=\) 1–2249 for rank \(=\) 6). Intuitively, respondents are more likely to select the opt-out choice for less preferred alternatives. The pooling hypothesis is rejected for all rankings. Hence, preferences are not stable across the choices made below and above the opt-out choice. It can be concluded that the decision rules that determine preferences are different across the relevant consideration set and the alternatives outside of the consideration set. The statistical significance of the test for the stability of the parameters increases as the number of rankings increase (i.e., using less preferred alternatives provides more evidence of non-stable parameters across the ranking stages). A stability of parameters test was also conducted following (Allison and Christakis 1994). The approach involves estimating stage dependent covariates with product terms for the parameters across stages. This approach resulted in the rejection of stability of preferences for all rankings across the two stages (below and above the opt-out choice). These results are available in an appendix. A test of the stability of parameters for the exploded BW ranking method was conducted and revealed that the parameters for the best alternative differ structurally from the parameters of the worst ranked alternative \(( {\chi ^{2}=221.75})\). What about the stability of parameters of going from the best alternative to pooling the second-best alternatives? Even going from the best ranked alternative to the second-best best ranked alternatives resulted in nonstable parameter estimates \(( {\chi ^{2}=79.84})\). Although using the proposed restricted choice set reduced the statistical significance of the stability test, the results were nevertheless the same; the parameters were not stable across the best-rank and the second-best rankings \(( {\chi ^{2}=70.38})\). The results challenge the common practice of pooling data from different rankings. In this case, only the best ranked alternative can be used because preferences are not stable across any of the ranking stages. The model with the highest predictive power comes from the proposed ranking method using only the best ranking alternative (Tjur \(=\) 0.309, compliance \(=\) 0.611). Using any additional rankings other than the best alternative would be inappropriate since it is clear that the decision rules governing preferences for the best alternative are different than all other alternatives. Nevertheless, if more than one ranking is used to model preferences, then better predictions are achieved by using the top two best ranked alternatives as supposed to the exploded BW.

Table 4 Random parameter rank-ordered logit estimates for the traditional ranking method with homogeneous rankings
Full size table
Table 5 Random parameter rank-ordered logit estimates for the proposed heterogeneous ranking method
Full size table

In order to capture individual heterogeneity of preferences, a random parameter ROL model was estimated. The Random Parameter ROL model of the exploded data was estimated in STATA 13.0 based on the procedure in Hole (2007) using 500 Halton draws. The estimated parameters for the RPROL are presented in Table 4. Table 5 presents the parameter estimates for the RPROL of the proposed ranking mechanism restricted to observations ranked higher than the no-product option.Footnote 3

Although the pattern is not always monotonic, a similar trend as in the constant parameter models is observed with a reduction of the standard errors of the parameter estimates as the number of rankings increases. The standard deviations of the random parameters are highly significant showing the presence of unobserved taste heterogeneity in the choice variable. The predictive power of the traditional ranking method and the proposed heterogeneous ranking method show a similar pattern as the constant parameter models, with decreases for the middle ranks and an increase in the prediction accuracy when using the worst alternative in the full ranking (rank \(=\) 6) compared to middle ranks (ranks 4–5). The exploded BW ranking showed similar results as before with lower Tjur’s \(R^{2}\) than the models with the best two alternatives. The compliance test also showed higher predictions of the chosen alternative using the best and second-best alternatives compared to the BW. If data augmentation is used and individual preference heterogeneity is incorporated in a random parameter framework, then using the top two (best) rankings results in better predictions than the BW method. The stability of the parameters hypothesis was tested using Allison and Christakis (1994) framework, and it was also rejected for all partial rankings (rank \(=\) 2–rank \(=\) 5) and the full rankings (rank \(=\) 6). Results of these tests are also available in “Appendix” section.

The proposed ranking elicitation mechanism robustly provided the best prediction accuracy compared to conventional full and partial ranking methods including the exploded BW method. There is supporting evidence for relaxing the assumption that respondents know their utility and are able to rank the same number of options. The compliance test also showed that if the models are used to predict the chosen alternative, using the best and second-best alternatives always have higher compliance of predicting the chosen alternative compared to exploded BW models. The results also provide robust evidence of differences in error variance scale and nonstable underlying utility for the alternatives ranked above and below the no-product option and for the best and worst ranked alternatives in exploded BW methods. Differences in preferences across ranking stages, including exploded BW types, may be due to respondents not knowing their utility for some of the alternatives, general misconceptions of the elicitation mechanism (Cason and Plott 2014), or complexity, tediousness and high cognitive costs of the ranking task itself. The results stand as a warning about equating ranking choices to true underlying utility preferences across different ranking elicitation stages or mechanisms without properly testing for symmetry and stability of the underlying preferences.

4 Summary and conclusions

The use of surveys to elicit consumer preferences using ranking mechanisms is very common in the literature. When full rankings are available, additional preference information can be analyzed by including more than just the most preferred alternative. Data collection is expensive, and additional rankings are usually elicited as a data augmentation tool to reduce the number of participants in surveys or economic experiments or to reduce the number of tasks a participant faces. The ranked-ordered logit model allows for the analysis of additional ranking data by using the full set of available alternatives in the choice set. All of the ranking elicitation mechanisms in the literature assume that respondents know their utility for and are able to rank the same number of choices. However, there are some reasons why using the full set of alternatives may not be appropriate. This article introduced a simple survey elicitation mechanism that allows for heterogeneity in the number of rankings for each participant, thus relaxing the assumption that respondent know the utility and are able to rank the same number of alternatives. The method consists of a two-step process where respondents determine a consideration choice set composed of alternatives they would purchase. This is empirically tested by adding an additional alternative in the choice set for an opt-out ‘no-product’ option to serve as a natural endogenous break point for relevant alternatives. A heteroscedastic error variance model with a scale parameter for alternatives ranked below and above the opt-out choice was not statistically significant for rank=1 through rank \(=\) 5, suggesting preferences are symmetrical for alternatives ranked above and below the opt-out choice for ranks \(=\)1–5. Scale differences were found for the full ranking model (rank \(=\)6). The scale was higher for alternatives ranked higher than no-product (lower variance) in the full ranking model. More importantly, a test of the stability of parameters across ranking stages showed nonstable parameters for alternatives ranked below and above the ‘no-product’ alternative; statistical significance increased as the number of rankings increases. Utility preferences were not stable across best and worst ranked alternatives. Furthermore, even going from the best ranked alternative to the top two alternatives resulted in nonstable preferences. These results challenge the common practice of pooling data from different rankings into a single model without properly accounting for symmetry and testing for the stability of the underlying preferences across ranking stages. For the empirical dataset analyzed, only the best ranked alternative can be used because preferences are not stable across any of the ranking stages. The model with the highest predictive power comes from the proposed ranking method using the best ranking alternative. Using any additional rankings other than the best alternative would be inappropriate since it is clear that the decision rules governing preferences for the best alternative are different than all other alternatives.