Is productivity diverging in the EU? Evidence from 11 Member States

Abstract

An argument that received a lot of attention in the political and economic discussion surrounding the recent crisis in the EU is that diverging trends in productivity across member countries will undermine the viability of the common currency. This article examines the issue of convergence in multifactor productivity using sector-level data from 11 EU Member States. A state-space model is developed, and formal Bayesian model comparisons are performed to infer whether productivity is diverging, both at the aggregate level and at a sector-by-sector basis. The data point toward diverging productivity at the aggregate level, but suggest the opposite for many individual sectors.

1 Introduction

The recent economic crisis in Europe has led to a renewed interest in the theory of optimum currency areas (OCA). As originally introduced by Mundell (1961) and extended in a first wave by McKinnon (1963) and Grubel (1970), there is no role in this theory for long-term productivity differentials between the political entities comprising an OCA. The costs of committing to a fixed exchange-rate regime are due to temporary asymmetric shocks in demand or productivity and the inherent downward inflexibility of wages and price levels. Nevertheless, the political and, sometimes, economic discussion around the economic crisis and the viability of the common currency were partly directed toward diverging productivity levels across EU Member States, most often using the unit labor cost as the single measure of productivity.

Although initially absent from the theory of OCAs, long-term productivity differentials may play a role in both the frequency and intensity of asymmetric shocks, especially when one looks at the specific components of the economy. For example, the probability of a shock being asymmetric is higher when the relative shares of two economic sectors are very different among the members of a common currency area (Alesina et al. 2003). Thus, the benefits of the members of the common currency area specializing in the sectors where they have a comparative advantage may be partially offset by the increased risk of asymmetric shocks (Krugman 1993; Frankel and Rose 1997). But, a common currency could induce specialization by lowering the cost of international trade or incapacitate monetary measures to protect local infant industries. If, on top of that, different industries experience different rates of productivity growth and compositional changes toward industries of ‘a highly innovative nature’ (van Ark 1990) occur at different rates across members, productivity differentials in the total economy will increase. Lastly, differences in productivity levels before a shock occurs may require different policy interventions in different members of the common currency area (Mélitz 1991), increasing the costs of giving up regional monetary authority.

When viewed in a dynamic setting, an asymmetric shock within a common currency area, in conjunction with the inability of implementing country-specific monetary policies, could put in motion a cycle of events that may lead to divergence in productivity. Such a shock would create unemployment in one region/country, say A, or inflationary pressures in another, say B. If wages are inflexible downward and factors of production are, at least partly, mobile across regions/countries, then resources will move from A toward B. If there are no quality differences in the factors of production, this move would be enough to restore equilibrium. On the other hand, if the factors of production differ in quality, the most productive resources will be the first to move away from A in the event of an adverse shock. Apart from region/country A being striped from human and possibly physical capital, differences in productivity will be further fueled by the fact that these resources will be put in use in region/country B, especially if inter-industry mobility is high. Similar cycles of events that lead to divergence have also been encountered in models of inter-regional/international trade (Krugman 1991) and endogenous growth (Romer 1986, 1990; Grossman and Helpman 1990), but the effects are amplified in the case of fixed exchange rates due to short-term unemployment inducing factor mobility.

On the other hand, a fixed exchange-rate regime could induce convergence in productivity. By lowering transaction costs, a fixed exchange rate increases international trade and foreign direct investment (Petroulas 2007), which, in turn, speeds-up technology spill-overs (Haskel et al. 2007). Furthermore, as trade intensity is positively correlated with the synchronization of business cycles between trade partners, at least for European economies (Frankel and Rose 1997; Abbott et al. 2008), migration of resources is likely to be limited. Finally, Christopoulos and Tsionas (2005) find that high inflation affects productivity negatively and argue that the Maastricht convergence criteria, which emphasize nominal convergence, are likely to lead to convergence in the real economy.¹

Viewed from either a theoretical or an empirical perspective, whether productivity converges across EU Member States remains an open question. In this article, I provide formal tests on whether productivity in manufacturing and selected services sectors has been converging or diverging across 11 EU Member States, since the Maastricht Treaty was signed in 1992. The Maastricht Treaty opened the way to the European Monetary Union and sparked a series of structural changes within the EU Member States in preparation of an entirely new economic environment. Although the Euro as a currency did not exist before 2000 and some countries in the sample have not adopted the common currency even today, exchange rates became largely inflexible due to the Maastricht convergence criteria. The focus is on manufacturing because output from this sector is easily tradeable, thus, providing for better conditions for inter-country competition. The analysis extends to a group of services sectors for which a well-defined market exists. This is done so that value added for the sectors considered in the analysis can be measured in terms of market value, rather than input costs.²

Contrary to the popular discussion, rather than labor productivity, I use multifactor productivity as an indicator of competitiveness.³ This choice is motivated by the fact that unit labor cost differences can be attributed to both technology differences and differences in capital intensity, while it is difficult to fully disentangle the effects of technical change and capital deepening on labor productivity (Wolff 1991). Instead, because multifactor productivity is based on the specification of a production function, it can be viewed as a measure that, at least partly, accounts for differences in capital intensity and, contrary to growth-accounting methods, the results depend less on short-run fluctuations in input price ratios.

Studies on the convergence of productivity across countries are abundant. Islam (1999, (2003a, (2003b) reviews the relevant literature. Many studies on productivity convergence, however, simply calculate productivity indexes across countries, but stop short of performing a formal test on convergence. The inherent problem in this line of literature is that multifactor productivity levels are not observed in the data and calculating productivity indexes requires strong assumptions (Di Liberto et al. 2008). Development accounting (Klenow and Rodríguez-Clare 1997; Hall and Jones 1999; Caselli 2005), in particular, assumes a constant-returns-to-scale Cobb–Douglass technology and decomposes output per worker into physical capital intensity, human capital and residual productivity. The input elasticities used for the decomposition are usually based on factor shares in total income or obtained from the literature and, because multifactor productivity is calculated rather than estimated, this measure absorbs any statistical noise from the data-generating process. Even if one is willing to accept these assumptions, formal tests on convergence are plagued by the generated regressors problem. Furthermore, if no form of dependence over time is assumed when productivity is estimated/calculated, a second-stage regression of productivity on its past values would, at best, reveal that the first stage is inefficient in not exploiting this time dependence or, at worst, even contradict the first-stage assumptions. On a related stream of the literature, productivity growth rates, rather than levels, are calculated, most often using growth accounting. But again, no formal tests on convergence can be performed as such tests would require productivity levels, not growth rates.

In this article, I treat productivity levels as latent data which, however, can be inferred from the observed data once a functional form is assumed for the representation of the production technology. The hypothesis of $\beta$-convergence (Barro and Sala-i-Martin 1992; Mankiw et al. 1992) in multifactor productivity is tested using a single-step approach and Bayesian model comparison techniques, while accounting for statistical noise in the data-generating process. Furthermore, the analysis is performed both at the levels of total manufacturing and total services and at a sector-by-sector basis.⁴ Any combination of convergence or divergence in productivity at the two levels of aggregation could occur, but the implications depend on the level the analysis is performed. Divergence at the sector level would imply that differences in technology levels across countries or the social and entrepreneurial environment are the driving forces behind productivity differences. On the other hand, divergence at the aggregate level could be attributed to additional factors. In particular, if productivity exhibits a tendency to converge at the sector level, then divergence at the aggregate level could still be observed simply because of varying productivity growth rates across sectors and a high degree of specialization of the Member States in specific sectors.

The remainder of this article is organized as follows: the next section presents the model specification and assumptions and makes the connection between parameter values and theoretical implications. Section 3 presents the statistical assumptions of the model, as well as, the estimation and inference methods. Section 4 describes the data, while the results are presented and discussed in Sect. 5. Section 6 summarizes the major findings and draws conclusions.

2 Model specification and theoretical considerations

Consider a Translog specification of the aggregate production function:

$$\begin{aligned} \log y_{ it }= & {} \log A_{ it } + \beta _{K} \log K_{ it } + \beta _{L} \log L_{ it } \nonumber \\&+\,\beta _{ KK } \log ^2 K_{ it } + \beta _{KL} \log K_{ it }\log L_{ it } + \beta _{ LL } \log ^2 L_{ it } + \varepsilon _{ it } \end{aligned}$$

(1)

where y is value added, K is capital stock and L labor use, i indexes countries and t time and $\varepsilon _{ it }$ is a white-noise error term. $A_{ it }$ is the unobserved productivity level for country i in year t. The following partial-adjustment process is imposed on $\log A_{ it }$:

$$\begin{aligned} \log A_{ it } - \log A_{i,t-1} = \lambda \left( \log A_{i,t-1}^* - \log A_{i,t-1} \right) + v_{ it } \end{aligned}$$

(2)

where $\log A_{i,t-1}^*$ is the log-productivity level that is expected or feasible in period $t-1$ and could depend on country characteristics, while $v_{ it }$ is another white-noise error term. This process implies that the productivity growth rate between periods $t-1$ and t is proportional to the distance between the actual log-productivity and its expected level in period $t-1$. $\lambda$ in the last expression is the speed-of-adjustment parameter.

The partial-adjustment process in (2) forms the basis for testing for $\beta$-convergence in productivity and, with the exception of the presence of statistical noise, it is similar to the expressions used in empirical studies that test for $\beta$-convergence in income per capita.⁵ The primary difference is that empirical studies in the economic growth literature refer to the Solow–Swan model to justify the specification of the steady state. In lack of such theoretical background, the specification of the steady state of productivity has to be ad hoc.⁶

Although the existence of a steady state for productivity is treated here as an empirical question, a specification of the steady state is required for this question to be answered. Toward this end, the steady state is defined as a function of time and its interactions with the stock of capital and labor use in period t:

$$\begin{aligned} \log A^*_{ it } = \delta + \gamma _t t + \gamma _K t\log K_{ it } + \gamma _L t\log L_{ it } \end{aligned}$$

(3)

By restricting $\gamma _K$ and $\gamma _L$ to zero, this specification reproduces the process of neutral technological progress assumed in the neoclassical growth model: $A\left( t\right) = A\left( 0\right) \cdot e^{\gamma _t t}$. The interactions of time with the factors of production are included here to capture any input-augmenting technical progress. Only economic fundamentals enter the specification, and no attempt is made to account for cross-country differences in the institutional environment or other characteristics. In this way, the statistical analysis that follows performs tests on whether convergence takes place unconditional on any country differences, other than in input endowments.

Substitution of the steady state in the partial-adjustment process in (2) leads to the autoregressive process:

$$\begin{aligned} \log A_{ it }= & {} \delta + \rho \log A_{i,t-1} + \gamma _t \left( t-1\right) \nonumber \\&+\,\gamma _K \left( t-1\right) \log K_{i,t-1} + \gamma _L \left( t-1\right) \log L_{i,t-1} + v_{ it } \end{aligned}$$

(4)

where $\rho \equiv 1 - \lambda$ is the persistence parameter. Successive substitution of $\log A_{ it }$ in this autoregressive process going back u time periods leads to:

$$\begin{aligned} \log A_{ it }= & {} \delta \left( \sum _{s=0}^{u-1}\rho ^s\right) + \rho ^u \log A_{i,t-u} + \gamma _t \left( \sum _{s=0}^{u-1}\rho ^s \left( t-s-1 \right) \right) \nonumber \\&+\,\gamma _K \left( \sum _{s=0}^{u-1}\rho ^s \left( t-s-1 \right) \log K_{i,t-s-1} \right) \nonumber \\&+\,\gamma _L \left( \sum _{s=0}^{u-1}\rho ^s \left( t-s-1 \right) \log L_{i,t-s-1} \right) + \left( \sum _{s=0}^{u-1}\rho ^s v_{i,t-s} \right) \end{aligned}$$

(5)

Restricting for a moment $\gamma _K$ and $\gamma _L$ to zero, three cases with respect to the values of $\rho$ and $\gamma _t$ are of interest regarding convergence in productivity across countries:

• (i) If $\rho <1$, letting u in (5) go to infinity leads to:

  $$\begin{aligned} \log A_{ it } = \left[ \frac{\delta -\gamma _t}{1-\rho } - \frac{\gamma _t\rho }{\left( 1-\rho \right) ^2} \right] + \left[ \frac{\gamma _t}{1-\rho } \right] t + \sum _{s=0}^{\infty }\rho ^s v_{i,t-s} \end{aligned}$$

  (6)

  In this case, log-productivity stochastically adjusts toward the line defined by the first two terms in (6). Although the process in (4) is non-stationary due to the non-zero trend, it still has the tendency to revert to $\frac{\delta + \gamma _t \left( t-1\right) }{1-\rho } - \frac{\gamma _t\rho }{\left( 1-\rho \right) ^2}$: if the productivity level for a given country and time period is below what this trend suggests, then it is expected that productivity will grow such that asymptotically it reaches the level described by this expression. The persistence of a deviation from expected log-productivity is measured by the value of $\rho$. This case corresponds to absolute $\beta$-convergence with a speed-of-convergence parameter equal to $\lambda =1-\rho$. Furthermore, unless $\gamma _t=0$, the adjustment is toward a target which moves over time, rather than a time-invariant steady state.

• (ii) If $\rho =1$ the summation series in (5) do not converge if u goes to infinity and one-time shocks in productivity persist indefinitely. Now (4) can be expressed as $\Delta \log A_{ it } = \delta + \gamma _t \left( t-1\right) + v_{ it }$ and productivity grows, in expectation, at a rate which is a linear function of time. Although neither $\beta$-convergence nor divergence takes place here, this case is theoretically appealing because it can capture any decline in the rate of productivity growth simply by a negative value for $\gamma _t$.⁷

• (iii) Lastly, if $\rho >1$, then irrespective of the value of $\gamma _t$, the effects of one-time productivity shocks escalate and the stochastic process in (4) explodes. This case corresponds to divergence in productivity with a gap in log-productivity among two countries widening exponentially over time.

Allowing for non-zero $\gamma _K$ and $\gamma _L$ only slightly changes the long-run behavior of $\log A$. The most interesting change occurs when $\rho <1$. In this case, $\beta$-convergence takes place, conditional on the levels of capital stock and labor use and the long-run expected value of log-productivity depends on the entire history of these two variables. Due to this dependence on factor endowments, the expected long-run level of $\log A$ may differ among countries.

In this article, I estimate and test the relative plausibility of models corresponding to the three cases presented above. Whether productivity gaps tend to shrink, widen or exhibit no tendency to change can be inferred by the value of $\rho$.

3 Estimation approach

Given that productivity is not observable in the data, I use a state-space representation of the model:

$$\begin{aligned} \log y_{ it }&= \log A_{ it } + \beta _{K} \log K_{ it } + \beta _{L} \log L_{ it } \nonumber \\&\quad +\beta _{ KK } \log ^2 K_{ it } + \beta _{KL} \log K_{ it }\log L_{ it } \nonumber \\&\quad +\beta _{ LL } \log ^2 L_{ it } + \varepsilon _{ it },&\varepsilon _{ it }\sim N\left( 0, \sigma _\varepsilon ^2\right) \end{aligned}$$

(7)

$$\begin{aligned} \log A_{ it }&= \delta + \rho \log A_{i,t-1} + \gamma _t \left( t-1\right) \nonumber \\&\quad +\gamma _K \left( t-1\right) \log K_{i,t-1} \nonumber \\&\quad +\gamma _L \left( t-1\right) \log L_{i,t-1} + v_{ it },&v_{ it }\sim N\left( 0, \sigma _v^2\right) \end{aligned}$$

(8)

$$\begin{aligned} \log A_{i1}&= \delta _1 + v_{i1},&v_{i1}\sim N\left( 0, \sigma _{v_1}^2\right) \end{aligned}$$

(9)

where (7) is the observed equation, (8) is the hidden-state equation and (9) initializes the stochastic process in period 1. This specification can be viewed as an autoregressive random-effects model: each country realizes an initial level of productivity according to Eq. (9), which then evolves according to the stochastic process described by Eq. (8).

Estimation of the model described by these three equations is feasible through linear Kalman filtering techniques. Such an approach would require integrating the hidden states out from the joined density of $\log y$ and $\log A$ and then maximizing the resulting integrated likelihood. However, to facilitate model comparison, a Bayesian approach is used in this article.

3.1 Complete-data likelihood and priors

Let $\varvec{\beta }$ and $\varvec{\gamma }$ be the $5\times 1$ and $3\times 1$ vectors, respectively, that contain the parameters associated with the capital and labor variables and their interactions and trend and its interactions, as they appear in Eqs. (7) and (8), and collect all parameters to be estimated in a vector $\varvec{\theta }\equiv \left[ \varvec{\beta }, \sigma _\varepsilon ^2, \delta , \varvec{\gamma }, \rho , \sigma _v^2, \delta _1, \sigma _{v_1}^2 \right] '$. The joint density of the observed data and hidden states is:

$$\begin{aligned}&{p}\left( \left\{ \log y_{ it }\right\} ,\left\{ \log A_{ it } \right\} \vert \varvec{\theta }\right) \nonumber \\&\quad = {p}\left( \left\{ \log y_{ it }\right\} \vert \left\{ \log A_{ it } \right\} , \varvec{\beta }, \sigma _\varepsilon ^2 \right) \times {p}\left( \left\{ \log A_{ it } \right\} \vert \delta , \varvec{\gamma }, \rho , \sigma _{v}^2, \delta _1, \sigma _{v_1}^2 \right) \nonumber \\&\quad = \left( 2\pi \sigma _\varepsilon ^2\right) ^{-IT/2} \exp \left\{ -\frac{1}{2\sigma _\varepsilon ^2} \sum _{i=1}^{I}\sum _{t=1}^{T}\varepsilon _{ it }^2\right\} \nonumber \\&\qquad \times \,\left( 2\pi \sigma _{v_1}^2 \right) ^{-I/2} \exp \left\{ -\frac{1}{2\sigma _{v_1}^2} \sum _{i=1}^{I}v_{i1}^2\right\} \nonumber \\&\qquad \times \,\left( 2\pi \sigma _v^2 \right) ^{-I(T-1)/2} \exp \left\{ -\frac{1}{2\sigma _v^2} \sum _{i=1}^{I}\sum _{t=2}^{T}v_{ it }^2\right\} \end{aligned}$$

(10)

where the first part is due to the normality of $\varepsilon _{ it }$, the second part due to (9) and the normality of $v_{i1}$ and the last part is due to the normality of $v_{ it }$. To proceed with estimation the following priors are imposed on the parameters:

• A multivariate normal density is used as the joint prior density of $\beta$s. The prior means for $\beta _K$ and $\beta _L$ are set equal to 0.5, while prior means for the remaining $\beta$s are set equal to zero. The prior covariance matrix is diagonal with entries on the diagonal equal to 100. The normal prior is conjugate, and the high prior variances placed on the parameters imply that prior beliefs will have negligible effects on the final results.

• An inverse-Gamma prior is used for $\sigma _\varepsilon ^2$ as this is conjugate. The shape and scale hyper-parameters of the prior are set equal to 0.1 and 0.001, leading to a very vague prior.

• Independent normal priors are placed on $\delta$, $\gamma$s and $\delta _1$ because these are conjugate. All prior means are set equal to 0 and all prior variances equal to 100.

• Independent inverse-Gamma priors are imposed on $\sigma _v^2$ and $\sigma _{v_1}^2$ as these are conjugate. For both parameters, the shape and scale hyper-parameters are set equal to 0.1 and 0.001, respectively.

• The prior for $\rho$ varies between models. For the case that corresponds to $\beta$-convergence $\rho$ has to be restricted on the unit interval. For this reason, a Beta prior with shape hyper-parameters equal to 8 and 1 is used to reflect prior expectations of high persistence in log-productivity levels. The case that corresponds to divergence requires $\rho$ to be above unity. To make the comparison between the two models as objective as possible, the problem is re-parameterized with $\rho =1+\sigma$ and a Beta(1,8) prior is placed on $\sigma$. In this way, both models incorporate prior beliefs that the value of $\rho$ is close to unity, but they impose antithetic priors along this point. When estimating the unit-root model, $\rho$ is not a parameter to be estimated and no prior is required.

Most priors used are conjugate and estimation can proceed via Gibbs sampling. The only exception is $\rho$, for which the full conditional does not belong to any known family. However, Metropolis–Hastings updates can be used for $\rho$ within the Gibbs algorithm.⁸ Log-productivity levels are treated as latent data in the model and integrating the hidden states from the likelihood involves a standard application of data augmentation (Tanner and Wong 1987). Country- and time-specific estimates of log-productivity can be obtained as a byproduct of the data-augmentation technique.

3.2 Log-marginal likelihood and model comparison

Model comparison is based on Bayes factors (Kass and Raftery 1995), in the spirit of unit-root tests as presented in Koop (1991, (1992). In short, the relative posterior probability of two competing models, ${\mathscr {M}}_1$ and ${\mathscr {M}}_2$, can be expressed as:

$$\begin{aligned} \frac{{p}\left( {\mathscr {M}}_1 \vert {\mathcal {D}} \right) }{{p}\left( {\mathscr {M}}_2 \vert {\mathcal {D}} \right) } = \frac{{p}\left( {\mathcal {D}} \vert {\mathscr {M}}_1 \right) }{{p}\left( {\mathcal {D}} \vert {\mathscr {M}}_2 \right) } \frac{\mathrm {Prob}\left( {\mathscr {M}}_1 \right) }{\mathrm {Prob}\left( {\mathscr {M}}_2 \right) } \end{aligned}$$

(11)

where ${\mathcal {D}}$ represents the (observed) data, and $\mathrm {Prob}\left( {\mathscr {M}}_j \right)$ is the prior probability of ${\mathscr {M}}_j$ being the true model. It is common practice to place equal prior probabilities on the competing models and this approach is taken here as well. ${p}\left( {\mathcal {D}} \vert {\mathscr {M}}_j \right)$ is the density of the data given ${\mathscr {M}}_j$, but marginally with respect to unobserved states and parameters:

$$\begin{aligned} {p}\left( {\mathcal {D}} \vert {\mathscr {M}}_j \right) = \int {p}\left( {\mathcal {D}} \vert \varvec{\theta }_j, {\mathscr {M}}_j \right) \pi \left( \varvec{\theta }_j \vert {\mathscr {M}}_j \right) \, \mathrm {d} \varvec{\theta }_j \end{aligned}$$

(12)

$\varvec{\theta }_j$ in the last equation is the parameter vector for model j and $\pi \left( \varvec{\theta }_j \vert {\mathscr {M}}_j \right)$ is the prior density placed on $\varvec{\theta }_j$ under model j. With equal prior model probabilities model comparison reduces to calculating the Bayes factor and, if one is willing to assume that the set of models is exhaustive, then posterior model probabilities can be obtained using the posterior odds ratio and the fact that probabilities sum to unity. Competing models are compared to each other after the unknown parameters are integrated out of the joint density of data and parameters. The integration is with respect to the priors placed on each model. Therefore, model comparison in this article is based on examining how well the data conform to alternative prior beliefs regarding the values of the parameters and, in particular, the value of $\rho$. No reference priors are available for the state-space model and, in this respect, the tests are not ‘objective’ in the sense Koop (1992) defines the term. Nevertheless, antithetic priors around unity are imposed on $\rho$ in the models of convergence and divergence, while all other priors are the same in all models.

Before proceeding with model comparison, the marginal density of the data with respect to the hidden states and parameters has to be calculated. This marginal density can be obtained in two steps. An approximation to the logarithm of the density of the data marginally with respect to both the hidden states and parameters can be obtained using the Laplace–Metropolis estimator (Lewis and Raftery 1997):

$$\begin{aligned} \log \left[ {p}\left( {\mathcal {D}}\vert {\mathscr {M}}_j \right) \right] \approx \frac{P}{2}\log \left[ 2\pi \right] + \frac{1}{2}\log \left[ \vert {\mathbf {H}}^*\vert \right] + \log \pi \left[ \varvec{\theta }^*_j\right] + \log {p}\left[ {\mathcal {D}}\vert \varvec{\theta }^*_j\right] \end{aligned}$$

(13)

where P is the dimension of $\varvec{\theta }_j$, $\varvec{\theta }^*_j$ is an MCMC estimator of $\varvec{\theta }_j$ that maximizes the integrated likelihood, ${p}\left[ {\mathcal {D}}\vert \varvec{\theta }^*_j\right]$, and ${\mathbf {H}}^*$ is the Hessian of the integrated likelihood evaluated at $\varvec{\theta }^*_j$. The integrated likelihood is the density of the data, marginally with respect to the hidden states, evaluated at $\varvec{\theta }^*_j$. Given that the hidden state enters the observed equation linearly and using the normality assumptions on the error terms, this last density can be evaluated using standard linear Kalman filtering techniques.⁹

3.3 Alternative specifications of the data-generating process

The state-space model specified in Eqs. (7)–(9) allows log-productivity to be country specific and to evolve over time, but it restricts the remaining parameters of the production function to be the same across countries. However, country heterogeneity could manifest itself in the data in alternative ways. To decide whether pooling together country data in a model such as the one described above, two additional data-generating processes are considered and the proposed models are compared to them.

First, country heterogeneity could be reflected on differences in the slope coefficients of the production function, as well as in the constant term. In a random-coefficients model (Hildreth and Houck 1968; Swamy 1970), each country is assumed to have its own vector of parameters. In a hierarchical specification, these country-specific vectors of parameters are drawn from a multivariate normal distribution:

$$\begin{aligned} \log y_{ it } = {\mathbf {x}}_{ it }'\varvec{\beta }_i + \varepsilon _{ it }, \quad \varvec{\beta }_i\sim N\left( {{\bar{\varvec{\beta }}}}, \varvec{{\varSigma }}\right) , \quad \varepsilon _{ it } \sim N\left( 0, \sigma _\varepsilon ^2\right) \end{aligned}$$

(14)

where y is, as before, value added, ${\mathbf {x}}_{ it }$ is a $k\times 1$ vector that stores the values of k independent variables for country i in period t and $\varvec{\beta }_i$ is a $k\times 1$ vector with the associated coefficients for country i. $\varvec{\beta }_i$ is a draw from a multivariate normal distribution with mean vector ${\bar{\varvec{\beta }}}$ and variance matrix $\varvec{{\varSigma }}$. The production function is specified as Translog in capital labor and time, but, contrary to the state-space model, the constant term is no longer autoregressive. This is because allowing for random coefficients deprives the productivity index, A, from its meaning as the sole technology index: if countries are allowed to have idiosyncratic slope coefficients, then technology differences and differences in productivity would stem from two sources.

The structural parameters in this hierarchical model are ${\bar{\varvec{\beta }}}$, $\sigma _\varepsilon ^2$ and $\varvec{{\varSigma }}$. In a Bayesian setting, the typical choice for the prior of $\varvec{{\varSigma }}$ is an inverse-Wishart distribution, because this is conjugate. The degrees-of-freedom parameter of the inverse-Wishart prior is set equal to 2k, while a diagonal matrix is used as the scale parameter, which restricts the variance of all $\beta _i$s except the constant term to be small, reflecting prior expectations of little variability in the production function parameters across countries. Similar priors as in the state-space models are used for the remaining parameters.

Lastly, the data could have been generated by a simple random-effects process where the country effects are restricted to be time invariant and the slope coefficients common to all countries:

$$\begin{aligned} \log y_{ it } = {\mathbf {x}}_{ it }'\varvec{\beta }+ \varepsilon _{ it } + \alpha _i, \quad \varepsilon _{ it }\sim N\left( 0, \sigma _\varepsilon ^2\right) , \quad \alpha _i \sim N\left( 0, \sigma _\alpha ^2\right) \end{aligned}$$

(15)

In this specification, $\alpha _i$ is a country-specific term that captures deviations of log-productivity from its average level (a constant term is included in ${\mathbf {x}}_{ it }$) and the production function is still assumed to be Translog in capital, labor and time. An inverse-Gamma prior is imposed on $\sigma _\alpha ^2$ with shape and scale parameters equal to 0.01.

The values of the log-marginal likelihood resulting from the random-effects and random-coefficients model can be estimated using the Laplace–Metropolis estimator given in Eq. (13). For both models, the latent data ($\varvec{\beta }_i$s in the random-coefficients and $\alpha _i$s in the random-effects model) can be integrated from the likelihood function analytically. Because the dependent variable in all five models considered is the same, these values of the log-marginal likelihood can be used directly to compare the models and to calculate posterior model probabilities.

4 Data

The data used for the empirical analysis are obtained from OECD’s Structural Analysis (STAN) database and are based on Revision 3 of the International Standard Industrial Classification (ISIC) system. Although STAN contains series starting as early as 1970, only data from 1993 until 2007 are extracted from the database. The time interval is restricted so that Germany is included in the analysis after the structural break due to its reunification and because series are incomplete for some countries prior to 1993. Four out of the EU-15 Member States have very incomplete series and are excluded altogether. Unfortunately, three out of the four excluded countries were at the center of the recent debate on productivity differentials: Greece, Ireland and Portugal. The fourth country excluded due to missing data is Luxembourg.

The data are at the 2-digit industry level as defined by ISIC Rev. 3, although some industries are combined due to data availability. Additionally, two aggregates of total manufacturing and total services are provided for the 11 countries considered in this study. Table 1 provides the correspondence between the industry codes and the official ISIC descriptions of the sectors, along with the abbreviations of the descriptions used throughout this paper.

Table 1 Codes and description of economic sectors under ISIC, Rev. 3

The variables used in the analysis are value added, labor use and stock of capital per sector. Value added and capital stock are measured in billions of constant Euros (2000 is the base year). For Denmark, Sweden and the UK, national currencies are converted to Euros/ECUs using the average annual exchange rates reported by Eurostat.

Labor input is reported by STAN in persons engaged in the industry. To account for within-country changes in human capital over time, the original labor variable was transformed to medium-skilled labor equivalents using data from the EU KLEMS database (O’Mahony and Timmer 2009). EU KLEMS provides information at the industry level on the shares of three types of labor (low-, medium- and high-skilled) in total hours worked and in total labor compensation. Medium-skilled labor equivalents are obtained using the transformation $L = \frac{s_\mathrm{M}}{c_\mathrm{M}} N$, where $s_\mathrm{M}$ is the share of medium-skilled labor in total hours worked, $c_\mathrm{M}$ is the share of medium-skilled labor in total labor compensation and N is the number of persons engaged in the industry.¹⁰ This transformation accounts for changes in the composition of labor over time, but only within a country. No effort, whatsoever, is made to account for cross-country differences in human capital because the definitions of labor types in EU KLEMS differ among countries. Therefore, any differences in productivity levels that result from the models are partly due to differences in initial endowments of human capital.

There are two particularities regrading the capital variable. The stock of capital is not reported for all sectors in the case of France, and these sectors are excluded from the analysis. The stock of capital series for the Netherlands do not go back to 1993 for all sectors. Nevertheless, deflated values of gross capital formation and capital consumption are used to construct an approximation to the stock of capital.

Summary statistics of the variables for the aggregates of total manufacturing and total services are reported in Table 2. The data are characterized by large variability, most of which, however, is due to differences in the size of the sectors across countries, rather than over time. Regarding the measurement of labor, only small increases appear from the original labor variable to the medium-skilled equivalents. This is because the ratio of shares of medium-skilled labor in total hours worked and total labor compensation is, for most countries and sectors, close to unity, although increasing over time.

Table 2 Summary Statistics of the Models’ Variables

One of the main arguments in this article is that, although productivity could be converging across countries at the sector level, divergence could be taking place at the aggregate levels because sectors experience different productivity growth rates and the shares of sectors in total manufacturing or total services differ among countries. To examine this claim, the data are analyzed in two phases. First, the models described in Sect. 2 are applied to total manufacturing and total services data for all 11 countries in the dataset. This analysis considers convergence in productivity assuming that there exists a production function at the aggregate level. Next, sector-by-sector models are run for all countries with available data, assuming that there exists a production function at the sector level and allowing for different factor elasticities and parameter values, in general, across industries. In both levels of analysis, the models are compared to a random-coefficients specification that relaxes the assumption that the parameters of the production functions are common to all countries.

To facilitate interpretation of the results, the shares of sectors in the value added of their respective aggregates, for each country and for the last year of available data (2007), are presented in Table 3. On average, firms classified under Machinery&Equipment and Chemical&Fuel contribute the most in the value added of total manufacturing. Remarkable differences appear in the shares of the capital-intensive industries (Machinery&Equipment and Transport Equipment). On the other hand, smaller differences in shares among countries are observed for the services sectors.

Table 3 Share of each sector in total-manufacturing and services value added in 2007 (%)

The data used in this study cover a transitional period after the structural break introduced by the Maastricht Treaty. This break can be viewed as a shock to the system and, assuming that the adjustment process of productivity toward its steady state does not differ between periods of transition in non-fundamental economic quantities (institutions, etc.) and periods of relative tranquility, this shock introduces variability in the data that will facilitate estimation if the models’ parameters. On the other hand, due to the short time span, the data may not contain enough information to provide conclusive evidence in favor of a single model. Posterior model probabilities, however, quantify the uncertainty with respect to the true model (convergence, unit root or divergence) and reflect the degree to which the data can distinguish between the competing models.

5 Results and discussion

The results presented in this section are based on 600,000 retained draws from the posterior distribution of the models’ parameters. One in every ten draws from the posterior is retained to reduce loss of precision due to the draws being autocorrelated. Table 4 reports the parameter estimates from the three models applied to the total manufacturing data. The model that imposes $\rho =1$ results in factor elasticities¹¹ close to $\frac{1}{3}$ and $\frac{2}{3}$ for capital and labor, respectively, while deviations from this norm are observed for the models that impose convergence and divergence. For the model that imposes $\rho >1$, in particular, the elasticity with respect to capital is estimated considerably higher, implying increasing returns to scale. The estimate of $\rho$ in the first model is very close to unity, already suggesting that the data would favor the model of divergence. Formal model comparison verifies this observation: the first row of Table 5 provides very strong evidence in favor of the model that implies divergence.

Table 4 Parameter estimates for total manufacturing

Turning to the task of testing convergence in productivity at a sector-by-sector basis, Table 5 reports the posterior probabilities of the three models when applied to the sector-level data and including all countries in the sample.¹² Although for many sectors, the data do not provide conclusive evidence in favor of a particular model, the 12 individual sectors are split almost equally among the three competing models. The data support the model that implies convergence for Manufacturing N.E.C. and for three out of four services sectors. These sectors either experienced slow rates of innovation in the last 20 years, or the innovations are easily transferable across borders. On the contrary, the model that imposes divergence is favored by the data for sectors that have experienced substantive innovations over the last decades: Chemical&Fuel (which includes pharmaceuticals), Machinery&Equipment (which includes electronics) and Transport Equipment.

Table 5 Posterior model probabilities

Table 6 Average multifactor productivity growth rates (%) per sector and country

Country- and time-specific estimates of log-productivity levels can be obtained from the estimation process as a byproduct of the data-augmentation technique. Table 6 reports the average (over time) multifactor productivity growth rates per sector and country.¹³ The first row of the table corresponds to total manufacturing and suggests an average productivity growth rate of 2.7 %. Productivity growth in the services aggregate is much lower. However, large differences appear across countries, with Finland and Sweden experiencing growth rates around 6 % for total manufacturing, while the rate for Italy is below 1 % and for Spain it is even negative. The growth rates for total manufacturing for Finland and Sweden are driven mostly from the extremely high productivity growth in Machinery&Equipment and the large shares of this sector in the two economies. In turn, the extremely high growth rates for this sector are most likely due to the innovations in electronics and telecommunications equipment that took place during the period covered by the data.

In the sector dimension, average productivity growth rates vary from as low as −0.3 % for Hotels&Restaurants to as high as 4.7 % for Machinery&Equipment. In general, productivity growth rates appear to be higher in sectors that have been largely transformed by the innovations in information technology (Machinery&Equipment, Chemical&Fuel) and the advent of the Internet (Financial Services). On the other hand, the low or negative productivity growth rates for some sectors are mostly due to increases in input use rather than declining output value. For Spain, in particular, the rate of increase in human capital was very high during the period covered by the data, which leads to a fast growth in labor use, measured in medium-skilled equivalents. This, in turn, results in negative estimates of productivity growth for most sectors in the country.

Differences in productivity growth rates among countries are, for most sectors, far from negligible. Further, some patterns seem to emerge. For example, productivity change is negative in Italy and Spain even in industries where the average productivity growth rates are well above 1 %, while industries in these two countries consistently experience lower productivity growth than the sample average. On the contrary, productivity growth for most industries in Austria, Finland and Sweden is above the sample average. The last three countries became members of the EU in 1995, and the increased growth rates could be attributed to catching up in terms of technology or expansion in the enlarged market.

Fig. 1

Evolution of $\log A$ in total manufacturing per country

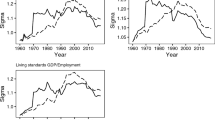
The vastly different productivity growth rates among countries reported in Table 6, even at the sector level, do not necessarily contradict the hypothesis of $\beta$-convergence per se. Under $\beta$-convergence countries with positive deviations from the expected productivity level should experience, in expectation, lower than average productivity growth rates. The converse is true for countries with negative deviations. However, in the context of the application, this argument would require Italy and Spain to have the highest productivity levels in the sample, while Sweden and Finland the lowest, a claim that is unlikely to be true. To examine this issue further, Fig. 1 presents the evolution of $\log A$ in total manufacturing per country. From this figure, it is apparent that the opposite is true: Italy and Spain start in 1993 with the lowest productivity levels in the sample and after 10 years of very low or negative growth rates they are left behind from the majority of the countries.¹⁴ On the contrary, the considerably faster productivity growth rates experienced by Finland and Sweden led them to the top of the list with the most productive countries. Furthermore, the results in Table 5 suggest that convergence is most likely to take place in sectors for which the growth rates do not vary vastly across countries.

Table 7 Posterior model probabilities excluding Italy and Spain

To examine whether the data from Italy and Spain are driving the results toward divergence, the entire analysis is repeated, this time excluding these two countries. Table 7 reports the posterior probabilities of the three models when applied to sector-level and aggregate data for this subsample. This time the model that imposes a unit root is favored by the data for both aggregates, although the evidence is not conclusive. Furthermore, for all sectors except hotels and restaurants the probability mass has moved toward the model of convergence.

Table 8 Average multifactor productivity growth rates (%) per sector and country, excluding Italy and Spain

Finally, productivity growth rates for the models applied to the subsample that excludes Italy and Spain are reported in Table 8. As expected, average productivity growth rates are now higher. A comparison of the productivity growth rates and the shares of industries in total-manufacturing value added leads to a couple of observations. First, with some exceptions, countries tend to experience higher-than-average productivity growth rates in the industries with higher-than-average shares within the country. The causality behind the correlation between growth rates and shares could run in both directions. On one hand, economic activity within a country could be specialized in the sectors for which the country has a comparative advantage in terms of generating innovations. On the other hand, it could be the case that economies of scale in specific sectors, especially with respect to R&D, are leading to a faster rate of innovations. Second, for most countries the sector-specific growth rates weighted by the sector shares provide a good predictor of the growth rate in the two aggregates (as estimated using the total-manufacturing and total services data). Given that the data favor the unit-root models at the disaggregate level and the rather large differences (among sectors) in productivity growth rates, this observation implies that non-convergence at the aggregate level is, to a large extend, driven by differences (among countries) in the shares of individual sectors.

6 Conclusions

This article examines the issue of convergence in multifactor productivity across 11 EU Member States. Two possible reasons for divergence are identified: (1) the level of technology or the social and entrepreneurial environment differ among countries, leading to divergent trends in productivity in each sector alone, or (2) different sectors experience different rates of productivity growth which, when coupled with high specialization of each Member State in particular sectors, leads to divergence at the aggregate level. A novel model is developed around the problem of testing whether convergence or divergence takes place and Bayesian model comparisons are performed, both at the sector and total manufacturing/services levels.

In general, the data provide strong evidence against the hypothesis of convergence in productivity at the aggregate levels and both possible reasons for divergence could contribute to this result. First, productivity levels, as well as growth rates for Italy and Spain are lower than the sample mean for almost all sectors considered. This finding suggests that country-wide characteristics, not specific to particular sectors, prevent these two countries from catching up with the remaining Member States. These characteristics could include aspects of the institutional environment or, given the measure of labor input used in this study, low initial levels of human capital. When these two countries are dropped from the sample, the data favor the model that implies neither convergence nor divergence at the aggregate level.

Second, when examining each sector in isolation, the data favor the model of convergence for more than half of the industries considered in this study and the unit-root model for the remaining industries. Therefore, non-convergence at the aggregate level in the reduced sample (excluding Italy and Spain) is unlikely to be driven by country-wide characteristics. Given the large differences in productivity growth rates across sectors and the different shares of each sector in their respective aggregates, the findings of this study point toward attributing the absence of convergence at the aggregate level to sector-specific characteristics, coupled with the specialization of particular Member-State economies in specific sectors.