1 Introduction

Since the deregulation of electricity markets in the 1990s, electricity spot price forecasting has attracted a lot of attention. A generator, a utility company or a large industrial customer able to forecast the volatile wholesale prices with a reasonable accuracy can adjust its bidding strategy and own production or consumption schedule to maximize profits in day-ahead trading. However, in contrast to other tradable commodities, electricity is very special (Eydeland and Wolyniec 2003; Kaminski 2013; Weron 2006). It is non-storable (economically) while power system stability requires a constant balance between production and consumption. At the same time, electricity demand is dependent on weather (temperature, wind speed, precipitation, etc.) and the intensity of business activities (working hours, weekdays vs. weekends, holidays and near-holidays, etc.). On one hand, these specific characteristics result in extreme—unobserved in any other market—spot price volatility, on the other, they have motivated intensive research efforts towards short-term forecasting of electricity prices, for a recent comprehensive review see Weron (2014).

A wide range of econometric or statistical models have been suggested in the literature, including (auto-)regressive models, (seasonal) ARIMA, AR-GARCH, jump-diffusions, factor models and regime-switching models (see e.g. Bierbrauer et al. 2007; Conejo et al. 2005; Garcia-Martos et al. 2012; Karakatsani and Bunn 2008; Kristiansen 2012; Maciejowska and Weron 2013; Misiorek et al. 2006; Weron and Misiorek 2008). However, in terms of predicting spot price movements, each model specification yields a different forecast. Despite the diversity of models it is impossible to select the most reliable one. For instance, Aggarwal et al. (2009) compared results from as many as 47 publications and concluded: there is no systematic evidence of out-performance of one model over the other models on a consistent basis. This fact is a good motivation for considering combining electricity spot price forecasts. Surprisingly, this approach has not been undertaken in the literature until very recently, see Bordignon et al. (2013), Nowotarski et al. (2014) and Raviv et al. (2013). All three cited papers yield similar conclusions—they support the benefits of combining forecasts for deriving more accurate and more robust point forecasts of electricity spot prices.

However, in some applications, such as risk management or bidding with a safety margin, one is more interested in predicting the variability of future price movements than simply point estimates. From a practical point of view prediction intervals (PI), and density forecasts even more so, provide additional information on the evolution of future prices. In particular, they allow for a better assessment of future uncertainty and for planning of different strategies for the range of possible outcomes indicated by the interval forecast (Chatfield 2000). While there are a variety of empirical studies on forecasting electricity spot prices, interval or density forecasts have not been investigated very extensively to date. Most notable exceptions include Bunn et al. (2013), Misiorek et al. (2006), Nogales and Conejo (2006), Weron and Misiorek (2008) and Wu et al. (2013). Yet, to our best knowledge, prediction intervals have not been considered in the context of combining electricity spot price forecasts. It should be noted, though, that the idea of combining interval forecasts is not new by itself (see e.g. Timmermann 2006; Wallis 2005).

The contribution of the article is twofold. First, we address the above mentioned unresolved issue of constructing PI from combined electricity spot price forecasts. We do this by constructing empirical PI—as in Weron and Misiorek (2008)—for two methods of forecast averaging, i.e. simple average and least absolute deviation (LAD), that proved to be robust and accurate in our recent point forecasting study (Nowotarski et al. 2014). Second, we propose a new method for constructing prediction intervals using the concept of quantile regression and a pool of point forecasts of individual (i.e. not combined) time series models. The latter can be viewed as a natural extension of LAD averaging to an arbitrary quantile.

The remainder of the paper is structured as follows. In Sect. 2, we present the electricity price data used in this study. In Sect. 3, we first present two benchmark individual models (ARX and SNARX) and two averaging schemes (SIMPLE and LAD). Then we introduce the new method—Quantile Regression Averaging (QRA)Footnote 1—for constructing PI from point forecasts of individual methods. In Sect. 4, we evaluate the forecasting performance of the five tested approaches for computing PI in terms of unconditional and conditional coverage. Finally, in Sect. 5, we wrap up the results and conclude.

2 The data

The electricity spot price data was downloaded from the GDF Suez website (www.gdfsuezenergyresources.com) and contains hourly day-ahead locational marginal prices (LPMs) for the Jersey Central Power and Light Company (JCPL) of the Pennsylvania–New Jersey–Maryland (PJM) Interconnection (U.S.). The time series of hourly air temperatures (in Fahrenheit degrees) for New York City was obtained from NOAA’s National Climatic Data Center (www.ncdc.noaa.gov).

We should note here that the spot electricity market is actually a day-ahead market that does not allow for continuous trading. This is a result of system operators requiring advance notice in order to verify that the schedule is feasible and lies within transmission constraints. In a day-ahead market agents submit their bids and offers for delivery of electricity during each hour (or half-hour in some markets) of the next day before a certain market closing time. Thus, when dealing with the forecasting of intraday prices it is important to recall that prices for all spot contracts of the next day are determined at the same time using the same available information (Bierbrauer et al. 2007; Peña 2012; Weron 2006). The system price is then calculated as the equilibrium point for the aggregated supply and demand curves and for each of the hourly (or half-hourly) intervals.

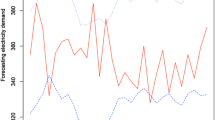
The dataset used in this study comprises hourly price and temperature data for the period August 22, 2010–January 14, 2012, see Fig. 1. The prices and temperatures were preprocessed in the standard way for ‘missing’/‘doubled’ values resulting from changes to/from the daylight saving time: the ‘missing’ values were interpolated from the two neighboring observations while the ‘doubled’ values were averaged to yield one observation for the doubled hour (as in Nowotarski et al. 2014; Weron and Misiorek 2008). The logarithms of hourly temperatures \(T_t\) (in Fahrenheit) were used as the exogenous variable in the time series models for the log-prices (no additional transformations were required since the temperatures were above \(1^{\circ }\)F in the studied period). This selection was motivated by a roughly linear dependence between these two variables. The mean log-price and the median log-temperature were removed to center the data around zero, as in Conejo et al. (2005) and Misiorek et al. (2006).

Fig. 1
figure 1

JCPL (PJM) hourly system prices (in USD/MWh) and hourly air temperatures (in Fahrenheit) for the period August 22, 2010–January 14, 2012. The first vertical dotted line marks the start of the forecasting period for individual models, the second—the beginning of the validation window for obtained prediction intervals

Full size image

In Fig. 1 the studied dataset is split into three subsets. The first date—August 22, 2010—marks the start of the calibration period for the 12 individual models (for model definitions see Sect. 3.1). The first prediction of these models is made for February 11, 2011 (the second date). Then the window is expanded by one day, the individual models are recalibrated and spot price predictions are made for February 12, 2011, etc. Consequently, the first combined forecast (using SIMPLE and LAD averaging) is made for February 11, 2011, the next for February 12, 2011, etc. Finally, the third date in Fig. 1—September 23, 2011—marks the first day for which PI are calculated. This is done using either (i) ARX and SNARX individual models and the empirical scheme for computing PI from the models’ point forecasting errors, (ii) SIMPLE and LAD averaging and the empirical scheme for computing PI from the errors of the combined point forecasts or (iii) point forecasts of all 12 individual models and quantile regression, i.e. the new Quantile Regression Averaging (QRA) approach. The PI validation period lasts until January 14, 2012, and includes 114 days.

3 The techniques

3.1 Individual models

A typical and obvious feature shared by all empirical applications using forecast averaging is that results depend on the specific choice of individual models. Thus, the set of individual techniques considered here includes the 12 models analyzed by Weron and Misiorek (2008) and then used in the context of averaging point forecasts by Nowotarski et al. (2014): autoregressive models (AR, ARX—the latter with temperature as the eXogenous variable), spike preprocessed autoregressive models (p-AR, p-ARX; where the model structure was estimated after replacing price spikes with less extreme observations), threshold autoregressive models (TAR, TARX), mean-reverting jump diffusions (MRJD, MRJDX) and two classes of semiparametric autoregressive models (IHMAR, IHMARX, SNAR, SNARX; introduced by Weron and Misiorek 2008). In this study, we also use two of those individual models—ARX and SNARX—as benchmarks for comparison of the prediction intervals.

The ARX autoregressive model structure is given by the following formula:

$$\begin{aligned} p_t&= \phi _1 p_{t-24} + \phi _2 p_{t-48} + \phi _3 p_{t-168} + \phi _4 mp_t \nonumber \\&+ \psi _1 z_t +d_1 D_{\textit{Mon}} +d_2 D_{\textit{Sat}} +d_3 D_{\textit{Sun}} +\varepsilon _t. \end{aligned}$$
(1)

The lagged log-prices \(p_{t-24}\), \(p_{t-48}\) and \(p_{t-168}\) account for the autoregressive effects of the previous days (the same hour yesterday, two days ago and one week ago), while \(mp_t\) is the minimum of the previous day’s 24 hourly log-prices and creates a link between bidding and price signals from the entire previous day (for discussions on the choice of this ‘link’ variable see Kristiansen 2012; Weron and Misiorek 2008). The variable \(z_t\) refers to the logarithm of the hourly temperature. The three dummy variables—\(D_{Mon}\), \(D_{Sat}\) and \(D_{Sun}\) (for Monday, Saturday and Sunday, respectively)—account for the weekly seasonality. Finally, the \(\varepsilon _t\)’s are assumed to be independent and identically distributed (i.i.d.) with zero mean and finite variance. Model parameters are estimated in Matlab by minimizing the Final Prediction Error (FPE) criterion. Construction of empirical PI boils down to taking a desired quantile of the in-sample residuals, which resembles estimating Value-at-Risk via historical simulation, see Weron and Misiorek (2008).

The smoothed nonparametric ARX (or SNARX) model relaxes the normality assumption needed for the maximum likelihood estimation in the ARX model. It has the same functional form (1) but the parameter estimates are obtained from a numerical maximization of the empirical likelihood as suggested by Cao et al. (2003) and in the context of electricity price forecasting by Weron and Misiorek (2008). The empirical prediction intervals are constructed in the same way as for ARX. Note that SNARX was recommended by Weron and Misiorek as the best individual model out of the 12 considered specifications, mainly due to its good PI performance.

3.2 Combining point forecasts

The idea of combining forecasts goes back to the late 1960s, with the works of Bates and Granger (1969) and Crane and Crotty (1967). Since then, many authors have suggested the superior performance of forecast combinations over the use of individual models, see e.g. Clemen (1989), de Menezes et al. (2000), Timmermann (2006) and references therein. Despite this popularity, combining forecasts has not been discussed widely in the context of electricity spot prices. Only very recently Bordignon et al. (2013), Nowotarski et al. (2014) and Raviv et al. (2013) have provided empirical support for the benefits of combining forecasts to obtain better point predictions of electricity spot prices.

In this paper we focus on computing prediction intervals derived from combined spot price forecasts and on evaluating their performance. To achieve this we examine two averaging schemes—SIMPLE averaging and least absolute deviation or LAD regression—that have been found by Nowotarski et al. (2014) to provide accurate and robust results. SIMPLE averaging is the most natural approach to combining forecasts and boils down to computing the (arithmetic) mean of all forecasts produced by the individual models. It is highly robust and is widely used in business and economic forecasting, see e.g. Clemen (1989) and Genre et al. (2013).

Another popular averaging method is based on classical linear regression. In this approach, the individual forecasts are regressors and the corresponding observed spot price is the dependent variable. The idea was first described by Crane and Crotty (1967), but it was the influential paper of Granger and Ramanathan (1984) to inspire more research effort in this direction. Since then, this way of averaging took on numerous variations according to different findings from different datasets. In this study we decide to follow an alternative proposed by Nowotarski et al. (2014) and replace the ordinary least squares approach with the absolute loss function. The resulting scheme is called least absolute deviation or LAD regression. An advantage of using the absolute loss function is its robustness to electricity price spikes. Indeed, a model that performs well in general, yet significantly underperforms on specific dates, is punished harder by the quadratic loss function. As a consequence it leads to a relatively large decrease of this model’s weight, while using the absolute loss function yields a relatively smaller decrease of the weight.

The forecasting setup is the following. First, for each day \(t\) we compute \(M=12\) individual day-ahead price forecasts \(\widehat{p}_{1t},\dots ,\widehat{p}_{Mt}\) of the 12 individual models (see Sect. 3.1). Then we combine them to yield a spot price forecast:

$$\begin{aligned} \widehat{p}_t^c = \varvec{\widehat{p}_t w_t} = \sum _{i = 1}^M w_{it} \widehat{p}_{it}, \end{aligned}$$
(2)

where \(w_{it}\) is the weight assigned at time \(t\) to forecast \(i\). We calculate the weights recursively at each time step, using data from the first prediction day (indicated by the first dotted vertical line in Fig. 1) until \(t-24\) (i.e. 24 h prior to the hour we forecast the price for). Like for individual forecasts, when predicting the price for hour \(h\), we utilize past price values only for that particular hour, i.e. we split our data into 24 time series. As our main interest here are prediction intervals (not point forecasts), given weights at time \(t\), we obtain the empirical prediction intervals by computing a quantile of the distribution of in-sample residuals of the averaged forecasts (2), i.e. analogously as for ARX and SNARX (see Sect. 3.1).

3.3 Quantile regression and forecast averaging

The quantile regression model introduced by Koenker and Basset (1978) has been widely used in many financial and economic applications, out of which the most intuitive may be Value-at-Risk as it simply concerns a quantile of a portfolio (Bunn et al. 2013). Quantile regression allows us to describe the conditional distribution of the dependent variable given its explanatory variables. Our idea here is to apply quantile regression to point (not interval!) forecasts of the individual models, i.e. to use the individual point forecasts as independent variables and the corresponding observed spot price as the dependent variable. Note that our method—dubbed Quantile Regression Averaging (QRA)—yields an interval forecast of the spot price, but does not use the PI of the individual methods. This is an important point, since as Wallis (2005) remarks: combining intervals directly will not in general give an interval with the correct probability. For instance, Granger et al. (1989) attempt to overcome this difficulty by estimating combining weights from data on past forecasts that in effect recalibrate the forecast quantiles, which is a cumbersome solution.

In our case the averaging problem is given by:

$$\begin{aligned} Q_p(q|\varvec{\widehat{p}_t}) = \varvec{\widehat{p}_t w_q} , \end{aligned}$$
(3)

where \(Q_p(q|\cdot )\) is the conditional \(q\)th quantile of the electricity spot price distribution, \(\varvec{\widehat{p}_t}\) are the regressors (explanatory variables) and \(\varvec{w_q}\) is a vector of parameters (\(q\) in the subscript emphasizes the fact that the parameters are varying for different quantiles). The weights are estimated by minimizing the loss function for a particular \(q\)th quantile:

$$\begin{aligned}&\min \limits _{\varvec{w_t}} \left[ \sum \limits _{\{t:p_t \ge \varvec{\widehat{p}_t w_t}\}}^{ } q |p_t - \varvec{\widehat{p}_t w_t}| + \sum \limits _{\{t:p_t < \varvec{\widehat{p}_t w_t}\}}^{ } (1-q)|p_t - \varvec{\widehat{p}_t w_t}| \right] \nonumber \\&\quad =\min \limits _{\varvec{w_t}} \left[ \sum \limits _{t}^{} (q - 1\!\!1_{p_t < \varvec{\widehat{p}_t w_t}}) (p_t - \varvec{\widehat{p}_t w_t}) \right] . \end{aligned}$$
(4)

Finally, note that the LAD regression may be viewed as a special case of quantile regression by taking the quantile to be the median, i.e. \(q=0.5\). Indeed, for \(q=0.5\) the right hand side of formula (4) under the minimum reduces to \(\sum _t^{ } \frac{1}{2} |p_t - \varvec{\widehat{p}_t w_t}|\) and, hence, we obtain the absolute loss function (up to a constant). That said, the proposed method is a natural extension of the averaging problem, where the point of interest is a point forecast.

It should be also emphasized that the QRA-based 50 % PI are not the same as the LAD-based 50 % PI. The former are based on running quantile regression for \(q=0.25\) and \(q=0.75\), the latter on running quantile regression for \(q=0.5\) and then taking the 25 and 75 % quantiles of the distribution of forecast errors (i.e. residuals).

4 Results

First, we evaluated the quality of the interval forecasts by comparing the nominal coverage to the true coverage. Thus, for the two individual models (ARX and SNARX) and for the three averaging schemes (SIMPLE, LAD and QRA) we calculated PIs and determined the percentage of coverage of the 50 and 90 % two sided day-ahead PI by the actual spot price. If the model implied interval forecasts were accurate then the percentage of coverage should match the nominal values. For each model, \(24\times 114\) hourly values were determined and compared to the actual spot price. The unconditional coverage is summarized in the upper part of Table 1 and in Table 2. Interestingly, all models have overall a slightly higher coverage than nominal (for some hours the coverage is lower than nominal, though), possibly due to a less volatile spot price in the PI validation period as compared to the calibration period, see Fig. 1. For both analyzed levels (50 and 90 %) the best results were achieved by QRA, while the worst by ARX.

Table 1 Upper part: Unconditional coverage of the 50 and 90 % two-sided day-ahead PIs by the actual spot price for all considered models.   Lower part:  Descriptive statistics of the PI width
Full size table
Table 2 Unconditional coverage (in percent) of the 50 and 90 % two-sided day-ahead PIs by the actual spot price for all five considered methods, independently for each of the 24 h
Full size table

Next, we applied the approach of Christoffersen (1998) to test the unconditional and conditional coverage. This model independent approach is designed to overcome the clustering effect. The tests are carried out in the likelihood ratio (LR) framework. Three LR statistics are calculated: for unconditional coverage, independence and conditional coverage. The former two are distributed asymptotically as \(\chi ^2(1)\) and the latter as \(\chi ^2(2)\). If we condition on the first observation, then the conditional coverage LR test statistics is the sum of the other two. It should be noted that the independence test and hence the conditional coverage test is conducted only with respect to the first order dependency of exceedances. As Clements and Taylor (2003) show, the test can be easily modified to measure higher order dependency; see Maciejowska et al. (2014) for a sample application of this approach in the context of electricity price forecasting and Berkowitz et al. (2011) for a review of more complex tests. For simplicity of exposition we present here only the results of the conditional coverage test based on the first order test for independence, however, the conclusions are qualitatively the same if higher order dependency is tested.

The conditional and unconditional coverage LR statistics are plotted in Fig. 2. We repeat the methodology of Weron and Misiorek (2008) and conduct the tests separately for the 24 hourly time series. It would not make sense to compute the statistics jointly for all hours, since, by construction, the forecasts for consecutive hours are correlated—predictions for all 24 h of the next day are made at the same time using the same information set.

Fig. 2
figure 2

The conditional coverage (left panels) and unconditional coverage (right panels) LR statistics for the PI obtained from the five considered forecasting models. The solid (dashed) horizontal lines represent the 5 % (1 %) significance level of the appropriate \(\chi ^2\) distribution. All test values exceeding 20 are set to 20

Full size image

According to Christoffersen’s test statistics, QRA-based PI were the best among the tested approaches. Apart from two (four) peak hours, the QRA-based PI were not rejected by the conditional coverage (unconditional coverage) test at the 1 % level. For a majority of hours, they were not rejected at the 5 % level as well. On the other hand, the ARX model turned out to be the worst out of all analyzed methods according to the unconditional coverage test, with the null hypothesis rejected in 21 and 17 out of 24 cases, respectively for the 50 and 90 % PI at 5 % confidence level. Empirical prediction intervals derived from SIMPLE averaging yielded better results than ARX. However, for the hours from 11 to 16 the SIMPLE averaging implied PI were generally too wide, see also the lower part of Table 1 and Fig. 3. As a result the test statistics were in excess of 20 and the null hypotheses were rejected for the two analyzed PI coverages (50 and 90 %). Moreover, for those hours SIMPLE based 90 % PI had a 100 % coverage. For the rest of the day the method performed slightly better, especially during night and early morning hours. The LAD regression did not perform much better. The test statistics were similar to those achieved by SIMPLE and better than the benchmark ARX.

Fig. 3
figure 3

Boxplots of widths of the prediction intervals (PI) for the five considered forecasting models

Full size image

Finally note that the best individual method according to Weron and Misiorek (2008)—SNARX—performed worse than QRA, but better than the remaining three approaches. The SNARX based PI were on average narrower and less volatile than QRA-based, but their median was higher than that of QRA-based PI, see Table 1. It seems as if QRA yields PI which adapt themselves better to the changing price dynamics than those obtained from the SNARX model.

5 Conclusions

This paper examines possible accuracy gains from forecast averaging in the context of interval forecasts of electricity spot prices. While there is a significant number of studies on the use of forecast combinations for constructing interval forecasts of economic and financial variables, to our best knowledge, there are no publications where this approach would be tested on the extremely volatile electricity spot price data. Our paper can be considered as an extension of the empirical studies of Weron and Misiorek (2008) and Nowotarski et al. (2014). In the former article the same individual models were evaluated in a point and interval forecasting exercise. The smoothed nonparametric autoregressive SNARX model came out as the best in terms of PIs. In the latter paper the same individual models were used as the building blocks for eight approaches to combining point forecasts. The SIMPLE and LAD averaging schemes turned out to be relatively accurate and robust ways to combine electricity spot price forecasts.

In this study we (i) construct empirical PI from combined electricity spot price forecasts, utilizing SIMPLE and LAD averaging, and (ii) propose a new method—Quantile Regression Averaging (QRA)—for constructing prediction intervals using the concept of quantile regression and a pool of point forecasts of individual (i.e. not combined) time series models. It turns out that the empirical PI from combined forecasts outperform ARX model implied PI, in terms of both the unconditional and conditional coverage, but are outperformed by the SNARX based PI. However, the QRA-based PI are found to be more accurate than those of the semiparametric SNARX model. The latter fact is particularly appealing since SNARX yielded the most accurate PI of out the 12 individual models used in this study. In other words, the Quantile Regression Averaging approach we propose here—which is obviously dependent on the quality of the point forecasts of the individual models—outperformed the best individual model.