Demand creation and location: a variable consumer-distribution approach in spatial competition

Abstract

This paper deals with a variable spatial distribution of consumers according to the location decisions of firms in spatial competition. Specifically, we present a location-then-quantity game in which some of the consumers are attracted to the firms’ locations. We show that all firms agglomerate in a circular city when the transport cost is low. This is in sharp contrast to the results shown in previous studies with fixed distributions of consumers, where such a full agglomeration never occurs in equilibrium. Welfare analysis shows excess dispersion compared with the second-best scenario.

Appendix

1.1 Proof of Proposition 1

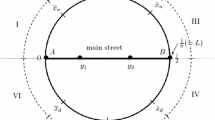
Without the loss of generality, let $x_{2}=0$ and $0\le x_{1}=x\le 1/2$. We will compute the best response of firm $1$ against $x_{2}=0$, and let $x_{1}^{*}=\arg \max \Pi _{1}^{*}(x)$ denotes the best response. Then, we have $108b\times \Pi _{1}^{*}(x)/a^{2}=12\left( 2n+1\right) -6\tau \left( 4nx+1\right) +\tau ^{2}\left( 1+12\left( 5n+2\right) x^{2}-32x^{3}\right)$.

Note that $\Pi _{1}^{*}(x)$ is cubic and the coefficient of $x^{3}$ in $\Pi _{1}^{*}(x)$ is negative. We readily have $\partial \Pi _{1}^{*}(x)/\partial x<0$ if $\tau \le 16n/\left( 5n+2\right) ^{2}$; thus, $x_{1}^{*}=0$. If otherwise $16n/\left( 5n+2\right) ^{2}<\tau , \, \partial \Pi _{1}^{*}(x)/\partial x=0$ yields a local maximizer of $\Pi _{1}^{*}(x)$ as $\hat{x}^{A}=(5n+2+\sqrt{\left( 5n+2\right) ^{2}-16n/\tau })/8$. With $\left. \partial \Pi _{1}^{*}(x)/\partial x\right| _{x=0}<0$, we can classify the solution of the maximization problem into three cases:

• (i) full agglomeration: $x_{1}^{*}=0\Leftrightarrow \hat{x}^{A}\ge 1/2$ and $\Pi _{1}^{*}(0)\ge \Pi _{1}^{*}(1/2)$; or $0<\hat{x}^{A}<1/2$ and $\Pi _{1}^{*}(0)\ge \Pi _{1}^{*}(\hat{x}^{A})$.

• (ii) full dispersion: $x_{1}^{*}=1/2\Leftrightarrow \hat{x}^{A}\ge 1/2$ and $\Pi _{1}^{*}(1/2)\ge \Pi _{1}^{*}(0)$.

• (iii) partial agglomeration: $x_{1}^{*}=\hat{x}^{A}(\!<\!1/2)\Leftrightarrow 0<\hat{x}^{A}<1/2$ and $\Pi _{1}^{*}(\hat{x}^{A})\ge \Pi _{1}^{*}(0)$.

Due to the symmetry, the best response of firm $2$ must be $x_{2}^{*}=0$ when firm $1$ is located at $x_{1}^{*}$ that is derived above in each case. By reducing and arranging the above conditions, we have the result.

1.2 Proof of Lemma 1

Without the loss of generality, we assume $0\le x_{1}=x\le 1/2$ and $x_{2}=0$. Substituting the quantity equilibrium obtained in (4), (5), and (6) into the consumer surplus, we have $\text{ CS }=a^{2}g_{B}(x)/54b$, where $g_{B}(x)=4\tau ^{2}x^{3}+3(2n-1)\tau ^{2}x^{2}-24n\tau x+\tau ^{2}-6\tau +12(2n+1)$ and $\partial g_{B}(x)/\partial x=6\left[ 2\tau ^{2}x^{2}+(2n-1)\tau ^{2}x-4n\tau \right]$. $\partial g_{B}(x)/\partial x=0$ yields two local extremizers as $\check{x}^{B}=(1-2n-\sqrt{d^{B}})/4$ and $\hat{x}^{B}=(1-2n+\sqrt{d^{B}})/4$, where $d^{B}=(1-2n)^{2}+32(n/\tau )>0$. Under $n>0$ and $0<\tau <1$, we readily have $\check{x}^{B}<0$ and $1/2< \hat{x}^{B}$. Because of the positive coefficient of $x^{3}$ in $g_{B}(x), \, g_{B}(x)$ is monotonically decreasing in $x\in [0,1/2]$. Therefore, full agglomeration maximizes consumer surplus.

1.3 Proof of Proposition 3

Without the loss of generality, $x_{2}=0$ and $0\le x_{1}=x\le 1/2$. Then, the social surplus (SS) is rewritten by $54b\times \text{ SS }(x)/a^{2}=-28\tau ^{2}x^{3}+3(22n+7)\tau ^{2}x^{2}-48n\tau x+2\tau ^{2}-12\tau +24(2n+1)$.

Note that $\text{ SS }(x)$ is cubic and the coefficient of $x^{3}$ in $\text{ SS }(x)$ is negative. If $\tau \le 448n/\!\left( 22n+7\right) ^{2}$, then $\partial \text{ SS }(x)/\partial x<0$; thus, $\text{ SS }(x)$ is maximized at $x=0$. If otherwise $448n/\!\left( 22n+7\right) ^{2}<\tau , \,\partial \text{ SS }(x)/\partial x=0$ yields a local maximizer of $\text{ SS }(x)$ as $\hat{x}^{C}=(22n+7+\sqrt{\left( 22n+7\right) ^{2}-448n/\tau })/28$. With $\left. \partial \text{ SS }(x)/\partial x\right| _{x=0}<0$, we can analyze three cases like “Appendix 8.1.

• (i) full agglomeration: $\arg \max \text{ SS }(x)=0\Leftrightarrow \hat{x}^{C}\ge 1/2$ and $\text{ SS }(0)\ge \text{ SS }(1/2)$; or $0<\hat{x}^{C}<1/2$ and $\Pi _{1}^{*}(0)\ge \Pi _{1}^{*}(\hat{x}^{C})$.

• (ii) full dispersion: $\arg \max \text{ SS }(x)=1/2\Leftrightarrow \hat{x}^{C}\ge 1/2$ and $\text{ SS }(1/2)\ge \text{ SS }(0)$.

• (iii) partial agglomeration: $\arg \max \text{ SS }(x)=\hat{x}^{C}(\!<\!1/2) \Leftrightarrow \hat{x}^{C}<1/2$ and $\text{ SS }(\hat{x}^{C})\ge \Pi _{1}^{*}(0)$.

By reducing and arranging the above conditions, we have the result.

1.4 Proof of Proposition 4

(We apply the same notations as in the duopoly case.) The total number of the firms is $m$, and let $j=\{1,2,\ldots ,m\}$ and $x_{j}$ denote the firm’s index and the location of firm $j$, respectively. Inverse demand function at $z$ is revised as $P(z)=a-b\sum _{j}q_{j}(z)$, where $q_{j}(z)$ is supply amount of firm $j$ at $z$. The total profit of firm $i$ is given by $\Pi _{i}=\int _{0}^{1}\pi _{i}(z)\text{ d }z+n\pi _{i}(x_{i})+n\sum _{j\ne i}\pi _{i}(x_{j})$, where $\pi _{i}(z)=q_{i}(z)[P(z)-T(x_{i},z)]$ is the local profit for firm $i$ at $z$. Then, the similar calculations yield equilibrium supply amount at $z$ as $q_{i}^{*}(z)=[a-mT(x_{i},z)+\sum _{j\ne i}T(x_{j},z)]/\left( m+1\right) b$.

Here, we require $\tau <2/m$ for each market to be served by all firms, irrespective of the locations of the firms. Substituting the above equilibrium quantity into the profit functions, we can rewrite the local and the total profits for firm $i$ as $\pi _{i}^{*}(z)=b\left[ q_{i}^{*}(z)\right] ^{2}$ and $\Pi _{i}^{*}(x_{i})=\int _{0}^{1}\pi _{i}^{*}(z)\text{ d }z+n\pi _{i}^{*}(x_{i})+n\sum _{j\ne i}\pi _{i}^{*}(x_{j})$, respectively. Then, we check the relocation incentive for a firm when all firms agglomerate at a location. Without the loss of generality, all firms agglomerate at $0$ and we analyze the optimal location for firm $1$ with $0\le x_{1}=x\le 1/2$. Then, we have the profit function of firm $1\, (\Pi _{1}^{*})$ as $12b\left( 1+m\right) ^{2}\times \Pi _{1}^{*}(x)/a^{2}=12\left( 1+mn\right) -6\tau \left[ 1+4(m-1)^{2}nx\right] +\tau ^{2}\left[ 1+12\left( m-1\right) \left( m^{2}n+mn+m-n\right) x^{2}-16m\left( m-1\right) x^{3}\right]$.

Note that the profit function is cubic and the coefficient of $x_{1}^{3}$ is negative, and $\left. \partial \Pi _{1}^{*}/\partial x\right| _{x=0}<0$.

Let $d^{D}$ be a discriminant of $\partial \Pi _{1}^{*}/\partial x_{1}=0$. If $d^{D}\le 0$, then the optimal location $x_{1}^{*}=0$. When $d^{D}>0, \,\partial \Pi _{1}^{*}/\partial x=0$ yields the local minimizer and the local maximizer as $\check{x}^{D}$ and $\hat{x}^{D}$, respectively ($0<\check{x}^{D}<\hat{x}^{D}$). For $x=0$ to be the optimal location, we require $\Pi _{1}^{*}(0)>\Pi _{1}^{*}(1/2)$ if $\hat{x} ^{D}\ge 1/2$, or $\Pi _{1}^{*}(0)>\Pi _{1}^{*}(\hat{x}^{D})$ if $\hat{x}^{D}<1/2$. By reducing these conditions, we have $0<\tau <T(m,n)\implies \arg \max \Pi _{1}^{*}(x)=0$, where

$$\begin{aligned}&T(m,n)\\&\quad =\left\{ \begin{array}{ll} 32(m-1)mn/3(m^{2}n+mn+m-n)^{2} &{}\quad \text{ when }\;0<n\le m/3(m^{2}+m-1) \\ 12(m-1)n/\left( 3m^{2}n+3mn+m-3n\right) &{}\quad \text{ when }\;m/3(m^{2}+m-1)<n \end{array} \right. . \end{aligned}$$

For any $m\ge 3$ and for any $n>0, \,T(m,n)>0$. This implies that if the transport cost is sufficiently low such that $\tau <T(m,n)$ and $\tau <2/m$, full agglomeration is a location equilibrium.

1.5 Proof of Proposition 5

We show three lemmas in the linear city.

Lemma 2

Central agglomeration is an equilibrium for all $n>0$ and for all $0<\tau <1/2$.

Proof

Without the loss of generality, let firm $2$ be located at $1/2$ ($x_{2}=1/2$) and $0\le x_{1}=x\le 1/2$. We have the total profit for firm $1\, (\Pi _{1}^{*})$ as $27b\times \Pi _{1}^{*}(x)/a^{2}=4\tau ^{2}x^{3}+3\tau [(5n+2)\tau -4)]x^{2}+3\tau \left[ (5\tau -2)n-3\tau +4\right] x+ \left[ 3(5\tau ^{2}-4\tau +8)n+11\tau ^{2}-18\tau +12\right] /4$.

Note that $\Pi _{1}^{*}$ is cubic, the coefficient of $x^{3}$ is positive, and $\left. \partial \Pi _{1}^{*}/\partial x\right| _{x=1/2}>0$. If the discriminant of $\partial \Pi _{1}^{*}/\partial x=0$ is zero or negative ($4(6-5\tau -\sqrt{11-10\tau })/25\tau \le n\le 4(6-5\tau +\sqrt{11-10\tau })/25\tau$), then $\Pi _{1}^{*}$ is non-decreasing, i.e., $\arg \max \Pi _{1}^{*}(x)=1/2$.

Suppose that the discriminant is positive, and let $\check{x}^{E1}$ and $\hat{x}^{E1}$ ($\check{x}^{E1}\le \hat{x}^{E1}$) denote the local maximizer and the local minimizer of $\Pi _{1}^{*}$, respectively. When $n<4(6-5\tau -\sqrt{11-10\tau })/25\tau$, we readily have $\check{x} ^{E1}>1/2$, which means $\Pi _{1}^{*}$ is increasing in $x$ under $x\le 1/2$. Hence, $\arg \max \Pi _{1}^{*}(x)=1/2$. When $n>4(6-5\tau + \sqrt{11-10\tau })/25\tau$, we readily have $\check{x}^{E1}<0$ and $\Pi _{1}^{*}(1/2)\ge \Pi _{1}^{*}(0)$, which also means $\Pi _{1}^{*}$ is increasing in $x$ under $x\le 1/2$. Hence, $\arg \max \Pi _{1}^{*}(x)=1/2$. In any cases, the best response for firm $1$ against $x_{2}=1/2$ is $x_{1}=1/2$. Due to symmetry, we have the result.$\square$

Lemma 3

Full dispersion is an equilibrium if and only if $\max \left\{ \frac{6n}{ 15n+2},\frac{n+2}{5n+1}\right\} \le \tau <1/2$ and $n>1$.

Proof

Without the loss of generality, let firm $2$ be located at $1$ ($x_{2}=1$) and $x_{1}=x$. The total profit for firm $1$ ($\Pi _{1}^{*}$) is given by $27b\times \Pi _{1}^{*}(x)/a^{2}=4\tau ^{2}x^{3}+3\tau (5n\tau -4)x^{2}-6\tau \left[ (5\tau -1)n+\tau -2\right] x+3\left[ (5\tau ^{2}-2\tau +2)n+\tau ^{2}-\tau +1\right]$.

Note that $\Pi _{1}^{*}$ is cubic and the coefficient of $x^{3}$ is positive. If the discriminant of $\partial \Pi _{1}^{*}/\partial x=0$ is zero or negative, then $\Pi _{1}^{*}$ is non-decreasing, i.e., $\arg \max \Pi _{1}^{*}(x)\ne 0$. Suppose that the discriminant is positive, and let $\check{x}^{E2}$ and $\hat{x}^{E2}$ ($\check{x}^{E2}\le \hat{x} ^{E2}$) denote the local maximizer and the local minimizer of $g_{E}(x)$, respectively. For $\arg \max \Pi _{1}^{*}(x)=0$ to hold, we require that $\Pi _{1}^{*}(0)\ge \Pi _{1}^{*}(1)$ and $\check{x}^{E2}\le 0$. Tedious calculations yield $\Pi _{1}^{*}(0)\ge \Pi _{1}^{*}(1)\iff \tau \ge 6n/(15n+2)$ and $\check{x}^{E2}\le 0\iff \tau \ge (n+2)/(5n+1)$. When $n\le 1$, these conditions violate the full-coverage condition $\tau <1/2$. In other words, full dispersion is an equilibrium for any $\tau$ satisfying the above conditions only when $n>1$.$\square$

Lemma 4

Except for full dispersion and central agglomeration, there is no equilibrium.

Proof

Without the loss of generality, $0\le x_{1}=x\le x_{2}=y\le 1$. Tedious calculations yield the total profit for firm $1\, (\Pi _{1}^{*})$ as $27b\times \Pi _{1}^{*}(x,y)/a^{2}=4\tau ^{2}x^{3}+3\tau [(5n-4y+4)\tau -4)]x^{2}+6\tau \left[ 2+n-\tau (1+(5n+2)y-2y^{2})\right] x+3+\tau (-3-6y+6y^{2})+3n(2-2\tau y+5\tau ^{2}y^{2})+\tau ^{2}(1+3y+3y^{2}-4y^{3}),$and the total profit for firm $2$ as $\Pi _{2}^{*}(x,y)=\Pi _{1}^{*}(1-y,1-x)$. Note that $\Pi _{1}^{*}$ and $\Pi _{2}^{*}$ are cubic, the coefficient of $x^{3}$ in $\Pi _{1}^{*}$ is positive, but the coefficient of $y^{3}$ in $\Pi _{2}^{*}$ is negative. First, we can show that $\left. \partial \Pi _{1}^{*}/\partial x\right| _{x=0}\le 0$ and $\partial \Pi _{2}^{*}/\partial y=0$ for $y<1$ are incompatible. Then, there is no corner solution except for full dispersion. Second, we have $\partial \Pi _{1}^{*}/\partial x+\partial \Pi _{2}^{*}/\partial y=12a^{2}\tau (\tau -2)(x+y-1)/27b$. Hence, if there is an inner solution, we require $y=1-x$, which means the equilibria are symmetric. For symmetric equilibria (full dispersion and central agglomeration excepted) to be established, we must find a solution of the first-order condition $\left. \partial \Pi _{1}^{*}/\partial x\right| _{y=1-x}=0$ with $0<x<1/2$. From the condition, we readily have the local maximizer of $\Pi _{1}^{*}$ as $x^{E3}=(2+\tau -5n\tau -\sqrt{4-4(3+7n)\tau +(3+5n)^{2}\tau ^{2}})/8\tau$. Next, when we compute two conditions of $x^{E3}>0$ and $x^{E3}<1/2$, we can show that these are incompatible. This indicates nonexistence of equilibria.$\square$

These three lemmas establish Proposition 5.

1.6 Proof of Proposition 6

As in Sect. 5, we define the social welfare in the linear city (the detail computation omitted). Without the loss of generality, $0\le x_{1}=x\le x_{2}=y\le 1$. Then, the social surplus ($\text{ SS }$) is given by $54b\times \text{ SS }(x,y)/a^{2}=24+6n(8+8\tau (x-y)+11\tau ^{2}(x-y)^{2})-24\tau (1-x+x^{2}-y+y^{2})+\tau (8+14x^{3}+x^{2}(33-42y)-12y+33y^{2}-14y^{3}+6x(-2-7y+7y^{2})$.

First, due to $\partial \text{ SS }/\partial x+\partial \text{ SS }/\partial y=12a^{2}\tau (\tau -2)(-1+x+y)/27b$, interior solutions, if any, must satisfy $x+y=1$ because $\partial \text{ SS }/\partial x=\partial \text{ SS }/\partial y=0$ is required by the first-order conditions. In other words, interior solutions are symmetric with regard to the center. We can readily confirm that there are no corner solutions ($x=0$ or $y=1$). Hence, we seek a symmetric solution. Substituting $1-x$ for $y$ in $g_{H}$ and solving $\partial \text{ SS }/\partial x=0$, we have the local maximizer as $x^{F}=(4+(5-22n)\tau -\sqrt{d^{F}})/28\tau$. where $d^{F}=16-8(9+50n)\tau +(9+22n)^{2}\tau ^{2}$. When $d^{F}\le 0, \,\arg \max \text{ SS }(x)=1/2.$ Next, we analyze two cases of $d^{F}>0$ as follows. (i) $n>(100+12\sqrt{56-77\tau }-99\tau )/242$. In this case, we have $x^{F}<0$ and $\text{ SS }(1/2)>\text{ SS }(0)$. This means $\arg \max \text{ SS }(x)=1/2$. (ii) $n<(100-12\sqrt{ 56-77\tau }-99\tau )/242$. In this case, we have $x^{F}>1/2$ when $\tau <4/9$ and $0<x^{F}<1/2$ when $\tau >4/9$. The former means $\arg \max \text{ SS }(x)=1/2$. In the latter case, we have $\text{ SS }(1/2)\gtrless \text{ SS }(x^{F})\iff 8\sqrt{ 7(244-297\tau )}+33(9+22n)\tau \gtrless 356$. By arranging the above findings, we have the result.