Multi-resolution topology optimization using adaptive isosurface variable grouping (MTOP-aIVG) for enhanced computational efficiency

Abstract

Because finite elements and density elements are separated in multi-resolution topology optimization (MTOP), a relatively fewer number of finite elements can be used, thereby significantly reducing computing cost in finite element analysis (FEA) during topology optimization. However, for large-scale problems, numerous design variables are still required to precisely represent the optimum topology. This causes a dominant computational burden in design optimization. In this paper, an efficient multi-resolution topology optimization (MTOP) using adaptive isosurface variable grouping (aIVG) is proposed to alleviate the above computational burden in topology optimization by grouping design variables of similar grouping criteria into a single grouped design variable. Adaptive isosurface variable grouping is performed according to the grouping criterion which can be calculated using design variables and their sensitivities. Numerical examples such as 2D and 3D compliance minimization, 2D compliant mechanism, 2D multiple displacement constraints, and 3D thermal compliance minimization demonstrate that the proposed MTOP-aIVG significantly reduces computation time in optimization by virtue of using a reduced number of design variables.

Appendix. Details of MTOP formulation

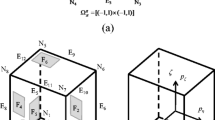
For a 2D quadrilateral element with 5 × 5 density variables (Fig. 32), a density element stiffness matrix using the Gauss-Legendre quadrature can be expressed as

$$ {\mathbf{K}}_d^e={\int}_{P_r}^{p_{r+1}}{\int}_{q_s}^{q_{s+1}}{\mathbf{B}}^T\mathbf{CB}\left|\mathbf{J}\right| d\xi d\eta =\frac{A^e}{4}{\int}_{P_r}^{p_{r+1}}{\int}_{q_s}^{q_{s+1}}{\mathbf{B}}^T\mathbf{CB} d\xi d\eta $$

(A1)

where A^e is the area of a finite element in physical coordinate; m and n are the numbers of quadrature points in ξ and η coordinates, respectively; and w_i and w_j are the weighting coefficients at the ith and jth quadrature, respectively. Also, in Eq. (A1),

$$ {a}_i=\frac{p_{r+1}-{p}_r}{2}{\xi}_i+\frac{p_{r+1}+{p}_r}{2}\kern0.62em \mathrm{and}\kern0.5em {b}_i=\frac{q_{s+1}-{q}_s}{2}{\eta}_i+\frac{q_{s+1}+{q}_s}{2}\kern0.62em \mathrm{for}\kern0.5em 1\le r\le G\kern0.5em \mathrm{and}\kern0.5em 1\le s\le G $$

(A2)

where p_r is the rth coordinate value in the ξ axis; q_s is the sth coordinate value in the η axis; G is the number of density elements in a finite element in each axis direction (5 in Fig. 32); ξ_i and η_j are the ith and jth quadrature position in ξ-η coordinate, respectively.

Fig. 32

Relation between the finite element layer and density element layer: a density variables in one finite element and b node position in the isoparametric element

To improve the computational efficiency in the optimization loop, the element stiffness matrix can be re-expressed in terms of precomputed terms and density variables. This study utilizes the modified SIMP (Sigmund 2007), where the elastic stiffness is expressed as

$$ E\left({\rho}_i\right)={E}_{\mathrm{min}}+\left({E}_0-{E}_{\mathrm{min}}\right){\left({\rho}_i\right)}^p,\kern0.48em {\rho}_i\in \left[0,1\right] $$

(A3)

where E_min is the minimum value of the Young’s modulus of the material; E₀ is the original Young’s modulus; and p is a penalization constant which is typically set to 3. Then, using Eqs. (2), (A1), and (A3), the element stiffness matrix in MTOP can be expressed as

$$ {\mathbf{K}}^e=\sum \limits_{k=1}^{{N_d}^e}\underset{{\Omega_d}^e}{\int }{\mathbf{B}}^T\mathbf{CB}d{\Omega_d}^e=\sum \limits_{k=1}^{{N_d}^e}\left\{{\left.{\mathbf{L}}_{\mathrm{min}}\right|}_d+\left({\left.{\mathbf{L}}_0\right|}_d-{\left.{\mathbf{L}}_{\mathrm{min}}\right|}_d\right){\left({\rho_d}^e\right)}^p\right\} $$

(A4)

where

$$ {\displaystyle \begin{array}{c}{\mathbf{L}}_{{\left.\min \right|}_d}=\underset{\Omega_d^e}{\int }{\mathbf{B}}^T{\mathbf{C}}_{\mathrm{min}}\mathbf{B}d{\Omega}_d^e\\ {}\simeq \frac{A^e}{4}{\left(\frac{1}{G}\right)}^2\sum \limits_{i=1}^m\sum \limits_{j=1}^n{w}_i{w}_j\mathbf{B}{\left({a}_i,{b}_j\right)}^T{\mathbf{C}}_{\mathrm{min}}\mathbf{B}\left({a}_i,{b}_j\right)\end{array}} $$

(A5)

$$ {\displaystyle \begin{array}{c}{\mathbf{L}}_{{\left.0\right|}_d}=\underset{\Omega_d^e}{\int }{\mathbf{B}}^T{\mathbf{C}}_0\mathbf{B}d{\Omega}_d^e\\ {}\simeq \frac{A^e}{4}{\left(\frac{1}{G}\right)}^2\sum \limits_{i=1}^m\sum \limits_{j=1}^n{w}_i{w}_j\mathbf{B}{\left({a}_i,{b}_j\right)}^T{\mathbf{C}}_0\mathbf{B}\left({a}_i,{b}_j\right)\end{array}} $$

(A6)

C_min is the constitutive matrix for the minimum Young’s modulus E_min; C₀ is the constitutive matrix for Young’s modulus E₀; and ρ_d^e is the density of the d^th density element which belongs to the eth finite element. Using the adjoint method, sensitivities of the objective and constraint functions with respect to the dth density variable (ρ_d^e) are given by

$$ \frac{\partial C}{{\partial \rho}_d^e}=-{\left({\mathbf{u}}^e\right)}^T\frac{\partial {\mathbf{K}}_d^e}{\partial {\rho}_d^e}{\mathbf{u}}^e=-{\left({\mathbf{u}}^e\right)}^T\left\{p{\left({\rho}_d^e\right)}^{p-1}\left({\mathbf{L}}_{0\mid d}-{\mathbf{L}}_{\min \mid d}\right)\right\}{\mathbf{u}}^e $$

(A7)

and

$$ \frac{\partial g}{\partial {\rho_d}^e}=\frac{\partial }{\partial {\rho_d}^e}\left(\sum \limits_{e=1}^{N^e}\sum \limits_{d=1}^{{N_d}^e}{\rho_d}^e{v_d}^e-{V}^{\ast}\right)={v_d}^e $$

(A8)

respectively.