Torque control strategy and optimization for fuel consumption and emission reduction in parallel hybrid electric vehicles

Abstract

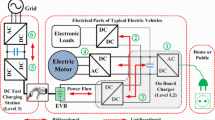
To reduce fuel consumption and exhaust emissions in hybrid electric vehicles (HEVs), it is important to develop a well-organized energy management system (EMS). This paper proposes a torque control strategy coupled with optimization for a parallel HEV. A torque control strategy is developed first. In particular, a function to control the driving condition, called the internal combustion engine (ICE) torque control function, is introduced. This function controls the driving conditions (electric motor (EM) driving, ICE driving, and ICE driving assisted by EM) for reducing fuel consumption and exhaust emissions. This function depends on several design variables that should be optimized. Numerical simulation of HEV using Matlab/Simulink is so computationally intensive that a sequential approximate optimization (SAO) using a radial basis function network (RBF) is adopted to determine the optimal values of these design variables. As the result, the optimal ICE torque control function is determined with a small number of simulation runs. In this paper, CO₂ and NO_x emissions are minimized simultaneously for reducing the fuel consumption and exhaust emission. Through numerical simulations using typical driving cycles, the trade-off between CO₂ and NO_x emissions is clarified and the validity of the proposed torque control strategy coupled with the proposed optimization is examined.

Appendix sequential approximate optimization with radial basis function network

1.1 A.1 Radial basis function network and width in the gaussian kernel

The RBF network is a three-layer feed-forward network. Given the training data expressed by {x _j , y _j }(j = 1, 2, ⋯, m), where m represents the number of sampling points, the output of the network ỹ(response surface) is given by

$$ \widehat{y}\left(\mathbf{x}\right)={\displaystyle {\sum}_{j=1}^m{w}_jK\left(\mathbf{x},{\mathbf{x}}_j\right)} $$

(A1)

where m denotes the number of sampling points, K(x, x _j ) is the j-th basis function, and w _j denotes the weight of the j-th basis function. The following Gaussian kernel is generally used as the basis function:

$$ K\left(\mathbf{x},{\mathbf{x}}_j\right)= \exp \left(-\frac{{\left(\mathbf{x}-{\mathbf{x}}_j\right)}^T\left(\mathbf{x}-{\mathbf{x}}_j\right)}{r_j^2}\right) $$

(A2)

In (A2), x _j represents the j-th sampling point, and r _j is the width of the j-th basis function. The response y _j is calculated at the sampling point x _j . The learning of RBF network is usually accomplished by solving

$$ E={\displaystyle {\sum}_{j=1}^m{\left({y}_j-\widehat{y}\left({\mathbf{x}}_j\right)\right)}^2}+{\displaystyle {\sum}_{j=1}^m{\lambda}_j{w}_j^2}\to \min $$

(A3)

where the second term is introduced for the purpose of the regularization. It is recommended that λ _j in (A3) is sufficient small value (e.g., λ _j =1.0 × 10⁻²). Thus, the learning of RBF network is equivalent to finding the weight vector w. The necessary condition of (A3) result in the following equation.

$$ \mathbf{w}={\left({\mathbf{H}}^T\mathbf{H}+\boldsymbol{\Lambda} \right)}^{-1}{\mathbf{H}}^T\mathbf{y} $$

(A4)

where H, Λ and y are given as follows:

$$ \mathbf{H}=\left[\begin{array}{cccc}\hfill K\left({\mathbf{x}}_1,{\mathbf{x}}_1\right)\hfill & \hfill K\left({\mathbf{x}}_1,{\mathbf{x}}_2\right)\hfill & \hfill \cdots \hfill & \hfill K\left({\mathbf{x}}_1,{\mathbf{x}}_m\right)\hfill \\ {}\hfill K\left({\mathbf{x}}_2,{\mathbf{x}}_1\right)\hfill & \hfill K\left({\mathbf{x}}_2,{\mathbf{x}}_2\right)\hfill & \hfill \cdots \hfill & \hfill K\left({\mathbf{x}}_2,{\mathbf{x}}_m\right)\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill K\left({\mathbf{x}}_m,{\mathbf{x}}_1\right)\hfill & \hfill K\left({\mathbf{x}}_m,{\mathbf{x}}_2\right)\hfill & \hfill \cdots \hfill & \hfill K\left({\mathbf{x}}_m,{\mathbf{x}}_m\right)\hfill \end{array}\right],\;\boldsymbol{\Lambda} =\left[\begin{array}{cccc}\hfill {\lambda}_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {\lambda}_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda}_m\hfill \end{array}\right] $$

(A5)

$$ \mathbf{y}={\left({y}_1,{y}_2,\cdots, {y}_m\right)}^T $$

(A6)

It is clear from (A4) that the learning of RBF network is equivalent to the matrix inversion (H ^T H + Λ)⁻¹. The new sampling points are added through the SAO process. Using the RBF network, it is easy to calculate the weight vector w, because the additional learning is reduced to the incremental calculation of the matrix inversion.

The width in the Gaussian kernel plays an important role for good approximation. The first author of this paper has proposed the following simple estimate of the width (Kitayama et al. 2011):

$$ \begin{array}{cc}\hfill {r}_j=\frac{d_{j, \max }}{\sqrt{n}\sqrt[n]{m-1}}\hfill & \hfill j=1,2,\cdots, m\hfill \end{array} $$

(A7)

where r _j denotes the width of the j-th Gaussian kernel, and d _j,max denotes the maximum distance between the j-th sampling point and the other sampling points. (A7) is applied to each Gaussian kernel individually, and can deal with the non-uniform distribution of sampling points.

1.2 A.2 Density function using RBF network

In the SAO, it is important to find out the unexplored region for global approximation. The Kriging can achieve this objective with the expected improvement (EI) function. In order to find out the unexplored region with the RBF network, we have developed a function called the density function (Kitayama et al. 2011). The basic idea is very simple. The local maxima are generated at the sampling points. To achieve this objective, every output y of the RBF network is replaced with +1. The procedure to construct the density function is summarized as follows:

• (D-STEP1) The following vector y ^D is prepared at the sampling points.

  $$ {\mathbf{y}}^D={\left(1,1,\cdots, 1\right)}_{m\times 1}^T $$

  (A8)

• (D-STEP2) The weight vector w ^D of the density function D(x) is calculated as follows:

  $$ {\mathbf{w}}^D={\left({\mathbf{H}}^T\mathbf{H}+\boldsymbol{\Lambda} \right)}^{-1}{\mathbf{H}}^T{\mathbf{y}}^D $$

  (A9)

• (D-STEP3) The density function D(x) is minimized.

  $$ D\left(\mathbf{x}\right)={\displaystyle {\sum}_{j=1}^m{w}_j^DK\left(\mathbf{x},{\mathbf{x}}_j\right)}\to \min $$

  (A10)

• (D-STEP4) The point minimizing D(x) is taken as the new sampling point.

Figure 15 shows an illustrative example in one dimension. The black dots denote the sampling points. It is found from Fig. 5 that local minima are generated around the unexplored region. The RBF network is basically the interpolation between sampling points: therefore, points A and B in Fig. 15 are the lower and upper bounds of the design variables of the density function.

Fig. 15

Illustrative example of density function