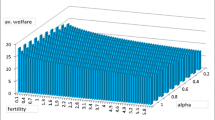
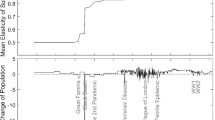
Abstract
Parenthood postponement is a key demographic trend of the last three decades. In order to rationalize that stylized fact, we extend the canonical model by Barro and Becker (Econometrica 57:481–501, 1989) to include two—instead of one—reproduction periods. We examine how the cost structure of early and late children in terms of time and goods affects the optimal fertility timing. Then, we identify conditions that guarantee the existence and uniqueness of a stationary equilibrium with a stationary cohort size. Finally, we examine how the model can rationalize the observed postponement of births, and we highlight two plausible causes: (1) a general rise in the cost of children in terms of goods and (2) a decline in the degree of family altruism.







Similar content being viewed by others
Notes
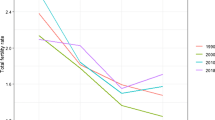
The total fertility rate measures the average number of children a woman has on her life cycle, while assuming that she survives during the entire reproduction period and faces age-specific fertility rates during the whole reproduction period. The data are from Lee (2003).
Data source: United Nations Population Division/DESA 2008.
Data source: United Nations Population Division/DESA 2008.
That stationary population assumption, which allows us to focus only on the birth timing problem, is actually quite plausible given the finiteness of the Earth. One could hardly imagine an ever growing population living on a fixed space.
D’Albis et al. (2010) focus on optimal life-cycle fertility in a continuous time OLG model, under the assumption of a decreasing relationship between the total number of children and the timing of births. Pestieau and Ponthiere (2014) focus on the optimal fertility timing in an OLG model à la Samuelson (1975) and examine whether the Serendipity Theorem still holds in a broader demographic environment with several reproduction periods instead of one.
We assume, without loss of generality, that N 0 = 1, and that m 0 = 0.
Note that this altruistic weighting function presupposes a strictly positive number of descendants, that is, either n t > 0 or m t > 0. This is a weak requirement, since a model of endogenous fertility does not make sense if the population becomes extinct.
Indeed, in the Barro-Becker model, we have N t+1 = n t N t , so that \(a(\cdot )=\alpha /\left [ {N}_{t}^{1-\varepsilon }{n}_{t}^{\varepsilon }{N}_{t}^{\varepsilon }\right ] =\alpha /{N}_{t}{n}_{t}^{\varepsilon }\), implying \( a\left (\cdot \right ) {N}_{t+1}=\alpha g_{t+1}^{1-\varepsilon }=\alpha {n}_{t}^{1-\varepsilon }\). Here, that formula is generalized, to obtain \( a\left (\cdot \right ) {N}_{t+1}=\alpha g_{t+1}^{1-\varepsilon }\) even when g t+1≠n t as a consequence of m t > 0.
For a study of stability in a four-period OLG model with two reproduction periods, see Pestieau and Ponthiere (2014). Those authors showed that, under exogenous fertility profile, there exists no stable stationary equilibrium when all births are located in the second reproduction period (i.e., n = 0). Note, however, that this section focuses, as the previous one, on an interior optimum, at which n > 0.
Note that this effect is larger when B (the time cost of late children) is larger.
On the contrary, a rise in the time cost of late children B tends to raise the LHS of Eq. 38, while letting the RHS unchanged, and tends thus to reduce κ ∗. We thus obtain, here again, that the costs of early and late children have opposite effects on κ ∗.
For instance, a larger rise in the cost of children could still do the job in the presence of some TFP growth.
References
Barro R, Becker G (1989) Fertility choice in a model of economic growth. Econometrica 57(2):481–501
Cigno A, Ermisch J (1989) A microeconomic analysis of the timing of births. Eur Econ Rev 33:737–760
D’Albis H, Augeraud-Véron E, Schubert K (2010) Demographic-economic equilibria when the age at motherhood is endogenous. J Math Econ 46(6):1211–1221
de la Croix D, Michel P (2001) A theory of economic growth. Dynamics and policy with overlapping generations. Cambridge University Press, Cambridge
Doepke M (2005) Child mortality and fertility decline: does the Barro-Becker model fit the facts? J Popul Econ 18(2):337–366
Ehrlich I, Lui F (1991) Intergenerational trade, longevity and economic growth. J Polit Econ 99:1029–1060
Ermisch J (1988) The econometric analysis of birth rate dynamics in Britain. J Hum Res 23(4):563–576
Ermisch J, Ogawa N. (1994) Age at motherhood in Japan. J Popul Econ 7:393–420
Fernald J (2011) Utilization-adjusted quarterly TFP series for the US business sector. Federal Reserve Bank of San Francisco
Gustafsson S (2001) Optimal age at motherhood. Theoretical and empirical considerations on postponement of maternity in Europe. J Popul Econ 14(2):225–247
Happel S, Hill J, Low S (1984) An economic analysis of the timing of childbirth. Popul Stud 38:299–311
Heckman J, Walker J (1990) The relationship between wages and income and the timing and spacing of births: evidence from Swedish longitudinal data. Econometrica 58:1411–1441
Human Fertility Database (2012) Max Planck Institute for Demographic Research (Germany) and Vienna Institute of Demography (Austria). www.humanfertility.org (Accessed 13 Jan 2012)
Joshi H (2002) Production, reproduction, and education: women, children and work in a British perspective. Popul Dev Rev 28:445–474
Lee R (2003) The demographic transition. Three centuries of fundamental change. J Econ Persp 17(4):167–190
Pestieau P, Ponthiere G (2014) Optimal fertility along the life cycle. Econ Theory 55:185–224
Putnam R (2000) Bowling alone. New-York, Simon & Schuster
Samuelson P (1975) The optimum growth rate for population. Int Econ Rev 16: 531–538
Schultz T P (1985) Changing world prices, women’s wages and the fertility transition: Sweden 1860-1910. J Polit Econ 93:1126–1154
United Nations Population Division/DESA - Fertility and Family Planning Section: World Fertility Data (2008) http://www.un.org/esa/population/publications/WFD%202008/Main.html
Acknowledgments
The authors are most grateful to David de la Croix, Andreas Irmen, Holger Strulik, Bertrand Wigniolle, and two anonymous referees for their helpful comments on this manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: Alessandro Cigno
Appendix
Appendix
Proof of Lemma 1
In order to compare the derivatives \(\frac {\partial {N}_{t+1+j}}{\partial {n}_{t} }\) and \(\frac {\partial {N}_{t+1+j}}{\partial m_{t}}\), remember that \( {N}_{t+1}={N}_{t}g_{t+1}={N}_{t}\left ({n}_{t}+\frac {m_{t}{N}_{t-1}}{{N}_{t}}\right ) \). Hence, we have
or, in general terms,
Thus, whether the marginal impact of raising early fertility is larger than the marginal impact of raising late fertility depends on whether the cohort size is growing over time or not. If N t > N t − 1 or g t > 1, we necessarily have, everything else being unchanged, that \(\frac {\partial {N}_{t+1+j}}{\partial {n}_{t}}>\frac {\partial {N}_{t+1+j}}{\partial m_{t}}\).
Proof of Proposition 1
From the condition
the existence of a stationary equilibrium with a stationary cohort size requires κ to satisfy the condition:
Let us denote the LHS by φ(κ)≡A κ η(1 − η)B + E − α η A κ η − 1 e and the RHS by ψ(κ)≡α η(1 − η)b A 2 κ 2η − 1.
Three cases can arise, depending on \(\eta \gtreqqless 1/2\).
When η < 1/2, we have φ(0) = −∞ and φ(+∞) = +∞. We also have φ′(κ) = A η κ η − 1(1 − η)B − (η − 1)α η A κ η − 2 e > 0.
Regarding ψ(κ), we have ψ(0) = + ∞ and ψ(+∞) = 0. We also have ψ′(κ) = α η(1 − η)(2η − 1)b A 2 κ 2η − 2 < 0.
Given that φ(0) < ψ(0) and that φ(+∞) > ψ(+∞), it follows that there exists, by continuity, a level of κ such that φ(κ) = ψ(κ). Moreover, given the strict monotonicity of φ(κ) and ψ(κ), the intersection of φ(κ) and ψ(κ) is unique.
When η = 1/2, we have φ(0) = −∞ and φ(+∞) = +∞. We also have φ′(κ) = A η κ η − 1(1 − η)B − (η − 1)α η A κ η − 2 e > 0.
Regarding ψ(κ), we have ψ(0) = α η(1 − η)b A 2 < 0 and ψ(+∞) = α η(1 − η)b A 2 < 0. We also have ψ′(κ) = 0.
Given that φ(0) < ψ(0) and that φ(+∞) > ψ(+∞), it follows that there exists, by continuity, a level of κ such that φ(κ) = ψ(κ). Moreover, given the strict monotonicity of φ(κ), the intersection of φ(κ) and ψ(κ) is unique.
When η > 1/2, we have φ(0) = −∞ and φ(+∞) = +∞. We also have φ′(κ) = A η κ η − 1(1 − η)B − (η − 1)α η A κ η − 2 e > 0 and φ″(κ) = A η(η − 1)κ η − 2(1 − η)B − (η − 1)(η − 2)α η A κ η − 3 e < 0.
Regarding ψ(κ), we have ψ(0) = 0 and ψ(+∞) = +∞. We also have ψ′(κ) = α η(1 − η)(2η − 1)b A 2 κ 2η − 2 < 0 and ψ″(κ) = α η(1 − η)(2η − 1)(2η − 2)b A 2 κ 2η − 3 < 0.
Note that, when κ → 0, we have φ′(κ) = A η κ η − 1(1 − η)B − (η − 1)α η A κ η − 2 e = +∞ > ψ′(κ) = α η(1 − η)(2η − 1)b A 2 κ 2η − 2 = 0.
Note also that, when κ → +∞, we have φ′(κ) = A η κ η − 1(1 − η)B − (η − 1)α η A κ η − 2 e = 0 < ψ′(κ) = α η(1 − η)(2η − 1)b A 2 κ 2η − 2 < 0.
We thus have φ(0) < ψ(0), with φ′(κ) > ψ′(κ) when κ → 0 and φ′(κ) < ψ′(κ) when κ → +∞.
Given that φ(0) < ψ(0), as well as φ′(κ) > 0, φ″(κ) < 0, ψ′(κ) > 0 and ψ″(κ) < 0, three distinct cases can arise: either no intersection of φ(κ) and ψ(κ), or a single intersection of φ(κ) and ψ(κ), or a double intersection of φ(κ) and ψ(κ). In the first case, we have that, for all κ > 0, it is the case that φ(κ) < ψ(κ). The two other cases can be described as follows. For low levels of κ, we have φ(κ) < ψ(κ), but the higher slope of φ(κ) for low levels of κ makes the φ(κ) curve intersect the ψ(κ) from below. That intersection occurs for low levels of κ, for which φ′(κ) > ψ′(κ). Let us denote that intersection by κ −. At that intersection, φ(κ) crosses ψ(κ) from below, since we initially have φ(0) < ψ(0). Then, two cases can arise. First, it is possible that the two curves φ(κ) and ψ(κ) do not intersect any more, the curve ψ(κ) remaining is always below φ(κ). Alternatively, φ(κ) and ψ(κ) may intersect a second time. Those two cases can arise, since we know that, although φ′(κ) > ψ′(κ) at κ = κ −, we have φ′(κ) = 0 < ψ′(κ) when κ → +∞. Hence, it can be the case that there exists a second intersection, which can be denoted by κ +.
Let us now concentrate on condition (36). The existence of a stationary equilibrium with a stationary cohort size requires condition (36) to be satisfied. Since the stationarity of the cohort size requires κ = κ ∗, it follows that there exists a stationary equilibrium with stationary population size if and only if there exists some interior level of early fertility n ∗ ∈ ]0, 1[ such that the following condition holds:
In general terms, that condition can be rewritten as
Further simplifications yield
Denote \(A^{\frac {2-\sigma }{1-\sigma }}(1-\eta )\left (\eta \beta \right )^{ \frac {1}{1-\sigma }}\)by Γ and \(\left [ \eta A\beta \right ]^{\frac {1}{ 1-\sigma }}\) by Θ. That condition can be rewritten as follows. There exists some interior level of early fertility n ∈ ]0, 1[ such that
Denote the LHS by
and the RHS by
We have \(\chi \left (0\right ) =A\eta \kappa ^{\ast \eta }(2-B)+\Theta \kappa ^{\ast \frac {\eta -\sigma }{1-\sigma }}(2-B)+A(1-\eta )\kappa ^{\ast \eta }(1-B)-E\gtrless 0\) and \(\chi \left (1\right ) =A\eta \kappa ^{\ast \eta }(2-b)+\Theta \kappa ^{\ast \frac {\eta -\sigma }{1-\sigma }}(2-b)+e\Theta \kappa ^{\ast \frac {\eta -1}{1-\sigma }}+A(1-\eta )\kappa ^{\ast \eta }>0\).
Note also that, under B ≥ b, we have
We have also \(\phi \left (0\right ) =\kappa ^{\ast \frac {2\eta -\eta \sigma -1 }{1-\sigma }}\Gamma >0\) and \(\phi (1)=\kappa ^{\ast \frac {2\eta -\eta \sigma -1}{1-\sigma }}(1-b)\Gamma >0\), as well as
Hence, two sufficient conditions for the existence and uniqueness of n ∗ are χ(0) < ϕ(0) and χ(1)>ϕ(1). In formulas
and
When those two conditions are satisfied, we have that there exists a stationary equilibrium with a stationary cohort size.
Proof of Corollary 1
Let us start from expression (36):
Isolating n yields
Given that κ = κ ∗ at the equilibrium, we obtain n ∗ by replacing κ by κ ∗ in that expression. Similar substitutions can be made for the special cases of no time cost and no resource cost of children.
Proof of Lemma 2
Regarding \(\frac {\partial \frac {{N}_{t+s-1}}{{N}_{t+s}}}{\partial {n}_{t}}\), we have, for s = 0:
For s = 1, s = 2, and s = 3:
Hence, for s > 1, we have
Regarding \(\frac {\partial \frac {{N}_{t+1+s}}{{N}_{t+s}}}{\partial {n}_{t}}\), we have, for s = 0:
For s = 1, s = 2, and s = 3:
Hence, for s > 0, we have
Regarding \(\frac {\partial \frac {{N}_{t+s-1}}{{N}_{t+s}}}{\partial m_{t}}\), we have, for s = 0:
For s = 1, s = 2, and s = 3:
Hence, for s > 1, we have
Finally, regarding \(\frac {\partial \frac {{N}_{t+1+s}}{{N}_{t+s}}}{\partial m_{t}} \), we have, for s = 0:
For s = 1, s = 2, and s = 3:
Hence, for s > 0, we have
Proof of Proposition 2
Take the expression for κ t+1 at g = 1, x t − 1 = x t = x t+1 and κ = κ ∗. Isolating n yields
When B − b ≥ 0, that expression is unambiguously increasing in x:
Rights and permissions
About this article
Cite this article
Pestieau, P., Ponthiere, G. Optimal life-cycle fertility in a Barro-Becker economy. J Popul Econ 28, 45–87 (2015). https://doi.org/10.1007/s00148-014-0511-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00148-014-0511-2