Reconciling Non-malleability with Homomorphic Encryption

Abstract

Homomorphic encryption schemes are useful in designing conceptually simple protocols that operate on encrypted inputs. On the other hand, non-malleable encryption schemes are vital for designing protocols with robust security against malicious parties, in a composable setting. In this paper, we address the problem of constructing public-key encryption schemes that meaningfully combine these two opposing demands. The intuitive tradeoff we desire in an encryption scheme is that anyone should be able to change encryptions of unknown messages $m_1, \ldots , m_k$ into a (fresh) encryption of $T(m_1, \ldots , m_k)$ for a specific set of allowed functions T, but the scheme should be otherwise “non-malleable.” That is, no adversary should be able to construct a ciphertext whose value is related to that of other ciphertexts in any other way. For the case where the allowed functions T are all unary, we formulate precise definitions that capture our intuitive requirements and show relationships among these new definitions and other more standard ones (IND-CCA, gCCA, and RCCA). We further justify these new definitions by showing their equivalence to a natural formulation of security in the framework of Universally Composable security. Next, we describe a new family of encryption schemes that satisfy our definitions for a wide variety of allowed transformations T and prove their security under the Decisional Diffie-Hellman (DDH) assumption in two groups with related sizes. Finally, we demonstrate how encryption schemes that satisfy our definitions can be used to implement conceptually simple protocols for non-trivial computation on encrypted data, which are secure against malicious adversaries in the UC framework without resorting to general-purpose multi-party computation or zero-knowledge proofs. For the case where the allowed functions T are binary, we show that a natural generalization of our definitions is unattainable if some T is a group operation. On the positive side, we show that if one of our security requirements is relaxed in a natural way, we can in fact obtain a scheme that is homomorphic with respect to (binary) group operations, and non-malleable otherwise.

1 Introduction

A recurring theme in cryptography is the tension between security and functionality features. We explore this theme in the context of the fundamental cryptographic task of encryption. On the one hand, a strong security guarantee for encryption must rule out “malleability”—the ability to manipulate encrypted data (without being able to decrypt it); on the other hand, computing on encrypted data—in particular, homomorphic encryption¹—mandates such an ability.

In the rich literature on encryption spanning the last three decades, the notion of non-malleability and that of homomorphic encryption have both been well developed, but there has been little success in marrying the two. For instance, IND-CCA2 security (as well as the few simple relaxations thereof) rules out the possibility of manipulating encrypted data in any way, while IND-CPA security (used for all homomorphic encryption schemes to date) permits every possible kind of manipulation. In many applications of homomorphic encryptions (e.g., [25]), CPA security is indeed sufficient, but for others (e.g., [27]) it is not. In practical terms, this means that protocols that use homomorphic encryption usually have to employ the heavy machinery of zero-knowledge proofs or verifiable secret sharing to achieve security against malicious adversaries.

In this work, we evolve definitions and tools to bring the opposing notions of non-malleability and homomorphic encryption together. To reconcile the tension between these notions would be to ensure that encrypted data can be manipulated, but only in some pre-specified manner. While adding such a sharp security guarantee to homomorphic encryption, to be useful, one must still retain all the traditional secrecy properties of homomorphic encryptions, including unlinkability: homomorphic encryption schemes hide not only the underlying plaintext, but also the “history” of a ciphertext—i.e., whether it was derived by encrypting a known plaintext, or by applying a homomorphic operation applied to some other ciphertext(s). Such schemes have been extensively studied for a long time and have a wide variety of applications (cf. [6, 22, 25, 26, 34, 40–42, 61, 62]). We develop the appropriate definitions of non-malleability and unlinkability for homomorphic encryptions as well as a family of efficient encryption schemes that fit our definitions, under standard algebraic intractability assumptions. We demonstrate the use of such a scheme with a simple and efficient “opinion poll” protocol, secure against active adversaries, which would not be possible using existing notions of homomorphic encryptions (unless used in conjunction with tools like zero-knowledge proofs). We also study the limits of non-malleability that can be achieved by homomorphic encryption schemes.

Challenges The first challenge is formally defining (in a convincing way) the intuitive requirement that a scheme “allow particular features but forbid all others.” The definitions of non-malleability available in the literature completely break down if one tries to naturally generalize them to a setting where the messages can be non-trivially modified. In particular, the definitions of CCA1, CCA2, gCCA [2, 63], and Replayable-CCA (RCCA) [18] security all use an experiment with a common structure wherein the adversary is given access to a decryption oracle for ciphertexts which are not “derived” from a challenge ciphertext; the test for derivation can be carried out publicly or (in the case of RCCA) using the private key of the encryption. But for unlinkable homomorphic encryption, such a test is impossible as the encryption scheme itself provides ways to mask derivation. A key insight we obtain is to go beyond the traditional structure of these experiments and require that an encryption scheme includes two procedures (not used in normal operation) that can be used to construct “rigged” challenge ciphertexts and to detect/trace derivation from such ciphertexts. This definition goes well beyond the usual structure of the previous definitions, but collapses to them when the homomorphic operations are removed. We arrive at this seemingly unnatural definition by means of considering the secure realization of a natural functionality in the Universal Composition framework.

Our second challenge is in meeting such a definition—i.e., an encryption scheme that permits a particular set of (unlinkable) homomorphic operations, but is non-malleable with respect to all other operations. We do this based on standard assumptions (DDH) and reasonably efficiently (with a small constant number of group elements per ciphertext and exponentiations per encryption). We stress that even if the set of allowed operations is very simple, supporting it can be very involved. Indeed, the problem of constructing a rerandomizable RCCA encryption scheme considered in a series of works [18, 36] and resolved in [54] corresponds to the simplest special case of our definitions, where only the identity operation is permitted.

Our Results We give several new security definitions to precisely capture the desired requirements in the case of unary homomorphic operations (those which transform a single encryption of m to an encryption of T(m), for a particular set of functions T). We provide two new indistinguishability-based security definitions. The first definition, called Homomorphic-CCA (HCCA) security, formalizes the intuition of “non-malleability except for certain prescribed operations,” and the second definition, called unlinkability, formalizes the intuition that ciphertexts do not leak their “history.” To justify our non-malleability definition, we show that it subsumes the standard IND-CCA, gCCA [2, 63], and Replayable-CCA (RCCA) [18] security definitions (Theorem 4.1). We further show that our two new security requirements imply a natural definition of security in the Universal Composition framework (Theorem 4.4).

Our main result is to describe a family of encryption schemes which achieve our definitions for a wide range of allowed (unary) homomorphism operations. The construction, which is a careful generalization of the rerandomizable RCCA-secure scheme of [54], is secure under the DDH assumption in two cyclic groups of related size; its supported homomorphic features are certain operations related to the group operation in one of the underlying groups (in the simplest case, the group operation itself).

To demonstrate the practical utility of our definitions, we show a simple, intuitive protocol for an anonymous opinion polling functionality, which uses unlinkable, HCCA-secure encryption as a key component. Even though the component encryption scheme supports only unary operations, we are able to perform non-trivial computations on a set of independently encrypted inputs, crucially using the scheme’s homomorphic features. Furthermore, because of the strong non-malleability guarantee, this simple protocol achieves UC security against malicious adversaries without resorting to the overhead of zero-knowledge proofs or general-purpose multi-party computation. We note that the homomorphic operations required for this protocol are also achieved by our construction.

Finally, we consider extending our definitions to the case of binary homomorphic operations (those which combine pairs of ciphertexts). We show that the natural generalization of our UC security definition to this scenario is unachievable for a large class of useful homomorphic operations (Theorem 8.1). However, we also give a positive result when one of our requirements is slightly relaxed. In particular, if we allow a ciphertext to leak only the number of homomorphic operations that were applied to obtain the ciphertext, then it is possible to construct a homomorphic scheme that supports the binary group operation (that is, it is possible to obtain ${{\textsf {Enc}}} (\alpha * \beta )$ from ${{\textsf {Enc}}} (\alpha )$ and ${{\textsf {Enc}}} (\beta )$, but no other operations are possible).

Related Work The ability to modify or compute with encrypted data has found tremendous use in applications, in various forms—homomorphic encryptions (e.g.,[29, 31, 52]), rerandomizable encryption [34, 36], proxy reencryption [7, 17], searchable encryption [21, 64], predicate encryption [12], etc. Security notions and schemes for regular encryption developed and matured over many years [5, 14, 23, 28, 33, 51, 58, 60], while security definitions for homomorphic encryption have lagged behind. In particular, to date, homomorphic encryptions are almost exclusively held to the weak standard of IND-CPA security.

However, it was recognized that in many security applications heuristic assumptions of non-malleability were implicit, and a systematic approach to understanding and limiting the extent of malleability in homomorphic encryption is important. For instance, Klonowski et al. [45] proposed using a rerandomizable RSA signature for strengthening the security of a rerandomizable encryption scheme of Golle et al. [34] (proposed for use in mixnets [20], with applications to RFID tag anonymization, and originally with only CPA security); but Danezis [27] showed that this still leaves vulnerabilities against practical chosen-ciphertext attacks. In another approach, Wikström [66], considered giving a few non-malleability guarantees (but without giving a comprehensive definition of non-malleability) for ElGamal encryption. Starting from the other extreme, [2, 63] proposed benignly malleable (also called gCCA) security as a relaxation of CCA security, which was further relaxed in the definition of Replayable-CCA (RCCA) security [18]. RCCA security allows a scheme to have homomorphic operations which preserve the underlying plaintext, but enforces non-malleability “everywhere else.” However, as mentioned above, these relaxations do not readily generalize to the setting of homomorphic encryption (see Sect. 3.1). Using the UC framework to define security of encryption schemes was already considered in [14, 16, 18, 53].

Our encryption scheme is based on the Cramer–Shoup scheme [23, 24], which in turn is modeled after ElGamal encryption [29]. The security of these schemes and our own is based on the DDH assumption (see, e.g., [8]).

Since the preliminary publication of this work (in particular, in [57]), the idea of cryptography that is “non-malleable except for a specified set of homomorphic operations” has been explored for other primitives. Chase et al. [19] define such a security notion for malleable non-interactive proofs and (among other results) use such proofs in a general framework for achieving our notion of unlinkable HCCA security for encryption.² Ahn et al. [1] define such a security notion for malleable signatures and give a variety of constructions. Finally, Boneh, Segev, and Waters [11] consider a related notion of “non-malleability except for certain homomorphic operations” for encryption. They consider a weaker form of unlinkability than the one we consider here (in fact, ciphertexts in their scheme grow with the number of homomorphic operations applied), but are able to achieve a general feasibility result starting from fully homomorphic encryption.

Prior Publication The definitions in Sects. 3–4 and main construction in Sect. 5 previously appeared as [56]. The construction significantly generalizes the rerandomizable, RCCA-secure scheme that appeared in [54]. The material in Sects. 7–8 previously appeared as [57]. All of the results appeared in the second author’s Ph.D. dissertation [59].

2 Preliminaries

We call a function $\nu$ negligible if, for all $c>0$, we have $\nu (\lambda ) < 1/\lambda ^c$ for all but finitely many values of $\lambda \in {\mathbb {N}}$. When $\nu$ and $\mu$ are functions (typically in an implicit security parameter $\lambda$), we write $\nu \approx \mu$ to mean that $| \nu - \mu |$ is a negligible function. A probability $\nu$ is overwhelming if $\nu \approx 1$.

When X is a finite set, we write $x \leftarrow X$ to indicate that x is chosen uniformly at random from X. When A is a probabilistic algorithm, we write $x \leftarrow A (z)$ to indicate that x is the outcome of evaluating A (with uniformly chosen random coins) on input z. We write PPT to mean probabilistic polynomial time.

2.1 Homomorphic Encryption Syntax

An encryption scheme consists of three polynomial-time procedures: ${{\textsf {KeyGen}}}$, ${{\textsf {Enc}}}$, and ${{\textsf {Dec}}}$. ${{\textsf {KeyGen}}}$ and ${{\textsf {Enc}}}$ are probabilistic, while ${{\textsf {Dec}}}$ is deterministic. We denote by ${\mathcal {M}}$ the message space of an encryption scheme (in our constructions, the message space depends on the public key, so ${\mathcal {M}} = {\mathcal {M}} _{pk}$; for simplicity we keep this relationship implicit), and let $\bot$ denote a special error indicator symbol not in ${\mathcal {M}}$.

Fig. 1

Illustration of the syntax and correctness of a (unary) homomorphic encryption scheme

The correctness condition for an encryption scheme is that: for all $\lambda \in {\mathbb {N}}$, all $({pk}, {sk})$ in the support of ${{\textsf {KeyGen}}} (1^\lambda )$, and every plaintext ${\textsf {msg}} \in {\mathcal {M}}$, we have ${{\textsf {Dec}}} _{sk} ({{\textsf {Enc}}} _{pk} ({\textsf {msg}})) = {\textsf {msg}}$, with probability 1 over the randomness of ${{\textsf {Enc}}}$.

A homomorphic scheme includes an additional probabilistic, polynomial-time “ciphertext transformation” procedure ${{\textsf {CTrans}}}$ and a set ${\mathcal {T}}$ of “allowable plaintext transformations.” More specifically, ${\mathcal {T}}$ is a set of k-ary, deterministic, polynomial-time functions from $({\mathcal {M}} \cup \{\bot \})^k$ to ${\mathcal {M}} \cup \{\bot \}$. (As above, since ${\mathcal {M}}$ depends on the public key, ${\mathcal {T}}$ and k too depend on the public key.)

The correctness condition for a homomorphic encryption scheme is that: for all $\lambda \in {\mathbb {N}}$, all $({pk}, {sk})$ in the support of ${{\textsf {KeyGen}}} (1^\lambda )$, all (purported) ciphertexts $\zeta _1, \ldots , \zeta _k$, and every $T \in {\mathcal {T}}$, we have

$$\begin{aligned} {{\textsf {Dec}}} _{sk} ({{\textsf {CTrans}}} _{pk} (\zeta _1, \ldots , \zeta _k, T))=T\big ({{\textsf {Dec}}} _{sk} (\zeta _1), \ldots , {{\textsf {Dec}}} _{sk} (\zeta _k)\big ), \end{aligned}$$

with probability 1 over the randomness of ${{\textsf {CTrans}}}$.³ If the correctness condition holds, we say that the encryption scheme is ${\mathcal {T}}$ homomorphic, or homomorphic with respect to ${\mathcal {T}}$ (Fig. 1).

In our main construction, we consider the case for $k=1$ (i.e., unary-homomorphic encryption); later we also consider the $k=2$ case.

2.2 Decisional Diffie–Hellman (DDH) Assumption (in Related Groups)

Let ${\textsf {DHGen}}$ be an algorithm that on input $1^\lambda$ outputs a triple $({\mathbb {G}}, g, p)$, where ${\mathbb {G}}$ is (the description of) a cyclic group of prime order p, $g$ is a generator of ${\mathbb {G}}$, and $\lceil \log (p+1) \rceil = \lambda$. We require that ${\mathbb {G}}$ admit operations (multiplication and membership testing) that are polynomial time in $\lambda$.

Definition 2.1

(DDH assumption). The Decisional Diffie–Hellman (DDH) assumption for ${\textsf {DHGen}}$ is that, for all non-uniform PPT algorithms ${{\mathcal {A}}}$, we have:

$$\begin{aligned}&\Pr [ ({\mathbb {G}},g,p) \leftarrow {\textsf {DHGen}} (1^\lambda ); a,b \leftarrow {\mathbb {Z}}_p:~ {{\mathcal {A}}} (({\mathbb {G}},g,p),g ^a, g ^b, g ^{ab}) = 1 ] \\&\quad \approx \Pr [ ({\mathbb {G}},g,p) \leftarrow {\textsf {DHGen}} (1^\lambda ) ; a,b,c \leftarrow {\mathbb {Z}}_p:~{{\mathcal {A}}} (({\mathbb {G}},g,p),g ^a, g ^b, g ^c) = 1 ]. \end{aligned}$$

Our main construction requires two cyclic groups with a specific relationship: ${\mathbb {G}}$ of prime order p, and $\widehat{{\mathbb {G}}}$ of prime order q, where $\widehat{{\mathbb {G}}}$ is a subgroup of ${\mathbb {Z}}^*_p$. We require the DDH assumption to hold in both groups (with respect to the same security parameter).

More formally, let ${\textsf {RG-DHGen}}$ be an algorithm that on input $1^\lambda$ outputs a tuple $({\mathbb {G}}, g, p, \widehat{{\mathbb {G}}},\widehat{g}, q)$, where: ${\mathbb {G}}$ is (the description of) a cyclic group of prime order p; $g$ is a generator of ${\mathbb {G}}$; $\lceil \log (p+1) \rceil = \lambda$; $\widehat{{\mathbb {G}}}$ is (the description of) a cyclic group of prime order q; $\widehat{g}$ is a generator of $\widehat{{\mathbb {G}}}$; and $\widehat{{\mathbb {G}}}$ is a subgroup of ${\mathbb {Z}}^*_p$.

Definition 2.2

(RG-DDH assumption). Let ${\textsf {RG-DHGen}}$ be as above. The Decisional Diffie–Hellman assumption in Related Groups (RG-DDH) for ${\textsf {RG-DHGen}}$ is that, for all non-uniform PPT algorithms ${{\mathcal {A}}}$, we have:

$$\begin{aligned}&\Pr \left[ \begin{array}{r} ({\mathbb {G}},g,p,\widehat{{\mathbb {G}}},\widehat{g},q) \leftarrow {\textsf {RG-DHGen}} (1^\lambda ); \\ a,b \leftarrow {\mathbb {Z}}_p;~~ x,y\leftarrow {\mathbb {Z}}_q \end{array} : ~ {{\mathcal {A}}} \left( ({\mathbb {G}},g,p,\widehat{{\mathbb {G}}},\widehat{g},q),g ^a, g ^b, g ^{ab}, \widehat{g} ^x, \widehat{g} ^y, \widehat{g} ^{xy}\right) = 1 \right] \\&\quad \approx \Pr \left[ \begin{array}{r} ({\mathbb {G}},g,p,\widehat{{\mathbb {G}}},\widehat{g},q) \leftarrow {\textsf {RG-DHGen}} (1^\lambda ); \\ a,b,c \leftarrow {\mathbb {Z}}_p;~~ x,y,z\leftarrow {\mathbb {Z}}_q \end{array} : ~ {{\mathcal {A}}} \left( ({\mathbb {G}},g,p,\widehat{{\mathbb {G}}},\widehat{g},q),g ^a, g ^b, g ^{c}, \widehat{g} ^x, \widehat{g} ^y, \widehat{g} ^{z}\right) = 1 \right] . \end{aligned}$$

Cunningham Chains As a concrete choice of parameters, recall that the DDH assumption is conjectured to hold in ${\mathbb {QR}}^*_p$ (the group of quadratic residues modulo p) when p and $\frac{p-1}{2}$ are prime (i.e., p is a safe prime). Thus given a sequence of primes $(q, 2q+1, 4q+3)$, the two groups $\widehat{{\mathbb {G}}} = {\mathbb {QR}}^*_{2q+1}$ and ${\mathbb {G}} = {\mathbb {QR}}^*_{4q+3}$ satisfy the needs of our construction. A sequence of primes of this form is called a Cunningham chain (of the first kind) of length 3 (see [3, 47, Sec. 2.5]). At the time of publication, the largest known Cunningham chain of this kind has q of over 34,800 bits in length.

2.3 Existing Security Definitions for Encryption

Several existing security definitions for encryption —CCA security, benignly malleable (gCCA) security [2, 63], and Replayable-CCA (RCCA) security [18]—follow a similar paradigm: The adversary has access to a decryption oracle and receives an encryption of one of two messages of her choice. Her task is to determine which of the two messages has been encrypted, and we say that security holds if no adversary can succeed with probability significantly better than chance.

Since the adversary can simply submit the challenge ciphertext to the decryption oracle, it is necessary to restrict this oracle in some way. The differences among these three security definitions are in how the decryption oracle is restricted. This restriction corresponds intuitively to identifying when a ciphertext has been (potentially) derived from the challenge ciphertext.

We can abstract all three notions of security into the following definitional framework. Let ${\mathcal {E}} = ({{\textsf {KeyGen}}},{{\textsf {Enc}}},{{\textsf {Dec}}})$ denote an encryption scheme. We define a stateful oracle ${\mathcal {O}}^{{\mathcal {E}},{\mathcal {G}}}_{\lambda ,b}$ parametrized by a bit b and a “guarding predicate” ${\mathcal {G}}$ (defined later, depending on the security notion) as follows.

Definition 2.3

(Encryption Security). Let ${\mathcal {E}} = ({{\textsf {KeyGen}}},{{\textsf {Enc}}},{{\textsf {Dec}}})$ be an encryption scheme. We say that ${\mathcal {E}}$ is ${\textsf {X}}$ -secure (for ${\textsf {X}} \in \{\text{ CCA }, {{{{\mathcal {R}}}}\text {-DR}}, \text{ RCCA }\}$) if, for all non-uniform PPT adversaries ${{\mathcal {A}}}$, we have

$$\begin{aligned} \Pr \left[ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{\mathcal {G}}}_{\lambda ,0}}(1^\lambda ) = 1\right] \approx \Pr \left[ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{\mathcal {G}}}_{\lambda ,1}}(1^\lambda ) = 1\right] , \end{aligned}$$

where ${\mathcal {G}}$ is specified differently for different X as follows:

$$\begin{aligned} \begin{array}{cl} {\textsf {X}} &{} {\mathcal {G}} ({sk},\zeta ,{\zeta ^*},{\textsf {msg}} _0,{\textsf {msg}} _1): \\ \hline CCA &{} \zeta \overset{\scriptstyle {\text {?}}}{=} {\zeta ^*} \\ {{{{\mathcal {R}}}}\text {-DR}} &{} {{\mathcal {R}}} (\zeta , {\zeta ^*}) \overset{\scriptstyle {\text {?}}}{=} 1 \\ RCCA &{} {{\textsf {Dec}}} _{sk} (\zeta ) \overset{\scriptstyle {\text {?}}}{\in } \{ {\textsf {msg}} _0, {\textsf {msg}} _1 \} \end{array} \end{aligned}$$

${\mathcal {E}}$ is said to be gCCA-secure if it is ${{{{\mathcal {R}}}}\text {-DR}}$-secure for some polynomial-time computable predicate ${{\mathcal {R}}}$ such that ${{\mathcal {R}}} (\zeta ,{\zeta ^*}) = 1 \Rightarrow {{\textsf {Dec}}} _{sk} (\zeta ) = {{\textsf {Dec}}} _{sk} ({\zeta ^*})$.

2.4 Universal Composability Framework

We assume some familiarity with the framework of universally composable (UC) security; for a full treatment, see [14]. We use the notation ${{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {A}}},\pi ,{\mathcal {F}} ]$ to denote the probability that the environment outputs 1, in an interaction involving environment ${{\mathcal {Z}}}$, a single instance of an ideal functionality ${\mathcal {F}}$, parties running protocol $\pi$, adversary ${{\mathcal {A}}}$. Technically the expression ${{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {A}}},\pi ,{\mathcal {F}} ]$ denotes a function of the global security parameter $\lambda$, which we will leave implicit. We consider security only against static adversaries, who corrupt parties only at the beginning of a protocol execution. ${\pi }_{\mathsf{dummy}}$ denotes the dummy protocol which simply relays messages between the environment and the functionality.

A protocol $\pi$ is a UC-secure protocol for functionality ${\mathcal {F}}$ in the ${\mathcal {G}}$-hybrid model if for all non-uniform PPT adversaries ${{\mathcal {A}}}$, there exists a non-uniform PPT simulator ${{\mathcal {S}}}$ such that for all non-uniform PPT environments ${{\mathcal {Z}}}$, we have that ${{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {A}}},\pi ,{\mathcal {G}} ] \approx {{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {S}}},{\pi }_{\mathsf{dummy}},{\mathcal {F}} ]$ (i.e., the interactions are indistinguishable in the security parameter $\lambda$). The former interaction (involving $\pi$ and ${\mathcal {G}}$) is called the real process, and the latter (involving ${\pi }_{\mathsf{dummy}}$ and ${\mathcal {F}}$) is called the ideal process.

We consider a communication network for the parties in which the adversary has control over the timing of message delivery. In particular, there is no guarantee of fairness in output delivery.

3 New Security Definitions for Homomorphic Encryption

In this section, we present our formal security definitions. The first two are indistinguishability-based definitions—i.e., in the traditional mold of security games—to capture non-malleability and unlinkability, respectively. The third is a definition in the Universal Composition framework that combines both these guarantees.

3.1 Homomorphic-CCA (HCCA) Security

Our first indistinguishability-based security definition formalizes the intuitive notions of message privacy and “non-malleability other than certain operations.”

A natural idea for formalizing our desired notion of non-malleability is to start with the standard CCA security experiment and sufficiently relax it. Indeed, this is the approach taken in the definitions of benignly malleable (gCCA) security [2, 63] and Replayable-CCA (RCCA) security [18], which allow for a scheme to be only “mostly” non-malleable. In these security experiments (Sect. 2.3), the decryption oracle is guarded so as not to decrypt ciphertexts that may be legitimate “derivatives” of the challenge ciphertext. In CCA security, the only derivative is the challenge ciphertext itself; in gCCA, derivatives are those which satisfy a particular binary relation with the challenge ciphertext; in RCCA, derivatives are those which decrypt to either of the two adversarially chosen plaintexts.

However, the same approach of guarding the decryption oracle fails in the case of more general homomorphic encryption. As an example, suppose that the set of allowed transformations is complete in the sense that, for every pair of messages $m, m'$, there is an allowed transformation T such that $T(m) = m'$. Suppose further that the scheme supports such operations in a rerandomizable/unlinkable way. (Some instantiations of our main construction have these two properties.) Then, every ciphertext in the support of the ${{\textsf {Enc}}}$ operation is a possible derivative of every other ciphertext. Letting the decryption oracle refuse to decrypt possible derivatives in such a scenario would essentially weaken the security requirement to IND-CCA1 (i.e., “lunchtime attack”) security, which is unsatisfactory.

Our approach to identifying “derivative” ciphertexts is completely different, and as a result our definition initially appears incomparable to these other standard definitions. However, Theorem 4.1 demonstrates that our new definition gives a generic notion of non-malleability which subsumes these existing definitions.

Overview and Intuition The formal definition, which we call Homomorphic-CCA (HCCA) security, appears below. Informally, in the security experiment we identify derivative ciphertexts not for normal encryptions, but for special “rigged” ciphertexts. These rigged ciphertexts are analogous to, for instance, the simulated view in the definition of zero-knowledge proofs, in that they are used only to formalize the security definition, and are not used in the execution of the scheme itself.

When $b=0$ in the experiment, the adversary simply receives an encryption of his chosen plaintext ${\textsf {msg}} ^*$ and gets access to an unrestricted decryption oracle. However, when $b=1$ in the experiment, instead of an encryption of ${\textsf {msg}} ^*$, the adversary receives a “rigged” ciphertext, generated by ${{\textsf {RigEnc}}}$ without knowledge of ${\textsf {msg}} ^*$. Such a rigged ciphertext need not encode any actual message, so if the adversary asks for it (or any of its derivatives) to be decrypted, we must compensate for the decryption oracle’s response in some way, or else it would be easy to distinguish the $b=0$ and $b=1$ cases. For this purpose, the ${{\textsf {RigEnc}}}$ procedure also produces some (secret) extra state information, which makes it possible to identify (via a corresponding ${{\textsf {RigExtract}}}$ procedure) all ciphertexts derived from that particular rigged ciphertext, as well as how (i.e., via which allowable transformation) they were derived. So in the $b=1$ scenario, the decryption oracle first uses ${{\textsf {RigExtract}}}$ to check whether the given ciphertext was derived via a homomorphic operation of the scheme, and if so, compensates in its response. For example, if it is discovered (via ${{\textsf {RigExtract}}}$) that the query ciphertext was derived by applying transformation T to the challenge ciphertext, then the decryption oracle should respond with $T({\textsf {msg}} ^*)$, to mimic the $b=0$ case.

It is easily seen that if an adversary can reliably maul an encryption of ${{\textsf {Enc}}} ({\textsf {msg}})$ (for unknown ${\textsf {msg}}$) into an encryption of a related message $T({\textsf {msg}})$, but ${{\textsf {RigExtract}}}$ is forbidden from outputting T, then there is a straightforward way for an adversary to distinguish between $b=0$ and $b=1$ in the experiment. Conversely, if ${{\textsf {RigExtract}}}$ never outputs T, and yet no adversary has non-negligible advantage in the HCCA experiment, then (intuitively) the scheme must be non-malleable with respect to T. Thus by restricting the range of the ${{\textsf {RigExtract}}}$ procedure in the security definition, we enforce a limit on the malleability of the scheme.

Finally, because ${{\textsf {RigExtract}}}$ uses the private key, as well as secret auxiliary information from ${{\textsf {RigEnc}}}$, we provide an oracle for these procedures. We do so in a “guarded” way that keeps the auxiliary shared information hidden from the adversary in the experiment. Looking ahead, these oracles are necessary in future security proofs (specifically, the proof of Theorem 4.4). Briefly, when considering interactions that involve many ciphertexts, we would like to replace each one with a rigged ciphertext. Doing so via a standard hybrid argument, we must provide a way for a simulator to generate rigged ciphertexts and later use ${{\textsf {RigExtract}}}$ to test for derivative ciphertexts. By defining “guarded” variants of the ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ oracles), we provide this bare functionality within the HCCA experiment.⁴

Formal Definition We now formally define the HCCA security notion. For a unary homomorphic encryption scheme ${\mathcal {E}} = ({{\textsf {KeyGen}}},{{\textsf {Enc}}},{{\textsf {Dec}}},{{\textsf {CTrans}}})$ and additional algorithms ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$, we define the following stateful oracle:

⁵

We point out one subtle but important detail. The set ${{\mathcal {R}}}$ denotes the “rigged” ciphertexts generated by the oracle (via ${{\textsc {rigenc}}}$ queries). Note that, in the case of $b=1$, both ${{\textsc {rigenc}}}$ and ${{\textsc {challenge}}}$ oracle queries use the ${{\textsf {RigEnc}}}$ procedure internally. But only the ${{\textsc {rigenc}}}$ queries add elements to ${{\mathcal {R}}}$, so only ${{\textsc {rigenc}}}$-generated ciphertexts can be checked for derivatives by the adversary.

Without this behavior—i.e., if we did indeed add $({\zeta ^*}, S^*)$ to ${{\mathcal {R}}}$ in the case of $b=1$—then a trivial query to ${{\textsc {rigextract}}}$ involving the challenge ciphertext ${\zeta ^*}$ would easily distinguish $b=0$ from $b=1$.

Definition 3.1

Let ${\mathcal {T}}$ be a set of (unary) transformations. A homomorphic encryption scheme ${\mathcal {E}}$ is ${\mathcal {T}}$ -Homomorphic-CCA-secure (${\mathcal {T}}$ -HCCA-secure) if there are PPT algorithms ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$, with $\mathrm {range}({{\textsf {RigExtract}}}) \subseteq {\mathcal {T}} \cup \{\bot \}$, such that for all non-uniform PPT adversaries ${{\mathcal {A}}}$, we have:

$$\begin{aligned} \Pr [ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{{\textsf {RigEnc}}},{{\textsf {RigExtract}}}}_{\lambda ,0}}(1^\lambda ) = 1] \approx \Pr [ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{{\textsf {RigEnc}}},{{\textsf {RigExtract}}}}_{\lambda ,1}}(1^\lambda ) = 1], \end{aligned}$$

3.2 Unlinkability

Triviality of HCCA Without Unlinkability HCCA security by itself is actually trivial to achieve. Take any space of transformations ${\mathcal {T}}$ and modify any CCA-secure encryption scheme by including an additional kind of ciphertext of the form $(\zeta , T)$, where $\zeta$ is a ciphertext in the original scheme and T is a description of a transformation in ${\mathcal {T}}$. To decrypt a ciphertext of this new form, first decrypt $\zeta$ and then if $T \in {\mathcal {T}}$, apply T to the result. The scheme has a homomorphic transformation procedure: ${{\textsf {CTrans}}} _{pk} (\zeta , T) = (\zeta ,T)$, and ${{\textsf {CTrans}}} _{pk} ((\zeta ,T),T') = (\zeta , T'\circ T)$.

It is not hard to see that such a scheme achieves HCCA security with respect to ${\mathcal {T}}$. ${{\textsf {RigEnc}}}$ should encrypt some fixed message and use the ciphertext itself as the auxiliary information S. Then on input $(\zeta , T), S$, the ${{\textsf {RigExtract}}}$ procedure should return T if $T \in {\mathcal {T}}$ and $\zeta = S$, and return $\bot$ otherwise. Clearly such a scheme is of limited interest—instead of actually applying a transformation to the underlying plaintext, the ${{\textsf {CTrans}}}$ operation simply defers the transformation until the time of decryption. Furthermore, transformed ciphertexts look noticeably different from plain ciphertexts.

We therefore focus on encryption schemes which are HCCA-secure while also satisfying a further requirement that transformed ciphertexts “look like” normal ciphertexts. A similar definition (called compactness) was also needed by Gentry [31] to avoid the same kind of degenerate case described here. However, in Gentry’s work the focus is solely on expressivity of the homomorphic operation, and not on any privacy guarantee provided by the homomorphic operation. As such, Gentry’s definition is somewhat incomparable to ours.

Unlinkability Overview Our main definition, called unlinkability, captures the strong notion that a ciphertext not leak anything at all about its history (i.e., whether it was generated using ${{\textsf {Enc}}}$ or via ${{\textsf {CTrans}}}$ and from which other ciphertext by applying which transformation). However, there would seem to be an apparent contradiction between the HCCA definition given above and this intuitive notion of unlinkability. HCCA security demands that it is possible to reliably track transformations applied to ciphertexts (i.e., via ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$), while unlinkability demands that ciphertexts not reveal whether they were generated via a transformation. To reconcile this, we require unlinkability to apply only to ciphertexts that successfully decrypt under a private key chosen by the challenger. This excludes linkability via the ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ procedures, since tracking ciphertexts using ${{\textsf {RigExtract}}}$ in general requires the tracking party to know the private key.

Our formal definition of unlinkability is given below. We note that the definition is more than just a correctness property, as it involves the behavior of the scheme’s algorithms on maliciously crafted ciphertexts.⁶ The security experiment also includes a decryption oracle, making it applicable even to adversaries with chosen-ciphertext attack capabilities.

Formal Definition For a unary homomorphic encryption scheme ${\mathcal {E}} = ({{\textsf {KeyGen}}},{{\textsf {Enc}}},{{\textsf {Dec}}},{{\textsf {CTrans}}})$ and a set of transformations ${\mathcal {T}}$, we define the following stateful oracle:

Definition 3.2

Let ${\mathcal {T}}$ be a set of (unary) transformations. A homomorphic encryption scheme ${\mathcal {E}}$ is ${\mathcal {T}}$ -unlinkable if, for all non-uniform PPT adversaries ${{\mathcal {A}}}$, we have:

$$\begin{aligned} \Pr \left[ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{\mathcal {T}}}_{\lambda ,0}}(1^\lambda ) = 1\right] \approx \Pr \left[ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{\mathcal {T}}}_{\lambda ,1}}(1^\lambda ) = 1\right] , \end{aligned}$$

Compatibility of Unlinkability and HCCA Security We have defined unlinkability and HCCA security with the intent that ${\mathcal {T}}$ unlinkability and ${\mathcal {T}}$-HCCA security (for the same ${\mathcal {T}}$) are compatible. If a scheme is ${\mathcal {T}}$-unlinkable and ${\mathcal {T}} '$-HCCA-secure, then at least intuitively ${\mathcal {T}} \subseteq {\mathcal {T}} '$. However, the definitions allow some pathological counterexamples to this claim.⁷ Still, we can prove the following conceptually similar claim:

Lemma 3.3

Let T be a (unary) plaintext transformation over a message space ${\mathcal {M}}$. We say that $T \in _\epsilon {\mathcal {T}} '$ if there exists an efficiently samplable distribution over $T' \in {\mathcal {T}} '$ such that $\Pr [ T(m) \ne T'(m) ] < \epsilon$ for every efficiently samplable distribution over $m \in {\mathcal {M}}$. We also say ${\mathcal {T}} \mathrel {\begin{array}{c} \textstyle \subset \\ \textstyle \sim \end{array}}_\epsilon {\mathcal {T}} '$ if for every $T \in {\mathcal {T}}$, we have $T \in _\epsilon {\mathcal {T}} '$.

In our setting, ${\mathcal {T}}$ and ${\mathcal {M}}$ depend on the public key of a scheme, so we write ${\mathcal {T}} _{pk}$. Let $\lambda ({pk})$ denote the security parameter inherent in ${pk}$.

If a scheme is ${\mathcal {T}} _{{pk}}$-unlinkable and ${\mathcal {T}} '_{{pk}}$-HCCA-secure, then there exists a negligible function $\epsilon$ such that ${\mathcal {T}} _{{pk}} \mathrel {\begin{array}{c} \textstyle \subset \\ \textstyle \sim \end{array}}_{\epsilon (\lambda ({pk}))} {\mathcal {T}} '_{{pk}}$.

Proof

For every $T \in {\mathcal {T}} _{pk}$ and every distribution $\mathcal D$ over ${\mathcal {M}} _{pk}$, consider the following adversary in the HCCA experiment. It samples $m^*$ according to ${\mathcal {D}}$ and sends a query ${{\textsc {challenge}}} (m^*)$, receiving response ${\zeta ^*}$. It computes $\zeta ' \leftarrow {{\textsf {CTrans}}} _{pk} ({\zeta ^*}, T)$ and sends a query ${{\textsc {dec}}} (\zeta ')$. The adversary outputs 1 iff the result is $T(m^*)$.

When $b=0$ in the HCCA experiment, the adversary outputs 1 with overwhelming probability by the fact that the scheme is unlinkable with respect to transformation T. When $b=1$, the game handles the ${{\textsc {dec}}} (\zeta ')$ query by running $T' \leftarrow {{\textsf {RigExtract}}} _{sk} (\zeta ', S^*)$ and outputting $T'(m^*)$. Note that the distribution by which $T'$ is computed is:

$$\begin{aligned} ({\zeta ^*},S^*) \leftarrow {{\textsf {RigEnc}}};\quad T' \leftarrow {{\textsf {RigExtract}}} _{sk} ({{\textsf {CTrans}}} _{pk} ({\zeta ^*},T), S^*);\quad \text{ return } T', \end{aligned}$$

which is independent of $m^*$. Note also that $T' \in {\mathcal {T}} '_{pk}$ by the constraints of the ${\mathcal {T}} '_{pk}$-HCCA game. It is with respect to this distribution on $T'$ that we have $T \in _\epsilon {\mathcal {T}} '_{pk}$, where $\epsilon$ is the (negligible) advantage of the adversary in the HCCA experiment (i.e., the probability that $T(m^*) \ne T'(m^*)$). As T was arbitrary in ${\mathcal {T}} _{pk}$, we get the claim from the lemma. $\square$

A scheme that simultaneously achieves both HCCA security and unlinkability with respect to the same space of transformations ${\mathcal {T}}$ yields a very sharp dichotomy between malleability and non-malleability. Namely, transforming ciphertexts according to operations in ${\mathcal {T}}$ is possible, as a highly expressive feature of the scheme, whereas transforming ciphertexts in any other way is impossible, even by adversaries. In this work, we focus on schemes which satisfy both conditions with respect to the same transformation space.

Robustness Against Malicious Keys Our UC-based security definition that follows also requires some significantly weaker condition to hold in the presence of maliciously generated public keys.

Definition 3.4

A homomorphic encryption scheme ${\mathcal {E}}$ is rerandomizing if for all (possibly malicious) ${pk}$, all $T \in {\mathcal {T}}$, and all ${\textsf {msg}} \in {\mathcal {M}}$, the following distributions are identical:

• Sample $\zeta \leftarrow {{\textsf {Enc}}} _{pk} ({\textsf {msg}})$ and $\zeta ' \leftarrow {{\textsf {CTrans}}} _{pk} (\zeta ,T)$. Output $(\zeta , \zeta ')$.

• Sample $\zeta \leftarrow {{\textsf {Enc}}} _{pk} ({\textsf {msg}})$ and $\zeta ' \leftarrow {{\textsf {Enc}}} _{pk} (T({\textsf {msg}}))$. Output $(\zeta , \zeta ')$.

In some cases, a public key may be extremely malformed, so that the ${{\textsf {Enc}}}$ and ${{\textsf {CTrans}}}$ algorithms become somewhat undefined. For example, the public key may not include the expected (number of) group elements. In this case, we can assume without loss of generality that both ${{\textsf {Enc}}}$ and ${{\textsf {CTrans}}}$ output an error indicator $\bot$.

3.3 Defining Security Using an Ideal Functionality

We also define the “Homomorphic Message Posting” functionality ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ in the framework of Universally Composable security [14] as a natural security definition encompassing both unlinkability and our desired notion of non-malleability. The complete definition appears in Fig. 2.

Fig. 2

UC ideal functionality ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$

${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ allows parties to post private messages for a designated receiver, as on a bulletin board. Messages are represented by abstract handles which reveal no information about the message (they are generated by the adversary without knowledge of the message). Only the designated receiver is allowed to obtain the corresponding message for a handle. To model the homomorphic features, the functionality allows parties to post messages derived from other handles. The functionality is parameterized by the set of allowed transformations ${\mathcal {T}}$. When a party provides a previously posted handle and a transformation $T \in {\mathcal {T}}$, the functionality retrieves the message m corresponding to the handle and then acts as if the party had actually requested T(m) to be posted. The sender does not need to know, nor is it told, the underlying message m of the existing handle.

${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ models the non-malleability we require, since the only way a posted message can influence a subsequent message is via an allowed transformation.

The functionality also models unlinkability by internally behaving identically (in particular, in its interaction with the adversary) for the two different kinds of posts. The only exception is that corrupt parties may generate “dummy” handles which look like normal handles but do not contain any message. When a party derives a new handle from such a dummy handle, the adversary learns the transformation. To see why it is unavoidable to inform the adversary when a dummy handle is reposted, consider an adversary who does the following: She generates a totally independent keypair (which she does not reveal) and broadcasts an encryption of m under that key. Then all derivatives will be noticeable to the adversary, as they will decrypt successfully under this new key. This tradeoff between notifying the adversary when dummy handles are reposted, and not notifying when non-dummy handles are reposted, mirrors the tradeoff between our indistinguishability definitions. In our security proofs, this additional dummy handle feature is crucial.

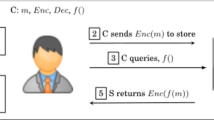
Homomorphic Encryption Schemes and Protocols for ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ The UC framework defines when a protocol is said to securely realize the functionality ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$: for every PPT adversary in the real-world interaction (using the protocol), there exists a PPT simulator in the ideal-world interaction with ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$, such that no PPT environment can distinguish between the two interactions. We associate homomorphic encryption schemes with candidate protocols for ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ in the following natural way (for simplicity assume all communication is on an authenticated broadcast channel). To setup an instance of ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$, a party generates a keypair and broadcasts the public key. To post a message, a party encrypts it under the public key and broadcasts the resulting ciphertext. The “derived post” feature is implemented via the ${{\textsf {CTrans}}}$ procedure. To retrieve a message from a handle, the receiver decrypts it using the private key. For simplicity of notation, when using an encryption scheme ${\mathcal {E}}$, we shall denote this protocol also by ${\mathcal {E}}$.

Broadcasting Versus Non-broadcasting For simplicity, we have defined our ideal UC functionality ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ in a broadcasting way; that is, that the adversary is notified every time an honest party generates a handle. This design choice leads to a simple functionality and a proof of equivalence (Theorem 4.4) that is relatively free of deep subtleties; however, as pointed out in [53], this paradigm does not allow the most flexibility.

A more general-purpose functionality would be a non-broadcasting one in which parties can privately (i.e., without the adversary being notified) generate new handles and then have arbitrary control over how the handles are sent to other parties. If a handle never reaches the adversary, the adversary should not know that it was ever generated.

Since in ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ the adversary is assumed to have control over the generation of handles, a functionality in the non-broadcasting paradigm lets the adversary register a handle-generating algorithm during the setup phase. This handle-generation algorithm is then executed locally by the functionality, without interacting with the adversary. Functionalities of this kind have been previously used for encryption and signatures [14, 16, 18, 53]. An analog of Theorem 4.4 holds for such a non-broadcasting definition of ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$.⁸

4 Relationships Among Security Definitions

To understand our new security definitions, we prove some relationships among them and among the more established definitions of CCA, gCCA [2, 63], and RCCA [18] security.

4.1 HCCA Generalizes Existing Non-malleability Definitions

Theorem 4.1

CCA, gCCA, and RCCA security⁹ can be obtained as special cases of the HCCA definition, by appropriately restricting ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$.

Proof

The restrictions on ${{\textsf {RigExtract}}}$ are progressively relaxed as we go from CCA to gCCA to RCCA, making it explicit that the non-malleability requirements get weaker in that order.

First, we modify the original definitions of CCA, gCCA and RCCA security (Sect. 2.3) so that they are similar to that of HCCA security. Instead of the adversary providing two challenge plaintexts, we modify the definition so that the plaintext ${\textsf {msg}} _0$ is fixed arbitrarily (and publicly known), and the adversary provides only ${\textsf {msg}} _1$. The modified definition is equivalent to the original definition (in which the adversary chooses both plaintexts).¹⁰ We can further modify the experiment so that when the adversary submits the challenge ciphertext to the decryption oracle, the response is ${\textsf {msg}} _1$ (regardless of whether ${\textsf {msg}} _0$ or ${\textsf {msg}} _1$ was chosen), instead of “${{\textsf {guarded}}}$.” In the case of CCA and gCCA definitions, this is a cosmetic change since the adversary can itself predict when the response will be “${{\textsf {guarded}}}$.” In the case of RCCA security, the legitimate guarded decryption oracle never responds with ${\textsf {msg}} _1$, and hence again, using ${\textsf {msg}} _1$ to indicate “${{\textsf {guarded}}}$ ” in the experiment does not the change the security definition.

Now we shall argue that each of the modified CCA, gCCA and RCCA experiments is equivalent to HCCA security, with appropriate restrictions on ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$.

CCA security. The modified CCA experiment can be directly obtained as a special case of the HCCA game as follows: ${{\textsf {RigEnc}}}$ generates an encryption of ${\textsf {msg}} _0$, and uses the ciphertext itself as the auxiliary information. ${{\textsf {RigExtract}}}$ simply checks if an input ciphertext is identical to this auxiliary information; if so, it reports the identity transformation (indicating that the given ciphertext encodes the same plaintext as the output of ${{\textsf {RigEnc}}}$); otherwise, it outputs $\bot$.

Note that the auxiliary information shared between ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ is in fact known to the adversary and that ${{\textsf {RigExtract}}}$ does not use the private key at all. Thus, without loss of generality the adversary makes no ${{\textsc {rigenc}}}$ or ${{\textsc {rigextract}}}$ queries. With this simplification, the resulting HCCA game is exactly equivalent to the modified CCA experiment described above.

gCCA security. The modified gCCA experiment for a particular (polynomial-time computable) equivalence relation R is equivalent to the HCCA experiment with the following ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$: as above ${{\textsf {RigEnc}}}$ generates an encryption of ${\textsf {msg}} _0$, and uses the ciphertext itself as the auxiliary information; but ${{\textsf {RigExtract}}}$ checks if an input ciphertext and the ciphertext in the auxiliary information satisfy the relation R; if so, it reports the identity transformation and otherwise, it outputs $\bot$.

Note that the gCCA security definition holds if indistinguishability holds in the (modified) gCCA experiment for equivalence relation R that can be computed in polynomial time given the public key, and such that $R(\zeta ,{\zeta ^*}) = 1 \Rightarrow {{\textsf {Dec}}} _{sk} (\zeta ) = {{\textsf {Dec}}} _{sk} ({\zeta ^*})$. That is, if we restrict ${{\textsf {RigEnc}}}$ to be the above one and ${{\textsf {RigExtract}}}$ to be of the above form with any arbitrary R satisfying the above conditions, then the resulting HCCA game is exactly the gCCA security definition. As above, the adversary need not make any ${{\textsc {rigenc}}}$/${{\textsc {rigextract}}}$ queries.

RCCA security. Consider ${{\textsf {RigEnc}}}$ which encrypts a random plaintext and sets that plaintext as the auxiliary information. Also, consider ${{\textsf {RigExtract}}}$ which simply decrypts the given ciphertext and checks whether the result equals the auxiliary information. If they are equal it reports the identity transformation, and otherwise outputs $\bot$.

In this case, ${{\textsf {RigExtract}}}$ does use the private key, but only to implement ${{\textsf {Dec}}}$ as a black box. Thus in the HCCA game with these ${{\textsf {RigEnc}}}$/${{\textsf {RigExtract}}}$ oracles, the adversary can simulate the effect of any ${{\textsc {rigenc}}}$/${{\textsc {rigextract}}}$ queries using only ${{\textsc {dec}}}$ queries. Again, with the above ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ procedures and with the adversary asking no ${{\textsc {rigenc}}}$ or ${{\textsc {rigextract}}}$ queries, the resulting HCCA experiment is equivalent to the modified RCCA experiment. The rigged ciphertext is generated using a randomly chosen plaintext so that it is unlikely that the adversary produces a ciphertext containing that plaintext (such a ciphertext would “fool” ${{\textsf {RigExtract}}}$). $\square$

Note that in all the three cases, when formulated as a restricted HCCA experiment, ${{\textsf {RigExtract}}}$ is allowed to output only $\bot$ or the identity transformation. This highlights the fact that schemes satisfying these security definitions are not malleable in ways which alter the message. Also, note that all of these special cases of HCCA involve a ${{\textsf {RigEnc}}}$ procedure which simply create a normal encryption of some plaintext. But in showing HCCA security of our construction (Sect. 5), we exploit the flexibility of the full HCCA definition to achieve larger classes of transformations, by letting ${{\textsf {RigEnc}}}$ generate a “ciphertext” that is not in the range of ${{\textsf {Enc}}} (\cdot )$.

Rerandomizable RCCA An extra requirement on RCCA encryption, namely rerandomizability, was introduced in [18] (called “secretly randomizable”) and later considered by [36, 54]. Briefly, rerandomizable RCCA security demands that given any ciphertext in the support of ${{\textsf {Enc}}} (m)$, anyone should be able to freshly sample the distribution of ${{\textsf {Enc}}} (m)$ (rerandomizability), but the scheme is non-malleable in ways which alter the plaintext (RCCA security).

Rerandomizable RCCA security corresponds to the special case of unlinkable HCCA security, where the only allowed transformation is the identity transformation. For historical reasons, we shall use the term “rerandomizable RCCA” security, but for the general case, we prefer the term “unlinkable,” as it emphasizes the concrete security end goal (for which appropriate ways of rerandomization serve as a means).

4.2 [R]CCA From HCCA

Given a (not necessarily unlinkable) HCCA-secure scheme satisfying a reasonable condition on its allowed transformations, we show a black-box construction of a CCA-secure and an RCCA-secure scheme.

Let ${\mathcal {E}} = ({{\textsf {KeyGen}}},{{\textsf {Enc}}},{{\textsf {Dec}}},{{\textsf {CTrans}}})$ be a ${\mathcal {T}}$-HCCA-secure scheme with the following properties:

• The message space ${\mathcal {M}}$ is isomorphic to $A \times B$. That is, there are efficiently computable maps between ${\mathcal {M}}$ and $A \times B$. Without loss of generality, we assume ${\mathcal {M}} = A \times B$.

• For all $T \in {\mathcal {T}}$, there exists a function $t: B \rightarrow B$ such that $T(a,b) = (a,t(b))$. That is, each transformation preserves the A-component of the plaintext.

In this case, an RCCA-secure [18] scheme can be obtained from ${\mathcal {E}}$ in the following way:

• To encrypt $m \in A$, choose an arbitrary $b \in B$ and output ${{\textsf {Enc}}} _{pk} (m,b)$

• To decrypt a ciphertext $\zeta$, compute $(a,b) \leftarrow {{\textsf {Dec}}} _{sk} (\zeta )$ and output a.

It is straightforward to see that the resulting scheme is RCCA-secure with message space A.

Then from a result of Canetti, Krawczyk, and Nielsen [18], the RCCA-secure scheme can be used to construct a CCA-secure scheme.

CHK Transformation RCCA-secure and CCA-secure encryption can also be obtained from an HCCA-secure encryption of the above kind, using a simple modification of the Canetti–Halevi–Katz (CHK) transformation [15]. A similar black-box transformation appeared independently in [49].

Briefly, let ${\mathcal {E}}$ be as above, and let $\Sigma = ({{\textsf {SigGen}}},{{\textsf {Sign}}},{{\textsf {Ver}}})$ be an one-time signature scheme whose space of verification keys is a subset of A.¹¹ Then the new CCA-secure scheme ${\mathcal {E}} ^{{\textsc {chk}}}$, with message space B, is as follows:

• ${{\textsf {KeyGen}}} ^{{\textsc {chk}}}$: same as ${{\textsf {KeyGen}}}$.

• ${{\textsf {Enc}}} ^{{\textsc {chk}}}_{pk} ({\textsf {msg}})$: Run $(vk,ssk) \leftarrow {{\textsf {SigGen}}}$. Compute $\zeta \leftarrow {{\textsf {Enc}}} _{pk} (vk,{\textsf {msg}})$ and $\sigma \leftarrow {{\textsf {Sign}}} _{ssk}(\zeta )$, then output $(vk, \zeta , \sigma )$.

• ${{\textsf {Dec}}} ^{{\textsc {chk}}}_{sk} (vk,\zeta , \sigma )$: If ${{\textsf {Ver}}} _{vk}(\zeta , \sigma ) \ne 1$, then output $\bot$. Else, compute $(vk', {\textsf {msg}}) \leftarrow {{\textsf {Dec}}} _{sk} (\zeta )$. If the decryption fails, or if $vk \ne vk'$, then output $\bot$. Otherwise, output ${\textsf {msg}}$.

If $\Sigma$ is unforgeable, then ${\mathcal {E}} ^{{\textsc {chk}}}$ is RCCA-secure; if $\Sigma$ is strongly unforgeable, then ${\mathcal {E}} ^{{\textsc {chk}}}$ is CCA-secure. The proof closely follows those of [15, 49] and is left as an exercise for the reader.

Black-Box Separation from CPA Security Given the black-box separation results of [32], our construction above implies that there is no shielding¹² black-box construction of a HCCA-secure scheme satisfying the condition above from a CPA-secure scheme.

We leave open the question of whether there exists a black-box reduction from CPA security to HCCA security with respect to, say, a group operation over the plaintext space (that is, the plaintext space is a group ${\mathbb {G}}$, and the set of allowed operations are $x \mapsto \sigma x$ for all choices of $\sigma \in {\mathbb {G}}$; such a scheme would not satisfy the properties described in this section).

4.3 Restricting the Transformation Space

In general, one cannot easily modify a ${\mathcal {T}} _1$-unlinkable-HCCA-secure scheme into a ${\mathcal {T}} _2$-unlinkable-HCCA-secure scheme, even if ${\mathcal {T}} _2 \subseteq {\mathcal {T}} _1$. The problem of “disabling” the transformations in ${\mathcal {T}} _1 {\setminus } {\mathcal {T}} _2$ while at the same time maintaining those in ${\mathcal {T}} _2$ appears just as challenging as constructing a ${\mathcal {T}} _2$-unlinkable-HCCA scheme from scratch. However, a simple black-box transformation is possible for the special case where ${\mathcal {T}} _2$ is a singleton set containing only the identity transformation. Recall that this special case is known as rerandomizable RCCA security [18].

Definition 4.2

Let ${\mathcal {E}} = ({{\textsf {KeyGen}}}, {{\textsf {Enc}}}, {{\textsf {Dec}}}, {{\textsf {CTrans}}})$ be a unary homomorphic encryption scheme, and let ${\mathcal {E}} '= ({{\textsf {KeyGen}}} ', {{\textsf {Enc}}} ', {{\textsf {Dec}}} ')$ be a (not necessarily homomorphic) encryption scheme. We define the encapsulation of ${\mathcal {E}} '$ inside ${\mathcal {E}}$, denoted ${\mathcal {E}} \circ {\mathcal {E}} '$, to be a unary homomorphic encryption scheme, given by the following algorithms:

• ${{\textsf {KeyGen}}} ^*$: Run $(pk, sk) \leftarrow {{\textsf {KeyGen}}}$ and $(pk', sk') \leftarrow {{\textsf {KeyGen}}} '$. Output ${pk} = (pk, pk')$ and ${sk} = (sk, sk')$.

• ${{\textsf {Enc}}} ^*_{pk,pk'}({\textsf {msg}}) = {{\textsf {Enc}}} _{pk}( {{\textsf {Enc}}} '_{pk'} ({\textsf {msg}}))$.

• ${{\textsf {Dec}}} ^*_{sk,sk'}(\zeta ) = {{\textsf {Dec}}} '_{sk'}( {{\textsf {Dec}}} _{sk} (\zeta ))$, where we let ${{\textsf {Dec}}} '_{sk'}(\bot )=\bot$ for simplicity.

• ${{\textsf {CTrans}}} ^*$: same as ${{\textsf {CTrans}}}$.

Theorem 4.3

If ${\mathcal {E}} ^H$ is a ${\mathcal {T}}$-unlinkable-HCCA-secure scheme (for any ${\mathcal {T}}$) and ${\mathcal {E}} ^R$ is a (not necessarily rerandomizable) RCCA-secure scheme, then ${\mathcal {E}} ^H \circ {\mathcal {E}} ^R$ is rerandomizable RCCA-secure.

Intuitively, the outer scheme’s unlinkability is preserved by the encapsulation, but the inner scheme’s non-malleability renders useless all transformations but the identity transformation.

Note that RCCA security without rerandomizability is a weaker requirement than CCA security [18]. Thus, for example, an unlinkable HCCA-secure scheme encapsulating a plain CCA-secure encryption scheme will yield a rerandomizable RCCA-secure encryption scheme.

Proof

For clarity, we superscript with “H” the algorithms of ${\mathcal {E}} ^H$, and superscript with “R” the algorithms of ${\mathcal {E}} ^R$. We write the keys of ${\mathcal {E}} ^H$ as (hpk, hsk), and similarly the keys of ${\mathcal {E}} ^R$ as (rpk, rsk). We write the algorithms of the encapsulated scheme ${\mathcal {E}} ^H \circ {\mathcal {E}} ^R$ without superscripts.

Note that ${{\textsf {CTrans}}} ^H$ accepts possibly many allowed transformations as input when viewed in the context of ${\mathcal {E}} ^H$. However, in the context of the encapsulated scheme ${\mathcal {E}} ^H \circ {\mathcal {E}} ^R$, ${{\textsf {CTrans}}} = {{\textsf {CTrans}}} ^H$ is only meaningful when called with the identity transformation. We note that to achieve HCCA security with respect to ${\mathcal {T}}$, ${\mathcal {T}}$ must indeed contain the identity function (since the adversary can simply send the challenge ciphertext itself as a ${{\textsc {dec}}}$ query). It is easy to see that the unlinkability of the outer scheme (with respect to the identity transformation) is preserved by the construction.

To show RCCA security (HCCA security with the identity function as the only allowed transformation), we must demonstrate appropriate ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ procedures for the new scheme. Let $({{\textsf {RigEnc}}} ^H,{{\textsf {RigExtract}}} ^H)$ and $({{\textsf {RigEnc}}} ^R,{{\textsf {RigExtract}}} ^R)$ be the procedures guaranteed by the two schemes, respectively. Then the new scheme satisfies HCCA security with the following procedures:

• ${{\textsf {RigEnc}}} _{hpk,rpk}$ does the following: Run $(\zeta ,S_H) \leftarrow {{\textsf {RigEnc}}} ^H_{hpk}$ and $(\zeta _R,S_R) \leftarrow {{\textsf {RigEnc}}} ^R_{rpk}$. Set $S=(S_H,\zeta _R,S_R)$ and output $(\zeta , S)$.

• ${{\textsf {RigExtract}}} _{hsk,rsk}(\zeta , S)$ does the following: Parse S as $(S_H,\zeta _R,S_R)$. Run $T\leftarrow {{\textsf {RigExtract}}} ^H_{hsk}(\zeta ,S_H)$. If $T=\bot$, output $\bot$; otherwise output ${{\textsf {RigExtract}}} ^R_{rsk}( T ( \zeta _R), S_R)$, which must be either the identity function or $\bot$, by the RCCA security of the inner scheme.

Consider a hybrid HCCA experiment where the challenge ciphertext is generated from ${\textsf {msg}} ^*$ as:

• Run $(\zeta ^*,S^*) \leftarrow {{\textsf {RigEnc}}} ^H_{hpk}$ and $\zeta ^*_R \leftarrow {{\textsf {Enc}}} ^R_{rpk}({\textsf {msg}} ^*)$. Remember $\zeta ^*_R$ and output $\zeta ^*$.

and a query of the form ${{\textsc {dec}}} (\zeta )$ is implemented as:

$$\begin{aligned} {{\textsc {dec}}} (\zeta ) = {\left\{ \begin{array}{ll} {{\textsf {Dec}}} ^R_{rsk}( T (\zeta ^*_R) ) &{} \text{ if } \bot \ne T\leftarrow {{\textsf {RigExtract}}} ^H_{hsk}(\zeta ,S^*) \\ {{\textsf {Dec}}} ^R_{rsk}( {{\textsf {Dec}}} ^H_{hsk} (\zeta )) &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$

It is straightforward to verify that this hybrid experiment is indistinguishable from both the $b=0$ and $b=1$ branches of the HCCA experiment instantiated with the new scheme and its ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ procedures described above. $\square$

4.4 Unlinkable HCCA Implies the UC Definition

Theorem 4.4

Every ${\mathcal {T}}$-homomorphic encryption scheme which is HCCA-secure, unlinkably homomorphic (with respect to ${\mathcal {T}}$), rerandomizing, and satisfies the correctness properties, is a UC-secure realization of ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$, against static (non-adaptive) corruptions.

Let ${\mathcal {E}} =({{\textsf {KeyGen}}},{{\textsf {Enc}}},{{\textsf {Dec}}},{{\textsf {CTrans}}})$ be an unlinkably homomorphic, HCCA-secure encryption scheme (with allowable homomorphisms ${\mathcal {T}}$). To prove Theorem 4.4, we must demonstrate for any real-world adversary ${{\mathcal {A}}}$ a corresponding ideal-world adversary (simulator) ${{\mathcal {S}}}$, so that for all PPT environments ${{\mathcal {Z}}}$, ${{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {A}}},{\mathcal {E}},{{\mathcal {F}}}_{{\textsc {bcast}}} ] \approx {{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {S}}},{\pi }_{\mathsf{dummy}},{\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}} ]$. Here, “${\mathcal {E}}$ ” is overloaded to denote the natural protocol that uses the encryption scheme ${\mathcal {E}}$, as described in Sect. 3.3. We also assume that all communication is done on an authenticated broadcast channel, denoted ${{\mathcal {F}}}_{{\textsc {bcast}}}$.

In the case where the recipient P is corrupt, the simulation is trivial. Each time it is asked to generate a handle, it is given the underlying message. Each time the adversary itself outputs a ciphertext, the simulator can register it as a dummy handle, after which it is notified each time that handle is ${{\textsc {repost}}}$ ’ed. We now focus on the case where P is not corrupt.

Overview We construct the simulator ${{\mathcal {S}}}$ in a sequence of hybrids. We give a brief overview of these hybrids now, highlighting the subtleties that arise.

• 0. We begin with the real-world interaction, involving the adversary ${{\mathcal {A}}}$ attacking the scheme ${\mathcal {E}}$ being executed over the broadcast channel ${{\mathcal {F}}}_{{\textsc {bcast}}}$. For convenience, we can write this as an interaction between an ideal-world adversary ${{\mathcal {S}}} _{0}$ attacking a functionality ${{\mathcal {F}}}_{{\textsc {0}}}$, which is a variant of ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ modified to give all of the honest parties’ inputs to ${{\mathcal {S}}} _{0}$. When an honest party ${{\textsc {post}}}$ s a message ${\textsf {msg}}$, the simulator ${{\mathcal {S}}} _{0}$ generates the corresponding handle via ${{\textsf {Enc}}} _{pk} ({\textsf {msg}})$; similarly handles for ${{\textsc {repost}}}$-ed handles are generated via ${{\textsf {CTrans}}}$.

  One subtlety here is that when the adversary outputs a ciphertext, it must be posted to ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$. The simulator decrypts it to decide whether to post it as a legitimate message or a dummy handle. Even if the ciphertext is adversarially generated (and perhaps not in the range of ${{\textsf {Enc}}} _{pk} (\cdot )$), as long as ${{\textsf {Dec}}} _{sk} (\zeta ) \ne \bot$ it will be interpreted as a non-dummy handle.

• 1. In the protocol, ${{\textsc {post}}}$ commands are handled via ${{\textsf {Enc}}}$, and ${{\textsc {repost}}}$ commands are handled via ${{\textsf {CTrans}}}$. By the unlinkability of the scheme, (intuitively), these two cases generate indistinguishable outputs, provided that the handle being reposted contains a valid message. Thus, when given a command $({{\textsc {repost}}}, {\textsf {handle}}, T)$ command for a non-dummy handle, we allow the functionality (called ${{\mathcal {F}}}_{{\textsc {1}}}$ after this modification) to give the simulator the same output as if the command $({{\textsc {post}}}, T({\textsf {msg}}))$ was received (the behavior used by ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$).

  Importantly, non-dummy handles (even those adversarially generated) must satisfy ${{\textsf {Dec}}} _{sk} (\zeta ) \ne \bot$, and so the unlinkability property holds. We use the fact that unlinkability applies even in the presence of a decryption oracle, since the remainder of the simulation uses ${{\textsf {Dec}}}$ throughout. At this point, the simulator never needs to use the ${{\textsf {CTrans}}}$ function.

• 2. ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ does not reveal the messages (plaintexts) that are posted, yet so far we have a hybrid in which the simulator is given these messages to appropriately generate handles via ${{\textsf {Enc}}}$. In this step, we apply the HCCA security property on each handle generated by the simulator. Intuitively, HCCA security implies that we can replace a valid encryption with a rigged encryption (which can be generated without knowledge of the plaintext) as long as we appropriately compensate on decryption queries (using ${{\textsf {RigExtract}}}$).

  More formally, we consider a sequence of hybrids; in the kth hybrid, the first k (honestly generated) handles are generated via ${{\textsf {RigEnc}}}$, and the rest with ${{\textsf {Enc}}}$. We also replace all decryptions with a process in which we first use ${{\textsf {RigExtract}}}$ to check whether the input was a derivative of one of these k rigged ciphertexts. To show that the kth and $(k+1)$th hybrids are indistinguishable, we apply HCCA security. The oracle queries ${{\textsc {rigenc}}}$ and ${{\textsc {rigextract}}}$ provide the basic functionality required by the simulator (namely, generating rigged ciphertexts and later identifying their derivatives).

Hybrid 0 (correctness) We define a functionality ${{\mathcal {F}}}_{{\textsc {0}}}$ that behaves exactly like ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ except in the following aspects:

• 1. When an honest party sends a command $({{\textsc {post}}},{\textsf {msg}})$ to ${{\mathcal {F}}}_{{\textsc {0}}}$, the functionality sends $({{\textsc {extra}}},{{\textsc {post}}},{\textsf {msg}})$ to the adversary.

• 2. When an honest party sends a command $({{\textsc {repost}}},{\textsf {handle}})$ to ${{\mathcal {F}}}_{{\textsc {0}}}$, the functionality sends $({{\textsc {extra}}},{{\textsc {repost}}},{\textsf {handle}})$ to the adversary.

We emphasize that these values sent to the adversary are in addition to what ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ would normally send (i.e., ${{\textsc {handle-req}}}$ commands).

Given an adversary ${{\mathcal {A}}}$ (attacking the real-process interaction) we define a simulator ${{\mathcal {S}}} _{0}$ as follows:

• 1. If ${{\mathcal {A}}}$ broadcasts $({{\textsc {id-announce}}},P,{\textsf {id}})$ on behalf of corrupt P then ${{\mathcal {S}}} _{0}$ sends a command ${{\textsc {setup}}}$ to the functionality (on behalf of P) and responds to $({{\textsc {id-req}}},P)$ with ${\textsf {id}}$. Internally ${{\mathcal {S}}} _{0}$ sets ${pk} = {\textsf {id}}$.

• 2. Otherwise, when ${{\mathcal {S}}} _{0}$ receives a command $({{\textsc {id-req}}},P)$ from the functionality (i.e., on behalf of an honest party), it generates a keypair $({pk}, {sk}) \leftarrow {{\textsf {KeyGen}}}$ and sends ${pk}$ to the functionality. It then internally simulates to ${{\mathcal {A}}}$ that party P broadcast ${pk}$ to ${{\mathcal {F}}}_{{\textsc {bcast}}}$. Note that ${sk}$ is only defined in the simulation in the case where the receiver P is honest.

• 3. When ${{\mathcal {S}}} _{0}$ receives commands $({{\textsc {handle-req}}},{\textsf {sender}})$ and $({{\textsc {extra}}},{{\textsc {post}}},{\textsf {msg}})$ from the functionality, it computes ${\textsf {handle}} \leftarrow {{\textsf {Enc}}} _{pk} ({\textsf {msg}})$ and sends ${\textsf {handle}}$ to the functionality. It also internally simulates to ${{\mathcal {A}}}$ that ${\textsf {sender}}$ broadcast ${\textsf {handle}}$ to ${{\mathcal {F}}}_{{\textsc {bcast}}}$.

• 4. When ${{\mathcal {S}}} _{0}$ receives commands $({{\textsc {handle-req}}},{\textsf {sender}})$ and $({{\textsc {extra}}},{{\textsc {repost}}},{\textsf {handle}})$ from the functionality, it computes ${\textsf {handle}} ' \leftarrow {{\textsf {CTrans}}} ({\textsf {handle}}, T)$ and sends ${\textsf {handle}} '$ to the functionality. It also internally simulates to ${{\mathcal {A}}}$ that ${\textsf {sender}}$ broadcast ${\textsf {handle}} '$ to ${{\mathcal {F}}}_{{\textsc {bcast}}}$.

• 5. When the adversary broadcasts a ciphertext $\zeta$ on ${{\mathcal {F}}}_{{\textsc {bcast}}}$, ${{\mathcal {S}}} _{0}$ does the following:

  • If the receiver P is corrupt, or if P is honest but ${{\textsf {Dec}}} _{sk} (\zeta ) = \bot$, then ${{\mathcal {S}}} _{0}$ sends $({{\textsc {dummy}}}, \zeta )$ to the functionality on behalf of ${{\mathcal {A}}}$.

  • Otherwise, P is honest and ${{\textsf {Dec}}} _{sk} (\zeta ) = {\textsf {msg}} \ne \bot$. In this case, ${{\mathcal {S}}} _{0}$ sends $({{\textsc {post}}},{\textsf {msg}})$ to the functionality on behalf of ${{\mathcal {A}}}$. The functionality will immediately ask for a handle for this post (via a ${{\textsc {handle-req}}}$ command), to which ${{\mathcal {S}}} _{0}$ responds with $\zeta$.

Claim 4.5

For any given PPT adversary, let ${{\mathcal {F}}}_{{\textsc {0}}}$ and ${{\mathcal {S}}} _{0}$ be as described above. Then for all PPT environments ${{\mathcal {Z}}}$, ${{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {A}}},{\mathcal {E}},{{\mathcal {F}}}_{{\textsc {bcast}}} ] \equiv {{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {S}}} _{0},{\pi }_{\mathsf{dummy}},{{\mathcal {F}}}_{{\textsc {0}}} ]$.

Proof

This follows from the correctness properties of encryption scheme ${\mathcal {E}}$ and the fact that ${{\mathcal {S}}} _{0}$ exactly emulates the real-world actions of all parties. $\square$

Hybrids(1, k) (unlinkable homomorphism) Let N be a (polynomial) bound on the number of commands sent to the functionality in the interactions we consider. Then we define

to be identical to ${{\mathcal {F}}}_{{\textsc {0}}}$ except in the following behavior:

• 1. When an honest party ${\textsf {sender}}$ sends a command $({{\textsc {repost}}},{\textsf {handle}},T)$, and the following are true:

  • $({\textsf {handle}},{\textsf {msg}})$ is internally recorded, where ${\textsf {msg}} \ne \bot$

  • this is the jth time such a command has been sent, where $j \le k$

  then instead of sending $({{\textsc {extra}}}, {{\textsc {repost}}}, {\textsf {handle}})$ to the adversary, it sends $({{\textsc {extra}}}, {{\textsc {post}}}, T({\textsf {msg}}))$.

Claim 4.6

For any given PPT adversary ${{\mathcal {A}}}$, let ${{\mathcal {S}}} _{0}$, ${{\mathcal {F}}}_{{\textsc {0}}}$, and

be as described above. Then for all PPT environments ${{\mathcal {Z}}}$:

Proof

The first statement follows from the definition of ${{\mathcal {F}}}_{{\textsc {1,0}}}$. To show the second statement, we consider two cases:

Case 1: the receiver P is corrupt. Note that the difference between hybrids is only relevant when an honest party reposts a handle for which ${\textsf {msg}} \ne \bot$. But when the receiver is corrupt, this can only happen when the original handle was produced from an honest party (the simulator will use a dummy handle, with ${\textsf {msg}} = \bot$ for any ciphertext broadcast by the adversary).

Then the difference between the hybrids is whether the simulator computes the $(k+1)$th handle via ${\textsf {handle}} ' \leftarrow {{\textsf {CTrans}}} ({\textsf {handle}},T)$ or via ${\textsf {handle}} ' \leftarrow {{\textsf {Enc}}} _{pk} (T({\textsf {msg}}))$, where ${\textsf {handle}}$ was originally generated via ${\textsf {handle}} \leftarrow {{\textsf {Enc}}} _{pk} ({\textsf {msg}})$. From the rerandomizing property of the ${{\textsf {CTrans}}}$ procedure, these two distributions are identically distributed (even when ${pk}$ is maliciously generated).

Case 2: the receiver P is honest. In this case, we reduce to the unlinkability security definition. Consider an adversary ${{\mathcal {A}}} ^*$ participating in the unlinkability game which carries out the interaction between

and the honest parties—with one small change described below. To do so, ${{\mathcal {A}}} ^*$ uses the public key ${pk}$ and ${{\textsf {Dec}}}$ oracle provided in the game. At the end, ${{\mathcal {A}}} ^*$ takes the output of ${{\mathcal {Z}}}$ to be its own output.

However, in the $(k+1)$th execution of item 1 from above, ${{\mathcal {A}}} ^*$ sends ${\textsf {handle}}$ as its challenge in the unlinkability game. By construction, item 1 above only occurs when an honest party sends a command $({{\textsc {repost}}}, {\textsf {handle}})$ for a non-dummy handle ${\textsf {handle}}$. As such, ${{\textsf {Dec}}} _{sk} ({\textsf {handle}}) \ne \bot$, as required in the unlinkability game. Say ${{\mathcal {A}}} ^*$ receives ${\textsf {handle}} '$ as the response; then it takes ${\textsf {handle}} '$ to be the response of ${{\mathcal {S}}} _{0}$.

Now, it is easy to see that the output of ${{\mathcal {A}}} ^*$ is distributed exactly as

where b is the choice bit in the unlinkability game. The claim then follows by the unlinkability of the scheme. $\square$

Hybrids (2, k) (HCCA security) As before, let N be a (polynomial) bound on the number of commands sent to the functionality in the interactions we consider. Then we define

to be identical to

except that it does not deliver to the adversary the first k messages of the form $({{\textsc {extra}}}, {{\textsc {post}}}, {\textsf {msg}}))$. Note that messages of this form can be triggered by either a ${{\textsc {post}}}$ or ${{\textsc {repost}}}$ command by an honest party.

Now we define ${{\mathcal {S}}} _{2}$ to act identically to ${{\mathcal {S}}} _{0}$, with the following exceptions when the receiver P is honest:

• 1. When ${{\mathcal {S}}} _{2}$ receives a request of the form $({{\textsc {handle-req}}},{\textsf {sender}})$ from the functionality with no corresponding message of the form $({{\textsc {extra}}},{{\textsc {post}}},\cdot )$, it computes $({\textsf {handle}}, S) \leftarrow {{\textsf {RigEnc}}} _{pk}$ and uses ${\textsf {handle}}$ as the message’s handle. It internally keeps track of $({\textsf {handle}}, S)$ for later use.

• 2. When the adversary broadcasts a ciphertext $\zeta$, the simulator ${{\mathcal {S}}} _{2}$ does the following: For each $({\textsf {handle}}, S)$ recorded above, ${{\mathcal {S}}} _{2}$ computes $T \leftarrow {{\textsf {RigExtract}}} _{sk} (\zeta ,S)$. If for some $({\textsf {handle}}, S)$ we have $T\ne \bot$, then ${{\mathcal {S}}} _{2}$ sends $({{\textsc {repost}}},{\textsf {handle}}, T)$ to the functionality and uses $\zeta$ as the corresponding handle. If all of these calls to ${{\textsf {RigExtract}}}$ produce $\bot$, then ${{\mathcal {S}}} _{2}$ proceeds just as ${{\mathcal {S}}} _{0}$ (i.e, attempts to decrypt $\zeta$ under ${sk}$ and so on).

When the receiver P is corrupt, note that the simulator can simply use the $({{\textsc {get}}},{\textsf {handle}})$ command to obtain the plaintext of any ciphertext. So we can trivially modify the simulator to obtain the information that is missing in these new hybrids, and proceed as before.

Claim 4.7

For any given PPT adversary ${{\mathcal {A}}}$, let ${{\mathcal {S}}} _{1}$, ${{\mathcal {F}}}_{{\textsc {1}}}$, ${{\mathcal {S}}} _{2}$ and ${{\mathcal {F}}}_{{\textsc {2}}}$ be as described above. Then for all PPT environments ${{\mathcal {Z}}}$,

Proof

The first statement follows from the definition of ${{\mathcal {F}}}_{{\textsc {2,0}}}$, since ${{\mathcal {S}}} _{2}$ never calls ${{\textsf {RigEnc}}}$ (and hence there are no opportunities to execute ${{\textsf {RigExtract}}}$ in item 2 above).

To show the second statement, consider an adversary ${{\mathcal {A}}} ^*$ participating in the HCCA game which carries out the interaction between

and the honest parties, with the following change. The $(k+1)$th time the functionality would have generated a message of the form $({{\textsc {extra}}}, {{\textsc {post}}}, {\textsf {msg}} ^*)$, ${{\mathcal {A}}} ^*$ sends ${\textsf {msg}} ^*$ as the challenge in the HCCA game. It receives ${\textsf {handle}} ^*$ in return and takes this to be the handle generated by ${{\mathcal {S}}} _{2}$ for the corresponding ${{\textsc {handle-req}}}$. At the end, ${{\mathcal {A}}} ^*$ takes the output of ${{\mathcal {Z}}}$ to be its own output.

We must show that ${{\mathcal {A}}} ^*$ can indeed carry out the desired interaction in the context of an HCCA experiment. It can use the ${{\textsf {GDec}}}$ oracle as its decryption oracle. In steps 1 and 2 above, the values S are used only internally to ${{\mathcal {S}}} _{2}$; in particular, they are not given to the underlying adversary ${{\mathcal {A}}}$. It suffices to simply have the ability to generate rigged ciphertexts and later test whether another ciphertext is a derivative of that ciphertext. Indeed, the ${{\textsc {rigenc}}}$ and ${{\textsc {rigextract}}}$ oracle queries provide this functionality.

It is easy to see that when $b=0$ in the HCCA game, the output of ${{\mathcal {A}}} ^*$ is distributed exactly as

It suffices to show that when $b=1$ the output of ${{\mathcal {A}}} ^*$ is distributed exactly as

.

When $b=1$ in the HCCA game, the $(k+1)$th ciphertext is a rigged ciphertext, for which ${{\mathcal {S}}} _{2}$ does not know the corresponding $S^*$ value. Note that ${{\mathcal {S}}} _{2}$ uses the decryption oracle only in step 2 above (in the parenthetical remark). When $b=1$ the ${{\textsf {GDec}}}$ oracle first uses ${{\textsf {RigExtract}}}$ to check whether the input is derived from ${\textsf {handle}} ^*$. If so, then $T({\textsf {msg}} ^*)$ is returned and ${{\mathcal {S}}} _{2}$ sends $({{\textsc {post}}}, T({\textsf {msg}} ^*))$ to the functionality.

By comparison, in the interaction

${{\mathcal {S}}} _{2}$ knows the value $S^*$ corresponding to the rigged ciphertext ${\textsf {handle}} ^*$. Then in step 2 above, ${{\mathcal {S}}} _{2}$ will itself use ${{\textsf {RigExtract}}}$ to check whether the input is a derivative of ${\textsf {handle}} ^*$. If it is derived via T, then ${{\mathcal {S}}} _{2}$ will send $({{\textsc {repost}}}, {\textsf {handle}} ^*, T)$ to the functionality.

In all other cases (say, a ciphertext is not identified as a derivative of ${\textsf {handle}} ^*$), the two interactions are identical. The key observation is that the commands $({{\textsc {post}}}, T({\textsf {msg}} ^*))$ and $({{\textsc {repost}}}, {\textsf {handle}} ^*)$ have exactly the same effect in

(in previous hybrid steps we have eliminated any external difference in behaviors between these two commands).

Thus, we see that the output of ${{\mathcal {A}}} ^*$ is distributed exactly as

, where b is the choice bit in the HCCA game. The claim then follows by the HCCA security of the scheme. $\square$

Concluding the Proof Combining the above claims, we get that for all adversaries ${{\mathcal {A}}}$, there exists a simulator ${{\mathcal {S}}} _{2}$ such that

for all environments ${{\mathcal {Z}}}$. Note that

and ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ in fact have identical behaviors (in particular,

never sends any messages of the form $({{\textsc {extra}}},\cdot )$ to the adversary). So letting ${{\mathcal {S}}} ={{\mathcal {S}}} _{2}$ completes the proof.

5 Main Construction: An Unlinkable, HCCA-secure Scheme

Our main result is a family of encryption schemes which achieve both HCCA security and unlinkable homomorphism, with respect to a wide range of (unary) transformations, under the RG-DDH assumption (Definition 2.2).

We begin with a high-level overview of the scheme.

5.1 Overview

We motivate the design of our construction, first focusing on the special case of rerandomizable, RCCA encryption. In this case, the only allowed operation is rerandomizability; that is, anyone can maul an encryption of (unknown) m into another freshly random encryption of m, yet the scheme is non-malleable in ways that alter the plaintext. This is the case considered in [54] and constitutes one of the simplest instantiations of our scheme.

Starting with Cramer–Shoup. We recall the well-known scheme of Cramer and Shoup [23], which serves as a conceptual starting point for our construction. In a group ${\mathbb {G}}$, a Cramer–Shoup encryption of $m \in {\mathbb {G}}$ has the following form:

$$\begin{aligned} g_1^x, g_2^x, m C^x, (DE^\mu )^x, \end{aligned}$$

where $\mu$ is a hash of the first three ciphertext elements; $g_1$ and $g_2$ are random generators of ${\mathbb {G}}$; and C, D, and E are values from the public key.

Two Strands for Rerandomizability To make the scheme rerandomizable (that is; allow anyone to “refresh” the randomness used during ciphertext generation), we use what we call a “double-strand” technique. This method, previously used by Golle et al. [34] to make ElGamal rerandomizable, involves double the size of the ciphertext to assist in randomization. Now, an encryption of m has the form:

$$\begin{aligned} g_1^x, g_2^x, m C^x, (DE^\mu )^x, \\ g_1^y, g_2^y, \quad C^y, (DE^\mu )^y. \end{aligned}$$

If we label the ciphertext as $(\mathbf{X}, \mathbf{Y})$, where $\mathbf{X}$ and $\mathbf{Y}$ are each a vector of 4 group elements, then we can see that the new ciphertext $(\mathbf{X} \cdot \mathbf{Y}^s, \mathbf{Y}^t)$ (operations taken component-wise) resembles an encryption of m with randomness $x' = x+sy$ and $y' = yt$. However, the ciphertext has changed so, as such, the value of $\mu$ is now inconsistent. Instead, we let $\mu$ be a hash (or any injective encoding) of the plaintext m, a value that is invariant under this rerandomization operation. Intuitively, the Cramer–Shoup paradigm makes the ciphertext non-malleable with respect to $\mu$.

Note that there is a fundamental asymmetry between the two “strands” $\mathbf{X}$ and $\mathbf{Y}$. In particular, we rerandomize x additively (to $x' = x+sy$) and y multiplicatively (to $y' = yt$). We could not, for instance, easily rerandomize x to tx, as it would presumably have the side effect of raising the (unknown) “payload” m to the t power.

Tying the Strands Together The scheme, as described above, is rerandomizable but not RCCA-secure. Note that if $\zeta = (\mathbf{X}, \mathbf{Y})$ and $\zeta '= (\mathbf{X}', \mathbf{Y}')$ are ciphertexts, then ${{\textsf {Dec}}} _{sk} (\mathbf{X}, \mathbf{Y}') \ne \bot$ if and only if $\zeta$ and $\zeta '$ encode the same plaintext (i.e., the respective $\mu$ values coincide). In the presence of a ${{\textsf {Dec}}}$ oracle, this property leads to a simple “strand mixing-and-matching” attack in the RCCA/HCCA security game.

To thwart such an attack, there must be some shared randomness correlating the two strands, so that they are only useful together. We do so by adding an additional element of randomness u to the ciphertexts, yielding the following form:

$$\begin{aligned} g_1^{xu}, g_2^{xu}, m C^x, (DE^\mu )^x,&\\ g_1^{yu}, g_2^{yu}, \quad C^y, (DE^\mu )^y;&~{{\textsf {MEnc}}} (u). \end{aligned}$$

Here ${{\textsf {MEnc}}}$ denotes an auxiliary encryption scheme, with properties to be enumerated later. The key point is that sharing a common value u, the two strands can carry out the rerandomization as above, rerandomizing $x' = x+sy$ and $y' = yt$. However, the new value u must also be rerandomized. This can be carried out multiplicatively (i.e., $u' = \sigma u$) by raising the appropriate values to the $\sigma$ power, and exploiting a homomorphic property of ${{\textsf {MEnc}}}$. Note that the “payload-carrying” component of the ciphertext is not raised to any power.

For this to actually work, ${{\textsf {MEnc}}}$ must satisfy some special properties:

• It must be rerandomizable itself (i.e., to refresh the randomness hidden inside the notation ${{\textsf {MEnc}}} (u)$)

• It must be homomorphic with respect to the operation ${{\textsf {MEnc}}} (u) \leadsto {{\textsf {MEnc}}} (\sigma u)$, to refresh the choice of u.

• The operation $u \mapsto \sigma u$ must coincide with multiplication in ${\mathbb {Z}}^*_p$ (where p is the order of the Cramer–Shoup group), as that is the operation that occurs when manipulating u “in the exponent.” Thus the plaintext space of the ${{\textsf {MEnc}}}$ scheme (the domain of u) must be a subgroup of ${\mathbb {Z}}^*_p$.

For these reasons, we require a hardness assumption in two groups of related size (one group for Cramer–Shoup, and the other group for this auxiliary scheme ${{\textsf {MEnc}}}$). As outlined in Sect. 2.2, one suggested choice of such groups are the groups of quadratic residues mod $2q+1$ and mod $4q+3$, where $(q, 2q+1, 4q+3)$ is a Cunningham chain.

We note that the ${{\textsf {MEnc}}}$ does not need to be HCCA-secure (which would certainly lead to a chicken-and-egg problem). The ${{\textsf {MEnc}}}$ scheme does need some restriction on its malleability, but the condition is significantly weaker than HCCA security. Our construction uses “Cramer–Shoup lite” for ${{\textsf {MEnc}}}$.

“Twisting” the First Strand As described so far, the scheme is not quite RCCA-secure. Suppose $(\mathbf{X}, \mathbf{Y}, U)$ is a ciphertext, and an adversary has a guess m for the underlying plaintext of this ciphertext. The related ciphertext $(\mathbf{X}^2, \mathbf{Y}, U)$ is almost a valid ciphertext, except that its plaintext payload has been squared and is thus inconsistent with $\mu$. However, the adversary can divide off its guess of m from the 3rd component; the resulting ciphertext will be valid (i.e., the ${{\textsf {Dec}}}$ oracle will return a non-$\bot$ response) if and only if the adversary’s guess for m was correct. This leads to a successful attack in the RCCA/HCCA game.

To thwart this kind of attack, we add something to the first strand which prevents rerandomizing the first strand multiplicatively. Finally, our ciphertexts take this form:

$$\begin{aligned} \begin{array}{lclrcc} g_1^{(x+z_1)u}, &{} \ldots , &{} g_4^{(x+z_4)u}, &{} m C^x, &{} (DE^\mu )^x, &{} \\ g_1^{yu}, &{} \ldots , &{} g_4^{yu}, &{} C^y, &{} (DE^\mu )^y; &{}~{{\textsf {MEnc}}} (u). \end{array} \end{aligned}$$

Here, $\vec {z} = (z_1, \ldots , z_4)$ is some fixed, public constant; $\vec {z} = (0,0,0,1)$ is a suitable choice. The scheme has been expanded to use 4 generators rather than 2, and this serves a technical purpose of providing more dimensions of freedom in the underlying linear algebra. The key is that squaring each component in the first strand would also double this additive $\vec {z}$ vector. The fact that $\vec {z}$ is linearly independent of (1, 1, 1, 1) makes it infeasible for the adversary to compensate accordingly in the payload-carrying component.¹³

Beyond Rerandomizable RCCA The scheme as described above is in fact the instantiation of our construction for the special case of rerandomizable RCCA security (and the scheme from [54]). Intuitively, the components of the scheme enforce that the only way to generate a valid ciphertext is to: rerandomize the first strand additively (using the second strand), and rerandomize the second strand multiplicatively (using only the second strand).

This “additive-only” property of the first strand means that, intuitively, the payload cannot be raised to a power. We also have that the scheme is non-malleable with respect to $\mu$. Thus, setting $\mu$ to be different invariants of the plaintext, we achieve a scheme that is non-malleable except in ways that multiply the plaintext by a known constant, while preserving an invariant.

A similar variation the Cramer–Shoup hashing was used in [49] to construct an encryption scheme which is non-malleable with respect to public “tags.” In our construction, however, the tag/invariant is a function of the (private) plaintext.

5.2 Details

We now present the details of the main construction.

Notation and Supported Transformations Let “$*$” denote the group operation in the product group ${\mathbb {G}} ^n$ defined by $(\alpha _1, \ldots , \alpha _n) * (\beta _1, \ldots , \beta _n) = (\alpha _1\beta _1, \ldots \alpha _n\beta _n)$.

For $\tau \in {\mathbb {G}} ^n$, define $T_\tau$ to be the “multiplication-by-$\tau$” transformation in ${\mathbb {G}} ^n$; i.e., $T_\tau (m) = \tau * m$. We also let $T_\tau (\bot ) = \bot$ for simplicity. Now let ${\mathbb {H}}$ be a subgroup of ${\mathbb {G}} ^n$. Our construction provides a scheme whose message space is ${\mathcal {M}} = {\mathbb {G}} ^n$, and whose set of allowable transformations is ${\mathcal {T}} _{\mathbb {H}} = \{ T_\tau \,|\, \tau \in {\mathbb {H}} \}.$ By choosing ${\mathbb {H}}$ appropriately, we can obtain the following notable classes ${\mathcal {T}} _{\mathbb {H}}$:

• The identity function alone (i.e., rerandomizable RCCA security), by setting ${\mathbb {H}} = \{1\}$.

• All transformations $T_\tau$ (that is, all component-wise multiplications in ${\mathbb {G}} ^n$), by setting ${\mathbb {H}} = {\mathbb {G}} ^n$.

• “Scalar multiplication” of tuples in ${\mathbb {G}} ^n$ by coefficients in ${\mathbb {G}}$, by setting ${\mathbb {H}} = \{ (s,\ldots , s) \,|\, s \in {\mathbb {G}} \}$.

Auxiliary “Cramer–Shoup Lite” (CSL) Scheme We present the “Cramer–Shoup lite” (CSL) [24] scheme, which is used as a component in our main construction. We crucially use the fact that it is CCA1-secure, and malleable (though not HCCA-secure) under particular transformations.

It is not hard to see that if $U$ is in the support of ${{\textsf {MEnc}}} _{\widehat{pk}} (u)$ (with randomness $v$), then ${{\textsf {MCTrans}}} _{\widehat{pk}} (U,T_\sigma )$ is in the support of ${{\textsf {MEnc}}} _{\widehat{pk}} (\sigma u)$, corresponding to random choice $v ' = v + s$.

We emphasize that this CSL scheme does not achieve our desired definitions of an HCCA-secure scheme, because given an encryption of $u$ and a value $r \in {\mathbb {Z}}_q$, one can easily construct an encryption of $u ^r$, and exponentiation by r is not an allowed transformation. Our main construction uses only the $T_\sigma$ transformations of CSL as a feature, although the security analysis must account for the fact that other kinds of transformations may be possible.

Main Construction We now present our main construction, which uses the previous CSL scheme as a component.

^{14 15}

It is not hard to see that if $\zeta$ is in the support of ${{\textsf {Enc}}} _{pk} (m_1, \ldots , m_n)$, say, with random choices $x$, $y$, and $u$, then the above ciphertext is in the support of ${{\textsf {Enc}}} _{pk} (\tau _1 m_1, \ldots , \tau _n m_n)$, corresponding to random choices $x ' = x + sy$, $y ' = ty$, and $u ' = \sigma u$.

6 Security Proof for Main Construction

In this section, we prove the security properties of our main construction. Throughout the proof, we continue to use the notational conventions of Sect. 5.

Theorem 6.1

The construction in Sect. 5 satisfies the correctness properties for a homomorphic encryption scheme, is ${\mathcal {T}} _{\mathbb {H}}$-unlinkable and ${\mathcal {T}} _{\mathbb {H}}$-HCCA-secure, under the RG-DDH assumption.

Since the proof is rather lengthy, we first give a high-level conceptual overview of the important steps. The correctness properties follow from straightforward inspection of the scheme’s routines. We now focus on the HCCA security requirement. Later, we will show how the arguments used to prove HCCA security can be very easily modified to show the unlinkability requirement.

6.1 Rigged Ciphertexts (${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$)

To prove HCCA security, we must demonstrate suitable ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ procedures for use in the HCCA security experiment (Definition 3.1). First, we define some useful subroutines that are common to both the “rigged” and standard encryption procedures, so that the distinction between rigged and standard ciphertexts is clearer:

Intuitively, the $D E ^\mu$ component is the core of our scheme’s non-malleability, following the Cramer–Shoup paradigm, as explained in the scheme’s motivation above. Thus, ${{\textsf {GenCiph}}} _{pk} ((m_1, \ldots , m_n), \mu )$ generates a ciphertext with plaintext $\vec {m}$, which is non-malleable with respect to the quantity $\mu$. Then ${{\textsf {Integrity}}} _{sk} (\zeta ,u,\mu )$ determines whether the given ciphertext encodes the specified non-malleability quantity $\mu$.

Using these subroutines, we can rewrite the scheme’s ${{\textsf {Enc}}}$ and ${{\textsf {Dec}}}$ routines as follows:

Now, we define the ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ procedures for use in our security proof:

Intuitively, a rigged ciphertext is one whose non-malleability value $\mu$ is a random value, rather than a function of the message as in the normal scheme. If a purported ciphertext is observed which encodes the same value of $\mu$ (S), we conclude that the ciphertext in question was derived from the rigged one. By inspecting and comparing the purported plaintexts of the two ciphertexts, we can determine the transformation that was applied.

6.2 Proof Overview

Recall that to prove HCCA security we must show that the advantage of any adversary in the HCCA game (with ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ as described above) is negligible. We do so by considering the following sequence of hybrid interactions, which at this high level follow the general approach used by Cramer and Shoup to show the CCA security of their scheme:

Hybrid 0 This hybrid is simply the HCCA game, using ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ from above.

Hybrid 1 (Alternative Encryption) This hybrid is the same as above, except in how the challenge ciphertext is generated. Recall that in the HCCA game, the adversary submits a plaintext ${\textsf {msg}}$ and receives the challenge ciphertext ${\zeta ^*}$, generated either via ${{\textsf {Enc}}} _{pk} ({\textsf {msg}})$ or ${{\textsf {RigEnc}}} _{pk}$. In either case, ${\zeta ^*}$ is generated by a suitable call to the ${{\textsf {GenCiph}}}$ subroutine.

Hybrid 1 differs from Hybrid 0 in that this particular call to ${{\textsf {GenCiph}}}$ is replaced with an alternative version (called ${{\textsf {AltGenCiph}}}$), as follows: Instead of using the same random exponent $x$ in ciphertext components $g _{1} ^{(x +z_{1})u}, \ldots , g _{4} ^{(x +z_{4})u}$ and the same random exponent $y$ in components $g _{1} ^{y u}, \ldots , g _{4} ^{y u}$, the alternate procedure uses independently random exponents for each of these components. This is analogous to the first step in the CCA-security proof of standard Cramer–Shoup: the challenge ciphertext is generated as $(g _{1} ^{x_{1}}, g _{2} ^{x_{2}}, \ldots )$ instead of $(g _{1} ^{x}, g _{2} ^{x}, \ldots )$.

This alternative way of generating the challenge ciphertext must then use the private key instead of the public key to ensure that the resulting ciphertext still decrypts successfully. A corresponding change is also made in the way the auxiliary CSL ciphertext is generated.

Hybrids 0 and 1 are indistinguishable by the DDH assumption in ${\mathbb {G}}$ and $\widehat{{\mathbb {G}}}$. Furthermore, if ${\zeta ^*}$ denotes the challenge ciphertext in Hybrid 1, then we show that $({pk}, {\zeta ^*})$ are distributed independently of the values $(u, \mu , b)$, where $u$ and $\mu$ are values chosen during ciphertext generation, and b is the choice bit in the HCCA game. Again, this reasoning is analogous to that of the standard Cramer–Shoup proof: there, the modified challenge ciphertext is distributed independently of the choice bit b.

Hybrid 2 (Alternative Encryption $+$ Decryption) It is not enough that $({pk}, {\zeta ^*})$ are distributed independent of the choice bit b. The adversary’s view also includes responses to oracle queries, which are implemented using the private key and may therefore leak information about b. Hybrid 2 addresses the potential information leaked by these decryption-like oracles.

In the security proof for Cramer–Shoup, these oracle queries are handled in the following way. Define a Cramer–Shoup ciphertext as bad if it has the form $(g _{1} ^{x_{1}}, g _{2} ^{x_{2}}, \ldots )$, where $x_{1} \ne x_{2}$. Using a purely statistical argument, Cramer and Shoup show that the decryption oracle will respond with $\bot$ with overwhelming probability,¹⁶ in response to any bad ciphertext query. Thus we may replace the decryption oracle with an oracle which simply checks whether the query is in the range of ${{\textsf {Enc}}} _{pk} (\cdot )$, and if so, returns the appropriate value of m. Of course, this oracle would require exponential time, but, crucially, it can be implemented using the public key only. In other words, the responses from oracle queries cannot leak more information than ${pk}$, which we already established was distributed independently of the choice bit b, so the adversary’s entire view is independent of the choice bit.

Our proof follows a similar approach of defining alternative (exponential-time) decryption procedures, which use only the public key. Like the proof of Cramer–Shoup, the bulk of our proof centers on defining when a query is bad, and then showing that the relevant oracles will respond with $\bot$ with overwhelming probability on all bad queries.

However, our situation is considerably more complicated than the one arising in the Cramer–Shoup security proof:

• In the Cramer–Shoup case, a ciphertext of the form $(g _{1} ^{x_{1}}, g _{2} ^{x_{2}}, \ldots )$ has either $x_{1} = x_{2}$ or $x_{1} \ne x_{2}$. The space of possible values $(x_{1}, x_{2})$ is 2-dimensional. Our situation is complicated by the fact that we have an analogous 4-dimensional space. We also have two places in the ciphertext (corresponding to randomness $x$ and $y$) where we must characterize these encryption exponents.

  More discussion of the relevant subtleties is deferred to Sect. 6.5, where the required linear-algebraic understanding has been developed.

• In the HCCA game, ${{\textsc {dec}}}$ queries are answered differently depending on the choice bit b. We must show an indistinguishable (exponential-time) alternative oracle which uses only ${pk}$ (and in particular, not b). Looking ahead, the alternative oracle will simply check whether the query ciphertext is in the range of ${{\textsf {Enc}}} _{pk} (\cdot )$ or in the range of ${{\textsf {CTrans}}} _{pk} ({\zeta ^*}, \cdot )$. The analysis must account for why any other purported ciphertext would cause a ${{\textsc {dec}}}$ query to output $\bot$ with overwhelming probability.

Unlinkability We have given the outline of how we prove the HCCA security of our construction. To prove unlinkability, we apply the reasoning from the HCCA proof in a similar way.

Consider the unlinkability experiment (Definition 3.2). Here, the adversary must provide a challenge ciphertext $\zeta$, to which the condition ${{\textsf {Dec}}} _{sk} (\zeta ) \ne \bot$ is checked. If the check succeeds, then the game continues, and the ciphertext is either transformed via ${{\textsf {CTrans}}}$, or reencrypted.

Now consider replacing the ${{\textsf {Dec}}}$ oracle with the (exponential-time) alternate decryption oracle used in Hybrid 2 of the HCCA proof. By the same argument as in that proof, we see that this hybrid experiment is indistinguishable from the original experiment. However, now when the adversary provides a challenge ciphertext $\zeta$, the condition that is checked is “is $\zeta$ in the range of ${{\textsf {Enc}}} _{pk} (\cdot )$?”

We can now apply the straightforward correctness property of ${{\textsf {CTrans}}}$; namely, that the two distributions ${{\textsf {Enc}}} _{pk} (T({{\textsf {Dec}}} _{sk} (\zeta )))$ and ${{\textsf {CTrans}}} _{pk} (\zeta ,T)$ are identical. As such, the adversary has no advantage in the unlinkability game (after replacing the decryption oracle with the alternative one from the HCCA proof).

6.3 Linear Algebra Characterization of Our Scheme

Before proceeding to the full details of the security proof, we first give an alternate characterization of our construction using linear algebra, which will be vitally useful in the security proof.

Public-Key Constraints First we examine what information is revealed to the adversary about the private key by the public key.

Let $({\vec {a}},{\vec {b}})$ be a CSL private key and $(\widehat{g} _{1},\widehat{g} _{2},A,B)$ be the corresponding CSL public key. Also let $({\vec {c}} _1, \ldots , {\vec {c}} _n,{\vec {d}},{\vec {e}})$ be a private key and $(g _{1},\ldots ,g _{4},C _1,\ldots ,C _n,D,E)$ be the corresponding public key. Then the relationship between the private and public keys is given by the following linear equations (the first equation is in the field of order q, and the second is in the field of order p):¹⁷

$$\begin{aligned} \begin{bmatrix} {\vec {1}}&\\&{\vec {1}} \end{bmatrix} \begin{bmatrix} \widehat{G}&\\&\widehat{G} \\ \end{bmatrix} \begin{bmatrix} {\vec {a}} ^\top \\ {\vec {b}} ^\top \end{bmatrix}&= \begin{bmatrix} \log A \\ \log B \end{bmatrix}, \text{ where } \widehat{G} = \begin{bmatrix} \log \widehat{g} _{1}&0 \\ 0&\log \widehat{g} _{2} \end{bmatrix} \nonumber \\ \begin{bmatrix} {\vec {1}} \\&\ddots \\&{\vec {1}} \end{bmatrix} \begin{bmatrix} G \\&\ddots \\&G \\ \end{bmatrix} \begin{bmatrix} {\vec {c}} _1^\top \\ \vdots \\ {\vec {c}} _n^\top \\ {\vec {d}} ^\top \\ {\vec {e}} ^\top \\ \end{bmatrix}&= \begin{bmatrix} \log C _1 \\ \vdots \\ \log C _n \\ \log D \\ \log E \\ \end{bmatrix}, \text{ where } G = \begin{bmatrix} \log g _{1}&\cdots&0 \\ \vdots&\ddots&\vdots \\ 0&\cdots&\log g _{4} \end{bmatrix} \end{aligned}$$

(6.1)

We call these constraints the public-key constraints.

Strands We introduce the notion of strands, which allow us to characterize the linear-algebraic dependence of ciphertext on the public key and the challenge ciphertext.

Definition 6.2

Let $U = (V_{1},V_{2},A_V,B_V)$ be a CSL ciphertext. The CSL strand of $U$ with respect to a public key $(\widehat{g} _{1},\widehat{g} _{2},A,B)$ is:

$$\begin{aligned} {\vec {v}}&= (v_{1}, v_{2}), \text{ where } v_{j} = \log _{\widehat{g} _{j}} V_{j} \end{aligned}$$

Observe that:

• Ciphertexts generated by ${{\textsf {MEnc}}} _{\widehat{pk}}$ have a strand (with respect to ${\widehat{pk}}$) where $v_{1} = v_{2}$; that is, the strand is a scalar multiple of the all-ones vector ${\vec {1}}$.

• If the CSL strand of $U$ (w.r.t. ${\widehat{pk}}$) is ${\vec {v}}$, then ${{\textsf {MCTrans}}} _{\widehat{pk}} (U,T_\sigma )$ produces a ciphertext whose strand (w.r.t. ${\widehat{pk}}$) is ${\vec {v}} +r{\vec {1}}$, for a random choice $r \in {\mathbb {Z}}_q$.

For ciphertexts in the main scheme, we define a similar notion of strands. However, in such a ciphertext, the first strand is “masked” by $u$ and $z_{i}$’s, and the second strand is masked by $u$.

Definition 6.3

Let $\zeta = ({\vec {X}},{\vec {C}} _X,P_{X};{\vec {Y}},{\vec {C}} _Y,P_{Y};U)$ be a ciphertext in the main scheme. The strands of $\zeta$ with respect to a public key $(g _{1},\ldots ,g _{4},C _1,\ldots , C _n, D,E)$ and a value $u \in \widehat{{\mathbb {G}}}$ are:

$$\begin{aligned} {\vec {x}}&= (x_{1}, \ldots , x_{4}), \text{ where } x_{i} = (\log _{g_{i}} X_{i})/u- z_{i} \\ {\vec {y}}&= (y_{1}, \ldots , y_{4}), \text{ where } y_{i} = (\log _{g_{i}} Y_{i})/u \end{aligned}$$

Again, we have the following observations:

• In ciphertexts generated by ${{\textsf {Enc}}} _{pk}$, both strands (with respect to ${pk}$ and $u = {{\textsf {MDec}}} _{\widehat{sk}} (U)$, where $U$ is the final component of the ciphertext) are scalar multiples of the all-ones vector.

• If the strands of $\zeta$ are ${\vec {x}}$ and ${\vec {y}}$ (w.r.t. ${pk}$ and $u$), then ${{\textsf {CTrans}}} _{pk} (\zeta ,T_{\vec {\tau }})$ produces a ciphertext whose two strands (w.r.t. ${pk}$ and $\sigma u$, where $\sigma$ is the value chosen in ${{\textsf {CTrans}}}$) are ${\vec {x}} +s{\vec {y}}$ and $t{\vec {y}}$, for a random choice of $s \in {\mathbb {Z}}_p, t\in {\mathbb {Z}}^*_p$.

Looking ahead, one way to interpret the role of ${\vec {z}}$ and $u$ in our construction is that they ensure that any way of modifying a ciphertext’s strands other than $({\vec {x}},{\vec {y}}) \leadsto ({\vec {x}} +s{\vec {y}}, t{\vec {y}})$ will cause the ciphertext to be invalid.

Decryption Constraints Let ${\widehat{sk}} = ({\vec {a}},{\vec {b}})$ be a CSL private key, let $U = (V_{1},V_{2},A_V,B_V)$ be a CSL ciphertext, and let ${\vec {v}}$ be its strand with respect to the corresponding public key. Then ${{\textsf {MDec}}} _{\widehat{sk}} (U) = u \ne \bot$ if and only if the following constraints hold in the field of order q:

$$\begin{aligned} \begin{bmatrix} {\vec {v}}&\\&{\vec {v}} \\ \end{bmatrix} \begin{bmatrix} \widehat{G}&\\&\widehat{G} \\ \end{bmatrix} \begin{bmatrix} {\vec {a}} ^\top \\ {\vec {b}} ^\top \end{bmatrix} = \begin{bmatrix} \log (A_V/u) \\ \log B_V \\ \end{bmatrix} \end{aligned}$$

(6.2)

Similarly, let ${sk} = ({\widehat{sk}},{\vec {c}} _1, \ldots , {\vec {c}} _n,{\vec {d}}, {\vec {e}})$ be a private key and $\zeta = ({\vec {X}},{\vec {C}} _X,P_{X};{\vec {Y}},{\vec {C}} _Y,P_{Y};U)$ be a ciphertext such that ${{\textsf {MDec}}} _{\widehat{sk}} (U) = u \ne \bot$. Let ${\vec {x}}$ and ${\vec {y}}$ denote the strands of ${\zeta ^*}$ with respect to the public key and $u$.

Then ${{\textsf {PurpMsg}}} _{sk} (\zeta ,u) = (m_1, \ldots , m_n)$ and ${{\textsf {Integrity}}} _{sk} (\zeta , u, \mu ) = 1$ if and only if ${\vec {y}}$ is a nonzero vector and the following constraints hold in the field of order p:

$$\begin{aligned} \begin{bmatrix} {\vec {x}}&\\&\ddots&\\&{\vec {x}} \\ {\vec {y}}&\\&\ddots&\\&{\vec {y}} \\&&{\vec {x}}&\mu {\vec {x}} \\&&{\vec {y}}&\mu {\vec {y}} \\ \end{bmatrix} \begin{bmatrix} G&\\&\ddots&\\&G \\ \end{bmatrix} \begin{bmatrix} {\vec {c}} _1^\top \\ \vdots \\ {\vec {c}} _n^\top \\ {\vec {d}} ^\top \\ {\vec {e}} ^\top \\ \end{bmatrix} = \begin{bmatrix} \log (C_{X,1}/m_1) \\ \vdots \\ \log (C_{X,n}/m_n) \\ \log C_{Y,1} \\ \vdots \\ \log C_{Y,n} \\ \log P_{X} \\ \log P_{Y} \\ \end{bmatrix} \end{aligned}$$

(6.3)

We call each constraint in these systems of equations a decryption constraint, and refer to them by the name of the ciphertext component that is involved in the right-hand side ($A_V$, $P_{X}$, etc.).

Ciphertexts generated by ${{\textsf {GenCiph}}}$ have strands that are scalar multiples of the all-ones vector. As such, the corresponding decryption constraints are linearly dependent on the public-key constraints. Thus, such a ciphertext does not provide any additional information about the private key to the adversary, which is logical since these ciphertexts are generated with the public key alone.

Looking ahead, in Hybrid 1 the challenge ciphertext will be generated in an alternative way, so that its decryption constraints are linearly independent of the public-key constraints with high probability. The linear independence helps to information-theoretically hide the plaintext and other information contained in the ciphertext, but also gives the adversary more constraints on the private key. The fact that ciphertexts in our scheme give constraints relating to both ${\vec {x}}$ and ${\vec {y}}$ is one of the reasons our construction uses four generators $g _{1}, \ldots , g _{4}$ instead of the typical two generators in the Cramer–Shoup construction. We need a large enough vector space so that $\{{\vec {1}}, {\vec {x}}, {\vec {y}} \}$ can all be linearly independent (in fact, they must also be linearly independent of ${\vec {z}}$ for additional reasons).

Correctness Properties Under this linear-algebraic interpretation of our scheme, it is easy to see the correctness of the homomorphic transformation operations.

Lemma 6.4

For all keypairs $({\widehat{pk}},{\widehat{sk}})$, all (purported) CSL ciphertexts $U$, and all $U '$ in the support of ${{\textsf {MCTrans}}} (U,T_\sigma )$, we have ${{\textsf {MDec}}} _{\widehat{sk}} (U ')= T_\sigma ( {{\textsf {MDec}}} _{\widehat{sk}} (U) )$.

Proof

If ${\vec {v}}$ is the CSL strand of $U$, then the strand of $U '$ is ${\vec {v}} + r {\vec {1}}$ for some $r\in {\mathbb {Z}}_q$. Consider any decryption constraint on $U '$. The left-hand side of the constraint is the left-hand side of the corresponding constraint from $U$ plus r times the left-hand side of the corresponding public-key constraint. By the definition of ${{\textsf {MCTrans}}}$, the right-hand side of the constraint is also a combination of the right-hand sides of these two constraints with the same coefficients (with one of the constraints being further offset by $\sigma$). $\square$

Lemma 6.5

For all keypairs $({pk},{sk})$, all (purported) ciphertexts $\zeta$, and all $\zeta '$ in the support of ${{\textsf {CTrans}}} _{pk} (\zeta , T_{\vec {\tau }})$, we have ${{\textsf {Dec}}} _{sk} (\zeta ')= T_{\vec {\tau }} ( {{\textsf {Dec}}} _{sk} (\zeta ) )$.

Proof

First, by the above lemma, the CSL component of $\zeta$ ’ will fail to decrypt if and only if the CSL component of $\zeta$ fails to decrypt.

Otherwise, the two strands of $\zeta '$ (with respect to the decryption of its CSL component) are linear combinations of the strands of $\zeta$ (with respect to the decryption of its CSL component). A similar argument to above shows that a decryption check fails on $\zeta '$ if and only if the same check fails on $\zeta$; and that the ratios of the purported plaintexts are ${\vec {\tau }}$. $\square$

6.4 Hybrid 1: Alternate Encryption

As outlined above, we consider a hybrid interaction wherein ${{\textsf {GenCiph}}}$ is replaced by an alternative procedure when generating the challenge ciphertext ${\zeta ^*}$. We now describe this procedure ${{\textsf {AltGenCiph}}}$. As a component, it uses ${{\textsf {AltMEnc}}}$, a corresponding alternate encryption procedure for the CSL scheme. Both of these procedures use the secret key instead of the public keys to generate ciphertexts.

Using the terminology of the previous section, we see that these alternate encryption procedures generate a ciphertext whose strands are random, whereas standard ciphertexts have strands which are scalar multiples of all-ones vectors. The remainder of the ciphertexts are “reverse-engineered” using the private key to ensure that the decryption constraints are satisfied.

Hybrid 1 Formally, we define a Hybrid challenge oracle, as follows:

$\underline{\widehat{{\mathcal {O}}}^{{\textsf {hyb-1}}}_{\lambda ,b}:}$

All queries are answered identically to ${\mathcal {O}}^{{\mathcal {E}},{{\textsf {RigEnc}}},{{\textsf {RigExtract}}}}_{\lambda ,b}$, except that when responding to a ${{\textsc {challenge}}}$ query, the implicit call to ${{\textsf {GenCiph}}} _{pk}$ (from either ${{\textsf {RigEnc}}}$ or ${{\textsf {Enc}}}$) is replaced with an identical call to ${{\textsf {AltGenCiph}}} _{sk}$.

Lemma 6.6

Let ${\mathcal {E}}$ denote our main construction. For every non-uniform PPT adversary ${{\mathcal {A}}}$ and $b \in \{0,1\}$, we have

$$\begin{aligned} \Pr [ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{{\textsf {RigEnc}}},{{\textsf {RigExtract}}}}_{\lambda ,b}}(1^\lambda ) = 1] \approx \Pr [ {{\mathcal {A}}} ^{\widehat{{\mathcal {O}}}^{{\textsf {hyb-1}}}_{\lambda ,b}}(1^\lambda ) = 1] \end{aligned}$$

under the RG-DDH assumption.

Proof

Under the RG-DDH assumption, the following two distributions are indistinguishable (the proof of their indistinguishability is left as an exercise for the reader):

Now consider a simulator which receives a sample from either ${\mathcal {D}}_0$ or ${\mathcal {D}}_1$; say:

$$\begin{aligned} \Big ( ({\mathbb {G}},g,p,\widehat{{\mathbb {G}}},\widehat{g},q);~ \widehat{g} _{1}, \widehat{g} _{2}; ~ V_{1}, V_{2}; ~ g _{1}, \ldots , g _{4}; ~ \overline{X}_{1}, \ldots , \overline{X}_{4}; ~ \overline{Y}_{1}, \ldots , \overline{Y}_{4} \Big ) \end{aligned}$$

The simulator then simulates the HCCA game with ${{\mathcal {A}}}$. It uses $(\widehat{g} _{1},\widehat{g} _{2})$ as the corresponding part of the CSL public key, and generates the remainder of the keypair (${\vec {a}},{\vec {b}}$) honestly. To simulate the encryption of $u ^*$ from the challenge ciphertext with this keypair, the simulator uses ${{\textsf {AltMEnc}}}$ with the input values $V_{1},V_{2}$.

Similarly, we take $(g _{1},\ldots ,g _{4})$ as the corresponding part of the public key and generate the remainder of the keypairs (${\vec {c}} _i$, ${\vec {d}}$, ${\vec {e}}$) honestly. To simulate the encryption of the challenge ciphertext, we use ${{\textsf {AltGenCiph}}}$ with these private keys and the input values $\overline{X}_{1},\ldots ,\overline{X}_{4},\overline{Y}_{1},\ldots ,\overline{Y}_{4}$.

If the above tuple is sampled according to ${\mathcal {D}}_0$, then the challenge ciphertext is statistically indistinguishable from one generated using ${{\textsf {GenCiph}}}$ (the distribution is identical when conditioned to avoid the negligible-probability event that $\overline{Y}_{1} =\cdots =\overline{Y}_{4} =1$). If the above tuple is instead sampled according to ${\mathcal {D}}_1$, then the challenge ciphertext is distributed identically to an encryption from ${{\textsf {AltGenCiph}}}$.

The rest of this simulation of the HCCA game can be implemented in polynomial time, so the claim follows from the RG-DDH assumption. $\square$

Lemma 6.7

In the Hybrid 1 experiment, conditioned on an overwhelming probability event, the values $({\zeta ^*}, {pk})$ are distributed independently of the values $(u, b)$, where $u \in \widehat{{\mathbb {G}}}$ is the randomness chosen when generating ${\zeta ^*}$, and b is the choice bit in the game.

Further, when $b=1$, the value $\mu \in {\mathbb {Z}}_p$ used to generate ${\zeta ^*}$ is chosen at random, and we have that $({\zeta ^*}, {pk})$ are distributed independently of $(u, \mu )$.

Proof

Given a CSL ciphertext from ${{\textsf {AltMEnc}}}$ with strand ${\vec {v}}$, the set $\{{\vec {v}},{\vec {1}} \}$ forms a basis for the 2-dimensional space of CSL strands, with overwhelming probability. The adversary’s view of the CSL private key $({\vec {a}},{\vec {b}})$ is constrained by the public key constraints in Eq. (6.1) and the decryption constraints given by ${\zeta ^*}$ in Eq. (6.3), that is:

$$\begin{aligned} \begin{bmatrix} {\vec {1}}&\\&{\vec {1}} \\ {\vec {v}}&\\&{\vec {v}} \\ \end{bmatrix} \begin{bmatrix} \widehat{G}&\\&\widehat{G} \\ \end{bmatrix} \begin{bmatrix} {\vec {a}} ^\top \\ {\vec {b}} ^\top \end{bmatrix} = \begin{bmatrix} \log A \\ \log B \\ \log (A_V/u) \\ \log B_V \end{bmatrix}. \end{aligned}$$

Note that the leftmost matrix has full rank when ${\vec {v}}$ and ${\vec {1}}$ are linearly independent.

Similarly, let ${\zeta ^*}$ be a ciphertext generated by ${{\textsf {AltGenCiph}}}$. For every $u \in \widehat{{\mathbb {G}}}$, we have that, with overwhelming probability, $\{{\vec {x}},{\vec {y}},{\vec {1}},{\vec {z}} \}$ form a basis for the 4-dimensional space of strands, where ${\vec {x}}$ and ${\vec {y}}$ are the strands of the challenge ciphertext with respect to $u$,¹⁸ and ${\vec {z}}$ is the fixed parameter of the scheme (recall that we require ${\vec {z}}$ to be linearly independent of ${\vec {1}}$). Then the adversary’s view of the private key is constrained as follows:

$$\begin{aligned} \begin{bmatrix} {\vec {1}} \\&\ddots \\&&{\vec {1}} \\ {\vec {x}}&\\&\ddots&\\&{\vec {x}} \\ {\vec {y}}&\\&\ddots&\\&{\vec {y}} \\&&{\vec {x}}&\mu {\vec {x}} \\&&{\vec {y}}&\mu {\vec {y}} \\ \end{bmatrix} \begin{bmatrix} G&\\&\ddots&\\&G \\ \end{bmatrix} \begin{bmatrix} {\vec {c}} _1^\top \\ \vdots \\ {\vec {c}} _n^\top \\ {\vec {d}} ^\top \\ {\vec {e}} ^\top \\ \end{bmatrix} = \begin{bmatrix} \log C _1 \\ \vdots \\ \log C _n \\ \log D \\ \log E \\ \log (C_{X,1}/m_1) \\ \vdots \\ \log (C_{X,n}/m_n) \\ \log C_{Y,1} \\ \vdots \\ \log C_{Y,n} \\ \log P_{X} \\ \log P_{Y} \end{bmatrix}, \end{aligned}$$

where $(m_1, \ldots , m_n)$ and $\mu$ were the inputs to ${{\textsf {AltGenCiph}}}$. Note that when $\{{\vec {1}},{\vec {x}},{\vec {y}} \}$ are linearly independent, the leftmost matrix has full rank for every $\mu \in {\mathbb {Z}}_p$.

The overwhelming event mentioned in the statement of the lemma is that $\{{\vec {1}}, {\vec {v}} \}$ and $\{{\vec {1}},{\vec {x}},{\vec {y}},{\vec {z}} \}$ are basis sets of their respective vector spaces. Hereafter, we condition on this event.

When $b=0$ in the HCCA game, the challenge ciphertext is generated with $(m_1, \ldots , m_n)$ and $\mu = {\textsf {H}} ({{\textsf {canonize}}} (m_1, \ldots , m_n))$, where $(m_1, \ldots , m_n)$ was provided by the adversary. The value $u$ is chosen at random in $\widehat{{\mathbb {G}}}$; for every $u \in \widehat{{\mathbb {G}}}$ there are an equal number of solutions for the private keys in this system of equations, since the leftmost matrix has full rank. In other words, after fixing $b=0$ and fixing $({\zeta ^*}, {pk})$, every possible $u \in \widehat{{\mathbb {G}}}$ is equally likely.

When $b=1$ in the HCCA experiment, the challenge ciphertext is generated using ${{\textsf {RigEnc}}}$; that is, with $(m_1, \ldots , m_n) = (1, \ldots 1)$ and $\mu$ is chosen at random. Again $u$ is chosen at random in $\widehat{{\mathbb {G}}}$. For every $u \in \widehat{{\mathbb {G}}}$ and $\mu \in {\mathbb {Z}}_p$, there are an equal number of solutions for the private keys in this system of equations, since again the leftmost matrix is nonsingular. Thus fixing $b=1$ and fixing $({\zeta ^*}, {pk})$, every possible setting of $(u \in \widehat{{\mathbb {G}}}, \mu \in {\mathbb {Z}}_p)$ is equally likely.

Finally, by the same reasoning, there are an equal number of solutions for the private keys consistent with $b=0$ as for $b=1$. Thus $({\zeta ^*}, {pk})$ is distributed independently of b. $\square$

6.5 Hybrid 2: Alternative Encryption $+$ Decryption

As outlined above, we next consider a hybrid in which ${{\textsc {dec}}}$ and ${{\textsc {rigextract}}}$ queries are answered in a different way. In this section, we let ${\zeta ^*}$ denote the challenge ciphertext in the Hybrid 1 experiment, which was generated using ${{\textsf {AltGenCiph}}}$ (called from either ${{\textsf {Enc}}}$ or ${{\textsf {RigEnc}}}$).

Bad Queries Our arguments in this section generally follow the same structure. The adversary’s view induces a set of public-key constraints and decryption constraints (from ${\zeta ^*}$) on the private key values.

In the HCCA security experiment, fix a public key pk and, if a ${{\textsc {challenge}}}$ query has been made, fix a challenge ciphertext ${\zeta ^*}$ as well. Call a query $\zeta$ to ${{\textsc {dec}}} (\cdot )$ or a query $(\zeta ', \zeta )$ to ${{\textsc {rigextract}}} (\cdot ,\cdot )$ a bad query if the oracle responds with $\bot$ with overwhelming probability, taken over private keys that are consistent with the public key and ${\zeta ^*}$.

The simplest way a ciphertext can be bad is if one of its decryption integrity constraints (Eqs. 6.2 and 6.3) is linearly independent of the constraints given by the public key and challenge ciphertext. In that case, only a negligible fraction of consistent private keys are further consistent with these linearly independent constraints. Thus much of this section involves showing that ciphertexts not of a certain form have linearly independent decryption constraints and are therefore bad.

Hybrid 2 We define Hybrid 2 to be identical to Hybrid 1, except that oracle queries of the following form are handled using the following (exponential-time) procedures. More formally, define the following stateful oracle:

To prove the indistinguishability of Hybrids 1 and 2, it suffices to show that the alternative oracles’ responses match those of the standard oracles, with overwhelming probability. In particular, we establish the following: (1) that these alternative oracles respond with $\bot$ if and only if the query was a bad query as identified above; and (2) that on non-bad queries these alternative oracles give the same response as do the normal oracles.

Properties of CSL Decryption The CSL auxiliary encryption scheme is clearly malleable, being a simple variant of the ElGamal scheme. However, we show that it is malleable only in the following restricted sense. Even when the plaintext of a CSL ciphertext is information-theoretically hidden (i.e., distributed independently of one’s view), it is possible to determine the relationship between two ciphertexts using an exponential-time procedure. This limitation on CSL’s malleability turns out to be crucial in our analysis of the main scheme.

In the next two lemmas, let $U ^*$ be the CSL ciphertext that was generated in response to a ${{\textsc {challenge}}}$ query in Hybrid 1, using ${{\textsf {AltMEnc}}}$ on input $u ^*$.

Lemma 6.8

Fix a CSL public key $(\widehat{g} _{1},\widehat{g} _{2},A,B)$ and challenge ciphertext $U ^* = (V_{1} ^*,V_{2} ^*,A_V ^*,B_V ^*)$, and let $U = (V_{1},V_{2},A_V,B_V)$ be an additional given CSL ciphertext. Then with overwhelming probability there exist values $\pi = \pi (U)$ and $\sigma =\sigma (U)$ such that the purported plaintext of $U$ is $\sigma \cdot {{\textsf {MDec}}} _{\widehat{sk}} (U ^*)^\pi$, for all private keys ${\widehat{sk}}$ consistent with the public key and with the decryption constraints of $U ^*$.

Note that even though the “correct” value of ${{\textsf {MDec}}} _{\widehat{sk}} (U ^*)$ is distributed independently of public key and $U ^*$, the values $\pi$ and $\sigma$ are nevertheless fixed.

Proof

Let ${\vec {v}} ^*$ be the strand of $U ^*$, and let ${\vec {v}}$ be the strand of $U$. As before, we condition on the overwhelming probability event that $\{{\vec {1}},{\vec {v}} ^*\}$ form a basis for the space of strands. Then we may write ${\vec {v}} = \pi {\vec {v}} ^* + \epsilon {\vec {1}}$ for some unique $\pi , \epsilon$. Set $\sigma = A_V/ (A_V ^*)^\pi A ^\epsilon$. The purported plaintext of $U$ is computed as follows:

$$\begin{aligned} \frac{A_V}{ V_{1} ^{a_{1}} V_{2} ^{a_{2}} } = \frac{A_V}{ \left[ (V_{1} ^*)^{a_{1}} (V_{2} ^*)^{a_{2}} \right] ^\pi \left[ \widehat{g} _{1} ^{a_{1}} \widehat{g} _{2} ^{a_{2}} \right] ^\epsilon } = \frac{A_V}{ \left[ A_V ^* / {{\textsf {MDec}}} _{\widehat{sk}} (U ^*) \right] ^\pi A ^\epsilon } = \sigma \cdot {{\textsf {MDec}}} _{\widehat{sk}} (U ^*)^\pi \end{aligned}$$

$\square$

Lemma 6.9

Let $U$ be a CSL ciphertext with $\pi$ and $\sigma$ as above, and suppose that ${{\textsf {MDec}}} _{\widehat{sk}} (U) \ne \bot$ with noticeable probability over the choice of private keys ${\widehat{sk}}$ consistent with ${\widehat{pk}}$ and $U ^*$. Then

$$\begin{aligned} \text{ If } \pi = 0&\text{ then } U \text{ is } \text{ in } \text{ the } \text{ support } \text{ of } {{\textsf {MEnc}}} _{\widehat{pk}} (\sigma ). \\ \text{ If } \pi = 1&\text{ then } U \text{ is } \text{ in } \text{ the } \text{ support } \text{ of } {{\textsf {MCTrans}}} (U ^*,T_\sigma ). \end{aligned}$$

Proof

As above, let ${\vec {v}} = \pi {\vec {v}} ^* + \epsilon {\vec {1}}$ be the CSL strand of $U$, where ${\vec {v}} ^*$ is the CSL strand of $U ^*$. Then $\Pr [ {{\textsf {MDec}}} _{\widehat{sk}} (U) = \bot ] \in \{0,1\}$, since ${{\textsf {MDec}}} (U) \ne \bot$ if and only if $B_V = (B_V ^*)^\pi B^\epsilon$, regardless of the private key.

If $\pi =0$, then the strand of $U$ is a multiple of ${\vec {1}}$, say, ${\vec {v}} = v{\vec {1}}$. Then it is straightforward to see that $U$ decrypts to $\sigma$ with non-negligible probability only if $U = {{\textsf {MEnc}}} _{\widehat{pk}} (\sigma ; v)$.

If $\pi =1$, then ${\vec {v}} = {\vec {v}} ^* + \epsilon {\vec {1}}$. Then it is straightforward to check that $U$ decrypts to $\sigma u ^*$ only if $U = {{\textsf {MCTrans}}} (U ^*, T_\sigma ; \epsilon )$. $\square$

Classifying Bad Queries All of the oracles whose behavior is different between Hybrids 1 and 2 involve calls to ${{\textsf {Integrity}}} _{sk}$ to check certain decryption constraints. We extend the definition of bad queries to these calls to ${{\textsf {Integrity}}}$. A pair $(\zeta ,\mu )$ is integrity-bad if ${{\textsf {Integrity}}} _{sk} (\zeta , {{\textsf {MDec}}} _{\widehat{sk}} (U), \mu ) = 0$, where U is the CSL ciphertext contained in $\zeta$, with overwhelming probability over the choice of private keys consistent with the public key and challenge ciphertext. For convenience of notation, we assume ${{\textsf {Integrity}}} _{sk} (\zeta ,\bot ,\mu ) = 0$.

Throughout this section, we use the following standard notation to refer to the public key and ciphertexts being considered:

• ${pk} = (g _{1},\ldots , g _{4},C _1, \ldots , C _n,D,E)$ is the public key.

• ${\zeta ^*} = ({\vec {X}} ^*, {\vec {C}} _X ^*, P_{X} ^*; {\vec {Y}} ^*, {\vec {C}} _Y ^*, P_{Y} ^*; U ^*)$ is the challenge ciphertext generated using ${{\textsf {AltGenCiph}}}$, with random choice of $\mu ^*$.

• $\zeta = ({\vec {X}}, {\vec {C}} _X, P_{X}; {\vec {Y}}, {\vec {C}} _Y, P_{Y}; U)$ is a purported ciphertext given as a query to an oracle.

Lemma 6.10

A pair $(\zeta ,\mu )$ is integrity-bad unless there exists $\sigma \in \widehat{{\mathbb {G}}}$ such that one of the following cases holds:

• 1. $U$ is in the support of ${{\textsf {MEnc}}} _{\widehat{pk}} (\sigma )$; and there exists $x \in {\mathbb {Z}}_p, y \in {\mathbb {Z}}^*_p$ such that $X_{j} = g_{j} ^{ (x+z_{j}) \sigma }$ and $Y_{j} = g_{j} ^{y\sigma }$, for $j = 1, \ldots , 4$ (similar to ciphertexts generated by ${{\textsf {GenCiph}}}$)

• 2. $U$ is in the support of ${{\textsf {MCTrans}}} (U ^*, T_\sigma )$; and there exists $s \in {\mathbb {Z}}_p, t \in {\mathbb {Z}}^*_p$ such that $X_{j} = (X_{j} ^* (Y_{j} ^*)^s)^\sigma$ and $Y_{j} = (Y_{j} ^*)^{t\sigma }$, for $j = 1, \ldots , 4$; and $\mu = \mu ^*$ (similar to ciphertexts generated by applying ${{\textsf {CTrans}}}$ to ${\zeta ^*}$).

Note that all of the relationships listed in Lemma 6.10 refer to components of ${pk}$, ${\zeta ^*}$, and $\zeta$. These values are well defined from the point of view of the adversary. In particular, there is no reference to values like $u ^*$ or $\mu ^*$, which are distributed independently of the adversary’s view.

Proof

The random choice of $u ^*$ used to generate ${\zeta ^*}$ is independent of the adversary’s view (Lemma 6.7). However, $u ^*$ is related to the fixed values ${\vec {X}} ^*$ and ${\vec {Y}} ^*$ via $X_{j} ^* = g_{j} ^{(x_{j} ^* + z_{j})u ^*}$ and $Y_{j} ^* = g_{j} ^{y_{j} ^*u ^*}$, where ${\vec {x}} ^*$ and ${\vec {y}} ^*$ are the (unknown) strands of ${\zeta ^*}$.

Similarly, when submitting a ciphertext $\zeta$ to an oracle, the adversary supplies the fixed components $U$, ${\vec {X}}$, and ${\vec {Y}}$. The CSL component $U$ encodes a value $u$ which is related to $u ^*$ as $u = \sigma (u ^*)^\pi$ for some $\sigma$ and $\pi$. As before, although $u ^*$ (and perhaps subsequently $u$) may be distributed independently of the adversary’s view, the relationship between them—namely, $\sigma$ and $\pi$—is well defined given the adversary’s view. Furthermore, the strands of $\zeta$ are ${\vec {x}}$ and ${\vec {y}}$, which are related to the fixed values ${\vec {X}}$ and ${\vec {Y}}$ via $X_{j} = g_{j} ^{(x _j+z_j)(\sigma (u ^*)^\pi )}$ and $Y_{j} = g_{j} ^{y _j(\sigma (u ^*)^\pi )}$.

Thus each of the vectors $({\vec {x}} ^*+{\vec {z}})u ^*$, ${\vec {y}} ^*u ^*$, $({\vec {x}} +{\vec {z}})(\sigma (u ^*)^\pi )$, and ${\vec {y}} (\sigma (u ^*)^\pi )$ is well defined given ${pk}, {\zeta ^*}, \zeta$. With overwhelming probability in the Hybrid 1 experiment, the fixed vectors $\{ ({\vec {x}} ^*+{\vec {z}})u ^*, {\vec {y}} ^*u ^*, {\vec {z}}, {\vec {1}} \}$ are a basis for the space of all strands. We condition on this event, and then we can write the fixed vectors $({\vec {x}} +{\vec {z}})u$ and ${\vec {y}} u$ in terms of this basis as follows:

$$\begin{aligned} ({\vec {x}} + {\vec {z}})(\sigma (u ^*)^\pi )&= \alpha \Big (({\vec {x}} ^*+{\vec {z}})u ^*\Big ) + \beta ({\vec {y}} ^*u ^*) + \gamma {\vec {1}} + \delta {\vec {z}} \\ {\vec {y}} (\sigma (u ^*)^\pi )&= \alpha '\Big (({\vec {x}} ^*+{\vec {z}})u ^*\Big ) + \beta '({\vec {y}} ^*u ^*) + \gamma ' {\vec {1}} + \delta ' {\vec {z}} \end{aligned}$$

We have simply expressed fixed vectors in terms of a basis of four fixed vectors, so the coefficients of these linear combinations are also fixed given ${pk}$, $\zeta$, and ${\zeta ^*}$. Solving explicitly for ${\vec {x}}$ and ${\vec {y}}$ in terms of the alternative basis $\{{\vec {1}},{\vec {x}} ^*,{\vec {y}} ^*,{\vec {z}} \}$, we then have:

$$\begin{aligned} {\vec {x}}&= \frac{\gamma }{\sigma (u ^*)^\pi } {\vec {1}} + \frac{\alpha }{\sigma (u ^*)^{\pi -1}} {\vec {x}} ^* + \frac{\beta }{\sigma (u ^*)^{\pi -1}} {\vec {y}} ^* + \left( \frac{\alpha }{\sigma (u ^*)^{\pi -1}} + \frac{\delta }{\sigma (u ^*)^\pi } -1 \right) {\vec {z}} \nonumber \\ {\vec {y}}&= \frac{\gamma '}{\sigma (u ^*)^\pi } {\vec {1}} + \frac{\alpha '}{\sigma (u ^*)^{\pi -1}} {\vec {x}} ^* + \frac{\beta '}{\sigma (u ^*)^{\pi -1}} {\vec {y}} ^* + \left( \frac{\alpha '}{\sigma (u ^*)^{\pi -1}} + \frac{\delta '}{\sigma (u ^*)^\pi } \right) {\vec {z}} \end{aligned}$$

(6.4)

In summary, it would be convenient to characterize bad queries in terms of their strands. But a query $\zeta$ may be derived in some arbitrary way from ${\zeta ^*}$, whose strands are (to some degree) information-theoretically hidden. Still, the relationship between the strands of $\zeta$ and ${\zeta ^*}$ is well defined (given the adversary’s view) and can be uniquely described by the ten parameters $\sigma$, $\pi$, $\alpha$, $\beta$, $\gamma$, $\delta$, $\alpha '$, $\beta '$, $\gamma '$, and $\delta '$ described above. Our analysis proceeds by showing that only very specific settings of these ten parameters can lead to $\zeta$ being a non-bad query. Any ciphertext $\zeta$ of the wrong form will fail one of its decryption constraints with overwhelming probability over the independent randomness in the private key.

The relevant constraints and linear dependence. Hereafter, we will assume that all of the decryption constraints on $\zeta$ are satisfied with non-negligible probability and use this fact to deduce that $\zeta$ must have one of the two desired forms.

The most relevant decryption constraints are the following, which involve the $P_{X}$ and $P_{Y}$ components of the ciphertext:

$$\begin{aligned} \begin{bmatrix} {\vec {x}}&\mu {\vec {x}} \\ {\vec {y}}&\mu {\vec {y}} \end{bmatrix} \begin{bmatrix} G \\&G \end{bmatrix} \begin{bmatrix} {\vec {d}} ^\top \\ {\vec {e}} ^\top \end{bmatrix} \overset{\scriptstyle {\text {?}}}{=} \begin{bmatrix} \log P_{X} \\ \log P_{Y} \end{bmatrix} \end{aligned}$$

(6.5)

These constraints involve the ${\vec {d}}$ and ${\vec {e}}$ components of the private key, which, from the adversary’s view, are constrained by the public key and challenge ciphertext ${\zeta ^*}$ as follows:

$$\begin{aligned} \begin{bmatrix} {\vec {1}} \\&{\vec {1}} \\ {\vec {x}} ^*&\mu ^* {\vec {x}} ^* \\ {\vec {y}} ^*&\mu ^* {\vec {y}} ^* \end{bmatrix} \begin{bmatrix} G \\&G \end{bmatrix} \begin{bmatrix} {\vec {d}} ^\top \\ {\vec {e}} ^\top \end{bmatrix} = \begin{bmatrix} \log D \\ \log E \\ \log P_{X} ^* \\ \log P_{Y} ^* \end{bmatrix} \end{aligned}$$

(6.6)

In order for Eq. (6.5) to be satisfied with non-negligible probability, the following conditions must hold:

• First, the two constraints in Eq. (6.5) must be linear combinations of the public constraints in Eq. (6.6). As described above, a linearly independent decryption constraint can only be satisfied with negligible probability, since the “correct” value of the left-hand side will be randomly distributed, while the ciphertext provides a fixed value for the right-hand side. The constraint would only hold with negligible probability.

• Not only must the constraints of Eq. (6.5) be linearly dependent on those of Eq. (6.6), but the coefficients of this linear dependence must be well defined from the adversary’s view. Recall that the value $u ^*$ is distributed independently of the adversary’s view. So if a constraint was linearly dependent on the equations in Eq. (6.6), but one of the coefficients of that dependence was, say, $u ^*$, then the new decryption constraint could not hold with non-negligible probability. In this case, there would be a different “correct” value of the constraint on the left-hand side for each different choice of $u ^* \in \widehat{{\mathbb {G}}}$. Again, the right-hand side of the constraint would be fixed with respect to $u ^*$, and equality could only happen with negligible ($1/|\widehat{{\mathbb {G}}} |$) probability.

In short, $[{\vec {x}}\ \mu {\vec {x}} ]$ and $[{\vec {y}}\ \mu {\vec {y}} ]$ must be fixed linear combinations of $\{ [{\vec {1}} \vec {0}], [\vec {0} {\vec {1}} ], [{\vec {x}} ^*\ \mu ^*{\vec {x}} ^*], [{\vec {y}} ^*\ \mu ^*{\vec {y}} ^*]\}$. If we substitute for ${\vec {x}}$ and ${\vec {y}}$ according to the relationships in Eq. (6.4), we have that the following expressions must be fixed linear combinations of $\{ [{\vec {1}}\ \vec {0}], [\vec {0}\ {\vec {1}} ], [{\vec {x}} ^*\ \mu ^*{\vec {x}} ^*], [{\vec {y}} ^*\ \mu ^*{\vec {y}} ^*]\}$:

$$\begin{aligned}{}[{\vec {x}}\ \mu {\vec {x}} ]&= \frac{\gamma }{\sigma (u ^*)^\pi } [{\vec {1}}\ \mu {\vec {1}} ] + \frac{1}{\sigma (u ^*)^{\pi -1}} \Big ( \alpha [{\vec {x}} ^* \ \mu {\vec {x}} ^*] + \beta [{\vec {y}} ^*\ \mu {\vec {y}} ^*] \Big ) \nonumber \\&\quad + \left( \frac{\alpha u ^* + \delta }{\sigma (u ^*)^\pi } - 1 \right) [{\vec {z}}\ \mu {\vec {z}} ] \nonumber \\ [{\vec {y}}\ \mu {\vec {y}} ]&= \frac{\gamma '}{\sigma (u ^*)^\pi } [{\vec {1}}\ \mu {\vec {1}} ] + \frac{1}{\sigma (u ^*)^{\pi -1}} \Big ( \alpha ' [{\vec {x}} ^* \ \mu {\vec {x}} ^*] + \beta ' [{\vec {y}} ^*\ \mu {\vec {y}} ^*] \Big ) + \frac{\alpha ' u ^* + \delta '}{\sigma (u ^*)^\pi } [{\vec {z}}\ \mu {\vec {z}} ] \end{aligned}$$

(6.7)

In particular, these expressions must be linear combinations whose coefficients are fixed over random choice of $u ^*$.

We now break down the analysis of these constraints according to the value of $\pi$.

The case of $\pi =0$. In this case, if the CSL component $U$ is to be decrypted successfully, then $U$ must be in the support of ${{\textsf {MEnc}}} _{{\widehat{pk}}}(\sigma )$, from Lemma 6.9.

Substituting $\pi =0$ in Eq. (6.7) leaves the following expression:

$$\begin{aligned}{}[{\vec {x}}\ \mu {\vec {x}} ]&= \frac{\gamma }{\sigma } [{\vec {1}}\ \mu {\vec {1}} ] + \frac{u ^*}{\sigma } \Big ( \alpha [{\vec {x}} ^* \ \mu {\vec {x}} ^*] + \beta [{\vec {y}} ^*\ \mu {\vec {y}} ^*] \Big ) + \left( \frac{\alpha u ^* + \delta }{\sigma } - 1 \right) [{\vec {z}}\ \mu {\vec {z}} ] \\ [{\vec {y}}\ \mu {\vec {y}} ]&= \frac{\gamma '}{\sigma } [{\vec {1}}\ \mu {\vec {1}} ] + \frac{u ^*}{\sigma } \Big ( \alpha ' [{\vec {x}} ^* \ \mu {\vec {x}} ^*] + \beta ' [{\vec {y}} ^*\ \mu {\vec {y}} ^*] \Big ) + \left( \frac{\alpha ' u ^* + \delta '}{\sigma } \right) [{\vec {z}}\ \mu {\vec {z}} ] \end{aligned}$$

Again, this expression must be a fixed linear combination of $\{ [{\vec {1}}\ \vec {0}], [\vec {0}\ {\vec {1}} ], [{\vec {x}} ^*\ \mu ^*{\vec {x}} ^*], [{\vec {y}} ^*\ \mu ^*{\vec {y}} ^*]\}$. However, $[{\vec {z}}\ \mu {\vec {z}} ]$ is linearly independent of the required set, so the coefficients of $[{\vec {z}}\ \mu {\vec {z}} ]$ in the above expression must be zero with non-negligible probability over the choice of $u ^*$. This is only possible when $\alpha = \alpha ' = \delta ' = 0$ and $\delta =\sigma$. Furthermore, the other coefficients in which $u ^*$ appears must be fixed with non-negligible probability over the choice of $u ^*$. This is only possible when further $\beta =\beta '=0$. Then we must have $\gamma ' \ne 0$, since otherwise ${\vec {y}}$ is the all-zeroes vector and the ciphertext is rejected outright.

Substituting these values, we have that ${\vec {x}} = (\gamma /\sigma ){\vec {1}}$ for some $\gamma$, and ${\vec {y}} = (\gamma '/\sigma ){\vec {1}}$ for some $\gamma ' \ne 0$. In terms of the original values from the ciphertext, this implies that there exists a fixed $x \in {\mathbb {Z}}_p$ and $y\in {\mathbb {Z}}^*_p$ such that $X_{j} = g_{j} ^{ (x+z_{i})\sigma }$ and $Y_{j} = g_{j} ^{ y\sigma }$ for all j. In addition, we have shown that $U$ is in the support of ${{\textsf {MEnc}}} _{\widehat{pk}} (\sigma )$. This is the first desired case from the lemma statement.

The case of $\pi =1$. In this case, if the CSL component $U$ is to be decrypted successfully, then $U$ must be in the support of ${{\textsf {MCTrans}}} _{{\widehat{pk}}}(U ^*, T_\sigma )$, from Lemma 6.9.

Substituting $\pi =1$ in Eq. (6.7) leaves the following expression:

$$\begin{aligned}{}[{\vec {x}}\ \mu {\vec {x}} ]&= \frac{\gamma }{\sigma u ^*} [{\vec {1}}\ \mu {\vec {1}} ] + \frac{1}{\sigma } \Big ( \alpha [{\vec {x}} ^* \ \mu {\vec {x}} ^*] + \beta [{\vec {y}} ^*\ \mu {\vec {y}} ^*] \Big ) + \left( \frac{\alpha u ^* + \delta }{\sigma u ^*} - 1 \right) [{\vec {z}}\ \mu {\vec {z}} ] \\ [{\vec {y}}\ \mu {\vec {y}} ]&= \frac{\gamma '}{\sigma u ^*} [{\vec {1}}\ \mu {\vec {1}} ] + \frac{1}{\sigma } \Big ( \alpha ' [{\vec {x}} ^* \ \mu {\vec {x}} ^*] + \beta ' [{\vec {y}} ^*\ \mu {\vec {y}} ^*] \Big ) + \frac{\alpha ' u ^* + \delta ' }{\sigma u ^*} [{\vec {z}}\ \mu {\vec {z}} ] \end{aligned}$$

As in the previous case, the coefficients of $[{\vec {z}}\ \mu {\vec {z}} ]$ must be zero with non-negligible probability over the choice of $u ^*$. This is only possible when $\alpha ' = \delta = \delta '=0$ and $\alpha =\sigma$. Then, the other coefficients in which $u ^*$ appears must be fixed with non-negligible probability over the choice of $u ^*$. This is only possible when further $\gamma =\gamma ' = 0$. Then we must have $\beta ' \ne 0$, since otherwise ${\vec {y}}$ is the all-zeroes vector and the ciphertext is rejected outright. Since $\beta '$ is nonzero, we must have that $\mu = \mu ^*$; otherwise $[{\vec {y}}\ \mu {\vec {y}} ] = (\beta '/\sigma )[{\vec {y}} ^*\ \mu {\vec {y}} ^*]$ would be linearly independent of the allowed basis vectors.

Substituting these values, we have that ${\vec {x}} = {\vec {x}} ^* + (\beta /\sigma ){\vec {y}} ^*$ for some $\beta$, and ${\vec {y}} = (\beta '/\sigma ){\vec {y}} ^*$ for some $\beta ' \ne 0$. In terms of the original values from the ciphertext, this implies that there exists a fixed $s \in {\mathbb {Z}}_p$ and $t\in {\mathbb {Z}}^*_p$ such that $X_{j} = (X_{j} ^*(Y_{j} ^*)^s)^\sigma$ and $Y_{j} = (Y_{j} ^*)^{t\sigma }$ for all j. In addition, we have shown that $\mu = \mu ^*$ and that $U$ is in the support of ${{\textsf {MCTrans}}} _{{\widehat{pk}}}(U ^*, T_\sigma )$. This is the second desired case from the lemma statement.

The case of $\pi \not \in \{0,1\}$. We have assumed that the ciphertext satisfies its decryption constraints with non-negligible probability, so it suffices to show a contradiction. This would prove that all oracle queries having $\pi \not \in \{0,1\}$ are in fact bad queries. We now establish the desired contradiction, after conditioning the entire Hybrid 1 HCCA experiment on an overwhelming-probability event.

First, recall the expressions in Eq. (6.7), in particular the expression for $[{\vec {y}}\ \mu {\vec {y}} ]$. By the same reasoning as in the previous two cases, we must have $\alpha '=\delta '=0$ so that the coefficient of $[{\vec {z}}\ \mu {\vec {z}} ]$ is zero. Suppose $\mu \ne \mu ^*$. Then $[{\vec {y}} ^*\ \mu {\vec {y}} ^*]$ in the expression in Eq. (6.7) is linearly independent of the allowed basis for this expression. Thus the coefficient of $[{\vec {y}} ^*\ \mu {\vec {y}} ^*]$ in the expression must be zero, which is only possible when $\beta '=0$. Then since $(u ^*)^\pi$ is uniformly distributed in $\widehat{{\mathbb {G}}}$, we must have $\gamma ' = 0$ to fix the remaining coefficient in the expression. But then, ${\vec {y}}$ is the all-zeroes vector and the ciphertext is rejected outright.

Therefore we must have $\alpha '=\delta '=0$ as well as $\mu = \mu ^*$. We now consider the decryption constraints on $P_{Y}$ and $C_{Y,1}$, which are as follows (substituting for ${\vec {y}}$ given that $\alpha '=\delta '=0$):

$$\begin{aligned} \begin{bmatrix} \log C_{Y,1} \\ \log P_{Y} \end{bmatrix}&\overset{\scriptstyle {\text {?}}}{=} \begin{bmatrix} {\vec {y}} \\&{\vec {y}}&\mu {\vec {y}} \end{bmatrix} \begin{bmatrix} G \\&G \\&G \end{bmatrix} \begin{bmatrix} {\vec {c}} _1^\top \\ {\vec {d}} ^\top \\ {\vec {e}} ^\top \end{bmatrix} \\&= \begin{bmatrix} \frac{\gamma '}{\sigma (u ^*)^\pi }&0&\frac{\beta '}{\sigma (u ^*)^{\pi -1}}&0 \\ 0&\frac{\gamma '}{\sigma (u ^*)^\pi }&0&\frac{\beta '}{\sigma (u ^*)^{\pi -1}} \end{bmatrix} \begin{bmatrix} {\vec {1}} \\&{\vec {1}}&\mu ^* {\vec {1}} \\ {\vec {y}} ^* \\&{\vec {y}} ^*&\mu ^* {\vec {y}} ^* \end{bmatrix} \begin{bmatrix} G \\&G \\&G \end{bmatrix} \begin{bmatrix} {\vec {c}} _1^\top \\ {\vec {d}} ^\top \\ {\vec {e}} ^\top \end{bmatrix} \\&= \begin{bmatrix} \frac{\gamma '}{\sigma (u ^*)^\pi }&0&\frac{\beta '}{\sigma (u ^*)^{\pi -1}}&0 \\ 0&\frac{\gamma '}{\sigma (u ^*)^\pi }&0&\frac{\beta '}{\sigma (u ^*)^{\pi -1}} \end{bmatrix} \begin{bmatrix} \log C _1 \\ \log (D E ^{\mu ^*}) \\ \log C_{Y,1} ^* \\ \log P_{Y} ^* \end{bmatrix} \end{aligned}$$

We can simplify these constraints and write them as follows:

$$\begin{aligned} \begin{array}{rrr} (\sigma \log P_{Y})(u ^*)^\pi &{} {} - (\beta '\sigma \log P_{Y} ^*)u ^* &{} {} - (\gamma ' \log (D E ^{\mu ^*})) = 0 \\ (\sigma \log C_{Y,1})(u ^*)^\pi &{} {} - (\beta '\sigma \log C_{Y,1} ^*)u ^* &{} {} - (\gamma ' \log C _1) = 0 \end{array} \end{aligned}$$

Note that these are polynomials in $u ^*$ of degree $\pi$, whose coefficients are fixed. No terms collect together, as $\pi \not \in \{0,1\}$. We are assuming that these two polynomials in $u ^*$ are simultaneously satisfied with non-negligible probability. However, this assumption results in a contradiction, after conditioning the entire interaction on an overwhelming-probability event:

• If one of the polynomials is not identically zero but has some coefficient equal to zero, then that polynomial is equivalent to (i.e, has the same roots as) an affine function of one of the terms $\{ u ^*, (u ^*)^\pi , (u ^*)^{\pi -1}\}$, with otherwise fixed coefficients. Since $u ^*$ is uniform in $\widehat{{\mathbb {G}}}$, then each of $\{ u ^*, (u ^*)^\pi , (u ^*)^{\pi -1}\}$ is also distributed uniformly (though their joint distribution is not uniform). We have an affine function of one term, which is uniformly distributed, so the equation is satisfied with only negligible probability.

• If neither polynomial has a zero coefficient, and the two polynomials are not scalar multiples of each other, then some linear combination of the constraints is an affine function in one of the terms $\{ u ^*, (u ^*)^\pi \}$, otherwise with fixed coefficients. Whenever the two original polynomial equations are simultaneously satisfied, this linear combination of the two is also satisfied. For the same reason as the previous case, however, this affine function can only be satisfied with negligible probability.

• If neither polynomial has a zero coefficient, and the two polynomials are scalar multiples of each other, then their pairs of corresponding coefficients have the same ratios. In particular, we have the following equality (after cancelation):

  $$\begin{aligned} \frac{\log (D E ^{\mu ^*})}{\log C _1} = \frac{\log P_{Y} ^*}{\log C_{Y,1} ^*} \end{aligned}$$

  The challenge ciphertext (including the components $P_{Y} ^*$ and $C_{Y,1} ^*$) is generated after $C _1$, $D$, $E$, and $\mu ^*$ are fixed. Thus it is only with negligible probability over the randomness of ${{\textsf {AltGenCiph}}}$ that $C_{Y,1} ^*$ and $P_{Y} ^*$ satisfy this condition. We therefore condition the entire HCCA experiment on this event not happening.

• The only other remaining case is that one polynomial is identically zero. Since $\sigma \ne 0$ (it is from $\widehat{{\mathbb {G}}}$, a subgroup of ${\mathbb {Z}}^*_p$), we must have either $P_{Y}$ or $C_{Y,1}$ equal to zero. It is straightforward to see that either of these events happens only with negligible probability over the randomness of the key generation. We therefore condition the entire HCCA experiment on this event not happening.

We have reached a contradiction by assuming that a ciphertext with parameter $\pi \not \in \{0,1\}$ satisfies its decryption constraints with non-negligible probability. Thus ciphertexts with this property are always bad queries to ${{\textsf {Integrity}}}$. $\square$

We now use this characterization of integrity-bad values to show that the alternate oracles in Hybrid 2 give responses that are consistent with the normal oracles in Hybrid 1.

Lemma 6.11

Let ${\mathcal {E}}$ denote our main construction. For every non-uniform PPT adversary ${{\mathcal {A}}}$ and $b \in \{0,1\}$, we have (unconditionally):

$$\begin{aligned} \Pr [ {{\mathcal {A}}} ^{\widehat{{\mathcal {O}}}^{{\textsf {hyb-1}}}_{\lambda ,b}}(1^\lambda ) = 1 ] \approx \Pr [ {{\mathcal {A}}} ^{\widehat{{\mathcal {O}}}^{{\textsf {hyb-2}}}_{\lambda ,b}}(1^\lambda ) = 1 ]. \end{aligned}$$

Proof

We prove the claim by showing that the oracle responses in Hybrid 2 match those of Hybrid 1, with overwhelming probability. More specifically, we will establish two claims about Hybrid 2:

• The alternative oracles (${{\textsc {dec}}}$ and ${{\textsc {rigextract}}}$) return $\bot$ if and only if the query was a bad query, or some other negligible-probability event happens (i.e., the adversary has solved discrete logarithm or found a hash collision).

• For non-bad queries, the alternative oracles’ responses match those of Hybrid 1.

Hence, the two hybrids agree on responses to non-bad oracle queries. For bad oracle queries, we point out that the alternative oracles in Hybrid 2 do not use the secret key at all. So the adversary’s view contains no information about the secret key beyond public information ${pk}$ and ${\zeta ^*}$. Bad queries are defined as queries to which $\bot$ is the correct answer, with overwhelming probability over the secret key conditioned on ${pk}$ and ${\zeta ^*}$. This describes the situation now in Hybrid 2, and so we get that oracle answers to bad queries are consistent with Hybrid 1 with overwhelming probability.

We proceed by considering a non-bad query. The alternative oracles that we consider (${{\textsc {dec}}}$ and ${{\textsc {rigextract}}}$) both invoke the ${{\textsf {Integrity}}}$ subroutine (${{\textsf {Integrity}}}$ may be called twice while servicing a ${{\textsc {dec}}}$ query: once from ${{\textsf {Dec}}}$ and once from ${{\textsf {RigExtract}}}$). Assuming the initial oracle query is non-bad, each call to ${{\textsf {Integrity}}}$ must involve a $(\zeta , \mu )$ pair which is not integrity-bad. So we may apply the characterization of Lemma 6.10 with respect to the queried ciphertexts.

We establish the above claims about Hybrid 2, considering 3 cases of queries:

${{\textsc {dec}}}$ queries when $b=0$. In this case, the challenge ciphertext ${\zeta ^*}$ was generated using ${{\textsf {AltGenCiph}}} _{sk} ( (m^*_1, \ldots , m^*_n), \mu ^*)$, where ${{\textsf {msg}} ^*} = (m^*_1, \ldots , m^*_n)$ is the plaintext given by the adversary in its ${{\textsc {challenge}}}$ query, and $\mu ^* = {\textsf {H}} ( {{\textsf {canonize}}} (m^*_1, \ldots , m^*_n))$.

In Hybrid 1, these queries are answered using the standard ${{\textsf {Dec}}}$ oracle. On input query $\zeta$, it computes the purported plaintext $(m_1, \ldots , m_n)$ and calls ${{\textsf {Integrity}}}$ using the value $\mu = {\textsf {H}} ({{\textsf {canonize}}} (m_1, \ldots , m_n))$. By our assumption, $(\zeta ,\mu )$ is not integrity-bad. As such, it satisfies either case 1 or case 2 of Lemma 6.10:

• In case 1, the ${\vec {X}}$, ${\vec {Y}}$, and $U$ components of $\zeta$ are as they would be if generated by ${{\textsf {Enc}}} _{pk} (\cdot )$. It is straightforward to verify that the remaining components of $\zeta$ lead to a purported plaintext $(m_1, \ldots , m_n)$ and satisfied integrity constraints with $\mu = {\textsf {H}} ({{\textsf {canonize}}} (m_1, \ldots , m_n))$ if and only $\zeta$ is in the support of ${{\textsf {Enc}}} _{pk} (m_1, \ldots , m_n)$. The oracle’s response in this case is $(m_1, \ldots , m_n)$.

• In case 2, the ${\vec {X}}$, ${\vec {Y}}$, and $U$ components of $\zeta$ are as they would be if generated by ${{\textsf {CTrans}}} _{pk} ({\zeta ^*},\cdot )$. In case 2, we must also have $\mu = \mu ^*$. By the collision resistance of ${\textsf {H}}$, this implies ${{\textsf {canonize}}} (m_1, \ldots , m_n) = {{\textsf {canonize}}} (m^*_1, \ldots , m^*_1)$ with overwhelming probability; that is, ${\vec {\tau }} = (m^*_1,\ldots , m^*_n) * (m_1, \ldots , m_n)^{-1} \in {\mathbb {H}}$ so $T_{\vec {\tau }}$ is an allowed transformation. Then the ${\vec {C}} _X$ components are as they would be if generated by ${{\textsf {CTrans}}} _{pk} ({\zeta ^*}, T_{\vec {\tau }})$. It is straightforward to see that the remaining integrity constraints are satisfied if and only if $\zeta$ is in the support of ${{\textsf {CTrans}}} _{pk} ({\zeta ^*}, T_{\vec {\tau }})$. The oracle’s response in this case is ${\vec {\tau }} * (m^*_1, \ldots , m^*_n)$.

Summarizing, the only non-bad queries in this case are those ciphertexts in the supports of ${{\textsf {Enc}}} _{pk} (\cdot )$ and ${{\textsf {CTrans}}} _{pk} ({\zeta ^*},\cdot )$. We see that the responses given in Hybrid 2 match those described above for queries of the specified form.

${{\textsc {dec}}}$ queries when $b=1$. In this case, the challenge ciphertext ${\zeta ^*}$ was generated using ${{\textsf {AltGenCiph}}} _{sk} ((1,\ldots ,1), \mu ^*)$ for a random choice of $\mu ^*$.

In Hybrid 1, these queries are answered using a combination of ${{\textsf {RigExtract}}}$ and ${{\textsf {Dec}}}$. On input query $\zeta$, it first calls ${{\textsf {Integrity}}}$ with value $\mu ^*$. If this fails, then ${{\textsf {Integrity}}}$ is called with a value $\mu$ derived from the ciphertext’s purported plaintext. Again by our assumption, one of the pairs $(\zeta , \mu ^*)$, $(\zeta , \mu )$ must not be integrity-bad: Lemma 6.10.

• If $\zeta$ satisfies case 1 of Lemma 6.10, then the ciphertext information-theoretically fixes at most one value $\mu$ such that ${{\textsf {Integrity}}} _{sk} (\zeta ,\cdot ,\mu )$ can return 1. Since $\mu ^*$ is distributed independently of the adversary’s view, the first call to ${{\textsf {Integrity}}}$ which uses $\mu ^*$ will fail with overwhelming probability.

  Then ${{\textsf {RigExtract}}}$ calls ${{\textsf {Dec}}}$ directly, and the analysis is identical to the previous case. We must have that $\zeta$ is in the support of ${{\textsf {Enc}}} _{pk} (m_1, \ldots , m_n)$, and the final oracle response is $(m_1, \ldots , m_n)$.

• If $\zeta$ satisfies case 2 of Lemma 6.10, then indeed $(\zeta , \mu ^*)$ may not be integrity-bad. Then the ${\vec {X}}$, ${\vec {Y}}$, and $U$ components of $\zeta$ are as they would be if generated by ${{\textsf {CTrans}}} _{pk} ({\zeta ^*},\cdot )$. It is straightforward to verify that ${{\textsf {Integrity}}}$ succeeds only if the ciphertext components ${\vec {C}} _Y$, $P_{X}$, and $P_{Y}$ are further consistent with ${{\textsf {CTrans}}} _{pk} ({\zeta ^*},\cdot )$. Finally, ${{\textsf {RigExtract}}}$ verifies that the purported plaintext of $\zeta$ is ${\vec {\tau }} \in {\mathbb {H}}$. These events happen if and only if $\zeta$ is in the support of ${{\textsf {CTrans}}} _{pk} ({\zeta ^*},T_{\vec {\tau }})$ for $T_{\vec {\tau }} \in {\mathcal {T}}$. In this case, the oracle response is ${\vec {\tau }} * (m^*_1, \ldots , m^*_n)$. However, if the oracle reaches the point where it passes $\zeta$ to ${{\textsf {Dec}}}$, then the oracle will call ${{\textsf {Integrity}}}$ on a value $\mu$ derived from the purported plaintext of $\zeta$. As in the previous case, a ciphertext whose ${\vec {X}}$, ${\vec {Y}}$, and $U$ components satisfy case 2 of Lemma 6.10 information-theoretically fixes a purported plaintext, and thus this value $\mu$. Only with negligible probability will this fixed value $\mu$ equal $\mu ^*$, which is distributed independently of the adversary’s view. Thus the second call to ${{\textsf {Integrity}}}$ cannot succeed with more than negligible probability.

As in the $b=0$ case, the only non-bad queries are those ciphertexts in the supports of ${{\textsf {Enc}}} _{pk} (\cdot )$ and ${{\textsf {CTrans}}} _{pk} ({\zeta ^*},\cdot )$. Again, the responses in this case match those of Hybrid 2 oracle.

${{\textsc {rigextract}}}$  queries: In Hybrid 1, the oracle is implemented as follows. On input $(\zeta ,\zeta ')$, it finds $(\zeta ',S)$ recorded internally, then calls ${{\textsf {RigExtract}}}$, which in turn calls ${{\textsf {Integrity}}}$ using value S. This value S was chosen at random during a previous ${{\textsc {rigenc}}}$ query. By our assumption, $(\zeta , S)$ is not integrity-bad.

• If the query satisfies case 1 of Lemma 6.10, then by analogous reasoning as in the previous cases, $\zeta$ must be in the support of ${{\textsf {CTrans}}} _{pk} (\zeta ', T_{\vec {\tau }})$ (equivalently, the support of ${{\textsf {GenCiph}}} _{pk} ({\vec {\tau }},S)$) for some $T_{\vec {\tau }} \in {\mathcal {T}}$. The oracle’s response in this case is $T_{\vec {\tau }}$.

• If the query satisfies case 2 of Lemma 6.10, then we must have $\mu ^*$ (used to generate the challenge ciphertext ${\zeta ^*}$) equal to S (used to generate rigged ciphertext $\zeta '$ in a previous ${{\textsc {rigenc}}}$ query). We consider two cases, depending on b:

  When $b=1$, consider that $\zeta '$ was generated using ${{\textsf {GenCiph}}}$ rather than ${{\textsf {AltGenCiph}}}$. Therefore, the value S is information-theoretically fixed given ${pk}$ and $\zeta '$. Then $\mu ^* = S$ only with negligible probability, since S is fixed and $\mu ^*$ is distributed independently at random.

  When $b=0$, $\mu ^*$ is computed as ${\textsf {H}} ({{\textsf {canonize}}} (m_1^*, \ldots , m_n^*))$, where ${{\textsf {msg}} ^*} = (m_1^*, \ldots , m_n^*)$ is the plaintext given by the adversary in its ${{\textsc {challenge}}}$ query. We argue that $\mu ^* = S$ can happen only with negligible probability. If $\zeta '$ was generated after the ${{\textsc {challenge}}}$ query, then $\mu ^* = S$ with negligible probability simply because $\mu ^*$ is fixed before S is chosen at random. Otherwise, if $\zeta '$ is generated after the ${{\textsc {challenge}}}$ query, then information about S is given to the adversary, although only “in the exponent” of ${\mathbb {G}}$. Here it is important that the challenge oracle does not reveal S to the adversary in ${{\textsc {rigenc}}}$ queries. For the adversary to be given a random S in the exponent and subsequently be able to specify $(m_1^*, \ldots , m_n^*)$ such that $S = {\textsf {H}} ({{\textsf {canonize}}} (m_1^*, \ldots , m_n^*))$, the adversary must essentially solve the discrete logarithm problem in ${\mathbb {G}}$.¹⁹ In a group such as ${\mathbb {G}}$ in which the DDH assumption holds, this can only happen with negligible probability.

In summary, the only non-bad queries here are those in which $\zeta$ is in the support of ${{\textsf {CTrans}}} _{pk} (\zeta ',T)$ for $T \in {\mathcal {T}}$. Clearly the output of the alternate Hybrid 2 oracle is consistent with the Hybrid 1 oracle in this case. $\square$

6.6 Completing the Proof

We can now complete the proof of HCCA security:

Proof of Theorem 6.1

By Lemmas 6.6 and 6.11, we have that

$$\begin{aligned} \Pr \left[ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{{\textsf {RigEnc}}},{{\textsf {RigExtract}}}}_{\lambda ,b}}(1^\lambda ) = 1 \right] \approx \Pr \left[ {{\mathcal {A}}} ^{\widehat{{\mathcal {O}}}^{{\textsf {hyb-2}}}_{\lambda ,b}}(1^\lambda ) = 1 \right] \end{aligned}$$

for all adversaries ${{\mathcal {A}}}$ and $b\in \{0,1\}$. It suffices to show that the adversary’s advantage in Hybrid 2 is zero; that is,

$$\begin{aligned} \Pr \left[ {{\mathcal {A}}} ^{\widehat{{\mathcal {O}}}^{{\textsf {hyb-2}}}_{\lambda ,0}}(1^\lambda ) = 1 \right] = \Pr \left[ {{\mathcal {A}}} ^{\widehat{{\mathcal {O}}}^{{\textsf {hyb-2}}}_{\lambda ,1}}(1^\lambda ) = 1 \right] \end{aligned}$$

In Hybrid 2, the adversary sees only the public key, challenge ciphertext, and responses to ${{\textsc {dec}}}$, ${{\textsc {rigenc}}}$, ${{\textsc {rigextract}}}$ queries. However, responses to these three kinds of queries are computed using only the public key, challenge plaintext, and challenge ciphertext. Thus, the adversary’s entire view is a function of the public key and challenge ciphertext. From Lemma 6.7, we see that the public key and challenge ciphertext (hence, the adversary’s entire view) are distributed independently of the choice bit b.

7 Opinion Polling Protocol Application

We now present an “opinion poll” protocol that elegantly illustrates the power of HCCA-secure encryption. The protocol is motivated by the following scenario:

A pollster wishes to collect information from many respondents. However, the respondents are concerned about the anonymity of their responses. Indeed, it is in the interest of the pollster to set things up so that the respondents are guaranteed anonymity, especially if the subject of the poll is sensitive personal information. To help collect responses anonymously, the pollster can enlist the help of an external tabulator. The respondents require that the external tabulator too does not see their responses and that if the tabulator is honest, then responses are anonymized for the pollster (i.e., so that he cannot link responses to respondents). The pollster, on the other hand, does not want to trust the tabulator at all: If the tabulator tries to modify any responses, the pollster should be able to detect this so that the poll can be invalidated.

More formally, we give a secure protocol for the UC ideal functionality ${\mathcal {F}}_{{\textsf {poll}}}$, described in Fig. 3, where $P_{{\textsf {client}}}$ is the pollster, $P_{{\textsf {server}}}$ is the tabulator, and $P_1, \ldots , P_n$ are the respondents.

Fig. 3

UC ideal functionality ${\mathcal {F}}_{{\textsf {poll}}}$

Verifiable Shuffling, Mix-Nets, and Voting Our opinion poll functionality can be viewed as an instantiation of verifiable shuffling (see e.g., [35, 38]). In a verifiable shuffle, a server takes in a collection of ciphertexts and outputs a random permutation in such a way that other parties are convinced that the shuffling server did not cheat; i.e., a shuffler cannot tamper with or omit any input ciphertext.

Verifying a shuffle typically involves using special-purpose zero-knowledge proofs, which are generally interactive and complicated. Even protocols whose verification is non-interactive rely on a common reference string setup [37]. Our approach is novel in that the shuffle’s integrity can be verified without any zero-knowledge proof mechanism. Instead we leverage the strong limitations that the encryption scheme places on a malicious shuffler, resulting in a very efficient and simple protocol, which is secure even in the UC framework with no setups.

Verifiable shuffles are used in mix-nets [20] and in voting protocols. However, in our setting the shuffle is only verified to the pollster, and not to the respondents. In an election, the respondents also have an interest in the integrity of the shuffle (to know that their votes are included in the tally). We note that an election protocol (in which all participants receive guaranteed correct results) is not possible in the UC framework without trusted setups, given the impossibility results of [55].

The Protocol Our protocol is described in detail in Fig. 4. The main idea is to use an HCCA-secure, transformation-hiding scheme, whose message space ${\mathbb {G}} ^2$ (for a cyclic group ${\mathbb {G}}$), and whose only allowed operations are those of the form $(m,r) \mapsto (m, rs)$ for a fixed group element s. In other words, anyone can apply the group operation to (multiply) the second plaintext component with a known value, but the first component is completely non-malleable, and the two components remain “tied together.” Our construction from Sect. 5 can easily accommodate these requirements, for instance, by setting parameter ${\mathbb {H}} = \{1\} \times {\mathbb {G}}$.

To initiate the opinion poll, the pollster generates a (multiplicative) secret sharing $r_1, \ldots , r_n$ of a random secret group element R, then sends to the ith respondent a share $r_i$. Each respondent sends ${{\textsf {Enc}}} (m_i, r_i)$ to the tabulator, where $m_i$ is his response to the poll. Now the tabulator can blindly rerandomize the shares of R (multiply the ith share by a random $s_i$, such that $\prod _i s_i = 1$), shuffle the resulting ciphertexts, and send them to the pollster. The pollster will ensure that the shares encode the secret R and accept the results.

The security of the protocol is informally argued as follows. A corrupt pollster only sees a random permutation of the responses, and a completely random sharing of R. There is no way to link any responses to the $r_i$ shares he originally dealt to the respondents, either by looking at the new shares of R or via the encryption scheme itself (we assume that the respondents send their ciphertexts to the tabulator through a secure channel). The tabulator sees only encrypted data and in particular has no information about the shares $r_i$. The only way the tabulator could successfully generate ciphertexts whose second components are shares of R is by making exactly one of his ciphertexts be derived from each respondent’s ciphertext. By the non-malleability of the encryption scheme, each response $m_i$ is inextricably “tied to” the corresponding share $r_i$ and cannot be modified, so each respondent’s response must be represented exactly once in the tabulator’s output without tampering. Finally, observe that the responses of malicious respondents must be independent of honest parties’ responses—by “copying” an honest respondent’s ciphertext to the tabulator, a malicious respondent also “copies” the corresponding $r_i$, which would cause the set of shares to be inconsistent with overwhelming probability.

Fig. 4

Opinion poll protocol

Theorem 7.1

If ${\mathcal {E}}$ is HCCA-secure and unlinkable with parameters as described above, and $|{\mathbb {G}} |$ is superpolynomial in the security parameter, then our protocol is a secure realization of ${\mathcal {F}}_{{\textsf {poll}}}$, in the point-to-point secure-channels model, against static adversaries.²⁰

Proof

Given a real-world adversary ${{\mathcal {A}}}$, we construct an ideal-world simulator ${{\mathcal {S}}}$. We break the proof down into 4 cases according to which parties ${{\mathcal {A}}}$ corrupts:

Case 1: If ${{\mathcal {A}}}$ corrupts neither $P_{{\textsf {server}}}$ nor $P_{{\textsf {client}}}$, then suppose by symmetry that ${{\mathcal {A}}}$ corrupts some input parties $P_1, \ldots , P_k$. Then the main task for ${{\mathcal {S}}}$ is to extract the inputs of each corrupt $P_i$ and send them to ${\mathcal {F}}_{{\textsf {poll}}}$. ${{\mathcal {S}}}$ simply does the following:

• 1. On receiving $({{\textsc {setup}}}, P_{{\textsf {client}}}, P_{{\textsf {server}}}, P_1, \ldots , P_n)$ from ${\mathcal {F}}_{{\textsf {poll}}}$, generate $({pk},{sk}) \leftarrow {{\textsf {KeyGen}}}$. Choose random $r_1, \ldots , r_k \leftarrow {\mathbb {G}}$ and simulate that $P_{{\textsf {client}}}$ broadcast $({pk},P_{{\textsf {server}}})$ and sent $r_i$ to each corrupt input party $P_i$.

• 2. Whenever corrupt party $P_i$ sends a ciphertext $C_i$ to $P_{{\textsf {server}}}$:

  • (a) If ${{\textsf {Dec}}} _{sk} (C_i) = \bot$, then send $({{\textsc {input}}},\bot )$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of $P_i$. Otherwise let $(m_i, r'_i) \leftarrow {{\textsf {Dec}}} _{sk} (C_i)$.

  • (b) If this is the last party $i \in \{1,\ldots ,k\}$ to send a ciphertext to $P_{{\textsf {server}}}$, and $\prod _i r'_i \ne \prod _i r_i$, then send $({{\textsc {input}}},\bot )$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of $P_i$.

  • (c) Otherwise, send $({{\textsc {input}}}, m_i)$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of $P_i$.

It is straightforward to see that in the cases where ${{\mathcal {S}}}$ sends $({{\textsc {input}}}, \bot )$, then by the honest behavior of $P_{{\textsf {server}}}$ and $P_{{\textsf {client}}}$, the protocol would have mandated that $P_{{\textsf {client}}}$ refuse the output.

Case 2: If ${{\mathcal {A}}}$ corrupts $P_{{\textsf {client}}}$ and (without loss of generality) input parties $P_1, \ldots , P_k$, then ${{\mathcal {S}}}$ does the following:

• When corrupt $P_{{\textsf {client}}}$ broadcasts $({pk},P_{{\textsf {server}}})$ and sends $r_i$ to each honest input party $P_i$, send $({{\textsc {setup}}}, P_{{\textsf {client}}}, P_{{\textsf {server}}}, P_1, \ldots , P_n)$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of $P_{{\textsf {client}}}$.

• When a corrupt input party $P_i$ sends a ciphertext $C_i$ to honest $P_{{\textsf {server}}}$, send $({{\textsc {input}}},m_0)$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of $P_i$, where $m_0$ is any arbitrary fixed message.

• When ${\mathcal {F}}_{{\textsf {poll}}}$ gives the final output to ${{\mathcal {S}}}$, remove as many $m_0$’s from the output list as there are corrupt input parties. Arbitrarily order the remaining outputs as $m_{k+1}, \ldots , m_n$. For each $i \in [n]$, choose a random $s_i$ such that $\prod _i s_i = 1$. Simulate that $P_{{\textsf {server}}}$ sends a random permutation of $\{ {{\textsf {Enc}}} _{pk} (m_i, r_is_i) ~|~ i>k \} \cup \{ {{\textsf {CTrans}}} (C_i, s_i) ~|~ i \le k\}$ to $P_{{\textsf {client}}}$.

Since $P_{{\textsf {client}}}$ is corrupt, ${{\mathcal {S}}}$ can legally obtain the set of honest input parties’ inputs. The only difference therefore between the view of ${{\mathcal {A}}}$ in the real world and our simulation is that in the real world, $P_{{\textsf {client}}}$ sees ${{\textsf {CTrans}}} ({{\textsf {Enc}}} _{pk} (m_i, r_i), s_i)$ for each honest party $P_i$, while in the simulation, $P_{{\textsf {client}}}$ sees ${{\textsf {Enc}}} _{pk} (m_i, r_i s_i)$. By the unlinkability property of the scheme, this difference is indistinguishable, even when $P_{{\textsf {client}}}$ maliciously chooses ${pk}$. Also in the simulation, each $m_i$ is paired with a potentially different $r_i$ than might be the case in the real-world protocol (since the simulator receives a shuffled list of $m_i$ values). However, the distribution of $(m_i, r_is_i)$ pairs is independent of the initial assignments of $m_i$’s to $r_i$’s.

Case 3: If ${{\mathcal {A}}}$ corrupts $P_{{\textsf {server}}}$ and input parties $P_1, \ldots , P_k$, then ${{\mathcal {S}}}$ does the following:

• When ${\mathcal {F}}_{{\textsf {poll}}}$ gives $({{\textsc {setup}}}, P_{{\textsf {client}}}, P_1, \ldots , P_n)$ to ${{\mathcal {S}}}$, generate $({pk},{sk}) \leftarrow {{\textsf {KeyGen}}}$. Pick random $r_1, \ldots , r_n \leftarrow {\mathbb {G}}$ and simulate that $P_{{\textsf {client}}}$ broadcast $({pk},P_{{\textsf {server}}})$ and sent $r_i$ to each corrupt $P_i$.

• When ${\mathcal {F}}_{{\textsf {poll}}}$ gives $({{\textsc {inputfrom}}}, P_i)$ to ${{\mathcal {S}}}$ for an honest party ($i > k$), generate $(C_i,S_i) \leftarrow {{\textsf {RigEnc}}} _{pk}$ and simulate that $P_i$ sent $C_i$ to $P_{{\textsf {server}}}$. Remember $S_i$.

• When $P_{{\textsf {server}}}$ sends $P_{{\textsf {client}}}$ a list of ciphertexts $(C'_1, \ldots , C'_n)$, do the following for each i:

  • – If ${{\textsf {Dec}}} _{sk} (C'_i) \ne \bot$, then set $(m_i, r'_i) \leftarrow {{\textsf {Dec}}} _{sk} (C'_i)$.

  • – Else, if ${{\textsf {RigExtract}}} _{sk} (C'_i, S_j) \ne \bot$ for some j, set $r'_i := r_i \cdot {{\textsf {RigExtract}}} _{sk} (C'_i, S_j)$.

  • – If both these operations fail, send ${{\textsc {cancel}}}$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of $P_{{\textsf {server}}}$.

  If $\prod _i r'_i \ne \prod _i r_i$ or for some $j>k$, there is more than one i such that ${{\textsf {RigExtract}}} _{sk} (C'_i,S_j) \ne \bot$, then send ${{\textsc {cancel}}}$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of $P_{{\textsf {server}}}$. Otherwise, let $\sigma$ be any permutation on [n] that maps each $j > k$ to the unique i such that ${{\textsf {RigExtract}}} _{sk} (C'_i, S_j) \ne \bot$. Send $({{\textsc {input}}}, m_{\sigma (i)})$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of corrupt $P_i$ ($i \le k$), and then send ${{\textsc {ok}}}$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of $P_{{\textsf {server}}}$, with $\sigma$ as the permutation that ${\mathcal {F}}_{{\textsf {poll}}}$ expects.

In this case, the primary task of ${{\mathcal {S}}}$ is to determine whether the corrupt $P_{{\textsf {server}}}$ gives a valid list of ciphertexts to $P_{{\textsf {client}}}$. Applying the HCCA definition in a sequence of hybrid interactions, we see that the behavior of the real-world interaction versus this simulation interaction is preserved when appropriately replacing ${{\textsf {Enc}}}$/${{\textsf {Dec}}}$ with ${{\textsf {RigEnc}}}$/${{\textsf {RigExtract}}}$.

Note that the adversary’s view is independent of $r_{k+1}, \ldots , r_n$. If ${{\textsf {Dec}}} _{sk} (C'_i)\ne \bot$, then the corresponding $r'_i$ value computed by the simulator is also independent of $r_{k+1}, \ldots , r_n$. Thus the only way $\prod _i r_i = \prod _i r'_i$ can be satisfied with non-negligible probability is if for each honest party $P_j$, exactly one i satisfies ${{\textsf {RigExtract}}} _{sk} (C'_i, S_j) \ne \bot$. In this case, there will be exactly as many $m_i$’s as corrupt players, and the simulator can legitimately send these to ${\mathcal {F}}_{{\textsf {poll}}}$ as instructed (with the appropriate permutation).

Case 4. If ${{\mathcal {A}}}$ corrupts $P_{{\textsf {server}}}$, $P_{{\textsf {client}}}$, and input parties $P_1, \ldots , P_k$, then ${{\mathcal {S}}}$ can legitimately obtain each honest input party’s input, so simulation is relatively straightforward. More formally, ${{\mathcal {S}}}$ does the following:

• Send $({{\textsc {setup}}}, P_{{\textsf {client}}}, P_{{\textsf {server}}}, P_1, \ldots , P_n)$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of $P_{{\textsf {client}}}$.

• Send $({{\textsc {input}}}, m_0)$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of each corrupt input party $P_i$, where $m_0$ is an arbitrary fixed message.

• After receiving $({{\textsc {inputfrom}}}, P_i)$ for all honest input parties $P_i$, send ${{\textsc {ok}}}$ to ${\mathcal {F}}_{{\textsf {poll}}}$ on behalf of $P_{{\textsf {server}}}$, and give the identity permutation as $\sigma$.

• After receiving $(m_1, \ldots , m_n)$ as output, we know that party $P_i$ was invoked with input $m_i$, so we can perfectly simulate the honest parties to ${{\mathcal {A}}}$. $\square$

Boolean or on Encrypted Data Using a similar technique, we can obtain a UC-secure protocol for a boolean-or functionality. This functionality is identical to ${\mathcal {F}}_{{\textsf {poll}}}$ except that $P_{{\textsf {server}}}$ also gets to provide an input (i.e., we identify $P_{{\textsf {server}}}$ with $P_0$), and instead of giving $(m_{\sigma (0)}, \ldots , m_{\sigma (n)})$, it gives $\bigvee _i m_i$ as the output to $P_{{\textsf {client}}}$.

We can achieve this new functionality with a similar protocol—this time, using an encryption scheme that is unlinkable HCCA-secure with respect to all group operations in ${\mathbb {G}} ^2$. $P_{{\textsf {client}}}$ sends shares $r_i$ to the input parties as before. The input parties send ${{\textsf {Enc}}} _{pk} (m_i,r_i)$ to $P_{{\textsf {server}}}$, where $m_i = 1$ if $P_i$’s input is 0, and $m_i$ is randomly chosen in ${\mathbb {G}}$ otherwise. Then, $P_{{\textsf {server}}}$ rerandomizes the $r_i$ shares as before and also randomizes the $m_i$’s in the following way: $P_{{\textsf {server}}}$ multiplies each $m_i$ by $s_i$ such that $\prod _i s_i = 1$ if $P_{{\textsf {server}}}$ ’s input is 0, and $\prod _i s_i$ is random otherwise ($P_{{\textsf {server}}}$ can randomize both sets of shares simultaneously using the homomorphic operation). $P_{{\textsf {client}}}$ receives the processed ciphertexts and ensures that $\prod _i r'_i = 1$. Then if $\prod _i m_i =1$, it outputs 0, else it outputs 1.

We note that this approach to evaluating a boolean or (where the induced distribution is a fixed element if the result is 0, and is random if the result is 1) has previously appeared elsewhere, e.g., [10, 13, 43].

8 Beyond Unary Transformations

Many interesting applications of homomorphic encryptions involve (at least) binary operations—those which accept encryptions of plaintexts $m_0$ and $m_1$ and output a ciphertext encoding $T(m_0,m_1)$. A common example is ElGamal encryption, where T is the group operation of the underlying cyclic group. In this section, we examine the possibility of extending our results to schemes with binary transformations.

Before presenting our results, we must first define appropriate extensions of our definitions to the case of binary homomorphic operations. Developing appropriate (and succinct) indistinguishability-style definitions appears to be a difficult task. Thus, the results in this section use security formulations as ideal functionalities in the UC model, as in Sect. 3.3.

8.1 Negative Result for Binary Group Operations

For an impossibility result, we make the security requirements on the ideal functionality as weak as possible. Throughout this subsection, we consider an ideal functionality ${\mathcal {F}}$ similar to ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$, with the following properties:

• Any party may post a new handle by either providing a plaintext message, or by providing a list of existing handles and a circuit where each fan-in-2 gate is associated with a transformation $T \in {\mathcal {T}}$, and each input gate associated with a handle. In the latter case, the message for the new handle is calculated in the natural way, by feeding as input to the circuit the messages internally recorded for each given handle.

• Only the “owner” of the functionality can obtain the message corresponding to each handle. All other parties simply receive notification that the handle was generated.

• Handles are generated by the adversary, without knowledge of the corresponding plaintext message, or which of the two ways the handle was produced.

For simplicity, we have not considered the functionality’s behavior on handles originally posted by the adversary (so-called dummy handles in the case of ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$). However, our impossibility results do not depend on these details, and one may consider the weakest possible ideal functionality, which reveals everything to the adversary when honest parties try to use dummy handles.

We can now formalize our impossibility result:

Theorem 8.1

There is no secure realization of ${\mathcal {F}}$ via a homomorphic encryption scheme, when ${\mathcal {T}}$ contains a group operation on the message space, and the size of the message space is superpolynomial in the security parameter.

The main observation is that each handle (ciphertext) must have a bounded length independent of its “history” (i.e., whether it was generated via the homomorphic reposting operation and if so, which operations applied to which existing handles) and thus can only encode a bounded amount of information about its history. We show that any simulator for ${\mathcal {F}}$ must be able to extract a reasonable history from any handle output by the adversary.

However, when a group operation is an allowed transformation, there can be far more possible histories than can be encoded in a single handle. For example, if n handles have been generated, then there are at least $2^n$ distinct histories for a newly posted handle (combine an arbitrary subset of those handles, using the group operation). We show that the simulator must be able to reliably distinguish between each possible history. By setting n sufficiently large, we achieve a contradiction whereby $2^n$ exceeds the number of possible ciphertexts!

We note that this “overabundance of histories” does not happen in the case of unary transformations. The simulator does not need to distinguish between the transformation “multiply by rs” and the composition of transformations “multiply by r” and “multiply by s.” The simulator does need to identify which ciphertext was transformed, but this leads to $n \cdot N$ total histories that the simulator must distinguish, where n is the number of handles generated so far (polynomial in the security parameter), and N is the size of the group (exponential in the security parameter, but fixed before the ciphertext length is determined). This number does not grow fast enough to exceed the number of possible ciphertexts.

Proof

We will construct an environment that will distinguish between the ideal interaction with ${\mathcal {F}}$ and the real-world protocol interaction involving any homomorphic encryption scheme. Let $\otimes$ be the group operation over message space ${\mathcal {M}}$.

The environment invokes an interaction with two honest parties Alice and Bob, and a dummy adversary Carol. The environment instructs Bob to ${{\textsc {setup}}}$ an instance of the functionality, then chooses d random messages $m_1, \ldots , m_d \leftarrow {\mathcal {M}}$, where d is a parameter to be fixed later, and instructs Alice to ${{\textsc {post}}}$ each of them. Then, the environment chooses a random $S \subseteq \{1, \ldots , d\}$ and then, given the handles for the posted messages, internally runs the encryption scheme algorithm to obtain a ciphertext $h^*$ encoding $\bigotimes _{i \in S} m_i$. The environment can do this locally because this protocol implements the ${{\textsc {repost}}}$ operation via a non-interactive procedure ${{\textsf {CTrans}}}$. Finally, the environment instructs the adversary to broadcast the resulting handle/ciphertext $h^*$ and then instructs Bob to open it. The environment outputs 1 if Bob outputs $\bigotimes _{i\in S} m_i$.

Clearly in the real-world interaction, the environment outputs 1 with overwhelming probability, by the correctness of the encryption scheme’s homomorphic operation. We will show that any sound simulator results in a contradiction.

Suppose there is a valid simulator for the protocol. After receiving $h^*$, the simulator must provide to ${\mathcal {F}}$ a legal circuit $T'$ such that $T'(m_1, \ldots , m_d) = \bigotimes _{i \in S} m_i$ with overwhelming probability. From the definition of ${\mathcal {F}}$, the initial d handles are generated without knowledge of the underlying plaintext, so the simulator’s view is independent of the choice of $m_1, \ldots , m_d$. Thus the simulator must in fact specify a legal circuit $T'$ such that $T'(m_1, \ldots , m_d) = \bigotimes _{i \in S} m_i$, with overwhelming probability over the random choice of $m_1, \ldots , m_d$.

Note that in a group, if we have $S \ne S' \subseteq \{1, \ldots , d\}$, then the probability (taken over choice of $m_1, \ldots , m_d$) that $\bigotimes _{i \in S} m_i = \bigotimes _{i \in S'} m_i$ is negligible. So any function $T'$ can agree with a function of the form $\bigotimes _{i \in S'}$ on an overwhelming fraction of inputs for at most one choice of $S'$. Thus the simulator’s choice of circuit $T'$ uniquely determines the subset S chosen by the environment.

However, let $\ell (k)$ be a polynomial bound on the length of handles in the given encryption scheme (when the security parameter is k). Let us specify $d = \ell (k) +1$, then the environment remains polynomial time in k. There are $2^{\ell (k)+1}$ choices of the subset S by the environment. However, there are at most $2^{\ell (k)}$ possible values for the handle $h^*$, which is the only part of the simulator’s view that depends on the choice of S. There is at least one bit of uncertainty in the simulator’s view about the environment’s choice of S, so the simulator cannot determine S with probability greater than $\frac{1}{2}$. This contradicts the fact that the simulator’s choice of $T'$ uniquely determines the environment’s choice of S.

From this contradiction, we see that no sound simulation is possible against this environment, which can successfully distinguish between the real and ideal interactions with probability at least $\frac{1}{2}$. $\square$

8.2 Positive Result for a Relaxation of Unlinkability

The impossibility result of the previous section leaves open the possibility of achieving a relaxation of the unlinkability requirement. We consider a relaxation similar to Sander, Young, and Yung [62]; namely, we allow the ciphertext to leak the number of operations applied to it (i.e., the depth of the circuit applied), but no additional information. To make this requirement more formal, we associate a length parameter with each ciphertext. If a length-$\ell$ and a length-$\ell '$ ciphertext are combined, then the result is a length $\ell +\ell '$ ciphertext. Our security definition insists that ciphertexts reveal (at most) their associated length parameter.

The main idea in our construction is to encode a group element m into a length-$\ell$ ciphertext as a vector $\big ({{\textsf {Enc}}} (m_1), \ldots , {{\textsf {Enc}}} (m_\ell )\big )$, where the $m_i$’s are a random multiplicative sharing of m in the group and ${{\textsf {Enc}}}$ is HCCA-secure with respect to the group operation. To “multiply” two such encrypted encodings, we can simply concatenate the two vectors of ciphertexts together and rerandomize the new set of shares (multiply the ith component by $s_i$, where $\prod _i s_i = 1$) to bind the sets together.

The above outline captures the main intuition, but our actual construction uses a slightly different approach to ensure UC security. In the scheme described above, anyone can split the vector $\big ({{\textsf {Enc}}} (m_1), \ldots , {{\textsf {Enc}}} (m_\ell )\big )$ into two smaller vectors that encode two (random) elements whose product is m. We interpret this as a violation of our desired properties, since it is a way to derive two encodings whose values are related to a longer encoding. To avoid the problem of “breaking apart” ciphertexts, we instead encode m as $\big ({{\textsf {Enc}}} (\alpha _1, \beta _1), \ldots , {{\textsf {Enc}}} (\alpha _\ell ,\beta _\ell )\big )$, where the $\alpha _i$’s and $\beta _i$’s form two independently random multiplicative sharings of m. Rerandomizing these encodings is possible when we use a scheme that is homomorphic with respect to the group operation in ${\mathbb {G}} ^2$ (i.e., by setting the parameter ${\mathbb {H}} = {\mathbb {G}} ^2$ in our construction). Intuitively, these encodings cannot be split up in such a way that the first components and second components are shares of the same value. Note that it is crucial that the $(\alpha _i, \beta _i)$ pairs cannot themselves be “broken apart.”

Security Definition The functionality, called $\mathcal {F}_{\mathbb {G}}$, is given in full detail in Fig. 5. Below we explain and motivate the details of the definition.

Fig. 5

UC ideal functionality $\mathcal {F}_{\mathbb {G}}$, parameterized by a cyclic group ${\mathbb {G}}$

Following our desired intuition, users can only generate new messages in two ways (for uniformity, all handled in the same part of the functionality’s code). A user can simply post a message by supplying a group element m (this is the case where $k=0$ in the user’s ${{\textsc {post}}}$ command). Alternatively, a user can provide a list of existing handles along with a group element m. If all these handles correspond to honestly generated posts, then this has the same effect as if the user posted the product of all the corresponding messages (though note that the user does not have to know what these messages are to do this). We model the fact that handles reveal nothing about the message by letting the adversary choose the actual handle string, without knowledge of the message. The designated recipient can obtain the message by providing a handle to the functionality. Note that there is no way (even for corrupt parties) to generate a handle derived from existing handles in a non-approved way.

As in ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$, adversaries can also post dummy handles, which contain no message. When a user posts a derived message using such a handle, the resulting handle also contains no message. When the handle is used in a derived ${{\textsc {post}}}$ command, the adversary is informed. The adversary also gets access to an “intermediate” handle corresponding to all the non-${{\textsc {dummy}}}$ handles that were combined in the ${{\textsc {post}}}$ request. Still, the adversary learns nothing about the messages corresponding to these handles.

The Construction Let ${\mathcal {E}} = ({{\textsf {KeyGen}}}, {{\textsf {Enc}}}, {{\textsf {Dec}}}, {{\textsf {CTrans}}})$ be an unlinkable HCCA-secure scheme, whose message space is ${\mathbb {G}} ^2$ for a cyclic group ${\mathbb {G}}$, and whose allowed (unary) transformations are all group operations in ${\mathbb {G}} ^2$. We suppose the ${{\textsf {CTrans}}}$ operation accepts arguments as ${{\textsf {CTrans}}} (C, (r,s))$, where $r,s\in {\mathbb {G}}$ specify the transformation $(\alpha ,\beta ) \mapsto (r\alpha , s\beta )$. We abbreviate the ${{\textsf {CTrans}}} (C, (r,s))$ operation as “$(r,s) * C$”. Thus $(r,s)*{{\textsf {Enc}}} _{pk} (\alpha ,\beta )$ is indistinguishable from ${{\textsf {Enc}}} _{pk} (r\alpha ,s\beta )$, in the sense of the unlinkability definition.

The new scheme ${\mathcal {E}} ^*$ is given by the following algorithms:

We note that the syntax of ${{\textsf {CTrans}}} ^*$ can be naturally extended to support multiplying several ciphertexts and/or a known group element at once, simply by composing the operations described above.

Theorem 8.2

If ${\mathcal {E}}$ is unlinkable and HCCA-secure with respect to ${\mathbb {G}} ^2$, where $|{\mathbb {G}} |$ is superpolynomial in the security parameter, then ${\mathcal {E}} ^*$ (as described above) is a secure realization of $\mathcal {F}_{\mathbb {G}}$, with respect to static corruptions.

Proof

Let ${\mathcal {E}} = ({{\textsf {KeyGen}}}, {{\textsf {Enc}}}, {{\textsf {Dec}}}, {{\textsf {CTrans}}})$ be the unlinkable HCCA-secure scheme used as the main component in our construction, and let ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ be the procedures guaranteed by HCCA security.

We proceed by constructing an ideal-world simulator for any arbitrary real-world adversary ${{\mathcal {A}}}$. The simulator ${{\mathcal {S}}}$ is constructed by considering a sequence of hybrid functionalities that culminate in $\mathcal {F}_{\mathbb {G}}$. These hybrids differ from $\mathcal {F}_{\mathbb {G}}$ only in how much they reveal in their ${{\textsc {handle-req}}}$ requests to the adversary.

Correctness. Note that $\mathcal {F}_{\mathbb {G}}$ only makes two kinds of ${{\textsc {handle-req}}}$ requests: those containing a lone message, and those containing a list of handles.

Let ${{\mathcal {F}}}_{{\textsc {1}}}$ be the functionality that behaves exactly as $\mathcal {F}_{\mathbb {G}}$, except that every time it sends a ${{\textsc {handle-req}}}$ to the simulator, it also includes the entire party’s input that triggered the ${{\textsc {handle-req}}}$. Define ${{\mathcal {S}}} _{1}$ to be the simulator that internally runs the adversary ${{\mathcal {A}}}$, and does the following:

• When ${{\mathcal {F}}}_{{\textsc {1}}}$ gives $({{\textsc {id-req}}}, P)$ to ${{\mathcal {S}}} _{1}$, it generates a keypair $({pk},{sk}) \leftarrow {{\textsf {KeyGen}}}$ and responds with ${pk}$. It simulates to ${{\mathcal {A}}}$ that party P broadcast ${pk}$.

• When ${{\mathcal {F}}}_{{\textsc {1}}}$ gives a ${{\textsc {handle-req}}}$ to ${{\mathcal {S}}} _{1}$, it generates the handle appropriately—with either ${{\textsf {Enc}}} ^*_{pk}$ or ${{\textsf {CTrans}}} ^*$ on an existing handle, depending on the party’s original command which is included in the ${{\textsc {handle-req}}}$. It simulates to ${{\mathcal {A}}}$ that the appropriate party output the handle.

• When ${{\mathcal {A}}}$ broadcasts a length-$\ell$ ciphertext C, ${{\mathcal {S}}} _{1}$ tries to decrypt it with ${{\textsf {Dec}}} ^*_{sk}$. If it decrypts (say, to m), then ${{\mathcal {S}}} _{1}$ sends a $({{\textsc {post}}},\ell ,m)$ command to ${{\mathcal {F}}}_{{\textsc {1}}}$ and later gives C as the handle; else it sends $({{\textsc {dummy}}},\ell ,C)$.

${{\mathcal {S}}} _{1}$ exactly simulates the honest parties’ behavior in the real-world interaction. By the correctness properties of ${\mathcal {E}} ^*$, the outputs of the honest ideal-world parties match that of the real world, except with negligible probability; thus, ${{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {A}}},{\mathcal {E}} ^*,{{\mathcal {F}}}_{{\textsc {bcast}}} ] \approx {{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {S}}} _{1},{\pi }_{\mathsf{dummy}},{{\mathcal {F}}}_{{\textsc {1}}} ]$ for all environments ${{\mathcal {Z}}}$.

Unlinkability. Let ${{\mathcal {F}}}_{{\textsc {2}}}$ be exactly like ${{\mathcal {F}}}_{{\textsc {1}}}$, except for the following change: For requests of the form $({{\textsc {handle-req}}}, {\textsf {sender}}, \ell , m)$, ${{\mathcal {F}}}_{{\textsc {2}}}$ does not send the handles that caused this request. That is, whereas ${{\mathcal {F}}}_{{\textsc {1}}}$ would tell the simulator that the handle is being requested for a ${{\textsc {post}}}$ command combining some non-dummy handles, ${{\mathcal {F}}}_{{\textsc {2}}}$ would instead act like ${\textsf {sender}}$ had sent $({{\textsc {post}}}, \ell , m)$ (that this is closer to what $\mathcal {F}_{\mathbb {G}}$ does; internally behaving identically for such requests). Let ${{\mathcal {S}}} _{2} = {{\mathcal {S}}} _{1}$, since ${{\mathcal {F}}}_{{\textsc {1}}}$ is only sending one fewer type of ${{\textsc {handle-req}}}$ to the simulator.

By a standard hybrid argument, we can see that ${{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {S}}} _{1},{\pi }_{\mathsf{dummy}},{{\mathcal {F}}}_{{\textsc {1}}} ] \approx {{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {S}}} _{2},{\pi }_{\mathsf{dummy}},{{\mathcal {F}}}_{{\textsc {2}}} ]$ for all environments ${{\mathcal {Z}}}$. The hybrids are over the number of ${{\textsc {post}}}$ requests affected by this change. Consecutive hybrids differ by whether a single handle was generated by ${{\textsf {Enc}}} ^*$ or by ${{\textsf {CTrans}}} ^*$. The only handles that are affected here are non-${{\textsc {dummy}}}$ handles and thus ciphertexts which decrypt successfully under ${sk}$. Thus distinguishing between consecutive hybrids can be reduced to succeeding in the unlinkability experiment (by further hybridizing over the individual ${{\textsf {Enc}}}$ ciphertext components).

HCCA. If the owner P of the functionality is corrupt, then ${{\mathcal {S}}} _{2}$ is already a suitable simulator for $\mathcal {F}_{\mathbb {G}}$, and we can stop at this point.

Otherwise, the difference between $\mathcal {F}_{\mathbb {G}}$ and ${{\mathcal {F}}}_{{\textsc {2}}}$ is that $\mathcal {F}_{\mathbb {G}}$ does not reveal the message in certain ${{\textsc {handle-req}}}$ requests. Namely, those in which the simulator receives $({{\textsc {handle-req}}}, {\textsf {sender}}, \ell )$.

Let ${{\mathcal {S}}} _{3}$ be exactly like ${{\mathcal {S}}} _{2}$, except for the following changes: Each time ${{\mathcal {S}}} _{2}$ would generate a ciphertext component via ${{\textsf {Enc}}} _{pk} (\alpha ,\beta )$, ${{\mathcal {S}}} _{3}$ instead generates it with ${{\textsf {RigEnc}}} _{pk}$. It keeps track of the auxiliary information S and records $(S,\alpha ,\beta )$ internally. Also, whenever ${{\mathcal {S}}} _{2}$ would decrypt a ciphertext component using ${{\textsf {Dec}}} _{sk}$, ${{\mathcal {S}}} _{3}$ instead decrypts it via:

$$\begin{aligned} D(C) = {\left\{ \begin{array}{ll} (r\alpha , s\beta ) &{} \text{ if } (S,\alpha ,\beta ) \text{ is } \text{ recorded } \text{ s.t. } (r,s) \leftarrow {{\textsf {RigExtract}}} _{sk} (C,S) \\ {{\textsf {Dec}}} _{sk} (C) &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

By a straightforward hybrid argument (in which distinguishing between adjacent hybrids reduces to success in a single instance of the HCCA experiment), we have that ${{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {S}}} _{2},{\pi }_{\mathsf{dummy}},{{\mathcal {F}}}_{{\textsc {2}}} ] \approx {{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {S}}} _{3},{\pi }_{\mathsf{dummy}},{{\mathcal {F}}}_{{\textsc {2}}} ]$ for all environments ${{\mathcal {Z}}}$.

We now examine when a ciphertext given by the adversary is successfully decrypted by the simulator (and thus given to the functionality as a ${{\textsc {post}}}$ instead of as a ${{\textsc {dummy}}}$ handle).

Given a ciphertext (sequence of HCCA ciphertexts) $C=(C_1, \ldots , C_\ell )$, ${{\mathcal {S}}} _{3}$ first decrypts each $C_i$ to obtain $(\alpha '_i, \beta '_i) = D(C_i)$. The overall decryption succeeds if $\prod _i (\alpha '_i/\beta '_i) = 1$.

Suppose the internal records $(S,\alpha ,\beta )$ are labeled as $(S_j,\alpha _j,\beta _j)$ for $j\ge 1$. Then for some constants $r,s \in {\mathbb {G}}$ and exponent $p \in \{0,1\}$, we have that $\alpha '_i/\beta '_i = (r/s) (\alpha _j / \beta _j)^p$. Now, let $\gamma '_i = \alpha '_i/\beta '_i$. We denote $\gamma '_i$ as a linear function in a single formal variable of the form $\gamma _j = \alpha _j/\beta _j$. The adversary’s view is independent of the choice of $\gamma _j$’s, except for the fact that $\prod _{j \in J} \gamma _j = 1$ for some disjoint sets J.

Recall that the overall decryption of C is successful if $\prod _i \gamma '_i =1$. However, note that if is only with negligible probability that $\prod _i \gamma '_i = 1$ when evaluated on the simulator’s choice of $\gamma _j$’s, but $\prod _j \gamma '_i \ne 1$ as a polynomial. Thus consider a simulator ${{\mathcal {S}}} _{4}$ that sends $({{\textsc {dummy}}}, C)$ to the functionality whenever $\prod _i \gamma '_i \ne 1$, as a polynomial (accounting for the constraints on $\gamma _j$’s). This simulator’s behavior differs from ${{\mathcal {S}}} _{3}$ with only negligible probability.

Suppose $\prod _i \gamma '_i = 1$ as a polynomial, and let J be such that that we have a constraint of the form $\prod _j \gamma _j = 1$. Then for all $j \in J$, there exists $n_J$ such that $\bot \ne {{\textsf {RigExtract}}} _{sk} (C_i,S_j)$ for exactly $n_J$ values of i. In other words, for each $j \in J$, the variable $\gamma _j$ appears in the expansion of $\prod _i \gamma '_i$ with the same multiplicity. Then ${{\mathcal {S}}}$ 4 can do the following when ${{\mathcal {A}}}$ outputs a ciphertext $C = (C_1, \ldots , C_\ell )$:

• If for some $C_i$, we have $D(C_i) = \bot$, the ciphertext is invalid; send $({{\textsc {dummy}}}, C)$ to the functionality.

• Otherwise, compute $(\alpha '_i,\beta '_i) = D(C_i)$. If $\prod _i \alpha '_i / \beta '_i \ne 1$, when viewed as a polynomial in variables $\alpha _j/\beta _j$, then send $({{\textsc {dummy}}}, C)$ to the functionality.

• Otherwise, let I be the set of indices such that $\bot \ne (\alpha '_i, \beta '_i) \leftarrow {{\textsf {Dec}}} _{sk} (C_i)$. Let $(r_i, s_i) \leftarrow {{\textsf {RigExtract}}} _{sk} (C_i, S_j)$ for each $i \not \in I$. We have that $\prod _{i \in I} (\alpha '_i/\beta '_i) = 1$ and $\prod _{i \not \in I} (r_i/s_i) = 1$ by the above argument. Then send $({{\textsc {post}}}, \ell , m_0,$H ) to the functionality, where $m_0 = \prod _{i \in I} \alpha _i \prod _{i \not \in I} r_i$ and H contains with multiplicity $n_J$ the handle that resulted when $\{ (\alpha _j, \beta _j) \mid j \in J\}$ were generated.

Except with negligible probability, ${{\mathcal {S}}} _{4}$ interacts identically with the functionality as ${{\mathcal {S}}} _{3}$. However, note that ${{\mathcal {S}}} _{4}$ does not actually use the $\alpha _j, \beta _j$ values that are recorded for each call to ${{\textsf {RigEnc}}}$. Thus ${{\mathcal {S}}} _{4}$ can be successfully implemented even if the functionality does not reveal m in messages of the form $({{\textsc {handle-req}}}, {\textsf {sender}}, \ell , m)$. Therefore ${{\mathcal {S}}} _{4}$ is a suitable simulator for $\mathcal {F}_{\mathbb {G}}$ itself, and ${{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {S}}} _{3},{\pi }_{\mathsf{dummy}},{{\mathcal {F}}}_{{\textsc {2}}} ] \approx {{\textsc {exec}}} [{{\mathcal {Z}}},{{\mathcal {S}}} _{4},{\pi }_{\mathsf{dummy}}, \mathcal {F}_{\mathbb {G}}]$ for all environments ${{\mathcal {Z}}}$. $\square$

9 Conclusion and Open Problems

Improved Constructions A natural next step is to address encryption schemes whose homomorphic operations are more expressive. Currently, all of our constructions support homomorphic transformations related to a group operation. Homomorphic operations involving other algebraic structures (ring, field, or vector space operations) may also prove useful in protocol applications.

Our construction of a transformation-hiding HCCA-secure scheme is quite efficient, having only a small additive overhead over a comparable CCA-secure scheme. However, our unlinkable scheme is much more impractical than the state of the art for CCA security. We leave open the problem of whether an “algebraic” property like unlinkability can be achieved using generic hardness assumptions like enhanced trapdoor permutations (or projective hash schemes or even CCA-secure encryption).

Anonymity In some applications, it is useful for an encryption scheme to have the additional property of receiver-anonymity (also known as key-privacy), as introduced by Bellare et al. [4]. Receiver-anonymity means, essentially, that in addition to hiding the underlying plaintext message, a ciphertext does not reveal the public key under which it was encrypted. Encryption schemes with this property are important tools in the design of many systems [30]. The special case of rerandomizable, anonymous, RCCA-secure encryption has interesting applications in mix-nets [34] and anonymous P2P routing [54].

In an anonymous, unlinkable, HCCA-secure scheme, the ${{\textsf {CTrans}}}$ feature of the scheme should not require the correct public key in order to function. That is, the homomorphic operation should be oblivious to the identity of the receiver.

To add the requirement of receiver-anonymity to our definitions, we consider an anonymous, multi-user variant of the ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ UC functionality. This variant allows multiple users to register IDs, and senders to post messages destined for a particular ID. The functionality does not reveal the handle’s recipient in its ${{\textsc {handle-announce}}}$ broadcasts (or in its ${{\textsc {handle-req}}}$ requests to the adversary).

Our indistinguishability-based security definition can be extended in a simple way to account for receiver-anonymity. We call a homomorphic encryption scheme HCCA-anonymous if it is HCCA secure and if the ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ procedures from the HCCA security definition can be implemented without the public or private keys (i.e, ${{\textsf {RigEnc}}}$ takes no arguments and ${{\textsf {RigExtract}}}$ takes only a ciphertext and a saved state).

We also consider an additional correctness requirement on schemes, which is natural in the context of multiple users: With overwhelming probability over $({pk},{sk}) \leftarrow {{\textsf {KeyGen}}}$ and $({pk} ',{sk} ') \leftarrow {{\textsf {KeyGen}}}$, we require that ${{\textsf {Dec}}} _{{sk} '}({{\textsf {Enc}}} _{pk} ({\textsf {msg}}))=\bot$ for every ${\textsf {msg}} \in {\mathcal {M}}$, with probability 1 over the randomness of ${{\textsf {Enc}}}$. In other words, ciphertexts honestly encrypted for one user do not successfully decrypt for another user.

Via a similar argument to the proof of Theorem 4.4, it can be seen that any HCCA-anonymous, unlinkable scheme which satisfies the additional correctness property is a secure realization of the anonymous variant of ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$.

Note that this notion of anonymity is a chosen-ciphertext and not a chosen-plaintext (simple ciphertext indistinguishability) one. Our construction does not achieve HCCA-anonymity, since it is possible to combine a ciphertext with a public key and obtain a valid ciphertext if and only if the original ciphertext was encrypted under that public key.

While our scheme can be easily modified to not require the public key as input to ${{\textsf {CTrans}}}$ (by adding a “second strand” to the CSL ciphertext, since the CSL public key is the only part of the key used by ${{\textsf {CTrans}}}$), this change does not result in a fully HCCA-anonymous construction. An adversary can determine whether a ciphertext $\zeta$ is valid under public key ${pk}$ by applying ${{\textsf {CTrans}}}$ with that public key. By sending the result to a decryption oracle, the adversary can tell whether the ciphertext was consistent with the public key. The technical barrier to achieving anonymity in our construction is that the CSL component is receiver-anonymous, but only in a chosen-plaintext sense, not in the chosen-ciphertext sense that would be required. Indeed, it appears as though a significantly different approach is needed to achieve HCCA-anonymity.

We consider it an interesting and important open problem to construct an anonymous, unlinkably homomorphic HCCA encryption scheme, for any ${\mathcal {T}}$.

Repost-test In ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$, when an honest party Alice receives a post from Bob and then another from Carl, Alice has no way of knowing if Carl’s message was derived from Bob’s (via ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ ’s ${{\textsc {repost}}}$ feature), or via an independent ${{\textsc {post}}}$ command. In fact, the only time ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ informs a recipient that a ${{\textsc {repost}}}$ occurred is for the adversary’s dummy handles.

We can easily modify our schemes and ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ to provide such a feature for honest parties. We call this feature repost-test. In this variant of ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$, the recipient may issue an additional command $({{\textsc {test}}}, {\textsf {handle}} _1, {\textsf {handle}} _2)$. The functionality returns a boolean indicating whether the two handles were the result of reposting a common handle (it keeps extra book-keeping to track the ancestor of each ${{\textsc {repost}}}$-generated handle).

To realize this modified functionality, we start with a realization of ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ on message space ${\mathcal {M}}^{n+1}$, where ${\mathcal {M}}$ has superpolynomial size. Suppose every $T \in {\mathcal {T}}$ always preserves the $(n+1)$th component of the message. Then let ${\mathcal {T}} '$ be the restrictions of $T \in {\mathcal {T}}$ to the first n components.

We may then use ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ to obtain a secure realization of ${\mathcal {F}}_{\text{ hmp }}^{{\mathcal {T}} '}$ with repost-test feature in the following way: To post a message $(m_1, \ldots , m_n) \in {\mathcal {M}}^n$, choose a random $m_{n+1} \leftarrow {\mathcal {M}}$ and post $(m_1, \ldots , m_{n+1})$ to ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$. When reading a message, ignore the last component. To perform the repost-test on two handles, simply check whether the last components of their corresponding messages are equal.

Appendix: Relaxations of Unlinkability

1.1 Definitions

Unlinkability is a strong security guarantee that considers even maliciously crafted ciphertexts. We also consider a relaxation of unlinkability which is implied by simple indistinguishability properties of the scheme’s ${{\textsf {CTrans}}}$ procedure (and thus potentially easier to achieve), but is nonetheless useful.

For a unary homomorphic encryption scheme ${\mathcal {E}} = ({{\textsf {KeyGen}}},{{\textsf {Enc}}},{{\textsf {Dec}}},{{\textsf {CTrans}}})$ and a set of transformations ${\mathcal {T}}$, we define the following stateful oracle:

Definition 10.1

Let ${\mathcal {T}}$ be a set of (unary) transformations. A homomorphic encryption scheme ${\mathcal {E}}$ is ${\mathcal {T}}$ -weakly unlinkable if, for all non-uniform PPT adversaries ${{\mathcal {A}}}$, we have:

$$\begin{aligned} \Pr \left[ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{\mathcal {T}}}_{\lambda ,0}}(1^\lambda ) = 1\right] \approx \Pr \left[ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{\mathcal {T}}}_{\lambda ,1}}(1^\lambda ) = 1\right] , \end{aligned}$$

Unlike the stronger variant, weak unlinkability is implied by a simple correctness condition: namely, that for all transformations $T \in {\mathcal {T}}$, plaintexts ${\textsf {msg}} \in {\mathcal {M}}$, and ciphertexts $\zeta \leftarrow {{\textsf {Enc}}} _{pk} ({\textsf {msg}})$, the distributions of ${{\textsf {Enc}}} _{pk} (T({\textsf {msg}}))$ and ${{\textsf {CTrans}}} _{pk} (\zeta , T)$ are identical.

Connection to the UC Definition If a scheme achieves only weak unlinkability, then Theorem 4.4 can be proven with respect to a slight relaxation of the UC functionality. In the ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$ UC functionality, call a handle adversarially influenced if:

• it is the result of a ${{\textsc {post}}}$ or ${{\textsc {repost}}}$ command issued by a corrupt party,

• or it is the result of a $({{\textsc {repost}}}, {\textsf {handle}})$ command, where ${\textsf {handle}}$ is adversarially influenced.

An encryption scheme which is HCCA-secure and only weakly unlinkably homomorphic is a secure realization of a variant of ${\mathcal {F}}_{{\textsc {hmp}}}^{\mathcal {T}}$, in which the adversary is notified every time an adversarially influenced handle is reposted (in the same way it is notified when its dummy handles are reposted). The proof is very similar to that of Theorem 4.4, except that unlinkability is only applied to handles which are not adversarially influenced (i.e., a ciphertext which was generated by the simulator honestly using ${{\textsf {Enc}}}$).

Transformation-Hiding Transformation-hiding is a weaker requirement than unlinkability. As such, it admits a much more efficient construction than our main construction. However, the requirement is still useful in protocols such as the one in Sect. 7.

In the two “unlinkability” definitions, an adversary cannot tell, given two ciphertexts, whether one ciphertext was derived from the other via the ${{\textsf {CTrans}}}$ operation. By contrast, in the definition of transformation-hiding we relax this requirement so that, given only a single ciphertext, an adversary cannot tell whether the ciphertext was derived by encrypting a plaintext, or by encrypting and then transforming it via ${{\textsf {CTrans}}}$.

For a unary homomorphic encryption scheme ${\mathcal {E}} = ({{\textsf {KeyGen}}},{{\textsf {Enc}}},{{\textsf {Dec}}},{{\textsf {CTrans}}})$ and a set of transformations ${\mathcal {T}}$, we define the following stateful oracle:

Definition 10.2

Let ${\mathcal {T}}$ be a set of (unary) transformations. A homomorphic encryption scheme ${\mathcal {E}}$ is ${\mathcal {T}}$ -transformation-hiding if, for all non-uniform PPT adversaries ${{\mathcal {A}}}$, we have:

$$\begin{aligned} \Pr \left[ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{\mathcal {T}}}_{\lambda ,0}}(1^\lambda ) = 1\right] \approx \Pr \left[ {{\mathcal {A}}} ^{{\mathcal {O}}^{{\mathcal {E}},{\mathcal {T}}}_{\lambda ,1}}(1^\lambda ) = 1\right] , \end{aligned}$$

Note that the transformation-hiding experiment is identical to the weak-unlinkability experiment, except that the adversary does not receive $\zeta ^*_0$ in the transformation-hiding experiment. Thus transformation-hiding is a strictly weaker requirement.

Transformation-hiding is also implied by a simple indistinguishability criterion: namely, that for all transformations T and plaintexts ${\textsf {msg}}$, the distributions ${{\textsf {Enc}}} _{pk} (T({\textsf {msg}}))$ and ${{\textsf {CTrans}}} _{pk} ({{\textsf {Enc}}} _{pk} ({\textsf {msg}}), T)$ are identical, over the randomness of both ${{\textsf {Enc}}}$ and ${{\textsf {CTrans}}}$ in the second expression. In particular, ${{\textsf {CTrans}}}$ need not be randomized for a scheme to be transformation-hiding.

1.2 Achieving Transformation-Hiding

We describe an encryption scheme which is HCCA-secure with respect to any unary group operation and achieves the transformation-hiding property.

The construction Let ${\mathcal {E}} = ({{\textsf {KeyGen}}},{{\textsf {Enc}}},{{\textsf {Dec}}})$ be any RCCA-secure encryption scheme with message space ${\mathbb {G}}$, which is an abelian group with group operation “$*$.” Without loss of generality, we assume that ${\mathbb {G}}$ isomorphic to the direct product ${\mathbb {H}} _1 \times {\mathbb {H}} _2$, where ${\mathbb {H}} _1$ is a parameter of our scheme, and elements in ${\mathbb {G}}$ are represented as $(m_1, m_2) \in {\mathbb {H}} _1 \times {\mathbb {H}} _2$.²¹

For $t \in {\mathbb {H}} _1$, let $T_t$ denote the “multiplication-by-t” transformation $T_t(m_1, m_2) = (t * m_1, m_2)$. For simplicity, we let $T_t(\bot ) = \bot$.

Our construction has message space ${\mathcal {M}}$ and supports transformations ${\mathcal {T}} = \{ T_t \mid t \in {\mathbb {H}} _1 \}$. The construction is specified by the following algorithms:

• ${{\textsf {KeyGen}}} ^*$: Same as ${{\textsf {KeyGen}}}$.

• ${{\textsf {Enc}}} ^*_{pk} (m_1, m_2)$: Choose random $r \leftarrow {\mathbb {H}} _1$, and set $s = m_1 * r \in {\mathbb {H}} _1$. Output $({{\textsf {Enc}}} _{pk} (r, m_2), s)$.

• ${{\textsf {Dec}}} ^*_{sk} (\zeta , s)$: Decrypt $(r, m_2) \leftarrow {{\textsf {Dec}}} _{sk} (\zeta )$, and output $\bot$ if the decryption fails. Otherwise, output $(s * r^{-1}, m_2)$.

• ${{\textsf {CTrans}}} ^*((\zeta , s), T_t)$: Output $(\zeta , s*t)$.

Intuitively, our desired transformations preserve the ${\mathbb {H}} _2$-component of the plaintext, but allow the group operation to be applied to the ${\mathbb {H}} _1$-component. Thus our encryption scheme places the ${\mathbb {H}} _2$-component of the plaintext into the RCCA-secure encryption. We also place inside the RCCA encryption a random one-time pad that masks the ${\mathbb {H}} _1$-component of the plaintext. The masked ${\mathbb {H}} _1$-component is provided in the clear of the ciphertext, so that anyone can apply the appropriate algebraic operations to it.

Theorem 10.3

The above construction is HCCA-secure with respect to ${\mathcal {T}}$, and is transformation-hiding.

Proof

First, it is easy to see that the scheme is transformation-hiding, since the distributions of ${{\textsf {Enc}}} ^*_{pk} ( T_t(m_1, m_2))$ and ${{\textsf {CTrans}}} ^*({{\textsf {Enc}}} ^*_{pk} (m_1, m_2), T_t)$ are identical.

To show that the scheme is HCCA-secure, we must demonstrate appropriate ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ procedures. Let ${{\textsf {RigEnc}}}$ and ${{\textsf {RigExtract}}}$ be the procedures guaranteed by the RCCA security of the component scheme ${\mathcal {E}}$. We define the following procedures:

• ${{\textsf {RigEnc}}} ^*_{pk}$: Choose random $s \leftarrow {\mathcal {T}} _1$ and compute $(\zeta ,S) \leftarrow {{\textsf {RigEnc}}} _{pk}$. Output $(\zeta ,s)$ and private information (S, s).

• ${{\textsf {RigExtract}}} ^*_{sk} ( (\zeta ',s'); (S,s) )$: If ${{\textsf {RigExtract}}} _{sk} (\zeta '; S) = \bot$, then output $\bot$. Otherwise, the output of ${{\textsf {RigExtract}}} _{sk} (\zeta '; S)$ is the identity transformation, by the RCCA security of ${\mathcal {E}}$. In that case, output $t = s' * s^{-1}$.

We must prove that the two branches of the HCCA experiment are indistinguishable. First consider the branch $b=1$ of the experiment that involves ${{\textsf {RigEnc}}} ^*$. We can equivalently write the branch as follows:

• Responding to ${{\textsc {challenge}}}$ query: Given message $(m^*_1, m^*_2)$, choose random $r \leftarrow {\mathcal {T}} _1$ and set $s = m^*_1 * r$. Compute $({\zeta ^*},S) \leftarrow {{\textsf {RigEnc}}} _{pk}$, and output $({\zeta ^*},s)$.

• Responding to ${{\textsc {dec}}} (\zeta ', s')$ queries: If ${{\textsf {RigExtract}}} _{sk} (\zeta '; S) \ne \bot$, then compute $t = s' * s^{-1}$. Then output $(m^*_1 * t, m^*_2)$. Otherwise, set $(r', m_2') \leftarrow {{\textsf {Dec}}} _{sk} (\zeta ')$. If this decryption fails, output $\bot$; otherwise output $(s' * (r')^{-1}, m_2')$.

As in the proof of Theorem 4.1, we can assume that the adversary makes no ${{\textsc {rigenc}}}$ or ${{\textsc {rigextract}}}$ queries since the ${{\textsf {RigExtract}}}$ of an RCCA scheme uses the private key only to call ${{\textsf {Dec}}} _{sk}$ as a black box. Now, we have simply filled in details of the HCCA experiment, but generated the value s slightly differently than in ${{\textsf {RigEnc}}} ^*$. However, the value s is still uniform in ${\mathbb {H}} _1$, so this does not affect the outcome of the experiment.

However, suppose we modify this branch as follows: Let ${\zeta ^*}$ be instead generated via ${{\textsf {Enc}}} _{pk} (r,m^*_2)$; and in ${{\textsc {dec}}}$ queries we remove the condition that checks ${{\textsf {RigExtract}}}$. By the RCCA security of ${\mathcal {E}}$, this difference is indistinguishable, since whenever ${{\textsf {RigExtract}}} _{sk} (\zeta ';S) \ne \bot$ in the ${{\textsc {dec}}}$ response algorithm above, we have that ${{\textsf {Dec}}} _{sk} (\zeta ') = (r, m^*_2)$ in the modified interaction, so the other clause of the ${{\textsc {dec}}}$ response algorithm will give a consistent answer.

But in this modified interaction, the challenge ciphertext is generated according to the honest ${{\textsf {Enc}}} ^*$ procedure, and ${{\textsc {dec}}}$ queries are implemented exactly as ${{\textsf {Dec}}} ^*$. Thus the modified experiment is exactly the $b=0$ branch of the HCCA experiment. We established that the two branches of the experiment are indistinguishable, thus the scheme is HCCA-secure. $\square$