Automata Evaluation and Text Search Protocols with Simulation-Based Security

Abstract

This paper presents efficient protocols for securely computing the following two problems: (1) The fundamental problem of pattern matching. This problem is defined in the two-party setting, where party $P_1$ holds a pattern and party $P_2$ holds a text. The goal of $P_1$ is to learn where the pattern appears in the text, without revealing it to $P_2$ or learning anything else about $P_2$’s text. This problem has been widely studied for decades due to its broad applicability. We present several protocols for several notions of security. We further generalize one of our solutions to solve additional pattern matching-related problems of interest. (2) Our construction from above, in the malicious case, is based on a novel protocol for secure oblivious automata evaluation which is of independent interest. In this problem, party $P_1$ holds an automaton and party $P_2$ holds an input string, and they need to decide whether the automaton accepts the input, without learning anything else. Our protocol obtains full security in the face of malicious adversaries.

1 Introduction

Secure two-party computation is defined as joint computation of some function over private inputs. This joint computation must satisfy at least privacy (no other information is revealed beyond the output of the function) and correctness (the correct output is computed). In order to achieve this, the parties engage in a communication protocol. Today’s standard definition (cf. [7] following [4, 12, 30]) formalizes security by comparing the execution of such protocol to an “ideal execution” where a trusted third party helps the parties compute the function. Specifically, in the ideal world, the parties just send their inputs over perfectly secure communication lines to a trusted party, who then computes the function honestly and sends the output to the designated party. Informally, the real protocol is defined to be secure if all adversarial attacks on a real protocol can also be carried out in the ideal world; of course, in the ideal world, the adversary can do almost nothing and this guarantees that the same is also true in the real world. This definition of security is often called simulation-based because security is demonstrated by showing that a real protocol execution can be “simulated” in the ideal world.

Secure two-party computation has been extensively studied, and it is known that any efficient two-party functionality can be securely computed [14, 17, 36]. However, these are just feasibility results that demonstrate secure computation is possible, in principle, though not necessarily in practice. One reason is that the results mentioned above are generic, i.e., they do not exploit any structural properties of the specific function being computed. A long series of research efforts has been focused on finding efficient protocols for specific functions; and constructing such protocols is crucial if secure computation is ever to be used in practice.

1.1 Text Search

In this work, we consider the classic problem of pattern matching. In this problem, one party holds a text $T$ of length $\ell$ whereas the other party holds a pattern $p$ of length $m$, where these lengths are mutually known. The aim is for the party holding the pattern to learn all the locations of the pattern in the text (and there may be many), while the other party learns nothing about the pattern. Pattern matching has been widely studied for decades due to its broad applicability, but rarely in a secure context.

Earlier text search algorithms were sequential, where the text is searched by scanning for all occurrences of a particular pattern. Efficient variants of this approach analyze the pattern string to enable $O(\ell )$ scanning to skip regions of text whenever possible matches are provably not possible. Included in this category are the widely studied Knuth–Morris–Pratt [27] that uses automata evaluation, which we implement here securely (but less efficiently), Boyer–Moore [6] and more recently, Factor Oracle [1]-based algorithms. Algorithms based instead upon the analysis of the text to be searched are categorized as index-based, including suffix tree-based algorithms which build a data structure in $O(\ell )$ time and storage [31]. Nevertheless, these algorithms do not appear to be amendable to secure computation with reasonable computational properties. Finally, for completeness, algorithms used frequently for natural languages use partial inverted indexes such as $n$-grams, and were suggested in [15] in a similar security context. However, the probabilistic properties of these techniques cannot be easily bounded in running time or in security properties for general texts.

1.2 Our Contribution

1.2.1 Secure Text Search

• 1. Secure text search with honest-but-curious and one-sided simulatability Our starting point is an efficient protocol (cf. Sect. 3.1) that computes the pattern matching function in the “honest-but-curious” setting over a binary alphabet.¹ This solution offers linear communication in the input lengths and computation complexity of $O(m+\ell )$ modular exponentiations and $O(m\ell )$ modular multiplications. Informally, our protocol instructs the party that inputs the pattern to prepare two lists of ciphertexts so that one list is associated with zero and the other is associated with one. For each pattern location $i$, an encryption of zero is placed in the $i$th position of the list for which the current pattern bit $p_i$ matches the value that is associated with that list. The other party then uses these lists in order to generate for each text location, an encryption of the Hamming distance between the pattern and the text starting from this location. These are used to determine the matched text positions. We then demonstrate how the security of this solution can be extended to the case of one-sided simulation (with similar costs), where full simulation is provided for one of the malicious corruption cases, while only privacy (via computational indistinguishability) is guaranteed for the other corruption case.² For example, the secrecy of the inputs is always guaranteed, but in one of the corruption cases, the adversary can behave inappropriately causing the honest party to output an incorrect value. The workload of $P_1$ in our protocols is $O(m+\ell )$ modular exponentiations, whereas the workload of $P_2$ is $O(m+\ell )$ exponentiations and $O(m\ell )$ modular multiplications.

• 2. In Sect. 3.2, we consider solutions (using our protocol from Item 1), for three generalizations of the pattern matching problem:

  • (i) Approximate text search Recent applications e.g., computational biology, text editing, meteorology and more, have shown that a more generalized theoretical notion of string matching is required. In approximate matching, one defines a distance metric between the strings and finds all the text locations where the pattern matches the text by a pre-specified distance. For example, an additional public parameter $\rho$, which determines the number of differences that can be tolerated, is introduced (where a difference is defined by the specified metric). The most natural metric is the Hamming distance that counts the number of mismatches between two strings. The best algorithm for solving text search with mismatches in an insecure setting is the solution by Amir et al. [2], which introduces a solution in $O(\ell \sqrt{\rho \log \rho })$ time. We show how to adapt our one-sided simulation solution for this problem, obtaining $O(m + \ell )$ exponentiations, $O(m\ell )$ modular multiplications and $O(\rho \ell )$ communication.

  • (ii) Text search with wildcards This variant was developed with the aim to introduce improved algorithms for approximate text search. Here, a wildcard symbol is introduced in the pattern, so that it matches against any character when comparing against the text. In an insecure setting, this problem can be solved in time that is linear in the lengths of the text and pattern and the number of occurrences [32]. Our solution obtains similar costs to the overhead introduced by our one-sided simulation protocol since essentially the protocols are almost identical.

  • (iii) Text search with larger alphabet We further extend our basic protocol to deal with a larger alphabet $\varSigma$ as in the DNA example from below. In an insecure setting, this problem can be solved in $O(|\varSigma |\ell )$ time by extending the binary solutions. Our solution inflates the costs of our protocols from the binary case by a multiplicative factor $|\varSigma |$.

• 3. Secure text search against malicious adversaries Trying to adapt our solution for the malicious setting introduces quite a few subtleties and requires the use of a different technique. The main difficulty is with respect to the party that inputs the text. Since it must be ensured that a well-defined text is used during the protocol execution. Although this can always be achieved using generic zero-knowledge proofs to demonstrate correct behavior, it is not immediately clear how to do so efficiently. To achieve full simulation, we introduce a second independent protocol (cf. Sect. 5), which employs several other novel sub-protocols, including a protocol to prove that a correct pattern-specific automaton was constructed. Specifically, our protocol securely implements the [27] protocol that reduces the pattern matching problem to the composition of a pattern-specific automaton with the text $T$. The communication complexity of our protocol is $O(m\ell )$, and the round complexity is $O(\ell )$, where the round complexity is derived from the fact that the automaton must be evaluated sequentially.³ In addition, the number of exponentiations induced by our protocol is $O(m\ell )$. This result is based on our contribution in the following section regarding oblivious automata evaluation.

1.2.2 Oblivious Automata Evaluation

We develop a protocol for two parties (one holding an automaton $\varGamma$ and another holding an input text $T$) to securely compute the evaluation of $\varGamma$ on $T$ with full simulation in the presence of malicious behavior. This protocol can be of independent interest beyond the pattern matching application and can be considered an extension of the work by Ishai and Paskin [24], which considered the model of obliviously evaluating branching programs (a deterministic automaton is a special case of a branching program). In the model of [24], the communication is proportional to the input for the branching program and independent of the description of the program. Still, only privacy is guaranteed, and not correctness nor independence of inputs. In contrast, our protocol achieves full security but the amount of communication is proportional to the size of the automaton’s description times the length of the input to the automaton. Similarly, the number of exponentiations is a factor of these two parameters. We provide a detailed analysis below in Sect. 1.5.

1.3 Motivation

Secure pattern matching has many potential applications. Consider, for example, the hypothetical case of a hospital holding a DNA database of all the participants in a research study, and a researcher wanting to determine the frequency of the occurrence of a specific gene. This is a classical pattern matching application, which is, however, complicated by privacy considerations. The hospital may be forbidden from releasing the DNA records to a third party. Likewise, the researcher may not want to reveal what specific gene she is working on nor trust the hospital to perform the search correctly.

It would seem that existing honest-but-curious solutions would work here. However, the parties may be motivated to produce invalid results, so a proof of accurate output might be as important as the output itself. Moreover, there is also a need to make sure that the data on which the protocol is run is valid. For example, a rogue hospital could sell “fake” DNA databases for research purposes. Perhaps some trusted certification authorities might one day pre-certify a database as being valid for certain applications. Then, the security properties of our protocol could guarantee that only valid data is used in the pattern matching protocol. (The first step of our protocol is for the hospital to publish an encryption of the data, this could be replaced by publication of encrypted data that was certified as correct.)

1.4 Related Work

The idea to use oblivious automata evaluation, and also the study of secure pattern matching, originated in [34]. In this paper, the authors present secure protocols in the honest-but-curious setting and require linear communication complexity, and multiplicative computation complexity (in the number of states and the input length for the automaton). We note that adapting these constructions to the malicious setting is much more challenging. First, due to the requirement that the automaton must be valid (according to some specifications described in Sect. 5). Furthermore, the parties’ inputs to the oblivious transfers must be consistent. We thus take a different approach and show how to tolerate malicious behavior.

The problem of secure pattern matching was also studied by Hazay and Lindell [18], who used oblivious pseudorandom function (PRF) to evaluate every block of size $m$ bits from the text. Their protocol achieves the weaker notion of one-sided simulation and requires $O(\ell )$ exponentiations and $O(m\ell )$ multiplications for both parties. It is not immediately clear how to efficiently extend their solution so that it achieves fully simulatable security, since the inputs to the PRF must be consistent in the sense that every two consecutive blocks overlap in $m-1$ bits. We further note that this approach is not useful in solving the first two generalizations specified in Item 1.2.1, since the PRF evaluations of any two strings that their Hamming distance is small (say the two strings differ in only one bit) yield two strings that look independent.

In [26], Katz and Malka considered a generalization of the basic pattern matching problem, denoted text processing. For example, the party who holds the pattern has some additional information $y$ with the aim to learn a function of the text and $y$, for the text locations where the pattern matches. They showed how to modify Yao’s garbled circuit approach to obtain a protocol where the size of the garbled circuit is linear in the number of occurrences of $p$ in $T$ (rather than linear in the length of $T$). The costs of their constructions are dominated by the size of the circuit times the number of occurrences $u$. Moreover, they assume a common input of some threshold on the number of occurrences. Their solutions are applied in the one-sided simulation setting.

In a follow-up work [22], Hazay and Toft presented an improved protocol that solves the basic pattern matching problem in the malicious setting with $O(m\ell )$ multiplications. This analysis holds also for the honest-but-curious setting, as well as with one-sided simulation. Their solution takes a different approach by converting the binary representation of the pattern and the text into field elements. Hazay and Toft further presented solutions for approximate text search and text search with wildcards that incur $O(m\ell )$ modular exponentiations (in both honest-but-curious and malicious settings).

The works by Jarrous and Pinkas [25] and by Vergnaud [35] solve variants of the basic problem. In the former work, the authors solve the hamming distance problem for two equal length strings against malicious adversaries. Their protocol requires a committed oblivious transfer for each bit. Moreover, the costs of their protocol are inflated by a statistical parameter $s$ for running a subprotocol for the oblivious polynomial evaluation functionality [19] (namely, the protocol requires $O(sd)$ exponentiations, where $d$ is the degree of the polynomial, i.e., the input length). In the context of approximate pattern matching, their protocol requires $O(sm\ell )$ exponentiations. The latter work solves the problem of pattern matching with wildcards in the presence of malicious adversaries by taking a different approach of Fast Fourier Transform and implementing this technique securely. This paper presents protocols that exhibit linear communication and $O(\ell \log m)$ modular exponentiations.

Finally, a more recent paper by Baron et al. [3] studies the problem of text search with wildcards in a more general sense of non-binary alphabet, implementing a different algorithm based on linear algebra formulation and additive homomorphic encryption. This protocol requires $O(m+\ell )$ communication complexity and $O(m\ell )$ modular multiplications in the malicious setting.

1.5 Efficiency Comparison

The state-of-the-art generic construction for secure two-party computation is a recent work by Lindell and Pinkas [29]. They propose a protocol that follows the methodology Yao’s protocol and is secure in the presence of malicious adversaries under the DDH assumption. In order to cope with malicious behavior, this protocol carries out a basic cut-and-choose test on the garbled Boolean circuit construction of Yao. This means that a party $P_1$ has to construct $s$ copies of a garbled circuit, sending them to $P_2$, who then asks $P_1$ to open half of them in order to verify their correctness. For example, the computation/communication costs are inflated by this security parameter $s$. Recent developments [28] reduce the cut-and-choose parameter into 40 (with some additional overhead). We thus compare our protocols that compute the oblivious automaton evaluation and pattern matching functionalities with the [28] generic two-party constant round protocol.

oblivious automata evaluation We note that a circuit that computes the oblivious automaton evaluation functionality would require $O(\ell Q\log Q)$ gates for a $Q$-states automaton evaluated over a binary input of length $\ell$.⁴ Notably, it is possible to generate a circuit of size $O(\ell Q)$ that computes this functionality but this circuit depends on the automaton’s description (and leaks information about its structure). Now, since we need to preserve the secrecy of the automaton, we need to consider a circuit that operates as a universal circuit, in the sense that it takes these inputs and evaluates the automaton on the input string. This accounts for an extra $\log Q$ factor and implies that the number of multiplications in [28] is dominated by $O(s\ell Q\log Q)$. Moreover, the number of exponentiations used in this protocol is dominated by $24.5s\ell + 18\ell +$ 5,520s.

On the other hand, our protocol for oblivious automata evaluation does not apply a cut-and-choose strategy. Having $P_1,P_2$ hold inputs of lengths $\ell , Q$, and our protocol incurs communication and computation costs of $O(\ell Q)$, where this constant mostly depends on the overhead of randomly permuting the automaton. By the analysis of [13], we get that this overhead of the ZK proof for shuffling is dominated by $30Q$ exponentiations (for permuting a pair of vectors each time). Thus, overall cost is dominated by $120\ell Q$ exponentiations and $O(\ell Q)$ multiplications. Nevertheless, the round complexity of our protocol is $O(\ell )$ since the automaton must be evaluated sequentially, while the round complexity of [29] is constant.

Text search We conclude with a discussion of our solutions for the basic pattern matching problem and its variants. The best known circuit that computes the classic pattern matching functionality requires $O(nm)$ gates since the circuit compares the pattern against every text location. In the honest-but-curious setting, Yao’s technique induces a protocol that uses $O(nm)$ symmetrical key operations and $O(m)$ exponentiations that can be made independent of the input length (where the later is obtained by employing the ideas of extended oblivious transfer [23], but also requires an additional assumption on the hash function). In the malicious setting, this overhead grows by a factor of a statistical parameter $s$ (see the analysis in the previous section). Our constructions for the honest-but-curious and one-sided simulation settings require $O(m+\ell )$ modular exponentiations for party $P_1$ and $O(m\ell )$ modular multiplications and $O(\ell )$ exponentiations for party $P_2$. Our protocols achieve better overhead than the protocols of [34] and [18], where the former requires $O(m\ell )$ exponentiations and the later requires $O(m+\ell )$ exponentiations and $O(m\ell )$ multiplications for both parties. Our protocol for the malicious setting requires $O(m\ell )$ exponentiations and takes a different approach than the protocol in [22] that requires $O(m\ell )$ modular multiplications and constant round complexity, and outperforms our protocol.

Generic protocols achieve the same overhead for the pattern matching variants considered in this paper, as in the case of computing the standard pattern matching problem since circuit size is about $O(m\ell )$ gates. Moreover, the protocols by Vergnaud [35] for computing approximate pattern matching and pattern matching with wildcards with one-sided simulation require $O(\ell \log m)$ exponentiations (in comparison with $O(m+\ell )$ exponentiations in our protocol). The one-sided simulation variant of [22] protocols for these problems require $O(m\ell )$ exponentiations. Finally, the work of [3] studies pattern matching with wildcards in the malicious setting that requires $O(m+\ell )$ exponentiations for non-binary alphabets.

1.6 A Road Map

In Sect. 2, we present basic definitions and useful tools that we use in our constructions. In Sect. 3, we present a honest-but-curious secure protocol for the pattern matching problem (cf. Sect. 3.1). We further extend this solution and show how to obtain one-sided simulation security. In Sect. 3.2, we consider generalizations of the basic problem. In Sect. 4, we present a protocol for the oblivious automata evaluation problem with full security against malicious adversaries. In Sect. 5, we show how to use our protocol from Sect. 4 within a larger protocol for the pattern matching problem in the malicious setting.

2 Definitions and Tools

Throughout the paper, we denote the security parameter by $n$. Although not explicitly specified, input lengths are always assumed to be bounded by some polynomial in $n$. A probabilistic machine is said to run in polynomial-time (PPT) if it runs in time that is polynomial in the security parameter $n$ alone. We denote by $a\leftarrow A$ the random choice of $a$ from a set $A$.

A function $\mu (\cdot )$ is negligible in $n$ if for every polynomial $p(\cdot )$ there exists a value $N$ such that $\mu (n)<\frac{1}{p(n)}$ for all $n>N$; i.e., $\mu (n) = n^{-\omega (1)}$. Let $X=\{X(a,n)\}_{a\in \{0,1\}^*,n\in N}$ and $Y=\{Y(a,n)\}_{a\in \{0,1\}^*,n\in N}$ be distribution ensembles. We say that $X$ and $Y$ are computationally indistinguishable, denoted $X\mathop {\equiv }\limits ^\mathrm{c}Y$, if for every polynomial non-uniform distinguisher $D$ there exists a negligible $\mu (\cdot )$ such that

$$\begin{aligned} \Bigl |\Pr [D(X(a,n))=1]-\Pr [D(Y(a,n))=1]\Bigr |<\mu (n) \end{aligned}$$

for every $n\in N$ and $a\in \{0,1\}^*$.

2.1 Secure Two-Party Computation with Malicious Adversaries

In this section, we briefly present the standard definition for secure multiparty computation and refer to [17, Chap. 7] for more details and a motivating discussion.

Two-party computation A two-party protocol can be systematically analyzed by characterizing the protocol as a random process that maps pairs of inputs to pairs of outputs (one for each party). We refer to such a process as a functionality and denote it as $f:\{0,1\}^*\times \{0,1\}^*\rightarrow \{0,1\}^*\times \{0,1\}^*$, where $f = (f_1,f_2)$. That is, for every pair of inputs $(x,y)$, the output is a random variable $(f_1(x,y),f_2(x,y))$ ranging over pairs of strings where $P_1$ receives $f_1(x,y)$ and $P_2$ receives $f_2(x,y)$. We sometimes denote such a functionality by $(x,y) \mapsto (f_1(x,y),f_2(x,y))$.

Security of protocols (informal) The security of a protocol is analyzed by comparing what an adversary can do in a real protocol execution to what it can do in an ideal scenario that is secure by definition. This is formalized by considering an ideal computation involving an incorruptible trusted third party to whom the parties send their inputs. The trusted party computes the functionality on the inputs and returns to each party its respective output. A protocol is secure if any adversary interacting in the real protocol (where no trusted third party exists) can do no more harm than if it was involved in the above-described ideal computation.

Execution in the ideal model In an ideal execution, the parties send their inputs to the trusted party who computes the output. An honest party just sends the input that it received, whereas a corrupted party can replace its input with any other value of the same length. Let $f$ be a two-party functionality where $f = (f_1,f_2)$, let $\mathcal{A}$ be a non-uniform probabilistic polynomial-time machine and let $I\subseteq [2]$ be the set of corrupted parties (either $P_1$ is corrupted, or $P_2$ is corrupted, or neither). Then, the ideal execution of $f$ on inputs $(x,y)$, auxiliary input $z$ to $\mathcal{A}$ and security parameter $n$, denoted ${\mathbf {IDEAL}}_{f,\mathcal{A}(z),I}(x,y,n)$, is defined as the output pair of the honest party and the adversary $\mathcal{A}$ from the above ideal execution.

Execution in the real model In the real model, there is no trusted third party and the parties interact directly. The adversary $\mathcal{A}$ sends all messages in place of the corrupted party and may follow an arbitrary polynomial-time strategy. In contrast, the honest parties follow the instructions of the specified protocol $\pi$.

Let $f$ be as above and let $\pi$ be a two-party protocol for computing $f$. Furthermore, let $\mathcal{A}$ be a non-uniform probabilistic polynomial-time machine and let $I$ be the set of corrupted parties. Then, the real execution of $\pi$ on inputs $(x,y)$, auxiliary input $z$ to $\mathcal{A}$ and security parameter $n$, denoted ${\mathbf {REAL}}_{\pi ,\mathcal{A}(z),I}(x,y,n)$, is defined as the output vector of the honest party and the adversary $\mathcal{A}$ from the real execution of $\pi$.

Security as emulation of a real execution in the ideal model Having defined the ideal and real models, we can now define the security of protocols. Loosely speaking, the definition asserts that a secure multi-party protocol (in the real model) emulates the ideal model (in which a trusted party exists). This is formulated by saying that adversaries in the ideal model are able to simulate executions of the real-model protocol.

Definition 2.1

Let $f$ and $\pi$ be as above. Protocol $\pi$ is said to securely compute $f$ with abort in the presence of malicious adversaries if for every non-uniform probabilistic polynomial-time adversary $\mathcal{A}$ for the real model, there exists a non-uniform probabilistic polynomial-time adversary $\mathcal{SIM}$ for the ideal model, such that for every $I\subseteq [2]$,

where $|x|=|y|$.

2.2 Sequential Composition

Sequential composition theorems are useful tools that help in writing proofs of security. The basic idea behind these composition theorems is that it is possible to design a protocol that uses an ideal functionality as a subroutine and then analyze the security of the protocol when a trusted party computes this functionality. For example, assume that a protocol is constructed that uses the secure computation of some functionality as a subroutine. Then, first we construct a protocol for the functionality in question and then prove its security. Next, we prove the security of the larger protocol that uses the functionality as a subroutine in a model where the parties have access to a trusted party computing the functionality. The composition theorem then states that when the “ideal calls” to the trusted party for the functionality are replaced by real executions of a secure protocol computing this functionality, the protocol remains secure.

The hybrid model The aforementioned composition theorems are formalized by considering a hybrid model where parties both interact with each other (as in the real model) and use trusted help (as in the ideal model). Specifically, the parties run a protocol $\pi$ that contains “ideal calls” to a trusted party computing some functionalities $f_1,\ldots ,f_m$. These ideal calls are just instructions to send an input to the trusted party. Upon receiving the output back from the trusted party, the protocol $\pi$ continues. We stress that honest parties do not send messages in $\pi$ between the time that they send input to the trusted party and the time that they receive back output (this is because we consider sequential composition here). Of course, the trusted party may be used a number of times throughout the $\pi$-execution. However, each time is independent (i.e., the trusted party does not maintain any state between these calls). We call the regular messages of $\pi$ that are sent among the parties standard messages and the messages that are sent between parties and the trusted party ideal messages.

Let $f_1,\ldots ,f_m$ be probabilistic polynomial-time functionalities and let $\pi$ be a two-party protocol that uses ideal calls to a trusted party computing $f_1,\ldots ,f_m$. Furthermore, let $\mathcal{A}$ be a non-uniform probabilistic polynomial-time machine and let $I$ be the set of corrupted parties. Then, the $f_1,\ldots ,f_m$-hybrid execution of $\pi$ on inputs $(x,y)$, auxiliary input $z$ to $\mathcal{A}$ and security parameter $n$, denoted ${\mathbf {HYBRID}}^{f_1,\ldots ,f_m}_{\pi ,\mathcal{A}(z),I}(x,y,n)$, is defined as the output vector of the honest party and the adversary $\mathcal{A}$ from the hybrid execution of $\pi$ with a trusted party computing $f_1,\ldots ,f_m$.

Sequential modular composition Let $f_1,\ldots ,f_m$ and $\pi$ be as above, and let $\rho _1,\ldots ,\rho _m$ be protocols. Consider the real protocol $\pi ^{\rho _1,\ldots ,\rho _m}$ that is defined as follows: all standard messages of $\pi$ are unchanged. When a party $P_i$ is instructed to send an ideal message $\alpha _i$ to the trusted party to compute functionality $f_j$, it begins a real execution of $\rho _j$ with input $\alpha _i$ instead. When this execution of $\rho _j$ concludes with output $\beta _i$, party $P_i$ continues with $\pi$ as if $\beta _i$ was the output received by the trusted party (i.e., as if it were running in the $f_1,\ldots ,f_m$-hybrid model). Then, the composition theorem of [7] states that if $\rho _j$ securely computes $f_j$ for every $j\in \{1,\ldots ,m\}$, then the output distribution of a protocol $\pi$ in a hybrid execution with $f_1,\ldots ,f_m$ is computationally indistinguishable from the output distribution of the real protocol $\pi ^{\rho _1,\ldots ,\rho _m}$. This holds for security in the presence of malicious adversaries [7] and one-sided simulation when considering the corruption case that has a simulator (an easy corollary from [7]).

2.3 One-Sided Simulation for Two-Party Protocols

Two of our protocols achieve a level of security that we call one-sided simulation. In these protocols, $P_2$ receives output while $P_1$ should learn nothing. In one-sided simulation, full simulation is possible when $P_2$ is corrupted. However, when $P_1$ is corrupted, we only guarantee privacy, meaning that $P_1$ learns nothing whatsoever about $P_2$’s input (this is straightforward to formalize because $P_1$ receives no output). This is a relaxed level of security and does not achieve everything we want; for example, independence of inputs and correctness are not guaranteed. Nevertheless, for this level of security, we are able to construct highly efficient protocols that are secure in the presence of malicious adversaries.

Formally, let ${\mathbf {REAL}}_{\pi ,\mathcal{A}(z),i}(x,y,n)$ denote the output of the honest party and the adversary $\mathcal{A}$ (controlling party $P_i$) after a real execution of protocol $\pi$, where $P_1$ has input $x, P_2$ has input $y, \mathcal{A}$ has auxiliary input $z$, and the security parameter is $n$. Let ${\mathbf {IDEAL}}_{f,\mathcal{SIM}(z),i}(x,y,n)$ be the analogous distribution in an ideal execution with a trusted party who computes $f$ for the parties. Finally, let ${\mathbf {VIEW}}^\mathcal{A}_{\pi ,\mathcal{A}(z),i}(x,y,n)$ denote the view of the adversary after a real execution of $\pi$ as above. Then, we have the following definition:

Definition 2.2

Let $f$ be a functionality where only $P_2$ receives output. We say that a protocol $\pi$ securely computes $f$ with one-sided simulation if the following holds:

• 1. For every non-uniform PPT adversary $\mathcal{A}$ controlling $P_2$ in the real model, there exists a non-uniform PPT adversary $\mathcal{SIM}$ for the ideal model, such that

  $$\begin{aligned}&\left\{ {\mathbf {REAL}}_{\pi ,\mathcal{A}(z),2}(x,y,n)\right\} _{x,y,z\in \{0,1\}^*,n\in N}\\&\quad \mathop {\equiv }\limits ^\mathrm{c}\left\{ {\mathbf {IDEAL}}_{f,\mathcal{SIM}(z),2}(x,y,n)\right\} _{x,y,z\in \{0,1\}^*,n\in N} \end{aligned}$$

  where $|x|=|y|$.

• 2. For every non-uniform PPT adversary $\mathcal{A}$ controlling $P_1$, and every polynomial $p(\cdot )$

  $$\begin{aligned}&\left\{ {\mathbf {VIEW}}^\mathcal{A}_{\pi ,\mathcal{A}(z),1}(x,y,n)\right\} _{x,y,y^{\prime },z\in \{0,1\}^*,n\in N}\nonumber \\&\quad \mathop {\equiv }\limits ^\mathrm{c}\left\{ {\mathbf {VIEW}}^\mathcal{A}_{\pi ,\mathcal{A}(z),1}(x,y^{\prime },n)\right\} _{x,y,y^{\prime },z\in \{0,1\}^*,n\in N} \end{aligned}$$

  (1)

  where $|x|=|y|=|y^{\prime }|$.

Note that the ensembles in Eq. (1) are indexed by two different inputs $y$ and $y^{\prime }$ for $P_2$. The requirement is that $\mathcal{A}$ cannot distinguish between the case that $P_2$ used the first input $y$ or the second input $y^{\prime }$ for any pair $y,y^{\prime }$ such that $|y|=|y^{\prime }|$.

2.4 Finite Automata

A deterministic finite automaton is described by a tuple $\varGamma =(Q,\varSigma ,\varDelta ,q_0,F)$, where $Q$ is the set of states, $\varSigma$ is an alphabet of inputs, $\varDelta :Q \times \varSigma \rightarrow Q$ denotes a state-transition table, $q_0\in Q$ is the initial state, and $F\subseteq Q$ is the set of final (or accepting) states. Without loss of generality, in this work we consider only automata with complete transition tables, where there exists a transition at each state for every input $\sigma \in \varSigma$. We also consider the notation of $\varDelta (q_0,(\sigma _1,\ldots ,\sigma _\ell ))$ to denote the result of the automaton evaluation on $\sigma _1,\ldots ,\sigma _\ell$, for $\sigma _i\in \varSigma$. Every automaton specifies a language, which is the (potentially infinite) set of strings accepted by the automaton.

2.5 Hardness Assumptions

Our constructions rely on the DDH assumption formalized below.

Definition 2.3

(DDH) We say that the decisional Diffie–Hellman (DDH) problem is hard relative to ${\mathbb G}=\{{\mathbb G}_n\}$ if for all polynomial-sized circuits $\mathcal{A}=\{\mathcal{A}_n\}$ there exists a negligible function $\mathsf{negl}$ such that

$$\begin{aligned} \Big |\Pr \left[ \mathcal{A}({\mathbb G},q,g,g^x,g^y,g^z)=1\right] - \Pr \left[ \mathcal{A}({\mathbb G},q,g,g^x,g^y,g^{xy})=1\right] \Big | \le \mathsf{negl}(n), \end{aligned}$$

where $q$ is the order of ${\mathbb G}$ and the probabilities are taken over the choices of $g$ and $x,y,z\leftarrow {\mathbb Z}_q$.

2.6 Public-Key Encryption Schemes

We begin by specifying the definitions of public-key encryption (PKE) and IND-CPA security. We then describe the El Gamal PKE and conclude this section with definitions for homomorphic PKE and threshold PKE, demonstrating that El Gamal meets these definitions.

Definition 2.4

(PKE) We say that $\Pi =(G, E, D)$ is a public-key encryption scheme if $G, E, D$ are polynomial-time algorithms specified as follows:

• $G$, given a security parameter $n$ (in unary), outputs keys $(pk,sk)$, where $pk$ is a public-key and $sk$ is a secret key. We denote this by $(pk,sk)\leftarrow G(1^n)$.

• $E$, given the public-key $pk$ and a plaintext message $m$, outputs a ciphertext $c$ encrypting $m$. We denote this by $c\leftarrow E_{pk}(m)$; and when emphasizing the randomness $r$ used for encryption, we denote this by $c\leftarrow E_{pk}(m;r)$.

• $D$, given the public-key $pk$, secret key $sk$ and a ciphertext $c$, outputs a plaintext message $m$ s.t. there exists randomness $r$ for which $c = E_{pk}(m;r)$ (or $\bot$ if no such message exists). We denote this by $m \leftarrow D_{pk,sk}(c)$.

For a public-key encryption scheme $\Pi =(G, E, D)$ and a non-uniform adversary $\mathcal{A}=(\mathcal{A}_1,\mathcal{A}_2)$, we consider the following IND-CPA game:

$$\begin{aligned}&(pk,sk)\leftarrow G(1^n).\\&(m_0,m_1,history)\leftarrow \mathcal{A}_1(pk),\text{ s.t. }|m_0|=|m_1|.\\&c\leftarrow E_{pk}(m_b), \text{ where }\, b\leftarrow \{0,1\}.\\&b^{\prime }\leftarrow \mathcal{A}_2(c,history).\\&\mathcal{A}\, \text{ wins }\,\text{ if }\,b^{\prime }=b. \end{aligned}$$

Denote by $\mathsf{AdvCPA}_{\Pi ,\mathcal{A}}(n)$ the probability that $\mathcal{A}$ wins the IND-CPA game.

Definition 2.5

(IND-CPA security) A public-key encryption scheme $\Pi =(G, E, D)$ is IND-CPA secure, if for every non-uniform adversary $\mathcal{A}=(\mathcal{A}_1,\mathcal{A}_2)$ there exists a negligible function $\mathsf{negl}$ such that $\mathsf{AdvCPA}_{\Pi ,\mathcal{A}}(n) \le \frac{1}{2} + \mathsf{negl}(n)$.

2.6.1 The El Gamal Encryption Scheme

We consider the following modification of the El Gamal encryption scheme [11]. The public-key is the tuple $pk=\langle {\mathbb G},q,g,h\rangle$ and the corresponding private key is $sk=\langle {\mathbb G},q,g,x\rangle$, where ${\mathbb G}$ is a cyclic group of prime order $q$ with a generator $g$ (we assume multiplication and group membership can be performed efficiently in ${\mathbb G}$). In addition, it holds that $h=g^x$.

Encryption of a message $m \in \{1,\ldots ,q^{\prime }\}$ (with $q^{\prime } \ll q$) is performed by choosing $r\leftarrow {\mathbb Z}_q$ and computing $E_{pk}(m;r)=\langle g^r,h^r\cdot g^m\rangle$. Decryption of a ciphertext $c=\langle c_1,c_2 \rangle$ is performed by computing $g^m = c_2 \cdot c_1^{-x}$ and then finding $m$ by exhaustive search. Thus, this scheme works only for small integer domains (i.e., $q^{\prime }$ must be small) which is the case for our protocol. We point out that the reason we modify El Gamal in this way (by encrypting $g^m$ rather than $m$) is to make it additively homomorphic. Finally, we note that a zero encryption corresponds to a Diffie–Hellman tuple, i.e., $E_{pk}(0;r)=\langle g^r,h^r\cdot g^0\rangle = \langle g^r,h^r\rangle$. The security of this scheme relies on the hardness of solving the DDH problem specified in Definition 2.3.

We define the following two properties and show how they are easily met by the El Gamal scheme.

Homomorphic PKE We abuse notation and use $E_{pk}(m)$ to denote the distribution $E_{pk}(m;r)$ where $r$ is chosen uniformly at random. Define homomorphic encryption as follows.

Definition 2.6

A public-key encryption scheme $(G, E, D)$ is homomorphic if, for all $n$ and all $(pk, sk)$ output by $G(1^n)$, it is possible to define groups ${\mathbb M}, {\mathbb C}$ such that:

• The plaintext space is ${\mathbb M}$, and all ciphertexts output by $E_{pk}(\cdot )$ are elements of ${\mathbb C}$.

• For any $m_1, m_2 \in {\mathbb M}$ and $c_1, c_2 \in {\mathbb C}$ with $m_1 = D_{ps,sk}(c_1)$ and $m_2 = D_{pk,sk}(c_2)$, it holds that

  $$\begin{aligned} \left\{ pk,c_1,c_1 \cdot c_2\} \equiv \{pk,E_{pk}(m_1),E_{pk}(m_1 + m_2)\right\} \end{aligned}$$

  where the group operations are carried out in ${\mathbb C}$ and ${\mathbb M}$, respectively.

Our modification of El Gamal is homomorphic with respect to component-wise multiplication (in ${\mathbb G}$) of ciphertexts. We denote by $c_1\cdot _{\mathbb G}c_2$ the respective multiplications of $c_1^1\cdot c_2^1$ and $c_1^2\cdot c_2^2$ where $c_i=\langle c_i^1,c_i^2\rangle =E_{pk}(m_i)$, such that the multiplication result yields the encryption of $m_1+m_2$.

Threshold PKE We consider two functionalities: One for securely generating a secret key while keeping it a secret from both parties, whereas the second functionality jointly decrypts a given ciphertext. We denote the key generation functionality by ${\mathcal{F}_{\scriptscriptstyle \mathrm {KEY}}}$, which is defined as follows:

$$\begin{aligned} (1^n,1^n) \mapsto \left( (pk,sk_1),(pk,sk_2)\right) , \end{aligned}$$

(2)

where $(pk, sk) \leftarrow G(1^n)$, and $sk_1$ and $sk_2$ are random shares of $sk$. The decryption functionality $\mathcal{F}_{\scriptscriptstyle \mathrm {DEC}}$ is defined by

$$\begin{aligned} (c,pk) \mapsto \left( (m:c=E_{pk}(m)),-\right) , \end{aligned}$$

(3)

It is well known how to design an efficient threshold El Gamal scheme in the malicious setting based on the protocol of Diffie and Hellman [10]. Informally, generating the shares for the key can be done by sequentially having each party $P_i$ (starting with $P_1$) pick a random element $x_i\leftarrow {\mathbb Z}_q$ and publish $g^{x_i}$ together with a zero-knowledge proof of knowledge of $x_i$, so that the public-key equals $g^{x_1+x_2}$ (see Sect. 2.7 for more details of the zero-knowledge proof). To ensure a simulation, $P_1$ must commit to its share first and decommit this commitment after $P_2$ sends its share. Decryption of a ciphertext $c=\langle c_1,c_2\rangle$ follows by computing $c_2\cdot (c_1^{x_1}\cdot c_1^{x_2})^{-1}$, where each party sends $c_i$ to the power of its share. We denote these protocols by $\pi _{\scriptscriptstyle \mathrm {KEY}}$ and $\pi _{\scriptscriptstyle \mathrm {DEC}}$, respectively, and assume that they can be computed with simulation-based security in the presence of malicious attacks.

2.7 Zero-Knowledge Proofs and Proofs of Knowledge

Our protocols employ zero-knowledge proofs (of knowledge) for assuring correct behavior. Before getting into more details, we formally define zero-knowledge and knowledge extraction as stated in [16]. We then conclude with a definition of a $\varSigma$-protocol which constitutes a zero-knowledge proof of a special type.

Definition 2.7

(Interactive proof system) A pair of ppt interactive machines $(P,V)$ is called an interactive proof system for a language $L$ if there exists a negligible function $\mathsf{negl}$ such that the following two conditions hold:

• 1. Completeness: For every $x\in L$,

  $$\begin{aligned} \Pr [\langle P,V\rangle (x)=1]\ge 1-\mathsf{negl}(|x|) \end{aligned}$$

• 2. Soundness: For every $x\notin L$ and every interactive ppt machine $B$,

  $$\begin{aligned} \Pr [\langle B,V\rangle (x)=1]\le \mathsf{negl}(|x|) \end{aligned}$$

Definition 2.8

(Zero-knowledge) Let $(P,V)$ be an interactive proof system for some language $L$. We say that $(P,V)$ is computational zero-knowledge if for every ppt interactive machine $V^{*}$ there exists a ppt algorithm $M^{*}$ such that

$$\begin{aligned} \{\langle P,V^{*}\rangle (x)\}_{x\in L}\mathop {\equiv }\limits ^\mathrm{c}\{\langle M^{*}\rangle (x)\}_{x\in L} \end{aligned}$$

where the left term denotes the output of $V^{*}$ after it interacts with $P$ on common input $x$, whereas the right term denotes the output of $M^{*}$ on $x$.

Definition 2.9

(Knowledge extraction) Let $\mathcal{R}$ be a binary relation and $\kappa \rightarrow [0,1]$. We say that an interactive function $V$ is a knowledge verifier for the relation $\mathcal{R}$ with knowledge error $\kappa$ if the following two conditions holds:

• Non-triviality: There exists an interactive machine $P$ such that for every $(x,y)\in \mathcal{R}$, (implying that $x\in L_R$), all possible interactions of $V$ with $P$ on common input $x$ and auxiliary input $y$ are accepting.

• Validity (with error $\kappa$): There exists a polynomial $q(\cdot )$ and a probabilistic oracle machine $K$ such that for every interactive function $P$, every $x\in L_R$, and every machine $K$ satisfies the following condition: Denote by $p(x,y,r)$ the probability that the interactive machine $V$ accepts, on input $x$, when interacting with the prover specified by $P_{x,y,r}$. If $p(x,y,r)>\kappa (|x|)$, then, on input $x$ and with access to oracle $P_{x,y,r}$, machine $K$ outputs a solution $s\in \mathcal{R}(x)$ within an expected number of steps bounded by

  $$\begin{aligned} \frac{q(|x|)}{p(x,y,r)-\kappa (|x|)} \end{aligned}$$

  The oracle machine $K$ is called a universal knowledge extractor.

Let $\mathcal{R}$ be an $\mathcal {NP}$ relation associated with the language $L_{\mathcal{R}} = \{x |~\exists w~s.t.~(x,w) \in \mathcal{R}\}$. Then, we define the zero-knowledge proof knowledge functionality for $\mathcal{R}$ by $\mathcal{F}^\mathcal{R}_{{\scriptscriptstyle \mathrm {ZKPoK}}}((x,w),x) \mapsto (-,(x,b))$ where $b=1$ if $\mathcal{R}(x,w) =1$ and $b=0$ if $\mathcal{R}(x,w)=0$.

Definition 2.10

($\varSigma$-protocol) A protocol $\pi$ is a $\varSigma$-protocol for relation $\mathcal{R}$ if it is a three-round public-coin protocol and the following requirements hold:

• Completeness: If $P$ and $V$ follow the protocol on input $x$ and private input $w$ to $P$ where $(x,w)\in \mathcal{R}$, then $V$ always accepts.

• Special soundness: There exists a polynomial-time algorithm $A$ that given any $x$ and any pair of accepting transcripts $(a,e,z), (a,e^{\prime },z^{\prime })$ on input $x$, where $e\ne e^{\prime }$, outputs $w$ such that $(x,w)\in \mathcal{R}$.

• Special honest-verifier zero knowledge: There exists a ppt algorithm $M$ such that

  $$\begin{aligned} \left\{ \langle P(x,w),V(x,e)\rangle \right\} _{x\in L_R} \equiv \left\{ M(x,e) \right\} _{x\in L_R} \end{aligned}$$

  where $M(x,e)$ denotes the output of $M$ upon input $x$ and $e$, and $\langle P(x,w),V(x,e)\rangle$ denotes the output transcript of an execution between $P$ and $V$, where $P$ has input $(x,w), V$ has input $x$, and $V$’s random tape (determining its query) equals $e$.

A generic, efficient technique that enables the transformation of any $\varSigma$-protocol into a zero-knowledge proof (of knowledge) can be found in [20]. This transformation requires an additional 5 (or 6 for a proof of knowledge) exponentiations.

Next, we describe the following standard $\varSigma$-protocols used in our constructions:

Protocol	Relation/language	References
$\pi _{\scriptscriptstyle \mathrm {DL}}$	$\mathcal{R}_{\scriptscriptstyle \mathrm {DL}}=\left\{ (({\mathbb G},q,g_1,g_2),x)\mid g_2=g_1^x \right\}$	[33]
$\pi _{\scriptscriptstyle \mathrm {DH}}$	$\mathcal{R}_{\scriptscriptstyle \mathrm {DH}}=\left\{ (({\mathbb G},q,g_1,g_2,g_3,g_4),x)\mid g_2=g_1^x \wedge g_4=g_3^x\}\right\}$	[9]
$\pi _{\scriptscriptstyle \mathrm {NZ}}$	$\mathrm{L}_{\scriptscriptstyle \mathrm {NZ}}=\left\{ ({\mathbb G}, q, g, h,\langle \alpha ,\beta \rangle )\mid \exists ~(m\not =0, r)\text{ s.t. } \alpha =g^r,\; \beta = h^r g^m\right\}$	[21]

All these proofs require constant round complexity and a constant number of exponentiations.

We further employ the following zero-knowledge proofs in our constructions:

• 1. A zero-knowledge proof $\pi _{\scriptscriptstyle \mathrm {ENC}}$ for the following language that is associated with a homomorphic encryption $\Pi =(G,E,D)$ relative to a ciphertext group ${\mathbb C}$ and group operation $\cdot$. Specifically, let $C_i=[c_{i,1},\ldots ,c_{i,Q}]$ for $i \in \{0,1\}$ and $C^{\prime }=[c_1^{\prime },\ldots ,c_Q^{\prime }]$ be three vectors of $Q$ ciphertexts each. We want to prove that $C^{\prime }$ is the “re-encryption” of the same messages encrypted in either $C_0$ or $C_1$, or in other words, there exists an index $i\in \{0,1\}$ such that for all $j, c_j^{\prime }$ was obtained by multiplying $c_{i,j}$ by a random encryption of $0$. More formally,

  $$\begin{aligned} \mathrm{L}_{\scriptscriptstyle \mathrm {ENC}}= \left\{ (pk,C_0,C_1,C^{\prime })\big |\exists ~(i,\{r_j\}_j)\, \text{ s.t. }\quad \text{ for }\,\text{ all } j: c_j^{\prime }= c_{i,j} \cdot E_{pk}(0;r_j) \right\} . \end{aligned}$$

  In the proof, the joint statement is a collection of three vectors, and the prover produces proofs that the third vector is a randomized version of either the first or the second vector. When using the El Gamal encryption, the proof boils down to proving that either $C^{\prime }/C_0$ or $C^{\prime }/C_1$ is a Diffie–Hellman tuple (when division is computed component-wise). This enables us to extract the bit $i$, but not the entire witness for $\mathrm{L}_{\scriptscriptstyle \mathrm {ENC}}$. We note that this is sufficient for our purposes. We continue with our protocol,

Protocol 1

($\varvec{\pi }_{\scriptscriptstyle \mathrm {ENC}}$—A Zero-Knowledge Proof for $\mathrm{L}_{\scriptscriptstyle \mathrm {ENC}}$):

• Joint statement The set $({\mathbb G},q,g,h,C_0,C_1,C^{\prime })$ for $pk=\langle {\mathbb G},q,g,h\rangle$ a public-key for El Gamal .

• Auxiliary input for the prover An index $i$ and a set $\{r_j\}_j$ as in $\mathrm{L}_{\scriptscriptstyle \mathrm {ENC}}$.

• The protocol

• (a) Let $Q$ denote the number of elements in each vector. Then the verifier picks random strings $r_{0,1},\ldots ,r_{0,Q},r_{1,1},\ldots ,r_{1,Q}\leftarrow {\mathbb Z}_q$ and sends these values to the prover.

• (b) Let $C_i=[c_{i,1},\ldots ,c_{i,Q}]$ for $i \in \{0,1\}$ and $C^{\prime }=[c_1^{\prime },\ldots ,c_Q^{\prime }]$. The parties compute the sets $c_0=\prod _{j=1}^Q (c_{0,j}\cdot _{\mathbb G}(1/c^{\prime }_j))^{r_{0,j}}$ and $c_1=\prod _{j=1}^Q (c_{1,j}\cdot _{\mathbb G}(1/c^{\prime }_j))^{r_{1,j}}$.

• (c) The prover performs a zero-knowledge proof of knowledge proving that either $\langle pk,c_0\rangle$ or $\langle pk,c_1\rangle$ is a Diffie–Hellman tuple.

Note that the first message sent by the verifier is not part of the challenge but used to reduce the size of the proven statement.

Proposition 2.1

Assume that the DDH assumption holds relative to ${\mathbb G}$. Then, Protocol 1 is a statistical zero-knowledge proof for $\mathrm{L}_{\scriptscriptstyle \mathrm {ENC}}$ with perfect completeness and negligible soundness error. It is further a proof of knowledge of the index $i$ within the prover’s witness.

It is easy to verify that the verifier is always convinced by an honest prover. The combined argument for zero-knowledge can be derived from [8].⁵ The fact that index $i$ can be extracted is due to the proof of knowledge property of the Diffie–Hellman proof from Step 1c.

• 2. Let $\Pi =(G,E,D)$ be a homomorphic encryption relative to a ciphertext group ${\mathbb C}$ and group operation $\cdot$, and let $C=\{c_{i,j}\}_{j,i}$ and $C^{\prime }=\{c^{\prime }_{i,j}\}_{j,i}$ be two sets of encryptions, where $j\in \{1,\ldots ,Q\}$ and $i\in \{0,1\}$. Then, we consider a zero-knowledge proof of knowledge $\pi _{\scriptscriptstyle \mathrm {PERM}}$ for proving that $C$ and $C'$ correspond to the same decryption vector up to some permutation. Meaning that,

  $$\begin{aligned} \mathcal{R}_{\scriptscriptstyle \mathrm {PERM}}=\left\{ \Bigl (pk,C,C^{\prime }\Bigr ), \Bigl (\pi ,\{r_{j,i} \}_{j,i}\Bigr ) \big |\forall ~i,j,~\{c_{j,i} = c^{\prime }_{\pi (j),i} \cdot E_{pk}(0;r_{j,i})\}_j \right\} \end{aligned}$$

  where $\pi$ is a one-to-one mapping over the elements $\{1,\ldots ,Q\}$. Specifically, we prove that $C'$ is obtained from $C$ by randomizing all the ciphertexts and permuting their indices. We require that the same permutation is applied for both vectors. The problem in which a single a vector of ciphertexts is randomized and permuted is defined by

  $$\begin{aligned} \mathcal{R}_{\scriptscriptstyle \mathrm {PERM}}^1&= \left\{ \Bigl (pk, (c_1,\ldots ,c_Q),(\tilde{c}_1,\ldots ,\tilde{c}_Q)\Bigr ), \right. \\&\quad \left. \Bigl (\pi ,(r_1,\ldots ,r_Q)\Bigr )\big | \forall ~i,j, \tilde{c}_j=c_{\pi (j)} \cdot E_{pk}(0;r_j)\right\} . \end{aligned}$$

  and has been widely studied in the literature. The state-of-the-art protocol is in [5]. In this work, we will use a simpler and slightly less efficient (but still good for our purposes) protocol by Groth and Lu [13]. They presented an efficient zero-knowledge proof of knowledge $\pi _{\scriptscriptstyle \mathrm {PERM}}^1$ for $\mathcal{R}_{\scriptscriptstyle \mathrm {PERM}}^1$ with linear computation and communication complexity, and constant number of rounds. The reason we use a slightly less efficient protocol is due to the fact that it is easy to show that this proof is applicable to the case where the same permutation is applied to more than one vector of ciphertexts (as we require), and because it can be applied to the El Gamal encryption scheme.

3 Secure Text Search with One-Sided Simulatability

The pattern matching problem is defined as follows: given a binary text $T$ of length $\ell$ and a binary pattern $p$ of length $m$, find all the locations in the text where pattern $p$ appears in the text. Stated differently, for every $i=1,\ldots ,\ell -m+1$, let $T_i$ be the substring of length $m$ that begins at the $i$th position in $T$. Then, the basic problem of pattern matching is to return the set $\{i \mid T_i=p\}$. Formally, we consider the functionality $\mathcal{F}_{\scriptscriptstyle \mathrm {PM}}$ defined by

$$\begin{aligned} ((p,\ell ),(T,m))\mapsto \left\{ \begin{array}{ll} (\{i \mid T_i=p_1\ldots p_m\},-) &{}\quad \hbox {if}\, |p|= m\, \hbox {and}\, |T|= \ell \\ (|T|,|p|) &{}\quad \hbox {otherwise} \end{array}\right. \end{aligned}$$

where $T_i$ is defined as above.

Note that $P_2$, which holds the text, learns nothing about the pattern held by $P_1$, whereas the only information that $P_1$ learns about the text is the locations where its pattern matches. As discussed in the introduction, this problem has been intensively studied and can be solved optimally in an insecure environment in time that is linear in length of the text and the number of occurrences.

3.1 Secure Text Search against Honest-But-Curious Adversaries

In this section, we present an algorithm for secure text search that is secure in the presence of honest-but-curious adversaries. Our protocol employs the properties of homomorphic encryption to compute the sum of the differences between the pattern and the text. Informally, party $P_1$ computes a matrix $\varPhi$ of size $2\times m$ that includes an encryption of zero in the position $(i,j)$ if $p_j=i$, and an encryption of one otherwise. Given $\varPhi$, party $P_2$ creates a new encryption $e_k$ for every text location $k$ that corresponds to the inner product of the encryptions at locations $(t_{k+j-1},j)$ for all $j\in \{1,\ldots ,m\}$. By definition, $e_k$ encrypts the Hamming distance between $p$ and $T_k$. Therefore, if $p$ matches $T_k, e_k$ is a random encryption of zero. Figure 1 illustrates the approach schematically, and Protocol $\pi _{\scriptscriptstyle \mathrm {SIMPLE}}$ introduces it formally.

Fig. 1

Text search in the honest-but-curious setting

Protocol 2

($\varvec{\pi }_{\scriptscriptstyle \mathrm {SIMPLE}}$—Honest-But-Curious Secure Text Search)

• Inputs The input of $P_1$ is a binary search string $p= p_1,\ldots ,p_m$ and $\ell$, whereas $P_2$’s input is a binary text string $T=t_1,\ldots ,t_\ell$ and $m$.

• Conventions The parties jointly agree on a group ${\mathbb G}$ of prime order $q$ and a generator $g$ for the El Gamal encryption. Party $P_1$ generates a key pair $(pk,sk)\leftarrow G(1^n)$ and publishes $pk$. Finally, unless written differently, $j\in \{1,\ldots ,m\}$ and $i\in \{0,1\}$.

• The protocol

  • 1. Encryption of pattern Party $P_1$ builds a $2\times m$ matrix of ciphertexts $\varPhi$ defined by,

    $$\begin{aligned} \varPhi (i,j) = \left\{ \begin{array}{ll} E_{pk}(0) &{}\quad p_j = i \\ E_{pk}(1) &{}\quad \mathrm{otherwise} \end{array} \right. \end{aligned}$$

    The matrix $\varPhi$ is sent to party $P_2$.

  • 2. Scanning of text For each offset $k\in \{1,\dots ,\ell -m+1\}, P_2$ computes

    $$\begin{aligned} e_k = \prod _{j=1}^{m} \varPhi \left( t_{k+j-1},j\right) \end{aligned}$$

    Note that for each offset $k$, it holds that $T_k$ matches pattern $p$ if and only if $e_k = E_{pk}(0)$.

  • 3. Masking of terms Due to the fact that the decryption of $e_k$ reveals the number of matched elements at text location $k$, party $P_2$ masks this result through scalar multiplication. In particular, $P_2$ sends the set $\{e^{\prime }_k = (e_k)^{r_k}\cdot E_{pk}(0;r^{\prime }_k)\}_k$ where $r_k,r^{\prime }_k$ are random strings chosen independently from ${\mathbb Z}_q$ for each $k$.

  • 4. Obtaining result $P_1$ uses $sk$ to decrypt the values of $e^{\prime }_k$ and outputs

    $$\begin{aligned} \left\{ k~|~D_{pk,sk}(e^{\prime }_k)=0\right\} \!. \end{aligned}$$

Clearly, if both parties are honest then $P_1$ outputs a correct set of indexes with overwhelming probability (an error may occur with negligible probability if $(e_k)^r$ is an encryption of zero even though $e_k$ is not). We now state the following theorem,

Theorem 3.1

Assume that the DDH assumption holds relative to ${\mathbb G}$. Then Protocol $\pi _{\scriptscriptstyle \mathrm {SIMPLE}}$ securely computes $\mathcal{F}_{\scriptscriptstyle \mathrm {PM}}$ in the presence of honest-but-curious adversaries.

In case $P_1$ is corrupted, statistical security is obtained by sending an encryption of zero for the matched text locations, and an encryption of a random element in ${\mathbb Z}_q$ for all other locations. In case $P_2$ is corrupted, security is obtained via a reduction to the IND-CPA security of $(G,E,D)$ by simply defining a simulator that sends encryptions of zero. The formal proof is straightforward and is therefore omitted.

One-sided simulation security We point out that if party $P_1$ proves that it computed matrix $\varPhi$ correctly, then we can also guarantee full simulation with respect to a corrupted $P_1$. This can be achieved by having $P_1$ prove, using the zero-knowledge proof of knowledge $\pi _{\scriptscriptstyle \mathrm {PERM}}$ (cf. Sect. 2.7), that for every $j$ the pair $\varPhi (0,j),\varPhi (1,j)$ is a permuted pair of the ciphertexts $E_{pk}(0),E_{pk}(1)$. In addition, we add two checks in the protocol where the parties verify whether the vectors sizes received from the other party are consistent with the lengths $\ell$ and $m, P_1$ and $P_2$ are given, respectively.

Constructing a simulator for the case of a corrupted $P_2$ is more challenging since the protocol does not guarantee that $P_2$ computes $\{e^{\prime }_k\}_k$ relative to a well-defined binary string $T$. In particular, $P_2$ may compute every ciphertext $e^{\prime }_k$ using a different $m$ bits string. We are not aware of any alternative for proving consistency relative to $P_2$’s behavior, rather than using generic zero-knowledge proofs of knowledge which do not provide an efficient approach. Therefore, we only consider privacy for this case. Let $\pi ^{\prime }_{\scriptscriptstyle \mathrm {SIMPLE}}$ denote the modified version of $\pi _{\scriptscriptstyle \mathrm {SIMPLE}}$ with the additional zero-knowledge proof of knowledge $\pi _{\scriptscriptstyle \mathrm {PERM}}$ used by $P_1$. We conclude with the following claim,

Theorem 3.2

Assume that the DDH assumption holds relative to ${\mathbb G}$. Then Protocol $\pi ^{\prime }_{\scriptscriptstyle \mathrm {SIMPLE}}$ securely computes $\mathcal{F}_{\scriptscriptstyle \mathrm {PM}}$ with one-sided simulation.

Proof Sketch

Assume $P_1$ is malicious. Then, we define a simulator $S$ that plays the role of $P_2$ and builds a view for $P_1$ that is (computationally) indistinguishable from the view of the real protocol without knowing the real input text held by $P_2$. The crucial point is that at the end of Step 1 (which in $\pi ^{\prime }_{\scriptscriptstyle \mathrm {SIMPLE}}$ includes also the zero-knowledge proof of knowledge $\pi _{\scriptscriptstyle \mathrm {PERM}}$), the simulator can learn the input of $P_1$ by extracting it from $\pi _{\scriptscriptstyle \mathrm {PERM}}$. At this point, the simulator is also given the output of the protocol by the trusted party, i.e., $S$ knows in which locations of the input text of $P_2$ the pattern appears. $S$ then chooses a text $T^{\prime }$ which contains the pattern in the exact same locations but is otherwise an arbitrary string $p^{\prime }\ne p$. It then runs the rest of the protocol using $T^{\prime }$. It is easy to verify that the view of $P_1$ produced by $S$ is statistically close to the real view.

In case $P_2$ is corrupted, the privacy of $P_1$ follows from the IND-CPA security of El Gamal and the zero-knowledge property of $\pi _{\scriptscriptstyle \mathrm {PERM}}$. Specifically, the simulator sends encryptions of zero and invokes the simulator for $\pi _{\scriptscriptstyle \mathrm {PERM}}$ for proving the correctness of $\varPhi$

$\square$.

We remark that protocol $\pi ^{\prime }_{\scriptscriptstyle \mathrm {SIMPLE}}$ takes a different approach than the one-sided simulatable protocol of [18], that computes the pattern matching functionality using oblivious PRF evaluation. One advantage of our protocol is that it can be easily extended for handling generalizations of the basic pattern matching problem (as shown in Sect. 3.2). This does not seem to be the case for the [18] protocol since the PRF evaluations of two strings that their Hamming distance is small yield two strings that look independent. Furthermore, in order to evaluate the PRF, the [18] protocol requires $\ell$ OT evaluations. This overhead implies that both parties must compute $O(\ell )$ exponentiations.

Efficiency We first note that the protocol $\pi ^{\prime }_{\scriptscriptstyle \mathrm {SIMPLE}}$ is constant round. The overall communication cost is $O(m+\ell )$ group elements, whereas the computation cost is $O(m+\ell )$ modular exponentiations and $(m\ell )$ multiplications, as $P_2$ computes the multiplication of $m$ ciphertexts (component-wise) for each text location. The additional cost of $\pi _{\scriptscriptstyle \mathrm {PERM}}$ is linear in the length of the pattern.

3.2 Generalizations of the Pattern Matching Problem

In this section, we study three generalizations of the classic pattern matching problem, to other problems of practical interest. We show how to modify our solution from the prior section to solve these problems.

Approximate Text Search In approximate matching, one defines a distance metric between the strings and finds all the text locations where the pattern matches the text by a pre-specified distance. For example, an additional public parameter $\rho$, which determines the number of differences that can be tolerated, is introduced (where a difference is defined by the specified metric). The most natural metric is the Hamming distance that counts the number of mismatches between two strings. Specifically, $P_1$ learns all the text locations in which the Hamming distance between the pattern and the substring at these text locations is smaller equal to $\rho$. More formally, we consider the functionality for approximate text search $\mathcal{F}_{\scriptscriptstyle \mathrm {APM}}$ that is defined by

$$\begin{aligned}&((p,\ell ,\rho ),(T,m,\rho ^{\prime }))\\&\quad \mapsto \left\{ \begin{array}{ll} (\{i \mid d(T_i,(p_1,\ldots ,p_m))\le \rho \},-) &{}\quad \hbox {if}\, |p|= m, |T|=\ell \, \hbox {and}\, \rho =\rho ^{\prime }\\ (|T|,|p|) &{}\quad \text{ otherwise } \\ \end{array}\right. \end{aligned}$$

where $d(x,y)$ denotes the Hamming distance of two binary strings $x$ and $y$ of the same length, and $T_i$ is the substring of length $m$. The best algorithm for solving text search with mismatches in an insecure environment is the solution by Amir et al. [2] who introduced a solution whose time complexity is $O(\ell \sqrt{\rho \log \rho })$. We show that a simple modification to our protocol yields a protocol that computes this functionality as well. Upon completing its computations and before masking the terms as in Step 3 of $\pi ^{\prime }_{\scriptscriptstyle \mathrm {SIMPLE}}$ and condition that $\rho =\rho ^{\prime }$, party $P_2$ produces $\rho +1$ ciphertexts from each ciphertext $e_k$ by subtracting from its plaintext all values between $[0,\ldots ,\rho ]$. Finally, it masks and rerandomizes these ciphertexts and randomly shuffles the result. Denote this modified protocol by $\pi _{\scriptscriptstyle \mathrm {APM}}$.

Then, simulation for a corrupted $P_1$ is not changed as now, and the simulator receives from the trusted party all the text locations where the pattern matches with at most $\rho$ mismatches. The proof for the case that $P_2$ is corrupted follows from above. Then it holds that

Theorem 3.3

Assume that the DDH assumption holds relative to ${\mathbb G}$. Then, Protocol $\pi _{\scriptscriptstyle \mathrm {APM}}$ securely computes $\mathcal{F}_{\scriptscriptstyle \mathrm {APM}}$ with one-sided simulation.

Note that both the computation and communication complexities are $O(m\ell )$. Specifically, the overhead of $P_2$ is dominated by $O(m\ell )$ multiplications and $O(m+\ell )$ exponentiations.

Text search with wildcards This variant was developed with the aim to introduce improved algorithms for approximate text search. Here, a wildcard symbol is introduced in the pattern, so that it matches against any character when comparing against the text. In an insecure setting, this problem can be solved in time that is linear in the lengths of the text and pattern, and the number of occurrences [32]. We note that in protocol $\pi ^{\prime }_{\scriptscriptstyle \mathrm {SIMPLE}}$, a wildcard can be introduced by having $P_1$ send two encryptions of zero instead of a pair of encryptions of zero and one. By doing so, we ensure that regardless of the text bit, $P_2$ will not count it as a mismatch. Denote this modified protocol by $\pi _{\scriptscriptstyle \mathrm {WC}}$, then it holds that

Theorem 3.4

Assume that the DDH assumption holds relative to ${\mathbb G}$. Then, Protocol $\pi _{\scriptscriptstyle \mathrm {WC}}$ securely computes the pattern matching problem with wildcards with one-sided simulation.

The security proof is as above except that $P_1$ uses a slightly different proof of knowledge. In particular, it proves the statement that for every $j$, the pair $\{\varPhi (0,j),\varPhi (1,j)\}$ is either a permuted pair of the encryptions $\{E_{pk}(0),E_{pk}(1)\}$ or it corresponds to a pair of zero encryptions. The number of exponentiations required from $P_2$ is $O(m\ell )$ and the communication is $O(m+\ell )$ group elements.

Larger alphabets Recalling that protocol $\pi ^{\prime }_{\scriptscriptstyle \mathrm {SIMPLE}}$ compares binary strings and computes the pattern matching functionality for the binary alphabet. However, in some scenarios, the pattern and the text are defined over a larger alphabet $\varSigma$, (e.g., when searching in a DNA database the alphabet is of size four.)

When $T$ and $p$ are drawn from a $|\varSigma |$-ary alphabet, protocol $\pi _{\scriptscriptstyle \mathrm {SIMPLE}}$ can be extended to this case, where $\varPhi$ is a $q\times m$ matrix. In this case, $P_1$ must prove that each row of $\varPhi$ is a permutation of a vector of $q$ elements of the form $\{ E_{pk}(0),E_{pk}(1),\ldots ,E_{pk}(1)\}$, using $\pi _{\scriptscriptstyle \mathrm {PERM}}$, with a single encryption of zero and $q-1$ encryptions of one. The size of the alphabet appears as a multiplicative cost for both the computation and communication measures. The security proof is not appreciably different from the binary case.

4 Secure Oblivious Automata Evaluation

In this section, we present a secure protocol for oblivious automata evaluation in the presence of malicious adversaries. In this functionality, $P_1$ inputs a description of an automaton $\varGamma =(Q,\varSigma ,\varDelta ,q_0,F)$, and $P_2$ inputs a string $t$. The result of the protocol is that $P_1$ receives $\varGamma (t)$, while $P_2$ learns nothing. Formally, we define this problem via the functionality

$$\begin{aligned} \mathcal{F}_{\scriptscriptstyle \mathrm {AUTO}}:(\varGamma =(Q,\varSigma ,\varDelta ,q_0,F),(t,|Q|,|F|))\mapsto \left\{ \begin{array}{ll} ((\text{ accept },|t|),-) &{}\quad \text{ if }\,\varGamma (t)\in F\\ ((\text{ no-accept },|t|),-) &{}\quad \text{ otherwise } \\ \end{array}\right. \end{aligned}$$

where $\varGamma (t)$ denotes the final state in the evaluation of $\varGamma$ on $t$. The reason we require from the party who holds $\varGamma$ to learn the outcome and not the other way around is due to employing this protocol in our main construction for computing text search. There, the party with the pattern designs an automaton for its specific input and should learn outcome of the its automaton evaluation on the text. In order to enable $P_2$ to learn the outcome, a simple modification is required in the last step of our protocol.

W.l.o.g., we consider the following simplifying assumptions. First, we assume that $\varSigma =\{0,1\}$ (our construction can be proven for any fixed alphabet) and that the transition table is complete, where there exists a transition at each state for every input $\sigma \in \varSigma$. To simplify the description, we assume that each row is described using three columns: the current state denoted by column $\epsilon$, the next state in case of reading a zero denoted by column $\mathbf{0}$ and the next state in case of reading a one denoted by column 1, so that each bit has its own column and the overall number of rows is now $|Q|$. We furthermore assume that the names of the states $\{q_0,q_1,\ldots ,q_{|Q|-1}\}$ are the integers taken from $\{1,\ldots ,{|Q|}\}$, respectively (i.e., the initial state is labeled $1$). Finally, we assume that $|Q|$ and $|F|$ are public (for $|F|$ the number of states in $F$). For the sake of generality, we note that keeping $|F|$ private can be easily dealt by having $P_1$ send a vector of $|Q|$ encryptions for which the $i$th encryption is a zero encryption only if $q_i\notin F$. Otherwise, it is an encryption of $q_i$ (this can be verified using a simple zero-knowledge proof).

Recall that our starting point is the protocol from [34]. Their idea is to have the parties share the current machine state, such that by the end of the $k$th iteration, the party with the automaton knows a random string $r_k$, whereas the party with the input for the automaton learns $q_k+r_k$. The parties complete each iteration by running an oblivious transfer in which the next state is now shared between them. The fact that the parties are honest-but-curious significantly simplifies their construction. Unfortunately, we cannot see any natural way to extend their technique to the malicious adversary case (even when using oblivious transfer that is resilient to malicious attacks). Coping with such behavior is much more challenging. First due to the requirement that the automaton must be valid (according to some specifications described in Sect. 5). Furthermore, the parties’ inputs to the oblivious transfers must be consistent. In this paper, we take a different approach to obtain security against malicious adversaries.

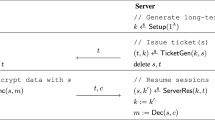
A high level description We begin by briefly motivating our construction; see Fig. 2 as well. At the beginning of the protocol, $P_1$ and $P_2$ jointly generate a public-key $(G,E,D)$ for the threshold El Gamal encryption scheme (denoted by the sub-protocol $\pi _{\scriptscriptstyle \mathrm {KEY}}$). Next, party $P_1$ encrypts its transition table $\varDelta$ and the set of accepting states $F$, and sends it to $P_2$. Note that this immediately allows $P_2$ to find the encryption of the next state $c_{\varDelta (1,t_1)}=\varDelta (1,t_1)$, by selecting it from the encrypted matrix (since it can identify the encrypted next state associated with the specific state and bit). $P_2$ rerandomizes this encryption and shows it to $P_1$. The protocol continues in this fashion for $\ell$ iterations (the length of the text).⁶

Fig. 2

Construction of determinized KMP automata for pattern 1100011001

Assume that at the outset of each iteration $i$, the parties know an encryption of the current state and their goal is to find an encryption of the next state. $P_2$ selects from the matrix the encrypted column that corresponds to the next state according to its input $t_i$ (as it only knows an encryption of the current state). Then, using the homomorphic properties of El Gamal , the parties obliviously select the correct next state; this stage involves the following computations. Let $c_{\varDelta (1,t_\xi -1)}$ denote an encryption of the current state after the partial automaton evaluation $\varDelta (1,t_1,\ldots ,t_{\xi -1})$. Then, the parties compute first the set $C=\{c_{\varDelta (1,\xi -1)}\cdot _G E_{pk}(g^{{q_j}^{-1}};0)\}_j$ where only one ciphertext in this set will be an encryption of $0$, indicating the position of the current state. In order to learn the encryption of the next state, the parties have to randomly permute the transition table and mask column $C$, so that when being decrypted, it will not reveal any useful information about the secret inputs of the parties. The protocol concludes by the parties jointly checking if the encrypted state that is produced within the final iteration is in the encrypted list of accepting states.

More specifically, there are several technical challenges in constructing such a secure protocol. In particular, the identification of the next encrypted state without leaking additional information requires a couple of rounds of interaction between the parties in which they mask and permute the ciphertext vector containing all possible states, in order to “destroy any link” between their input and the next encrypted state. Moreover, in order to protect against malicious behavior, zero-knowledge proofs are included at each step to make sure the parties behave according to the protocol specifications.

We are now ready to present a formal description of our protocol.

Protocol 3

($\varvec{\pi }_{\scriptscriptstyle \mathrm {AUTO}}$—Secure Oblivious Automata Evaluation)

• Inputs The input of $P_1$ is a description of an automaton $\varGamma =(Q,\{0,1\},\varDelta ,q_0,F)$, and the input of $P_2$ is a binary string $t=t_1,\ldots ,t_\ell$.

• Auxiliary Inputs ${|Q|}$ and $|F|$ for $P_2$ and the security parameter $1^n$ for both.

• Conventions We assume that the parties jointly agree on a group ${\mathbb G}$ of prime order $q$ and a generator $g$ for the threshold El Gamal encryption scheme. Both parties check every received ciphertext for validity and abort if an invalid ciphertext is received. We further assume that the description of the automaton does not include unreachable states. Finally, unless written differently, ${j\in \{1,\ldots ,{|Q|}\}}$ and $i\in \{0,1\}$.

• The protocol:

• 1. El Gamal key setup The parties engage in an execution of protocol $\pi _{\scriptscriptstyle \mathrm {KEY}}$ and generate a public-key $pk$ and two shares $x_1$ for $P_1$ and $x_2$ for $P_2$.

• 2. Encrypting $P_1$’s transition table and accepting states

  • (a) $P_1$ encrypts each entry in its transition table $\varDelta$ under $pk$ component-wise. Denote this set of ciphertexts by $E_\varDelta =(C_\epsilon ,C_0,C_1)$, denoting columns $\epsilon , 0$ and $1$, respectively. $P_1$ also sends the list of encrypted accepting states denoted by $E_F=\{E_{pk}(f)\}_{f\in F}$. For simplicity, we assume that the randomness of the ciphertexts encrypting column $C_\epsilon$ is known (note that this column “encrypts” the publicly known states $\{1,\ldots ,|Q|\}$ in some fixed order).

  • (b) For every encryption $\langle c_1,c_2\rangle \in E_\varDelta ~\cup ~E_F, P_1$ proves the knowledge of $\log _g c_1$ using $\pi _{\scriptscriptstyle \mathrm {DL}}$.

  • (c) Proving the validity of the encrypted transition matrix $P_1$ proves that $E_\varDelta$ is a set of encryptions for values from the set $\{1,\ldots ,|Q|\}$. It first sorts the ciphertexts within columns $C_0$ and $C_1$ according to their plaintexts (i.e., in a non-decreasing order), denotes the sorted vector by $c_1,\ldots ,c_{2\cdot |Q|}$. $P_1$ multiplies every encryption in this set with a random encryption of 0, sends it to $P_2$ and proves: (1) firstly that this vector is a permutation of $C_0$ and $C_1$ using $\pi _{\scriptscriptstyle \mathrm {PERM}}$. (2) That $\tilde{c}_\tau =c_\tau /c_{\tau -1}\in \{E_{pk}(0),E_{pk}(1)\}$ for $\tau \in \{2,\ldots ,2|Q|\}$ using $\pi _{\scriptscriptstyle \mathrm {DH}}$. For example, by proving that either $(pk,\tilde{c}_\tau )$ or $(pk,\tilde{c}_\tau /E_{pk}(1))$ is a Diffie–Hellman tuple and finally, (3) that $c_1$ and $c_{2\cdot |Q|}$ encrypt plaintexts from $\{1,\ldots ,|Q|\}$ (to ensure that $P_1$ does not use states taken from a different range) by running a combined argument for $\pi _{\scriptscriptstyle \mathrm {DH}}$ (see Footnote 5 for more details about such an argument).

• 3. First iteration

  • (a) $P_2$ chooses the encryption of the next state $c_{\varDelta (1,t_1)}=E_{pk}(\varDelta (1,t_1))$. It then defines $c_1=c_{\varDelta (1,t_1)} \cdot _{\mathbb G}E_{pk}(0;r)$ for a fresh uniform $r$, i.e., a random encryption of the next state and sends it to $P_1$.

  • (b) $P_2$ proves that $D_{pk,sk}(c_1) \in \{D_{pk,sk}(c_{\varDelta (1,0)}),D_{pk,sk}(c_{\varDelta (1,1)})\}$ using the zero-knowledge proof of knowledge $\pi _{\scriptscriptstyle \mathrm {ENC}}$.

• 4. Iterations $\{2,\ldots ,\ell \}$ for every $\xi \in \{2,\ldots ,\ell \}$, let $c_{\varDelta (1,t_{\xi -1})}$ denote the encryption of the current state after the partial automaton evaluation $\varDelta (1,(t_1,\ldots ,t_{\xi -1}))$. Then, the parties continue as follows:

  • (a) Subtracting column $C_\epsilon$ from the current state The parties compute the vector of encryptions $C=\{c_{\varDelta (1,\xi -1)}/c_{j,\epsilon }\}_j$ for every ciphertext $c_{j,\epsilon }\in C_\epsilon$. Note that only one ciphertext will denote an encryption of zero, and that indicates the position corresponding to the current state.

  • (b) Picking column $C_{t_\xi }$: $P_2$ sends $P_1$ a randomized version of column $C_{t_\xi }$, denoted $B_{t_\xi }$, and proves correctness using the zero-knowledge proof of knowledge $\pi _{\scriptscriptstyle \mathrm {ENC}}$.

  • (c) $P_2$ permutes columns $C$ and $B_{t_\xi }$: $P_2$ chooses a random permutation $\pi$ over $\{1,\ldots ,{|Q|}\}$ and sends $P_1$ a randomized version of the permuted columns $(C_\pi ,C_{\pi ,t_\xi })=(\pi (C),\pi (B_{t_\xi }))$. $P_2$ proves its computations using a zero-knowledge proof of knowledge $\pi _{\scriptscriptstyle \mathrm {PERM}}$.

  • (d) $P_1$ permutes columns $C_\pi$ and $C_{\pi ,t_\xi }$: If $P_1$ accepts the proof $\pi _{\scriptscriptstyle \mathrm {PERM}}$, it continues similarly by randomizing and permuting $(C_{\pi ^{\prime }},{C}_{\pi ^{\prime },t_\xi })=(\pi ^{\prime }(C_\pi ),\pi ^{\prime }({C}_{\pi ,t_\xi }))$ using a new random permutation $\pi ^{\prime }$. $P_1$ proves its computations using a zero-knowledge proof of knowledge $\pi _{\scriptscriptstyle \mathrm {PERM}}$.

  • (e) Masking column $C_\epsilon$ The parties take turns in masking $C_{\pi ^{\prime }}$ (a permutation over column $C_\epsilon$).

    • (i.) More specifically, for every $c_{\pi ^{\prime }} \in C_{\pi ^{\prime }}, P_2$ chooses $x,r\leftarrow {\mathbb Z}^*_q$ and computes $c^{\prime }_{\pi ^{\prime }}=c^x_{\pi ^{\prime }}\cdot E_{pk}(0;r)$ (component-wise). It then proves that $(c_{\pi ^{\prime }},c^{\prime }_{\pi ^{\prime }})$ forms a Diffie–Hellman tuple using $\pi _{\scriptscriptstyle \mathrm {DH}}$. Notice that the ciphertext that denotes an encryption of zero will not be influenced by the masking, while the others are mapped to a random value.

    • (ii.) $P_1$ repeats this step and masks the result yielding a new vector $\bar{C}$.

  • (f) Decrypting column $\bar{C}$ The parties decrypt vector $\bar{C}$ by running $\pi _{\scriptscriptstyle \mathrm {DEC}}$ on each element $\bar{c} \in \bar{C}$, where $P_2$ decrypts using its share first.

  The parties choose the $j$th ciphertext to be $c_{\varDelta (1,t_\xi )}\in C_{\pi ^{\prime },t_\xi }$ for which $D_{pk,sk}(\bar{c}_j)=0$ (with high probability there will be only one such ciphertext).

• 5. Verifying output Upon completing the $\ell$th iteration the parties hold a ciphertext $c_{\varDelta (1,t_\ell )}$ that denotes the encryption of $\varDelta (1,t)$. To check if this is an accepting state the parties do the following:

  • (a) They compute the ciphertext vector $C_F=\{c_{\varDelta (1,t_\ell )}/c\}_{c\in E_F}$. Notice that $\varDelta (1,t)$ is accepting if and only if one of these ciphertexts is an encryption of zero.

  • (b) $P_2$ masks $C_F$ as in Step 4e and proves correctness using $\pi _{\scriptscriptstyle \mathrm {DL}}$. Let $C_F^{\prime }$ be the result vector.

  • (c) $P_2$ permutes $C^{\prime }_F$ and proves correctness using $\pi ^1_{\scriptscriptstyle \mathrm {PERM}}$. Let $C_{F,\pi }$ be the resulting vector.

  • (d) The parties run $\pi _{\scriptscriptstyle \mathrm {DEC}}$ to decrypt all the ciphertexts in $C_{F,\pi }$, where $P_2$ decrypts using its share first and the result going only to $P_1$ that outputs accept if and only if one of the plaintexts equals zero.

We continue with the following claim,

Theorem 4.1

Assume that the DDH assumption holds relative to ${\mathbb G}$. Then $\pi _{\scriptscriptstyle \mathrm {AUTO}}$ securely computes $\mathcal{F}_{\scriptscriptstyle \mathrm {AUTO}}$ in the presence of malicious adversaries.

Intuitively it should be clear from the IND-CPA security of the encryption scheme that the automaton and the text remain secret. Consider first the case in which $P_1$ is corrupted, and we need to simulate the role of $P_2$. The simulator is going to choose an arbitrary input and run $P_2$’s code on it (while forcing a correct outcome for $P_1$). Then, to prove that this view is indistinguishable from a real view, we need to show a reduction to the encryption scheme. In particular, our reduction should enable the simulator to decrypt without actually knowing the secret key, since the parties must run a decryption in each iteration in order to locate the encryption of the next state. Moreover, decryptions must be computed for the ciphertexts received from the challenger during the reduction, for which the simulator has no control.

We approach this technicality via a sequence of hybrid games in which indistinguishable changes are introduced to the way the simulator works, but still allowing it to complete the simulated execution. More specifically, we first instruct the simulator to decrypt without using its share (but still introducing the same view) and then show how to create a view that is independent of the honest party’s input. This enables us to replace the simulated input with a real one. As for the case that $P_2$ is corrupted, the proof follows the same outline mainly because, even though $P_2$ does not receive an output, it still sees intermediate decryptions of column $\bar{C}$. Our goal is to prove that these decryptions do not contribute any information about $P_1$’s input.

4.1 Proof of Theorem 4.1

We separately prove security in the case that $P_1$ is corrupted and the case that $P_2$ is corrupted. Our proof is in a hybrid model where a trusted party implements the relations $\mathcal{R}_{\scriptscriptstyle \mathrm {DL}}, \mathcal{R}_{\scriptscriptstyle \mathrm {DH}}, \mathcal{R}_{\scriptscriptstyle \mathrm {PERM}}$ and $\mathcal{R}^1_{\scriptscriptstyle \mathrm {PERM}}$ (namely, the zero-knowledge proof of knowledge functionality that corresponds to these relations).

Party $P_1$ is corrupted Let $\mathcal{A}$ denote an adversary controlling $P_1$. We construct a simulator $\mathcal{SIM}$ as follows,

• 1. $\mathcal{SIM}$ is given a description of an automaton $\varGamma =(Q,\{0,1\},\varDelta ,q_0,F)$ and $\mathcal{A}$’s auxiliary input and invokes $\mathcal{A}$ on these values.

• 2. $\mathcal{SIM}$ invokes the simulator for $\pi _{\scriptscriptstyle \mathrm {KEY}}$ and extracts the adversary’s share $x_1$. $\mathcal{SIM}$ records this value, picks $x_2\leftarrow {\mathbb Z}_q$ and completes the execution of $\pi _{\scriptscriptstyle \mathrm {KEY}}$ with this share. Let $pk=g^{x_1+x_2}$ denote the public-key generated in this execution.

• 3. $\mathcal{SIM}$ receives from $\mathcal{A}$ ciphertexts $E_{\varDelta _\mathcal{A}}$ and $E_{F_\mathcal{A}}$ and verifies the proofs for a valid automaton. If the verification fails $\mathcal{SIM}$ sends $\bot$ to the trusted party for $\mathcal{F}_{\scriptscriptstyle \mathrm {AUTO}}$ and halts. $\mathcal{SIM}$ decrypts $E_{\varDelta _\mathcal{A}}$ and records the transition matrix $\varDelta _\mathcal{A}$. If the recorded set $\varDelta _\mathcal{A}$ does not constitute a valid transition matrix $\mathcal{SIM}$ outputs fail. $\mathcal{SIM}$ similarly computes the set of accepting states $F_\mathcal{A}$ (as $\mathcal{A}$ may send encryptions of invalid accepting states, $\mathcal{SIM}$ records only the valid states that correspond to values within $\{1,\ldots ,Q\}$).

• 4. $\mathcal{SIM}$ sends $\varGamma _\mathcal{A}=(Q,\{0,1\},\varDelta _\mathcal{A},q_0,F_\mathcal{A})$ to its trusted party. If it receives back the message “accept” and $\ell$, it chooses an arbitrary string $t^{\prime }=t^{\prime }_1\ldots t^{\prime }_\ell$ for which $\varGamma _\mathcal{A}(t^{\prime })\in F_\mathcal{A}$. Else, it chooses a string $t^{\prime }=t^{\prime }_1\ldots t^{\prime }_\ell$ such that $\varGamma _\mathcal{A}(t^{\prime })$ is not an accepting state. This is done by mapping the automaton into a graph and then searching for a path from the initial state to each one of the accepting/non-accepting states of length $\ell$.

• 5. $\mathcal{SIM}$ completes the execution as the honest $P_2$ would on this input. Specifically, in the first iteration, $\mathcal{SIM}$ chooses $c_{\varDelta _\mathcal{A}(1,t^{\prime }_1)}$ and sends $\mathcal{A}$ ciphertext $c_1=c_{\varDelta _\mathcal{A}(1,t^{\prime }_1)}\cdot E_{pk}(0)$. It then invokes the simulator for $\pi _{\scriptscriptstyle \mathrm {ENC}}$ while playing the role of the prover, for proving that it computed $c_{\varDelta _\mathcal{A}(1,t^{\prime }_1)}$ correctly.

• 6. In every iteration $\xi , \mathcal{SIM}$ plays the role of the honest $P_2$ on its input determined above, emulating the ideal computations of $\mathcal{R}_{\scriptscriptstyle \mathrm {PERM}}$ and $\mathcal{R}_{\scriptscriptstyle \mathrm {DH}}$. It further invokes the simulator for the zero-knowledge proof $\pi _{\scriptscriptstyle \mathrm {ENC}}$ when required in the protocol.

• 7. $\mathcal{SIM}$ outputs whatever $\mathcal{A}$ does.

We first note that $\mathcal{SIM}$ outputs fail with negligible probability due to the fact that in the real execution $P_2$ accepts an invalid automaton description only with a negligible probability due to the negligible soundness error of $\pi _{\scriptscriptstyle \mathrm {PERM}}$ and $\pi _{\scriptscriptstyle \mathrm {DL}}$. In particular, if $\mathcal{A}$ sends an encryption of a value not in $\{1,\ldots ,Q\}$, then the proof fails since either there exists an index $\tau$ in which $\tilde{c}_i$ is not an encryption of zero or one, or $c_1$ and $c_{2\cdot |Q|}$ are not encryptions of an element from $\{1,\ldots ,2|Q|\}$. Next, we show that the output distribution of $\mathcal{A}$ in the hybrid and the simulated executions are computationally indistinguishable. Recall that $\mathcal{SIM}$ plays against $\mathcal{A}$ with input $t^{\prime }$ so that $\varGamma _\mathcal{A}(t)\in F_\mathcal{A}$ if and only if $\varGamma _\mathcal{A}(t^{\prime })\in F_\mathcal{A}$ where $t$ is the input of the real $P_2$. The intuition of the proof follows from the security of El Gamal, where the adversary should not be able to distinguish between an encrypted path of the automaton that was computed relative to $t$ or $t^{\prime }$. Formally, we define a sequence of hybrid games and denote by the random variable $\mathrm{H}^{\mathcal{A}(z)}_\ell (\varGamma =(Q,\{0,1\},\varDelta ,q_0,F),t,n)$ (for a fixed $n$) the output of $\mathcal{A}$ in hybrid game ${\mathrm {H}}_\ell$.

Formally, we consider the following sequence of games.

Game ${\mathrm {H}}_0$ The simulated execution as described above.

Game ${\mathrm {H}}_1$ In this game, we define a simulator $\mathcal{SIM}_1$ similarly to simulator $\mathcal{SIM}$ with the following modifications.

• 1. In Step 3a (i.e., in the first iteration), $\mathcal{SIM}_1$ sends an encryption to a random plaintext instead of $c_{\varDelta _\mathcal{A}(1,t^{\prime }_1)}$, for $t^{\prime }=t^{\prime }_1,\ldots ,t^{\prime }_\ell$ the arbitrary input picked by the simulator. $\mathcal{SIM}_1$ then invokes the simulator for the proof $\pi _{\scriptscriptstyle \mathrm {ENC}}$.

• 2. Next, for each iteration $2\le \xi \le \ell , \mathcal{SIM}_1$ does not send a random permutation of columns $C,C_{t^{\prime }_\xi }$ in Step 4c. Instead, $\mathcal{SIM}_1$ sends two vectors of $|Q|$ ciphertexts encrypting random plaintexts. Moreover, in Step 4f, $\mathcal{SIM}_1$ decrypts column $\bar{C}$ as follows. It picks a random index $k\in \{1,\ldots ,|Q|\}$ and forces the decryption of $\bar{c}_k=\langle \bar{c}_{k_1},\bar{c}_{k_2}\rangle \in \bar{C}$ into zero by sending

  $$\begin{aligned} e_2=\frac{\bar{c}_{k_2}}{\left( \bar{c}_{k_1}^{x_1}\cdot g^m\right) } = \frac{\bar{c}_{k_2}}{\left( \bar{c}_{k_1}^{x_1}\cdot g^0\right) } = \frac{\bar{c}_{k_2}}{\bar{c}_{k_1}^{x_1}}, \end{aligned}$$

  for $m=0$ and $x_1$ the adversary’s secret key share. Note that if the adversary decrypts correctly then the outcome is $g^0$ since it computes $\bar{c}_{k_2}/(\bar{c}_{k_1}^{x_1} \cdot e_2) = g^0$.

• 3. Similarly, in Step 5c, $\mathcal{SIM}_1$ sends a random vector of ciphertexts rather than the permuted outcome $C_{F,\pi }$ and forces the decryption of one of these ciphertexts into zero as done in the previous step.

We claim that the adversary’s views in the games ${\mathrm {H}}_0$ and ${\mathrm {H}}_1$ are computationally indistinguishable due to the IND-CPA security of the El Gamal scheme. For example, a distinguisher $D_E$ can be constructed as follows. Upon receiving public-key $pk$ from its oracle, $D_E$ invokes the simulator for $\pi _{\scriptscriptstyle \mathrm {KEY}}$ and forces the shared public-key to be $pk$. It further records the adversary secret key share $x_1$ and the transition table it extracts in Step 2b. Next, in the first iteration $D_E$ outputs messages $\varDelta _\mathcal{A}(1,t{c}_1)$ and $s$ for $s\leftarrow {\mathbb Z}_q$, receiving back from its oracle ciphertext $e$.⁷ $D_E$ forwards $\mathcal{A}$ in Step 3a ciphertext $e$ and invokes the simulator for $\pi _{\scriptscriptstyle \mathrm {ENC}}$. Then, in each iteration $2\le \xi \le \ell , D_E$ sends to its oracle two vectors of size $2|Q|$: (i) the first vector corresponds to a random permutation $\pi$ of columns $C_\epsilon ,C_{t{c}_\xi }$. (ii) The second vector corresponds to a set of random plaintexts. $D_E$ forwards $\mathcal{A}$ the oracle’s response and emulates the ideal calls for the zero-knowledge proofs. Finally, in the decryption of Step 4f, $D_E$ decrypts ciphertext $\bar{c}_k$ as in game ${\mathrm {H}}_1$ except that it picks index $k\in \{1,\ldots ,|Q|\}$ to be the index that would have been decrypted by simulator $\mathcal{SIM}$ when running on input $t^{\prime }$ (i.e., the index that corresponds to plaintext $\varDelta _\mathcal{A}(1,t^{\prime }_\xi )$ if the oracle indeed encrypts the second set of messages. Clearly, $D_E$ does not know that, but pretends that this is the case). We recall that $D_E$ extracts the permutations applied by the adversary in Step 4d, so it is able to compute this index efficiently. Similarly in Step 5d, $D_E$ decrypts the ciphertext that corresponds to the final state $\varDelta _\mathcal{A}(1,t^{\prime })$ (again, assuming that the oracle encrypts the second set of messages.)

We now prove that $\mathcal{A}$’s view distributes either according to game ${\mathrm {H}}_0$ with $\mathcal{SIM}$ or according to game ${\mathrm {H}}_1$ with $\mathcal{SIM}_1$. Note first that the differences between the two executions are with respect to the permuted ciphertexts and the way decryption follows. For example, if $D_E$ receives from its oracle encryptions of $\varDelta _\mathcal{A}(1,t^{\prime }_1)$ and the permuted columns $C_\epsilon ,C_{t^{\prime }_\xi }$, then the result is a view as in the simulation with $\mathcal{SIM}$. To see this, note that the ciphertexts received from $D_E$’s oracle distribute as in game ${\mathrm {H}}_0$ since they correspond to the encryptions of the evaluation of the automaton on $t^{\prime }$. In addition, $D_E$ decrypts the ciphertexts that correspond to $\{\varDelta _\mathcal{A}(1,t^{\prime }_\xi )\}_\xi$ by sending $\bar{c}_{k_2}/(\bar{c}_{k_1}^{x_1}\cdot g^0)$ in each iteration. Now, since $D_E$ decrypts as if the oracle sends these sets of encryptions, it holds that $D_E$ decrypts correctly (without knowing). For example, it sends

$$\begin{aligned} \frac{\bar{c}_{k_2}}{\bar{c}_{k_1}^{x_1}\cdot g^0} = \frac{\bar{c}_{k_1}^x \cdot g^0}{\bar{c}_{k_1}^{x_1}\cdot g^0} = \bar{c}_{k_1}^{x_2} \end{aligned}$$

for $x=x_1+x_2$, which distributes identically to $\mathcal{SIM}$’s decryption message in the execution of $\pi _{\scriptscriptstyle \mathrm {DEC}}$.

On the other hand, the result is a view with ciphertexts that encrypt random plaintexts as required in game ${\mathrm {H}}_1$. Here, we need to ensure that the view distributes as in game ${\mathrm {H}}_1$. Note that the only difference with respect to the views generated by $D_E$ and $\mathcal{SIM}_1$ is regarding the way index $k$ is picked, since $D_E$ does not pick it uniformly. Nevertheless, since the index of $\varDelta _\mathcal{A}(1,t^{\prime }_\xi )$ is randomly permuted within column $C_{t^{\prime }_\xi }$ using a fresh permutation $\pi$, it amounts to picking this index at random.

Game ${\mathrm {H}}_2$ In this game, there is no trusted party and no honest $P_2$. Instead, we define a simulator $\mathcal{SIM}_2$ that uses the real input $t$ instead of the simulated input $t^{\prime }$. For example, this game is identical to game ${\mathrm {H}}_0$ with $\mathcal{SIM}$ except that $\mathcal{SIM}_2$ does not interact with a trusted party and plays the role of $\mathcal{SIM}$ with input $t$ rather than with $t^{\prime }$. The proof for which the views generated within games ${\mathrm {H}}_1$ and ${\mathrm {H}}_2$ are computationally indistinguishable follows the same argument from the proof that demonstrates computational indistinguishability with respect to the simulated view with $\mathcal{SIM}$ and the view generated in game ${\mathrm {H}}_1$.

Game ${\mathrm {H}}_3$ In this game, we define a simulator $\mathcal{SIM}_3$ that uses its share of the secret key to decrypt correctly. We claim that the adversary’s views generated in games ${\mathrm {H}}_2$ and ${\mathrm {H}}_3$ are identical. This is due to the fact that the simulator decrypts correctly in both games. Specifically, in game ${\mathrm {H}}_2$, the simulator decrypts the ciphertexts it picks in Steps 4f and 5d correctly, since it knows the plaintexts.

Game ${\mathrm {H}}_4$ In this game, we define a simulator that invokes the real prover for $\pi _{\scriptscriptstyle \mathrm {ENC}}$ instead of the simulator. Computational indistinguishability follows straightforwardly due to the zero-knowledge property of $\pi _{\scriptscriptstyle \mathrm {ENC}}$.

Finally, note that the distribution induced by game ${\mathrm {H}}_4$ is identical to the distribution generated in the hybrid execution. This concludes the proof for the case when $P_1$ is corrupted.

Party $P_2$ is corrupted Let $\mathcal{A}$ denote an adversary controlling $P_2$, we construct a simulator $\mathcal{SIM}$ for $P_1$ as follows.

• 1. $\mathcal{SIM}$ is given a string $t_1,\ldots ,t_\ell$ and $\mathcal{A}$’s auxiliary input $(|Q|,|F|)$, and invokes $\mathcal{A}$ on these values.

• 2. $\mathcal{SIM}$ picks $x_1\leftarrow {\mathbb Z}_q$ and invokes the simulator for $\pi _{\scriptscriptstyle \mathrm {KEY}}$. $\mathcal{SIM}$ extracts the adversary’s share $x_2$ and records this value. It then completes the execution of $\pi _{\scriptscriptstyle \mathrm {KEY}}$ with its share. Let $pk=g^{x_1+x_2}$ denote the public-key generated in this execution.

• 3. $\mathcal{SIM}$ encrypts an arbitrary automaton $\varGamma ^{\prime }=(Q^{\prime },\{0,1\},\varDelta ^{\prime },q_0,F^{\prime })$ with $|Q^{\prime }|=|Q|$ and $|F^{\prime }|=|F|$ and sends its encryption. It emulates the ideal calls for $\mathcal{R}_{\scriptscriptstyle \mathrm {PERM}}$ and $\mathcal{R}_{\scriptscriptstyle \mathrm {DH}}$ approving the validity of the description of the automaton.

• 4. In every iteration $\xi , \mathcal{SIM}$ records $t_{\xi _\mathcal{A}}$ by extracting it from the proof $\pi _{\scriptscriptstyle \mathrm {ENC}}$ that $\mathcal{A}$ runs in Step 4b (for the first iteration $\mathcal{SIM}$ extracts $t_{1_\mathcal{A}}$ in Step 3b). $\mathcal{SIM}$ sends $t_{1_\mathcal{A}},\ldots ,t_{\ell _\mathcal{A}}$ to the trusted party.

• 5. $\mathcal{SIM}$ completes the execution as the honest $P_1$ would on this input $\varGamma ^{\prime }$ while emulating the ideal calls for $\mathcal{R}_{\scriptscriptstyle \mathrm {PERM}}, \mathcal{R}^1_{\scriptscriptstyle \mathrm {PERM}}, \mathcal{R}_{\scriptscriptstyle \mathrm {DL}}$ and $\mathcal{R}_{\scriptscriptstyle \mathrm {DH}}$.

• 6. $\mathcal{SIM}$ outputs whatever $\mathcal{A}$ does.

Note that the difference between this simulated and the hybrid executions is within the fact that the simulation runs on an arbitrary encrypted automaton. Therefore, the reduction follows from the security of the El Gamal encryption scheme. More formally, recall that $P_2$ does not receive any output, thus it only learns the decryption results in Step 4f. Therefore, our goal is to prove that privacy is preserved in spite of these decryptions. The proof follows similarly to the proof of the prior corruption case. We denote by the random variable $\mathrm{H}^{\mathcal{A}(z)}_\ell (\varGamma =(Q,\{0,1\},\varDelta ,q_0,F),t,n)$ (for a fixed $n$) the view of $\mathcal{A}$ in the hybrid game ${\mathrm {H}}_\ell$.

Game ${\mathrm {H}}_0$ The simulated execution.

Game ${\mathrm {H}}_1$ In this game, we define a simulator $\mathcal{SIM}_1$ similarly to simulator $\mathcal{SIM}$ with the following modifications.

• 1. In Step 2, $\mathcal{SIM}_1$ sends ciphertexts that encrypt random plaintexts rather than using the fake automaton $\varGamma ^{\prime }=(Q^{\prime },\{0,1\},\varDelta ^{\prime },q_0,F^{\prime })$ the fake input that $\mathcal{SIM}$ inputs in game ${\mathrm {H}}_0$. $\mathcal{SIM}_1$ emulates the ideal calls in Step 2c, approving the validity of the description of the automaton.

• 2. For each iteration $2\le \xi \le \ell , \mathcal{SIM}_1$ continues as simulator $\mathcal{SIM}$ does. For example, follows the protocol instructions until Step 4f, where $\mathcal{SIM}_1$ decrypts column $\bar{C}$ as follows. It picks a random index $k\in \{1,\ldots ,|Q|\}$ and forces the decryption of $\bar{c}_k=\langle \bar{c}_{k_1},\bar{c}_{k_2}\rangle \in \bar{C}$ into zero by sending

  $$\begin{aligned} \frac{\bar{c}_{k_2}}{\left( \bar{c}_{k_1}^{x_1}\cdot g^m\right) } = \frac{\bar{c}_{k_2}}{\left( \bar{c}_{k_1}^{x_1}\cdot g^0\right) } = \frac{\bar{c}_{k_2}}{\bar{c}_{k_1}^{x_1}}, \end{aligned}$$

  for $m=0$ and $x_1$ is the adversary’s secret key share. Note that if the adversary decrypts correctly then the outcome is $g^0$ since it computes $\bar{c}_{k_2}/(\bar{c}_{k_1}^{x_1} \cdot e_2) = g^0$.

• 3. The rest of the simulation is as in game ${\mathrm {H}}_0$.

We claim that the adversary’s views in games ${\mathrm {H}}_0$ and ${\mathrm {H}}_1$ are computationally indistinguishable due to the IND-CPA security of the El Gamal scheme. For example, a distinguisher $D_E$ can be constructed as follows. Upon receiving public-key $pk$ from its oracle, $D_E$ invokes the simulator for $\pi _{\scriptscriptstyle \mathrm {KEY}}$ and forces the shared public-key to be $pk$. It further records the adversary secret key share $x_2$. $D_E$ sends to its oracle two vectors of size $2|Q|+|F|$: (i) The first vector corresponds to the fake automaton description $\varGamma ^{\prime }=(Q^{\prime },\{0,1\},\varDelta ^{\prime },q_0,F^{\prime })$. (ii) The second vector corresponds to a random set of plaintexts. $D_E$ forwards the adversary the oracle’s response and emulates the ideal calls for $\mathcal{R}_{\scriptscriptstyle \mathrm {PERM}}$ and $\mathcal{R}_{\scriptscriptstyle \mathrm {DH}}$ approving the validity of the description of the automaton. Next, in each iteration $1\le \xi \le \ell , D_E$ extracts $t_{\xi _\mathcal{A}}$ and verifies the proofs $\pi _{\scriptscriptstyle \mathrm {ENC}}$, and aborts if verification fails. It then permutes columns $C_\pi$ and $C_{\pi ,t_\xi }$ correctly.

Finally, in the decryption of Step 4f, $D_E$ decrypts ciphertext $\bar{c}_k$ as in game ${\mathrm {H}}_1$ except that it picks index $k\in \{1,\ldots ,|Q|\}$ to be the index that would have been decrypted by simulator $\mathcal{SIM}$ when running on input $\varDelta ^{\prime }$ (i.e., the index that corresponds to plaintext $\varDelta ^{\prime }(1,t_{\xi _\mathcal{A}})$ if the oracle indeed encrypts the first set of messages. Clearly, $D_E$ does not know that, but pretends that this is the case). We recall that $D_E$ extracts the permutations applied by the adversary in Step 4c so it is able to compute this index efficiently. The rest of the proof follows similarly as in the former corruption case.

Game ${\mathrm {H}}_2$ In this game, there is no trusted party and no honest $P_1$. Instead, we define a simulator $\mathcal{SIM}_2$ that uses the real input $\varGamma =(Q,\{0,1\},\varDelta ,q_0,F)$ instead of the simulated input $\varGamma ^{\prime }=(Q^{\prime },\{0,1\},\varDelta ^{\prime },q_0,F^{\prime })$. For example, this game is identical to game ${\mathrm {H}}_0$ with $\mathcal{SIM}$ except that $\mathcal{SIM}_2$ does not interact with a trusted party and plays the role of $\mathcal{SIM}$ with input $\varGamma =(Q,\{0,1\},\varDelta ,q_0,F)$ rather than with a fake input $\varGamma ^{\prime }=(Q^{\prime },\{0,1\},\varDelta ^{\prime },q_0,F^{\prime })$. The proof for which the views generated within games ${\mathrm {H}}_1$ and ${\mathrm {H}}_2$ are computationally indistinguishable follows the same argument from the proof that demonstrates computational indistinguishability with respect to the simulated view with $\mathcal{SIM}$ and the view generated in game ${\mathrm {H}}_1$.

Game ${\mathrm {H}}_3$ In this game, we define a simulator $\mathcal{SIM}_3$ that uses its share of the secret key to decrypt correctly. We claim that the adversary’s views generated in games ${\mathrm {H}}_2$ and ${\mathrm {H}}_3$ are identical. This is due to the fact that the simulator decrypts correctly in both games. Specifically, in game ${\mathrm {H}}_2$, the simulator decrypts the ciphertexts it picks in Steps 4f and 5d correctly, since it knows the plaintexts.

Finally, note that the distribution induced by game ${\mathrm {H}}_3$ is identical to the distribution generated in the hybrid execution. This concludes the proof for the case when $P_2$ is corrupted.

4.2 Efficiency

We present a brief analysis of our protocol; a comprehensive analysis can be found in the introduction. Our protocol runs $O(\ell )$ rounds where $\ell$ is the length of the text. This round complexity is inherent from the fact that the parties cannot initiate a new iteration before visiting the previous one. Looking ahead, when using this protocol for text search the round complexity can be reduced into $O(m)$ (i.e., the length of the pattern) using standard techniques of splitting the text into blocks of size $2m$; see Sect. 5.2 for more details. We note that the length of the pattern is typically very small, usually a constant. Moreover, the overall number of exponentiations in protocol $\pi _{\scriptscriptstyle \mathrm {VALIDAUTO}}$ is $O(m\ell )$.

4.3 Dealing with an Arbitrary Size Alphabet

Protocol $\pi _{\scriptscriptstyle \mathrm {AUTO}}$ can be naturally extended to dealing with arbitrary size alphabet by simply have $P_1$ send a larger table with a column for each symbol. The rest of the protocol is adapted similarly. Note that this will introduce a multiplicative factor $|\varSigma |$ within the overhead of the communication and computation costs, where $\varSigma$ is the alphabet.

5 Secure Text Search Against Malicious Adversaries

In this section, we present a secure version of the KMP algorithm [27] for computing the text search functionality in the presence of malicious adversaries. A toy example of the KMP algorithm is demonstrated in Fig. 3. Loosely speaking, the KMP algorithm searches for occurrences of a pattern $p$ of length $m$ within a text $T$ of length $\ell$, by employing the observation that when a mismatch occurs, the pattern itself embodies sufficient information to determine where the next match could begin, thus bypassing reexamination of previously matched characters. More formally, $P_1$, whose input is a pattern $p$, first constructs an automaton $\varGamma _p$ for $p$ as follows. Let $p_{\langle j\rangle }$ denote the length $j$ prefix $p_1,\ldots ,p_j$ of $p$. $P_1$ constructs a table $\Upsilon$ with $m$ entries where its $j$th entry contains a pointer to the last bit of the largest prefix of $p$ that matches a suffix of $p_{\langle j-1\rangle }$. For example, the $j$th entry points to the largest prefix $p_{\langle j^{\prime }\rangle }$ that matches a proper suffix of $p_{\langle j-1\rangle }$. The intuition behind this construction captures the following idea. Assume that one has already successfully compared the first $j-1$ bits of $p$ against the text, yet encountered a mismatch when compared the $j$th bit of $p$. Then, the automaton encodes the appropriate transition to the next potential match instead of comparing $p$ naively against the next text location. We remark that $\Upsilon$ can be easily constructed in time $O(m^2)$ by comparing $p$ against itself at every alignment.

Fig. 3

A high-level diagram of $\pi _{\scriptscriptstyle \mathrm {AUTO}}$

Next, $P_1$ constructs its automaton $\varGamma _p=(Q,\varSigma ,\varDelta ,q_0,F)$ based on $\Upsilon$. It first sets $|Q|=m+1$ and constructs the transition table $\varDelta$ as follows: for all $j\in \{1,\ldots ,m\}, \varDelta (q_{j-1}\times p_j)\rightarrow q_j$ (i.e., moving forwards) and $\varDelta (q_{j-1}\times {(1-p_j)})\rightarrow \Upsilon (j)$ (i.e., moving backwards), where $\Upsilon (j)$ denotes the $j$th entry in $\Upsilon$. In case we found a match and the automaton reaches the last state $q_m$, it can only go backwards, since the algorithm finds the largest prefix that matches a proper suffix of the pattern.

We denote the labels of the states $q_0,\ldots ,q_m\in Q$ by the sequential integers starting from $0$ to $m$. This way, if there is no matching prefix for $p_1,\ldots ,p_j$, the automaton goes back to the initial state $q_0$ and $\Upsilon (j)=0$. $P_1$ concludes the construction by setting $F=q_m$. If state $q_{m}$ is ever reached then there is a match. In order to ensure that $P_1$ and $P_2$ jointly evaluate the automaton on $P_2$’s text such that no information is revealed about either the text or the automaton (besides knowing if the final state is accepting or not), we use protocol $\pi _{\scriptscriptstyle \mathrm {AUTO}}$ from Sect. 4. This, however, is insufficient since $P_1$ must prove first that it constructed the automaton correctly according to the KMP specifications. In Sect. 5.1, we present a zero-knowledge proof of knowledge for proving that the automaton $P_1$ constructs is a correct KMP automaton. In Sect. 5.2, we give our complete construction for text search in the presence of malicious adversaries.

5.1 A Zero-Knowledge Proof of Knowledge for a Valid KMP Automaton

In this section, we present an efficient zero-knowledge proof of knowledge for the relation $\mathcal{R}_{\scriptscriptstyle \mathrm {VALIDAUTO}}$ defined by:

$$\begin{aligned} \left( \left( \left\{ Q_{i,j},r_{i,j}\right\} _{i,j}\right) ,\left( \left\{ c_{i,j}\right\} _{i,j},pk\right) \right) \mapsto \left\{ \begin{array}{ll} (-,1) &{}\quad \forall i,j~c_{i,j}=E_{pk}(Q_{i,j};r_{i,j})\;\text{ and } \\ &{}\quad \{Q_{i,j}\}_{i,j}~\text{ is }\,\text{ a }\,\text{ valid }\,\text{ KMP }\,\text{ automaton }\\ (-,0) &{}\quad \text{ otherwise } \end{array}\right. \end{aligned}$$

where $i\in \{0,1\},{j\in \{1,\ldots ,{|Q|}\}}, |Q|$ is the number of states in $Q$, and a valid KMP automaton is as specified above. This proof is needed in protocol $\pi _{\scriptscriptstyle \mathrm {PM}}$ from Sect. 5.2 to ensure the validity of the encrypted automaton that $P_1$ sends. We remark that it is unnecessary for this proof to be a proof of knowledge, as the knowledge extraction of the automaton can be performed within protocol $\pi _{\scriptscriptstyle \mathrm {AUTO}}$. Nevertheless, for the sake of modularity, we consider this property here as well. Our proof uses a zero-knowledge proof for the following language,

$$\begin{aligned} \mathrm{L}_{\scriptscriptstyle \mathrm {NZ}}=\left\{ ({\mathbb G}, g, q, h, h_1, h_2)\mid \exists ~(m\not =0, r)\,\text{ s.t. }\, \alpha =g^r,\; \beta = h^r g^m\right\} . \end{aligned}$$

An efficient constant round proof $\pi _{\scriptscriptstyle \mathrm {NZ}}$ with constant number of exponentiations, can be found in [21].

Our proof shows that an automaton $\varGamma$ corresponds to a well-defined string $p=p_1,\ldots ,p_{|Q|-1}$ and is computed correctly according to table $\Upsilon$ defined above. Recall that we assume w.l.o.g., that the transition table $\varDelta$ is complete and that it contains two columns corresponding to zero or one (i.e., whether the next bit from the input string is zero or one). Then, for every $j\in \{0,1,\ldots ,m\}$, there exists an entry in $\varDelta$ with two ciphertexts $c_{0,j}, c_{1,j}$, so that there exists an index $i$ in which $c_{i,j}$ denotes the encryption of state $q_j$ and $c_{i,j}$ denotes an encryption of $q_{\Upsilon (j)}$. In order to ensure that the proof does not leak any information about $p$, these checks must be performed obliviously, independent of the prefix. We therefore conduct a brute force search on the matched prefix against every suffix in which ultimately, the verifier accepts only if the conditions for $\mathcal{R}_{\scriptscriptstyle \mathrm {VALIDAUTO}}$ are met. For simplicity, our proof is not optimized; we give more details below how to improve it. We now continue with the formal description of our proof $\pi _{\scriptscriptstyle \mathrm {VALIDAUTO}}$ and its proof of security.

Protocol 4

($\varvec{\pi }_{\scriptscriptstyle \mathrm {VALIDAUTO}}$—A Zero-Knowledge Proof of Knowledge for $\mathcal{R}_{\scriptscriptstyle \mathrm {VALIDAUTO}}$):

• Joint statement A public-key $pk$ and a collection $\{c_{i,j}\}_{i,j}$ of $|Q|$ sets, each set is of size $2$ which corresponds to a row in the transition matrix $\varDelta$.

• Auxiliary input for the prover A collection $\{Q_{i,j},r_{i,j}\}_{i,j}$ of $|Q|$ sets, each set is of size $2$, such that $c_{i,j}=E_{pk}(Q_{i,j};r_{i,j})$ for all $i\in \{0,1\}$ and ${j\in \{1,\ldots ,{|Q|}\}}$.

• Convention We assume that the parties jointly agree on a group ${\mathbb G}$ of prime order $q$ and a generator $g$ for the threshold El Gamal encryption scheme. Both parties check every received ciphertext for validity, and abort if an invalid ciphertext is received. Finally, unless written differently, $i\in \{0,1\}$ and ${j\in \{1,\ldots ,{|Q|}\}}$.

• The protocol

• 1. For every $c_{i,j}=\langle \alpha _{i,j},\beta _{i,j}\rangle$, the prover $P$ proves the knowledge of $\log _g \alpha _{i,j}$ using $\pi _{\scriptscriptstyle \mathrm {DL}}$.

• 2. For every row $\varDelta _j=\{c_{0,j},c_{1,j}\}_{j=4}^{|Q|}$ in the transition matrix $P$ proves the following:⁸

  • (a) $P$ randomly permutes each entry in $\varDelta$ It first randomly permutes $c_{0,j}$ and $c_{1,j}$ and employs $\pi _{\scriptscriptstyle \mathrm {PERM}}$ to prove its computations.

  • (b) $P$ proves a forwards path It proves that there exists $b\in \{0,1\}$ in which $c_{b,j}=E_{pk}(j+1)$ by proving that $(pk,c_{b,j}/E_{pk}(j+1))$ is a Diffie–Hellman tuple.

  • (c) $P$ proves a backwards path $P$ proves the correctness of $c_{{1-b},j}$ in two steps: (1) It first proves that $c_{{1-b},j}$ is a valid entry in $\Upsilon$. (2) It then proves the maximality of this prefix. In order to prove this, we define a string $p=p_1,\ldots ,p_{|Q|-1}$, induced by the description of the automaton, as follows. Define (the encryption) $p_j$ by the (encrypted) column in which $c_{b,j}$ belongs to. For example, we let the prover permute the encryptions of the columns names zero/one, using the same permutation, and then take the column’s name associated with $c_{b,j}$ to be the encryption of $p_j$. Then, to complete the check, $P$ proves that $c_{{1-b},j}$ encrypts $r$, so that $p_{\langle r\rangle }$ corresponds to a suffix of $p_{\langle j-1\rangle }$. (Recall that $p_{\langle r\rangle }$ denotes the $r$th length prefix $p_1,\ldots ,p_r$ of $p_1,\ldots ,p_{j-1}$.)

  • (d) $V$ sends a challenge The verifier $V$ chooses $j$ random elements $u_1,\ldots ,u_{j-1}\leftarrow {\mathbb Z}_q^{*}$ and sends $\{u_{\alpha }\}_{\alpha =1}^{j-1}$ to $P$.

  • (e) Public computation Next, the parties compute ciphertexts $v_{\alpha ^{\prime }}=E_{pk}(\sum \nolimits _{k=1}^{\alpha ^{\prime }} u_k\cdot p_k)$ for all $\alpha ^{\prime }\in \{1,\ldots ,j-1\}$.

  • (f) Proving a valid entry in $\Upsilon$ $P$ proves that there exists $1\le k\le j-2$ for which $v^{\prime }_k$ is a ciphertext that encrypts zero and is defined as follows:

    $$\begin{aligned} v^{\prime }_k = \left( v_{j-k-1,j-1}\big /v_{1,k}\right) \cdot \left( c_{j,1-b}/g^k\right) . \end{aligned}$$

    The parties essentially compute the linear combination of all potential prefixes of $p_1,\ldots ,p_{j-1}$ and compare them against a suffix of this string. The multiplication with $(c_{j,1-b}/g^k)$ is to ensure that such a prefix is consistent with whatever is encrypted in the transition table. For $k=0$, the parties set $v^{\prime }_0=c_{j,1-b}$, Since if there is no matching prefix for any suffix of $p_{\langle j-1\rangle }$, this means that $c_{j,1-b}$ denotes an encryption of the initial state $q_0$ which equals zero.

  • (g) Proving $D_{pk,sk}(c_{1-b,j})$ is maximal Next $P$ proves that there does not exist an index $D_{pk,sk}(c_{j,1-b})< \varGamma \le j-2$ in which

    $$\begin{aligned} v_{j-\varGamma -1,j-1}\big /v_{1,\varGamma }=0 \end{aligned}$$

    yet $c_{j,1-b}/g^\varGamma \ne 0$, as this would imply that there exists a larger prefix $p_{\langle \varGamma \rangle }$ that matches a suffix of $p_{\langle j-1\rangle }$ yet, $D_{pk,sk}(c_{j,1-b})\ne \varGamma$. For every $1\le k\le j-3$ and $2\le k^{\prime }\le j-2$ the parties compute the ciphertext $v^{\prime }_k\cdot (v_{j-k^{\prime }-1,j-1}/v_{1,k^{\prime }})$ for which $P$ then proves that $e_{k,k^{\prime }}$ is not an encryption of zero using $\pi _{\scriptscriptstyle \mathrm {NZ}}$.

• 3. Output If all the proofs are successfully completed, $V$ outputs $1$. Otherwise it outputs $0$.

Theorem 5.1

Assume that the DDH assumption holds relative to ${\mathbb G}$. Then, $\pi _{\scriptscriptstyle \mathrm {VALIDAUTO}}$ is a computational zero-knowledge proof of knowledge for $\mathcal{R}_{\scriptscriptstyle \mathrm {VALIDAUTO}}$ with perfect completeness.

Proof

We first show perfect completeness. This is derived from the fact that we conduct a brute force search for the matched prefix of every suffix.

Zero Knowledge Let $V^{*}$ be an arbitrary probabilistic polynomial-time strategy for $V$. Then, a simulator $\mathcal{SIM}_{\scriptscriptstyle \mathrm {VALIDAUTO}}$ for this proof can be constructed using the simulators $\mathcal{SIM}_{\scriptscriptstyle \mathrm {DL}}, \mathcal{SIM}_{\scriptscriptstyle \mathrm {PERM}}, \mathcal{SIM}_{\scriptscriptstyle \mathrm {DH}}$ and $\mathcal{SIM}_{\scriptscriptstyle \mathrm {NZ}}$ from the corresponding proofs of $\pi _{\scriptscriptstyle \mathrm {DL}}, \pi _{\scriptscriptstyle \mathrm {PERM}}, \pi _{\scriptscriptstyle \mathrm {DH}}$ and $\pi _{\scriptscriptstyle \mathrm {NZ}}$. That is, $\mathcal{SIM}_{\scriptscriptstyle \mathrm {VALIDAUTO}}$ invokes $V^*$ and plays the role of the honest prover, except that in every zero-knowledge invocation it invokes the appropriate simulator. The executions are computationally indistinguishable via standard reductions to the security of the zero-knowledge proofs.

Knowledge Extraction We show the existence of a knowledge extractor $K$. Let $P^{*}_{x,\zeta ,\rho }$ be an arbitrary prover machine where $x=\mathrm{(}\{c_{i,j}\}_{i,j},pk\mathrm{)}, \zeta$ is an auxiliary input and $\rho$ is $P^{*}$’s random tape. Basically, the extractor $K$ extracts $\mathcal{P}^{*}$’s input from the zero-knowledge proof $\pi _{\scriptscriptstyle \mathrm {DL}}$ at the beginning of the protocol. In particular, for all $i,j, P^{*}$ proves the knowledge of the randomness $r_{i,j}$ used for the computation of the ciphertext $c_{i,j}$. This, in turn, enables $K$ to recover the plaintext $Q_{i,j}$ as well. It then continues playing the role of the honest verifier and aborts the execution if the honest verifier does. The fact that we perform a brute force search, combined with the fact that the randomness $\{u_\alpha \}_\alpha$ incorporated by the verifier, precludes the event in which equality does not hold yet the sum of the encryptions amount to zero. $\square$

Efficiency Note first that the round complexity of $\pi _{\scriptscriptstyle \mathrm {VALIDAUTO}}$ is constant, as the zero-knowledge proofs can be implemented in constant rounds and run in parallel for all $j$. As for the number of asymmetric computations, we note that an optimized construction achieves computation cost of $O(m^2)$ operations. This is due to the fact that there are $m$ distinct prefixes of $p$ for which their encryptions can be computed once for the entire execution. Moreover, for every $j$, there are $j-2$ prefixes to check against $p_1,\ldots ,p_{j-1}$. Therefore, the overall number of exponentiations is $O(m^2)$.

5.2 Text Search Protocol with Simulation-Based Security

In this section, we present our complete construction for securely evaluating the pattern matching functionality. Recall that our construction is presented in the malicious setting with full simulatability and is modular in the sub-protocols $\pi _{\scriptscriptstyle \mathrm {AUTO}}$ (cf. Sect. 4) and $\pi _{\scriptscriptstyle \mathrm {VALIDAUTO}}$ (cf. Sect. 5.1). Having described the sub-protocols incorporated in the our scheme, we are now ready to describe it formally. Our protocol is comprised out of two main phases: (i) the parties first engage in an execution of $\pi _{\scriptscriptstyle \mathrm {VALIDAUTO}}$ for which $P_1$ proves that it sent a valid KMP automaton. (ii) The parties run protocol $\pi _{\scriptscriptstyle \mathrm {AUTO}}$ which evaluates automaton $\varGamma$ on $P_2$’s private input. In order to reduce the round complexity of our protocol (which depends on the input length to the automaton), long texts are partitioned into $2m$ pieces and are handled separately so that the KMP algorithm is employed on each block independently (thus all these executions can be executed in parallel). That is, let $T=t_1,\ldots ,t_\ell$ then the text is partitioned into blocks $(t_1,\ldots ,t_{2m}),(t_{m+1},\ldots ,t_{3m}),(t_{2m},\ldots ,t_{4m})$ and so on, such that every two consecutive blocks overlap in $m$ bits. This ensures that all the matches will be found. Therefore, the total number of blocks is $\lceil \ell /m\rceil$. Details follow,

Protocol 5

$\varvec{\pi }_{\scriptscriptstyle \mathrm {PM}}$—Secure Text Search

• Inputs The input of $P_1$ is a binary pattern $p=p_1,\ldots ,p_m$, and the input of $P_2$ is a binary string $T=t_1,\ldots ,t_\ell$.

• Auxiliary Inputs The security parameter $1^n$ and the input sizes $\ell$ and $m$.

• The Protocol

  • 1. Preparing a KMP automaton $P_1$ constructs an automaton $\varGamma =(Q,\varSigma ,\varDelta , q_0,F)$ according to the KMP specifications based on its input $p$ and sends $P_2$ encryptions of the transition matrix $\varDelta$ and the accepting states, denoted by $E_\varDelta$ and $E_F$, respectively (recall that by our conventions $q_0=0, \varSigma =\{0,1\}, Q=[0,\ldots ,m]$, and $F=\{q_m\}$).

  • 2. Validating correctness of the automaton The parties engage in an execution of the zero-knowledge proof $\pi _{\scriptscriptstyle \mathrm {VALIDAUTO}}$ for which $P_1$ proves that $\varGamma$ was constructed correctly. That is, $P_1$ proves that the set $E_\varDelta$ corresponds to a valid KMP automaton for a well-defined input string of length $m$. If $P_2$’s output from this execution is $1$ the parties continue to the next step. Otherwise $P_2$ aborts.

  • 3. Partitioning the text $P_2$ sends encryptions of the bits of $T$ to $P_1$ and the parties partition the encrypted bits into $\ell /m$ blocks of length $2m$ in which every two consecutive blocks overlap in $m$ bits.

  • 4. Evaluating the automaton on the text The parties engage in $\ell /m$ parallel executions of $\pi _{\scriptscriptstyle \mathrm {AUTO}}$ on these blocks.⁹ For every $1\le i\le \lceil \ell /m\rceil$, let $\{\mathsf{output_j^i}\}_{j=1}^{m+1}$ denotes the set of outputs returned by $P_1$ upon completing the $i$th execution of $\pi _{\scriptscriptstyle \mathrm {AUTO}}$. Then $P_1$ returns $\{j~|~\mathsf{output_j^i}$ = “‘accept”$\}_{i=1,j=1}^{\lceil \ell /m\rceil ,m+1}$.

Theorem 5.2

Assume that the DDH assumption holds relative to ${\mathbb G}$. Then $\pi _{\scriptscriptstyle \mathrm {PM}}$ securely computes $\mathcal{F}_{\scriptscriptstyle \mathrm {PM}}$ in the presence of malicious adversaries.

The security proof for $\pi _{\scriptscriptstyle \mathrm {PM}}$ follows immediately from the proofs described for $\pi _{\scriptscriptstyle \mathrm {AUTO}}$ (cf. Sect. 4.1) and $\pi _{\scriptscriptstyle \mathrm {VALIDAUTO}}$ (cf. Sect. 5.1).

Efficiency we refer the reader to the analysis presented in the introduction and in Sect. 4 since the costs of protocol $\pi _{\scriptscriptstyle \mathrm {PM}}$ are dominated by the costs of $\pi _{\scriptscriptstyle \mathrm {VALIDAUTO}}$. The overall costs are amount to $O(m\cdot \ell +m^2)$ which typically amounts to $O(m\cdot \ell )$ since in most cases $m \ll \ell$.