Nonequilibrium thermodynamics and maximum entropy production in the Earth system

Abstract

The Earth system is maintained in a unique state far from thermodynamic equilibrium, as, for instance, reflected in the high concentration of reactive oxygen in the atmosphere. The myriad of processes that transform energy, that result in the motion of mass in the atmosphere, in oceans, and on land, processes that drive the global water, carbon, and other biogeochemical cycles, all have in common that they are irreversible in their nature. Entropy production is a general consequence of these processes and measures their degree of irreversibility. The proposed principle of maximum entropy production (MEP) states that systems are driven to steady states in which they produce entropy at the maximum possible rate given the prevailing constraints. In this review, the basics of nonequilibrium thermodynamics are described, as well as how these apply to Earth system processes. Applications of the MEP principle are discussed, ranging from the strength of the atmospheric circulation, the hydrological cycle, and biogeochemical cycles to the role that life plays in these processes. Nonequilibrium thermodynamics and the MEP principle have potentially wide-ranging implications for our understanding of Earth system functioning, how it has evolved in the past, and why it is habitable. Entropy production allows us to quantify an objective direction of Earth system change (closer to vs further away from thermodynamic equilibrium, or, equivalently, towards a state of MEP). When a maximum in entropy production is reached, MEP implies that the Earth system reacts to perturbations primarily with negative feedbacks. In conclusion, this nonequilibrium thermodynamic view of the Earth system shows great promise to establish a holistic description of the Earth as one system. This perspective is likely to allow us to better understand and predict its function as one entity, how it has evolved in the past, and how it is modified by human activities in the future.

Introduction

Thermodynamics is a fundamental theory of physics. Albert Einstein once said about the scope of thermodynamics (Klein 1967) that:

A theory is more impressive the greater the simplicity of its premises, the more different are the kinds of things it relates, and the more extended its range of applicability. Therefore, the deep impression which classical thermodynamics made on me. It is the only physical theory of universal content, which I am convinced, that within the framework of applicability of its basic concepts will never be overthrown.

This sounds profound, but how does it help us to better understand the functioning of the Earth system and the role that life plays in it? The parts of thermodynamics that we are usually most familiar with deal with equilibrium systems, systems that maintain a state of thermodynamic equilibrium (TE) and that are isolated, that is, they do not exchange energy or matter with their surroundings. In contrast, the Earth is a thermodynamic system for which the exchange of energy with space is essential. Earth system processes are fueled by absorption of incoming sunlight. Sunlight heats the ground, causes atmospheric motion, is being utilized by photosynthesis, and ultimately is emitted back into space as terrestrial radiation at a wavelength much longer than the incoming solar radiation. Without the radiative exchanges across the Earth–space boundary, not much would happen on Earth and the Earth would rest in a state of TE.

Furthermore, the atmospheric composition is clearly maintained in a state far from TE, as reflected, for instance, in the high abundance of 21% molecular oxygen and an average relative humidity of about 60% that is far from being saturated. If the Earth system would be at, or evolve towards, TE through time, molecular oxygen would react and its concentration would diminish in time. Water would evaporate from the oceans into the atmosphere to the point of saturation. Why is the Earth maintained in a state so far from TE?

Several researchers have explored the role and maintenance of life on Earth from a perspective of nonequilibrium thermodynamics. Boltzmann (1886) already noted that the organized structures associated with photosynthesizing plants thrive on converting low-entropy solar radiation into heat. Schrödinger (1944) applied nonequilibrium thermodynamics to the living cell and formulated that the cell’s ordered state is maintained by consuming low-entropy sources of free energy and exporting high-entropy waste to its surroundings. At a planetary scale, Lovelock (1965, 1975) noted that the Earth’s atmosphere is maintained far from TE in contrast to its planetary neighbors and proposed that the extent of disequilibrium is an indication of a planet’s habitability (Hitchcock and Lovelock 1967). This later led Lovelock (1972a, b) to develop the Gaia hypothesis, which states that the Earth’s unique state far from TE is maintained for and by life. Even though the Gaia hypothesis was met with skepticism and substantial criticism and is far from being accepted (Kirchner 1989, 1990, 2002; Lovelock 1989, 1990, 2003; Kleidon 2002; Lenton 2002; Volk 2002), it is possible to understand such anticipated behavior from the optimality associated with nonequilibrium thermodynamics as formulated by the proposed principle of maximum entropy production (MEP) (Kleidon 2004a, see below).

Systems that are maintained far from TE dissipate energy, resulting in entropy production. In this context, several, closely related principles have been suggested independently in different disciplines that closely relate to MEP. For instance, Lorenz (1960) suggested that the atmospheric circulation dissipates available potential energy as much as possible, while Paltridge (1975, 1978, 1979) suggests that the atmospheric circulation maximizes entropy production. Several authors have suggested the same organizing principles for biology (Lotka 1922a, b; Odum 1969, 1988; Ulanowicz and Hannon 1987; Schneider and Kay 1994; Loreau 1995). In this review, I focus on the proposed principle of MEP, as this is likely justified on more fundamental grounds (I use the term “proposed” to indicate that MEP is not yet well accepted and established). The MEP principle is a form of optimality that arises from nonequilibrium thermodynamics and is essentially a consequence of the second law of thermodynamics as extended to nonequilibrium systems (Sawada 1981; Dewar 2003, 2005a, b)—even though this has not yet been firmly established on theoretical grounds.

In this review, I will first provide a brief background of nonequilibrium thermodynamics, how systems evolve away and are maintained in a state far from TE, and how this relates to the MEP principle. While excellent reviews already exist regarding the application of MEP to turbulent processes in the climate system (Ozawa et al. 2003) and to the physical foundation (Martyushev and Seleznev 2006; Martyushev 2007), this review focuses on the broader role of nonequilibrium thermodynamics within the Earth system context. Specifically, the goals of this review are to illustrate in simple terms why we would expect systems to evolve away from TE, to provide the basis to evaluate the thermodynamic nature of Earth system processes far from TE, to give an overview of previous examples that demonstrate MEP, and to synthesize these applications of MEP into a more holistic view to compare it to the Gaia hypothesis. The review closes with a brief summary and conclusions.

Background

I give a rather general introduction to nonequilibrium thermodynamics in the following, with a focus on the understanding and illustration using a simple example rather than derivations. The derivations and inherent limitations are dealt with in the established literature, e.g., the textbook by Kondepudi and Prigogine (1998).

Equilibrium and nonequilibrium thermodynamics

The first and second laws of thermodynamics provide fundamental constraints on any process that occurs in nature. While the first law essentially states the conservation of energy, the second law makes a specific statement on the direction into which processes are likely to proceed. It states that the entropy of an isolated system, i.e., a system that does not exchange energy or mass with its surroundings, can only increase, or, in other words, that free energy and gradients are depleted in time. The entropy balance of an isolated system is expressed by:

$$ \label{eqn:entropy_isolated} \frac{dS}{dt} = \sigma, $$

(1)

where dS/dt is the change of the entropy of the system with time and σ is the entropy being produced by irreversible processes within the system. What the second law tells us is σ ≥ 0. I use the distinction here of S referring to the state of the system (its entropy), while σ refers to the irreversible nature of particular processes occurring within the system (their entropy production).

In the absence of external exchange fluxes, gradients would be dissipated in time, and hence, entropy production would diminish in time, reaching a state of TE. To sustain gradients and dissipative activity within the system, exchange fluxes with the surroundings are essential. These modify the entropy budget (Eq. 1) to:

$$ \label{eqn:entropy_nonisolated} \frac{dS}{dt} = \sigma - \text{NEE} $$

(2)

where the last term represents the net entropy exchange with the surroundings (or, more precisely, $\text{NEE}$ stands for the divergence of entropy fluxes, see, e.g., Kondepudi and Prigogine (1998), with the convention of net entropy export being positive). The rate of increase of the entropy of the surroundings is then NEE, so that the second law of the system plus surroundings is still fulfilled (i.e., $dS/dt + \text{NEE} = \sigma > 0$) even though the entropy of the local system under consideration may decrease in time.

A steady state of a system is reached when the entropy change averaged over sufficiently long time vanishes ($\overline{dS/dt} \approx 0$). In this steady state, the entropy production within the system is equal to the net entropy export (i.e., $\sigma = \text{NEE}$ in Eq. 2). Note that entropy production is closely related to the ability of a system to continuously perform work. In steady state, the rate at which work is performed (P = dW/dt, the “power” of a system) balances the rate at which free energy is dissipated. Dissipation D, e.g., the degradation of higher forms of energy to heat and the mixing of this heat with the surroundings, is then directly related to entropy production by (under isothermal conditions)

$$ \label{eqn:dissipation} \sigma = \frac{D}{T} $$

(3)

Since the term 1/T usually does not vary by much for typical temperatures of the Earth’s climate system, Eqs. 2 and 3 tell us that the ability of a system to perform work in steady state is directly related to its dissipation, entropy production, and the ability of the system to export entropy to its surroundings (i.e., $dW/dt = D \propto \sigma = \text{NEE}$).

The proposed principle of MEP

The proposed principle of MEP states that, if there are sufficient degrees of freedom within the system, it will adopt a steady state at which σ is maximized. While MEP has been proposed for concrete examples, in particular, poleward transport of heat in the climate system (Paltridge 1975, 1978, 1979), entropy production in steady state is a very general property of nonequilibrium thermodynamics, so that MEP should be applicable to a wide variety of nonequilibrium systems.

There is no firm foundation yet that systems indeed maximize entropy production, although recently, there has been substantial progress in supporting the MEP principle. Recent work in establishing its theoretical foundation (Dewar 2003, 2005a, b) is based on information theory (Shannon 1948a, b; Jaynes 1957a, b). This recent line of research essentially aims to establish an interpretation of MEP equivalent to the maximum entropy principle in equilibrium thermodynamic systems. In equilibrium statistical mechanics, the state of a system is characterized by microscopic variables, such as the position and velocity of every molecule of a gas, and by macroscopic variables, such as temperature, density, and pressure. The state of maximum entropy is then interpreted as the most probable macroscopic state, that is, the state that is represented by the vast majority of microscopic states (following Boltzmann’s famous relationship S = k ·logW, which relates thermodynamic entropy S to the probability of the macroscopic state W). Following this line of reasoning, Dewar’s work argues that the MEP state is the most probable out of many possible nonequilibrium steady states. However, the theoretical foundation for MEP is still work in progress, and some deficiencies have been pointed out (Grinstein and Linsker 2007; Bruers 2007).

To avoid confusion, note that MEP is very different from Prigogine’s principle of minimum entropy production (Prigogine 1947, 1955). Prigogine’s principle states that the steady state is one of minimum entropy production compared to transient states. When a steady-state condition is assumed, the minimum entropy production principle makes no further predictions about the nature of the emergent steady state, in particular if many steady state conditions are possible given the system’s boundary conditions. In contrast, MEP acts as a selection principle of the most probable out of many possible steady states. Some applications have invoked Prigogine’s principle of minimum entropy production to steady state configurations, e.g., in geomorphology, (Leopold and Langbein 1962), but possibly for the wrong reasons, as discussed further below.

A simple example

A simple model is now used to demonstrate the relationship between entropy, entropy export, entropy production, and their evolution in time (Fig. 1a). This model will serve as a basis for extending this model to real Earth system processes.

Fig. 1

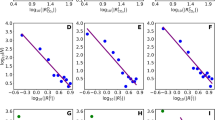
A conceptual model to demonstrate how a system can be maintained away from TE. a Schematic diagram of the system considered. b Time evolution of temperatures T _a , T _b and the heat flux F _ab (left) and entropy S and entropy production σ (right) in the case of an isolated system. c Same as b, but for a nonisolated system with an external flux F = 20 W m^− 2. The values used in the simulations are $T_{a}(0) = 38.7^\circ$C, $T_{b}(0) = -5.5^\circ$C, c = 2 ·10⁸ J K^− 1 m^− 2, k = 1 W m^− 2 K^− 1. Time is expressed in months. All fluxes are expressed per unit area, and both boxes are assumed to be of equal size. See text for further explanations and model equations

Imagine a system of two boxes A and B of same size and mass which is characterized by the respective temperatures T _a and T _b and a total heat capacity c of the boxes (assumed to be equal for simplicity). Initially, the boxes contain different amounts of heat, corresponding to temperatures T _a,0 and T _b,0.

We now consider the evolution of this system in three cases: (1) the case of an isolated system in which only the heat exchange flux F _ab between the boxes A and B is considered, (2) the case of a nonisolated system in which a given amount of heat is added to box A and removed from box B, and (3) the case where alternative pathways of heat loss allow for many possible steady states of the system.

Case 1: isolated system

In case 1, we deal with an isolated system, so that the change of temperatures of the two boxes is only related to the exchange flux of heat between the two boxes. The energy balances of the two boxes A and B are described by:

$$\label{eqn:eb_case1}\begin{array}{lll} c \cdot \frac{dT_{a}}{dt} & = & -F_{ab} \\ c \cdot \frac{dT_{b}}{dt} & = & F_{ab} \end{array} $$

(4)

The heat flux F _ab is expressed as F _ab  = k ·(T _a  − T _b ) with a certain conductivity k. Entropy is being produced as heat is removed from box A at a rate F _ab , and added to box B, where it mixes with the temperature T _b . The resulting entropy production can be derived from the thermodynamic definition of entropy as dS = δQ/T, where δQ is the change of heat content. When we remove heat δQ from box A during a time interval dt (of the amount δQ = F _ab ·dt), the change of entropy of box A is dS = − F _ab ·dt/T _a . The entropy of box B increases by dS = F _ab ·dt/T _b after the heat is mixed in box B. Hence, the resulting entropy production is:

$$ \label{eqn:diffusion} \sigma_{ab} = F_{ab} \cdot \left( \frac{1}{T_{b}} - \frac{1}{T_{a}} \right) $$

(5)

The change of entropy S of the total system (box A and B) with time is then:

$$ S(t) = c \cdot \ln T_{a}(t) + c \cdot \ln T_{b}(t) = S_{0} + \int_{t=0}^{t} \sigma(t^{\prime}) dt^{\prime}, $$

(6)

where S ₀ = c ln T _a,0 + c ·ln T _b,0 is the initial entropy of the system.

The time evolution of temperatures, heat flux, and entropy is shown in Fig. 1b. The values used are typical for climate applications when considering that, in the simple setup used here, the flux F only is the redistribution flux between the boxes. This is equivalent to the two-box model of poleward heat transport discussed below with the mean radiative forcing being subtracted. Note that σ is always positive but decreases with time and approaches 0 as the initial temperature gradient is depleted through flux F _ab . S increases with time reaching a maximum value, $S_{\text{max}}$.

The speed to TE depends on a mixing time scale $\tau_{\text{mix}}$, given by the ratio of difference in heat contents of boxes A and B to the magnitude of the heat exchange flux:

$$ \label{eqn:mixingtime} \tau_{\text{mix}} = \frac{c \cdot (T_{a} - T_{b})}{F_{ab}} = \frac{c}{k} $$

(7)

The steady-state, described by T _a  = T _b  = T and F = 0, does not depend on the value of $\tau_{\text{mix}}$, but only on the initial amount of heat within the system.

Case 2: nonisolated system

We now consider the case of a nonisolated system in which an external heat flux maintains a gradient between boxes A and B. Heat is added to box A at a given rate $F_{\text{in}}$ and is being removed from box B at a rate $F_{\text{out}}$. For simplicity, I will assume that the two fluxes balance: $F = F_{\text{in}} = F_{\text{out}}$. The energy balances (Eq. 4) are modified to account for the exchange of energy with the surroundings:

$$\label{eqn:eb_case2}\begin{array}{lll} c \cdot \frac{dT_{a}}{dt} & = & F - F_{ab} \\ c \cdot \frac{dT_{b}}{dt} & = & F_{ab} - F \end{array} $$

(8)

To express the change of entropy with time, we now need to consider the exchange fluxes across the system boundary (cf. Eq. 2). The net entropy exchange associated with the flux F is:

$$ \text{NEE} = \frac{F}{T_{b}} - \frac{F}{T_{a}}, $$

(9)

where we assume that the heat is added to box A at T _a and removed from box B at T _b for simplicity. The time evolution of entropy of the system is then given by:

$$ S(t) = S_{0} + \int_{t=0}^{t} (\sigma(t^{\prime}) - \text{NEE}(t^{\prime})) dt^{\prime} $$

(10)

Figure 1c shows the time evolution of the variables of our system for a given flux F. Entropy production σ approaches a steady-state value greater than zero with $\sigma = \text{NEE}$, entropy increases in time, but reaches a steady state of $S < S_{\text{max}}$, and a temperature gradient is maintained in steady state.

The extent to which the system is maintained away from TE depends on the strength of F, i.e., on the net entropy exchange at the system boundary. Here, we can define a forcing time scale $\tau_{\text{forc}}$, which describes the time scale at which the external flux builds up the initial temperature gradient within the system:

$$ \tau_{\text{forc}} = \frac{c \cdot (T_{a,0} - T_{b,0})}{F} $$

(11)

The ratio of the two time scales then indicates whether the system evolves from the initial state with $S = S_{\text{init}}$ to a state of higher or lower entropy. At $\tau_{\text{forc}} = \tau_{\text{mix}}$, S does not change in time, while $\tau_{\text{forc}} < \tau_{\text{mix}}$ results in a steady state in which S < S ₀. In other words, a system evolves towards lower entropy and away from TE when $\tau_{\text{forc}} < \tau_{\text{mix}}$. For this to take place, it requires that the system exchanges a relatively large amount of entropy with its surroundings. This then allows the system to maintain or increase the initial gradient within the system against the constant depletion of this gradient by the flux F _ab .

Case 3: nonisolated system with many possible steady states

While case 2 allows for the maintenance of a steady state away from TE, the system is fixed by the fluxes across the boundary. In particular, the flux F _ab between the boxes is fixed in steady state by the boundary condition $F = F_{\text{in}} = F_{ab} = F_{\text{out}}$. For case 3, we allow for alternative methods of heat loss from the system (Fig. 2a). In this configuration, the steady state condition $F_{\text{in}} = F_{\text{out},a} + F_{\text{out},b}$ can be met by a variety of states with 0 ≤ F _ab  ≤ F if it is possible for F _ab to take a range of values. This can, for instance, be achieved if we allow for mass flow between the boxes, which is associated with the generation of kinetic energy and its dissipation. In this case, k no longer corresponds to a fixed material property (the diffusivity), but rather to an effective (or eddy) diffusivity that is associated with the strength of macroscopic motion between the boxes. This effective eddy diffusivity accounts for a variety of different possible eddy structures in the case of turbulent motion that result in a range of possible steady state solutions.

Fig. 2

Modification of the conceptual model in Fig. 1 to demonstrate MEP. a The modified model allows for alternative methods of heat loss through boxes A and B. The steady state condition $F_{\text{in}} = F_{\text{out},a} + F_{\text{out},b}$ can be satisfied by a range of values of F _ab from 0 to $F_{\text{in}}$. b Sensitivity of the model to the flux F _ab by varying its conductivity k in terms of temperatures T _a , T _b , and flux F _ab (left) and entropy S, net entropy exchange $\text{NEE}$, and entropy production by mixing σ _a of $F_{\text{in}}$ within box A and by heat transport σ _ab (right)

In order to quantify the sensitivity of the thermodynamic state of the system to F _ab , Eq. 8 is extended to include the alternative pathways of heat loss:

$$\label{eqn:eb_case3}\begin{array}{lll} c \cdot \frac{dT_{a}}{dt} & = & F_{\text{in}} - F_{ab} - F_{\text{out},a} \\ c \cdot \frac{dT_{b}}{dt} & = & F_{ab} - F_{\text{out},b} \end{array} $$

(12)

with the fluxes $F_{\text{out},a}$ and $F_{\text{out},b}$ expressed as linearly dependent on the temperatures (with $F_{\text{out}} = a + b \cdot T_{a}$ and a = 12 W m^− 2, and b = 2.17 W m^− 2 K^− 1). These values have been chosen to be similar to the application to poleward heat transport in the Earth system, which is discussed further below.

The entropy flux associated with the influx of energy $F_{\text{in}}$ is taken to be fixed and characterized by a temperature $T_{\text{in}}$, so the net entropy exchange of the whole system is:

$$ \text{NEE} = \frac{F_{\text{out},a}}{T_{a}} + \frac{F_{\text{out},b}}{T_{b}} - \frac{F_{\text{in}}}{T_{\text{in}}} $$

(13)

In addition to the entropy production σ _ab due to heat exchange between boxes A and B as before, we also have entropy production σ _a by mixing the heat flux $F_{\text{in}}$ with the heat reservoir A:

$$ \sigma_{a} = F_{\text{in}} \cdot \left( \frac{1}{T_{a}} - \frac{1}{T_{\text{in}}} \right) $$

(14)

The resulting sensitivity of the steady state variables of our system to the effectiveness of mixing between the two boxes is shown in Fig. 2b. With a greater conductivity k and heat flux F _ab , the temperature difference T _a  − T _b decreases. As a result of the tradeoff between the thermodynamic force T _a  − T _b that drives the flux and the flux F _ab that depletes the force, a maximum in the associated entropy production σ _ab exists at intermediate values of flux and force—that is, a state of MEP associated with the flux F _ab . This flux–force tradeoff is typical for the emergence of MEP states.

We can understand the relationship between $\text{MEP}$—which is maximized at intermediate values of k—and $\text{NEE}$—which is maximized at maximum k—as follows: A greater heat flux F _ab results in a lower temperature T _a , so σ _a increases with k. The largest net entropy export is achieved at a flux that completely dissipates the temperature gradient T _a  − T _b . In this case, all entropy is produced by mixing within box A and none by the mixing between the boxes A and B. However, since we stated earlier that the “freedom” in F _ab originates, for instance, by motion, and motion is necessarily associated with friction and dissipation, this state seems to lie outside the range of possibilities, and the maximum possible heat transport achievable by motion in steady state would be the one of MEP.

Figure 2b shows that the MEP state also corresponds to the state of minimum entropy. This can be understood as follows: A small value of F _ab results in a large temperature difference, and most entropy is being produced in box A by mixing. Entropy export occurs mostly from A at a relatively high temperature because the small flux F _ab does not allow for high entropy export from box B. As F _ab increases, the heat loss efficiency of the system increases because heat is lost over a larger surface area (i.e., from boxes A and B). A larger flux F _ab allows the system to lose the same amount of heat at a lower global mean temperature. Since S = c ·ln T, it means that the total entropy of the system initially decreases with F _ab . However, with increasing flux F _ab , the temperature difference decreases as well. In the limit of high flux and a small temperature difference, all entropy is produced again in box A by mixing. Entropy export is maximized since it occurs at equal temperatures from both boxes. Since both boxes are at the same temperature at this extreme, the entropy of the system is again high. While this simple model suggests that $\text{MEP}$ also corresponds to a minimum value of S, that is, a state furthest from TE, with a reasonable explanation, this is clearly no definite proof that this is necessarily always so.

Summary

The simple model of this section illustrates how a flux through the system drives it away from TE. While this is no proof that all thermodynamic systems can be described in this way, I take this example as sufficiently justified to generalize it. The example demonstrates that processes within the model system are such that they aim to bring the system back to TE, thereby producing entropy. Hence, the maintenance of a state away from TE is fully consistent with the second law of thermodynamics. The flexibility of boundary conditions plays a critical part for the ability of a system to evolve away from TE. In our model, this was the case (3) in which heat could be lost at different temperatures depending on the internal configuration of heat redistribution (flux F _ab ). Flexible boundary conditions allow a system to increase entropy exchange across the system boundary, depending on its internal state. If feedbacks to the boundary conditions exist that allow for a greater entropy export with the surroundings, the system can achieve a state of MEP, which corresponds also to a state of lowest entropy, furthest away from TE.

We may also speculate that the flexibility of the boundary conditions (i.e. the sensitivity of the net entropy exchange $\text{NEE}$ to the fluxes and dissipation within the system) plays a critical role in setting limits on the emergent complexity of the system. This speculation is motivated by the suggestion that the resulting distance to TE is a measure of a system’s complexity (Lloyd and Pagels 1988). If we assume that more complex structures are also associated with higher levels of dissipation (as for instance shown by Zotin (1984) for organisms of different evolutionary ages and Chaisson (2001) for more general structures), then we could suspect that these more complex structures add degrees of freedom to the means of the system to redistribute energy, mass, and entropy. With greater degrees of freedom, MEP—as a suggested statistical principle similar to the maximum entropy approach in equilibrium thermodynamics—would be increasingly applicable. This would result in an interaction between the degrees of freedom within a system and its extent to produce entropy. This interaction would be mostly constrained by the sensitivity of the boundary conditions to the state of the system; hence, the boundary conditions and their sensitivity impose fundamental constraints and should be able to predict the system’s overall complexity and behavior.

While the simple model only dealt with heat content, exchange, and fluxes, it can easily be extended to mass exchange and a wealth of other Earth system processes. The basis for this is provided in the next section before specific applications of MEP are being reviewed.

Entropy production by Earth system processes

The majority of processes within the Earth system are irreversible. This irreversibility is expressed by their entropy production, which, in general, can be expressed as the product of a thermodynamic force multiplied by a thermodynamic flux. An estimate of the global entropy budget is shown in Fig. 3 assuming a steady state (i.e., $\overline{dS/dt} = 0$), based on a compilation of previous budgets (Nicolis and Nicolis 1980; Aoki 1983; Peixoto et al. 1991; Goody 2000; Kleidon and Lorenz 2005; Kleidon 2008a). In the following, we will go through the different kinds of processes and discuss the irreversibilities involved and the means to quantify the associated entropy production.

Fig. 3

Estimated entropy budget of Earth. The white arrows denote fluxes of solar radiation; black arrows, terrestrial radiation; and grey arrows, heat fluxes. F states the magnitude of the flux, T the characteristic temperature, Ω the solid angle, and F/T the associated entropy flux. The boxes denote dissipative processes with the associated magnitudes of the heat fluxes, temperature differences, and entropy production. Numbers do not necessarily balance due to uncertainties and rounding errors. The derivation of the estimates are described in the text. After Aoki (1983), Peixoto et al. (1991), and Kleidon (2008a)

Radiative transfer

Radiative exchange plays a critical role for the Earth system as it provides the means to exchange entropy with space. Once photons are emitted from the Sun’s surface towards Earth, the photon composition is increasingly out of TE as the radiative flux is diluted with increasing distance from the Sun’s surface. When this radiation is absorbed at a certain distance from the Sun, it cannot be reemitted in the same composition, but in one corresponding to the temperature for which the radiative flux would correspond to the flux emitted at a temperature given by the Stefan–Boltzmann law ($\sigma T_{e}^4$, with σ being the Stefan–Boltzmann constant). As the radiative flux decreases in density proportional to distance d squared, the corresponding equilibrium radiative temperature drops with distance as $T_{e} \propto d^{-1/2}$. This results in irreversibility associated with the absorption of solar radiation away from the Sun’s surface.

This irreversibility can also be understood when we consider what would happen to the solar photons if they were absorbed by means of electronic absorption. Electronic absorption of a solar photon by an atom or molecule would allow for an electron from a ground state to be raised to an excited state, with the gain in energy ${\mathit\Delta} E$ corresponding to ${\mathit\Delta} E = h \cdot \nu$, where h is Planck’s constant and ν is the frequency of the absorbed radiation. When the excited state decays, there may be many more ways for the electron to transition back to the ground state through some intermediate states. This path through a few intermediate states implies that the same amount of energy ${\mathit\Delta} E = h \cdot \nu$ that was absorbed would be emitted by a series of less energetic photons, i.e., ${\mathit\Delta} E = h \cdot \sum n_{i} \nu_{i}$. Hence, absorption and re-emission in total resulted in the conversion of one photon in many for a given amount of absorbed and re-emitted radiation ${\mathit\Delta} E$.

The entropy production associated with the absorption of radiation $\sigma_{\text{rad}}$ in steady state can be calculated from an expression similar to Eq. 5:

$$ \label{eqn:epradiation} \sigma_{\text{rad}} = F_{\text{rad}} \cdot \left( \frac{1}{T_{\text{abs}}} - \frac{1}{T_{\text{em}}} \right), $$

(15)

where $F_{\text{rad}}$ is the radiative flux, $T_{\text{em}}$ is the radiative temperature at which the radiation was emitted, and $T_{\text{abs}}$ is the temperature at which the radiation is absorbed. Note that, in some treatments, a factor of 4/3 in the entropy production associated with radiative transfer is included (Essex 1984). The additional term of 1/3 σT ⁴ stems from the contribution of the change in photon pressure during absorption (Press 1976) and is practically of no relevance to the energy exchanges on Earth. This contribution is therefore not discussed in the following considerations.

Another aspect of irreversibility of radiative processes is associated with the scattering of incoming radiation. Incoming solar radiation is constrained to a narrow solid angle. It illuminates the cross section of the Earth, but when emitted, it is emitted from the whole surface area of the Earth, since the Earth rotates sufficiently fast. The quantification of entropy production associated with scattering requires a more detailed treatment of radiation entropy that includes integration over the solid angle (Planck 1906; Wildt 1956; Press 1976).

Of the incoming flux of solar radiation of 341 W m^− 2, about 1/3 is scattered back to space, while the other 2/3 are absorbed in the atmosphere and at the surface. For the estimate of entropy production by scattering, it is assumed that the scattered solar radiation is scattered from a very narrow angle to the hemisphere, yielding about 26 mW m^− 2 K^− 1. Absorption in the atmosphere and at the surface add the largest contribution to planetary entropy production of 258 and 555 mW m^− 2 K^− 1, respectively. These contributions are large because solar radiation was emitted at the high temperature of the Sun of about 5,760 K and absorbed on Earth at relatively low temperatures of 252 and 288 K, respectively. Radiative exchange of terrestrial radiation produces much less entropy (of about 26 mW m^− 2 K^− 1) because temperature differences between the surface and the atmosphere are much less.

Further relevant research on entropy of radiation is found in Essex (1984), Callies and Herbert (1988), Lesins (1990), and Goody and Abdou (1996).

Diffusion of heat

When the Earth’s surface is heated, e.g., during periods of high solar radiation, and then cooled later at night or within the year by the emission of longwave radiation, the change of heating and cooling in time results in temporal changes in ground heat storage and diffusive heat exchange at the surface. Because heat is added to the surface at a different temperature compared to the time when it is removed, ground heat exchange is associated with irreversibility and entropy production.

The associated entropy production can be calculated from the time-varying ground heat flux G and the temperature gradient at the surface:

$$ \label{eqn:epdiffusion} \sigma_{\text{diff}} = G \cdot \nabla \left(\frac{1}{T}\right) $$

(16)

Note that $\overline{G} = 0$ in the climatological mean, i.e., we deal with diurnal, seasonal, or other periodic variations in heat storage here in the climatological mean and do not consider long-term climatic change.

The diurnal and seasonal cycles on Earth result in temporal heat storage changes of significant magnitude, resulting in entropy production in the order of 1 mW m^− 2 K^− 1 in the global mean, but with strong regional variations of low values in the tropics and high values of up to 14 mW m^− 2 K^− 1 found in the continental climates near the poles. The values used in Fig. 3 (box “diffusion”) are land averages computed from a detailed land surface model simulation by the author (unpublished results).

Motion

Uneven heating results in air temperature differences and density gradients, causing pressure gradient forces to accelerate air and water masses, thereby generating kinetic energy. Friction, mostly at the system boundary, causes momentum dissipation, which converts kinetic energy into heat, resulting in entropy production. Motion also transports heat (and mass), and mixing of heat (and mass) results in entropy production as well. These two forms of irreversibility are referred to as thermal and viscous dissipation, respectively.

Overall, the associated entropy production can be calculated from the associated heat flux $F_{\text{heat}}$ and their respective temperature differences:

$$ \sigma_{\text{heat}} = F_{\text{heat}} \cdot \left( \frac{1}{T_{\text{cold}}} - \frac{1}{T_{\text{warm}}} \right) $$

(17)

The contribution of viscous dissipation to the total entropy production can be quantified by the shear stress τ multiplied by the gradient in velocity u (Goody 2000; Ozawa et al. 2003):

$$ \label{eqn:epfriction} \sigma_{\text{fric}} = \frac{\tau \cdot \nabla u}{T} $$

(18)

This consideration applies to any motion: in the atmosphere, oceans, and the Earth’s mantle.

In the climate system, two major gradients in heating develop: in the vertical, convection transports heat and depletes the gradient caused by the heating of the ground by absorption of solar radiation and the cooling of the atmosphere aloft by longwave emission. The sensible heat flux from the surface to the atmosphere is in the order of 20 W m^− 2 with a typical temperature gradient of about ${\mathit\Delta} T = 8$ K; this contributes about 20 W m^− 2 ·(1/280 K − 1/288 K) = 2 W m^− 2 K^− 1 to the Earth’s entropy budget (see box “dry convection”). In the horizontal, the large-scale atmospheric and oceanic circulations transport heat from the warmer tropics to the colder poles. With a heat flux of about 10 W m^− 2 and a typical temperature gradient of about 45 K, this results in entropy production of about 6 W m^− 2 K^− 1 (see box “frictional dissipation”). Within the Earth, mantle convection transports heat from the interior to the crust. While the heat flux is small (in the order of 0.1 W m^− 2), the heat flux is driven by a large temperature gradient of about 5,000 K between the core and the surface. Hence, it contributes about 0.3 W m^− 2 K^− 1 to the Earth’s entropy budget.

Mass transfer

Mass fluxes play a key role in shaping global biogeochemical cycles—in particular, the global cycles of water and carbon—and the atmospheric composition. The atmospheric composition in turn has important consequences for the strength of the atmospheric greenhouse effect (water vapor, clouds, and carbon dioxide are important components of the greenhouse effect), and impact the overall reflectivity of the planet through effects on cloud cover. These material processes can be formulated in thermodynamic terms by using energy and mass exchanges and gradients in chemical potentials. The chemical potential describes the change of internal energy of the system associated with a change of mass. If we take Gibbs free energy as a basis, that is, the amount of energy that can be converted into work at constant temperature T and pressure p, the chemical potential is simply given by $\mu = \partial G/ \partial N$, with N being the number of particles (or moles) of a substance. For an ideal gas, the chemical potential expresses the amount of work required to compress the gas from an original pressure p ₀ to a pressure p:

$$ \label{eqn:muidealgas} \mu = \mu_{0} + R T \log p/p_{0}, $$

(19)

where μ ₀ is a reference chemical potential and R is the ideal gas constant.

Since all mass fluxes on Earth take place in the gravitational field of the Earth, one needs to use the modified chemical potential to properly account for gravity (Kondepudi and Prigogine 1998):

$$ \label{eqn:muidealgasgrav} \mu = \mu_{0} + R T \log p/p_{0} + g z, $$

(20)

where g is the gravitational constant and z is the height with respect to a reference height.

The entropy production of mass transfer—either by physical means such as diffusion, or by chemical means in terms of reaction rates—then results from a difference in chemical potentials and the mass flux of the substance. The resulting entropy production associated with a mass flux $F_{\text{mass}}$ in steady state can be expressed as:

$$ \sigma_{\text{mass}} = F_{\text{mass}} \frac{(\mu_{b}-\mu_{a})}{T}, $$

(21)

where T is the prevailing temperature and μ _a and μ _b are the chemical potentials that drive the flux.

If heat is being utilized or released, for instance, in chemical reactions, we also need to consider enthalpy fluxes in the entropy budget. This expression directly follows from the standard definition of the Gibbs free energy G = H − T S , with H = U + p V being the enthalpy exchange (i.e., change in internal energy and/or changes in pressure/volume work), T the temperature, and S the entropy. By taking the time derivative and division by temperature (assuming isothermal conditions), we obtain:

$$ \frac{1}{T} \cdot \frac{dG}{dt} = \frac{1}{T} \cdot \frac{dH}{dt} - \frac{dS}{dt}, $$

(22)

or, in slightly rearranged form:

$$ \label{eqn:gibbsdepletion} \frac{dS}{dt} = - \frac{1}{T} \cdot \frac{dG}{dt} + \frac{1}{T} \cdot \frac{dH}{dt} $$

(23)

Equation 23 is equivalent to Eq. 2: The first term on the right-hand side expresses the depletion of Gibbs free energy with time, resulting in entropy production within the system, which is exchanged with the environment by enthalpy exchange (the second term). Hence, we can view chemical reactions, e.g., the biogeochemical reactions of the carbon cycle, within this generalized framework of entropy production and associated changes in chemical potentials.

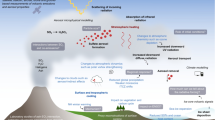
The use of chemical potentials, fluxes, and the resulting entropy production is demonstrated in the following using the global cycles of water and carbon. These cycles are summarized in Fig. 4 and are discussed in an analogy of an electric circuit, with a battery representing the corresponding electromotive force that drives the cycle out of TE, and resistances representing the dissipative processes within these cycles that deplete gradients and are directed to bring the cycle back to TE.

Fig. 4

Simplified diagram of the irreversible processes in the global water (a) and carbon (b) cycles. The cycles are drawn as electric circuits, with potentials being indicated as chemical potentials, resistances being the dissipative processes, and the batteries being the processes that generate the free energies and thereby drive these cycles (labeled by boxes with italic text). Dotted lines represent the compounds in gaseous state, dashed lines represent compounds in dissolved state, and solid lines represent liquid or solid states

The hydrologic cycle

The global hydrologic cycle consists of processes such as phase transitions from solid to liquid to gas as snow melts, water evaporates, and vapor condenses, transport of water vapor by the atmospheric circulation to higher altitudes and to land, binding of liquid water to the soil matrix on land and the flow of water in river systems back to the oceans (Fig. 4a).

In order to understand the irreversible nature of the hydrologic cycle, let us first consider the state of TE with respect to water. TE in the hydrologic cycle corresponds to an atmosphere that is saturated with respect to its water vapor content. At this state, the rate of condensation and precipitation balances evaporation, and these processes are therefore reversible at saturation. The hydrologic cycle is driven out of TE by the atmospheric circulation, as symbolized by the battery in Fig. 4a. Updrafts in the atmosphere cool air, thereby bringing water vapor to condensation in liquid or solid form. When this condensed moisture falls down through the atmosphere in the form of droplets, its net effect is such that it removes liquid water from the atmosphere in the updraft region. In regions of atmospheric downdrafts, these air masses then reach unsaturated conditions and are able to drive evaporation at the surface.

The strength of the “battery” depends primarily on the strength of the atmospheric circulation. The stronger the atmospheric circulation and the associated upward motions, the larger the droplets of liquid water need to be to overcome the uplift and to precipitate out of the atmosphere. Larger droplets in turn are less likely to be re-evaporated on their downfall; thus, this should enhance the ability of the atmosphere to lose its moisture more efficiently. This would result overall in air of a lower humidity when descending and a hydrologic cycle further away from TE with stronger dissipative activities.

Entropy production associated with dissipative processes in the hydrologic cycle can be quantified by using the chemical potential of water vapor in air for a given humidity $\text{RH}$ and temperature T:

$$ \label{eqn:chempotwater} \mu = R_{\emph{v}} T \log \text{RH} + g z + \mu_{0}, $$

(24)

where $R_{\emph{v}}$ is the gas constant for water vapor, z is the height above mean sea level, and μ ₀ is a reference potential (which is assumed to be zero in the following discussions).

As examples, these expressions can be used to calculate the entropy production $\sigma_{\text{evap}}$ associated with evaporating water at a rate E from a saturated surface into air of relative humidity $\text{RH}$:

$$ \sigma_{\text{evap}} = R_{\emph{v}} \cdot E \cdot \log \text{RH} $$

(25)

When vapor of two different air parcels with different vapor partial pressures are being mixed, entropy is produced by mixing:

$$ \label{eqn:h2omix} \sigma_{\text{mix}} = R_{\emph{v}} \cdot M \cdot \log e_{a}/e_{b}, $$

(26)

where M is the rate of mixing and e _a and e _b are the respective partial pressures. In both examples, it is assumed that the temperature T of the air does not change during the process.

The overall entropy production by the hydrologic cycle is 23 mW m^− 2 K^− 1 (see Fig. 3, box “hydrologic cycling”). This estimate is derived from the rate at which heat is added to the hydrologic cycle (79 W m^− 2) when water is evaporated, from the rate at which heat is removed from the hydrologic cycle when water condenses (the same 79 W m^− 2 in steady state), and from the temperatures at which these heat exchanges take place (288 and 266 K, respectively).

When we want to break down the contributions of individual processes to this total of 23 mW m^− 2 K^− 1, we need to consider the formulation using the chemical potentials as discussed above. Kleidon (2008b) uses climate model simulations to estimate entropy production by boundary layer mixing to be about 8 mW m^− 2 K^− 1, with rates over the ocean about twice the rate over land, although large geographical and seasonal variations exist. In the atmosphere, entropy production due to condensation of supersaturated vapor, water vapor diffusion, re-evaporation of condensed moisture in unsaturated regions of the atmosphere, and the frictional dissipation of falling raindrops is estimated to lie within the range of 13–17 mW m^− 2 K^− 1 (Goody 2000; Pauluis and Held 2002a, b; Pauluis 2005).

Once precipitation falls on land, its motion is driven by differences in height (i.e., gravitational potential) and by capillary and adhesive forces within the soil (which are commonly expressed by the soil’s matric potential). Irreversible processes include the wetting of soil, which corresponds to a phase change from free to bound liquid water, redistribution of soil moistures along gradients in chemical potential, and frictional dissipation of water flow within plants and river channels (Leopold and Langbein 1962; Kleidon et al. 2008; Kleidon and Schymanski 2008). Except for dissipation of kinetic energy by river flow, the magnitude of entropy production by these processes is generally much smaller than 1 mW m^− 2 K^− 1.

The carbon cycle

The global carbon cycle encompasses processes that shape the concentration of carbon dioxide in the Earth’s atmosphere and, thereby, plays a major role in shaping the strength of the atmospheric greenhouse effect. It consists of purely geophysical and geochemical processes, such as outgassing from the mantle, air–sea gas exchange, and the formation of carbonate by precipitation in the ocean, and of biological processes, in particular, photosynthesis and respiration, which represent most of biotic activity on Earth.

We start the thermodynamic view of the carbon cycle with the identification of the state of TE. The concentration of carbon dioxide in the atmosphere is in a state of TE when its concentration is in TE with the carbon content of the interior. Since the mantle of the Earth has a high temperature, the corresponding equilibrium partial pressure of carbon dioxide is much higher than the carbon dioxide concentration of the atmosphere over most of the recent history of the Earth.

There are two types of “batteries” that drive the carbon cycle on very different time scales (Fig. 4b):

• The biotic “battery”: On short time scales, the biotic “battery” represents photosynthetic activity in oceans and on land. Photosynthesis is the process by which life uses low-entropy sunlight to convert carbon dioxide and water from the environment into chemical free energy in the form of carbohydrates. The strength of this battery depends on environmental conditions. For present-day conditions, the primary limitation to photosynthetic activity in the oceans is the supply of nutrients (which relates to the strength of upwelling of deep, nutrient-rich water), while the primary limitations to photosynthetic activity on land are moisture availability in tropical and subtropical regions and cold temperatures in polar regions.

• The geologic “battery”: The geologic “battery” involves processes in the Earth’s interior and operates on long time scales. The geologic “battery” is associated with the initial heat content of the Earth’s interior, the resulting mantle convection, plate tectonics, and the related degassing of volatiles. Since carbonate rocks and sedimentary organic carbon are not stable at high temperatures, they release carbon dioxide. This release of carbon dioxide creates partial pressure gradients to the atmospheric concentrations that drive volcanic outgassing. The strength of this “battery” is ultimately related to the temperature difference between the interior and the surface as the main driving force for mantle convection. As the Earth looses its initial heat content in the interior, the strength of this battery has likely decreased over Earth’s history.

Entropy production associated with carbon exchange can be quantified in a similar way as for hydrologic fluxes, except that the partial pressure of carbon dioxide is used to express the chemical potential instead of vapor pressure:

$$ \label{eqn:chempotco2} \mu_{\text{CO2}} = R_{\text{CO2}} T \log e_{\text{CO2}} + g z, $$

(27)

where $R_{\text{CO2}}$ is the ideal gas constant for carbon dioxide and $e_{\text{CO2}}$ is the partial pressure of carbon dioxide. For instance, when the high concentrations of carbon dioxide in the soils of tropical rainforests mix with the carbon dioxide of the free atmosphere, entropy is being produced. This can be quantified as in Eq. 26:

$$ \sigma_{\text{mix}} = R_{\text{CO2}} \cdot M \cdot \log \frac{e_{\text{CO2,soil}}}{e_{\text{CO2,atm}}}, $$

(28)

where M is the rate of mixing.

For instance, if the carbon dioxide concentrations in the soil and air are $e_{\text{CO2,soil}} =$ 5,000 ppm and $e_{\text{\text{CO2,atm}}} = 360$ ppm, respectively, this yields an entropy production rate in the order of $\sigma_{\text{mix}} = 0.1$ mW m^− 2 K^− 1 with a soil respiration flux of M = 2 kgC m^− 2 year^− 1. Entropy production resulting from the respiration of carbohydrates involves the production of high-entropy compounds and the release of heat.

The overall contribution of the carbon cycle to the entropy budget as shown in Fig. 3 (box “carbon cycling”) is derived from the rate at which energy is added to the carbon cycle by photosynthesis, the rate at which energy is released by respiration, and the respective temperatures. Photosynthesis requires about 10 photons of 680 and 700 nm to fix one molecule of carbon dioxide. This yields a photon energy requirement of 1,710 kJ per mole of fixed carbon. Using global estimates of gross primary productivity of 120 GtC/year on land and 90 GtC/year in oceans results in an estimated 1.8 W/m² of solar radiation being utilized by photosynthesis, which is eventually respired into heat. Assuming that the solar photons used by photosynthesis are characterized by the emission temperature of the Sun of $T_{\text{sun}} =$ 5,760 K and that respiration takes place roughly at the surface temperature of the Earth $T_{\text{surf}} = 288$ K, we obtain a total entropy production of the carbon cycle of about 6 mW m^− 2 K^− 1.

Since carbohydrates only contain 479 kJ per mole of carbon, about 70% of the entropy production occurs during photosynthesis. The remaining entropy production of about 1.6 mW m^− 2 K^− 1 occurs when carbohydrates are used to construct and maintain biomass (autotrophic respiration), and dead biomass is decomposed (heterotrophic respiration). Diffusive processes play a minor role in terms of entropy production, as illustrated by the example above as an upper case of a large gradient and flux in a tropical rainforest ecosystem.

Applications

We can distinguish three types of applications of MEP to Earth system processes: (1) demonstration of the existence of MEP states (mostly for turbulent processes), (2) analysis of climate system behavior using MEP to parameterize turbulent processes, and (3) applicability of MEP to biotic processes within an Earth system context.

Demonstration of MEP states: background

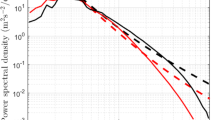
Most demonstrations of MEP for Earth system processes deal with turbulent processes. Any motion is associated with dissipation of kinetic energy. With turbulence, the intensity of energy dissipation is substantially increased compared to laminar flow. Many of the heat transport mechanisms in the Earth system are turbulent, and therefore, turbulence plays a major role. Turbulence is found in atmospheric motion at relatively small scales like convection cells in the vertical atmospheric column, and at large scales in the form of cyclones in the atmosphere and ocean gyres at mid-latitudes. Within the mantle, convection is the main form of heat loss from the interior. Even though the contribution of turbulent processes to the global entropy budget are relatively small (cf. Fig. 3), it can be shown that the presence of polar heat transport by motion nevertheless acts to enhance the overall radiative entropy export to space (see Fig. 5 and explanation below).

Fig. 5

Simple two-box models to illustrate states of MEP with respect to a large-scale poleward heat transport and b vertical convective heat transport. The thick dotted lines mark the boundaries of the systems under consideration. The thin boxes frame the energy balances of the two boxes for each system. White arrows represent solar radiation; black arrows, terrestrial radiation; and grey arrows, turbulent fluxes, which are used to demonstrate MEP. The figures on the right show the decrease of the temperature gradient with increased flux (solid line), entropy production by heat transport (dashed line), and the increase in planetary entropy production (dotted line). The symbols in a are F _TF : large-scale poleward heat flux; F _SW,T: insolation in the tropics; F _SW,P: insolation at the poles; T _T : tropical temperature; T _P : polar temperature; σ: Stefan–Boltzmann constant. The symbols in b are F _TF : convective flux; F _SW : solar heating of the surface; T _S : surface temperature; T _A : atmospheric temperature; ε: atmospheric opacity to longwave radiation (depends on strength of greenhouse effect). After Kleidon (2004a)

MEP is commonly demonstrated using relatively simple box models in which the heat fluxes between the boxes are varied to demonstrate the sensitivity of entropy production to the heat flux. Such simple models are used here to demonstrate MEP associated with horizontal and vertical motion in Fig. 5. Both examples closely resemble the simple model shown in Fig. 2, but consider the specifics of the actual radiative fluxes that heat and cool the surface and atmosphere of the Earth.

The first example shown in Fig. 5 deals with MEP associated with large-scale, horizontal heat transport from the tropics to the poles. Since tropical regions receive more solar radiation than polar regions due to the orientation of the surface to the incoming solar radiation, an imbalance in heating is generated. As in the case (3) of the simple example above, a redistribution of heat from the tropics to the poles increases entropy production and overall net entropy export to space. Also, the same tradeoff between flux and force exists: a greater heat flux reduces the temperature gradient and, thereby, the force that drives the generation of kinetic energy. A greater heat flux enhances the entropy export to space, but with an increasing share of entropy production by absorption rather than heat transport. Hence, a maximum in entropy production associated with poleward heat transport is found at intermediate values of heat flux and temperature gradient.

A similar tradeoff exists for turbulent heat transport in the vertical (Fig. 5b). The turbulent transport of heat from the surface to the atmosphere depletes the temperature gradient that drives the flow. As a result of this tradeoff, a maximum exists in the entropy produced by the vertical heat flux. Overall, the entropy export to space increases with increasing vertical heat flux. In the absence of a turbulent heat flux, radiation is emitted at a relatively high temperature of the surface. With increasing turbulent heat flux, more and more heat is emitted at the lower, atmospheric temperature, thus resulting in the enhanced entropy export to space in the presence of a turbulent heat flux. As with the case above, with greater values of vertical heat transport, entropy is being produced more and more by absorption of radiation; hence, a maximum in entropy production associated with vertical heat transport exists.

Demonstration of MEP states: examples

An MEP-like principle for the climate system was first proposed by Lorenz (1960), who argued that the atmospheric circulation is organized to maximize dissipation. Independently, Paltridge (1975, 1978, 1979) set up a simple multibox model to simulate the latitudinal transect of the climate system and showed that, by using MEP, one can get a realistic representation of the present-day climate in terms of the latitudinal variation of temperature and cloudiness. Since Paltridge’s seminal papers, several authors have confirmed and extended these results (Grassl 1981; Shutts 1981; Lin 1982; Mobbs 1982; Noda and Tokioka 1983; Wyant et al. 1988; Sohn and Smith 1993, 1994; Obrien and Stephens 1995; Pujol and Llebot 1999, 2000; Paltridge 2001; Lorenz et al. 2001; Lorenz 2002a, 2004; Kleidon et al. 2003, 2006; Murakami and Kitoh 2005; Ito and Kleidon 2005). Lin (1982) linked Paltridge’s work with the maximization of the generation of available potential energy, linking MEP with the energy cycle of Lorenz (1955). Wyant et al. (1988) explicitly included a seasonal cycle in the simulations and showed that the seasonal aspect of solar heating is an important factor in shaping the MEP state and the associated climate. Sohn and Smith (1993, 1994) also included oceanic heat transport and extended the energy balance model to two dimensions. Lorenz et al. (2001) showed that a simple, two-box model of planetary atmospheres can predict better temperature gradients by MEP than empirical modifications of eddy diffusion coefficients for Mars and Titan. Kleidon et al. (2003; Kleidon et al. (2006) used an atmospheric general circulation model to demonstrate that MEP states can be found in idealized model simulations if the strength of boundary layer friction is varied. The value obtained by MEP closely matched the empirical value used in the model. While Paltridge (1975) originally hypothesized maximum convective heat flux in the vertical, several authors have demonstrated that MEP is applicable to convection in the vertical as well (Ozawa and Ohmura 1997; Pujol and Fort 2002; Pujol 2003; Lorenz and Mckay 2003; Kleidon 2004a).

A few studies focused on potential applications of MEP to the ocean circulation (Polyakov 2001; Shimokawa and Ozawa 2001, 2002, 2005, 2007; Jupp and Schultz 2004). Polyakov (2001) used MEP to parameterize an ocean model and showed an improved simulated circulation of the arctic ocean. Jupp and Schultz (2004) found that the upper temperature of 400°C of seafloor vents can be explained by the nonlinear aspects of water in conjunction with the assumption that the fluid flow of the hydrothermal convection cell maximizes entropy production. In a series of papers, Shimokawa and Ozawa (Shimokawa and Ozawa 2001, 2002, 2005, 2007) showed with model simulations with an ocean general circulation model that the oceanic state of MEP is the most stable steady state among a series of possible steady-state solutions. An application of MEP to the nearshore fluid dynamics that shape beach profiles is given in Jenkins and Inman (2006).

The applicability of MEP to convection in the Earth’s mantle and earthquake dynamics has also been explored (Vanyo and Paltridge 1981; Lorenz 2002b; Main and Al-Kindy 2002, 2004; Main and Naylor 2008). Vanyo and Paltridge (1981) showed with a simulation model of viscous transport of the Earth’s mantle and core that the magnitude of maximum energy dissipation associated with mantle convection corresponds qualitatively well with estimates derived from observations. Lorenz (2002b) demonstrates with a simple model that the temperature profile with depth in the Earth’s interior can be reasonably reproduced by the assumption that the convective heat transport by mantle convection is governed by MEP. Main and Naylor (2008) showed that the observed power-law behavior in earthquake dynamics is consistent with MEP.

MEP states can also be demonstrated for Earth system processes that are indirectly related to turbulent processes or not turbulent at all. Wang et al. (2004, 2007) successfully tested the hypothesis that the evapotranspiration flux from land is maximized with field observations. Since evapotranspiration is directly linked to the turbulent transport of latent heat from the surface to the atmosphere, this maximization would correspond to MEP for a fixed gradient. Kleidon and Schymanski (2008) investigated potential applications of MEP in land surface hydrology. The key question in land surface hydrology is the partitioning of incoming precipitation into evapotranspiration and runoff. Similar tradeoffs exist as in the case of poleward heat transport, by which the mass fluxes deplete the thermodynamic forces (gradients in chemical potentials), thereby resulting in optimum states that maximize entropy production. They argued that, through soil heterogeneity and vegetation effects, degrees of freedom are introduced to the hydrologic fluxes to allow for this optimization to take place. If we express hydrologic fluxes as an electric network of resistances (e.g., as in Fig. 4), then this would follow directly from Kirchhoff’s loop law, which in turn has been derived from the assumption that currents are partitioned to maximize entropy production (Zupanovic et al. 2004).

Demonstration of MEP states: potential mechanism

These examples lead to the question of how fluids would be organized in such a way that the associated production of entropy is maximized. Theoretical and laboratory studies of fluid turbulence have looked into this question for quite some time. Malkus (1954, 1956) hypothesized that fluid flow in a Bérnard convection cell is organized in a way that maximizes the heat flux for a given temperature gradient (see also Busse 1968, 1970; Robert and Sommeria 1991, 1992; Sommeria 2005). Under this fixed boundary condition, MEP translates into the maximization of the flux, so that Malkus’ maximum flux hypothesis is consistent with MEP for fixed boundary conditions. Ozawa et al. (2001) related the maximum flux hypothesis to MEP in more detail (see also Schneider and Kay 1994). They argued that the maximization is achieved by the fluid system by creating steep gradients near the system boundary with critical stability numbers (e.g., Reynolds number, Nuesselt number, etc.) while creating large areas of uniformity within the system’s interior. Similar patterns of steep gradients at the boundary can be found, for instance, in the atmosphere near the surface, and at the polar front in the mid-latitude regions in winter. To resolve such steep gradients and how these vary in time, it is important to have a sufficiently high resolution in numerical simulation models. This has been demonstrated with model simulations by Kleidon et al. (2003), who investigated the sensitivity of entropy production to the spatial resolution of an atmospheric general circulation model. They found that entropy production by the atmospheric circulation increases with model resolution but saturates at a maximum value for a sufficiently high resolution. This result is consistent with the above line of reasoning.

MEP and climate system behavior

Another set of studies used MEP to describe processes such as heat transport for an analysis of the climate system to study theoretical issues, such as multiple steady states and long-term climate regulation.

Previous studies (Budyko 1969; Sellers 1969) have established that the Earth’s climate system can exhibit multiple steady states due to the positive ice–albedo feedback. Nicolis and Nicolis 1980 explored climate stability and the ice–albedo feedback from a perspective of entropy production, including the snowball Earth state. They found that the glaciated state is associated with enhanced entropy production. Gerard et al. (1990) investigated the role of MEP in the context of the ice–albedo feedback and found that the critical threshold at which global glaciation would occur is lowered when assuming MEP for poleward heat transport.

In a series of papers, Ou developed a simple model of the climate system and used MEP to parameterize poleward heat transport to investigate long-term climate stability with respect to cloud feedbacks and the implications for climate system functioning (Ou 2001, 2006, 2007). Ou (2001) argued that a shifting balance of high vs low clouds can result in climate-regulating behavior. Ou (2006, 2007) extended this work to explore the impacts for the hydrological cycle, including humidity profiles, atmospheric moisture transport, and ocean stratification. This work was able to derive basic, observed relationships from his simple model.

Some studies used MEP to parameterize heat transport in the conceptual Daisyworld model (Pujol 2002; Toniazzo et al. 2005; McDonald-Gibson et al. 2008) that was developed by Watson and Lovelock (1983) to demonstrate homeostatic behavior as postulated by the Gaia hypothesis. These studies found that the range of climate stability in Daisyworld was substantially enlarged when using MEP to parameterize the heat transport.

Other applications include, e.g., the investigation of the Lorenz attractor from a perspective of MEP (Nicolis 1999), the climate sensitivity to atmospheric $\text{CO}_{2}$ concentrations (Grassl 1981), and cloud cover sensitivity (Paltridge et al. 2007).

MEP and biotic processes in the Earth system

MEP associated with biotic processes are being discussed separately from the above examples because biotic activity is a biochemical process and is, thus, quite different from the purely physical processes discussed above. In the Earth system context, it is important to note that interactions take place between biotic activity and the physical and chemical characteristics of the Earth system at the larger to planetary scale (as already discussed in the context of the Gaia hypothesis and the thermodynamics of the carbon cycle above). For instance, the presence of vegetation affects physical properties and fluxes such as land surface albedo and evapotranspiration rate, while biotic carbon exchange strongly affects the global carbon cycle and the strength of the atmospheric greenhouse effect.

The thermodynamic nature of biotic activity—the sum of all organisms—and its maximization has been hypothesized for some time (Lotka 1922a, b; Odum 1969, 1988; Ulanowicz and Hannon 1987; Schneider and Kay 1994; Loreau 1995; Jorgensen and Svirezhev 2004; Schneider and Sagan 2005). What has been missing in some of these studies is a full treatment of the effects of biotic activity on its environmental boundary conditions, as well as a precise formulation of the effects in terms of nonequilibrium thermodynamics. In the following examples, thermodynamic considerations and tradeoffs within the boundary conditions are explicitly considered.

Meysman and Bruers (2007) described the decomposition of organic matter in ocean sediments as a thermodynamic process and applied MEP to a simple model to demonstrate that it is possible to describe this biotic process solely in terms of thermodynamic properties and fluxes. The maximum in entropy production associated with decomposition resulted from the tradeoff between reaction rate (the ecosystem metabolic rate) and resource availability in the steady state. They found reasonable agreement between the decomposition rates predicted by MEP and observed data.

Kleidon (2004a) explored the applicability of MEP at the planetary level (Fig. 6a). In this study, it is argued that a maximum in planetary entropy production should exist on Earth due to the tradeoff between decreasing reflective polar ice cover and increasing reflective tropical cloud cover with increasing surface temperature. Since life plays a critical role in driving changes in the global carbon cycle (see the “The carbon cycle” section), it affects the strength of the greenhouse effect and, thereby, surface temperature. Surface temperature in turn plays a critical role in shaping the magnitude of surface evaporation and for the maintenance of snow and ice. Using a simple model, it was demonstrated that MEP on the planetary scale can result in homeostatic behavior, as postulated by the Gaia hypothesis.

Fig. 6

Proposed states of MEP a at the planetary scale resulting from the contrasting effects of surface temperature on ice albedo and cloud albedo and b at the land surface resulting from the contrasting effects of vegetation productivity on surface albedo and evapotranspiration on overall absorption of solar radiation at the surface. After Kleidon (2004a) and Kleidon and Fraedrich (2005)

A similar larger-scale tradeoff between surface and cloud albedo results in optimum conditions on land (Kleidon and Fraedrich 2005), as illustrated in Fig. 6b. Vegetation directly shapes the evapotranspiration flux on land through several effects, such as rooting zone depth (available soil water for evapotranspiration) and stomatal functioning (regulation of evapotranspiration rate). The water loss from terrestrial vegetation is closely linked to its ability to photosynthesize: as carbon dioxide is taken up by leaves by photosynthesis, water vapor escapes from the leaves’ interior. At a larger scale, transpiration affects the concentration of water vapor in the atmospheric boundary layer, which in turn affects cloud cover and the amount of solar radiation at the surface available for photosynthesis. The link to MEP is made by recognizing that, in steady state, a maximization of photosynthesis is equivalent with a maximum in respiration. Hence, a maximum in photosynthesis would correspond to a state of MEP associated with biotic carbon exchange. This tradeoff results in an optimum transpiration rate, at which photosynthetic activity is maximized, although this maximum is sensitive to the extent to which water vs light limits productivity (which depends on the prevailing climatic conditions), and also depends on other limiting factors, e.g., nutrients. The existence of this maximum has been demonstrated by sensitivity simulations with a coupled climate–vegetation model (Kleidon 2004b).

Both examples shown in Fig. 6 illustrate that, through the process of biotic activity at the large to planetary scale, the entropy production of the whole system can be enhanced through enhanced absorption of solar radiation. The constraints imposed by water and light availability on vegetation productivity act as large-scale boundary conditions in these examples. The potential degrees of freedom that would allow for optimization to take place in biotic functioning have been demonstrated, for instance, by a set of sensitivity simulations with a coupled climate–vegetation model in which parameters of vegetation form and function (e.g., canopy roughness, partitioning of biomass among roots and shoots) have been varied within reasonable ranges (Kleidon 2006). The resulting simulated climates span a considerable range of different conditions that would be associated with vastly different levels of photosynthesis. Within this range, the maximization of photosynthesis would result in an overall increase in entropy production through enhanced absorption of sunlight compared to the abiotic state. This would then be fully consistent with the above examples in which a thermodynamic process that maximizes entropy production would also enhance planetary entropy production to the extent possible. While the examples cited above show that maximization of productivity under these large-scale constraints yield reasonable results, the mechanisms of how this maximization takes place (e.g., whether it requires sufficient diversity in the vegetative cover), as well as a full thermodynamic treatment of the biotic processes (which includes detailed treatments of plant ecophysiological processes such as photosynthesis, photorespiration, and linkages of ecophysiology to nutrient cycling and requirements), would still need to be further explored.

Implications

In this section, some of the important implications of MEP for Earth system functioning are being discussed under the presumption that MEP is justified sufficiently well and applicable to Earth system processes.

MEP and feedbacks

One of the most important implications of MEP is that it implies that the associated thermodynamic processes react to perturbations with negative feedbacks in the steady state behavior (Ozawa et al. 2003, Fig. 7a). This follows directly from the maximization of entropy production, which essentially corresponds to the maximization of the work done and the free energy dissipated by a process, as explained above. Imagine that a thermodynamic flux at MEP is perturbed and temporarily reduced (black arrow in Fig. 7a). This reduction in flux would result in a build-up of the thermodynamic force, e.g., temperature gradient in the case of poleward heat transport. In this case, the process would not generate as much kinetic energy as possible. The enhanced temperature gradient would then act to enhance the generation of kinetic energy, and thereby the flux, thus bringing it back to its optimal value and the MEP state. If the boundary conditions shape the optimum change (Fig. 7b), then a perturbation of the state would be amplified until the new optimum is reached, which could be interpreted as a positive feedback to the perturbation.

Fig. 7

Implications of MEP for feedbacks. a Maximization of entropy production for steady-state conditions implies a negative feedback to perturbations. The flux–force relationship is shown by the black solid line, and the associated entropy production by the black dotted line. A perturbation that temporarily reduces the flux (black arrow) would increase the thermodynamic force, which in turn would act to increase the flux, therefore resulting in a negative feedback (grey arrow). b When external conditions change in such a way that the tradeoff between flux and force shifts (grey lines: old state, black lines: new state), a perturbation of the flux would be enhanced until the flux reaches the new optimum value at which entropy production is at a maximum. This could be interpreted as a positive feedback to change

It is, however, not just the flux–force tradeoff that results in the negative feedbacks associated with MEP. A flux–force tradeoff for the example shown in Fig. 5 can result for many functional relationships for the flux F _tf . If this flux is expressed as F _tf  = k ·(T _t  − T _p ), as it is commonly done, then a flux–force tradeoff exists for any given value of k. What MEP states is that the functional relationship itself takes a shape that maximizes entropy production and thereby results in negative feedbacks. This maximization can be understood as the direct consequence of the system to achieve its most probable configuration of states, as in the case of equilibrium statistical mechanics, as discussed in the section on MEP above.

This discussion of feedbacks and MEP is quite different from the conventional treatment of feedbacks in climatology, which are usually based on temperature sensitivities (Hansen et al. 1984). In the usual analysis, the total change in temperature ${\mathit\Delta} T_{\text{total}}$ is expressed as the sum of the direct response of temperature to the change in external forcing (${\mathit\Delta} T_{0}$) and the contribution of feedbacks (${\mathit\Delta} T_{\text{feedbacks}}$): ${\mathit\Delta} T_{\text{total}} = {\mathit\Delta} T_{0} + {\mathit\Delta} T_{\text{feedbacks}}$. If the total change in temperature is expressed as ${\mathit\Delta} T_{\text{total}} = f \cdot {\mathit\Delta} T_{0}$, with f being the feedback factor, then a positive feedback is defined as f > 1, while a negative feedback is defined as f < 1. The feedback framework plays a very important role in the analysis of anthropogenic climatic change (e.g., Hansen et al. 1998; Friedlingstein et al. 2003, 2006).

In principle, one could develop a similar feedback framework using entropy production rather than temperature as the central metric under consideration. The change in entropy production ${\mathit\Delta} \sigma_{\text{total}}$ would then be expressed as the sum of the changes due to the external forcings and due to feedbacks: ${\mathit\Delta} \sigma_{\text{total}} = {\mathit\Delta} \sigma_{0} + {\mathit\Delta} \sigma_{\text{feedbacks}}$, or ${\mathit\Delta} \sigma_{\text{total}} = f \cdot {\mathit\Delta} \sigma_{0}$. In steady state, MEP would be associated with f < 1, i.e., a negative feedback as discussed above. In case of changes in the external forcing, these would result in a change in the boundary conditions while the feedback would be associated with the change in internal configuration of the flux and gradients. With a change in external forcing, the tendency of systems to maximize entropy production would then state that, after the change, the feedback factor would initially be f > 1. That is, a small change in the flux would be amplified since the flux is no longer at the MEP state. This tendency would continue up to the point when the flux again reached the optimum value, at which point the feedback factor would change to values of f ≤ 1. This points out that optimality is a strong nonlinear aspect that is unlikely to be adequately treated in a linearized feedback framework. However, more work needs to be done to place MEP and optimality into the common feedback framework.

MEP and Earth system evolution

As mentioned in the “Introduction,” the Gaia hypothesis attempts to explain why the Earth system has been maintained in a relatively stable state (i.e., is dominated by negative, stabilizing feedbacks) by linking life with the unique thermodynamic state of the Earth system. As sketched in Fig. 6, such behavior could be understood by the Earth system regulating into a planetary state of MEP through life.

However, the Earth system has changed dramatically in the past. The early Earth very likely had an atmosphere with a high carbon dioxide concentration and in which free oxygen was basically absent. Over time, carbon dioxide was removed to trace-gas amounts, while oxygen increased substantially during the great oxidation event some 2.3 billion years ago, and again about 0.5 billion years ago, to near current levels. So how can nonequilibrium thermodynamics inform us about how the evolution of the Earth system has proceeded in the past?

Kleidon (2009) proposes that the Earth system over time has evolved further away from the planetary TE state towards states of higher entropy production, and suggests that this overarching trend can be used to derive how the Earth’s environment has changed through time. Central here is that the reference states of TE with respect to motion and fluxes of water and carbon, as described in the section “Entropy production by earth system processes” above, are interconnected, as shown in Table 1. TE at the planetary scale would be associated with the absence of large-scale motion, since only in the absence of motion would there be no frictional dissipation, hence, no entropy production by motion. Such a state of an atmosphere at rest would be saturated with water vapor since atmospheric motion acts to dehumidify the atmosphere. A saturated atmosphere in turn would likely be associated with high cloud cover and no net exchange of moisture between the surface and the atmosphere. This implies that there is no continental runoff, and no associated cycling of rock-derived, geochemical elements. For the geologic carbon cycle, this implies no carbon sink, so that the atmospheric carbon dioxide concentration would be high, in turn resulting in a strong greenhouse effect and high surface temperatures. High surface temperatures would result in ice- and snow-free conditions. Overall, because of the high cloud cover, absorption of solar radiation would be low, as would be planetary entropy production. While it is unlikely that the Earth actually ever was in a state of TE, what is shown in Table 1 nevertheless provides an association of what the Earth’s environment should look like closer and further away from a state of planetary TE.

Table 1 Environmental conditions close and far from a state of planetary TE. After Kleidon (2009)

A basic positive feedback between the water, carbon, and atmospheric dynamics was also postulated to be modulated by life: Stronger atmospheric dynamics (“motion”) would result in an atmosphere in which the hydrologic variables would be maintained further away from TE, which would imply a drier atmosphere, higher fluxes of precipitation and evapotranspiration, higher ocean–land transport, etc. This in turn would drive the geologic carbon cycle to lower carbon dioxide concentrations, resulting in a weaker greenhouse effect, which in turn would cool the Earth. A cooler Earth could maintain more extensive snow and ice cover, thus enhancing the radiative forcing gradient between the tropics and the poles. This, in turn, would strengthen the atmospheric dynamics and close the positive feedback loop.

This positive feedback would cause fundamental, thermodynamic thresholds in the whole Earth system. These thresholds would imply that planetary entropy production would unlikely increase continuously during the evolution of the Earth system, but in a stepwise fashion. Once such a thermodynamic threshold is reached, the positive feedback would cause the Earth system to rapidly evolve to a state of higher entropy production, after which the system would be maintained in a stable, MEP state.

These climatic trends associated with how far the Earth system is maintained away from TE at the planetary level could help us to better reconstruct and understand the past evolution of the Earth system. This would, however, need to be further evaluated, e.g., with more detailed simulation models that explicitly consider the nonequilibrium thermodynamic nature of Earth system processes.

MEP and complex system theories

The MEP hypothesis provides the basis to unite previously suggested optimality approaches and complex systems theories with a unified, fundamental perspective of the nonequilibrium thermodynamic nature of the system under consideration.

Similar hypotheses to MEP have been suggested in the past. For instance, the “maximum power principle” was advocated by Odum (1988), in particular for biological systems, based on Lotka’s papers (Lotka 1922a, b). Since power is work performed in time, and in steady state, power equals dissipation, this principle states that systems dissipate as much as possible. As discussed above already, maximum dissipation is consistent with MEP at fixed temperatures.

Also, the “constructal law” of Bejan (Bejan 1996; Bejan and Lorente 2004, 2006; Reis and Bejan 2006), which states that “for a finite-size system to persist in time (to live), it must evolve in such a way that it provides easier access to the imposed currents that flow through it” (Bejan and Lorente 2004), is very closely related to MEP. While the term “access” is somewhat ill-defined, earlier work (Bejan 1996) refers to it as “entropy generation minimization.” This is, in fact, very closely related to MEP, except that the minimization is seen from a different perspective (and is unrelated to Prigogine’s principle of minimum entropy production). For a given rate of entropy production, e.g., in a power plant, the system is designed in a way to maximize the amount of useful work, so that the wasted (thermal) entropy production is minimized. Applied to the atmospheric circulation (Bejan and Reis 2005), this would imply that the entropy production by frictional dissipation is maximized, while the “waste” thermal entropy production is minimized. In this way, it seems that the “constructal law” can be seen as a complement to MEP.

Dewar (2003) has briefly discussed that self-organized criticality (SOC) (Bak et al. 1987, 1988) emerges from the special case of MEP in low flow conditions. SOC has been highly successful in explaining the fractal scaling relationships of many complex systems (Bak 1996; Turcotte 1999). As SOC has also been linked, for instance, to the organization of river networks and energetics (Leopold and Langbein 1962; Rodriguez-Iturbe et al. 1992a, b; Rodriguez-Iturbe and Rinaldo 2001; Miyamoto et al. 2005), it seems to closely relate to nonequilibrium thermodynamics and MEP. This linkage has recently been discussed with respect to earthquake dynamics (Main and Naylor 2008), but it would need to be further explored for the other examples for MEP given above.

Note also that the confusion of MEP with Prigogine’s principle of minimum entropy production can be resolved relatively easily. The examples shown in Figs. 1 and 2 clearly show in practical terms how a system evolves to a state of minimum entropy production in time until a steady state is reached (Fig. 1), while MEP selects among steady state solutions as shown in Fig. 2. For technical discussion on this topic, see Martyushev et al. (2007).

Challenges

As with any hypothesis that aims to be general and postulates simple behavior of complex systems, various criticisms have been raised. In terms of the recent theoretical work on MEP by Dewar (2003, 2005a, b), criticisms have been raised by Grinstein and Linsker (2007) and Bruers (2007). Grinstein and Linsker (2007) point out some technical flaws in the derivation of the linkage of MEP and SOC, while Bruers (2007) discusses some refinements of Dewar’s derivation.

Applications of MEP to atmospheric dynamics have been criticized by arguing that the solution of MEP does not account for the important role of rotation rate in the solution (Rodgers 1976; Goody 2007). This, however, is rather a limitation of the simple energy balance model used to demonstrate MEP, rather than a deficiency of the hypothesis per se. The demonstration of MEP in simulations with an atmospheric general circulation model (Kleidon et al. 2003, 2006) clearly shows that the effect of rotation rate can be included in the maximization.

Volk (2007) and Caldeira (2007) discuss Kleidon’s application of MEP at the planetary scale (Kleidon 2004a). Volk (2007) uses a thought experiment at aiming to show that MEP applied to biology is fundamentally mistaken and concludes that “MEP ...has no great relevance for discussions of biological evolution or the time history of the effects of life on the global system”. In his response, Kleidon (2007) points out the lack of appreciation of the thermodynamic nature of Earth system processes and several misunderstandings. Caldeira (2007) raises the comment that thermodynamics and MEP “may be true, but trivially so.”

Without going into much further detail on these discussions, one issue that becomes clear from these criticisms is that the thermodynamic basis of the Earth system far from TE seems to be mostly misunderstood and needs to be clarified further. At this point, no one would argue that MEP is well established and that applications are without their limitations. Hopefully, this review provides a basis to stimulate more informed discussions on the applicability of MEP and its relationship to other complex system theories.

Summary and conclusions

This review attempts to provide a basis for the thermodynamic nature of the Earth system and to quantify its entropy, distance to TE, and associated rates of entropy production. Such a quantification will allow us to take the meaning of entropy out of its sometimes esoteric use, discuss optimality principles such as MEP on solid thermodynamic grounds, and put these in context with what was originally formulated by the Gaia hypothesis. This in turn should help us to better understand the thermodynamic foundation of many Earth system processes, and the role that life plays in driving the Earth system away from TE. While this is still speculative though reasonable at this time, it is quite possible that, after such quantifications, Lovelock’s vision of the Earth system as expressed by the original formulation of the Gaia hypothesis may be closer to the truth than what some of its skeptics would expect.

At the same time, a more solid foundation of MEP is needed. Once this foundation is successfully established, it implies that the dynamical description of complex systems far from TE follow from the maximization of entropy production. This would have quite far-reaching implications for how we model the Earth system and understand Earth system change. It will provide us with a fundamental approach to understand the success of optimality approaches that have previously been used to understand complex systems. It should also yield us a better way to upscale microscopic dynamics to the macroscopic scale. Entropy production considerations could also result in a better selection of the best forecast simulation from an ensemble of weather prediction simulations (Tapiador and Gallardo 2006). The linkage between information entropy of wind speeds to maximum frictional dissipation (Lorenz 2002a) could explain observed frequency distributions. Nonequilibrium thermodynamic measures such as entropy production may also be a more useful property to express climate sensitivity than the conventional temperature measures, as it is closely associated with the dissipative activity of the process under consideration (Kleidon 2006). In a much wider context, thermodynamics can help us to explore the thermodynamic conditions of life in a cosmological context, specifically regarding the origins of free energy to fuel life (Lineweaver and Egan 2009).

In conclusion, nonequilibrium thermodynamics and MEP show great promise in allowing us to formulate a quantifiable, holistic perspective of the Earth system at a fundamental level. This perspective would allow us to understand how the Earth system organizes itself in its functioning, how it reacts to change, and how it has evolved through time. Further studies are needed to better establish the nonequilibrium thermodynamic basis of many Earth system processes, which can then serve as test cases for demonstrating the applicability and implications of MEP.