New Approach for Stability Analysis of Interconnected Nonlinear Discrete-Time Systems Based on Vector Norms

Abstract

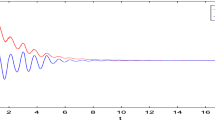
The stability analysis of interconnected large-scale systems is generally characterized by some degree of difficulty, specifically when the interconnections gather a large number of nonlinear subsystems and the couplings evolve according to nonlinear functions in time. In this paper, a novel systematic analysis procedure of fully interconnected discrete-time nonlinear systems with nonlinear interconnections is presented. First, a new arrow form representation of the interconnected system state space model is generated. The obtained generalized thin arrow state matrix is developed by combining the instantaneous subsystems characteristic polynomials, as well as a set of arbitrary and freely parameters. Then, the stability analysis is achieved using the comparison principle and vector norms by translating the stability properties of the lower-dimensional comparison system into those of the considered interconnected system. Aside the proposed systematic formulation and simplicity over existing techniques based mainly on LMIs, it is shown that through an appropriate choice of the model parameters, the developed stability conditions are opportune to locate interesting estimation of the stability domains. Lastly, two numerical examples are included to show the effectiveness of the proposed approach.

Appendices

Appendices

1.1 Appendix A1

The nonlinear system  (1) can be described, in state space, as

$$\begin{aligned} {S_i}:x_{k + 1}^i= & {} {A_{ii}}\left( . \right) x_k^i + {B_{ii}}\left( . \right) u_k^i \end{aligned}$$

(48)

$$\begin{aligned} {A_{ii}}\left( . \right)= & {} \left[ {\begin{array}{*{20}{c}} 0&{} \cdots &{}0&{}{\,\, - {a_{ii,{n_i}}}\left( . \right) } \\ 1&{}0&{} \vdots &{}{ - {a_{ii,{n_i} - 1}}\left( . \right) } \\ 0&{} {\ddots } &{}0&{} \vdots \\ 0&{}0&{}1&{}{\,\, - {a_{ii,1}}\left( . \right) } \end{array}} \right] ,\,\,{B_{ii}}\left( . \right) = \left[ {\begin{array}{*{20}{c}} {{b_{ii,{n_i}}}\left( . \right) } \\ {{b_{ii,{n_i} - 1}}\left( . \right) } \\ \vdots \\ {{b_{ii,1}}\left( . \right) } \end{array}} \right] \end{aligned}$$

(49)

with $x_k^i = {\left[ {x_{1,k}^i, \ldots ,x_{{n_i} - 1,k}^i,x_{{n_i},k}^i} \right] ^T} \in {\mathfrak {R}^{{n_i}}}$ the system ${S_i}$ state vector, ${A_{ii}}\left( . \right) \in {\mathfrak {R}^{{n_i} \times {n_i}}}$ and ${B_{ii}}\left( . \right) \in {\mathfrak {R}^{{n_i}}}$. A change of variables defined by $z_k^i = {P_i}x_k^i$

$$\begin{aligned} {P_i} = \left[ {\begin{array}{*{20}{c}} 0&{}0&{} \cdots &{}0&{}1 \\ 1&{}{{\alpha _{i,1}}}&{}{\alpha _{i,1}^2}&{} \cdots &{}{\alpha _{i,1}^{{n_i} - 1}} \\ \vdots &{} \vdots &{} \vdots &{} \cdots &{} \vdots \\ 1&{}{{\alpha _{i,{n_i} - 2}}}&{}{\alpha {{_{i,{n_i} - }^2}_2}}&{}{}&{}{\alpha _{i,{n_i} - 2}^{{n_i} - 1}} \\ 1&{}{{\alpha _{i,{n_1} - 1}}}&{}{\alpha {{_{i,{n_i} - }^2}_1}}&{} \cdots &{}{\alpha _{i,{n_i} - 1}^{{n_i} - 1}} \end{array}} \right] \end{aligned}$$

(50)

with $z_k^i \in {\mathfrak {R}^{{n_i}}}$, ${P_i} \in {\mathfrak {R}^{{n_i} \times {n_i}}}$ an invertible transformation and ${\alpha _{i,j}}$ , $j = 1,2, \cdots ,{n_i} - 1$ distinct constant arbitrary parameters, leads to the system dynamics

$$\begin{aligned} {S_i}:z_{k + 1}^i= & {} {F_{ii}}\left( . \right) z_k^i + {G_{ii}}\left( . \right) u_k^i \nonumber \\ {F_{ii}}\left( . \right)= & {} \,\left[ {\begin{array}{*{20}{c}}{\delta _{ii,{n_i}}^{}\left( . \right) }&{}{{\beta _{i,1}}}&{}{{\beta _{i,2}}}&{} \cdots &{}{{\beta _{i,{n_i} - 1}}}\\ {\gamma _{i,1}^{}\left( . \right) }&{}{{\alpha _{i,1}}}&{}{}&{}{}&{}{}\\ {\gamma _{i,2}^{}\left( . \right) }&{}{}&{}{{\alpha _{i,2}}}&{}{}&{}{}\\ \vdots &{}{}&{}{}&{} {\ddots } &{}{}\\ {\gamma _{i,{n_i} - 1}^{}\left( . \right) }&{}{}&{}{}&{}{}&{}{{\alpha _{i,{n_i} - 1}}}\end{array}} \right] ,\,\,{G_{ii}}\left( . \right) = \left[ {\begin{array}{*{20}{c}}{{\sigma _{ii}}\left( . \right) }\\ {\psi _{ii,1}^{}\left( . \right) }\\ {\psi _{ii,2}^{}\left( . \right) }\\ \vdots \\ {\psi _{ii,{n_i} - 1}^{}\left( . \right) }\end{array}} \right] \nonumber \\ \end{aligned}$$

(51)

with for $\forall j=1,2,\ldots ,{{n}_{i}}-1$,

$$\begin{aligned} {{\beta }_{i,j}}= & {} \prod \nolimits _{k=1,k\ne j}^{{{n}_{i}}-1}{{{({{\alpha }_{i,j}}-{{\alpha }_{i,k}})}^{-1}}}\\ {{\gamma }_{i,j}}(.)= & {} -{{P}_{{{A}_{ii}}}}(.,{{\alpha }_{i,j}})\\ {{\delta }_{ii,{{n}_{i}}}}(.)= & {} -{{a}_{ii,1}}(.)-\sum \nolimits _{p=1}^{{{n}_{i}}-1}{{{\alpha }_{i,p}}}\\ {{\psi }_{ii,j}}(.)= & {} {{R}_{ii}}(.,{{\alpha }_{i,j}})\\ {{\sigma }_{ii}}(.)= & {} {{b}_{ii,1}}(.) \end{aligned}$$

Polynomials ${{P}_{{{A}_{ii}}}}(\,.\,,{{\lambda }_{{}}})$ and ${{R}_{ii}}(\,.\,,{{\lambda }_{{}}})$ are defined by

$$\begin{aligned} {{P}_{{{A}_{ii}}}}(.,\lambda )=\lambda _{{}}^{{{n}_{i}}}+\sum \nolimits _{p=1}^{{{n}_{i}}}{{{a}_{ii,p}}(.){{\lambda }^{{{n}_{i}}-p}}} \end{aligned}$$

and

$$\begin{aligned} {{R}_{ii}}(.,{{\lambda }_{{}}})=\sum \nolimits _{p=1}^{{{n}_{i}}}{{{b}_{ii,m}}(.){{\lambda }^{{{n}_{i}}-p}}} \end{aligned}$$

where ${P_{{A_{ii}}}}(\,.\,,{\lambda _{}})$ denotes the instantaneous characteristic polynomial of the system ${S_i}$ described by (1), (48) or (51).

1.2 Appendix A2

Consider the discrete nonlinear Lur’e system described by means of the following block-oriented model of Fig. 8 where $f\left( . \right) :\mathfrak {R}\rightarrow \mathfrak {R}$ represents a nonlinear function, ${{B}_{0}}\left( s \right) ={{s}^{-1}}\left( 1-{{e}^{-Ts}} \right)$ a zero-order holder and ${{T}_{{}}}=0.2s$ the sampling time. $D\left( s\right) =s\left( 1+{{\tau }_{1}}s \right) \left( 1+{{\tau }_{2}}s \right)$ and $N\left( s\right) ={{\lambda }_{2}}{{s}^{2}}+{{\lambda }_{1}}s+{{\lambda }_{0}}$ are polynomials with constant parameters ${{\tau }_{1}}=0.1s$, ${{\tau }_{2}}=0.005s$, ${{\lambda }_{0}}=0.98$, ${{\lambda }_{1}}=0.098$ and ${{\lambda }_{2}}=4.7\,\,{{10}^{-4}}$.

Fig. 8

Studied third-order Lur’e system