1 Introduction

Input saturation exists in every practical control system and brings the great challenge to the designers. It will deteriorate the performance and even lead to the instability of the closed-loop system. If the control input saturates, the practical control system will not operate according to the way of the designed controller, which will cause the control mission fail and the major accident. Controller design considering the input saturation has been recognized to be a difficult problem. There has been a lot of work on this topic [1, 7, 10, 23]. For example, the scheduled low-and-high gain design technique was proposed in [12], a parametric Lyapunov equation-based low gain approach was given in [24], a saturated adaptive robust control (ARC) strategy was proposed in [16] and the saturated linear feedback control laws were established in [25]. Nevertheless, for the control system, the parameter uncertainties are always studied separately from the other requirements. It is necessary to consider the robust control simultaneously. Recent years, many results on the robust control for input saturated systems were available such as [20, 21].

When a system is affected by a disturbance, the system state will be translated far from the original trajectory. The control input will beyond the maximal control input, which causes the input saturation. The growth of the disturbance amplitude leads to the coherent large control motion and degrades the system performance. Thus, there are many methods on improving the disturbance attenuation performance of the saturated system, such as [4, 8, 14, 15].

Actuator failures are also inevitable for the control system in practical applications. The unexpected failure may cause substantial damage for the control system and may also influence the safety and accuracy of the control system. Hence, in addition to the input saturation, external disturbance and parameter uncertainties mentioned above, the reliability control against the possible actuator failure is also challenging to research. In the last decades, many results on reliable control have been reported, such as [2, 3, 18, 22, 26, 27].

The gain scheduling approach is one of the most popular nonlinear control design approaches and has been applied in many fields [11, 13]. There are many results on gain scheduling control [6, 8, 12, 17, 19].

From the above, there are few results of the input saturated systems focusing on strengthening the disturbance attenuation ability as strong as possible, improving the dynamic performance of the closed-loop system and removing the actuator failures, simultaneously. Motivated by the above discussions, we propose a reliable robust control for the input saturated system based on the discrete scheduling approach. The key idea of the proposed method is based on the LMIs, low gain feedback and gain scheduling. The low gain feedback is to design as small as possible control gain for avoiding actuator saturation. When the initial conditions are far from the origin, the control gain must be very small. However, as the state converges to the origin gradually, the amplitude of the control becomes smaller and smaller. Thus, the convergence rate of the closed-loop system is very slow. To solve this problem, we proposed the gain scheduling method to improve the dynamic performance of the closed-loop system. Moreover, by the designed discrete gain scheduling controller, we can use a series of nesting ellipsoid invariant sets to increase the disturbance performance as strong as possible. It means that the innermost invariant ellipsoid set needs to be minimized to strengthen the disturbance attenuation ability. The existence conditions for the admissible controllers are formulated as LMIs, and the controller can be computed by solving an optimization problem with the linear matrix inequality (LMI) constraints. Finally, the simulation results will be used to verify the effectiveness of the proposed approach.

The rest of the paper is organized as follows. Section 2 formulates the control problem. In Sect. 3, the reliable robust discrete gain scheduling controller is designed to solve the problem. A numerical simulation is given in Sect. 4. Section 5 concludes the paper.

Notation Throughout the paper, the notation used is fairly standard. \(A^{\mathrm {T}}\) denotes the transpose of matrix A and \(\mathrm {I} \left[ p,q\right] \) denotes the sets of integers \([p,p+1,\ldots ,q]\). Let \(\mathrm {diag}\{\ldots \}\) stand for a block-diagonal matrix; I refer to the identity matrix with compatible dimensions and \(\left\| \cdot \right\| \) denote the \(2-\) norm. The function \(\mathrm {sign}\) is defined as \(\mathrm {sign}(y)=1\) if \(y\ge 0\) and \(\mathrm {sign}(y)=-1\) if \(y<0\). The saturation function \(\mathrm {sat}:{R}^{m}\rightarrow {R}^{m}\) is a vector-valued standard saturation function,

$$\begin{aligned} \mathrm {sat}(u)=\left[ \begin{array}{cccc} \mathrm {sat}(u_{1})&\mathrm {sat}(u_{2})&\cdots&\mathrm {sat}(u_{m}) \end{array} \right] ^{\mathrm {T}}, \end{aligned}$$

and \(\mathrm {sat}(u_{i})=\mathrm {sign}(u_{i})\min \left\{ 1,\left| u_{i}\right| \right\} ,i\in 1,2,\ldots ,m.\) Here, we have slightly abused the notation by using \(\mathrm {sat}\left( \cdot \right) \) to denote both the scalar- and vector-valued functions.

2 System Description and Problem Formulation

Consider the system

$$\begin{aligned} \dot{x}=\left( A+{\Delta } A\right) x+B\mathrm {sat}\left( u\right) +B_{\omega }\omega , \end{aligned}$$
(1)

where \(x\in {R}^{n},u\in {R}^{m}\) and \(\omega \in {R}^{l}\) denote the state, the control input and the external disturbance, respectively. The matrix \({\Delta } A=MFE\) with \(F^{\mathrm {T}}F\le I\) and the matrices \(A, B, M, E, B_{\omega }\) are real constant matrices with appropriate dimensions. Assuming that the external disturbance \(\omega \) always belongs to the set W defined as

$$\begin{aligned} W=\left\{ \omega \in {R}^{l}\left| \omega ^{\mathrm {T}}\omega \le \omega _{0},\omega _{0}>0\right. \right\} . \end{aligned}$$
(2)

We have assumed in (1), without loss of generality, the unity saturation level. Non-unity saturation level can be absorbed by the matrix B and the feedback gain.

Considering the actuator failures, the controller can be described as

$$\begin{aligned} u={\varLambda } Kx, \end{aligned}$$
(3)

where

$$\begin{aligned} {\varLambda } =\mathrm {diag}\left\{ {\varLambda }_{1},{\varLambda } _{2},\ldots ,{\varLambda }_{m}\right\} , \end{aligned}$$
(4)

with \(0\le {\varLambda }_{li}\le {\varLambda }_{i}\le {\varLambda }_{ui}<\infty ,i\in \mathrm {I}\left[ 1,m\right] \) and the designed feedback gain is

$$\begin{aligned} K=\varsigma {\varLambda }_{0}^{-1}HP^{-1}, \end{aligned}$$
(5)

where \(H\in {R}^{m\times n} \) and \(P\in {R}^{n\times n}\). We denote \({\varLambda }_{i}\) as the possible failure of the i-th actuator. For instance, \({\varLambda }_{li}={\varLambda }_{ui}=1\) implies that there is no fault in the it-h actuator and \({\varLambda }_{li}={\varLambda } _{ui}=0\) denotes the i-th actuator is invalid completely. Furthermore, \(0<{\varLambda }_{li}< {\varLambda }_{ui}\) and \({\varLambda }_{i}\ne 0\) denote the partial failure of the \(i-\)th actuator.

With above parameters, we define the following matrices

$$\begin{aligned} {\varLambda }_{0}= & {} \mathrm {diag}\left\{ {\varLambda }_{01},{\varLambda }_{02},\ldots ,{\varLambda }_{0m}\right\} , \end{aligned}$$
(6)
$$\begin{aligned} S= & {} \mathrm {diag}\left\{ s_{1},s_{2},\ldots ,s_{m}\right\} , \end{aligned}$$
(7)

and

$$\begin{aligned} R=\mathrm {diag}\left\{ r_{1},r_{2},\ldots ,r _{m}\right\} , \end{aligned}$$
(8)

where

$$\begin{aligned} {\varLambda }_{0i}= & {} \frac{{\varLambda }_{li}+{\varLambda }_{ui}}{2}>0, i\in \mathrm {I}\left[ 1,m \right] , \end{aligned}$$
(9)
$$\begin{aligned} s_{i}= & {} \frac{{\varLambda }_{ui}-{\varLambda }_{li}}{{\varLambda }_{ui}+{\varLambda }_{li}}, i\in \mathrm {I}\left[ 1,m \right] , \end{aligned}$$
(10)

and

$$\begin{aligned} r_{i}=\frac{{\varLambda }_{i}-{\varLambda }_{0i}}{{\varLambda }_{0i}},i\in \mathrm {I}\left[ 1,m \right] . \end{aligned}$$
(11)

Proposition 1

According to the matrices defined above, we have

$$\begin{aligned} {\varLambda } ={\varLambda }_{0}\left( I+R\right) . \end{aligned}$$
(12)

Proof

According to (11), we have

$$\begin{aligned} r_{i}{\varLambda }_{0i}+{\varLambda }_{0i}={\varLambda }_{i}. \end{aligned}$$

In view of the diagonal matrices \({\varLambda }\), \({\varLambda }_{0}\) and R, obviously, we can get

$$\begin{aligned} {\varLambda } ={\varLambda }_{0}\left( I+R\right) . \end{aligned}$$

The proof is finished. \(\square \)

Similarly, we have the following proposition.

Proposition 2

The matrices R and S defined in (7) and (8) satisfy

$$\begin{aligned} \left( I+R\right) ^{\mathrm {T}}\left( I+R\right) \le \left( I+S\right) ^{\mathrm {T}}\left( I+S\right) \end{aligned}$$
(13)

and

$$\begin{aligned} R^{\mathrm {T}}R \le S^{\mathrm {T}}S\le I. \end{aligned}$$
(14)

The lemmas will be used in the following.

Lemma 1

[5] Let E, F and M be matrices of appropriate dimensions with \(\left\| F\right\| \le 1\). Then for any scaler \(\delta >0\), there holds

$$\begin{aligned} EFM+M^{\mathrm {T}}F^{\mathrm {T}}E^{\mathrm {T}}\le \delta ^{-1}EE^{\mathrm {T}}+\delta M^{\mathrm {T}}M. \end{aligned}$$

Lemma 2

[5] For a time-varying diagonal matrix \({\varPsi } \left( t\right) =\mathrm {diag}\left\{ \varphi _{1}\left( t\right) ,\varphi _{2}\left( t\right) ,\ldots ,\varphi _{m}\left( t\right) \right\} \) and two matrices R and S with appropriate dimensions, if \(\left| {\varPsi } \left( t\right) \right| \le V\), where V is a known diagonal matrix, then for any scalar \(\delta >0\), there holds

$$\begin{aligned} R{\varPsi } \left( t\right) S+S^{\mathrm {T}}{\varPsi }^{\mathrm {T}} \left( t\right) R^{\mathrm {T}}\le \delta RVR^{\mathrm {T}}+\delta ^{-1}S^{\mathrm {T}}VS. \end{aligned}$$

Lemma 3

[5] (Schur complement lemma) Let the partitioned matrix

$$\begin{aligned} A=\left[ \begin{array}{cc} A_{11} &{} A_{12} \\ A_{12}^{\mathrm {T}} &{} A_{22} \end{array} \right] \end{aligned}$$

be symmetric. Then \(A<0\) if and only if

$$\begin{aligned} A_{11}<0,S_{ch}\left( A_{11}\right) =A_{22}-A_{12}^{\mathrm {T}}A_{11}^{-1}A_{12}<0, \end{aligned}$$

or

$$\begin{aligned} A_{22}<0,S_{ch}\left( A_{22}\right) =A_{11}-A_{12}A_{22}^{-1}A_{12}^{\mathrm {T}}<0. \end{aligned}$$

We define the following several ellipsoidal sets \(\mathscr {E}_i,i\in \mathrm {I}[0,N]\), for \(\varsigma _{i}>0\)

$$\begin{aligned} \mathscr {E}_i=\left\{ x\in {R}^{n}:\varsigma _{i} x^{\mathrm {T}}P^{-1}_{i}x\le 1,P^{-1}_{i}>0\right\} , i\in \mathrm {I}[0,N], \end{aligned}$$
(15)

with

$$\begin{aligned} \varsigma _{j-1}P_{j-1}^{-1}-\varsigma _{j}P_{j}^{-1}<0,j\in \mathrm {I}[1,N]. \end{aligned}$$
(16)

The formula (16) indicates that the ellipsoids \(\mathscr {E}_{i}\) are nested, that is

$$\begin{aligned} \mathscr {E}_{N}\subset \mathscr {E}_{N-1}\subset \cdots \subset \mathscr {E}_{0}. \end{aligned}$$
(17)

The parameter \(\varsigma \) increases as follows

$$\begin{aligned} \varsigma _{j} =\varsigma _{0}+\frac{j}{N}\left( \varsigma _{N}-\varsigma _{0}\right) ,\;j\in \mathrm {I}\left[ 1,N\right] , \end{aligned}$$
(18)

and \(\varsigma _{0}\) can be computed by solving the following nonlinear equation

$$\begin{aligned} \varsigma _{0}x_{0}^{\mathrm {T}}P_{0}^{-1} x_{0}=1. \end{aligned}$$
(19)

Problem 1

Consider the input saturated system (1), design a reliable robust gain scheduled controller u based on the sets \(\mathscr {E}_i,i\in \mathrm {I}[0,N]\), such that, for \(\omega \in W\), every trajectory enters and remains in a as small as possible bounded set \(\mathscr {E}_{N}\) after some finite time.

Moreover, the proposed controller should satisfy the following requirements

  1. S1

    The relationship (17) must be satisfied;

  2. S2

    Removing the actuator fault;

  3. S3

    Guaranteeing the control input without saturation;

  4. S4

    A satisfactory dynamic performance;

  5. S5

    Strengthening the disturbance attenuation ability as strong as possible.

3 Main Results

Theorem 1

Consider the input saturated system (1). Let \(\delta _{1}>0\), \(\varepsilon _{1}>0 \) and \(\varsigma _{i}>0,i\in \mathrm {I}[0,N]\) be given. If there exist positive definite matrices \(P_{i}\in {R}^{n\times n}\) and matrices \(H_{i}\in {R}^{m\times n}\), that satisfy the matrix inequalities (16),

$$\begin{aligned} \left[ \begin{array}{cc} -\frac{1}{\varsigma _{i} }P_{i} &{} H_{i}^{\mathrm {T}}\left( I+S\right) ^{\mathrm {T}}\\ *&{} -I \end{array} \right] \le 0, \end{aligned}$$
(20)

and

$$\begin{aligned} {\varTheta } =\left[ \begin{array}{cc} {\varTheta }_{11}&\left[ \begin{array}{ccc} P_{i}E^{\mathrm {T}} &{} H_{i}^{\mathrm {T}}&{} B \end{array} \right] \\ *&{} {\varTheta }_{22} \end{array} \right] <0, \end{aligned}$$
(21)

where

$$\begin{aligned} {\varTheta }_{11}=A P_{i}+P_{i}A^{\mathrm {T}}+\delta _{1}MM^{\mathrm {T}}+\varsigma _{i}BH_{i}+\varsigma _{i}\left( BH_{i}\right) ^{\mathrm {T}}+\varsigma _{i}\omega _{0}P_{i}+B_{\omega }B_{\omega } ^{\mathrm {T}} \end{aligned}$$
(22)

and

$$\begin{aligned} {\varTheta }_{22} =\mathrm {diag}\left\{ -\delta _{1}I,-\frac{\varepsilon _{1}}{\varsigma _{i}}S^{-1},-\frac{1}{\varsigma _{i}\varepsilon _{1}}S^{-1}\right\} . \end{aligned}$$
(23)

Then the controller

$$\begin{aligned} u=\left\{ \begin{array}{c} u_{j-1}={\varLambda } K_{j-1}x,x\in \mathscr {C}_{j-1},j\in \mathrm {I}\left[ 1,N\right] , \\ u_{N}={\varLambda } K_{N}x,x\in \mathscr {E}_{N}, \end{array} \right. \end{aligned}$$
(24)

solves Problem 1, where \(K_{j-1}=\varsigma _{j-1}{\varLambda }_{0}^{-1}H_{j-1}P_{j-1}^{-1},K_{N}=\varsigma _{N}{\varLambda }_{0}^{-1}H_{N}P_{N}^{-1},\mathscr {C}_{j-1}=\mathscr {E}_{j-1}/\mathscr {E}_{j}\).

Proof

Define the following set

$$\begin{aligned} \mathscr {L}_{i} =\left\{ x\in {R}^{n}:\left\| {\varLambda } K_{i}x\right\| \le 1\right\} ,i\in \mathrm {I}[0,N], \end{aligned}$$
(25)

which indicates that the control input will not be saturated when \(x\in \mathscr {L}_{i}\). In view of Propositions 1 and 2, for any \(x \in \mathscr {E}_{i}\), we have

$$\begin{aligned} \left\| {\varLambda } K_{i}x\right\| ^{2}= & {} \left\| \varsigma _{i} \left( I+R\right) H_{i}P_{i}^{-1}x\right\| ^{2} \\\le & {} \varsigma _{i}^{2}x^{\mathrm {T}}P_{i}^{-1}H_{i}^{\mathrm {T}}\left( I+R\right) ^{\mathrm {T}}\left( I+R\right) H_{i}P_{i}^{-1}x \\\le & {} \varsigma _{i}^{2}x^{\mathrm {T}}P_{i}^{-1}H_{i}^{\mathrm {T}}\left( I+S\right) ^{\mathrm {T}}\left( I+S\right) H_{i}P_{i}^{-1}x \\= & {} \varsigma _{i} x^{\mathrm {T}}\widetilde{P}_{i}x, \end{aligned}$$

where \(\widetilde{P}_{i}=\varsigma _{i} P_{i}^{-1}H_{i}^{\mathrm {T}}\left( I+S\right) ^{\mathrm {T}}\left( I+S\right) H_{i}P_{i}^{-1}.\)

If \(\widetilde{P}_{i}\le P_{i}^{-1}\), then

$$\begin{aligned} \mathscr {E}_{i}\subseteq \mathscr {L}_{i}, \end{aligned}$$
(26)

which indicates that for any \(x\in \mathscr {E}_{i},\) the control input will not be saturated, that is

$$\begin{aligned} \mathrm {sat}(u)=u. \end{aligned}$$
(27)

According to Lemma 3 \(\widetilde{P}_{i}\le P_{i}^{-1}\) can be rewritten as

$$\begin{aligned} \left[ \begin{array}{cc} -\frac{1}{\varsigma _{i} }P_{i} &{} H_{i}^{\mathrm {T}}\left( I+S\right) ^{\mathrm {T}}\\ *&{} -I \end{array} \right] \le 0, \end{aligned}$$

which guarantees the requirement S3.

When \(x\in \mathscr {C}_{j-1}\), we have \(u=u_{j-1},j \in \mathrm {I}[1,N]\) and the closed-loop system is

$$\begin{aligned} \dot{x}=\left( A+{\Delta } A\right) x+B\mathrm {sat}\left( u_{j-1}\right) +B_{\omega }\omega . \end{aligned}$$
(28)

Considering the following Lyapunov function

$$\begin{aligned} V_{j-1}\left( x\right) =x^{\mathrm {T}}P^{-1}_{j-1}x. \end{aligned}$$
(29)

For any \(x\in \mathscr {C}_{j-1},\) the time-derivative of \(V_{j-1}\left( x\right) \) along the state trajectories of system (28) can be described as

$$\begin{aligned} \dot{V}_{j-1}\left( x\right)= & {} 2\dot{x}^{\mathrm {T}}P_{j-1}^{-1}x \\= & {} 2\left( \left( A+{\Delta } A\right) x+B\mathrm {sat}\left( u_{j-1}\right) +B_{\omega }\omega \right) ^{\mathrm {T}}P_{j-1}^{-1}x, \end{aligned}$$

in view of (26) and (27), we have

$$\begin{aligned} \dot{V}_{j-1}\left( x\right)= & {} 2\left( \left( A+MFE\right) x+Bu_{j-1}+B_{\omega }\omega \right) ^{\mathrm {T}}P_{j-1}^{-1}x \\= & {} x^{\mathrm {T}}\left( P_{j-1}^{-1}A+A^{\mathrm {T}}P_{j-1}^{-1}+P_{j-1}^{-1}\left( MFE\right) +\left( MFE\right) ^{\mathrm {T}}P_{j-1}^{-1}\right) x \\&+2\left( B{\varLambda }_{0}\left( I+R\right) K_{j-1}x\right) ^{\mathrm {T}}P_{j-1}^{-1}x+2\omega ^{\mathrm {T}} B_{\omega }^{\mathrm {T}}P_{j-1}^{-1}x \\= & {} x^{\mathrm {T}}\left( P_{j-1}^{-1}A+A^{\mathrm {T}}P_{j-1}^{-1}+P_{j-1}^{-1}\left( MFE\right) +\left( MFE\right) ^{\mathrm {T}}P_{j-1}^{-1}\right) x \\&+\,x^{\mathrm {T}}\left( P_{j-1}^{-1}\left( B{\varLambda }_{0}K_{j-1}\right) +\left( B{\varLambda }_{0}K_{j-1}\right) ^{\mathrm {T}}P_{j-1}^{-1}\right) x \\&+\,x^{\mathrm {T}}\left( P_{j-1}^{-1}\left( B{\varLambda }_{0}RK_{j-1}\right) +\left( B{\varLambda }_{0}RK_{j-1}\right) ^{\mathrm {T}}P_{j-1}^{-1}\right) x+2\omega ^{\mathrm {T}} B_{\omega }^{\mathrm {T}}P_{j-1}^{-1}x. \end{aligned}$$

In view of Lemmas 1, 2 and 3 and the fact \({\varLambda }_{0}R=R{\varLambda }_{0}\), we can obtain

$$\begin{aligned}&\dot{V}_{j-1}\left( x\right) \le x^{\mathrm {T}}\left( P_{j-1}^{-1}A+A^{\mathrm {T}}P_{j-1}^{-1}+\delta _{1}P_{j-1}^{-1}MM^{\mathrm {T}}P_{j-1}^{-1}+\delta _{1}^{-1}E^{\mathrm {T}}E+\right. \\&\qquad \varsigma _{j-1}P_{j-1}^{-1}BH_{j-1}P_{j-1}^{-1}+\varsigma _{j-1}P_{j-1}^{-1}\left( BH_{j-1}\right) ^{\mathrm {T}}P_{j-1}^{-1}+P_{j-1}^{-1}\left( BR{\varLambda }_{0}K_{j-1}\right) \\&\qquad \left. +\left( BR{\varLambda }_{0}K_{j-1}\right) ^{\mathrm {T}}P_{j-1}^{-1}\right) x+\omega \omega ^{\mathrm {T}}+x^{\mathrm {T}}P_{j-1}^{-1}B_{\omega }B_{\omega }^{\mathrm {T}}P_{j-1}^{-1}x \\&\quad \le x^{\mathrm {T}}\left( P_{j-1}^{-1}A+A^{\mathrm {T}}P_{j-1}^{-1}+\delta _{1}P_{j-1}^{-1}MM^{\mathrm {T}}P_{j-1}^{-1}+\delta _{1}^{-1}E^{\mathrm {T}}E+\right. \\&\qquad \varsigma _{j-1}P_{j-1}^{-1}BH_{j-1}P_{j-1}^{-1}{+}\varsigma _{j-1}P_{j-1}^{-1}\left( BH_{j-1}\right) ^{\mathrm {T}}P_{j-1}^{-1}{+}\varsigma _{j-1}\varepsilon _{1}x^{\mathrm {T}}P_{j-1}^{-1}BSB^{\mathrm {T}}P_{j-1}^{-1} \\&\qquad \left. +\varsigma _{j-1}\varepsilon _{1}^{-1}P_{j-1}^{-1}H_{j-1}^{\mathrm {T}}SH_{j-1}P_{j-1}^{-1}\right) x+\omega \omega ^{\mathrm {T}}+x^{\mathrm {T}}P_{j-1}^{-1}B_{\omega }B_{\omega }^{\mathrm {T}}P_{j-1}^{-1}x \\&\quad \le x^{\mathrm {T}}{\varSigma } x+\omega _{0}-\omega _{0}\varsigma _{j-1}x^{\mathrm {T}}P_{j-1}^{-1}x, \end{aligned}$$

where

$$\begin{aligned} {\varSigma }&=P_{j-1}^{-1}A+A^{\mathrm {T}}P_{j-1}^{-1}+\delta _{1}P_{j-1}^{-1}MM^{\mathrm {T}}P_{j-1}^{-1}+\varsigma _{j-1}P_{j-1}^{-1}BH_{j-1}P_{j-1}^{-1}\\ \nonumber&\quad +\varsigma _{j-1}P_{j-1}^{-1}\left( BH_{j-1}\right) ^{\mathrm {T}}P_{j-1}^{-1}+\varsigma _{j-1}\varepsilon _{1}x^{\mathrm {T}}P_{j-1}^{-1}BSB^{\mathrm {T}}P_{j-1}^{-1}+P_{j-1}^{-1}B_{\omega }B_{\omega }^{\mathrm {T}}P_{j-1}^{-1}\\ \nonumber&\quad +\delta _{1}^{-1}E^{\mathrm {T}}E+\varsigma _{j-1}\varepsilon _{1}^{-1}P_{j-1}^{-1}H_{j-1}^{\mathrm {T}}SH_{j-1}P_{j-1}^{-1}+\omega _{0}\varsigma _{j-1}P_{j-1}^{-1}. \end{aligned}$$

According to Lemma 3, we have

$$\begin{aligned} {\varSigma } =\left[ \begin{array}{cc} {\varSigma }_{11}&\left[ \begin{array}{ccc} E^{\mathrm {T}}&{} P_{j-1}^{-1}H_{j-1}^{\mathrm {T}}&{} P_{j-1}^{-1}B \end{array} \right] \\ *&{} {\varSigma }_{22} \end{array} \right] , \end{aligned}$$
(30)

where

$$\begin{aligned} {\varSigma }_{11}&=P_{j-1}^{-1}A+A^{\mathrm {T}}P_{j-1}^{-1}+\delta _{1}P_{j-1}^{-1}MM^{\mathrm {T}}P_{j-1}^{-1}+\varsigma _{j-1}P_{j-1}^{-1}BH_{j-1}P_{j-1}^{-1} \nonumber \\&+\varsigma _{j-1}P_{j-1}^{-1}\left( BH_{j-1}\right) ^{\mathrm {T}}P_{j-1}^{-1} \nonumber \\&+P_{j-1}^{-1}B_{\omega }B_{\omega }^{\mathrm {T}}P_{j-1}^{-1}+\omega _{0}\varsigma _{j-1}P_{j-1}^{-1}, \end{aligned}$$
(31)

and

$$\begin{aligned} {\varSigma }_{22}=\mathrm {diag}\left\{ -\delta _{1}I,-\frac{\varepsilon _{1}}{\varsigma _{j-1}}S^{-1},-\frac{1}{\varsigma _{j-1}\varepsilon _{1}}S^{-1}\right\} . \end{aligned}$$
(32)

Then, by pre- and post-multiplying \( T =\mathrm {diag}\left\{ P_{j-1},I\right\} \) and \(T^{\mathrm {T}}\) on both sides of \({\varSigma }\), we can get

$$\begin{aligned} {\varTheta }= & {} T{\varSigma } T^{\mathrm {T}} \\= & {} \left[ \begin{array}{cc} {\varTheta }_{11}&\left[ \begin{array}{ccc} P_{j-1}E^{\mathrm {T}} &{} H_{j-1}^{\mathrm {T}} &{} B \end{array} \right] \\ *&{} {\varTheta }_{22} \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} {\varTheta }_{11}&=AP_{j-1}+P_{j-1}A^{\mathrm {T}}+\delta _{1}MM^{\mathrm {T}}+\varsigma _{j-1}BH_{j-1}+\varsigma _{j-1}\left( BH_{j-1}\right) ^{\mathrm {T}} \\&+\varsigma _{j-1}\omega _{0}P_{j-1}+B_{\omega }B_{\omega }^{\mathrm {T}} \end{aligned}$$

and

$$\begin{aligned} {\varTheta }_{22} =\mathrm {diag}\left\{ -\delta _{1}I,-\frac{\varepsilon _{1}}{\varsigma _{j-1}}S^{-1},-\frac{1}{\varsigma _{j-1}\varepsilon _{1}}S^{-1}\right\} . \end{aligned}$$

According to (21), we have

$$\begin{aligned} {\varTheta }<0. \end{aligned}$$

When the state is on the boundary of \(\mathscr {E}_{j-1}\), we have the following equation

$$\begin{aligned} \varsigma _{j-1}x^{\mathrm {T}}P_{j-1}^{-1}x=1. \end{aligned}$$

Hence, we have

$$\begin{aligned} \dot{V}_{j-1}\left( x\right)&< \omega _{0}-\omega _{0}\varsigma _{j-1}x^\mathrm {T}P_{j-1}^{-1}x \\&=\omega _{0}-\omega _{0} \\&= 0, \end{aligned}$$

which denotes that \(\mathscr {E}_{j-1}\) is a strictly invariant set.

Fig. 1
figure 1

State trajectories of the closed-loop system with \(N=4\) and \(N=0\)

Full size image
Fig. 2
figure 2

Control input with \(N=4\) and \(N=0\)

Full size image
Fig. 3
figure 3

State trajectories, Case 1 denotes the control method in Theorem 1 with Algorithm 1 , Case 2 denotes the control method in Theorem 1 without Algorithm 1

Full size image

When \(x\in \mathscr {E}_{N}\), we have \(u={\varLambda } K_{N}x\) and the closed-loop system becomes

$$\begin{aligned} \dot{x}=\left( A+{\Delta } A\right) x+B\mathrm {sat}\left( {\varLambda } K_{N}x\right) +B_{\omega }\omega ,\; \forall x\in \mathscr {E}_{N}. \end{aligned}$$
(33)

Similarly to the case of \(x\in \mathscr {E}_{j-1}, j\in \mathrm {I}[1,N]\), the time-derivative of the Lyapunov function \( V_{N}\left( x\right) =x^{\mathrm {T}}P_{N}^{-1}x\) along the trajectories of system (33), we can get

$$\begin{aligned} \dot{V}_{N}\left( x\right) \le x^{\mathrm {T}}{\varTheta } x+\omega _{0}-\omega _{0}\varsigma _{N}x^\mathrm {T}P_{N}^{-1}x, \end{aligned}$$

where

$$\begin{aligned} {\varTheta }=\left[ \begin{array}{cc} {\varTheta }_{11}&\left[ \begin{array}{ccc} P_{N}E^{\mathrm {T}} &{} H_{N}^{\mathrm {T}}&{} B \end{array} \right] \\ *&{} {\varTheta }_{22} \end{array} \right] \end{aligned}$$

with \({\varTheta } _{11}=AP_{N}+P_{N}A^{\mathrm {T}}+\delta _{1}MM^{\mathrm {T}}+\varsigma _{N}BH_{N}+\varsigma _{N}\left( BH_{N}\right) ^{\mathrm {T}}+\varsigma _{N}\omega _{0}P_{N}+B_{\omega }B_{\omega } ^{\mathrm {T}}\) and

$$\begin{aligned} {\varTheta }_{22} =\mathrm {diag}\left\{ -\delta _{1}I,-\frac{\varepsilon _{1}}{\varsigma _{N}}S^{-1},-\frac{1}{\varsigma _{N}\varepsilon _{1}}S^{-1}\right\} . \end{aligned}$$

Observing that on the boundary of \(\mathscr {E}_{N}\), the following equation

$$\begin{aligned} \varsigma _{N}x^{\mathrm {T}}P_{N}^{-1}x=1 \end{aligned}$$

can be obtained. Thus, we have

$$\begin{aligned} \dot{V}_{N}\left( x\right)&<\omega _{0}-\omega _{0}\varsigma _{N}x^\mathrm {T}P_{N}^{-1}x \\&= 0. \end{aligned}$$

According to the LaSalle invariance principle [9], the state will eventually move to \(\mathscr {E}_{N}\) at finite time and stay in \(\mathscr {E}_{N}\) thereafter. The proof is finished.

Remark 1

It follows from Theorem 1 that \(\varsigma \) becomes larger and larger during the state convergence of the closed-loop system. The larger \(\varsigma \) can lead to a larger norm of the feedback gain \(K=\varsigma {\varLambda }_{0}^{-1}HP^{-1}\), which can increase the control force and improve the dynamic performance of the closed-loop system. Therefore, the requirement S4 is satisfied. The main aim of this paper is improving the dynamic performance of the closed-loop system. However, the cost of using controller (24) is not considered which we will study in the future.

In order to meet the requirement S5, the size of the set \(\mathscr {E}_{N}\) needs to be minimized. Summarizing above analysis, we have the following algorithm.

Algorithm 1

$$\begin{aligned} \underset{P_{N}>0,H_{N},G>0,\delta _{1}>0,\varepsilon _{1}>0,\varsigma _{N}>0 }{\min }\mu \end{aligned}$$

subject to

$$\begin{aligned}&\left[ \begin{array}{cc} -\frac{1}{\varsigma _{N} }P_{N} &{} H_{N}^{\mathrm {T}}\left( I+S\right) ^{\mathrm {T}}\\ *&{} -I \end{array} \right] \le 0, \\&\quad {\varTheta } =\left[ \begin{array}{cc} {\varTheta }_{11}&\left[ \begin{array}{ccc} P_{N}E^{\mathrm {T}} &{} H_{N}^{\mathrm {T}}&{} B \end{array} \right] \\ *&{} {\varTheta }_{22} \end{array} \right] <0 \end{aligned}$$

and

$$\begin{aligned} \mu G^{-1}-\frac{1}{\varsigma _{N}}P_{N}\ge 0, \end{aligned}$$
(34)

(34) guarantees \(\mathscr {E}_{N}\subset \mu \mathscr {G}\) where

$$\begin{aligned} {\varTheta }_{11}= & {} A P_{N}+P_{N}A^{\mathrm {T}}+\delta _{1}MM^{\mathrm {T}}+\varsigma _{N}BH_{N}+\varsigma _{N}\left( BH_{N}\right) ^{\mathrm {T}} \nonumber \\&+\varsigma _{N}\omega _{0}P_{N}+B_{\omega }B_{\omega }^{\mathrm {T}}, \end{aligned}$$
(35)
$$\begin{aligned} {\varTheta }_{22}=\mathrm {diag}\left\{ -\delta _{1}I,-\frac{\varepsilon _{1}}{\varsigma _{N}}S^{-1},-\frac{1}{\varsigma _{N}\varepsilon _{1}}S^{-1}\right\} \end{aligned}$$

and

$$\begin{aligned} \mathscr {G}=\left\{ x\in {R}^{n}\left| x^{\mathrm {T}}G x\le 1,G>0\right. \right\} . \end{aligned}$$

4 Numerical Simulations

In this section, we will give two examples to illustrate the effectiveness of the proposed method in Theorem 1 by considering Algorithm 1.

4.1 Example 1

The system is described by (1) with

$$\begin{aligned} A= & {} \left[ \begin{array}{cc} 0 &{} 1 \\ -2 &{} -3 \end{array} \right] ,B=\left[ \begin{array}{c} 1 \\ 0.5 \end{array} \right] ,B_{w}=\left[ \begin{array}{c} 0.5 \\ 0.2 \end{array} \right] , \\ M= & {} \left[ \begin{array}{cc} 0 &{} 0.1 \\ 1 &{} 0.3 \end{array} \right] ,F=0.1,E=\left[ \begin{array}{cc} 1 &{} 0.1 \\ 0.2 &{} 0.5 \end{array} \right] , \\ \omega= & {} 0.1,{\varLambda }_{li}=0.01,{\varLambda }_{ui}=1,{\varLambda }_{i}=0.5. \end{aligned}$$

Let \(N=4\), \(i\in \mathrm {I}[0,4]\), \(\delta _{1}=0.2\), \(\varepsilon _{1}=0.1\),

$$\begin{aligned} G=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array} \right] . \end{aligned}$$

The initial state of the system is

$$\begin{aligned} x\left( 0\right) =\left[ \begin{array}{c} -0.1 \\ -0.2 \end{array} \right] . \end{aligned}$$

With these parameters, by solving the LMIs, we can get the following designed feedback gains:

$$\begin{aligned} K_{0}= & {} \left[ \begin{array}{cc} -10.0160&-2.6902 \end{array} \right] , \\ K_{1}= & {} \left[ \begin{array}{cc} -11.6393&-2.7656 \end{array} \right] , \\ K_{2}= & {} \left[ \begin{array}{cc} -12.3872&-2.8174 \end{array} \right] , \\ K_{3}= & {} \left[ \begin{array}{cc} -13.0095&-2.8148 \end{array} \right] , \\ K_{4}= & {} \left[ \begin{array}{cc} -13.5884&-2.8118 \end{array} \right] . \end{aligned}$$

The norms of the gains are respectively

$$\begin{aligned} \left\| K_{0}\right\|= & {} 10.3710, \\ \left\| K_{1}\right\|= & {} 11.9634, \\ \left\| K_{2}\right\|= & {} 12.7036, \\ \left\| K_{3}\right\|= & {} 13.3105, \\ \left\| K_{4}\right\|= & {} 13.8763. \end{aligned}$$

Therefore, the larger value of \(\varsigma \) will lead to a larger norm of the feedback gain \(K=\varsigma {\varLambda }_{0}^{-1}HP^{-1}\), which increases the control force and improves the dynamic performance of the closed-loop system.

Fig. 4
figure 4

Relative positions in the X-axis, Y-axis and Z-axis with \(N=4\) and \(N=0\)

Full size image
Fig. 5
figure 5

Relative velocities in the X-axis, Y-axis and Z-axis with \(N=4\) and \(N=0\)

Full size image
Fig. 6
figure 6

Control accelerations in the X-axis, Y-axis and Z-axis with \(N=4\) and \(N=0\)

Full size image
Fig. 7
figure 7

Relative positions, Case 1 denotes the possible failure of the \(i-\)th actuator \({\varLambda }_{i}=0.5\), Case 2 denotes \({\varLambda }_{i}=0.1\)

Full size image
Fig. 8
figure 8

Relative velocities, Case 1 denotes the possible failure of the \(i-\)th actuator \({\varLambda }_{i}=0.5\), Case 2 denotes \({\varLambda }_{i}=0.1\)

Full size image

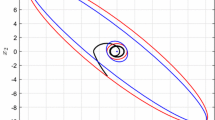
The state trajectories of the closed-loop system are plotted in Fig. 1. From Fig. 1, we can see that the state convergence time is about \(t=1\mathrm {s}\) by using the proposed gain scheduling method with \(N = 4\) which saves about \(1\mathrm {s}\) compared with the low gain feedback controller corresponding to \(N = 0\). From the control input curve recorded in Fig. 2, it can be seen that the control inputs do not exceed the maximal control inputs. Figure 3 illustrates that the proposed method with Algorithm 1 achieves a better disturbance attenuation performance.

4.2 Example 2

Considering the spacecraft rendezvous system [19] with

$$\begin{aligned} A=\left[ \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 3n^{2} &{} 0 &{} 0 &{} 0 &{} 2n &{} 0 \\ 0 &{} 0 &{} 0 &{} -2n &{} 0 &{} 0 \\ 0 &{} 0 &{} -n^{2} &{} 0 &{} 0 &{} 0 \end{array} \right] ,\text { }B=\left[ \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] , \end{aligned}$$
(36)
$$\begin{aligned} M=0.05\left[ \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] , E=0.02\left[ \begin{array}{cccccc} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \end{array} \right] , F=\left[ \begin{array}{ccc} 0.1 &{} 0 &{} 0 \\ 0 &{} 0.1 &{} 0 \\ 0 &{} 0 &{} 0.1 \end{array} \right] , \\ \end{aligned}$$
$$\begin{aligned} \omega = 0.1,{\varLambda }_{li}=0.01,{\varLambda }_{ui}=1,{\varLambda }_{i}=0.5. \end{aligned}$$
(37)

Supposing that the target spacecraft is on a geosynchronous orbit of radius \(R=42241\mathrm {km}\) with an orbital period of 24 hours. Thus, the angle velocity \(n=7.2722\times 10^{-5}\mathrm {rad/s}\) and the gravitational parameter \(\mu =3.986\times 10^{14}\mathrm {m^{3}/s^{2}}\). The initial state of the system is

$$\begin{aligned} x\left( 0\right) = \left[ \begin{array}{cccccc} 10&10&10&0.5&3&-1 \end{array} \right] ^{\mathrm {T}}. \end{aligned}$$

With these parameters, the positive definite matrices \(P_{i}, i\in \mathrm {I}[0,N]\) and the matrices \(H_{i}, i\in \mathrm {I}[0,N]\) can be computed accordingly. The resulting discrete gain scheduled controller can be constructed according to (24). For comparison purpose, the closed-loop system will also be simulated for \(N=0\) which corresponds to a low gain feedback controller. Let \(N=4\), \(i\in \mathrm {I}[0,4]\), \(\delta _{1}=0.2\), \(\varepsilon _{1}=0.1\).

From Figs. 4 and 5, we can see that the rendezvous mission is accomplished at about \(t_{\mathrm {f}}=100\mathrm {s}\) with \(N=4\) which saves about \(300\mathrm {s}\) comparing with \(N=0\). Figure 6 illustrates that the proposed controller not only makes better use of the actuator capacity, but also guarantees that the control inputs do not exceed the maximal control inputs provided by the thruster equipment. Figures 7 and 8 show that the rendezvous mission of the spacecraft can be finished in the two different cases. However, the rendezvous time would be longer and the disturbance attenuation ability would be degraded in the serious thruster failure case.

5 Conclusions

This paper has designed a reliable robust discrete gain scheduling controller for the systems with the input saturation, system uncertainty, external disturbance and actuator failures. The advantage of the proposed gain scheduling approach is that the convergence rate of the closed-loop system can be increased and the disturbance attenuation ability can also be strengthened. By the Lyapunov approach, the existence conditions for the admissible controllers are formulated as LMIs and the controller can be computed by solving an optimization problem with LMI constraints. The simulation results illustrate the effectiveness of the proposed method.