Abstract
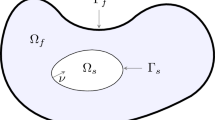
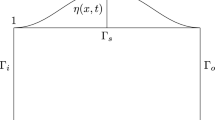
A coupled system of partial differential equations modeling the interaction of a fluid and a structure with delay in the feedback is studied. The model describes the dynamics of an elastic body immersed in a fluid that is contained in a vessel, whose boundary is made of a solid wall. The fluid component is modeled by the linearized Navier-Stokes equation, while the solid component is given by the wave equation neglecting transverse elastic force. Spectral properties and exponential or strong stability of the interaction model under appropriate conditions on the damping factor, delay factor and the delay parameter are established using a generalized Lax-Milgram method.
Similar content being viewed by others
References
Arendt W., Batty C.J.K.: Tauberian theorems and stability of one-parameter semigroups. Trans. Amer. Math. Soc. 360, 837–852 (1988)
Avalos G., Bucci F.: Rational rates of uniform decay for strong solutions to a fluid-structure PDE system. J. Differ. Equ. 258, 4398–4423 (2015)
Avalos G., Triggiani R.: The coupled PDE system arising in fluid-structure interaction, Part I: Explicit semigroup generator and its spectral properties. Contemp. Math. 440, 15–54 (2007)
Avalos G., Triggiani R.: Semigroup wellposedness in the energy space of a parabolic-hyperbolic coupled Stokes-Lamé PDE system of fluid-structure interaction. Discr. Cont. Dyn. Syst. 2, 417–447 (2009)
Avalos G., Triggiani R.: Rational decay rates for a PDE heat-structure interaction: a frequency domain approach. Evol. Equ. Control Theory 2, 233–253 (2013)
Avalos G., Triggiani R.: Fluid structure interaction with and without internal dissipation of the structure : A contrast study in stability. Evol. Equ. Control Theory 2, 563–598 (2013)
Avalos G., Lasiecka I., Trigianni R.: Higher regularity of a coupled parabolic-hyperbolic fluid structure interactive system. Georgian Math. J. 15, 403–437 (2008)
Barbu V., Grujić Z., Lasiecka I., Tuffaha A.: Existence of the energy-level weak solutions for a nonlinear fluid-structure interaction model. Contemp. Math. 440, 55–81 (2007)
Barbu V., Grujić Z., Lasiecka I., Tuffaha A.: Smoothness of weak solutions to a nonlinear fluid-structure interaction model. Indiana U. Math. J. 57, 1173–1207 (2008)
Datko R.: Not all feedback stabilized hyperbolic systems are robust with respect to small time delays in their feedback. SIAM J. Control Optim. 26, 697–713 (1988)
Datko R., Lagnese J., Polis P.: An example on the effect of time delays in boundary feedback stabilization of wave equations. SIAM J. Control Optim 24, 152–156 (1985)
Desch W., Fas̆angová E., Milota J., Propst G.: Stabilization through viscoelastic boundary damping: a semigroup approach. Semigroup Forum 80, 405–415 (2010)
Engel K.J., Nagel R.: One-Parameter Semigroups for Linear Evolution Equations, 2nd ed. Springer, Berlin (2000)
Du Q., Gunzburger M.D., Hou L.S., Lee J.: Analysis of a linear fluid-structure interaction problem. Discr. Contin. Dyn. Syst. 9, 633–650 (2003)
Horn R.A., Johnson C.R.: Matrix Analysis. Cambridge University Press, Cambridge (1985)
Kirane M., Said-Houari B.: Existence and asymptotic stability of a viscoelastic wave equation with delay. Z. Angew. Math. Phys. 62, 1065–1082 (2011)
LasieckaLu Y.: Asymptotic stability of finite energy in Navier Stokes-elastic wave interaction. Semigroup Forum 82, 61–82 (2011)
Lasiecka I., Lu Y.: Interface feedback control stabilization of a nonlinear fluid-structure interaction. Nonlinear Anal. 75, 1449–1460 (2012)
Lasiecka I., Seidman T.: Strong stability of elastic control systems with dissipative saturating feedback. Syst. Control Lett. 48, 243–252 (2013)
Lions J.L., Magenes E.: Non-Homogeneous Boundary Value Problems And Applications, Vol. 1. Springer, New York (1972)
Lyubich Y.I., Phong V.Q.: Asymptotic stability of linear differential equations in Banach spaces. Studia Matematica LXXXVII, 37–42 (1988)
Lu Y.: Stabilization of a fluid structure interaction with nonlinear damping. Control Cybern. 42, 155–181 (2013)
Lu Y.: Uniform decay rates for the energy in nonlinear fluid structure interaction with monotone viscous damping. Palest. J. Math. 2, 215–232 (2013)
Nicaise S., Pignotti C.: Stability and instability results of the wave equation with a delay term in boundary or internal feedbacks. SIAM J. Control Optim. 45, 1561–1585 (2006)
Peralta G., Propst G.: Stability and boundary controllability of a linearized model of flow in an elastic tube. ESAIM: Control Optim. Calc. Var. 21, 583–601 (2015)
Quarteroni A., Valli A.: Numerical Approximations of Partial Differential Equations. Springer, Heidelberg (2008)
Sohr H.: The Navier-Stokes Equations: An Elementary Functional Analytic Approach. Birkhäuser, Berlin (2001)
Temam R.: Navier-Stokes Equations, Theory and Numerical Analysis. AMS Chelsea Publishing, Providence (2001)
Tucsnak M., Weiss G.: Observation and Control for Operator Semigroups. Birkhäuser-Verlag, Basel (2009)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Peralta, G. A fluid–structure interaction model with interior damping and delay in the structure. Z. Angew. Math. Phys. 67, 10 (2016). https://doi.org/10.1007/s00033-015-0611-1
Received:
Revised:
Published:
DOI: https://doi.org/10.1007/s00033-015-0611-1