Skip to main content
SpringerLink
Log in

Reflection and Transmission Coefficients for an Incident Plane Shear Wave at an Interface Separating Two Dissimilar Poroelastic Solids

  • Published:
Pure and Applied Geophysics Aims and scope Submit manuscript

Abstract

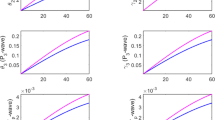
Using Biot’s poroelasticity theory, we derive expressions for the reflection and transmission coefficients for a plane shear wave incident on an interface separating two different poroelastic solids. The coefficients are formulated as a function of the wave incidence angle, frequency and rock properties. Specific cases calculated include the boundary between water-saturated sand and water-saturated sandstone and the gas–water interface in sand. The results show a very different interface response to that of an incident P wave. Plane SV wave incidence does not significantly excite the Biot slow P wave if the frequency of the wave is below the transition frequency. Above this frequency, an incident plane SV wave can generate a mode-converted slow Biot P wave which is actually a normal propagating wave and not highly attenuating as in the usual (diffusive) case. For an incident SV wave onto a gas–water interface, even at very high frequency, there is no significant Biot second P wave produced. For small incident angles, the gas–water interface is essentially transparent. With increasing angles, there can arise an unusual "definitive angle" in the reflection/transmission coefficient curves which is related to the change of fluid viscosity on both sides of the interface and provides a possible new means for underground fluid assessment.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  • Aki, K. and Richards, P.G. (1980). Quantitative Seismology: Theory and Methods-Vols. I–II, W.H. Freeman, San Francisco.

  • Biot, M.A. (1956a). Theory of propagation of elastic waves in a fluid-saturated porous solid: I- low frequency range. Journal of the Acoustical Society of America, 28(2):168–178.

  • Biot, M.A. (1956b). Theory of propagation of elastic waves in a fluid-saturated porous solid: II-higher frequency range. Journal of the Acoustical Society of America, 28(2):179–191.

    Google Scholar 

  • Denneman, A.I.M., Drijkoningen, G.G., Smeulders, D.M. and Wapenaar, K. (2002). Reflection and transmission of waves at a fluid/porous-medium interface. Geophysics 67:282–291.

  • Deresiewicz, H. and Skalak, R. (1963). On uniqueness in dynamic poroelasticity. Bulletin of Seismological Society of America, 53:783–788.

  • Dutta, N.C. and Odé, H. (1979a). Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (White model)-Part I: Biot theory. Geophysics, 44(11):1777–1788.

    Google Scholar 

  • Dutta, N.C. and Odé, H. (1979b). Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (White model)-Part II: Results. Geophysics, 44(11):1789–1805.

  • Dutta, N.C. and Odé H. (1983). Seismic reflections from a gas-water contact. Geophysics 48(2):148–162.

    Google Scholar 

  • Gassmann, F. (1951). Über die elastizität poröser medien: Viertel. Nat rurforsch. Ges., Zurich 96:1–23.

    Google Scholar 

  • Geertsma, J. and Smit, D.C. (1961). Some aspects of elastic wave propagation in fluid-saturated porous solids. Geophysics, 26(2):169–181.

    Google Scholar 

  • Gurevich, B. and Schoenberg, M. (1999). Interface conditions for Biot’s equations of poroelasticity. Journal of the Acoustical Society of America, 105:2285–2589.

    Google Scholar 

  • Gurevich, B., Ciz, R: and Denneman, A.I.M. (2004). Simple expressions for normal incidence reflection coefficients from an interface between fluid-saturated porous materials. Geophysics 69:1372–1377.

    Google Scholar 

  • Johnson, D. L., Koplik, J. and Dashen, R. (1978). Theory of dynamic permeability and tortuosity in fluid-saturated porous media. Journal of Fluid Mechanics, 176:379–402.

    Google Scholar 

  • Pride, S.R., Berryman, J.G. and Harris, J.M. (2004). Seismic attenuation due to wave-induced flow. Journal of Geophysical Research, 109:B01201:1–19.

    Google Scholar 

  • Quiroga-Goode, G. and Carcione, J.M. (1997). Heterogeneous modelling behaviour at an interface in porous media. Computational Geosciences, 1:109–125.

  • Santos, J.E., Corbero, J.M., Ravazolli, C.L. and Hensley, J.L. (1992). Reflection and transmission coefficients in fluid-saturated porous media. Journal of the Acoustical Society of America, 91(4):1911–1923.

    Google Scholar 

  • Sharma, M.D., Kaushik, V.P. and Gogna, M.L. (1990). Reflection and refraction of plane waves at an interface between liquid-saturated porous solid and viscoelastic solid. The Quarterly Journal of Mechanics and Applied Mathematics, 43(4):427–448.

    Google Scholar 

  • Sharma, M.D. and Saini, T. (1992). Pore alignment between two dissimilar saturated poroelastic media: Reflection and refraction at the interface. Int. J. Solids Structures, 29(11):1361–1377.

    Google Scholar 

  • Sharma, M.D. (2008). Wave propagation across the boundary between two dissimilar poroelastic solids. Journal of Sound and Vibration, 314:657–671.

    Google Scholar 

  • Wu, K.Y., Xue, Q. and Adler, L. (1990). Reflection and transmission of elastic waves from a fluid-saturated porous solid boundary. Journal of the Acoustical Society of America, 87(6):2349–2358.

    Google Scholar 

  • Yang, J. (1999). Importance of flow condition on seismic waves at saturated porous solid boundary. Journal of Sound and Vibration, 221(3):391–413.

    Google Scholar 

Download references

Acknowledgments

This research was supported by grants from the Australian Research Council and the Swiss National Science Foundation. One of us (XL) also wishes especially to acknowledge the University of Adelaide and the Faculty of Sciences for providing him with a postgraduate research scholarship during his doctoral studies. We very much appreciate the constructive comments of an anonymous reviewer and the editor, Dr. Arthur Snoke, which have improved the clarity of the manuscript.

Author information

Authors and Affiliations

  1. Department of Geology and Geophysics, University of Adelaide, Adelaide, 5005, Australia

    Xu Liu

  2. Institute of Geophysics, ETH Zurich, Sonneggstrasse 5, 8092, Zurich, Switzerland

    Stewart Greenhalgh

Authors
  1. Xu Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stewart Greenhalgh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stewart Greenhalgh.

Appendices

Appendix A: Biot’s Complex Wavenumbers, Dynamic Permeability and Constitutive Equations

The complex wavenumber for the Biot shear wave is given by:

$$ k_{\text{s}}^{2} = \frac{{\omega^{2} }}{\mu }\left(\rho - \frac{{\rho_{\text{f}}^{2} }}{q(\omega )}\right) $$
(47)

where ω is frequency; \( \rho_{\text{f}} \) and ρ is the density of the fluid and the average density of the composite; μ is the shear modulus of the solid frame; \( q(\omega ) = {{i\eta } \mathord{\left/ {\vphantom {{i\eta } {\omega \kappa (\omega )}}} \right. \kern-0pt} {\omega \kappa (\omega )}} \) and η is dynamic viscosity (or viscosity) and κ(ω) is the dynamic permeability (see later in this section).

The Biot slow P wave and the classic P wave have wavenumbers:

$$ k_{\text{d}}^{2} = \omega^{2} \frac{{c_{1} \delta_{22} - c_{3} \delta_{12} }}{{c_{1} c_{4} - c_{2} c_{3} }} $$
(48)
$$ k_{\text{c}}^{2} = \omega^{2} \frac{{c_{2} \delta_{21} - c_{4} \delta_{12} }}{{c_{3} c_{2} - c_{1} c_{4} }} $$
(49)

where

$$ \left. \begin{gathered} \delta_{11} = \rho \delta_{\text{d}} + \rho_{\text{f}} \quad \quad \quad c_{1} = (\lambda_{\text{c}} + 2\mu )\delta_{\text{d}} + \alpha M \hfill \\ \delta_{12} = \rho \delta_{\text{c}} + \rho_{\text{f}} \quad \quad \quad c_{2} = (\lambda_{\text{c}} + 2\mu )\delta_{\text{c}} + \alpha M \hfill \\ \delta_{21} = \rho_{\text{f}} \delta_{\text{d}} + q(\omega )\quad \quad c_{3} = \alpha M\delta_{\text{d}} + M \hfill \\ \delta_{22} = \rho_{\text{f}} \delta_{\text{c}} + q(\omega )\quad \quad c_{4} = \alpha M\delta_{\text{c}} + M \hfill \\ \end{gathered} \right\} $$
(50)
$$ \delta_{\text{c}} = \frac{{ - B - \sqrt {B^{2} - 4AC} }}{2A}\;\;{\text{and}}\;\;\delta_{\text{d}} = \frac{{ - B + \sqrt {B^{2} - 4AC} }}{2A} $$
(51)
$$ \left. \begin{gathered} A = \rho \alpha M - \rho_{\text{f}} (\lambda_{\text{c}} + 2\mu ) \hfill \\ B = \rho M - q(\omega )(\lambda_{\text{c}} + 2\mu ) \hfill \\ C = - q(\omega )\alpha M + M\rho_{\text{f}} \hfill \\ \end{gathered} \right\} $$
(52)
$$ \lambda_{\text{c}} = K_{\text{m}} - {{2\mu } \mathord{\left/ {\vphantom {{2\mu } 3}} \right. \kern-0pt} 3} + \alpha^{2} M $$
(54)
$$ \alpha = 1 - \frac{{K_{\text{m}} }}{{K_{\text{s}} }} $$
(55)
$$ \frac{1}{M} = \frac{\alpha }{{K_{\text{s}} }} + \text{n}\left(\frac{1}{{K_{\text{f}} }} - \frac{1}{{K_{\text{s}} }}\right) $$
(56)

Here, K s, \( K_{\text{f}} \) and \( K_{\text{m}} \) are the bulk modulus of the solid grain, the pore fluid and the solid frame, respectively.

The dynamic permeability can be viewed as static permeability κ 0 multiplied by a frequency correction factor (Johnson et al. 1978),

$$ \kappa (\omega ) = \kappa_{0} \left[ {\sqrt {1 - i\frac{4\omega }{{n_{\text{J}} \omega_{t} }}} - i\frac{\omega }{{\omega_{t} }}} \right]^{ - 1} $$
(57)
$$ \omega_{\text{t}} \, = \,\eta /(\rho_{\text{f}} F\kappa_{0} ) $$
(58)

Here, κ 0 is permeability; ω t is called the transition frequency or relaxation frequency (Pride et al. 2004) which separates the viscous force-dominated flow from the inertial force-dominated flow. The quantity \( n_{\text{J}} = {{\varLambda^{2} } \mathord{\left/ {\vphantom {{\varLambda^{2} } {\kappa_{0} F}}} \right. \kern-0pt} {\kappa_{0} F}} \), where Λ represents the pore volume-to-surface ratio and has the dimensions of length. F is the electric formation factor and it can also be related to the tortuosity T and porosity n through the relation: \( F = Tn^{ - 1} \).

Biot’s constitutive equations can be written as

$$ \tau_{ij} = 2\mu {\kern 1pt} e_{ij} + \delta_{ij} (\lambda_{c} e - \alpha M\zeta ) $$
(59)
$$ p_{f} = - \alpha Me + M\zeta $$
(60)

Here, \( \tau_{ij} \) = total stress in the medium (including the porous solid frame and the fluid filling the pores); p f = fluid pressure in the pores; e = div u; ζ = −div w;

$$ e_{ij} = \frac{1}{2} \left(\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}\right), $$
(61)

and

\( \delta_{ij} \) is the Kronecker delta symbol.

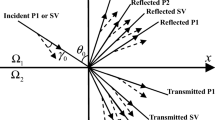
Appendix B: The Reflection and Transmission Coefficients for an Incident SH Wave

Because SH waves are decoupled from P-SV waves in isotropic media, and incident SH waves do not mode-convert to P or to SV waves, the boundary conditions, Eqs. 8 and 9a, which are just related to the compressional properties, are not required. So there will only be three waves to consider: incident SH, reflected SH and transmitted SH.

The relative fluid displacement for the incident SH shear wave w sh, is written as:

$$ {\mathbf{w}}_{\text{sh}} = A_{\text{sh}} \exp (il_{{1{\text{s}}}} y)\exp (im_{{1{\text{s}}}} x - i\omega {\kern 1pt} t){\hat{\mathbf{z}}} $$
(61)

Let w 1s be the reflected wave in medium 1, given by:

$$ {\mathbf{w}}_{{1{\text{s}}}} = B_{{1{\text{s}}}} \exp ( - il_{{1{\text{s}}}} y)\exp (im_{{1{\text{s}}}} x - i\omega {\kern 1pt} t){\hat{\mathbf{z}}} $$
(62)

Let w 2s be the transmitted waves in medium 2, given by:

$$ {\mathbf{w}}_{{2{\text{s}}}} = A_{{2{\text{s}}}} \exp (il_{{2{\text{s}}}} y)\exp (im_{{2{\text{s}}}} x - i\omega {\kern 1pt} t){\hat{\mathbf{z}}} $$
(63)

where l js and m js, (j = 1, 2) denote, respectively, the x- and y-components of the complex wave vector k js of medium j (The waves propagate in the x–y plane). The total wavenumber is given by:

$$ (l_{\text{js}} )^{2} + (m_{\text{js}} )^{2} = (k_{\text{js}} )^{2} $$
(64)

From the continuity condition of the solid frame displacement, Eq. (6) and the linear relationship, Eq. (4), which are valid for all x and t, we have:

$$ m_{{1{\text{s}}}} = m_{{1{\text{s}}}} $$
(65)
$$ \varGamma_{{1{\text{s}}}} (A_{\text{sh}} + B_{{1{\text{s}}}} ) = \varGamma_{{2{\text{s}}}} (A_{{2{\text{s}}}} ) $$
(66)

By the continuity condition of the total traction, Eq. 7, we have:

$$ \mu_{1} l_{{1{\text{s}}}} \varGamma_{{1{\text{s}}}} (A_{\text{sh}} - B_{{1{\text{s}}}} ) = \mu_{2} l_{{2{\text{s}}}} \varGamma_{{2{\text{s}}}} A_{{2{\text{s}}}} $$
(67)

By Eqs. 66 and 67, we get the transmission ratio of the relative fluid displacement A 2s/A sh,

$$ \frac{{A_{2} }}{{A_{\text{sh}} }} = \frac{{2\mu_{1} l_{{1{\text{s}}}} \varGamma_{{1{\text{s}}}} }}{{\left( {\mu_{1} l_{{1{\text{s}}}} + \mu_{2} l_{{2{\text{s}}}} } \right)\varGamma_{{2{\text{s}}}} }} $$
(68)

and the reflection ratio of the relative fluid displacement B 1s/A sh,

$$ \frac{{B_{{1{\text{s}}}} }}{{A_{\text{sh}} }} = \frac{{\left( {\mu_{1} l_{{1{\text{s}}}} - \mu_{2} l_{{2{\text{s}}}} } \right)}}{{\left( {\mu_{1} l_{{1{\text{s}}}} + \mu_{2} l_{{2{\text{s}}}} } \right)}} $$
(69)

According to Eq. 69, if the physical parameters of the two media are the same, the reflection goes to zero. Then, by Eq. 4, the transmission coefficient of the solid frame displacement is:

$$ T_{\text{sh}} = \frac{{A_{{2{\text{s}}}} \varGamma_{{2{\text{s}}}} }}{{A_{\text{sh}} \varGamma_{{1{\text{s}}}} }} $$
(70)

The reflection coefficient of the solid frame displacement is:

$$ R_{\text{sh}} = \frac{{B_{{1{\text{s}}}} }}{{A_{\text{sh}} }} $$
(71)

Appendix C: The Coefficients of the Boundary Conditions

The elements a ij of matrix A appearing in Eq. 31 are obtained as follows:

(i) Setting u 1x  = u 2x

$$ \begin{gathered} a_{11} = 1,\quad a_{12} = - \frac{{\varGamma_{{1{\text{c}}}} m}}{{\varGamma_{{1{\text{s}}}} l_{{1{\text{s}}}} }},\quad a_{13} = - \frac{{\varGamma_{{1{\text{d}}}} m}}{{\varGamma_{{1{\text{s}}}} l_{{1{\text{s}}}} }}, \hfill \\ a_{14} = \frac{{\varGamma_{{2{\text{s}}}} l_{{2{\text{s}}}} }}{{\varGamma_{{1{\text{s}}}} l_{{1{\text{s}}}} }},\quad a_{15} = \frac{{\varGamma_{{2{\text{c}}}} m}}{{\varGamma_{{1{\text{s}}}} l_{{1{\text{s}}}} }},\quad a_{16} = \frac{{\varGamma_{{2{\text{d}}}} m}}{{\varGamma_{{1{\text{s}}}} l_{{1{\text{s}}}} }} \hfill \\ \end{gathered} $$

(ii) Setting u 1y  = u 2y

$$ \begin{gathered} a_{21} = - 1,\quad \;\;a_{22} = - \frac{{\varGamma_{{1{\text{c}}}} l_{{1{\text{c}}}} }}{{\varGamma_{{1{\text{s}}}} m}},\quad a_{23} = - \frac{{\varGamma_{{1{\text{d}}}} l_{{1{\text{d}}}} }}{{\varGamma_{{1{\text{s}}}} m}}, \hfill \\ a_{24} = \frac{{\varGamma_{{2{\text{s}}}} }}{{\varGamma_{{1{\text{s}}}} }},\quad a_{25} = - \frac{{\varGamma_{{2{\text{c}}}} l_{{2{\text{c}}}} }}{{\varGamma_{{1{\text{s}}}} m}},\quad a_{26} = - \frac{{\varGamma_{{2{\text{d}}}} l_{{2{\text{d}}}} }}{{\varGamma_{{1{\text{s}}}} m}} \hfill \\ \end{gathered} $$

(iii) Setting τ 1yy  = τ 2yy

$$ \begin{gathered} a_{31} = 1,\quad a_{34} = \frac{{\mu_{2} \varGamma_{{2{\text{s}}}} l_{{2{\text{s}}}} }}{{\mu_{1} \varGamma_{{1{\text{s}}}} l_{{1{\text{s}}}} }},\quad \quad \hfill \\ a_{32} = \frac{{\left[ {\varGamma_{{1{\text{c}}}} (\lambda_{{1{\text{c}}}} + 2\mu_{1} ) + \alpha_{1} M_{1} } \right](k_{{1{\text{c}}}} )^{2} - \varGamma_{{1{\text{c}}}} 2\mu_{1} m^{2} }}{{\varGamma_{{1{\text{s}}}} 2\mu_{1} ml_{{1{\text{s}}}} }}, \hfill \\ a_{33} = \frac{{\left[ {\varGamma_{{1{\text{d}}}} (\lambda_{{1{\text{c}}}} + 2\mu_{1} ) + \alpha_{1} M_{1} } \right](k_{{1{\text{d}}}} )^{2} - \varGamma_{{1{\text{d}}}} 2\mu_{1} m^{2} }}{{\varGamma_{{1{\text{s}}}} 2\mu_{1} ml_{{1{\text{s}}}} }}, \hfill \\ a_{35} = \frac{{\varGamma_{{2{\text{c}}}} 2\mu_{2} m^{2} - \left[ {\varGamma_{{2{\text{c}}}} (\lambda_{{2{\text{c}}}} + 2\mu_{2} ) + \alpha_{2} M_{2} } \right](k_{{2{\text{c}}}} )^{2} }}{{\varGamma_{{1{\text{s}}}} 2\mu_{1} ml_{{1{\text{s}}}} }}, \hfill \\ a_{36} = \frac{{\varGamma_{{2{\text{d}}}} 2\mu_{2} m^{2} - \left[ {\varGamma_{{2{\text{d}}}} (\lambda_{{2{\text{c}}}} + 2\mu_{2} ) + \alpha_{2} M_{2} } \right](k_{{2{\text{d}}}} )^{2} }}{{\varGamma_{{1{\text{s}}}} 2\mu_{1} ml_{{1{\text{s}}}} }} \hfill \\ \end{gathered} $$

(iv) Setting τ 1xy  = τ 2xy

$$ \begin{gathered} a_{41} = - 1,\quad a_{42} = \frac{{\varGamma_{{1{\text{c}}}} 2ml_{{1{\text{c}}}} }}{{\varGamma_{{1{\text{s}}}} (l_{{1{\text{s}}}}^{2} - m^{2} )}},\quad a_{43} = \frac{{\varGamma_{{1{\text{d}}}} 2ml_{{1{\text{d}}}} }}{{\varGamma_{{1{\text{s}}}} (l_{{1{\text{s}}}}^{2} - m^{2} )}}, \hfill \\ a_{44} = \frac{{\varGamma_{{2{\text{s}}}} \mu_{2} (l_{{2{\text{s}}}}^{2} - m^{2} )}}{{\varGamma_{{1{\text{s}}}} \mu_{1} (l_{{1{\text{s}}}}^{2} - m^{2} )}},\quad a_{45} = \frac{{\varGamma_{{2{\text{c}}}} 2\mu_{2} ml_{{2{\text{c}}}} }}{{\varGamma_{{1{\text{s}}}} \mu_{1} (l_{{1{\text{s}}}}^{2} - m^{2} )}}, \hfill \\ a_{46} = \frac{{\varGamma_{{2{\text{d}}}} 2\mu_{2} ml_{{2{\text{d}}}} }}{{\varGamma_{{1{\text{s}}}} \mu_{1} (l_{{1{\text{s}}}}^{2} - m^{2} )}} \hfill \\ \end{gathered} $$

(v) Setting w 1y  = w 2y

$$ \begin{gathered} a_{51} = - 1,\quad a_{52} = - \frac{{l_{{1{\text{c}}}} }}{m},\quad a_{53} = - \frac{{l_{{1{\text{d}}}} }}{m}, \hfill \\ a_{54} = 1,\quad a_{55} = - \frac{{l_{{2{\text{c}}}} }}{m},\quad a_{56} = - \frac{{l_{{2{\text{d}}}} }}{m}, \hfill \\ \end{gathered} $$

(vi) Setting \( \frac{\partial }{\partial t}w_{2y} = \kappa_{12} (p_{1f} - p_{2f} ) \)

$$ \begin{gathered} a_{61} = 0,\quad a_{62} = \kappa_{12} (\alpha_{1} \varGamma_{{1{\text{c}}}} + 1)M_{1} (k_{{1{\text{c}}}} )^{2} \hfill \\ a_{63} = \kappa_{12} (\alpha_{1} \varGamma_{{1{\text{d}}}} + 1)M_{1} (k_{{1{\text{d}}}} )^{2} ,\quad a_{64} = \omega m \hfill \\ \end{gathered} $$
$$ \begin{gathered} a_{65} = - (\omega l_{{2{\text{c}}}} + \kappa_{12} (\alpha_{2} \varGamma_{{2{\text{c}}}} + 1)M_{2} k_{{2{\text{c}}}}^{2} ) \hfill \\ a_{66} = - (\omega l_{{2{\text{d}}}} + \kappa_{12} (\alpha_{2} \varGamma_{{2{\text{d}}}} + 1)M_{2} k_{{2{\text{d}}}}^{2} ) \hfill \\ \end{gathered} $$

For the sealed-pore boundary condition, \( \kappa_{12} = 0 \), then

$$ a_{61} = a_{62} = a_{63} = 0,\quad a_{64} = \omega m,\quad a_{65} = - \omega l_{{2{\text{c}}}} ,\quad a_{66} = - \omega l_{{2{\text{d}}}} $$

For the open-pore boundary condition, \( \kappa_{12} = \infty \), then

$$ \begin{gathered} a_{61} = a_{64} = 0, \hfill \\ a_{62} = (\alpha_{1} \varGamma_{{1{\text{c}}}} + 1)M_{1} k_{{1{\text{c}}}}^{2} ,\quad a_{63} = (\alpha_{1} \varGamma_{{1{\text{d}}}} + 1)M_{1} k_{{1{\text{d}}}}^{2} , \hfill \\ a_{65} = - (\alpha_{2} \varGamma_{{2{\text{c}}}} + 1)M_{2} k_{{2{\text{c}}}}^{2} ,\quad a_{66} = - (\alpha_{2} \varGamma_{{2{\text{d}}}} + 1)M_{2} k_{{2{\text{d}}}}^{2} \hfill \\ \end{gathered} $$

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liu, X., Greenhalgh, S. Reflection and Transmission Coefficients for an Incident Plane Shear Wave at an Interface Separating Two Dissimilar Poroelastic Solids. Pure Appl. Geophys. 171, 2111–2127 (2014). https://doi.org/10.1007/s00024-014-0844-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00024-014-0844-5

Keywords

Search

Navigation