Abstract
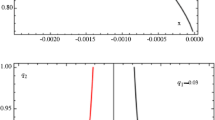
The restricted 3-body problem is generalised to include the effects of an inverse square distance radiation pressure force on the infinitesimal mass due to the large masses, which are both arbitrarily luminous. A complete solution of the problems of existence and linear stability of the equilibrium points is given for all values of radiation pressures of both liminous bodies, and all values of mass ratios. It is shown that the inner Lagrange point, L1, can be stable, but only when both large masses are luminous. Four equilibrium points, L6, L7, L8, and L9 can exist out of the orbital plane when the radiation pressure of the smaller mass is very high. Although L8 and L9 are always linearly unstable, L6 and L7 are stable for a small range of radiation pressures provided that both large masses are luminous.
Similar content being viewed by others
References
Buckingham, R. A.: 1957,Numerical Methods, Pitman Press.
Budding, E.: 1981, in E. B. Carling and Z. Kopal (eds.),Photometric and Spectroscopic Binary System, D. Reidel Publ. Co., Dordrecht, Holland.
Chernikov, Yu. A.: 1970,Soviet Astron.-A.J. 14, No. 1.
Danby, J. M. A.: 1962,Fundamentals of Celestial Mechanics, Macmillan Company, New York.
Friedman, L. D.: 1976, in G. A. Gary and K. S. Clifton (eds.),Proceedings of the Shuttle-Based Cometary Science Workshop George C. Marshall Space Flight Center, Alabama, NASA Publication No. 251.
Perezhogin, A. A.: 1976,Astron. J. Letters 2, 448.
Radzievskii, V. V.: 1950,Astron. Zh. 27, 250.
Radzievskii, V. V.: 1953,Astron. Zh. 30, 265.
Schuerman, D. W.: 1972,Astrophys. Space Sci. 19, 351.
Schuerman, D. W.: 1980,Astrophys. J. 238, 337.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Simmons, J.F.L., McDonald, A.J.C. & Brown, J.C. The restricted 3-body problem with radiation pressure. Celestial Mechanics 35, 145–187 (1985). https://doi.org/10.1007/BF01227667
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF01227667