Abstract
We present a new contact algorithm that endows the granular element method [1] with the ability to model non-convex particles using non-uniform rational basis splines. This significant extension allows for the representation of particle morphological features, namely, sphericity and angularity, to their fullest extent, with local contact rolling resistance and interlocking emanating directly from grain geometry. Both particle elasticity and friction at the contact level are treated implicitly and simultaneously, and the contact algorithm is cast into a mathematical programming-based contact dynamics framework. The framework provides the advantages of implicit time integrators (for e.g., stability and larger time steps) and ability to handle both rigid and highly stiff particles. By allowing for particle non-convexity, modeling flexibility is significantly enhanced, to a level that is comparable with isogeometric methods. As such, the transition from image data to particle shapes is greatly streamlined. More importantly, increased macroscopic strength in granular packings comprising of non-convex particles is fully captured. All the above capabilities are achieved under a very modest implementation effort.
Similar content being viewed by others
1 Introduction
The objective of this paper is to develop a new contact algorithm that endows the granular element method (GEM) [1] with the ability to model non-convex particles using non-uniform rational basis splines (NURBS). This significant extension allows for the representation of particle morphological features, namely, sphericity and angularity [2], to their fullest extent, with local contact rolling resistance and interlocking emanating directly from grain geometry. Both particle elasticity and friction at the contact level are treated implicitly and simultaneously, and the contact algorithm is cast into a mathematical programming-based contact dynamics framework. The framework provides the advantages of implicit time integrators (for e.g., stability and larger time steps) and ability to handle both rigid and highly stiff particles. By allowing for particle non-convexity, modeling flexibility is significantly enhanced, to a level that is comparable with isogeometric methods [3]. As such, the transition from image data to particle shapes is greatly streamlined. More importantly, increased macroscopic strength in granular packings comprising of non-convex particles is fully captured. All the above capabilities are achieved under a very modest implementation effort.
Recent discrete simulation approaches include techniques to represent complex particle morphology or shape, beyond discs/spheres and ellipses/ellipsoids, which are based mostly on the clustering or clumping technique [4, 5] and polyhedra approach [6–10]. Alternatives, which are essentially combinations of the aforementioned techniques, include spheropolyhedra [11, 12] and potential particles [13, 14]. All development work to date, however, have focused almost exclusively on the treatment of convex particles. Polyhedra have the capability to handle non-convex particles, but are still limited in resolution and discrete models tend to be very blocky, a result of the primitive simplexes underlying the geometry basis, as well as the complexity of the associated contact detection algorithms [15]. As a result, the shape representation capabilities of polyhedra have not been fully realized. By and large, clustering appears to be the most popular approach taken to handle non-convexity due to its simplicity (see for e.g., [16, 17]), although in actual simulations, the number of disks or spheres clustered to form a particle is usually small to minimize computational cost. While simple, clustering is unappealing because of its lack of continuity in the curvatures and tangents on the particle boundaries, which results in clustered particles appearing ‘clumpy’ at locations where spheres overlap or clump, and the curvature at any point on the resulting boundary always positive. The geometrical anomalies associated with the clustering technique prevents it from enabling higher fidelity contact mechanics calculations without further numerical treatment.
While the influence of particle morphology on properties such as strength, permeability, etc. is well established [2, 18], it appears that grain-scale modeling and characterization efforts have remained compartmentalized, as exemplified by a relative lack of connection between real experiments and numerical studies. In cases where discrete modeling of real granular materials with non-trivial geometries were attempted, crude discrete models with large geometrical biases and significantly calibrated parameters have been widely employed. Interestingly, the effects of geometrical bias on grain-scale response from use of simplified geometries are largely not discussed or quantified in the literature. It appears that the current gap between grain-scale modeling and characterization technologies is quite large. While imaging techniques are becoming increasingly sophisticated [19–23], there continues to be a lack of effort to bring discrete granular simulation technology closer to the engineering application level. The development to be discussed in this paper may help in narrowing the gap between grain-scale modeling and characterization.
Our earlier work on GEM has focused on particles geometries that are angular but strictly convex. While GEM has been shown to improve particle morphology representation beyond disks and spheres, it was still limited in two ways. First, the increase in rolling resistance of angular but convex geometries relative to disks is limited. For instance, rolling resistance provided by distributed contact reaction over flat boundaries cannot be represented using strictly convex shapes. Moreover, interlocking behavior between non-convex particles, which contributes significantly to mobilized strength and stability [16, 17], is not accounted for. Second, the generation of strictly convex NURBS shapes is very difficult and restrictive from a modeling perspective. This is even more so when dealing image data of real particle shapes and obtaining strictly convex boundaries through a fitting procedure is not possible in most cases. We emphasize that this difficulty is not due to the limitation of NURBS itself but rather the need to deal with contact algorithms for NURBS, which were undeveloped in GEM at the time. A contact algorithm capable of dealing with general non-convex NURBS particles, to be described in this paper, would eliminate the above two limitations. As a result, a more faithful representation on the contact force distributions over particle boundaries is obtained and the image data-to-analysis pipeline (see for e.g., [24]) is significantly streamlined.
In this work, we target applications with realistic material properties and deformation regimes in which standard DEM either performs poorly or simply fails; namely, in granular systems comprising of rigid or highly stiff particles and subjected to quasi-static or dynamic flow conditions. In the context of these applications, we build upon two important developments that allow us to extend GEM to handle non-convex particles:
-
We extend a variational formulation of granular contact dynamics (CD) recently developed for convex particles [25–28]. This particular formulation, which is employed in this paper, is appealing because it provides a way for CD to be easily implemented and solved using off-the-shelf mathematical programming solvers. The most prominent advantage of this formulation is its automatic inclusion of the quasi-static limit, enabling quasi-static modeling without the need for adjusting damping parameters or time step. The advantages of CD over DEM in the context of our current applications, as well as their differences, have been discussed in [28].
-
We generalize the node-to-surface approach typically used in the contact treatment of finite element models [29] to a ‘knot-to-surface’ approach to enable the contact treatment of non-convex particles described using NURBS. The latter is similar to that of a recent approach used in the contact treatment of frictionless bodies in isogeometric analysis [30]. The key difference and novelty here is on the simultaneous treatment of contact elasticity and frictional contact within the aforementioned CD formulation, as well as the ability to perform contact calculations for granular systems, which contain a large number of particles.
This paper describes the details on how each of the above items are implemented and is structured as follows. First, we describe the contact problem and summarize the variational formulation of the general contact problem for frictional particles in Sect. 2. Then, we lay out the implementation details of the proposed contact algorithm in Sect. 3. Finally, we present two numerical examples in Sect. 4 to demonstrate the effects of non-convexity before conclusions are drawn in Sect. 5. For clarity of presentation and implementation details, we limit our discussion to the two-dimensional case. An extension of the method to the three-dimensional setting is outlined in the Appendix at the end of this paper.
Remark 1
Isogeometric analysis is a computational mechanics technology that uses basis functions emanating from computer aided geometric design (CAGD), such as B-splines, NURBS, and T-splines. It has been shown that isogeometric analysis provides more precise and efficient geometric representations [3]. The advantages of isogeometric basis functions for the representation of particle morphology in discrete simulations have been discussed in [1, 31].
2 Governing equations for frictional particles
The formulations from [25–28] carry forward completely to the non-convex case without any change. As such, simplicity of implementation is retained. Here, we present a summary containing only those key equations required for the completeness of presentation. Quantities that are particular to the contact problem of non-convex particles are noted. Where necessary, we point the reader to the appropriate references for further details.
2.1 General contact problem definition
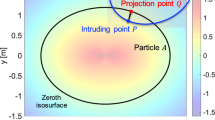
We consider a general two-particle contact problem, with the particles in question to be potentially contacting at the initial time \(t_0\). Referring to Fig. 1, let \(W_i\) be the set of potential contacts associated with particle \(i\) and denote by \(I \in W_i\) a particular contact point in the set. Following a master-slave approach to describe the contact problem [29], a contact point on the slave particle \(\Omega ^j\) is denoted by \(\varvec{x}\) while the contact point on the master particle is defined to be the closest point projection of \(\varvec{x}\) onto the boundary of the master particle:
As shown in Fig. 1, the contact plane at a potential contact point \(I\) is described on the master boundary \(\Gamma ^i\) by the normal \(\varvec{n}_0\) and tangent \(\varvec{t}_0\) at point \(\varvec{\bar{y}}\). The gap at time \(t_0\) is then defined as
with the non-penetration constraint requiring that \(g \ge 0\). The above convention is similar to that used in the definition of contact problems in the finite element method (FEM) [29]. The computation of the signed gap values and related contact quantities within the proposed contact algorithm is described in the next section.
2.2 Notation for general multi-particle system
To facilitate the variational formulation of the governing equations, we first set the notation for the general multi-particle system that will be used throughout this paper. A particle \(i\) has mass \(m^i\) and mass moment of inertia \(J^i\). The position and rotation of the particle are denoted by \(\varvec{x}^i=(x^i,y^i)^T\) and \(\alpha ^i\), respectively, and their corresponding translational and rotational velocities by \(\varvec{v}^i=(v_x^i,v_y^i)^T\) and \(\omega ^i\). We introduce the following matrix or vector quantities that cover general \(n\)-particle systems:
where \(\varvec{M}\) is the diagonal matrix containing the particle masses and \(\varvec{J}\) is the diagonal matrix containing the particle mass moments of inertia. The kinematical quantities are the vectors of particle translations \(\varvec{x}\) and rotations \(\varvec{\alpha }\), and their corresponding velocities \(\varvec{v}\) and \(\varvec{\omega }\). The contact quantities are given by the vectors \(\varvec{p},\; \varvec{q}\) and \(\varvec{g}\), which are the contact normal forces, shear forces and gap values, respectively, each at \(N\) number of contacts.
A quantity, which at the initial time is denoted by \(\Box _0\), would then be denoted at time \(t_0+\Delta t\) by \(\Box \). For example, \(\varvec{x}_0\) and \(\varvec{v}_0\) are the known positions and velocities at time \(t_0\) while \(\varvec{x}\) and \(\varvec{v}\) are the corresponding quantities at time \(t_0+\Delta t\). With this notation, an increment of a quantity will be denoted by \(\Delta \Box = \Box -\Box _0\).
2.3 Discrete update equations
Under the discretization of the equations of motion using the \(\theta \)-method [32], the resulting discrete update equations for translation and rotations are given by:
In the above, the matrices \(\bar{\varvec{M}}\) and \(\bar{\varvec{J}}\) contain the scaled particle masses and mass moments of inertia, respectively:
The effective translational force vector \(\bar{\varvec{f}}_0\) contains the external load vector \(\varvec{f}_\text {ext}\), which we have assumed to be constant (for e.g., due to gravity). The vector \(\bar{\varvec{m}}_0\), with \(\varvec{\omega }_0\) being the angular velocities, is the vector containing the external rotational moments, which may be applied on the particles.
The translational and angular velocities are calculated, respectively, as
where \(0 \le \theta \le 1\). The stability properties of the \(\theta \)-method are well known: for \(\theta = \frac{1}{2}\) an unconditionally stable and energy preserving scheme is recovered, for \(\theta > \frac{1}{2}\) the scheme is unconditionally stable and dissipative, and for \(\theta < \frac{1}{2}\) stability depends on the time step. In the context of binary collisions, the algorithmic energy dissipation that occurs for \(\theta > \frac{1}{2}\) can be related to the physical dissipation associated with impact and thus to the restitution coefficient. Indeed, as shown in [25], a value of \(\theta = \frac{1}{2}\) corresponds to an elastic collision while \(\theta = 1\) reproduces a perfectly inelastic collision.
2.4 Variational formulation of contact problem
Following the formulation procedure as described in [25–28], the resulting discrete mixed force-displacement problem including contact constraints takes the form:
With a slight abuse of notation, we have denoted the vector containing the absolute values of the shear forces by \(\Vert \varvec{q}\Vert \). The matrix \(\varvec{N}\) contains all the normals associated with potential contacts \(\varvec{n} = (n_x,n_y)^T\) while the matrix \(\widehat{\varvec{N}}\) has the same form contains entries \(\varvec{t} = (-n_y,n_x)^T\), i.e., the tangent vector defined as the \(90^{\circ }\) counterclockwise rotation of \(\varvec{n}\). We note the presence of the term with incremental shear \(\Delta \varvec{q} = \varvec{q}-\varvec{q}_0\), which requires the tracking of shear forces at contact points and makes the problem history-dependent.
In Eq. (7), the matrix \(\varvec{R}^q_0\) contains the contribution of the total angular momentum balance from the tangential forces and contains entries \(\varvec{R}^T_{iI}\varvec{n}_0\) where \(\varvec{R}_{iI}\) is the moment arm vector extending from the centroid of particle \(i\) to the contact point \(\varvec{\bar{y}}\). The matrix \(\varvec{R}^p_0\) contains the contribution of the total angular momentum balance from the normal contact forces and contains entries \(-\varvec{R}^T_{iI}\varvec{t}_0\). Both \(\varvec{R}^T_{iI}\varvec{n}_0\) and \(-\varvec{R}^T_{iI}\varvec{t}_0\) are signed moment arms and their signs depend on whether the associated contact force induces a positive (clockwise) or negative moment on the particle. A similar description applies to the slave particle using its contact normal \(-\varvec{n}_0\) and tangent \(-\varvec{t}_0\). The matrices \(\varvec{C}_N\) and \(\varvec{C}_T\) contain the compliances \(1/k_N\) and \(1/k_T\) on the diagonal, where \(k_N\) and \(k_T\) are the normal and tangential contact stiffnesses, respectively. Finally, the Coulomb criterion is imposed with \(\mu = \tan \phi \) being the effective inter-particle friction coefficient and \(\phi \) is the effective friction angle at the scale below the particle angularity level.
2.5 Optimality conditions
Following the approach in [25], the first-order KKT conditions associated with Eq. (7) comprise of linear moment balance:
balance of angular momentum:
sliding friction conditions:
where \(\varvec{s}\) is the slack vector, introduced to enforce equality, and kinematics:
where \(\text {sgn}\) is the signum function. The kinematics in Eqs. (12) and (13) pertain to the associated sliding rule, which leads to an apparent dilation proportional to the friction coefficient \(\mu \). However, as described in [25], this dilation can be viewed as an artifact of the time discretization which, with the exception of a few pathological cases, is gradually reduced as the time step is reduced. Moreover, it was shown in [25] that the dilation, even for rather large time steps, is negligible over a range of common conditions including both instances of highly dynamic and relatively unconfined flows as well as confined quasi-static deformation processes.
2.6 Force-based problem
Finally, it is possible to cast Eq. (7) in terms of the following force based problem:
where \(\varvec{t}\) are the dynamic forces associated with the rotations, i.e., torques.
2.7 Static limit
Omitting the dynamic forces \(\varvec{r}\) and \(\varvec{t}\) from Eq. (14) gives rise to the following static problem which is valid in the limit of \(\Delta t\) tending to infinity:
The above principle is useful for quasi-static problems governed by an internal pseudo-time rather than physical time. Examples include common soil mechanics laboratory tests such as triaxial tests, quasi-static soil-structure interaction problems such as cone penetration, and various applications in the earth sciences where the time scales are such that the deformations are of a quasi-static nature, e.g. [33, 34]. We note that in the quasi-static formulation, the accuracy of the scheme would then depend on the increment size of the applied boundary conditions (for e.g., wall displacements or stresses).
2.8 Solution procedure and computational complexity
We observe that Eqs. (14) and (15) are essentially standard quadratic programming problems. In this work, the primal-dual interior-point solver in MOSEK [35] is used for the solution of both problems. The solution and storage costs associated with these problems are usually justified by the larger analysis steps that can be taken when using implicit algorithms. This is more so for systems comprised of rigid or highly stiff particles in which explicit solution procedures perform poorly or simply fails. Moreover, large-scale mathematical programming solvers with sparse storage (for e.g., [35, 36]) are becoming widely available and increasingly efficient and robust. More recent solvers such as MOSEK [35] also include multi-core or multi-threaded capabilities.
The performance of the primal-dual interior-point method in the context of our proposed contact dynamics formulation has been described in detail in [25] and the following properties are summarized: (1) insensitivity of iteration count to problem size, (2) arithmetic complexity that is equivalent to standard Newton–Raphson schemes, and (3) highly robust (almost never fails or stalls). The overall cost is therefore comparable to implicit Newton–Raphson-type schemes used in nonlinear finite element analysis. For details on the fundamental theory and implementation of interior-point methods, we refer the reader to [37].
Schematic illustration of a NURBS curve. The curve degree \(p\) is 3 (cubic). The knots \(u_i\) and weights \(w_j\) are listed in the vectors \(U\) and \(w\), respectively. The kink in the curve is due to full multiplicity \(k=p=3\) in which the knot/parameter value \(u=0.75\) is repeated \(p=3\) times
3 Contact algorithm
The CD formulation of either Eq. (14) or (15) described in the previous section offers great simplicity and significant effort reduction in contact implementation in that the only required information are the signed gap values at the initial time \(\varvec{g}_0\). In this section, we describe the implementation of the proposed contact algorithm for the general contact problem described in Sect. 2.1 in the context of NURBS. We describe each of the required components for implementation followed by algorithm boxes to describe the procedures in detail.
3.1 Non-uniform rational basis-splines (NURBS)
The literature on NURBS is extensive and relatively mature, and our purpose here is not to present all of its elements but rather those that are needed for completeness of presentation. For an exhaustive description of NURBS, the reader is referred to [3, 38–40]. The NURBS curve is defined parametrically as
where \(u\) is the curve parameter, \(N_{i,p}\) is the \(i\)th B-Spline basis function of degree \(p\) defined by the Cox-de Boor recursion formula [41, 42] as follows:
and \(w_i \ge 0\) are the weights, which affect the effective contribution of control point \(\mathbf P_i\) on the overall shape of the curve \(\mathbf C(u)\). In the above, the degree \(p=0,1,2,3\), etc. refers to constant, linear, quadratic, cubic, etc., polynomials.
The key elements of NURBS are [40]:
-
1.
A set of \(n+1\) control points \(\mathbf {P}_i\) \((0 \le i \le n)\),
-
2.
A knot vector \(U\) of \(m+1\) knots \((0 = u_0 \le u_1 \le \cdots \le u_{m-1} \le u_m = 1)\), and
-
3.
A degree \(p\) satisfying \(m=n+o\) where \(o=p+1\) is the order of the curve.
The number of knots \(m+1\) must be equal to the number of control points \(n+1\) plus the curve order \(p+1\). The control points need not lie on the curve itself. Rather, control points act as a scaffold that controls the geometry [3]. Piecewise linear interpolation of the control points effectively furnishes a control polygon bounding the geometry. In our work, we describe all particle geometries using NURBS of cubic degree \(p=3\).
The curve parameter is described through the knots in the knot vector \(U\) of the B-Splines. The non-decreasing knots \(u_i\), \(i=0,1,...,m\) partitions the parameter space into segments of half-open intervals \([u_i,u_{i+1})\), which are also called knot spans. The knot span can be of zero length since the knots need not be distinct, i.e., they can be repeated. The number of times a knot value repeats itself is called multiplicity \(k\). We use the non-periodic (or clamped) NURBS, in which the knot vector takes the form
If the internal knots are uniformly spaced, the curve is infinitely continuously differentiable in the interior of a knot span, and \((p-k)\)-times continuously differentiable at a knot. If \(k=p\), we say that the knot has full multiplicity; the multiplicity cannot be greater than the degree. Multiplicity of knots provides a way to specify the continuity between segments. For example, a full multiplicity knot in the knot vector (away from the ends) means that a kink or cusp is present in the curve (see for e.g., Fig. 2). In general, the knots can be unequally spaced.
Finally, we close the curve using the following approach: the first and last control points are made coincident, i.e., \(\varvec{P}_0=\varvec{P}_n\) and the two coincident and adjacent control points are made collinear to maintain curvature continuity.
Remark 2
Polygonal bodies can be generated using NURBS curves having degree \(p=1\) and full multiplicity \(k=p\) at each internal knot. In this case, existing polyhedra-based contact algorithms are fully applicable. In this paper, we focus on the case of smooth non-convex bodies described using NURBS, with \(p > 1\) where the normals and tangents are well-defined everywhere on the boundary.
3.2 Boundary knot positioning
We generalize the node-to-surface approach typically used in the contact treatment of finite element models [29] to a ‘knot-to-surface’ approach to enable the contact treatment of non-convex particles described using NURBS. Following a master-slave approach, the contact points associated with the slave particle are represented by knots (i.e., parameter values) while the master boundary serves as the constraint boundary for non-penetration of contact points. This is necessary for computational tractability, as well as for tracking the incremental slip and contact gain or loss around non-convex boundaries of potentially contacting particles.
While similar to nodal discretization in FEM, we emphasize that the key difference here is that the positioning of contact points by knots does not change the particle geometry; the knot or parameter value simply runs continuously along the boundary. For simplicity, we have selected the knot positions a priori and in sufficient number (between 40 and 60 in our examples here) to represent the particle geometry and contact problem appropriately. More complicated schemes such as the adaptive positioning of contact points to reduce the number of knots, as well as more advanced interface contact discretization strategies may be possible; further research, however, is required to determine the feasibility of these ideas in the context of granular simulations.
3.3 Contact elasticity
In this paper, we have only considered the case of linear contact elasticity as shown in Fig. 3 but extension to nonlinear elasticity is entirely possible as is the consideration of more complex contact models incorporating hardening, viscous effects, etc.
The resulting scheme bears some similarity to standard DEM schemes in that the consideration of a finite contact stiffness implies the possibility for an elastically reversible inter-particle penetration. The inclusion of contact elasticity reproduces the more basic case of rigid particles in the limit of the contact stiffness tending to infinity. Moreover, in contrast to standard DEM, there are no algorithmic repercussions from operating with a large or, in the extreme case, infinite stiffness. Indeed, the same algorithm is used regardless of the contact stiffness, with perfect rigidity being a limiting case that allows for certain simplifications. For example, in the limiting case, both \(\varvec{C}_N\) and \(\varvec{C}_T\) in either Eq. (14) or (15) are zero, and the associated quadratic terms drop out from the formulation. In particular, this means that no information of the shear forces needs to be carried over from one time step to the next. As a result, contact stiffness values that are representative of real materials (for e.g., steel or rock) can be used without causing numerical difficulties.


The static problem described by Eq. (15) reveals a number of interesting properties related to the indeterminacy of force networks in granular media. It is well known that rigid particles lead to a situation where the force network solution is non-unique [43–46]. Setting \(\varvec{C}_N = \varvec{C}_T = \varvec{0}\) in Eq. (15) leads to a linear program where global optimality may be achieved by more than one set of forces. Conversely, for finite values of \(\varvec{C}_N\) and \(\varvec{C}_T\), the solution is unique, i.e. there is a unique set of contact forces leading to the optimal value of the objective function.
3.4 Implementation of contact algorithm
The key procedure required for the implementation of the proposed contact algorithm is the closest point projection (CPP) as described in Algorithm 1. Here, the contact points on the slave boundary are projected onto the master curve, from which the signed gap values can then be calculated. The minimization problem in Algorithm 1 can be solved using either gradient-based or derivative-free constrained optimization procedures. Here, we choose the derivative-free procedure since it is simpler and does not require the evaluation of the derivatives of the objective function. As a simple additional optimization, Algorithm 2 first isolates the spans that are nearest to a particular contact point by checking that the dot product of normals at a contact point and its corresponding closest-projected point is negative. This means that only the spans on the master curve that are within the direct sight of a contact point on the slave boundary are used in the CPP operation. Combining the above two algorithms, Algorithm 3 describes the global procedure to determine all the signed gaps over all particles, which are then stored in the vector \(\varvec{g}_0\) in either Eq. (14) or (15). The broad-phase contact detection aspect of Algorithm 3 is standard (see for e.g., [15]).
By considering the knot spans as segments, our proposed contact algorithm has essentially the same computational complexity as polyhedra-based approaches employed in either CD [9] or finite element contact algorithms [29]. We note that for a given prescribed resolution, however, NURBS has the advantage of carrying significantly less geometric information compared to polyhedra, i.e., less number of NURBS control points compared to number of polyhedra nodes [1]. For quasistatic applications, further efficiency enhancement to the proposed contact algorithm can be achieved by taking advantage of temporal coherence in which the configuration of particles from one time step to the next changes little. In this case, an incremental approach similar to that of [47] may be adapted to minimize the number of nearest span computations (Algorithm 2).
Remark 3
If the curves are locally convex, the separating hyperplane algorithm described in [31] can be employed as an additional refinement. For general smooth non-convex bodies, however, there is no local convexity everywhere in general. The proposed contact algorithm would handle this situation effectively and robustly.

4 Numerical examples
In this section, we present two examples that highlight the effects of particle morphology on the macroscopic response of granular assemblies, as well as the robustness of our proposed method. In particular, we compare responses of assemblies with three levels of particle angularity: discs, angular but (strictly) convex, and non-convex particles.
4.1 Biaxial compression
Biaxial compression simulations using the static limit formulation in Eq. (15) are carried out on a rectangular assembly of initial width \(W_0\) and initial height \(H_0\) containing 1,520 particles. First, an assembly with GEM non-convex particles is prepared using 16 different shapes. Then, two additional assemblies—one with angular convex GEM particles and another with discs—are also prepared. The particles in these assemblies are obtained by matching average particle diameters of the 16 non-convex shapes. Effectively, sphericity is kept constant and a comparison of effects of angularity is made. The three assemblies with their corresponding particle shapes are shown in Fig. 4.
The non-convex and angular GEM assemblies have an initial porosity of approximately 0.152, while the disc assembly has an initial porosity of approximately 0.176. The higher porosity of the disc assembly points to the inability of discs to match porosity by just simply matching average particle diameters. Indeed, a wider distribution of disc sizes would be required in this case to match the initial porosity of 0.152, which in turn would substantially increase the number of particles. In this regard, the use of discs to represent particle geometry introduces an unavoidable geometrical bias, which leads to packings with higher porosities [17]. Nevertheless, in this example, we retain the disc assembly for comparison with the other two GEM assemblies. Two inter-particle friction coefficients \(\mu =0.3\) and 0.5 are used to gauge the effect of inter-particle friction. The upper wall is moved downwards while the applied stress on the right wall \(\sigma _3\) is maintained at 125 units. A total of about 150 steps are used to impose a total axial strain of approximately 0.21. The left and bottom walls are stationary. All walls are frictionless.
To show the effects of particle elasticity, we perform the tests with several values of particle elasticity: \(k_N=\infty ,\; 10^8,\; 10^6,\; 10^5\). The tangential stiffness is set at \(k_T=2 k_N/3\), which is within the range for a physically consistent volumetric response in granular materials [26, 48]. At every time step, the current width \(W\) and current height \(H\) of the assembly box are tracked, and the stresses \(\sigma _1\) and \(\sigma _3\) computed using the contact forces of the particles impinging on the top and right walls, respectively. The results in terms of deviatoric stress \(\sigma _1 - \sigma _3\) versus axial strain, \(\epsilon _a = 1 - H/H_0\), and volumetric strain, \(\epsilon _v = 1 - WH/(W_0H_0)\), versus axial strain are shown in Figs. 5, 6, 7 and 8. We see that the macroscopic response at \(k_N=10^8\) is close to rigid. As \(k_N\) is lowered, a more elastic initial response is observed in which the sharp initial peak is progressively suppressed and the peak response lowers slightly. At \(k_N=10^5\), an initial slope in the deviatoric stress becomes visible and the corresponding volumetric strain response shows an initial compaction followed by volume expansion. The deformed configurations of the three assemblies for the case of \(k_N=10^8\) are shown in Fig. 4.
In all cases, we note the following observations. For a particular assembly, the macroscopic deviatoric stress reaches a constant value that is independent of the elastic properties while the rate of volumetric strain tends to zero, in agreement with standard continuum plasticity theories. Comparing across the three assemblies with different particle angularity levels, however, we observe that the both the peak strength and dilatancy increase with increasing angularity i.e. from discs to non-convex. This latter observation is consistent with experimental evidence of increased strength with increasing angularity of the particles [2].
4.2 Column drop test
We consider a column with an initial height to width ratio \(H_0/L_0\) of approximately 1.68. The base supporting the column has a friction coefficient of \(\mu _{\text {base}} = 0.5\) while a smooth vertical wall, representing a symmetry boundary, is placed on one side of the column. Three columns with 1520 particles of increasing angularity - disc, angular but convex, and non-convex, as shown at Step 0 in Figs. 9 and 10, are constructed using particles from the sixteen different shapes described in the biaxial test example. These particles are dropped into the rectangular box forming the column and letting them settle under gravity. Drop test simulations are then conducted by removing one of the side walls of the box and letting the column spread under gravity. The simulations are carried out using the dynamic formulation in Eq. (14) with \(\theta =0.7\) and a time step of \(\Delta t = 0.05\) for two inter-particle friction coefficients \(\mu = 0.5\) and \(\mu =0\). We set the contact elasticity to be \(k_N=10^8\) and \(k_T=2k_N/3\) for all columns.
Configurations of columns with inter-particle friction coefficient of \(\mu =0\) at step 3,200: approximate dimensions relative to column with non-convex particles. We note that at this point in time, the column with disc particles continues to flow; a final layer thickness of 1 particle is reached as the simulation is progressed
We compare the response evolutions of the angular GEM and disc columns against the non-convex GEM column as shown in Figs. 9 and 10. The final configurations of the three columns for \(\mu = 0.5\) are shown in Fig. 11. The slopes of the final spreads of the angular GEM and disc columns are approximately \(12^{\circ }\) and \(9^{\circ }\), respectively. More prominently, the slope in the non-convex GEM column is \(17^{\circ }\). This is a \(5^{\circ }\) and \(8^{\circ }\) increase from the angular GEM and disc columns, respectively, which are quite significant. Relative to the non-convex GEM column, the final spreads of the angular GEM and disc columns are approximately 14 and 45 percent wider. These observations are consistent with the increase of rolling resistance with increasing angularity.
For the case of \(\mu = 0\), the response evolutions of the angular GEM and disc columns as compared with the non-convex GEM column are shown in Figs. 12 and 13, with the final configurations of the GEM columns shown in Fig. 14. At Step 3,200, the two GEM columns have stopped flowing while the disc column continues to flow and as the simulation is progressed, a final layer thickness of 1 particle is reached. Essentially, without rolling resistance, the disc column simply ‘melts’ away. On the other hand, the GEM columns maintain a well-defined spread, even at zero inter-particle friction, due to the rolling resistance provided by angular and non-convex particles. As expected, the non-convex GEM column has a smaller spread due to increased angularity in the non-convex particles.
5 Conclusion
We have presented a new contact algorithm that enables the GEM to model non-convex particles. Its implementation is very simple, with the main operation being the closest point projection. The overall simplicity of GEM is retained by adopting a variational framework of contact dynamics, which allows the use of realistic contact stiffnesses and the system can be solved using reasonably large time steps. With this new contact algorithm, GEM is able to represent, through Non-Uniform Rational Basis Splines (NURBS), particle morphological features of sphericity and angularity to their fullest extent. Modeling flexibility is also greatly enhanced, streamlining the image data-to-analysis pipeline.
Through numerical simulations of the biaxial compression and column drop tests, we demonstrated and highlighted the ability of GEM to capture the effects of increased rolling resistance, associated with increased angularity in and interlocking between non-convex particles, on the macroscopic response. These effects are manifested macroscopically through an increase in the mobilized shear strength and dilatancy under biaxial compression, and a smaller spread and higher angle of response under a column drop test. These observations are consistent with reported experimental observations. The effect of geometrical bias from the use of discs to match average particle diameter on packing porosity, which in turn affects mobilized strength, is also noted.
In the present work, we have focused on the numerical verification aspect of GEM. Future research on GEM would include further algorithmic improvements on contact algorithms and solution procedures, as well as on the extension of non-convexity into the three-dimensional setting. At the present state, however, GEM has sufficient capabilities to allow for its application in lab-scale validation with experiments similar to that described in [49], and this endeavor is currently under preparation. While the comparison of numerical and experimental micromechanical quantities remains challenging due to system sensitivities and uncertainties, it is expected that GEM would be able to provide access to contact topologies, forces and kinematics that are unique to natural granular media with realistic particle morphologies. This would bring us a step closer toward the goal of complete characterization of natural granular media for engineering applications.
References
Andrade JE, Lim K-W, Avila CF, Vlahinic I (2012) Granular element method for computational particle mechanics. Comput Methods Appl Mech Eng 241–244:262–274
Cho GC, Dodds J, Santamarina JC (2006) Particle shape effects on packing density, stiffness, and strength: natural and crushed sands. J Geotech Geoenviron Eng 132(5):591–602
Hughes TJR, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: cad, finite elements, nurbs, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194:4135–4195
Ashmawy AK, Sukumaran B, Hoang AV (2003) Evaluating the influence of particle shape on liquefaction behavior using discrete element method. In: Proceedings of the thirteenth international offshore and polar engineering conference (ISOPE 2003) Honolulu
Garcia X, Latham J-P, Xiang J, Harrison JP (2009) A clustered overlapping sphere algorithm to represent real particles in discrete element modelling. Geotechnique 59:779–784
Cundall PA (1988) Formulation of a three-dimensional distinct element model—part i: a scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int J Rock Mech Min Sci 25(3):107–116
Zhao D, Nezami EG, Hashash YMA, Ghaboussi J (2006) Three-dimensional discrete element simulation for granular materials. Eng Comput 23:749–770
Alonso-Marroquin F, Herrmann HJ (2002) Calculation of the incremental stress-strain relation of a polygonal packing. Phys Rev E 66:021301
Dubois F, Jean M (2006) The non smooth contact dynamic method: recent lmgc90 software developments and application. In: Wriggers Peter, Nackenhorst Udo (eds) Analysis and simulation of contact problems. Lecture notes in applied and computational mechanics, vol 27. Springer, Berlin, pp 375–378
Peña AA, Lind PG, Herrmann HJ (2008) Modeling slow deformation of polygonal particles using dem. Particuology 6:506– 514
Pournin L, Liebling TM (2005) A generalization of distinct element method to three dimensional particles with complex shapes. In: Proceedings of Powders & Grains, Balkema, Leiden
Galindo-Torres SA, Pedroso DM (2010) Molecular dynamics simulations of complex-shaped particles using voronoi-based spheropolyhedra. Phys Rev E 81:061303
Houlsby GT (2009) Potential particles: a method for modelling non-circular particles in dem. Comput Geotech 36:953–959
Harkness J (2009) Potential particles for the modelling of interlocking media in three dimensions. Int J Numer Methods Eng 80(12):1573–1594
Ericson C (2004) Real-time collision detection (The Morgan Kaufmann Series in Interactive 3-D Technology) (The Morgan Kaufmann Series in Interactive 3D Technology). Morgan Kaufmann Publishers Inc., San Francisco
Saint-Cyr B, Delenne J-Y, Voivret C, Radjai F, Sornay P (2011) Rheology of granular materials composed of nonconvex particles. Phys Rev E 84:041302
Ludewig F, Vandewalle N (2012) Strong interlocking of nonconvex particles in random packings. Phys Rev E 85:051307
Garcia X, Akanji LT, Blunt MJ, Matthai SK, Latham JP (2009) Numerical study of the effects of particle shape and polydispersity on permeability. Phys Rev E 80:021304
Alshibli KA, Sture S, Costes NC, Frank ML, Lankton FR, Batiste SN, Swanson RA (2000) Assessment of localized deformations in sand using x-ray computed tomography. Geotech Test J ASCE 23:274–299
Ketcham RA, Carlson WD (2001) Acquisition, optimization and interpretation of x-ray computed tomographic imagery: applications to the geosciences. Comput Geosci 27:381–400
Oda M, Takemura T, Takahashi M (2004) Microstructure in shear band observed by microfocus x-ray computed tomography. Géotechnique 54:539–542
Wang L, Park JY, Fu Y (2005) Representation of real particles for dem simulation using x-ray tomography. Constr Build Mater 21:338–346
Hall SA, Bornert M, Desrues J, Pannier Y, Lenoir N, Viggiani G, Bésuelle P (2010) Discrete and continuum analysis of localized deformation in sand using x-ray micro ct and volumetric digital image correlation. Géotechnique 60:315–322
Andrade JE, Vlahinic I, Lim K-W, Jerves A (2012) Multiscale ‘tomography-to-simulation’ framework for granular matter: the road ahead. Géotech Lett 2:135–139
Krabbenhoft K, Lyamin AV, Huang J, Vicente da Silva M (2012) Granular contact dynamics using mathematical programming methods. Comput Geotech 241–244:262–274
Krabbenhoft K, Lyamin AV, Huang J, Vicente da Silva M (2012) Granular contact dynamics with particle elasticity. Granul Matter 14:607–619
Huang J, Vicente da Silva M, Krabbenhoft K (2013) Three-dimensional granular contact dynamics with rolling resistance. Comput Geotech 49:289–298
Lim K-W, Krabbenhoft K, Andrade JE (2014) A contact dynamics approach to the granular element method. Comput Methods Appl Mech Eng 268:557–573
Laursen TA (2002) Computational contact and impact mechanics: fundamentals of modeling interfacial phenomena in nonlinear finite element analysis. Springer, Berlin
Temizer I, Wriggers P, Hughes TJR (2011) Contact treatment in isogeometric analysis with nurbs. Comput Methods Appl Mech Eng 200(9–12):1100–1112
Lim K-W, Andrade JE (2014) Granular element method for three-dimensional discrete element calculations. Int J Numer Anal Methods Geomech 38:167–188
Wood WL (1990) Practical time-stepping schemes. Oxford University Press, Oxford
Souloumiac P, Leroy YM, Maillot B, Krabbenhoft K (2009) Predicting stress distributions in fold-thrust and accretionary wedges by optimisation. J Geophys Res 114:B09404
Souloumiac P, Krabbenhoft K, Leroy YM, Maillot B (2010) Failure in accretionary wedges with the maximum strength theorem. Comput Geosci 19:793–811
MOSEK ApS. MOSEK. http://mosek.com/products/mosek/
Sturm JF (1999) Sedumi 1.02: a matlab toolbox for optimization over symmetric cones. Optim Methods Softw 11–12:625–653
Wright SJ (1997) Primal-dual interior-point methods. Society for Industrial and Applied Mathematics, Philadelphia
Piegl L, Tiller W (1997) The NURBS book, 2nd edn. Springer-Verlag, New York
Shene C-K (2011) CS3621 Introduction to Computing with Geometry. Unit 7: NURBS Curves. http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/
Lowther J, Fisher J, Shene C-K (March 2004) If you know B-splines well, you also know nurbs!. SIGCSE Bull 36:343–347
Cox MG (1971) The numerical evaluation of B-splines. Technical report, National Physics Laboratory DNAC 4
De Boor C (1972) On calculation with B-splines. J Approx Theory 6:50–62
Radjai F, Brendel L, Roux S (1996) Nonsmoothness, indeterminacy, and friction in two-dimensional arrays of rigid particles. Phys Rev E 54:861–873
Snoeijer JH, Vlugt TJH, van Hecke M, van Saarloos W (2004) Force network ensemble: a new approach to static granular matter. Phys Rev Lett 92:054302
McNamara S, García-Rojo R, Herrmann H (2005) Indeterminacy and the onset of motion in a simple granular packing. Phys Rev E 72:021304
Unger T, Kertész J, Wolf DE (2005) Force indeterminacy in the jammed state of hard disks. Phys Rev Lett 94:178001
Li T-Y, Chen J-S (1998) Incremental 3D collision detection with hierarchical data structures. In: Proceedings of the ACM symposium on virtual reality software and technology, VRST ’98, ACM, pp 139–144
Mindlin RD (1949) Compliance of elastic bodies in contact. J Appl Mech 71:259–268
Calvetti F, Combe G, Lanier J (1997) Experimental micromechanical analysis of a 2D granular material: relation between structure evolution and loading path. Mech Cohes Frict Mater 2:121–163
Sintef, ICT, Department of Applied Mathematics, Norway. GoTools Geometry Toolkit. http://www.sintef.no/Projectweb/Geometry-Toolkits/GoTools/
Evans DJ, Murad S (1977) Singularity free algorithm for molecular dynamics simulation of rigid polyatomics. Mol Phys 34(2):327–331
Moler C, Loan CV (2003) Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later. SIAM Rev 45(1): 3–49
Author information
Authors and Affiliations
Corresponding author
Appendix 1: Three-dimensional formulation
Appendix 1: Three-dimensional formulation
The two-dimensional formulation discussed in this paper may be extended to three dimensions in a number of ways. All appropriate physical constraints of the three-dimensional contact problem can be found in [26] and hence, will not be repeated here. The exception here is that we need to deal with arbitrary-shaped three-dimensional particles in which the closest-point projection operation and integration of rotational degrees of freedom need special attention.
A detailed discussion of closest-point projection algorithms for NURBS surfaces is beyond the scope of this paper. The design of an efficient closest-point projection for contact operations in granular contact dynamics is currently in progress and will be reported as a separate publication. Here, we simply note that the minimum distance problem given by Eq. (1) and gap definition given by Eq. (2) remain unchanged and computationally feasible. Generally, a two-stage optimization procedure is required, first to isolate the potential area of global minima, followed by a local optimization procedure to finalize the location of the closest point on the master surface. Again, simplicity of implementation is maintained by casting the closest-point projection operation as a constrained optimization problem. In this area, several ideas from the realm of computer graphics may be applicable (see for e.g. [50]).
Kinematically, the non-trivial difference between the two- and three-dimensional case is a result of rotations of arbitrary-shaped particles. In the following, we outline one possible approach to integrate the rotational degrees of freedom in three dimensions. Without loss of generality, we consider the dynamic problem without contact elasticity. Unless otherwise noted, all quantities pertain to a single particle in the principal body frame.
The discretization of rotational equilibrium equations using the \(\theta \)-method gives
with the update equation for the (body frame) rotational degrees of freedom as (analogous to Eq. (6)b):
and where \(\varvec{I}\) is the time-independent tensor of (principal) inertia in the body frame, \(\varvec{m}_0\) are the external moments in the body frame, and \(\text {skew}\left[ \varvec{\omega }\right] \) is the skew-symmetric matrix defined by \(\text {skew}\left[ \varvec{\omega }\right] \varvec{\omega } = 0\). We observe that the rotational equilibrium equations are nonlinear due to the presence of the products of angular velocities. This nonlinearity can be accounted for within the mathematical programming framework proposed in this paper as follows. We first define the (nonlinear) residual equations as
A truncated Taylor expansion about the \(k\)th iterate \(\varvec{\omega }_k\) then gives the following iterative procedure for the (unconstrained) solution of \(\varvec{\omega }\)
where \(\varvec{J} = -\frac{\partial \varvec{r}}{\partial \varvec{\omega }}\). To cast this iterative procedure along with all the physical constraints of the problem as a quadratic programming problem, we note from Eq. (20) that the variation of \(\varvec{\omega }\) is simply (since \(\varvec{\omega }_0\) and \(\varvec{\alpha }_0\) are fixed)
which allows us to rewrite the iterative procedure in Eq. (22) as
where \(\bar{\varvec{J}}\) is the effective tensor of inertia, calculated to be
We see that Eq. (24)a has an identical structure to Eq. (9) except now the problem needs to be solved incrementally within each time step. The necessary modification to the formulation then entails defining an incremental problem within each time step and replacing the rotational equilibrium equations of the form given by Eq. (9) with Eq. (24)a.
We note several properties of the effective tensor of inertia given by Eq. (25) in relation to the proposed mathematical programming framework. First, the terms are functions of the body frame angular velocities. Second, the effective tensor of inertia is no longer diagonal. In the force-based problem described by Eq. (14), the inverse of the global moment of inertia matrix is required. However, recognizing that the global moment of inertia is now block diagonal, the inverse of the global moment of inertia is another block diagonal matrix, which is composed of the inverse of \(3 \times 3\) blocks and these can be calculated efficiently. Finally, the non-symmetry of \(\bar{\varvec{J}}\) poses no problem since the associated quadratic term for a non-symmetric matrix \(\varvec{Q}\) can be written as
which implies that a non-symmetric matrix \(\varvec{Q}\) can be replaced by \( \frac{1}{2}(\varvec{Q}+\varvec{Q}^T)\).
Computationally, a sequence of quadratic programming problems is solved within a time step for the incremental unknowns (\(\delta \varvec{x}\), \(\delta \varvec{\alpha }\)) until a prescribed tolerance is reached. We note that we can formulate the translational problem incrementally by simply replacing \(\Delta \varvec{x}\) with \(\delta \varvec{x}\); this is possible because the translational equilibrium equations already have a linear structure. Finally, we need to update the orientation of each particle. Here, a singularity-free quaternion approach [51] may be taken. We denote the quaternion vector representing the orientation of the particle as \(\varvec{z} = (z_i), i = 1,\ldots ,4\). The required orientation matrix of each particle can be calculated as a function of quaternion values as
In turn, the evolution of the quaternions can be expressed as a singularity-free set of equations as
where
The general solution is given by
Here, several choices of updating \(\varvec{z}\) exist. One possible choice is the generalized trapezoidal rule of the form
where we have used the same \(\theta \) parameter as in Eq. (20). In this case, one can update \(\varvec{z}\) as
Efficient algorithms for the computation of matrix exponentials can be found in [52].
Rights and permissions
About this article
Cite this article
Lim, KW., Krabbenhoft, K. & Andrade, J.E. On the contact treatment of non-convex particles in the granular element method. Comp. Part. Mech. 1, 257–275 (2014). https://doi.org/10.1007/s40571-014-0019-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40571-014-0019-2