Skip to main content
SpringerLink
Log in

Optimal homotopy asymptotic method for convective–radiative cooling of a lumped system, and convective straight fin with temperature-dependent thermal conductivity

  • Published:
Afrika Matematika Aims and scope Submit manuscript

Abstract

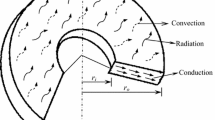
Here, the optimal homotopy asymptotic method (OHAM), one of the newest analytical methods which is powerful and easy-to-use, is applied to solve heat transfer problems with high nonlinearity order. In this research, the OHAM is used to investigate two problems: the temperature distribution equation in a convective straight fin with temperature-dependent thermal conductivity and the convective–radiative cooling of a lumped system with variable specific heat. The validity of our results is verified by numerical results. The OHAM provides us with a convenient way to control the convergence of approximation series and adjust convergence regions when necessary. This realizes using a number of auxiliary constants which are optimally determined. Thus, unlike perturbation methods, the OHAM does not depend on any small physical parameters and it is valid for both weakly and strongly nonlinear problems. It has been attempted to show the capabilities and wide-range applications of the OHAM in comparison with the previous methods in solving heat transfer problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A :

Area (m2)

A c :

Cross-sectional area of fin (m2)

b :

Fin length (m)

c :

Specific heat (J kg−1 K−1)

c a :

Specific heat at ambient temperature (J kg−1 K−1)

E :

Surface emissivity (W)

h :

Convection heat transfer coefficient (W m−2 K−1)

k :

Thermal conductivity of fin material (W m−1 K−1)

k a :

Thermal conductivity at ambient temperature (W m−1 K−1)

k b :

Thermal conductivity at base temperature (W m−1 K−1)

P :

Fin perimeter (m)

T :

Temperature (K)

T a :

Ambient temperature (K)

T b :

Base temperature of fin (K)

Ti :

Initial temperature (K)

T s :

Effective sink temperature (K)

V :

Volume (m3)

x :

Distance measured from fin tip (m)

β :

Volumetric thermal expansion coefficient (K−1)

θ :

Dimensionless temperature (–)

λ :

Slope of thermal conductivity-temperature curve (K−1)

ξ :

Dimensionless length (–)

ρ :

Density (kg m−3)

σ :

Stefan–Boltzman constant (–)

τ :

Dimensionless time (–)

ψ :

Thermo-geometric fin parameter (–)

References

  1. Aziz A., Na T.Y.: Perturbation Method in Heat Transfer. Hemisphere Publishing Corporation, Washington (1984)

    Google Scholar 

  2. Nayfeh AH.: Introduction to Perturbation Techniques. Wiley, New York (1979)

    Google Scholar 

  3. Rand R.H., Armbruster D.: Perturbation Methods, Bifurcation Theory and Computer Algebraic. Springer, Berlin (1987)

    Book  Google Scholar 

  4. He, J.H.: Non-perturbative methods for strongly nonlinear problems. Dissertation, de-Verlag im Internet GmbH, Berlin (2006)

  5. Bildik N., Konuralp A.: The use of variational iteration method, differential transform method and adomian decomposition method for solving different types of nonlinear partial differential equations. Int. J. Nonlinear Sci. Numer. Simul. 7, 65–70 (2006)

    Article  Google Scholar 

  6. Lyapunov A.M.: General Problem on Stability of Motion (English translation). Taylor and Francis, London (1992)

    Google Scholar 

  7. Karmishin A.V., Zhukov A.I., Kolosov V.G.: Methods of Dynamics Calculation and Testing for Thin-Walled Structures. Mashinostroyenie, Moscow (1990)

    Google Scholar 

  8. Adomian G.: Solving Frontier Problems of Physics: The Decomposition Method. Kluwer, Dordrecht (1994)

    MATH  Google Scholar 

  9. Liao, S.J.: The proposed homotopy analysis technique for the solution of nonlinear problems. Ph.D. Thesis, Shanghai Jiao Tong University (1992)

  10. Liao S.J.: Beyond Perturbation: Introduction to the Homotopy Analysis Method. Chapman and Hall/CRC Press, Boca Raton (2003)

    Book  Google Scholar 

  11. Liao S.J.: On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 147, 499–513 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  12. He J.H.: Variational iteration method for autonomous ordinary differential systems. Appl. Math. Comput. 114(2–3), 115–123 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  13. Marinca V., Herişanu N., Nemeş I.: Optimal homotopy asymptotic method with application to thin film flow. Cent. Eur. J. Phys. 6, 648–653 (2008)

    Article  Google Scholar 

  14. Marinca V., Herişanu N.: Application of optimal homotopy asymptotic method for solving nonlinear equations arising in heat transfer. Int. Commun. Heat Mass Transf. 35, 710–715 (2008)

    Article  Google Scholar 

  15. Marinca V., Herişanu N., Bota C., Marinca B.: Optimal homotopy asymptotic method to the steady flow of a fourth grade fluid past a porous plate. Appl. Math. Lett. 22, 245–251 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  16. Herişanu N., Marinca V., Dordea T., Madescu G.: A new analytical approach to nonlinear vibration of an electric machine. Proc. Romanian Acad. Ser. A 9(3), 229–236 (2008)

    Google Scholar 

  17. Marinca V., Herişanu N.: Determination of periodic solutions for the motion of a particle on a rotating parabola by means of the optimal homotopy asymptotic method. J. Sound Vib. 359, 1450–1459 (2010)

    Article  Google Scholar 

  18. He J.H.: A coupling method for homotopy technique and perturbation technique for nonlinear problem. Int. J. NonLinear Mech. 35, 37–43 (2000)

    Article  MATH  Google Scholar 

  19. He J.H.: Asymptotology by homotopy perturbation method. Appl. Math. Comput. 156, 591–596 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  20. He J.H.: Homotopy perturbation method for solving boundary problems. Phys. Lett. A 350, 87–88 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  21. Kern D.Q., Kraus D.A.: Extended Surface Heat Transfer. McGraw-Hill, New York (1972)

    Google Scholar 

  22. Aziz A., Enamul Hug S.M.: Perturbation solution for convecting fin with variable thermal conductivity. J. Heat Transf. 97, 300–310 (1975)

    Article  Google Scholar 

  23. Razelos P., Imre K.: The optimum dimension of circular fins with variable thermal parameters. J. Heat Transf. 102, 420–425 (1980)

    Article  Google Scholar 

  24. Laor K., Kalman H.: Performance and optimum dimensions of different cooling fins with a temperature-dependent heat transfer coefficient. Int. J. Heat Mass Transf. 39, 1993–2003 (1996)

    Article  Google Scholar 

  25. Yu L.T., Chen C.K.: Optimization of circular fins with variable thermal parameters. J. Franklin Inst. B 336, 77–95 (1999)

    Article  MATH  Google Scholar 

  26. Incropera F.P., Dewitt D.P.: Introduction to Heat Transfer, 3rd edn, pp. 114. Wiley, New York (1996)

    Google Scholar 

  27. Herisanu N., Marinca V.: Accurate analytical solutions to oscillators with discontinuities and fractional-power restoring force by means of the optimal homotopy asymptotic method. Comput. Math. Appl. 60, 1607–1615 (2010)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mechanical Engineering Department, Amirkabir University of Technology, 424 Hafez Avenue, 15875-4413, Tehran, Iran

    Saeed Dinarvand & Reza Hosseini

Authors
  1. Saeed Dinarvand
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Reza Hosseini
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Saeed Dinarvand.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dinarvand, S., Hosseini, R. Optimal homotopy asymptotic method for convective–radiative cooling of a lumped system, and convective straight fin with temperature-dependent thermal conductivity. Afr. Mat. 24, 103–116 (2013). https://doi.org/10.1007/s13370-011-0043-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13370-011-0043-9

Keywords

Mathematics Subject Classification (2000)

Search

Navigation