Perspective on Electrospray Ionization and Its Relation to Electrochemistry

Abstract

The phenomenon of electrospraying of liquids is presented from the perspective of the electrochemistry involved. Basics of current and liquid flow in the capillary and spray tip are discussed, followed by specifics of charging and discharging of the sprayed liquid surface. Fundamental theories and numerical modeling relating electrospray current to solution and spray parameters are described and then compared with our own experimentally obtained data. The method of mapping potentials and currents inside the electrospray capillary by using an inserted electrically-isolated small wire probe electrode is discussed in detail with illustrations from new and published data. Based on these experimentally obtained results, a new mathematical model is derived. The introduced “nonlinear resistor electrospray capillary model” divides the electrospray capillary into small sections, adds their contributions, and then, by transition to infinitely small section thickness, produces analytical formulas that relate current and potential maps to other properties of the electrospraying liquid: primarily conductivity and current density. The presentation of the model is undertaken from an elementary standpoint, and it offers the possibility to obtain quantitative information regarding operating parameters from typical analytical systems subjected to electrospray. The model stresses simplicity and ease of use; examples applying experimental data are shown and some predictions of the model are also presented. The developed nonlinear resistor electrospray capillary model is intended to provide a new quantitative basis for improving the understanding of electrochemical transformations occurring in the electrospray emitter. A supplemental material section gives full derivation of the model and discusses other consequences.

Introduction

Studies into electrochemistry/electrospray have dealt with electrochemical issues relating to standard redox cells, flow cells, homogeneous and heterogeneous reaction kinetics, and mass transport. These are combined with phenomena pertaining to liquid jet charging and instability, plus surface phenomena and gas-phase ion production. In this Perspective, we present observations and opinions based on our own experiments and studies of relevant literature. Our discussion will focus on electrochemical phenomena that accompany the liquid charging step of the electrospray process.

The electrospray phenomenon and, in general, electrified liquid jets, are topics of interest not only to mass spectrometrists who use them as a means to transfer ions from a liquid into the gas phase, but also to users of a large variety of other applications starting from jet printing through metal plating, polymer fiber production, to aerial spraying of fertilizers [1]. Flow phenomena in electrified liquids are studied in a discipline called electrohydrodynamics. This belabored field has a large body of literature that developed over time, heavy, often staggering, mathematics.

In the latter part of this Perspective, we present a simple mathematical model to not only qualitatively, but also quantitatively, assess experimental measurements of electrical potential and current within the ES emitter. The goal for developing the model was to have mathematical formulas that can describe the obtained potential and current maps, extract useful electrochemical parameters, and provide confidence that the observed trends in those maps conform to electrochemical principles. At the same time, the derived mathematical formulas are intended to be simple enough to be handled with minimum computational effort, yet precise enough to simulate maps with less error than observed during experimental acquisitions. A Supplemental Material section, which contains all of the details of mathematical formula derivations, accompanies this document.

A stable electrospray exists only when all relevant parameters fall within a certain narrow range of values. Often a sizeable change of one parameter necessitates a major adjustment of others in order to regain spray stability. In this Perspective, our intention is to take a fresh look at electrospray phenomena and operating parameters that are pertinent to solution conditions commonly found in analytical applications. Our presentation has been made as quantitative as possible, while striving to maintain an elementary approach. The intention was not to derive a model to compete with fundamental theories developed by researchers in the field of electrohydrodynamics but rather to present a “new view” in electrospray phenomena such that an experimentalist might consider an electrospray mass spectrometer as something more than a “black box” device.

This Perspective is not intended to be a comprehensive review or a tutorial of electrochemical cell coupling to mass spectrometry. It is meant to be a quantitative guide for mass spectrometry experimentalists who deal with electrochemical transformations of the sprayed liquid but have difficulty in exploiting its benefits or fighting its adverse effects. This Perspective also seeks to fill the gap between existing advanced theory and everyday analytical lab practice; thus, a goal here is to facilitate experimental implementation of existing theory to electrospray mass spectrometry practitioners. Because of this intentionally limited scope, our selection of literature is subjective and many important publications are neither quoted nor discussed. We refer the interested reader to a selection of published reviews pertaining to electrospray ionization and/or EC/ESI coupling available elsewhere [1–23]. The focus in the current paper is kept on features of electrochemistry/electrospray that have been largely neglected but might be important for analytical practice, especially if one considers how the development of electrochemical derivatization of analytes has become an established and fruitful method [24–38].

Electrospray as an Electrolytic Flow Cell

The Electrospray Process

Electrospray is a process of liquid nebulization induced by the pull of a nearby electric field [39–41]. The liquid exiting the capillary assumes a conical shape, referred to as a Taylor cone. Droplets of electrically charged liquid are expelled from the tip of the cone. There are a variety of spraying modes that have been classified by Clopeau and Prunet-Foch [42]. In our experiments, and in this publication, we deal only with the commonest and most investigated “cone-jet” mode. In this mode, a thin jet (or filament) of liquid emerges from the tip of the Taylor cone, with liquid jet break-up into droplets occurring further downstream (Figure 1). The process of liquid spraying in a gaseous atmosphere is the result of an interplay of forces acting in various directions, the principal force being the electric field interaction with charges on the surface acting to pull the liquid toward the counter-electrode, whereas surface tension works to keep the liquid in one piece and exerts a pull in the opposite direction. Only a certain combination of spray parameters leads to a stable cone-jet mode of spraying [43–51]; outside the stable region, the spray is either intermittent or it consists of multiple jets.

Figure 1

Taylor cone and related concepts

The jet carries away a net charge, so, except in special circumstances [52–54], the charge must be replenished at the incoming end (see discussion of this issue in reference [12]). This is accomplished through an electrochemical reaction at the surface of a metal capillary or on another conducting surface in the ES device with which the power supply is in electrical contact. If the flow of current is restricted, for example, by allowing the ES capillary to float at an ill-defined potential, the electrospray process will stop, as the capillary cannot be charged indefinitely. Thus, it is the electrochemistry at the capillary surface that permits transfer of the necessary charge to sustain the electrospray process. The charge flows from the metal capillary surface, through the electrolyte, to the surface of the Taylor cone.

Ambient Gas Adsorption

Despite the apparent look, ES does not produce a simple, unidirectional downstream transfer of liquid. While operating, the ES system undergoes a gradual change in composition and possibly in conductivity as a result of the inherent electrochemical processes.

The smaller diameter of the Taylor cone jet makes the linear velocity of liquid in the jet far greater than in the wider capillary. Liquid acceleration takes place principally on the outer layer or “skin” of the Taylor cone [55]. When the Taylor cone surface charge carriers accelerate, they transfer momentum to the inside liquid through a shearing stress. That momentum encounters another momentum vector from the opposite or internal side. The resulting momentum in the constrained geometry of the cone results in some liquid flow in backward and circular directions (Figure 1), but this flow encounters the primary liquid flow momentum vector further upstream. The inside volume of the Taylor cone thus has characteristics of a “whirlpool mixer” [56, 57].

The movement inside of the Taylor cone is easy to observe through a microscope by placement of some visible tracers [58, 59]. It becomes very clear that the hydrodynamic velocity of the internal liquid is far greater than the velocity of anticipated ion migration through the interior of the liquid in response to the imposed electric field. The complicated flow patterns inside the Taylor cone disrupt the orderliness of liquid arrival and departure at the ES capillary exit and, thus, cause band broadening that thereby degrades the resolution of separations performed by liquid chromatography or capillary electrophoresis instruments interfaced to ES-MS detectors. Realistic photographs of the cone-jet spray mode (including motion inside the cone) are available in many publications, including those of Zeleny that date back to 1917 [39, 40] as well as others [49, 55–67].

Back flow and lateral mass transfer have another practical consequence. Any liquid surface, charged or uncharged, exchanges molecules with the ambient gas as a result of adsorption and evaporation processes [68–73]. When liquid is electrosprayed, molecules of ambient gas are adsorbed at the Taylor cone’s surface; then, they are laterally transported to the inside bulk, and from there may move upstream and react with sample constituents either in solution or at the metal/solution interface. By placing a wire probe electrode inside the Taylor cone (detailed later in Figure 3), we were able to detect changes of electrode potential depending upon whether the ambient gas was pure nitrogen (an inert one) or air (containing reactive oxygen) [74]. Also, we have shown that the overall potential distribution in the cell [differential electrospray emitter potential (DEEP), see below] is affected by ambient gas adsorption through the Taylor cone skin, and that the effect of adsorbed oxygen from the air is very strong compared with the influence of molecular oxygen, which might have been initially dissolved in the solution prior to starting ES-MS. We have called this the “oxygen effect” [74]. The observed change of the electrochemical potential inside the Taylor cone is significant although gradual; upon initiation of electrospray, it takes hundreds of seconds to reach a steady state. The shift in electrical potential is a response of the system to the ambient gas change through either buildup or removal of electrolytically active species inside the Taylor cone and/or on the electrode surfaces. Recently, it has been experimentally proven that droplets formed by ESI can reverse direction [75] and be re-adsorbed onto the Taylor cone surface [43].

An instructive yet simple experiment demonstrates charging and discharging of the surfaces involved in the spray process. In Figure 2a, a stable cone-jet mode of spraying is established. The potential of the high voltage counter-electrode is stepped higher in increments, whereas the total current to the capillary is being measured. When the high voltage is stepped up, the current to the capillary suddenly jumps higher; next, in a few seconds, it decays back to a value slightly above that observed just before the step. During that time, the length of the Taylor cone becomes smaller and the cone angle increases (i.e., the initial elongation of the filament is followed by a slow reduction in Taylor cone volume). When the high voltage is reduced, the opposite process occurs: the jet filament length is temporarily reduced while the Taylor cone grows larger in volume and the current spikes in the opposite direction. Figure 2b shows the accounting of charge, which is measured by integrating the additional current generated in the transition time. After completing the entire cycle, the amount of extra charge removed from, and put into, the Taylor cone balances out.

Figure 2

(a) Total electrospray current (nA) vesus high voltage (V). Solution : MeOH with 225 μM KCl; positive ion mode. Distance between the end of capillary and high voltage counterelectrode is 6.9 mm. (b) Charge accumulation on the Taylor cone extracted by integration of current jumps in panel (a)

In the equivalent circuit of the electrospray device, the charge separation accompanying droplet formation that occurs at the end of the jet filament is believed to be the current limiting element [76–79]. The process of adjusting Taylor cone size and relevant current to a new, higher field is surprisingly slow. Nonfaradaic charging of the capillary metal interface will occur relatively quickly, but the main temporal limitation lies in adjustment of the jet filament to the new voltage conditions. The jet has sufficient flexibility to pass a higher current but its ability to pass a higher volume of liquid is far more limited. In the moments after a change in potential, liquid inflow keeps the whole Taylor cone surface in a field higher than otherwise determined by force equilibrium conditions, which pushes the current temporarily higher. As the volume is pumped out, the Taylor cone volume diminishes to a size determined by the steady state conditions.

The sluggishness of this Taylor cone size adjustment has the beneficial consequence that one can suddenly increase the high voltage without losing ES stability. A sudden increase of the electric field causes the filament to disintegrate at an extended distance. In reducing the electric field, the jet must not be allowed to shrink to zero length, where the stable cone-jet mode of spraying breaks down. Thus, electrospray in cone-jet mode must always be “jump started” to a higher electric field than the necessary minimum corresponding to a given set of operating parameters (e.g., see hysteresis in current-voltage plot in reference [80] and also reference [81, 82]).

The above description illustrates why a stable operation in cone-jet mode may be achieved only within a somewhat narrow range of parameters. When venturing outside of these limits, new phenomena may occur, as for example, crown mode spraying [42] or corona discharge. Only a narrow breadth of Taylor cone angles are stable, which leads to only a limited range of allowed electric potential gradients that can support a stable spray for a given range of electrolyte conductivities while employing a particular range of flow rates. Only under these conditions are there enough ions on the Taylor skin surface, and only then are they accelerated to a proper speed to transfer all the necessary momentum to the liquid to form a stable jet.

Electrodes in Electrospray

The electrospray device can be considered to be an electrolytic flow cell [76–78, 83]. The electrochemical cell must consist of an anode and a cathode. The anode is the electrode where electrons are transferred from solution to the electrode. The oxidizing electrode is an anode regardless of its potential with respect to the cathode and regardless of the polarity of charge on its surface [84–86]. A standard way to look at electrospray electrodes (in the positive ion spraying mode) is to assign the anode as the electrospray capillary. By contrast, the cathode, where ions are reduced, corresponds to the metal part(s) of the mass spectrometer where ions strike and accept electrons. The physical space between such electrodes consists of distinctively different regions. One part is a regular liquid, next is a gas that contains charged droplets, then solvated or “naked” ions under low pressure. The presence of the gaseous region in the heart of the system represents a substantial divergence from what one typically considers as constitutive elements of an electrochemical cell.

For a metal electrode, such as one found in a common electrolytic cell, a charged layer of a liquid is attracted by an electric field originating on the metal (charges in the bulk metal). In the Taylor cone, charges are influenced by the electric field produced by a distant source (charges in the metal of a high voltage counter-electrode). The liquid sides of these two kinds of interfaces have similar looks [87–89]. The role of the electrode in the electrochemical cell is to provide or remove charge. A metal electrode does this by electron transfer in the redox process occurring at the metal/electrolyte interface. The Taylor cone does it by removing charged ions through spraying them out of this part of the system to another part where they, in practice, do not influence the electric field inside. Because the Taylor cone removes not only charge but also mass, the mass must be constantly replenished by flow of electrolyte to the capillary. The Taylor cone surface is positively or negatively charged depending upon the polarity of operation. This surface charge counterbalances the external electric field to a large degree, but not completely. Some electric field still penetrates into the bulk electrolyte volume. This internal field is directed toward the charged Taylor cone skin surface.

Given these limitations, how can the potential at the Taylor cone skin be defined? In a regular electrochemical cell, potential difference can be easily measured by a voltmeter with one lead clipped to a reference electrode. This total potential difference between two electrodes is distributed according to Eq. 6, which is shown later in this article. This type of experiment cannot be done at the Taylor cone surface. There is no transfer of electrons on the Taylor cone skin; neither is there a chance that a Nernst-like equilibrium is being established. If one tries to probe the surface using a metallic connector, the latter will become an electrode in its own right; it will form a new current loop with the capillary or with the high voltage counter-electrode. We have observed that if our wire probe electrode tip punctures the Taylor cone skin, the potentiostat voltmeter reading jumps to a significantly higher value (e.g., 5 to 9 V); this value far exceeds that of the highest reading in a typical potential map (e.g., see Figure 5a and b), which is less than about 2 V.

Electrochemical Processes Inside the Electrospray Capillary

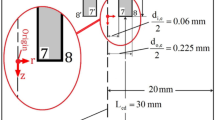
In our laboratory, we have constructed a device (Figure 3) capable of monitoring potential and current along the interior of an electrospray emitter [90, 91]. The device consists of a platinum wire probe electrode that is isolated from the surrounding platinum ES capillary. The potential difference, or the current flowing between the wire probe electrode and the grounded ES capillary, is measured as a function of movement of the disk-like wire probe along the interior of the ES capillary. A plot of potential difference versus distance from the ES capillary exit has been termed a differential electrospray emitter potential or “DEEP” map. Current maps consist of plots of current at zero potential difference between the wire probe and the ES capillary.

Figure 3

Experimental set–up. Capillary diameter is overstated for visibility. (a) gas inlet; (b) solution inlet; (c) wire probe electrode with silica shield; (d) wire probe electrode moving mechanism; (e) connecting cross; (f) electrochemical workstation; (g) high voltage supply; (h) reference electrode lead; (i) working electrode lead; (j) high voltage electrode; (k) Taylor cone skin—place where electrochemically active gas is absorbed; (l) end of wire probe electrode in contact with sprayed solution; (m) Faraday cage

The Electrospray Emitter as an Electrolytic Trough

If two electrodes made of the same metal are placed in an electrolyte solution, a voltmeter connected to the metals will not read a potential difference of zero. In reality, the two pieces of the same metal will become polarized and behave as anode and cathode. The measurement process itself will polarize them (solutions of low conductivity will render the polarization more visible, as will inexpensive voltmeters). Now consider three electrodes in the same solution with two of them performing electrolysis; current is passing between them. The reading of the voltmeter clipped between either of the current passing electrodes and the third one will represent the sum of the original polarization process plus the overpotential due to the passage of current.

The very old concept behind mapping currents and potentials in solution is that of the electrolytic trough [92]. It consists of a vessel containing any number of electrodes set at a variety of potentials. A probing electrode that meanders around the vessel can directly read the potential at any given point. Figure 4 is an actual experiment performed in a long, thin vessel. The electrodes are all made of the same metal (Pt); cathodes are of the same size, whereas the anode has the combined size of the two cathodes. The wire probe electrode is an isolated wire with only its tip in contact with the electrolyte. Current is set to be constant; it flows from the anode to the two cathodes. In the lower panel of Figure 4, one can see how current is split between the two cathodes. Although the potential of those cathodes (on the metal side) is the same, the potential very close to the cathode on the electrolyte side is different. Cathode number 1 is closer to the anode; it produces more current, and the current going from electrolyte to the metal of this cathode faces a larger overpotential. That extra amount of overpotential is equal to the ohmic drop (iR) of potential attributable to resistance of electrolyte between cathode number 1 and cathode number 2. The slope of the potential drop with distance between the two cathodes is less than that between cathode number 1 and the anode. Next, imagine that there are a greater number of small cathodes located side-by-side. The potential map will then take the form of short straight lines with gradually changing slope. In the limit of a continuous cathode, it will be a smooth curved line. A cathode can be rolled up to form a ring. Many rings can be joined to form a cylindrical tube. Our electrospray capillary fits this description of a cylindrical tube, and the wire probe in our measurement device can be considered as the probing electrode.

Figure 4

(a) Electrolytic trough—a simple system with two cathodes and an anode. A movable element (electrode) reads the potential on voltmeter V₂. No current flows through it, so its position does not change the total applied potential, which is read by voltmeter V₁. Total current is read by ammeter A, partial currents are read by ammeters A₁ and A₂. (b) The actual potential map for that electrolytic trough

Potential and Current Maps

The use of our wire probe electrode has permitted the acquisition of a great number of differential electrospray emitter potential (DEEP) maps in electrospray capillaries containing a variety of solutions [91, 93, 94]. Examples are given in Figure 5a and b. Positive ion mode (oxidative) maps have the same features as negative ion mode (reductive) maps.

Figure 5

Potential maps. (a) Negative ion mode, electrolyte: methanol/chloroform (50/50) with KCl concentration: 0, 50, 100, and 240 μM. (b) Combined metal–glass capillary in positive ion mode, electrolyte methanol 100% with KCl concentration from 33 to 450 μM. In the glass capillary region, the limiting molar conductivity of the electrolyte determined from the slope of the curve in the glass section is: Λ₀ = 141 [cm²Ω^–1 mol^–1]. (c) Decay constants extracted from potential maps with linear fits (see text for discussion)

Potential and current maps are strongly influenced by the concentration of the electrolyte. More concentrated (more conductive) electrolytes cause the potential to decay more slowly as one moves further into the capillary; less conductive solutions make potential maps drop off in a steeper fashion. In other words, upon entering the ES capillary, the potential map slope goes down more slowly for a more conductive electrolyte and the current is produced from deeper within.

When a nonionic (no change in solution conductivity), easily oxidizable species (one which does not require high potential to deliver the current), like the polycyclic aromatic hydrocarbon ‘rubrene,’ is added to the solution subjected to ES, a substantial decrease of the potential at the capillary exit is seen. The total electrospray current does not change; the reduction of potential is independent from the effects of conductivity change. The same potential reduction is seen when water is added to dry acetonitrile. The standard potential of the cell becomes lower, so the whole potential map is lowered [91].

Shown in Figure 6 is an example of a current map. Even if a potential map shows a high potential at a given position in the capillary, this does not mean that a high level of current will be produced there, as measured potential expresses only the ability to deliver current, whereas the actual magnitude of the current also depends upon other limitations, for example, mass transport or gas evolution. Current and potential maps are related to each other through the Butler-Volmer (B-V) equation (see Eq. 5 below). Because current is exponentially dependent on the potential, current maps will always be steeper than potential maps.

Figure 6

Current maps; positive ion mode. Solution: acetonitrile 100% with lithium trifluoromethylsulfonate 20, 50, and 100 μM. (a) Actual maps. (b) Data from panel a divided by the total electrospray current for the given concentrations (from Reference [93])

When current and potential maps are plotted against each other, they form a Tafel plot. In some instances, instead of forming a monotonically rising line, the plot makes unexpected turns. Such cases indicate that electrochemical conditions are not uniform throughout the whole length of the capillary; this occurs when the electrochemical reaction responsible for current production is not the same at different places in the ES capillary. So, despite the B-V relation, current and potential maps contain different information, and are thus complementary to one another.

The above conclusions about map slopes and their relation to solution conductivity can be conveniently discussed in terms of the dimensionless Wagner number (Wa) [95, 96], which is the ratio of polarization resistance (i.e., resistance of the interface at the electrode, R_η) to electrolyte resistance (R_s): Wa = R_η /R_s. When the Wagner number is large everywhere, that is, large for every locus of the electrode, current transport is governed by polarization resistance. In the extreme case, when the Wagner number approaches infinity, the current reflects electrode kinetics (i.e., after passing the interface, current flow through the electrolyte is practically unrestricted). Conversely, when the Wagner number is small, polarization of the interface does not influence the distribution; instead, only solution resistance matters and the problem of current distribution is reduced to the geometry of the electrochemical cell. In the extreme, when the Wagner number approaches zero, the whole cell behaves like a regular ohmic resistor. The Wagner number can be made smaller by raising the resistance of the electrolyte, but only when we deal with a very reactive species. Thus, not only do easily oxidizable species make maps with lower slopes, but also, the so called “ease of reduction” must be cast in relation to electrolyte conductivity. In sufficiently conductive electrolytes, readily oxidizable species do not cause lower slopes, but rather, they move the whole map downward.

Glass Capillary

In Fig. 5b is shown a map of potential inside the composite electrospray capillary. One part is a regular platinum capillary, a second part (closer to the exit) is made of glass. The inner part of the map corresponding to the metal region has the same features as maps obtained for the “metal only” capillaries. The outer (glass) part of the map is a straight line. This is exactly what is expected from a nonconductive tube filled with a liquid behaving like an ohmic conductor. The slope of the linear (glass) part of the map, with known internal diameter, can be used to calculate the conductivity of the solution. Indeed, this calculated conductivity gives values in excellent agreement with literature data [97–99] and by this, it demonstrates the soundness of the device and measurement method.

The DEEP map in Fig. 5b shows that when the wire probe enters the Taylor cone there is no change of slope. The map shows that the internal bulk of the Taylor cone has no special electrical properties and the cause of increased slopes on the metal capillary maps was due to a “back-shift” of our measuring device. The term "back-shift" signifies that the measured potential of our wire probe located in the middle of the ES capillary, concentric with the capillary axis, in fact corresponds to a potential at the metal/solution interface located at a point further upstream (back into the capillary). The second factor contributing to the slope increase inside the Taylor cone is the raised electrolyte resistance between the wire probe and the metal capillary electrode attributable to constricted geometry as the probe enters the cone. For a glass capillary, this effect appears relatively small because it adds to an already augmented resistance caused by a greater distance between the tip of the wire probe and the metal capillary contact. That is to say, when the electric contact is made elsewhere upstream (as is the case with the attached glass capillary), the ohmic drop must have a higher value. The glass capillary introduces an extra resistance created by the extra electrolyte that it contains. In order to overcome this extra resistance, a higher pseudo-potential at the Taylor cone is needed.

Extrapolation of the glass capillary potential map to the end of the Taylor cone is more precise than for a regular (metal) capillary because, here, the map is a straight line plot, and not a steeply rising function [91]. This extrapolation gives a Taylor cone surface “pseudo” potential of ~4 V. This number is called a pseudo-potential because it has the same effect as if there were a real electrode with this potential.

Skin Current and ES Capillary Front Surface

It has been observed many times that the shape and size of the electrospray capillary orifice influences the production of electrosprayed ions [1]. Tapered capillaries have been used, as have capillaries with special coatings [100]. The front capillary surface is particularly sensitive to conditions of electrospray. If it is made of metal, then, in close proximity to one another are: the metal surface, the ambient gas, and the charged liquid–gas interface. Compared with the inner surface of the capillary, the metal front surface is in better electrical contact with the jet filament because the resistive path along the skin is shorter than through the bulk. In addition, the skin is more conductive than the bulk because of the relative ease of movement of charge carriers. Thus, the portion of the total electrospray current that is transported through the skin from the front capillary surface to the jet is larger than would be expected to occur from simple geometric considerations. Actually, it is difficult to imagine that the current produced at the front surface sinks, in large part, into the bulk instead of flowing through the lowest resistance path (i.e., straight along the Taylor cone skin). The above shows that the skin can be a very conductive direct contact to the ES capillary, largely bypassing the electrolyte.

Our mapping methods are not capable of measuring skin current directly. Actually, the potential and current maps obtained were only maps of part of the total electrospray current. The remaining part, which flows directly from the front surface to the Taylor cone jet, was not directly measurable. Only when employing the attached glass capillary could the obtained maps be considered to be probing the total electrospray current because the glass capillary does not generate front surface current. Thus, a part of the current evades our measurement method in metal-only capillaries. We have noticed that even when our wire probe was placed in the interior of the Taylor cone, appearing geometrically much closer to the cone apex than the front surface, it was able to take up at best about 50%–60% of the total electrospray current. The remainder of the current was produced at the ES capillary, most importantly at the ES capillary front surface. This occurred despite the fact that the distance to the front surface from the Taylor cone apex was considerably greater than the distance from the wire electrode tip, plus the fact that the wire probe electrode surface area was also greater than the area of the capillary front surface. The underlying issue was not that of a simple current redistribution resulting from an excessive overpotential on the wire electrode because when the capillary was electrically disconnected, the wire probe was then able to conduct all of the current without any detrimental effects to spray stability, or to the shape or size of the Taylor cone. The magnitude of the total current was maintained regardless of the wire probe’s position, whether it extended into the Taylor cone or it was withdrawn deep inside the capillary.

Theories on Principles of the Electrospray Process

The stage for electrochemical processes to occur inside the electrospray capillary is set by a number of external parameters. One group relates to properties of the sprayed liquid such as conductivity, viscosity, surface tension, and electric permittivity, whereas the second group relates to the geometry of the sprayer and applied external potentials. From an electrochemistry standpoint, the primary information to be extracted from the comprehensive list of parameters is the total electrospray current (I_T) and the electrochemical potential at the very tip of the electrospray capillary (U₀) because these characteristics influence all other features of the ES electrochemical cell. Much theoretical work has been performed to mathematically describe trends related especially to ES current. Below is a brief account, but not a comprehensive review, of some selected important examples of such work that we are including to situate, and cast light upon, a new mathematical model to describe current and potential in ES emitters that we present later in this paper.

For historical reasons, we start with the Hendricks model [101, 102]. Here, the liquid surface of the Taylor cone is charged, stationary, and, at every point, in equilibrium with the external electric field, and is assumed to be equipotential. The model leads to a formula for total electrospray current, I_T [101]:

$$ {I}_T={\left[{\left(4\pi /\varepsilon \right)}^3{\left(9\gamma \right)}^2{\varepsilon}_0^5{Q}^4{\varLambda}_0^3{c}^3{E}^3\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$7$}\right.} $$

(1)

where E is the outside (gas side) electric field, Q is the solution flow rate, γ is the surface tension, ε₀ is the electrical permittivity of vacuum, ε is the relative permittivity, Λ₀ is the electrolyte limiting molar conductivity, and c is the concentration. If we plug in numbers for a typical electrospray solvent, methanol, we get a total electrospray current I_T = 7 nA. The result is less than the experimental value of 73.3 nA. The power dependence of total electrospray current on electrolyte conductivity is close to, but does not exactly agree with, experimental data. The equation indicates a power dependence of 3/7, whereas our experiments produce a square root (=1/2) dependence.

There are many more advanced treatments of the electrospray current flow. They were derived in the field of fluid electrodynamics. By thorough consideration of flow conditions and electric forces, exact relations of total current as a function of various fluid parameters were derived. A good deal of literature has been produced on this subject [18, 45, 63, 103].

For example, Fernandez de la Mora [63, 104] arrived at the conclusion that the original conditions for the equilibrium of forces formulated by Taylor for perfect conductors are essentially correct in solutions with high (but non-metallic) conductivities, but they are satisfied only in the apex region of the cone. Using dimensional analysis of the physical quantities involved, and casting them against his experimental work, he arrives at the conclusion that the total electrospray current scales as:

$$ {I}_T=f\left(\varepsilon \right)\sqrt{\frac{Q\gamma \kappa }{\varepsilon }} $$

(2)

where f(ε) is a function to be determined empirically through experiment, κ is the conductivity, and other symbols are as above. The power dependence of total current on conductivity and flow rate is ½, in agreement with experimental measurements. The author also divides the total current into the skin current that flows along the Taylor cone skin and the bulk current that flows through a body of liquid.

Gañan-Calvo et al.’s detailed model [55, 105–108] of total electrospray current is based on an extension of the classic work by Melcher and Warren [109–112] of the electric field surrounding the jet. The analysis leads to two limiting formulas for total electrospray current: one is for liquids of high conductivity and high viscosity [107]:

$$ {I}_T={I}_0\left(6.2\sqrt{\frac{Q}{Q_0\sqrt{\varepsilon -1}}}-2.o\right) $$

(3)

whereas the second applies to liquids of low viscosity and low conductivity:

$$ {I}_T={I}_0\left(11.0{\left(\frac{Q}{Q_0}\right)}^{\frac{1}{4}}-5.0\right) $$

(4)

where I₀ is reference current: I₀ = (ε₀*γ²/ρ)^1/2, [ρ is density (kg/m³)], and Q₀ is reference flow: Q₀ = ε₀*γ/(ρ*κ). This model also predicts a square root dependence of electrospray current on the conductivity and liquid flow rate and produces acceptable predictions of the total electrospray current.

A more recent comprehensive treatment of the problem by Higuera [113] addressed the current transported by the jet and the nearby cone apex. By setting equations accounting for the balance of forces present, followed by numerical simulation, he arrived at a result in which, indeed, the current is proportional to the square root of solution flow. But this result was only valid within a low flow rate regimen. When the flow rate was pushed higher, the accompanying current increase did not keep up, but instead, leveled off.

Jackson and Enke presented an equivalent circuit for the electrospray device [79] showing a single loop of current (i.e., the current in each portion is the same). The loop consists of the power supply that provides as much current as necessary for a preset voltage; the air gap is characterized as an element that poses resistance, but does not diminish the total current. The electrolytic solution creates ohmic resistance, and, lastly, the two electrodes, one in the ES capillary and the other one at the opposite end of the air gap, are each represented as resistors in series with batteries whose polarities oppose that of the power supply. This description of the electrodes is equivalent to assigning a half-cell potential (E^ø) to each electrode. The experimentally obtained curve for total current versus potential is a product of all current-potential curves for each element. This analysis is used to evaluate current versus potential for the charge separation process leading to the formation of electrospray droplets. This important charge separation process occurring in the electrospray current loop is deemed to be the feature that imposes a constant current on the ES device.

The Van Berkel group, among many other contributions to the electrochemistry/electrospray field [76–78, 114–120], attempted a full-scale numerical simulation of current and potential distribution in the electrospray capillary [121]. The project was based on solving the Laplace equation with boundary conditions corresponding to the actual geometric and flow conditions in the electrospray capillary. To this end, it was convenient to assign the tip of the ES filament as a “virtual cathode.” This was the mathematical equivalent of placing an electrode at the very end of the Taylor cone. The final result of Van Berkel and coworkers’ calculations was qualitatively correct. It had all the essential features of potential and current maps; however, owing to the employed assumptions, the magnitude of some numbers can be called into question. For the mixture of acetonitrile and water, the calculation predicted unrealistically high current densities very near to the capillary exit and the area close to the tip of the capillary produced an unrealistically large (compared with our experimental results) fraction of the total current. This probably came from the fact that the limiting current for water oxidation had been set at a high value. Another problematic theoretical result was the current map, which does not fall abruptly with movement toward the inside of the capillary but, instead, forms a short plateau. In our experimental measurements, no such plateau was found. We acknowledge that our measurements were done on a capillary with an internal diameter five times wider than the diameter used in the simulation, so the cross-section where the flow is unrestricted was larger. By contrast, in the small capillary used for calculation, a large fraction of the cross-section was taken to be a stagnant layer. The authors’ assumption concerning the thickness of the stagnant boundary layer was based on standard electrochemical values for common electrodes in stagnant solution, but for thin capillary flow conditions, the assigned stagnant layer thickness was likely an overestimation, leading to an underestimation of the depth of current production into the capillary.

“Nonlinear Resistor Electrospray Capillary Model” to Describe the Electrical Equivalent to the Electrospray Capillary

In order to precisely describe the distribution of potential inside the electrochemical cell, one has to solve the Laplace equation for electrical potential with appropriate boundary conditions [122, 123]. When the liquid in the cell is in motion, fluid dynamics equations must be included. In some rare cases of highly symmetric systems, a solution can be obtained in an analytical form [124–129]. In all other cases, one has to resort to numerical simulation, such as the work of Van Berkel et al. described above [121].

The values of the potential adopted by the capillary in the electrospray process have been shown to have a direct influence on the products detected [130]. Analyses of the electrochemical potential distribution along flow cell electrodes, such as the electrospray capillary, have been based on equations of hydrodynamics in combination with an account of electrical current flow. They required much effort and computer time and, even then, the outcome was a complicated function [131–136]. The results were strict but difficult to fathom. Here, we present a simple “nonlinear resistor electrospray capillary model” that has the advantage of employing mathematical formulas that can readily handle our experimentally generated data. In any instance, because of the nature in which they were obtained, our experimental numbers contain systematic and random errors; these errors are likely to be bigger than the compromised accuracy caused by the simplicity of the model.

Assumptions

The “nonlinear resistor electrospray capillary model” has been constructed by first dividing the electrospray capillary into a large number of sectors (Figure 7). Each sector represents an annulus with a uniform surface area and volume of electrolyte inside. Each sector has resistance R_s, which is the resistance of a cylinder of electrolyte and a second resistance, R_η, which is the resistance of the interface. R_s is assumed to be linear, according to Ohm’s law, meaning that a change of potential produces a linearly proportional change in current. R_η may or may not be linear depending on the particular circumstances. Because we can make the sector infinitely small, in the end, we can arrive at a mathematical formula describing the potential map: U(x) and current map: i(x), which then can be dealt with by regular calculus methods.

Figure 7

Electrical equivalent circuit of electrospray capillary. U_0: total potential, R_s: resistance of electrolyte in one capillary sector, R_ηi: resistance of interface in i^th capillary sector, I_T: total current flowing through capillary, ∆x: length of one sector

In employing the model, it is assumed that surface reactions satisfy Butler-Volmer (B-V) type kinetics. In principle, such kinetics are satisfied only when a reversible pair of redox reactants can be identified at the electrode, and when exchange current can flow in both directions. This may not always be the case in the electrospray capillary; nonetheless, this type of the B-V mathematical formula has proven to be useful. The equation is:

$$ i={i}_0S\left[\left(1-\frac{i}{i_{cL}}\right){e}^{-anF\left|{\eta}_c\right|/RT}-\left(1-\frac{i}{i_{aL}}\right){e}^{\left(1-a\right) nF\left|{\eta}_a\right|/RT}\right] $$

(5)

where i is current (A), i_cL is the cathodic limiting current (A), i_aL is the anodic limiting current (A), i₀ is exchange current density (A/cm²), S is the area of the electrode (cm²), n is the number of electrons in electrochemical reaction, R is the gas constant = 8.31451 (J*K^–1*mol^–1), T is temperature (K), F is the Faraday constant = 96,485 (C/mol), α is a symmetry factor of the electrochemical reaction (dimensionless), η_a is the anodic overpotential (V), η_c is the cathodic overpotential (V). If the reaction is symmetrical, that is α is equal to 0.5, and the limiting current is high compared with the total current, the exponents can be combined into a more easy to handle hyperbolic sinus function.

The total potential drop (U) through the cell consists of the sum of the potential drop at the anode, the potential drop through the electrolyte (i*R where i is the current and R is the resistance of the electrolyte), and the potential drop at the cathode. The potential drop at the electrodes consists of the standard potentials of the half-reactions (anodic E_a ^Ø ; cathodic E_c ^Ø) plus accompanying overpotentials (anodic η_a ; cathodic η_c) as shown below.

$$ U={E}_a^{\phi }+{E}_c^{\phi }+\left|{\eta}_a\right|+\left|{\eta}_c\right|+iR $$

(6)

The derivation of U(x) showing potential as a function of distance into the ES capillary contains a simplifying assumption that the standard potential of the overall reaction (that is the sum of anodic E_a ^Ø and cathodic E_c ^Ø) is zero. A proper standard potential for the reaction may be added, as needed and, in the end, it will not influence the slope of the potential or current map (see Eq. 15).

The above treatment (starting with Eq. 6) leads to a differential-integral equation (see Supplemental Material for all details) [127, 128, 137]:

$$ {\left(\frac{dU(x)}{dx}\right)}_{x=x}=-a+b{\displaystyle {\int}_0^x \sinh \left[\beta U(x)\right]dx} $$

(7)

$$ a=\frac{I_T}{\varLambda_0c\pi {r}_c^2}\left[\frac{V}{cm}\right] $$

(8)

$$ b=\frac{4{i}_0}{\varLambda_0c{r}_c}\left[\frac{V}{c{m}^2}\right] $$

(9)

where c = concentration of electrolyte (mol/cm³), β = nαF/(RT) (1/V) [for one electron (n = 1) symmetrical (α = 0.5) reaction β = 19.48 (1/V)], F (Faraday constant) = 96,485 (C/mol), R (gas constant) = 8.31451 ( JK^–1 mol^–1), T temperature (K), n = number of electrons (in electrochemical reaction), α = symmetry factor of electrochemical reaction, I_T = total electrospray current (A), i₀ = exchange current density (A/cm²), r_c = radius of the electrospray capillary [cm], and Λ₀ = limiting molar conductivity (cm²Ω^–1 mol^–1). Note also that integration is over dx, not over dU so it cannot be performed in a straightforward manner.

Linear Approximation

For small current densities and small overpotentials, we can apply a linear approximation to Eq. 7 by expanding the hyperbolic sinus function and dropping all higher terms. The linear approximation solution has all essential features of experimentally acquired potential maps. Later, we will show how non-linearity is dealt with in the solution by including extra corrective terms.

The linear approximation leads to a formula for a potential map in the form of a simple exponential decay:

$$ U(x)={U}_0{e}^{-\sqrt{\beta b}x};{U}_0=\frac{a}{\sqrt{\beta b}} $$

(10)

where U₀ is the value of the potential at the capillary tip, that is, at x = 0. For the total electrospray current we obtain:

$$ {I}_T=\xi \sqrt{c} $$

(11)

where ξ is a proportionally factor combining all other constants.

In the linear approximation, the total electrospray current is a square root function of concentration of electrolyte, provided that the U₀ term is the same in each case. Surprisingly, Eq. 11 has exactly the same square root dependence on the electrolyte conductivity as the formulas arrived at by advanced theoretical models. However, it has nothing to do with the actual physics of electrospraying and is only the consequence of electrical circuit considerations caused by a specific geometry of a tubular capillary.

The decay rate of U(x) in the potential maps in the linear approximation will be governed by a decay constant:

$$ \sqrt{\beta b}=\sqrt{\frac{4\beta {i}_0}{\varLambda_0c{r}_c}}\left[\frac{1}{cm}\right] $$

(12)

where all the terms have the same meaning as above. The larger this constant becomes, the faster the potential will decay from its maximum value, U₀, at the capillary tip. It is evident from the formula that the potential decay will be faster for a facile reaction (i.e., one which has a high exchange current density, i₀), and also will be faster for multi-electron reactions (β is multiplied by the number of electrons exchanged). In more conductive solutions, where c and/or Λ₀ is higher, the potential will decay more slowly and will penetrate more deeply into the capillary, and the current production will be spread more evenly along the capillary inner walls. In less conductive solutions, potential will decay faster and it will squeeze the current production into a smaller area at the capillary exit. Larger capillaries (large r_c) cause the potential to decay more slowly, whereas smaller capillaries make it decay more quickly, so small capillaries are the ones that squeeze current production to the very tip. This all is in good agreement with experimental data and intuitive understanding.

Decay rate is not a function of total electrospray current. It can be obtained by taking the derivative of the experimental potential map. A derivative is a good experimental parameter, better than, for example, the maximum potential U₀, because when calculating a derivative the constant factor (here: cell standard potential E^ø) drops out of the equation. Initially, U₀ was treated as overpotential in the sense of Eq. 6, where the sum of E_a ^ø and E_c ^ø was assumed to be zero. Now we see that this initial assumption was valid because the experimental potential maps preserve the value of the decay constant regardless of how we treat U₀, U(x), or cell standard potential. If the total current changes for a reason that will not depend on the above parameters, such as a change in external high voltage, the slope of the potential map at a given point x, within the ES capillary, will remain unchanged.

The pre-exponential factor, U₀, is the value of the potential (including any overpotential) at the capillary exit, point x = 0. It will grow as total electrospray current grows, but it will diminish when conductivity increases. If we take Eq. 10, explicitly expand constants a (Eq. 8) and b (Eq. 9) and replace the total current by relation from Eq. 11, we obtain:

$$ {U}_0=\frac{\xi }{\sqrt{4{\pi}^2\beta {i}_0{\varLambda}_0{r}_c^3}} $$

(13)

U₀ is not a function of total current, neither is it a function of solution concentration (however, it is a function of conductivity through Λ₀). Because U₀ is independent of total current, this derivation points to the conclusion that the potential maps for different concentrations of the same electrolyte ought to converge and cross at x = 0. If they do not, they probably correspond to different electrochemical reactions.

The derivative of potential (including any overpotential) at x = 0, according to Eq. 7 will always be equal to –a:

$$ {\left(\frac{dU(x)}{dx}\right)}_{x=0}=-a=-\frac{\xi }{\varLambda_0\pi {r}_c^2\sqrt{c}} $$

(14)

Thus, slopes of potential maps at x = 0 ought to form a straight line when plotted against 1/c^1/2.

In Figure 5c are two examples of the use of this simple theoretical nonlinear resistor electrospray capillary model to analyze experimental data. Decay constants of potential maps from Figure 5a and b are recovered and plotted against concentrations in Figure 5c. The curves shown in Figure 5a do not cross exactly at x = 0 but, instead, at some positive value. The reason for this small discrepancy is a systematic error of our method (the “back-shift”), which we have discussed previously in the section pertaining to the glass capillary emitter. For a solvent corresponding to the data in Figure 5a, the total current can be fitted by the formula I_T = 6.06*c^1/2 (where I_T is in A and c in μM). Figure 5c shows a straight line for the plot of this experimental data as the model predicts. From the value of the slope, after plugging in other required numbers, we get a current density for reduction: n*i₀ = 4.28*10^–7 (A/cm²). The second set of data shown in Figure 5c illustrates obtainment of the i₀ parameter from experimental decays plotted in Figure 5b. The dependence is also linear, the slope yields n*i₀ = 8.34*10^–7 (A/cm²). These values are typical for oxidation and reduction of methanol on a polycrystalline platinum surface. The essence here, however, is not to determine exchange current density, but rather, to demonstrate that the electrospray capillary is an electrochemical system that lends itself to measurement and simple analysis.

Complete Solution

The linear approximation is only an approximation; for a complete description we must solve Eq. 7. Of course, potential and current maps can be simulated and plotted with simple numerical routines. Nonetheless, only analytical solution can give an intuitive insight into how input parameters reflect on the final formula. The final solution (see Supplemental Material) is:

$$ U(x)=-\frac{2}{\beta } \ln \left[ \tanh \left(\sqrt{\beta b}x+\sqrt{\frac{b}{\beta {a}^2}}\right)\right] $$

(15)

This formula is straightforward and simpler than found in the literature [127, 128, 137]. After expansion of U(x) in a power series we see that:

$$ U(x)=\frac{4}{\beta }{e}^{-\sqrt{\beta b}\left(x+\frac{2}{\beta a}\right)}+\frac{4}{3\beta }{e}^{-3\sqrt{\beta }b\left(x+\frac{2}{\beta a}\right)}+\cdots $$

(16)

The first term in the series has exactly the same decay factor (β*b)^1/2 as in the linear solution. However, the series is converging slowly and many terms (about 20) must be used to see proper curvature of the potential map at low x values.

The full solution gives U₀ (for x = 0) in the explicit form:

$$ {U}_0=\frac{1}{\beta } \ln \left(\frac{\beta {I}_T^2}{4{\pi}^2{\varLambda}_0c{r}_c^3{i}_0}\right) $$

(17)

If we use formula 17 relating the total current to concentration: I_T = ξ*c^1/2 we get:

$$ {U}_0=\frac{1}{\beta } \ln \left(\frac{\beta {\xi}^2}{4{\pi}^2{\varLambda}_0{r}_c^3{i}_0}\right) $$

(18)

It is reminiscent of the linear approximation. U₀, the maximum potential at the entrance of the capillary, is not a function of electrolyte concentration (i.e., conductivity), meaning that even without the linear approximation (i.e., in the more general case), all potential (and current) maps ought to cross at x = 0 (ignoring back-shift). For a typical range of electrospray currents and typical reactions, one should not expect big changes in the value of U₀ because U₀ is a logarithmic function of exchange current density, i₀. To see a significant change in U₀ requires orders of magnitude of change in the value of i₀.

Further discussion of the nonlinear resistor electrospray capillary model, including how to use it to obtain a Tafel plot of the electrospray capillary, or to calculate the extent of the current production in the capillary, can be found in the Supplemental Material.

Conclusions

Electrospray is not only a nebulizing device, it is also an electrochemical device, and the results of its use in experimental practice show the work of both phenomena. Many researchers have enough good fortune using electrospray ionization as a “black box,” whereas others are adept at using an electrochemical cell coupled to an electrospray device to produce novel redox products that are detectable by a mass spectrometer. A large number of chemical reactions can be studied using a simple upstream “on-line” electrochemical cell, which can be independently driven by use of an electrochemical work station. Many intricacies of such coupling were thoroughly discussed in a book chapter by Van Berkel and Kertesz [78]. In addition to the compounds existing in the initial solution, adsorbed gases originating from the ambient gas atmosphere may offer yet another avenue to interesting electrochemistry, or additional solution chemistry, taking place in the vicinity of the Taylor cone.

The device (Figure 3) employed to map potential [91, 94] and current [93] in the ES emitter, and to uncover the “oxygen effect” of adsorbed ambient air [74] consists of a wire probe electrode placed along the central axis of the ES capillary. In addition to the above functions, the probe electrode can be used to alter the potential distributions and to produce current by electrochemically transforming molecules on its metal surface. This probe electrode can be polarized in any direction with respect to the ES capillary, thus allowing one to “steer” the electrochemical processes occurring at its surface and at the surface of the ES capillary. The probe reaction may actually reverse a previous electrochemical reaction that had occurred upstream at the ES capillary surface, or it may add a follow-up electrochemical step. Because the probe electrode can be moved, it can provide a temporal dimension when combined with other data. This experimental set-up offers the possibility to observe short-lived reaction intermediates that are not stable enough to survive solution transport, for example, if produced further upstream in a self-standing electrochemical flow cell.

Despite all of the above advances, there are still some areas in which better knowledge of electrochemical processes taking place in the electrospray capillary will be necessary to properly analyze obtained data (e.g., see a recent example pertaining to anodic oxidation of phenylenediamines during electrospray [138]). Studies of the kinetics of redox reactions are also possible, but they can quickly become quite complex: encompassing primary reactions occurring at the metal/solution interface as well as secondary chemical reactions, which in turn, may undergo electrochemical transformations that, yet again, engage in electron exchange. The electrospray process pushes those products into the gas phase, thereby stopping the sequence. To fully describe such redox transformations, one must be able to analyze not only the residence time of various species in solution but also the locations of electrochemical transformations, which reactions are producing the observed current at specific locations, and how much current is being produced at a given distribution of potentials. To advance this endeavor, the analysis of potential and current maps (performed above in terms of Wagner number) needs a quantitative dimension.

The proposed nonlinear resistor electrospray capillary model will serve to provide a basis for an improved understanding of electrochemical and follow-up chemical transformations occurring in the electrospray emitter while adding a numerical dimension to their comprehension. The developed model may be used to quantitatively examine the relationships between various electrochemical parameters including total electrospray current, solution conductivity, as well as current density and electrochemical potential at various points along the spray capillary. The model may further be employed to elucidate specific electrochemical parameters of the electrospray process, such as the calculation of the depth at which current production extends into the ES capillary. It may also be used to answer a question of the type: Over what distance into the capillary can one account for a specified percentage of the total current production? The magnitude of the current could be expressed as a function of the capillary diameter or, instead, be linked to the aspect ratio of the capillary. The term “non-linearity” in the model’s name refers to the non-linearity of the resistance at the metal–electrolyte interface with distance into the capillary. This non-linearity in the electrical scheme (Fig. 7) renders the model difficult to solve mathematically, and it is this aspect that has further-reaching consequences that are discussed in the accompanying Supplemental Material.