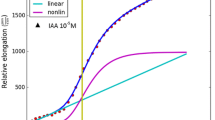
Abstract
If growing cells in plants are considered to be composed of increments (ICs) an extended version of the law of mass action can be formulated. It evidences that growth of plants runs optimal if the reaction–entropy term (entropy times the absolute temperature) matches the contact energy of ICs. Since these energies are small, thermal molecular movements facilitate via relaxation the removal of structure disturbances. Stem diameter distributions exhibit extra fluctuations likely to be caused by permanent constraints. Since the signal–response system enables in principle perfect optimization only within finite-sized cell ensembles, plants comprising relatively large cell numbers form a network of size-limited subsystems. The maximal number of these constituents depends both on genetic and environmental factors. Accounting for logistical structure–dynamics interrelations, equations can be formulated to describe the bimodal growth curves of very different plants. The reproduction of the S-bended growth curves verifies that the relaxation modes with a broad structure-controlled distribution freeze successively until finally growth is fully blocked thus bringing about “continuous solidification”.













Similar content being viewed by others
References
Bertallanaffy, V. L. (1957). Quantitative laws in metabolism and growth. Quarterly Review of Biology, 32, 217–231.
Schneider, M. K., Law, R., & Illian, J. B. (2006). Quantification of neighborhood-dependent plant growth by Bayesian hierarchical modelling. Journal of Ecology, 94, 310–321.
Hara, T. (1988). Dynamics of size structure in plant populations. Trends in Ecology & Evolution, 3, 129–133.
Weiner, J., Kinsman, S., & Williams, S. (1998). Modelling the growth of individuals in plant populations: local density variation in a strand population of Xanthium strumarium (Asteraceae). American Journal of Botany, 85, 1638–1645.
Weiner, J., & Thomas, S. W. (1986). Size variability and competition in plant monocultures. Oikos., 47, 211–222.
Banavar, J. R., Damuth, J., Maritan, A., & Rinaldo, A. (2002). Ontogenetic growth: Modelling universality and scaling. Nature., 420, 626–627.
Damgaard, C., Weiner, J., & Nagahshima, H. (2002). Modelling individual growth and competition in plant populations: growth curves of Chenopodium album. Journal of Ecology, 90, 666–671.
Jürgens, G. (2003). Growing up green: Cellular basis of plant development. Mechanisms of Development, 120, 1395–1406.
Green, P. B. (1976). Growth and cell pattern formation on an axis: Critique of concepts, terminology and modes of study. Botanical Gazette, 137, 187–202.
Cockcroft, C. E., den Boer, B. G. W., Healy, J. M. S., & Murrey, J. A. H. (2000). Cyclin D control of growth rate in plants. Nature., 405, 575–579.
Hara, T., & Yokozawa, M. (1994). Effects of physiological and environmental variations on size–structure dynamics in plant populations. Annals of Botany, 73, 39–51.
Schmid, I., & Kadzda, M. (2001). Vertical distribution and radial growth of coarse roots in pure and mixed stands of Fagus sylvatica and Picea abies. Canadian Journal of Forest Research, 3, 539–548.
Damgaard, C., & Weiner, J. (2008). Modeling of the growth of individuals in crowded plant populations. J Plant Ecolology, 1, 111–116.
Zeide, B. (1993). Analysis of growth equations. Forest Science, 39, 594–616.
Yeytman, B. A., & Cosgrove, D. J. (1998). A model of cell wall expansion based on thermodynamics of polymer networks. Biophysical Journal, 75, 2240–2250.
Kilian, H. G., Kemkemer, R., & Gruler, H. (2002). Universality and individuality as complementary factor to optimize and reproduce cell populations. Colloid and Polymer Science, 280, 1151–1156.
Kilian, H. G., Bartkowiak, D., Kaufmann, D., & Kemkemer, R. (2008). The general growth logistics of cell populations. Cell Biochemistry and Biophysics, 51, 51–66.
Kilian, H. G., Gruler, H., & Kemkemer, R. (2004). Relaxations processes during cell growth. Progress in Colloid and Polymer Science, 125, 198–205.
Pelling, A. E., Sehati, S. B., Gralla, B., Valentie, J. S., & Gimzewski, J. K. (2004). Local nanomechanical motion of the cell wall of Saccharomyces cerevisae. Science., 305, 1147–1150.
Volkov, I., Banavar, J. R., He, F., & Hubell, S. P. (2005). Density dependence explains tree species abundance and diversity in tropical forests. Nature, 438, 658–661.
Shemesh, T., Geiger, B., Bershatzky, A. D., & Kozlov, M. M. (2005). Focal adhesions as mechanosensors: A physical Mechanism. Proceedings of the National Academy of Sciences of the United States of America, 102, 12383–12388.
Sitte, P., Ziegler, H., Ehrendorfer, F., Bresinsky, A. (1997). Strasburger, Lehrbuch der Botanik. (34th ed., pp. 120, Fig. 1-42 B). Spektrum: Akademischer Verlag, Gustav Fischer.
Holmes, P., Goffard, N., Weiller, G. F., Rolfe, B. G., & Imin, N. (2008). Transcriptional profiling of Medicago truncatula root cells. BMC Plant Biology, 8, 21.
Micoulet, A., Spatz, J. P., & Ott, A. (2005). Mechanical response analysis and power generation by single-cell stretching. Chemical Physics and Physical Chemistry, 6, 663–670.
Koepf, M., & Kilian, H. G. (1999). Relaxation in the glass transition regime interpreted in terms of the aggregate model. Acta Polymerica, 59, 109–121.
Sitte, P., Ziegler, H., Ehrendorfer, F., & Bresinsky, A. (1997). Strasburger, Lehrbuch der Botanik (34th ed., pp. 400–411). Spektrum: Akademischer Verlag, Gustav Fischer.
Penel, C., Gaspae, Th, & Geppin, H. (1985). Rapid interorgan communications in higher plants with special reference to flowering. Biologia Plantarium., 27, 334–338.
Puig, S., Mira, H., Dorcey, E., Sancenón, V., Andrés-Colás, N., Garcia-Molina, A., et al. (2006). Higher plants possess two different types of ATX1-like copper chaperones. Biochemical and Biophysical Research Communications, 354, 385–390.
Mackenzie, S., & McIntosh, L. (1999). Higher plant mitochondria. Plant Cell, 11, 571–585.
McCrum, N. G., Read, B. E., & Williams, G. (1967). Anelastic and dielectric effects in polymer solids (p. 102). London: Wiley.
Brophy, C., Gibson, D. J., Wayne, P. M., & Connolly, J. (2008). How reproductive allocation and flowering probability of individuals in plant populations are affected by position in stand size hierarchy, plant size and CO2 regime. J Plant Ecology, 1, 207–215.
Hofmann, A. L. (2007). Untersuchungen zur Isolierung von Regulator-Genen des floralen Meristem-Identitäts-Gens FLORICAULA aus Antirrhinum majus (Thesis). (pp. 13–15) Köln: Matematisch-Naturwissenschaftliche Fakultät, Universität.
Ogle, K., & Pacala, S. W. (2009). A modeling framework of inferring tree growth and allocation from physiological, morphological and allometric traits. Tree Physiology, 29, 587–605.
Hozumi, K. (1987). Analysis of growth curve of stem volume in some woody species using the u–w diagram. The Botanical Magazine Tokyo, 100, 87–97.
Nagashima, H., Tereashima, I., & Katoh, S. (1995). Effects of plant density distributions of plant height in chenopodium album stands: analysis based on continuous monitoring of height-growth of individual plants. Annals of Botany, 75, 173–180.
Nagashima, H., & Terashima, I. (1995). Relationships between height, diameter and weight distributions of Chenopodium album plants in stands: effects of dimension and allometry. Annals of Botany, 75, 181–188.
Groover, A., & Robischon, M. (2006). Developmental mechanisms regulating secondary growth in woody plants. Current Opinion in Plant Biology, 9, 55–58.
Fehrmann, L. (2006). Alternative Methoden zur Biomassenschätzung auf Einzelbaumebene unter spezieller Berücksichtigung der k-Nearest Neighbour (k-NN) (Thesis). (pp. 59) Göttingen: Methode Fakultät für Forstwissenschaften und Waldökologie der Georg-August-Universität.
Koyama, T., & Hara, T. (1989). Frequency distribution of tree growth rate in natural forest stands. Annals of Botany, 64, 47–57.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Growth curves are calculated with Eq. 10. For biomass the parameter p was set equal to 3 while height was characterized by p = 1. All parameters except from p were assigned their values by educated guess and subsequent manual optimization.
To describe dbh or height distributions, Eq. 1 was subjected to an iterative non-linear fit procedure (Excel Solver). During iterations at constant values for ξ and y min the parameters p and βΔu 0 were modified until the deviation reduction converged towards 0.0001. These fits incorporate aberrant data points. To quantify this, we use the parameter γ which relates all deviations from the ideal size-distribution to the total plant mass.
Rights and permissions
About this article
Cite this article
Kilian, H.G., Kazda, M., Király, F. et al. On the Structure-Bounded Growth Processes in Plant Populations. Cell Biochem Biophys 57, 87–100 (2010). https://doi.org/10.1007/s12013-010-9087-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12013-010-9087-y