The Common Ancestor Process Revisited

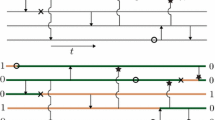
Abstract

We consider the Moran model in continuous time with two types, mutation, and selection. We concentrate on the ancestral line and its stationary type distribution. Building on work by Fearnhead (J. Appl. Probab. 39 (2002), 38–54) and Taylor (Electron. J. Probab. 12 (2007), 808–847), we characterise this distribution via the fixation probability of the offspring of all individuals of favourable type (regardless of the offspring’s types). We concentrate on a finite population and stay with the resulting discrete setting all the way through. This way, we extend previous results and gain new insight into the underlying particle picture.

Appendix

In Sect. 4.1, we have presented an alternative derivation of the boundary value problem for the conditional probability h. It remains to prove that $\lim_{N \to \infty} h^{N}_{k_{N}} = h(x)$, with x∈[0,1], 0<k _N <N, $\lim_{N \to \infty} \frac{k_{N}}{N} = x$ and h as given as in (7).

Since $h_{k}^{N} = \frac{k}{N} + \psi^{N}_{k}$ and h(x)=x+ψ(x), respectively, it suffices to show the corresponding convergence of the $\psi^{N}_{k}$. For ease of exposition, we assume here that the process is stationary.

Lemma 3

Let $\tilde{x}$ be as in (8). Then

$$ \lim_{N \to \infty} N \psi^N_{N-1} = \frac{\sigma}{1 + \theta \nu^{}_1}(1-\tilde{x}). $$

Proof

Since the stationary distribution $\pi^{N}_{Z}$ of $( Z^{N}_{t} )_{t \geqslant 0}$ (cf. (2)) satisfies

$$ \prod_{i=1}^{n-1} \frac{\lambda_i^{N}}{\mu_i^{N}} = \frac{\pi^N_Z (n)}{C_N} \frac{\mu^N_n}{\lambda^N_0}, $$

(47)

for 1⩽n⩽N, Eq. (30) leads to

$$\begin{aligned} N \psi^N_{N-1} &= \frac{Ns^{}_N}{1 + N u^{}_N \nu^{}_1} \frac{\sum_{n=1}^{N} \pi^N_Z(n) \mu^N_{n} \frac{N-n}{N}}{\sum_{n=1}^{N}\pi^N_Z(n) \mu^N_{n}} \\ &=\frac{Ns^{}_N}{1 + N u^{}_N \nu^{}_1} \frac{\sum_{n=1}^{N} \pi^N_Z(n) \frac{n(N-n)^2}{N^3} \bigl( 1 + \frac{N u^{}_N \nu^{}_1}{N-n} \bigr)}{\sum_{n=1}^{N}\pi^N_Z(n) \frac{n(N-n)}{N^2} \bigl(1 + \frac{N u^{}_N \nu^{}_1}{N-n} \bigr)} , \end{aligned}$$

where we have used (1) in the last step. The stationary distribution of the rescaled process $( X^{N}_{t} )_{t \geqslant 0}$ is given by $( \pi^{N}_{X} ( \frac{i}{N} ) )_{0 \leqslant i \leqslant N}$, where $\pi^{N}_{X} ( \frac{i}{N} ) = \pi^{N}_{Z} (i)$. Besides, the sequence of processes $(X^{N}_{t} )_{t \geqslant 0}$ converges to (X _t ) _t⩾0 in distribution, hence

$$\begin{aligned} \lim_{N \to \infty} N \psi^N_{N-1} &= \lim_{N \to \infty} \frac{N s^{}_N}{1 + N u^{}_N \nu^{}_1} \frac{\mathbb{E}_{\pi^N_X}\bigl( X^N ( 1- X^N )^2 ( 1 + \frac{u^{}_N \nu^{}_1}{1-X^N} ) \bigr)}{\mathbb{E}_{\pi^N_X}\bigl( X^N ( 1- X^N ) ( 1 + \frac{u^{}_N \nu^{}_1}{1-X^N} ) \bigr)} \\ &= \frac{\sigma}{1 + \theta \nu^{}_1} \frac{\mathbb{E}_{\pi^{}_X} ( X (1-X)^2 ) }{\mathbb{E}_{\pi^{}_X} ( X (1-X))} = \frac{\sigma}{1 + \theta \nu^{}_1}(1-\tilde{x}), \end{aligned}$$

as claimed. □

Remark 2

The proof gives an alternative way to obtain the initial value $a^{}_{1}$ (cf. (18)) of recursion (15).

Theorem 3

For a given x∈[0,1], let $( k_{N} )_{N \in \mathbb{N}}$ be a sequence with 0<k _N <N and $\lim_{N \to \infty} \frac{k_{N}}{N} = x$. Then

$$ \lim_{N \to \infty} \psi_{k_N}^N = \psi(x), $$

where ψ is the solution of the boundary value problem (11).

Proof

Using first Theorem 1, then (47), and finally (1), we obtain

$$\begin{aligned} \psi_k^N &= \frac{k(N-k)}{\mu_k^N} \sum _{n=1}^{N-k} \Biggl( \prod _{i=k+1}^{N-n} \frac{\lambda^N_i}{\mu^N_i} \Biggr) \biggl( \frac{\mu_{N-1}^N}{N-1} \psi^N_{N-1} - \frac{s^{}_N (n-1)}{N^2} \biggr) \\ &= \frac{k(N-k)}{\mu_k^N} \bigl( \mu^N_{k+1} \pi^N_Z (k+1) \bigr)^{-1} \\ &\quad {}\times \sum_{n=0}^{N-k-1} \mu^N_{N-n} \pi^N_Z (N-n) \biggl( \frac{\mu_{N-1}^N}{N-1} \psi^N_{N-1} - \frac{s^{}_N n}{N^2} \biggr) \\ &= \biggl( 1 + \mathcal{O} \biggl( \frac{1}{N} \biggr) \biggr) \biggl( \frac{k+1}{N} \frac{N-k-1}{N} \pi^N_Z (k+1) \biggr)^{-1} \\ & \hphantom{=} \times \frac{1}{N} \sum_{n=0}^{N-k-1} \pi^N_Z (N-n) \frac{N-n}{N} \frac{n}{N} \biggl( 1 + \frac{Nu^{}_N \nu^{}_1}{n} \biggr) \\ & \hphantom{= \times \frac{1}{N} \sum_{n=0}^{N-k-1}} \times \biggl( (1 + N u^{}_N \nu^{}_1) N \psi^N_{N-1} - N s^{}_N \frac{n}{N} \biggr). \end{aligned}$$

In order to analyse the convergence of this expression, define

$$\begin{aligned} S_1^N (k) &:= \frac{k+1}{N} \frac{N-k-1}{N} \pi^N_Z (k+1), \\ S_2^N (k) &:= \frac{1}{N} \sum _{n=0}^{N-k-1} \pi^N_Z (N-n) \frac{N-n}{N} \frac{n}{N} \biggl( (1 + N u^{}_N \nu^{}_1) N \psi^N_{N-1} - N s^{}_N \frac{n}{N} \biggr) \\ & \hphantom{:} = \int_0^1 T^N_k (y) \,dy, \\ S_3^N (k) &:= \frac{1}{N} \sum _{n=0}^{N-k-1} \pi^N_Z (N-n) \frac{N-n}{N} u^{}_N \nu^{}_1 \biggl( (1 + N u^{}_N \nu^{}_1) N \psi^N_{N-1} - N s^{}_N \frac{n}{N} \biggr) \\ & \hphantom{:} = \int_0^1 \tilde{T}_k^N (y) \,dy, \end{aligned}$$

with step functions $T^{N}_{k} : [0,1] \rightarrow \mathbb{R}$, $\tilde{T}^{N}_{k} : [0,1] \rightarrow \mathbb{R}$ given by

Consider now a sequence $( k_{N} )_{N \in \mathbb{N}}$ as in the assumptions. Then $\lim_{N \to \infty} \pi^{N}_{Z} (k_{N}) = \pi^{}_{X}(x)$ (cf. Durrett, 2008, p. 319), and due to Lemma 3

Since $T^{N}_{k}$ and $\tilde{T}^{N}_{k}$ are bounded, we have

$$\begin{aligned} \lim_{N \to \infty} S_2^N (k_N) &= \int_0^{1-x} \pi^{}_X (1-y) (1-y)y \bigl(\sigma (1- \tilde{x})- \sigma y \bigr) \,dy, \\ \lim_{N \to \infty} S_3^N (k_N) &=0, \end{aligned}$$

thus

$$ \lim_{N \to \infty} \psi^N_{k_N} = \bigl( x (1-x) \pi^{}_X (x) \bigr)^{-1} \int_0^{1-x} \pi^{}_X (1-y) (1-y)y \bigl(\sigma (1- \tilde{x})- \sigma y \bigr) \,dy. $$

Substituting on the right-hand side yields

$$\begin{aligned} \lim_{N \to \infty} \psi^N_{k_N} &= \bigl( x (1-x) \pi^{}_X (x) \bigr)^{-1} \sigma \int_x^1 \pi^{}_X(y)y(1-y) (y - \tilde{x}) \,dy \\ &= \bigl( x (1-x) \pi^{}_X (x) \bigr)^{-1} \sigma \biggl[ \int_0^1 \pi^{}_X (y) y (1-y) (y - \tilde{x})\,dy \\ &\quad {} + \int_0^x \pi^{}_X (y)y (1-y) ( \tilde{x}-y)\,dy \biggr] \\ &= \bigl( x (1-x) \pi^{}_X (x) \bigr)^{-1} \sigma \int_0^x \pi^{}_X (y) y (1-y) (\tilde{x}-y)\,dy = \psi(x) , \end{aligned}$$

where the second-last equality goes back to the definition of $\tilde{x}$ in (8), and the last is due to (7), (10), and (5). □