Skip to main content

Advertisement

SpringerLink
Log in

The Development of the STEM Career Interest Survey (STEM-CIS)

  • Published:
Research in Science Education Aims and scope Submit manuscript

Abstract

Internationally, efforts to increase student interest in science, technology, engineering, and mathematics (STEM) careers have been on the rise. It is often the goal of such efforts that increased interest in STEM careers should stimulate economic growth and enhance innovation. Scientific and educational organizations recommend that efforts to interest students in STEM majors and careers begin at the middle school level, a time when students are developing their own interests and recognizing their academic strengths. These factors have led scholars to call for instruments that effectively measure interest in STEM classes and careers, particularly for middle school students. In response, we leveraged the social cognitive career theory to develop a survey with subscales in science, technology, engineering, and mathematics. In this manuscript, we detail the six stages of development of the STEM Career Interest Survey. To investigate the instrument's reliability and psychometric properties, we administered this 44-item survey to over 1,000 middle school students (grades 6–8) who primarily were in rural, high-poverty districts in the southeastern USA. Confirmatory factor analyses indicate that the STEM-CIS is a strong, single factor instrument and also has four strong, discipline-specific subscales, which allow for the science, technology, engineering, and mathematics subscales to be administered separately or in combination. This instrument should prove helpful in research, evaluation, and professional development to measure STEM career interest in secondary level students.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. AMOS is the structural equation modeling software produced with IBM/SPSS.

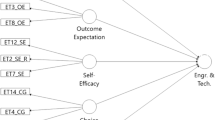
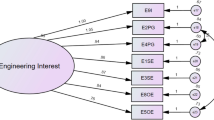
  2. Modification indices are reported in AMOS as chi square values with one degree of freedom. As such, a significant improvement in the model is signified by a chi square in excess of 3.84. In order to be very conservative with this process, and to model inter-item correlations that contributed substantially to model fit, we used a rule that we would examine inter-item correlations that resulted in a modification index (MI) of 8.00 or greater. Further, note that because these models were all single latent variable models with multiple measured variables that legitimately should be allowed to correlate, there is no conceptual issue with allowing items designed to measure a particular latent variable to correlate. We cannot model all possible correlations between items on a scale in CFA due to lack of degrees of freedom, and thus, the use of modification indices is merely an efficient method of identifying those items that, by allowing a nonzero correlation, significantly and substantially (and appropriately) improve model fit.

  3. Mahalanobis D 2 is a common index of whether an individual score is aberrant within the multivariate distribution of scores; higher numbers indicate the score is farther from the center of the multivariate distribution. Guidelines for assessing Mahalanobis D 2 suggest that a reasonable cutoff score is a chi square value that would be significant at p < .05 for the number of df equal to the number of variables or parameters estimated in the model.

  4. Note that Marsh et al. (2004) argue against strict cutoff scores or “golden rules,” and thus, these indices should be treated as the continuous variables they are, and interpreted in context.

References

  • American Association of State Colleges and Universities (2005, November/December). Strengthening the science and mathematics pipeline for a better America. Policy Matters, 2(11), 1–4. Retrieved from http://www.aascu.org/uploadedFiles/AASCU/Content/Root/PolicyAndAdvocacy/PolicyPublications/STEM%20Pipeline.pdf/.

  • American College Testing (2011). The condition of college and career readiness 2011. Retrieved January 3, 2012 from http://www.act.org/research/policymakers/cccr11/.

  • Archer, L. A., Osborn, J., Dillon, J., Willis, B., & Wong, B. (2010). “Doing” science versus “Being” a scientist: Examining 10/11-year-old schoolchildren's constructions of science through the lens of identity. Science Education, 94(4), 617–639.

    Article  Google Scholar 

  • Ashby Plant, E., Baylor, A. L., Doerr, C. E., & Rosenberg-Kima, R. B. (2009). Changing middle-school students' attitudes and performance regarding engineering with computer-based social models. Computers & Education, 53(2), 209–215.

    Article  Google Scholar 

  • Avery, L. M. (2013). Rural science education: Valuing local knowledge. Theory Into Practice, 52(1), 28–35.

    Article  Google Scholar 

  • Bandura, A. (1986). Social foundations of thought and action: A social cognitive theory. Englewood Cliffs: Prentice-Hall.

  • Baram–Tsabari, A., Sethi, R. J., Bry, L., & Yarden, A. (2009). Asking scientists: A decade of questions analyzed by age, gender, and country. Science Education, 93(1), 131–160.

    Article  Google Scholar 

  • Blanchard, M.R., Albert, J.L., Alsbury, T.L., Williams, B. (2012). NSF ITEST Annual Project Outcomes Report: Innovative technology experiences for students and teachers. STEM Teams: Promoting Science, Technology, Engineering, and Mathematics (STEM) career interest, skills, and knowledge through Strategic Teaming. Arlington: National Science Foundation.

  • Bowdich, S. (2009). Analysis of research exploring culturally responsive curriculum Hawaii. Paper presented to the Hawaii Educational Research Association Annual Conference, February 7, 2009.

  • Brotman, J. S., & Moore, F. M. (2008). Girls and science: A review of four themes in the science education literature. Journal of Research in Science Teaching, 45(9), 971–1002.

    Article  Google Scholar 

  • Business Europe (2011). Plugging the skills gap: The clock is ticking. Retrieved September 6, 2013 from http://www.businesseurope.eu/Content/Default.asp?pageid=568&docid=28659.

  • Byrne, B. M. (2010). Structural equation modeling with AMOS: Basic concepts, applications, and programming. New York: Routledge.

    Google Scholar 

  • Capobianco, B. M., Diefes-Dux, H. A., Mena, I., & Weller, J. (2011). What is an engineer? Implications of elementary school student conceptions for engineering education. Journal of Engineering Education, 100(2), 304–328.

    Article  Google Scholar 

  • Cataldi, E.F., Green, C., Henke, R., Lew, T., Woo, J., Shepherd, B., and Siegel, P. (2011). 2008–09 Baccalaureate and Beyond Longitudinal Study (BB:08/09): First Look (NCES 2011–236). US Department of Education. Washington: National Center for Education Statistics. Retrieved February 4, 2012 from http://nces.ed.gov/pubs2011/2011236.pdf.

  • Change the Equation. (2010). Change the Equation: Improving learning in science, technology, engineering, and mathematics. Retrieved December 28, 2012 at www.changetheequation.org.

  • Clark, L.A., & Watson, D. (1995). Constructing validity: Basic issues in objective scale development. Psychological Assessment, 7(3), 309–319.

    Google Scholar 

  • Drew, C., (2011, November 4). Why science majors change their minds (It's just so darn hard). The New York Times. Retrieved from http://www.nytimes.com/2011/11/06/education/edlife/why-science-majors-change-their-mind-its-just-so-darn-hard.html?pagewanted=all.

  • Eccles, J. S. (1994). Understanding women’s educational and occupational choices: Applying the Eccles et al. model of achievement related choices. Psychology of Women Quarterly, 18, 585–609.

    Google Scholar 

  • Fouad, N. A., Smith, P. L., & Enoch, L. (1997). Reliability and validity evidence for the Middle School Self-Efficacy Scale. Measurement and Evaluation in Counseling and Development, 30(1), 17–31.

    Google Scholar 

  • Fralick, B., Kearn, J., Thompson, S., & Lyons, J. (2009). How middle schoolers draw engineers and scientists. Journal of Science Education and Technology, 18(1), 60–73.

    Article  Google Scholar 

  • Frome, P. M., Alfed, C. J., Eccles, J. S., & Barber, B. L. (2006). Why don't they want a male dominated job? An investigation of young women who changed their occupational aspirations. Educational Research and Evaluation, 12, 359–372.

    Article  Google Scholar 

  • Gushue, G. V. (2006). The relationship of ethnic identity, career decision-making self-efficacy and outcome expectations among Latino/a high school students. Journal of Vocational Behavior, 68(1), 85–95.

    Article  Google Scholar 

  • Healy, J., Mavromaras, K., Zhu, R. (2011). Consultant report securing Australia's future STEM: Country comparisons. Retrieved September 6, 2011 from http://www.acolasecretariat.org.au/ACOLA/PDF/SAF02Consultants/Consultant%20Report%20-%20Australian%20Labour%20Market.pdf.

  • Hill, H. C. (2011). The nature and effects of middle school mathematics teacher learning experiences. Teachers College Record, 113(1), 205–234.

    Google Scholar 

  • Hill, C., Corbett, C., St Rose, A. (2010). Why so few? Women in science, technology, engineering, and mathematics. Washington: American Association of University Women. Retrieved March 22, 2011 at http://www.aauw.org/files/2013/02/Why-So-Few-Women-in-Science-Technology-Engineering-and-Mathematics.pdf.

  • Hu, L. T., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives. Structural Equation Modeling, 6(1), 1–55.

    Article  Google Scholar 

  • Johnson, D. G., & Miller, K. W. (2002). Is diversity in computing a moral matter? SIGCSE Bulletin, 34(2), 9–10.

    Article  Google Scholar 

  • Kier, M.W. (2013). Examining the effects of a STEM career video intervention on the interests and STEM professional identities of rural, minority middle school students. Dissertation study, NC State University.

  • Kitts, K. (2009). The paradox of middle and high school students' attitudes towards science versus their attitudes about science as a career. Journal of Geoscience Education, 57(2), 159–164.

    Article  Google Scholar 

  • Lent, R. W., Brown, S. D., & Hackett, G. (1994). Toward a unifying social cognitive theory of career and academic interest, choice, and performance. Journal of Vocational Behavior, 45, 79–122.

    Article  Google Scholar 

  • Lent, R. W., Brown, S. D., & Hackett, G. (2000). Contextual supports and barriers to career choice: A social cognitive analysis. Journal of Counseling Psychology, 47(1), 36.

    Article  Google Scholar 

  • Lent, R. W., Lopez, A. M., Lopez, F. G., & Sheu, H. B. (2008). Social cognitive career theory and the prediction of interests and choice goals in the computing disciplines. Journal of Vocational Behavior, 73(1), 52–62.

    Article  Google Scholar 

  • Marsh, H. W., Hau, K. T., & Wen, Z. (2004). In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler's (1999) findings. Structural Equation Modeling, 11(3), 320–341.

    Google Scholar 

  • Masnick, A., Valenti, S., Cox, B., & Osman, C. (2010). A multidimensional scaling analysis of students' attitudes about science careers. International Journal of Science Education, 32(5), 653–667.

    Article  Google Scholar 

  • National Academy of Sciences, Global Affairs, & Institute Of Medicine. (2011). Expanding underrepresented minority participation: America's science and technology talent at the crossroads. Washington: National Academy Press.

  • National Science Board (2010). Science and engineering indicators. Arlington: National Science Foundation (NSB 10-01).

  • National Science Foundation. (2009). Women, minorities, and persons with disabilities in science and engineering: 2009. Arlington: National Science Foundation. Retrieved January 8, 2013 at http://www.nsf.gov/statistics/wmpd.

  • Navarro, R. L., Flores, L. Y., & Worthington, R. L. (2007). Mexican American middle school students' goal intentions in mathematics and science: A test of the social cognitive career theory. Journal of Counseling Psychology, 54(3), 320–335.

    Article  Google Scholar 

  • Regisford, K. (2012, November 20). Life and work in a global city—The need to improve STEM education. The Recruitment & Employment Confederation. Retrieved November 2, 2012 from http://www.rec.uk.com/press/news/2253.

  • Schwab, K., & Sala-i-Martín, X. (2012). Insight Report: The Global Competitiveness Report 2012–2013. Geneva: World Economic Forum.

  • Scott, A. & Martin, A. (2012). Dissecting the data 2012: Examining STEM opportunities and outcomes for underrepresented students in California. Retrieved from May 15, 2012 from http://toped.svefoundation.org/wp-content/uploads/2012/04/Achieve-LPFIstudy032812.pdf.

  • Skamp, K. (2007). Conceptual learning in the primary and middle years: The interplay of heads, hearts, and hands-on science. Teaching Science, 53(3), 18–22.

    Google Scholar 

  • STEMconnector® (2012). Where are the STEM students? National Report, Washington. Retrieved September 6, 2012 from http://www.stemconnector.org/sites/default/files/store/STEM-Students-STEM-Jobs-Executive-Summary.pdf.

  • Stone, D.L., Johnson, R.D., Stone-Romero, E.F., Navas, D. (2005, February). Hispanic American and Anglo American beliefs, attitudes, and intentions to pursue careers in information technology. In E. McChrystal, A.Gujar, & C.Harmon (Chairs), Proceedings. Presentation conducted at the 26th annual Industrial Organizational/Organizational Behavior (IOOB) conference, Indialantic, FL.

  • Stout, J. G., Dasgupta, N., Hunsinger, M., & McManus, M. A. (2011). STEMing the tide: Using ingroup experts to inoculate women's self-concept in science, technology, engineering, and mathematics (STEM). Journal of Personality and Social Psychology, 100(2), 255.

    Article  Google Scholar 

  • TechWomen. (2013). www.techwomen.org.

  • Thomas, T., & Allen, A. (2006). Gender differences in students' perceptions of information technology as a career. Journal of Information Technology Education, 5, 165–178.

    Google Scholar 

  • Thompson, B., & Daniel, L. G. (1996). Factor analytic evidence for the construct validity of scores: A historical overview and some guidelines. Educational and Psychological Measurement, 56(2), 197–208.

    Article  Google Scholar 

  • Tyler-Wood, T., Knezek, G., & Christensen, R. (2010). Instruments for assessing interest in STEM content and careers. Journal of Technology and Teacher Education, 18(2), 341–363.

    Google Scholar 

  • US Bureau of Labor Statistics (2010). Occupational outlook handbook, (2010–2011 ed.). Office of Occupational Statistics and Employment Projections. Retrieved January 9, 2012 from http://www.bls.gov/oco/oco2003.htm.

  • Usher, E. L. (2009). Sources of middle school students' self-efficacy in mathematics: A qualitative investigation. American Educational Research Journal, 46(1), 275–314.

    Google Scholar 

  • VanLeuvan, P. (2004). Young women's science/mathematics career goals from seventh grade to high school graduation. The Journal of Educational Research, 97(5), 248–268.

    Article  Google Scholar 

  • Wells, B., Sanchez, A., & Attridge, J. (2007). Modeling student interest in science, technology, engineering and mathematics. IEEE Summit. “Meeting the growing demand for engineers and their educators,” Munich, Germany.

  • White House Office of Science and Technology Policy (2012, February 13). Preparing a 21st Century workforce: Science, Technology, Engineering, and Mathematics (STEM) education in the 2013 Budget. Retrieved May 30, 2012 from http://www.whitehouse.gov/sites/default/files/microsites/ostp/fy2013rd_stem.pdf.

  • Whitfield, A., Feller, R., & Wood, C. (2008). A counselor's guide to career assessment instruments. Broken Arrow: National Career Development Association.

    Google Scholar 

  • Zeldin, A., Britner, S., & Pajares, F. (2008). A comparative study of the self-efficacy beliefs of successful men and women in mathematics, science, and technology careers. Journal of Research in Science Teaching, 45(9), 1036–1058.

    Article  Google Scholar 

Download references

Acknowledgments

The authors wish to thank Michael D. Cobb for his helpful suggestions on the initial development of this instrument and all of the collaborators on this project who participated in this research. This research was funded by an ITEST grant (2010–2013) from the National Science Foundation (award number 1031118). The opinions expressed are those of the authors and do not represent the views of the National Science Foundation or North Carolina State University.

Author information

Authors and Affiliations

  1. Department of Curriculum and Instruction, Howard University, 2441 4th St. NW, Washington, DC, 20059, USA

    Meredith W. Kier

  2. Department of Science, Technology, Engineering, and Mathematics Education, North Carolina State University, Campus Box 7801, Raleigh, NC, 27695-7801, USA

    Margaret R. Blanchard

  3. College of Education & Human Development, University of Louisville, Louisville, KY, 40292, USA

    Jason W. Osborne

  4. Department of Computer Science, North Carolina State University, Campus Box 8206, Raleigh, NC, 27695-7801, USA

    Jennifer L. Albert

Authors
  1. Meredith W. Kier
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Margaret R. Blanchard
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jason W. Osborne
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jennifer L. Albert
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Meredith W. Kier.

Appendix

Appendix

STEM Career Interest Survey (STEM-CIS)

Optional Demographic Questions

  1. 1.

    Date

  2. 2.

    First name

  3. 3.

    Last name

  4. 4.

    Grade

  5. 5.

    Gender

  6. 6.

    Teacher

  7. 7.

    Race

  8. 8.

    Period

  9. 9.

    School

Directions: Students will complete the STEM-CIS online via iPod Touches or computers. Each question is a Likert scale with the following choices:

Strongly Disagree (1), Disagree (2), Neither Agree nor Disagree (3), Agree (4), Strongly Agree (5)

Science

  1. S1

    I am able to get a good grade in my science class.

  2. S2

    I am able to complete my science homework.

  3. S3

    I plan to use science in my future career.

  4. S4

    I will work hard in my science classes.

  5. S5

    If I do well in science classes, it will help me in my future career.

  6. S6

    My parents would like it if I choose a science career.

  7. S7

    I am interested in careers that use science.

  8. S8

    I like my science class.

  9. S9

    I have a role model in a science career.

  10. S10

    I would feel comfortable talking to people who work in science careers.

  11. S11

    I know of someone in my family who uses science in their career.

Mathematics

  1. M1

    I am able to get a good grade in my math class.

  2. M2

    I am able to complete my math homework.

  3. M3

    I plan to use mathematics in my future career.

  4. M4

    I will work hard in my mathematics classes.

  5. M5

    If I do well in mathematics classes, it will help me in my future career.

  6. M6

    My parents would like it if I choose a mathematics career.

  7. M7

    I am interested in careers that use mathematics.

  8. M8

    I like my mathematics class.

  9. M9

    I have a role model in a mathematics career.

  10. M10

    I would feel comfortable talking to people who work in mathematics careers.

  11. M11

    I know someone in my family who uses mathematics in their career.

Technology

  1. T1

    I am able to do well in activities that involve technology.

  2. T2

    I am able to learn new technologies.

  3. T3

    I plan to use technology in my future career.

  4. T4

    I will learn about new technologies that will help me with school.

  5. T5

    If I learn a lot about technology, I will be able to do lots of different types of careers.

  6. T6

    My parents would like it if I choose a technology career.

  7. T7

    I like to use technology for class work.

  8. T8

    I am interested in careers that use technology.

  9. T9

    I have a role model who uses technology in their career.

  10. T10

    I would feel comfortable talking to people who work in technology careers.

  11. T11

    I know of someone in my family who uses technology in their career.

Engineering

  1. E1

    I am able to do well in activities that involve engineering.

  2. E2

    I am able to complete activities that involve engineering.

  3. E3

    I plan to use engineering in my future career.

  4. E4

    I will work hard on activities at school that involve engineering.

  5. E5

    If I learn a lot about engineering, I will be able to do lots of different types of careers.

  6. E6

    My parents would like it if I choose an engineering career.

  7. E7

    I am interested in careers that involve engineering.

  8. E8

    I like activities that involve engineering.

  9. E9

    I have a role model in an engineering career.

  10. E10

    I would feel comfortable talking to people who are engineers.

  11. E11

    I know of someone in my family who is an engineer.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kier, M.W., Blanchard, M.R., Osborne, J.W. et al. The Development of the STEM Career Interest Survey (STEM-CIS). Res Sci Educ 44, 461–481 (2014). https://doi.org/10.1007/s11165-013-9389-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11165-013-9389-3

Keywords

Search

Navigation