1 Introduction

Most of financial institutions publish their financial reporting under the International Financial Reporting Standards (IFRS). It is even mandatory for companies which are listed at stock exchange or have issued bonds within the European Union. This new accounting framework modifies the perception of financial analysts and investors. Agostino et al. (2010) have carried out an empirical study of the value relevance of IFRS in the European banking industry.

Due to the present standards, these companies measure financial assets at fair value. As a matter of fact, even if bonds are eligible to the amortized cost through the Held-To-Maturity (HTM) category, the restrictions on this category have led financial institutions (and especially insurance company) to parsimoniously use this ability. As a consequence most of insurance companies financial assets are categorized as Available-For-Sale (AFS) and so measured at fair value.

In this category, financial assets are measured at fair value in the balance sheet. Nevertheless paragraph 55 of IAS 39 states that a gain or loss on an available-for-sale financial asset shall be recognized in other comprehensive income (OCI), except for impairment losses and foreign exchange gains and losses, until the financial asset is de-recognized. This constitutes the main difference with the Held-For-Trading (HFT) category which consists in a measurement at Fair Value through profit or loss. This latest category is much less used by financial institutions due to the volatility it generates in the result.

Table 1 shows the preponderance of this category among insurance companies.

Table 1 Some figures about insurance companies investments in 2011
Full size table

Figures are extracted from the 2011 reference document of each company.

As along as a financial asset classified as AFS belongs to a company, any gains or losses on this asset are not recognized in profit or loss. Unless any impairment losses occur. In such a case, IAS 39 states that the amount of the cumulative loss that is reclassified from equity to profit or loss (…) shall be the difference between the acquisition cost (net of any principal repayment and amortization) and current fair value, less any impairment loss on that financial asset previously recognized in profit or loss.

Paragraph 59 of IAS 39 states that A financial asset (…) is impaired and impairment losses are incurred if, and only if, there is objective evidence of impairment as a result of one or more events that occurred after the initial recognition of the asset (a "loss event") and that loss event (or events) has an impact on the estimated future cash flows of the financial asset (…) that can be reliably estimated. This principle is completed in paragraph 61 for equity instruments : A significant or prolonged decline in the fair value of an investment in an equity instrument below its cost is also objective evidence of impairment.

To resume, if for debt instruments classified as AFS, the impairment criterion is based on a loss event (this leads to consider the present impairment methodology for such instruments as "incurred approach" by opposition of an "expected approach"), IAS 39 gives a more precise double-criterion for considering impairment losses for an equity instrument. It is important to note that the two conditions do not necessarily to be concomitantly met in order to lead to an impairment loss (it is the case in some local accounting standards such as the French ones). This has been confirmed by an IFRIC Footnote 1 Update of July 2009. Moreover for those instruments, any impairment losses shall not be reversed through profit or loss (see Paragraph 69).

This situation is summarized in Table 2.

Table 2 Overview of IAS 39 impairment disposals
Full size table

As a consequence with the present standard, most of impairment losses on AFS financial assets come from equity instruments.

Table 3 compares, for some insurance companies, their 2011 result and the losses from AFS funds and equity securities impairment. The figures are extracted from the 2011 reference document of each company.

Table 3 Some figures about insurance companies investments in 2011
Full size table

We see that these impairment losses are far from being negligible compared to the result of these insurers. Also in this paper, we focus on equity instruments classified as available for sale.

The following questions are of interest for a company which holds equity instruments classified as AFS: what is the probability that an impairment occurs before the next financial reporting? What is the expected amount of such an impairment loss? What is its distribution function? To which parameters is this amount the most sensitive? These questions have been little addressed so far by practitioners and researchers. As a matter of fact, impairment rules of financial assets (and especially their level of strictness between different frameworks and economic situations) and their impact have been pointed out in studies about Fair Value Accounting (see for example (Laux and Leuz 2009; Jaggi et al. 2010) for an analysis of the role of Fair Value accounting in the recent financial crisis or (Bowen et al. 2009) for an examination of the economic consequences of relaxing fair value accounting and especially impairment rules during the financial crisis). Nevertheless the point of view of the reporting entity has been little addressed (see (Batens 2007) for a numerical approximation of the impairment losses over an equity securities portfolio). As impairment losses can have major consequences for financial reporting, it would be interesting for decision makers to have some quantitative indicators of impairment risk. They could sometimes change their asset allocation after analyzing impairment characteristics of their initial investment strategy.

After giving an overview of practices of financial institutions to consider what kind of decline leads to an impairment loss, the aim of our paper is to provide some answers to the above questions in the Black and Scholes model. Even if this model is far from being perfect (see Mozumder et al. 2013 for example), it is still widely used by insurance companies, sometimes with modifications like stochastic volatility or stochastic interest rates. Many insurance companies still use Black–Scholes model for financial planning. As our goal is to study impairments in the IFRS framework and not to build a more reliable risky asset model, we believe that the Black–Scholes approach is reasonable here and enables us to derive explicit expressions for some impairment characteristics. Introducing more sophisticated Lévy processes, regime switching, stochastic volatility or interest rates would require much more financial engineering and is left for future research. Computations would be more complicated and less tractable, but the same analysis would apply as we work in the real-world universe.

The two criteria and the form of the impairment losses are similar to those of the (probabilistic) payoff of a sum of three financial options. Among them the first one corresponds to a classical European put option (see Hull 2011). The two others are in the family of the barrier options: the rear-end up-and-out put option (see Hui 1997). We may observe that barrier options are useful for some accounting and tax issues. For example, Couch et al. (2012) present practical valuation formulas for tax shields of interest expense.

Using results about barrier options from Hui (1997), Chuang (1996) and Carr and Chou (1997), we give an analytical formula of the expectation of the next-year impairment losses for any equity security (even previously impaired) in the Black and Scholes model. Moreover we compute the cumulative distribution function of the next year impairment losses which enables a Chief Financial Officer (CFO) and a Chief Risk Officer (CRO) to measure the risk of any deviation in the profit or loss resulting from any impairment of such a security. For each characteristic, we give sensitivities on parameters. We also find a mean-preserving relation between the parameters of the impairment criteria and those of a simplified version (using only the significant decline criterion) that is easier to compute. These results are then illustrated on real securities from the French stock market. Some practitioners argue that such the above-mentioned proxy could be used in order to get a simpler formula. We show that such a proxy is only relevant when large impairment losses already occurred in the previous financial reporting statements, because differences between the results of the two methods are important when no large impairment has occurred yet. In order to get a more readable paper, the proofs of the results are given in the “Appendices”. Apart from solving this particular issue, another goal of this paper is to demonstrate how financial mathematics techniques can be applied to IFRS accounting problems, including impairment related ones.

2 Impairment of equity securities

The aim of this section is to give an overview of how financial institutions such as banks and insurance companies interpret Paragraph 61 of IAS 39 in order to determine the parameters to consider a significant or prolonged decline which leads to an impairment loss for an equity security.

A study of the auditing company (Grant 2009) indicates that these criteria have fallen within the following ranges:

  • significant between 20 and 30 %

  • prolonged between 9 and 12 months.

Nevertheless, as we can see in Table 4, these parameters are very volatile among financial institutions. Moreover some of them consider a third criterion which embrace both significant and prolonged decline: a prolonged decline under a significant fall in fair value since the acquisition time. We can observe that a wide range of criterion are practically used. Obviously the greater the significant (resp. the prolonged) parameter is, the later an impairment loss occurs and the greater the potential impaired amount may be. If one positions impairment risk in a risk map (whose axes correspond to probability of occurrence and expected severity if event occurs), it is going to lie close to different axes for different insurers (for equivalent previous impairments): for AXA it would be closer to the first axis, because this company tends to recognize impairments much faster (after a 20 % decrease or a 6-month prolonged decline) than Generali, who recognizes impairments only after a 50 % decrease or a 3-year prolonged decline. In Generali risk map, impairment risk would be closer to the second axis, because the probability of impairment is much smaller, but if this happened, the impairment amount would be much higher.

Table 4 Impairment parameters used by some insurance companies in 2011
Full size table

Decision makers need some quantitative analysis to complement this qualitative analysis in order to set up their trigger parameters. The computations we present in this paper enable CFO’s and CRO’s to quantify impairment risk and to choose their appropriate thresholds. In the numerical applications section, we carry out some sensitivity analysis and also provide concrete numbers for probability of impairment and expected severity given that event occurs for Axa and Generali trigger parameters in different stock price evolution and past impairment scenarios. The additional criterion that some companies consider seems like the trigger given by some local GAAP (French GAAP for example for which a continuously fall of 20 or 30 % during the last 6 months leads to an impairment loss).

Figures are extracted from the 2011 reference document of each company.

3 Theoretical results

3.1 Notation and model

We first give a mathematical framework in order to deal with the properties of the (probabilistic) next-year impairment loss of an equity security classified as AFS.

3.1.1 Notation

Let us denote by \(S=\left(S_t\right)_{0\leq t}\) the stock price at time t. We denote the acquisition date by t a  ≥ 0. We assume that we want to forecast next year impairments at some time t ≥ t a . Hereafter, we introduce all quantities that constitute the information of the Chief Financial Officer at time t (present).

With these notation, \(S_{t_a}\) is the acquisition cost of the stock and S t is the fair value of the stock at time t.

Let us denote by \(\Uplambda(S, t_a,t)\) the cumulative results obtained through the sum of profit and loss starting at time t a until now:

$$\Uplambda(S, t_a,t)=\sum _{s=\lfloor t_a \rfloor +1} ^{t} \lambda(S, t_a, s).$$
(1)

Remark 1

The above sum starts at the first integer valued date after the acquisition. In fact it is more general than that because times of annual accounts are not necessary integers. This detail has no influence on the results.

As there will be no possible confusion, we choose to use \(\Uplambda_t\).

Let us denote by \(\Upomega(S,t_a,t)\) the cumulative unrealized gains and losses deferred in Other Comprehensive Incomes (OCI) since t a .

We have the balance sheet equilibrium property:

$$S_t-S_{t_a}=\Upomega(S,t_a,t)+\Uplambda_t.$$
(2)

The unrealized gains and losses have to be reported either on past profit and loss or on OCI, since the financial asset is measured at fair value in the balance sheet.

To summarize, at time t, information available for the CFO corresponds to \(\mathcal{F}_t=\{S_{t_a}, S_t, \Uplambda_t \}\). Using this, we would like to forecast the following year impairments. According to what the CFO knows, probabilities have to be evaluated conditionally to information \(\mathcal{F}_t\) at time t.

3.1.2 Modeling the impairment triggers and losses

The aim of this subsection consists in modeling the impairment trigger and the resulting losses if any. We divide each impairment process into two steps. The first one deals with the (non-cumulative) couple of criteria on the fall (significant or prolonged).

The trigger for an impairment at time t + 1 can be written as:

$$\left\{ \begin{array}{l} S_{t+1} \leq (1-\alpha) S_{t_a}, \hbox{or};\\ \forall u \in \left] t+1-s, t+1 \right] , S_u \leq S_{t_a}, \end{array}\right.$$
(3)

where the parameters α and s are determined by the company.

  • Parameter \(\alpha \in \left]0,1\right[\) represents the relative level of fall in fair value since the acquisition date corresponding to significant decline.

  • Parameter 0 < s < 1 represents the minimum period before the financial reporting date that leads to consider that the decline is prolonged.

The second step is to determine if an impairment really occurs. For that, we have to test the following condition: \(S_{t+1} \leq S_{t_a} - \Uplambda_t\). Finally, for each t, we define J t+1 as the Bernoulli random variable that takes value 1 if some impairment occurs at time t + 1. This occurs if both the trigger condition is satisfied and \(\{ S_{t+1} \leq S_{t_a} - \Uplambda_t \}\).

Then, if an impairment is recognized, its value is denoted by λ t+1 and is equal to \(S_{t_a} - \Uplambda_t - S_{t+1}\). Without loss of generality, we have \(\lambda_{t+1} = (S_{t_a} - \Uplambda_t - S_{t+1})^+\) or, as for a European put option, λ t+1 = (K t  − S t+1)+, with \(K_t = S_{t_a} - \Uplambda_t\).

3.1.3 Stock price evolution

Let (W t )0 ≤ t be a standard Brownian motion. Let (S t )0 ≤ t be the price process of some asset in the Black–Scholes model (see Mozumder et al. (2013) for a recent comparative analysis of the calibration and performance of a variety of options pricing models) : for 0 ≤ t, we have, under the real-world probability,

$$\frac{dS_t}{S_t}=\mu dt+\sigma dW_t,$$
(4)

where (W t ) t ≥ 0 is a standard Brownian motion. We denote the risk-free interest rate by r.

3.2 Characteristics of the next-year impairment

We now provide in the Black and Scholes framework the main characteristics of the (potential) next year impairment losses. The main results are, for the next year reporting:

  • the probability that some impairment occurs,

  • the expectation of impairment losses,

  • the cumulative distribution function (c.d.f.) of impairment losses.

These results enable a CFO to analyze both the next year losses resulting from holding such an investment categorized as AFS and to determine some risk indicators in order to manage the risk of an impairment loss resulting from this equity securities. More precisely, the two first indicators enable the CFO and the CRO to position impairment risk on a risk map (chart whose coordinates correspond to probability of occurrence and expected severity of events). The last indicator enables them to take impairment risk into account in internal risk models, or to deal with the multi-period case by induction. Of course, if one knows the c.d.f., one knows everything, including the two first indicators. But it is much longer to compute the c.d.f. than the two first quantities, and it would be painful, and numerically complex to retrieve the expected value of impairments by integration of the survival function. Consequently, we analyze the three risk indicators separately and provide formulas and computation scheme for each of them.

3.2.1 Impairment probability

As we shall see in the sequel, the probability to recognize an impairment after one year can be interpreted as the probability that a complex option (involving both the final price and the maximum of the price during the end of the period) is in the money at maturity.

We express the probability to recognize an impairment in one year conditionally to \({\mathcal{F}_t, \mathbb{P} \left[ {J_{t+1} | \mathcal{F}_t} \right]=\mathbb{P}_t \left[ {J_{t+1}} \right]}\). Let us start by re-writing J t+1:

$$J_{t+1} = \left( S_{t+1} \leq (1-\alpha) S_{t_a}, S_{t+1} \leq K_t \right)\bigcup \left( \max_{t+1-s\leq u\leq t+1} S_u \leq S_{t_a} , S_{t+1} \leq K_t \right).$$

Then, it is easy to obtain, introducing \(m_t =\min \left( (1-\alpha) S_{t_a}, K_t \right)\):

$$\begin{aligned} {\mathbb{P}}_t \left[ {J_{t+1}} \right] &= {\mathbb{P}}_t \left[ { S_{t+1} \leq m_t} \right] + {\mathbb{P}}_t \left[ { \max_{t+1-s\leq u\leq t+1} S_u \leq S_{t_a}, S_{t+1} \leq K_t } \right]\\ &\quad- {\mathbb{P}}_t \left[ { \max_{t+1-s\leq u\leq t+1} S_u \leq S_{t_a},S_{t+1} \leq m_t } \right]. \end{aligned}$$

The next step is to retrieve an expression using the drifted Brownian motion and the joint law of its current maximum and its value. Details are provided in “Appendix 1”. We are then able to enunciate the following theorem:

Theorem 1

(Impairment probability) The probability to recognize an impairment at future time t + 1, given the information \(\mathcal{F}_t\) at time t, is given by

$$\begin{aligned} {\mathbb{P}}_t \left[ {J_{t+1}} \right] &= \left( \frac{S_{t_a}}{S_t}\right)^{k_1 - 1} \left[ \Uppsi_\rho \left( C , D(K_t) \right) - \Uppsi_\rho \left( C , D(m_t ) \right) \right]\\ &\quad+ \Upphi\left(- A(K_t) \right) + \Uppsi_\rho \left( B , A(K_t ) \right) - \Uppsi_\rho \left( B , A(m_t ) \right), \end{aligned}$$
(5)

where, for \(x\in\{ m_t , K_t \}\),

  • \(A(x)=\frac{\ln(S_t /x) + \mu}{\sigma} - \frac{\sigma}{2}, A^{\prime}(x)=A(x)+\sigma\),

  • \(B=\frac{\ln(S_t /S_{t_a}) + \mu (1-s)}{\sigma \sqrt{(1-s)}} - \frac{\sigma\sqrt{(1-s)}}{2}, B^{\prime}=B+\sigma\sqrt{(1-s)}\),

  • \(C=\frac{\ln(S_{t_a}/S_t) + \mu (1-s)}{\sigma \sqrt{(1-s)}} - \frac{\sigma\sqrt{(1-s)}}{2}, C^{\prime}=C+\sigma\sqrt{(1-s)}\),

  • \(D(x)=\frac{\ln(S_{t_a}^2/S_t x) + \mu}{\sigma} - \frac{\sigma}{2}, D^{\prime}(x)=D(x)+\sigma\),

  • \(k_1 = \frac{2\mu}{\sigma^2}\),

\(\Upphi\) denotes the c.d.f. of a standard normal distribution, and \(\Uppsi_\rho\) is the bivariate normal distribution function: for all \({x,y, \Uppsi_\rho (x,y) = \mathbb{P}_t \left[ {X\leq x, Y\leq y} \right]}\) where (X, Y) is a Gaussian vector with standard marginals and correlation ρ.

The proof is given in the “Appendices”.

Remark 2

This is also the probability to have non-null impairment:

$${\mathbb{P}}_t \left[ {J_{t+1}} \right]={\mathbb{P}}_t \left[ {\lambda_{t+1} \neq 0} \right].$$

Theorem 2

(Probability sensitivities) The impairment probability is decreasing in \(\alpha, \mu, \Uplambda\) and s. Moreover, it is convex in α,  μ and s.

Remark 3

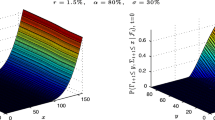
In Fig. 1, we observe that the probability to recognize an impairment next year is neither globally convex in σ, nor globally concave. Actually, we observe some (local) convexity in σ when μ is close to 0, and some (local) concavity for large values of μ. Moreover, there is an area where the first derivative of the sensitivity is not monotonous.

Fig. 1
figure 1

Probability to recognize an impairment next year as a function of μ and σ (left), and of \(\Uplambda\) and α (right)

Full size image

3.2.2 Expectation of the next-year impairment loss

The expectation of the next-year impairment loss looks like the price of a complex option, without discounting. Note that here however we are interested in the expectation under the real-world probability measure. Consequently, in the sequel, we decompose the payoff, in order to retrieve some simpler and known expressions. We denote \({\mathbb{E}_t}\) instead of \({\mathbb{E} \left[.|\mathcal{F}_t \right]}\) for simplicity, as we have done for probabilities.

Proposition 1

The payoff we are interested in is

$$\lambda_{t+1} = (K_t-S_{t+1})^+ {\bf 1} \left\{ \max_{t+1-s\leq u\leq t+1} S_u \leq S_{t_a} \cup S_{t+1} \leq (1-\alpha )S_{t_a} \right\},$$
(6)

with \(K_t =S_{t_a}-\Uplambda_t\). We have

$$\lambda_{t+1}=X_{t+1} + Y_{t+1} - Z_{t+1},$$

with

  • \(X_{t+1} = (K_t -S_{t+1})^+ {\bf 1} \left\{ \max_{t+1-s\leq u\leq t+1} S_u \leq S_{t_a} \right\}\),

  • \(Y_{t+1} = (K_t -S_{t+1})^+ {\bf 1} \left\{ S_{t+1} \leq (1-\alpha )S_{t_a} \right\}\),

  • and \(Z_{t+1} = (K_t -S_{t+1})^+ {\bf 1} \left\{ \max_{t+1-s\leq u\leq t+1} S_u \leq S_{t_a} \right\}.{\bf 1} \left\{ S_{t+1} \leq (1-\alpha )S_{t_a} \right\}\).

Remark 4

These three terms can be interpreted as payoffs of options with underlying asset S. The first one corresponds to a rear-end up-and-out put option (as it appears in (Hui 1997)), the second one to a classic European put option, and the third one is a bit more complicated: Z t+1 corresponds to the sum of the payoff of a rear-end up-and-out put option and of a compensating quantity. All the details can be found in “Appendix 2”.

Finally, again with \(m_t =\min \left( (1-\alpha) S_{t_a}, K_t \right)\), one may obtain the expected value of next year impairment.

Theorem 3

(Impairments expectation) The expectation of next-year impairment, given the information \(\mathcal{F}_t\) at time t, is given by

$$\begin{aligned} {\mathbb{E}}_t \left[ \lambda_{t+1}\right] &= S_t e^\mu \left( \frac{S_{t_a}}{S_t} \right)^{k_1 -1} \left[ \Uppsi_{-\rho} \left( C^{\prime} , -D^{\prime}(K_t ) \right) - \Uppsi_{-\rho} \left( C^{\prime} , -D^{\prime}(m_t ) \right) \right]\\ &\quad+S_t e^\mu \left[ \Uppsi_\rho\left( -B^{\prime}, - A^{\prime}(m_t ) \right) -\Upphi \left( -A^{\prime}(m_t ) \right) - \Uppsi_\rho \left( -B^{\prime} , -A^{\prime}(K_t ) \right)\right]\\ &\quad+K_t \left[\Uppsi_{\rho} \left( -B , -A(K_t ) \right) + \Upphi \left( -A(m_t ) \right) -\Uppsi_{\rho} \left( -B , -A(m_t ) \right) \right]\\ &\quad+ (K_t -m_t ) \left( \frac{S_{t_a}}{S_t} \right)^{k_1 -1}\left[\Upphi\left( -D(m_t ) \right) - \Uppsi_{\rho} \left( -C , -D(m_t ) \right) \right]\\ &\quad-K_t \left( \frac{S_{t_a}}{S_t} \right)^{k_1 -1} \Uppsi_{-\rho} \left( C, - D(K_t ) \right)+ m_t \left( \frac{S_{t_a}}{S_t} \right)^{k_1 -1} \Uppsi_{-\rho} \left( C, - D(m_t ) \right), \end{aligned}$$
(7)

where all constant numbers, variables and parameters are defined in Theorem 1.

Corollary 1

We can interpret the impairment as a financial product. Consequently, the "price" of this option - namely the expectation under risk neutral probability \({\mathbb{Q}}\) (cf. (Hull 2011)) of discounted value of the next-year impairment loss - is given by :

$$\begin{aligned} {\mathbb{E}}_t^{{\mathbb{Q}}} \left[e^{-r} \lambda_{t+1}\right] &= S_t \left( \frac{S_{t_a}}{S_t} \right)^{\tilde{k}_1 -1} \left[ \Uppsi_{-\rho} \left( \tilde{C}^{\prime} , -\tilde{D}^{\prime}(K_t ) \right) - \Uppsi_{-\rho} \left( \tilde{C}^{\prime} , -\tilde{D}^{\prime}(m_t ) \right) \right]\\ &\quad+S_t \left[ \Uppsi_\rho\left( -\tilde{B}^{\prime}, - \tilde{A}^{\prime}(m_t ) \right) -\Upphi \left( -\tilde{A}^{\prime}(m_t ) \right) - \Uppsi_\rho \left( -\tilde{B}^{\prime} , -\tilde{A}^{\prime}(K_t ) \right)\right]\\ &\quad+K_t e^{-r} \left[\Uppsi_{\rho} \left( -\tilde{B} , -\tilde{A}(K_t ) \right) + \Upphi \left( -\tilde{A}(m_t ) \right) -\Uppsi_{\rho} \left( -\tilde{B} , -\tilde{A}(m_t ) \right) \right]\\ &\quad+ (K_t -m_t ) e^{-r} \left( \frac{S_{t_a}}{S_t} \right)^{\tilde{k}_1 -1}\left[\Upphi\left( -\tilde{D}(m_t ) \right) - \Uppsi_{\rho} \left( -\tilde{C} , -\tilde{D}(m_t ) \right) \right]\\ &\quad-K_t e^{-r} \left( \frac{S_{t_a}}{S_t} \right)^{\tilde{k}_1 -1} \Uppsi_{-\rho} \left( \tilde{C}, - \tilde{D}(K_t ) \right)\\ &\quad+ m_t e^{-r} \left( \frac{S_{t_a}}{S_t} \right)^{\tilde{k}_1 -1} \Uppsi_{-\rho} \left( \tilde{C}, - \tilde{D}(m_t ) \right), \end{aligned}$$
(8)

where, for \(x\in\{ m_t , K_t \}\),

  • \(\tilde{A}(x)=\frac{\ln(S_t /x) + r }{\sigma} - \frac{\sigma}{2},\tilde{A}^{\prime}(x)=\tilde{A}(x)+\sigma\),

  • \(\tilde{B}=\frac{\ln(S_t /S_{t_a}) + r (1-s)}{\sigma \sqrt{(1-s)}} - \frac{\sigma\sqrt{(1-s)}}{2}, \tilde{B}^{\prime}=\tilde{B}+\sigma\sqrt{(1-s)}\),

  • \(\tilde{C}=\frac{\ln(S_{t_a}/S_t) + r (1-s)}{\sigma \sqrt{(1-s)}} - \frac{\sigma\sqrt{(1-s)}}{2}, \tilde{C}^{\prime}=\tilde{C}+\sigma\sqrt{(1-s)}\),

  • \(\tilde{D}(x)=\frac{\ln(S_{t_a}^2/S_t x) + r}{\sigma} - \frac{\sigma}{2}, \tilde{D}^{\prime}(x)=\tilde{D}(x)+\sigma\),

  • \(\tilde{k}_1 = \frac{2r}{\sigma^2}\),

\(\Upphi\) is the c.d.f. of a standard normal distribution, \(\rho=\sqrt{1-s}\) and \(\Uppsi_\rho\) is as above.

Theorem 4

(Expectation sensitivities) The impairment value is decreasing in \(\alpha, \mu, \Uplambda\) and s, and increasing in σ. Moreover, it is convex in α,  μ, σ and \(\Uplambda\), and concave in s.

The expected next year impairment is illustrated in Fig. 2 as a function of some key parameters. One can notice that its structure is quite simple in terms of μ and σ, but more complex in terms of \(\Uplambda\) and α as non-linearity comes from exotic optional-type behavior.

Fig. 2
figure 2

Average next-year impairment as a function of μ and σ (left), and of α and \(\Uplambda\) (right)

Full size image

3.2.3 Distribution of the next-year impairment

This analysis of this third impairment characteristic can be interpreted as a profit-and-loss analysis of some complex option. In order to give a more complete panel of characteristics of the next-year impairment, we have to study the distribution of its value. This is particularly important for future extensions to multi-year models. In the following section, we are able to give the cumulative distribution function of next-year impairment.

Theorem 5

(Distribution function of impairments) The cumulative distribution function of the next-year impairments, given the information \(\mathcal{F}_t\) at time t, is given by

$${\mathbb{P}}_t \left[ {\lambda_{t+1} \leq l} \right] = \left\{\begin{array}{ll} (1 - {\mathbb{P}}_t \left[ { J_{t+1} } \right]) + \Upphi \left( A( K_t - l ) \right) - \Upphi \left( A( K_t ) \right) &\\ + \left( \frac{S_{t_a}}{S_t} \right)^{k_1 - 1} \left[ \Uppsi_\rho \left( C , D(K_t) \right) - \Uppsi_\rho \left( C, D(K_t - l) \right) \right] &\\ + \Uppsi_\rho \left( B , A( K_t) \right) - \Uppsi_\rho \left( B, A(K_t - l) \right) &,\quad 0\leq l\leq K_t - m_t,\\ \Upphi \left( A(K_t - l) \right) &, \quad K_t-m_t< l\leq K_t, \end{array}\right.$$
(9)

where all constant numbers, variables and parameters are defined in Theorem 1.

In another way, we have

$${\mathbb{P}}_t \left[ {\lambda_{t+1} \leq l} \right] = \left\{\begin{array}{ll} \Upphi\left( A(K_t -l) \right) + \Uppsi_\rho \left( B , A(m_t ) \right) - \Uppsi_\rho \left( B , A(K_t -l ) \right) &\\ + \left( \frac{S_{t_a}}{S_t} \right)^{k_1 - 1} \left[ \Uppsi_\rho \left( C , D(m_t) \right) - \Uppsi_\rho \left( C, D(K_t - l) \right) \right] &, \quad 0\leq l\leq K_t - m_t,\\ \Upphi \left( A(K_t - l) \right) &,\quad K_t-m_t< l\leq K_t. \end{array}\right.$$
(10)

The proof is given in the “Appendices”.

3.3 A proxy method for already impaired equity securities

We have given closed formula for the probability, the expectation and the distribution function of the next-year impairment losses for an equity securities in a particular model. However, these formulas are quite complex and may be hard to extend to more sophisticated model, or to embed into some risk management or investment optimization software. Some insurance practitioners therefore use a simplification of the approach prescribed by the IFRS standards. In this section, we investigate the relevance of considering only the prolonged criterion (with an updated parameter) as a proxy. To do that, we look for a new α1, parameter of the significant criteria, that gives us the same impairment expectation (cf. Theorem 3) but without the prolonged criteria. In other words, the new impairment expectation is

$$\begin{aligned} {\mathbb{E}}_t \left[ \widetilde{\lambda}_{t+1}^{\alpha_1} \right] &= {\mathbb{E}}_t \left[ (K_t - S_{t+1})^+ {\bf 1} \left\{ S_{t+1} \leq (1-\alpha_1 )S_{t_a} \right\} \right]\\ &= -S_t e^\mu \Upphi \left( -A^{\prime}(m_t^{\alpha_1}) \right) + K_t \Upphi\left( -A(m_t^{\alpha_1}) \right), \end{aligned}$$

with \(m_t^{\alpha_1} = \min \left( K_t, (1-\alpha_1) S_{t_a} \right)\).

So we have to solve:

$$\begin{aligned} {\mathbb{E}}_t \left[ \widetilde{\lambda}_{t+1}^{\alpha_1} \right] &= S_t e^\mu \left( \frac{S_{t_a}}{S_t} \right)^{k_1 -1} \left[ \Uppsi_{-\rho} \left( C^{\prime} , -D^{\prime}(K_t ) \right) - \Uppsi_{-\rho} \left( C^{\prime} , -D^{\prime}(m_t ) \right) \right]\\ &\quad+S_t e^\mu \left[ \Uppsi_\rho\left( -B^{\prime}, - A^{\prime}(m_t ) \right) -\Upphi \left( -A^{\prime}(m_t ) \right) - \Uppsi_\rho \left( -B^{\prime} , -A'(K_t ) \right)\right]\\ &\quad+K_t \left[\Uppsi_{\rho} \left( -B , -A(K_t ) \right) + \Upphi \left( -A(m_t ) \right) -\Uppsi_{\rho} \left( -B , -A(m_t ) \right) \right]\\ &\quad+ (K_t -m_t ) \left( \frac{S_{t_a}}{S_t} \right)^{k_1 -1}\left[\Upphi\left( -D(m_t ) \right) - \Uppsi_{\rho} \left( -C , -D(m_t ) \right) \right]\\ &\quad-K_t \left( \frac{S_{t_a}}{S_t} \right)^{k_1 -1} \Uppsi_{-\rho} \left( C, - D(K_t ) \right)+ m_t \left( \frac{S_{t_a}}{S_t} \right)^{k_1 -1} \Uppsi_{-\rho} \left( C, - D(m_t ) \right) \end{aligned}$$
(11)

Remark 5

One can note, thanks to the expression of the impairment expectation, when the agent chooses \(\alpha_0 \leq \Uplambda/S_{t_a}\) as the initial parameter, then m t  = K t and so the expectation \({\mathbb{E}_t \left[ \lambda_{t+1} \right]}\) does not depend on s nor α0 anymore. It follows that the new α1 can be taken between 0 and \(\Uplambda/S_{t_a}\). Indeed, \(\forall \alpha_1 \leq \Uplambda/S_{t_a}\) then \({\mathbb{E}_t \left[ \widetilde{\lambda}_{t+1}^{\alpha_1} \right] = \mathbb{E}_t \left[ \lambda_{t+1} \right]}\). And so all those values can be solutions.

As a consequence, we will impose in the sequel that if \(\alpha_0 \leq \Uplambda/S_{t_a}, \alpha_1 = \alpha_0\).

Moreover, it is possible to verify that, if \(\alpha_0 > \Uplambda/S_{t_a}, \alpha_1 > \Uplambda/S_{t_a}\) too.

Expectation sensitivities given previously permit us to know that there is a unique solution.

As for the implicit volatility, it is also possible to give a theoretical formula.

Theorem 6

For all sets of parameters, we have

$$\alpha_1 = 1 - \frac{S_t}{S_{t_a}} {{\exp}} \left( (\mu - \frac{\sigma^2}{2}) + \sigma^2 (E_\xi - 1) \right),$$
(12)

with:

  • \(E_\xi = \frac{\partial \vert C^{(2)} - C^{(1)} \vert}{\partial \ln S_t}\);

  • \({C^{(1)} = \frac{\partial \mathbb{E}_t \left[ \lambda_{t+1} \right]}{\partial \ln S_t}}\);

  • \({C^{(2)} = \frac{\partial^2 \mathbb{E}_t \left[ \lambda_{t+1} \right]}{\partial (\ln S_t )^2}}\).

We obtain a closed-form expression for the new parameter α1, as a function of the parameters, and of E ξ. This last quantity depends on first and second derivatives of the impairment value with respect to S t (in fact its logarithm), the asset price at time t. So, if the agent owns a sufficient quantity of information to estimate (or to know) E ξ, she can explicitly determine α1.

But this formula is very hard to use in practice, because we need the knowledge of these derivatives. That is why we shall use numerical methods in the numerical illustration section, as for the implicit volatility.

4 Numerical illustrations and empirical study

We now want to study numerically next year impairment characteristics in concrete cases.

4.1 Data description

We have chosen stocks of French market CAC40: BNP Paribas, Bouygues, Carrefour, Pernod Ricard and Total.

The dataset consists of daily quotations starting at the fourth of January, 2010, and ending at the thirty-first of December, 2012. It almost corresponds to 3 entire years of data. These quotations are used in order to calibrate model parameters (volatility and drift) and give initial and terminal values. This period was impacted by the financial crisis. As volatilities may be higher than in normal periods, we expect to observe more important impairments. Annual volatilities are provided by the website Small Caps Vision. The value of \(\varvec{\mu}\) is obtained by adding a constant drift (3 %) to the volatility: if the volatility is σ, then μ = log (1 + 3 %) + σ2/2. The buying value \(S_{t_a}\) is the quotation of the stock at the date 01/4/2010. Those figures are summarized in Table 5.

Table 5 Used data
Full size table

The first step in this study is to study realized impairments in Table 6. Indeed, we apply our impairment criterion on the close values of the stocks. Remark that this is not perfect, because we are processing on discrete values and the barrier (in the prolonged criteria of impairment) has to be continuous, but this has minor effect on our results. Note that some stocks like BNP Paribas and Carrefour feature consequent impairments, while some others like Pernod Ricard do not feature any impairment in this particular case. As impairments have to be recognized securities by securities, part of the investment diversification effect is not fully recognized in the IFRS framework.

Table 6 Past impairment losses
Full size table

4.2 Next year impairment for various past impairment cases

After this step, at time t = 12/31/2012, we now compute the probability \({\mathbb{P}_t \left[ {J_{t+1}} \right]}\) to recognize an impairment next year, the expectation \({\mathbb{E}_t \left[ \lambda_{t+1}\right]}\) of next year impairment, as well as different Value-at-Risks at levels 80, 95 and 99.5 %. For the sake of brevity we only present results for Total in Table 7. We use standard trigger criteria, i.e. α = 0.3 and s = 0.5. We also use market parameters given previously and the historical buying value \(S_{t_a}\). We artificially vary \(\Uplambda\), set to 5, 10, 50 and 75 % of the buying value \(S_{t_a}\) (that do not correspond to the history of realized impairment between t a and t) in order to study next year impairments in different situations. When \(\Uplambda _t= 2.28975\), at least one small impairment occurred because of the prolonged depreciation criterion. The current price S t is now much lower than \(S_{t_a}\) and \(S_{t_a }-\Uplambda _t\), but still above 0.7 \(S_{t_a}\). It means in particular that the stock price crossed level \(S_{t_a}\) in the time interval [t − 0.5;t): the stock price went severely down during the last six-month period before t. In this case, the probability to recognize an impairment at time t + 1 is larger than 1/2, and the average impairment \({\mathbb{E}_t \left[ \lambda_{t+1}\right]}\) is approximately equal to 4. When \(\Uplambda _t= 22.8975,\) the probability to recognize an impairment next year is very low (smaller than 80bps), and \({\mathbb{E}_t \left[ \lambda_{t+1}\right]}\) is very small too. This is because at least one impairment has been recognized in the past due to the significant depreciation criterion. The last impairment occurred when the stock price was much lower (below 23) than the current price S t . The probability that S t+1 falls again below 23 is very small.

Table 7 Results for Total
Full size table

4.3 Next year impairments for different acquisition dates

In Table 8, we fix t = 12/31/2008 and we vary acquisition dates of stock Pernod Ricard (whose value is S t  = 49.26 at time t). We get then different values of \(S_{t_a}\) and corresponding values of \(\Uplambda_t\) according to the real evolution of stock Pernod Ricard between t a and t. For the first acquisition date, \(S_{t_a}\) = 41.98 and \(\Uplambda_t =0\). The probability to recognize an impairment in that case is below 10 %, because price went up between t a and t. For the second acquisition date, as \(S_{t_a}\) = 71.60 and \(\Uplambda_t = 22.34\), stock price has gone down and the last impairment occurred due to the significant depreciation criterion. The probability to recognize an impairment next year is very high (above 46 %). Note that the choice of the parameters (μ and σ) estimation period is crucial, because it strongly affects the probability to recognize an impairment next year.

Table 8 Results for Pernod Ricard, with σ = 31.38 % and μ = 7.88 %, in different scenarios
Full size table

4.4 Next year impairments with different trigger levels

We now compare impairment probabilities and potential sizes for two insurers, AXA and Generali, which feature very different impairment triggers: for AXA, we have α = 0.2 and s = 6 months, where for Generali we have α = 0.5 and s = 36 months. We can see in Table 9 that the probability to recognize an impairment is much smaller for Generali than for AXA. However, given that an impairment is recognized, the average impairment is likely to be larger for Generali than for AXA.

Table 9 Comparison of AXA and Generali impairment triggers: impairment probability and potential severity for 5 different stocks
Full size table

Remark 6

For the particular case studied appearing in Table 9, both companies have bought assets today (time t). In this framework, the impairment event of Generali is very easy to write, and so the probability and expectation.

Indeed, we have \(S_t=S_{t_a}, \Uplambda_t=0\),

$$\begin{aligned} J_{t+1}&=\left( S_{t+1} \leq (1-\alpha) S_{t_a} \right),\\ {\mathbb{P}}_t \left[ {J_{t+1}} \right]&= \Upphi \left( \frac{\ln(1-\alpha) -\mu}{\sigma} +\frac{\sigma}{2} \right), \end{aligned}$$

and

$${\mathbb{E}}_t \left[ \lambda_{t+1} \right] = -S_t e^\mu \Upphi \left( \frac{\ln (1-\alpha) - \mu }{\sigma} -\frac{\sigma}{2} \right) + S_t \Upphi\left( \frac{\ln (1-\alpha) - \mu }{\sigma} +\frac{\sigma}{2} \right).$$

Note that in some other cases, in particular when past impairments are different for AXA and Generali, one might get different results.

4.5 Illustration of the proxy

We have used the numerical MATLAB solver fzero in order to find α1. The precision of the method was the default precision of the software (i.e. 10−6): we have created a function that returns (original) impairments expectation for a parameters set and another one that returns new impairments expectation for a parameters set. In Fig. 3, we show how this new parameter α1 depends on values of s and (original) α0. It is of course increasing in α0 and s, without any systematic concavity or convexity.

Fig. 3
figure 3

α 1 as a function of α 0 when s = 0.3 (top left), s = 0.5 (top right), and s = 0.75 (bottom left). α 1 as a function of s when α 0 = 0.3 (bottom right)

Full size image

4.6 Quality of this proxy method

The approximation consists in making average impairments identical in both approaches. Here we would like to investigate its quality, through comparison of next year impairment distributions.

Quantiles of next year impairments conditioned to be positive are given in Table 10 for the proxy and for the rigorous approach.

Table 10 Quantiles of next year impairment (conditioned to be positive) with classical criterion and proxy criterion, in the central scenario \((S_t=95, \,\mu = \ln 0.08, \,\sigma = 0.25, S_{t_a} = 100, \,\Uplambda =5)\)
Full size table

One can see that the probability that an impairment occurs is always significantly smaller with the proxy than with the rigorous approach, and that consequently, if an impairment occurs, it is likely to be larger with the proxy than with the rigorous approach. This is in accordance with what we observed in Subsection 4.4 when we compared Axa and Generali impairment trigger levels. The differences are important at all interesting quantile levels for this particular value of \(\Uplambda =5\) that corresponds to one sixth of the distance α0 \(S_{t_a}\) between acquisition price \(S_{t_a}\) and the significant depreciation threshold (1 − α0) \(S_{t_a}\). We have tested many situations, not presented here for the sake of brevity. In all cases, the conclusion is the same: the quality of the proxy is very bad, except if past impairments are very large. We do not recommend to use it if

$$\frac{ \Uplambda }{\alpha_0 S_{t_a}} \le 90\,\%.$$

Consequently, this proxy might be acceptable only and interesting when \(\frac{ \Uplambda }{\alpha_0 S_{t_a}} \in (0.9;1)\), which is not going to happen very often. Besides, if this condition were true for one asset, it would be unlikely to be satisfied for all assets, and it would be hard to justify the use of the proxy for some assets but not for the other ones. The conclusion of this section is that the proxy is not suitable for this concrete impairment study, and that one cannot avoid complexity bred by the two impairment criteria in the IFRS framework. This confirms that sophisticated financial analysis is needed to correctly analyze impairment risk.

5 Conclusion

In this paper, we have given the probabilistic characterization of next-year impairment loss of any equity security, in the Black and Scholes framework. We have also studied a proxy that is often used by practitioners, and found that the quality of this proxy is not good, except when past impairments are large. More generally, our work shows how financial engineering techniques and complex financial option pricing naturally take place in modern accounting problems. In future work, we plan to extend our results in three different ways: studying the sum of discounted impairments in a multi-period setting, considering a portfolio of equity securities with dependence between stock returns (see (Batens 2007)), and testing whether more sophisticated stock price models leads to an effective improvement in the quality of the impairment losses prediction and probabilistic representation.