On the distribution of typical shortest-path lengths in connected random geometric graphs

Abstract

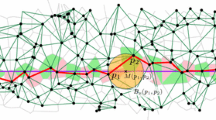
Stationary point processes in ℝ² with two different types of points, say H and L, are considered where the points are located on the edge set G of a random geometric graph, which is assumed to be stationary and connected. Examples include the classical Poisson–Voronoi tessellation with bounded and convex cells, aggregate Voronoi tessellations induced by two (or more) independent Poisson processes whose cells can be nonconvex, and so-called β-skeletons being subgraphs of Poisson–Delaunay triangulations. The length of the shortest path along G from a point of type H to its closest neighbor of type L is investigated. Two different meanings of “closeness” are considered: either with respect to the Euclidean distance (e-closeness) or in a graph-theoretic sense, i.e., along the edges of G (g-closeness). For both scenarios, comparability and monotonicity properties of the corresponding typical shortest-path lengths C ^e∗ and C ^g∗ are analyzed. Furthermore, extending the results which have recently been derived for C ^e∗, we show that the distribution of C ^g∗ converges to simple parametric limit distributions if the edge set G becomes unboundedly sparse or dense, i.e., a scaling factor κ converges to zero and infinity, respectively.