Two different types of optical hybrid qubits for teleportation in a lossy environment

Abstract

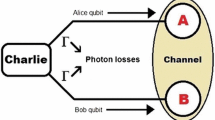
We investigate the performance of quantum teleportation under a lossy environment using two different types of optical hybrid qubits. One is the hybrid of a polarized single-photon qubit and a coherent-state qubit (type-I logical qubit), and the other is the hybrid of a qubit of the vacuum and the single-photon and a coherent-state qubit (type-II logical qubit). We show that type-II hybrid qubits are generally more robust to photon loss effects compared to type-I hybrid qubits with respect to fidelities and success probabilities of quantum teleportation.

Appendix

In this appendix, we present all possible teleported states, their probabilities of obtaining such particular outcomes and fidelities with the input state $|\phi (\tau )\rangle$ for the teleportation of type-II hybrid qubits. All the listed states are the final teleported states on which appropriate unitary transforms are applied. If the measurement results are revealed as $E_{1}\otimes O_{2}$, $E_{1}\otimes O_{3}$, $E_{2}\otimes O_{1}$ and $E_{2}\otimes O_{4}$, the final teleported states are

$$\begin{aligned} \rho ^T_1(\tau )&=|\mu |^2\rho _{++}\otimes |t\alpha \rangle \langle t\alpha | +|\nu |^2\rho _{--}\otimes |-t\alpha \rangle \langle -t\alpha | \nonumber \\&\quad +te^{-4|\alpha |^2r^2}\big (\mu \nu ^*\rho _{+-}\otimes |t\alpha \rangle \langle -t\alpha | +\mu ^*\nu \rho _{-+}\otimes |-t\alpha \rangle \langle t\alpha |\big ), \end{aligned}$$

(51)

with the probability

$$\begin{aligned} p_1(\tau )&=\mathrm{Tr}_{c,C}[\rho ^{1,2}]+\mathrm{Tr}_{c,C}[\rho ^{1,3}]+\mathrm{Tr}_{c,C}[\rho ^{2,1}]+\mathrm{Tr}_{c,C}[\rho ^{2,4}] \nonumber \\&=\frac{1}{4}\left( 1-e^{-2|\alpha |^2t^2}\right) \left( 1+te^{-2|\alpha |^2t^2}\right) . \end{aligned}$$

(52)

Their fidelities with the input state $|\phi (\tau )\rangle$ are calculated as

$$\begin{aligned} f_1(\tau )&=(|\mu |^4+|\nu |^4)\frac{1+t}{2} +2|\mu |^2|\nu |^2\bigg (\frac{1-t}{2}e^{-4|\alpha |^2t^2}+t\frac{t^2+t}{2}e^{-4|\alpha |^2r^2}\bigg ) \nonumber \\&\quad +\left( \mu ^2{\nu ^*}^2+{\mu ^*}^2\nu ^2 \right) t\frac{t^2-t}{2}e^{-4|\alpha |^2} +(\mu \nu ^*+\mu ^*\nu )\frac{r^2}{2}e^{-2|\alpha |^2t^2}. \end{aligned}$$

(53)

If the measurement results are revealed as $E_{1}\otimes O_{1}$, $E_{1}\otimes O_{4}$, $E_{2}\otimes O_{2}$ and $E_{2}\otimes O_{3}$, the final teleported states are

$$\begin{aligned} \rho ^T_2(\tau )&=|\mu |^2\rho _{++}^\prime \otimes |t\alpha \rangle \langle t\alpha | +|\nu |^2\rho _{--}^\prime \otimes |-t\alpha \rangle \langle -t\alpha | \nonumber \\&\quad +te^{-4|\alpha |^2r^2}\big (\mu \nu ^*\rho _{+-}\otimes |t\alpha \rangle \langle -t\alpha | +\mu ^*\nu \rho _{-+}\otimes |-t\alpha \rangle \langle t\alpha |\big ), \end{aligned}$$

(54)

where

$$\begin{aligned} \rho _{++}^\prime&=\frac{1+t}{2}|+\rangle \langle +|+\frac{1-t}{2}|-\rangle \langle -|-\frac{r^2}{2}|+\rangle \langle -|-\frac{r^2}{2}|-\rangle \langle +|,\end{aligned}$$

(55)

$$\begin{aligned} \rho _{--}^\prime&=\frac{1-t}{2}|+\rangle \langle +|+\frac{1+t}{2}|-\rangle \langle -|-\frac{r^2}{2}|+\rangle \langle -|-\frac{r^2}{2}|-\rangle \langle +|, \end{aligned}$$

(56)

with the probability

$$\begin{aligned} p_2(\tau )&=\mathrm{Tr}_{c,C}[\rho ^{1,1}]+\mathrm{Tr}_{c,C}[\rho ^{1,4}]+\mathrm{Tr}_{c,C}[\rho ^{2,2}]+\mathrm{Tr}_{c,C}[\rho ^{2,3}] \nonumber \\&=\frac{1}{4}\left( 1-e^{-2|\alpha |^2t^2}\right) \left( 1-te^{-2|\alpha |^2t^2}\right) , \end{aligned}$$

(57)

and the fidelities are

$$\begin{aligned} f_2(\tau )&=(|\mu |^4+|\nu |^4)\frac{1+t}{2} +2|\mu |^2|\nu |^2\bigg (\frac{1-t}{2}e^{-4|\alpha |^2t^2}+t\frac{t^2+t}{2}e^{-4|\alpha |^2r^2}\bigg ) \nonumber \\&\quad +\left( \mu ^2{\nu ^*}^2+{\mu ^*}^2\nu ^2 \right) t\frac{t^2-t}{2}e^{-4|\alpha |^2} -(\mu \nu ^*+\mu ^*\nu )\frac{r^2}{2}e^{-2|\alpha |^2t^2}. \end{aligned}$$

(58)

If the measurement results are revealed as $E_\mathrm{e}\otimes O_{1}$ and $E_\mathrm{e}\otimes O_{3}$, the final teleported states are

$$\begin{aligned} \rho ^T_3(\tau )&=|\mu |^2\rho _{++}\otimes |t\alpha \rangle \langle t\alpha | +|\nu |^2\rho _{--}\otimes |-t\alpha \rangle \langle -t\alpha | \nonumber \\&\quad +t^2e^{-4|\alpha |^2r^2}\big (\mu \nu ^*\rho _{+-}\otimes |t\alpha \rangle \langle -t\alpha | +\mu ^*\nu \rho _{-+}\otimes |-t\alpha \rangle \langle t\alpha |\big ), \end{aligned}$$

(59)

with the probability

$$\begin{aligned} p_3(\tau )=\mathrm{Tr}_{c,C}[\rho ^{\mathrm{e},1}]+\mathrm{Tr}_{c,C}[\rho ^{\mathrm{e},3}] =\frac{1}{4}\left( 1-e^{-2|\alpha |^2t^2}\right) ^2, \end{aligned}$$

(60)

and the fidelities are

$$\begin{aligned} f_3(\tau )&=(|\mu |^4+|\nu |^4)\frac{1+t}{2} +2|\mu |^2|\nu |^2\bigg (\frac{1-t}{2}e^{-4|\alpha |^2t^2}+t^2\frac{t^2+t}{2}e^{-4|\alpha |^2r^2}\bigg ) \nonumber \\&\quad +\left( \mu ^2{\nu ^*}^2+{\mu ^*}^2\nu ^2 \right) t^2\frac{t^2-t}{2}e^{-4|\alpha |^2} +(\mu \nu ^*+\mu ^*\nu )\frac{r^2}{2}e^{-2|\alpha |^2t^2}. \end{aligned}$$

(61)

If the measurement results are revealed as $E_\mathrm{e}\otimes O_{2}$ and $E_\mathrm{e}\otimes O_{4}$, the final teleported states are

$$\begin{aligned} \rho ^T_4(\tau )&=|\mu |^2\rho _{++}^\prime \otimes |t\alpha \rangle \langle t\alpha | +|\nu |^2\rho _{--}^\prime \otimes |-t\alpha \rangle \langle -t\alpha | \nonumber \\&\quad +t^2e^{-4|\alpha |^2r^2}\big (\mu \nu ^*\rho _{+-}\otimes |t\alpha \rangle \langle -t\alpha | +\mu ^*\nu \rho _{-+}\otimes |-t\alpha \rangle \langle t\alpha |\big ), \end{aligned}$$

(62)

with the probability

$$\begin{aligned} p_4(\tau )=\mathrm{Tr}_{c,C}[\rho ^{\mathrm{e},2}]+\mathrm{Tr}_{c,C}[\rho ^{\mathrm{e},4}] =\frac{1}{4}(1-e^{-2|\alpha |^2t^2})(1+e^{-2|\alpha |^2t^2}), \end{aligned}$$

(63)

and the fidelities are

$$\begin{aligned} f_4(\tau )&=(|\mu |^4+|\nu |^4)\frac{1+t}{2} +2|\mu |^2|\nu |^2\bigg (\frac{1-t}{2}e^{-4|\alpha |^2t^2}+t^2\frac{t^2+t}{2}e^{-4|\alpha |^2r^2}\bigg ) \nonumber \\&\quad +\left( \mu ^2{\nu ^*}^2+{\mu ^*}^2\nu ^2 \right) t^2\frac{t^2-t}{2}e^{-4|\alpha |^2} -(\mu \nu ^*+\mu ^*\nu )\frac{r^2}{2}e^{-2|\alpha |^2t^2}. \end{aligned}$$

(64)

Lastly, for the measurement results of $E_{1}\otimes O_\mathrm{e}$ and $E_{2}\otimes O_\mathrm{e}$, the final teleported states are

$$\begin{aligned} \rho ^T_5(\tau )&=\frac{1}{1-(\mu \nu ^*+\mu ^*\nu )r^2} \nonumber \\&\quad \times \bigg \{\bigg (|\mu |^2\frac{1+t}{2}-\mu \nu ^*\frac{r^2}{2}-\mu ^*\nu \frac{r^2}{2}+|\nu |^2\frac{1-t}{2}\bigg ) \rho _{++}^\prime \otimes |t\alpha \rangle \langle t\alpha | \nonumber \\&\quad +\bigg (|\mu |^2\frac{1-t}{2}-\mu \nu ^*\frac{r^2}{2}-\mu ^*\nu \frac{r^2}{2}+|\nu |^2\frac{1+t}{2}\bigg ) \rho _{--}^\prime \otimes |-t\alpha \rangle \langle -t\alpha | \nonumber \\&\quad +e^{-4|\alpha |^2r^2}\bigg [\bigg (\mu \nu ^*\frac{t^2+t}{2}+\mu ^*\nu \frac{t^2-t}{2}\bigg )\rho _{+-} \otimes |t\alpha \rangle \langle -t\alpha | \nonumber \\&\quad +\bigg (\mu \nu ^*\frac{t^2-t}{2}+\mu ^*\nu \frac{t^2+t}{2}\bigg )\rho _{-+}\otimes |-t\alpha \rangle \langle t\alpha |\bigg ]\bigg \} \end{aligned}$$

(65)

with the probability

$$\begin{aligned} p_5(\tau )=\mathrm{Tr}_{c,C}[\rho ^{1,\mathrm{e}}]+\mathrm{Tr}_{c,C}[\rho ^{2,\mathrm{e}}] =\frac{1}{2}e^{-2|\alpha |^2t^2}\left[ 1-(\mu \nu ^*+\mu ^*\nu )r^2 \right] , \end{aligned}$$

(66)

and the fidelities are

$$\begin{aligned} f_5(\tau )&=\frac{1}{1-(\mu \nu ^*+\mu ^*\nu )r^2} \bigg \{(|\mu |^4+|\nu |^4)\bigg [\bigg (\frac{1+t}{2}\bigg )^2+\bigg (\frac{1-t}{2}\bigg )^2e^{-4|\alpha |^2t^2}\bigg ] \nonumber \\&\quad +2|\mu |^2|\nu |^2\bigg [\frac{r^2}{4}\left( 1+e^{-2|\alpha |^2t^2}\right) ^2 +\bigg (\frac{t^2+t}{2}\bigg )^2e^{-4|\alpha |^2r^2}+\bigg (\frac{t^2-t}{2}\bigg )^2e^{-4|\alpha |^2}\bigg ] \nonumber \\&\quad +(\mu ^2{\nu ^*}^2+{\mu ^*}^2\nu ^2)\bigg [\frac{r^4}{2}e^{-2|\alpha |^2t^2} +\bigg (\frac{t^2+t}{2}\bigg )\bigg (\frac{t^2-t}{2}\bigg )\left( e^{-4|\alpha |^2r^2}+e^{-4|\alpha |^2}\right) \bigg ] \nonumber \\&\quad -(\mu \nu ^*+\mu ^*\nu )\frac{r^2}{2}\left( 1+e^{-2|\alpha |^2t^2}\right) \bigg (\frac{1+t}{2}+\frac{1-t}{2}e^{-2|\alpha |^2t^2}\bigg )\bigg \}. \end{aligned}$$

(67)