Skip to main content
SpringerLink
Log in

Estimation of seismic hazard and risks for the Himalayas and surrounding regions based on Unified Scaling Law for Earthquakes

  • Original Paper
  • Published:
Natural Hazards Aims and scope Submit manuscript

Abstract

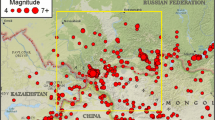
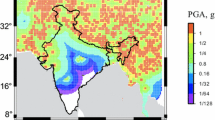
To estimate seismic hazard, the basic law of seismicity, the Gutenberg–Richter recurrence relation, is applied in a modified form involving a spatial term: \(\log N\left( {M,\;L} \right) = A - B\left( {M - 5} \right) + C\log L\), where N(M,L) is the expected annual number of earthquakes of a certain magnitude M within an area of linear size L. The parameters A, B, and C of this Unified Scaling Law for Earthquakes (USLE) in the Himalayas and surrounding regions have been studied on the basis of a variable space and time-scale approach. The observed temporal variability of the A, B, and C coefficients indicates significant changes of seismic activity at the time scales of a few decades. At global scale, the value of A ranges mainly between −1.0 and 0.5, which determines the average rate of earthquakes that accordingly differs by a factor of 30 or more. The value of B concentrates about 0.9 ranging from under 0.6 to above 1.1, while the fractal dimension of the local seismic prone setting, C, changes from 0.5 to 1.4 and larger. For Himalayan region, the values of A, B, and C have been estimated mainly ranging from −1.6 to −1.0, from 0.8 to 1.3, and from 1.0 to 1.4, respectively. We have used the deterministic approach to map the local value of the expected peak ground acceleration (PGA) from the USLE estimated maximum magnitude or, if reliable estimation was not possible, from the observed maximum magnitude during 1900–2012. In result, the seismic hazard map of the Himalayas with spatially distributed PGA was prepared. Further, an attempt is made to generate a series of the earthquake risk maps of the region based on the population density exposed to the seismic hazard.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Auden JB (1959) Earthquakes in relation to the Damodar Valley Project. Proc Symp Earthquake Engineering, 1st University of Roorkee, Roorkee

  • Bak P, Christensen K, Danon L, Scanlon T (2002) Unified Scaling Law for Earthquakes. Phys Rev Lett 88:178501–178504

    Article  Google Scholar 

  • Bhatia SC, Chetty TRK, Filimonov M, Gorshkov A, Rantsman E, Rao MN (1992) Identification of potential areas for the occurrence of strong earthquakes in Himalayan arc region. Proc Indian Acad Sci (Earth Planet Sci) 101(4):369–385

    Google Scholar 

  • Bhatia SC, Kumar R, Gupta HK (1999) A probabilistic seismic hazard map of India and adjoining regions. Ann Geophys 42:1153–1164

    Google Scholar 

  • Christensen K, Danon L, Scanlon T, Bak P (2002) Unified Scaling Law for Earthquakes. Proc Natl Acad Sci 99(suppl. 1):2509–2513

    Article  Google Scholar 

  • Davis C, Keilis-Borok V, Kossobokov V, Soloviev A (2012) Advance prediction of the March 11, 2011 Great East Japan earthquake: a missed opportunity for disaster preparedness. Int J Disaster Risk Reduct 1:17–32. doi:10.1016/j.ijdrr.2012.03.001

    Article  Google Scholar 

  • Deshikachar SV (1974) A review of the tectonic and geological history of eastern India in terms of ‘plate tectonics’ theory. J Geol Soc India 15:137–149

    Google Scholar 

  • Gansser A (1964) Geology of the Himalayas. Interscience, New York, p 289

    Google Scholar 

  • Gansser A (1977) The great suture zone between Himalaya and Tibet: a preliminary account. In: Jest C (ed) Himalaya: Science de la Terre, Colloq. Int. CNRS, 268: 181–192

  • Gaur VK, Chouhan RKS (1968) Quantitative measures of seismicity applied to Indian regions. Bull Indian Soc Earthq Technol 5:63–78

    Google Scholar 

  • Gorshkov A, Kossobokov V, Soloviev A (2003) 6. Recognition of earthquake-prone areas. In: Keilis-Borok VI, Soloviev AA (eds) nonlinear dynamics of the lithosphere and earthquake prediction. Springer, Heidelberg, pp 239–310

    Chapter  Google Scholar 

  • Gorshkov A, Parvez IA, Novikova O (2012) Recognition of earthquake-prone areas in the Himalaya: validity of the results. International J Geophys 2012, Article ID 419143, p 5. doi:10.1155/2012/419143

  • Gridded Population of the World, Version 3 (GPWv3) (2005) Palisades, NY: Socioeconomic Data and Applications Center (SEDAC), Columbia University. Available at http://sedac.ciesin.columbia.edu/gpw. 2012.05.29

  • Kaila KL, Rao M (1979) Seismic zoning maps of Indian subcontinent. Geophys Res Bull 17:293–301

    Google Scholar 

  • Keilis-Borok VI (1990) The lithosphere of the Earth as a nonlinear system with implications for earthquake prediction. Rev Geophys 28(1):19–34

    Article  Google Scholar 

  • Keilis-Borok VI, Kossobokov VG, Mazhkenov SA (1989) On similarity in spatial distribution of seismicity. In: Theory and algorithms of interpretation of geophysical data. Nauka, Moscow, pp 28–40 (Computational Seismology 22, in Russian)

  • Khattri KN (1987) Great earthquakes, seismicity gaps and potential for earthquake disaster along the Himalaya plate boundary. Tectonophysics 138:79–92

    Article  Google Scholar 

  • Khattri KN, Rogers AM, Perkins DM, Algermissen ST (1984) A seismic hazard map of India and adjacent areas. Tectonophysics 108:93–134

    Article  Google Scholar 

  • Kossobokov VG (1984) General features of the strongest (with M ≥ 8.2) earthquake-prone areas in the non-Alpine zone of the Transasian seismic belt. In: Keilis-Borok VI, Levshin AL (eds) Logical and computational methods in seismology (Comput Seismol 17). Nauka, Moscow, pp 69–72

    Google Scholar 

  • Kossobokov VG (2012) Earthquake prediction: 20 years of global experiment. Nat Hazards. doi:10.1007/s11069-012-0198-1

    Google Scholar 

  • Kossobokov VG, Mazhkenov SA (1988) Spatial characteristics of similarity for earthquake sequences: fractality of seismicity. Lecture notes of the workshop on global geophysical informatics with applications to research in earthquake prediction and reduction of seismic risk (15 Nov–16 Dec., 1988), ICTP, Trieste, p 15

  • Kossobokov VG, Mazhkenov SA (1994) On similarity in the spatial distribution of seismicity. Computational Seismology and Geodynamics. Am. Geophys. Un., The Union, Washington, DC, 1:6–15

  • Kossobokov VG, Nekrasova A (2003) Generalized Gutenberg-Richter recurrence law. Geophysical research abstracts, 5, abstracts of the contributions of the EGS-AGU-EGU Joint Assembly, Nice, France, 06–11 April, 2003 (CD-ROM): EAE03- A-06597

  • Kossobokov VG, Nekrasova AK (2005) Temporal variations in the parameters of the Unified Scaling Law for Earthquakes in the eastern part of Honshu Island (Japan). Doklady Earth Sci 405:1352–1356

    Google Scholar 

  • Kossobokov VG, Nekrasova A (2007) Unified scaling law for earthquakes: implications for seismic hazard and risk assessment. In: IUGG2007, July 2–13, 2007, Perugia, Italy. Abstracts, SS002–65

  • Kossobokov VG, Nekrasova AK (2012) Global seismic hazard assessment program maps are erroneous. Seism Instrum 48(2):162–170. doi:10.3103/S0747923912020065

    Article  Google Scholar 

  • Krishnan MS (1968) Geology of India and Burma. Higginbothams, Madras, p 536

    Google Scholar 

  • Lyubushin A, Parvez IA (2010) Map of seismic hazard of India using Bayesian approach. Nat Hazards 55:543–556

    Article  Google Scholar 

  • Mandelbrot BB (1982) The fractal geometry of nature. Freeman, New York, p 488

    Google Scholar 

  • Molchan G, Kronrod T, Panza GF (1997) Multi-scale seismicity model for seismic risk. Bull Seism Soc Am 87:1220–1229

    Google Scholar 

  • Nekrasova A (2008) Unified scaling law for earthquakes: application in seismic regions worldwide. PhD Thesis, M.V. Lomonosov Moscow State University, Moscow, p 200 (in Russian)

  • Nekrasova AK, Kosobokov VG (2006) General law of similarity for earthquakes: evidence from the Baikal region. Doklady Earth Sci 407A(3):484–485

    Article  Google Scholar 

  • Nekrasova A, Kossobokov V (2002) Generalizing the Gutenberg-Richter scaling law. EOS Trans AGU 83(47), Fall Meet Suppl, abstract NG62B-0958, 2002

  • Nekrasova A, Kossobokov V (2003) Generalized Gutenberg-Richter recurrence law: global map of parameters. Geophysical research abstracts, 5, abstracts of the contributions of the EGS–AGU–EGU Joint Assembly, Nice, France, 6-11 April, 2003 (CD-ROM): EAE03-A-03801

  • Nekrasova A, Kossobokov V, Peresan A, Aoudia A, Panza GF (2011) A multiscale application of the Unified Scaling Law for Earthquakes in the Central Mediterranean area and Alpine region. Pure Appl Geophys 168:297–327

    Article  Google Scholar 

  • Panza G, Irikura K, Kouteva-Guentcheva M, Peresan A, Wang Z, Saragoni R (eds) (2011) Advanced seismic hazard assessment. Pure Appl Geophys 168(1–4):752

  • Parvez IA (2007) On the Bayesian analysis of the earthquake hazard in the north–east Indian peninsula. Nat Hazards 40:397–412

    Article  Google Scholar 

  • Parvez IA, Ram A (1997) Probabilistic assessment of earthquake hazards in the north–east Indian Peninsula and Hidukush region. Pure Appl Geophys 149:731–746

    Article  Google Scholar 

  • Parvez IA, Ram A (1999) Probabilistic assessment of earthquake hazards in the Indian subcontinent. Pure Appl Geophys 154:23–40

    Article  Google Scholar 

  • Parvez IA, Gusev AA, Panza GF, Petukhin AG (2001) Preliminary determination of the interdependence among strong motion amplitude, earthquake magnitude and hypocentral distance for the Himalayan region. Geophys J Int 144:577–596

    Article  Google Scholar 

  • Parvez IA, Vaccari F, Panza GF (2003) A deterministic seismic hazard map of India and adjacent areas. Geophys J Int 155:489–508

    Article  Google Scholar 

  • Turcotte DL (1997) Fractals and chaos in Geology and Geophysics, 2nd edn. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Turcotte DL (1999) Seismicity and self-organized criticality. Phys Earth Planet Int 111:275–294

    Article  Google Scholar 

  • Wadia DN (1975) Geology of India. Tata McGraw-Hill, New Delhi, p 508

    Google Scholar 

  • Wyss M, Nekrasova A, Kossobokov V (2012) Errors in expected human losses due to incorrect seismic hazard estimates. Nat Hazards 62(3):927–935. doi:10.1007/s11069-012-0125-5

    Article  Google Scholar 

Download references

Acknowledgments

The authors acknowledge the financial support from the RFBR-DST Project “Seismic hazard and risk assessment based on pattern recognition: Himalayas and adjacent territories” (Grants RFBR No. 11-05-92691 and DST No. INT/RFBR/P-109). We also would like to thank two anonymous reviewers for their constructive suggestions and critical reviews to improve the quality of the manuscript.

Author information

Authors and Affiliations

  1. CSIR Centre for Mathematical Modelling and Computer Simulation, Bangalore, India

    Imtiyaz A. Parvez

  2. Institute of Earthquake Prediction Theory and Mathematical Geophysics, RAS, Moscow, Russian Federation

    Anastasia Nekrasova & Vladimir Kossobokov

  3. Institut de Physique du Globe de Paris, Paris, France

    Vladimir Kossobokov

Authors
  1. Imtiyaz A. Parvez
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Anastasia Nekrasova
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vladimir Kossobokov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Imtiyaz A. Parvez.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Parvez, I.A., Nekrasova, A. & Kossobokov, V. Estimation of seismic hazard and risks for the Himalayas and surrounding regions based on Unified Scaling Law for Earthquakes. Nat Hazards 71, 549–562 (2014). https://doi.org/10.1007/s11069-013-0926-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11069-013-0926-1

Keywords

Search

Navigation