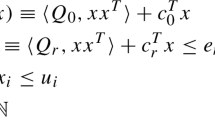Abstract
In deterministic continuous constrained global optimization, upper bounding the objective function generally resorts to local minimization at several nodes/iterations of the branch and bound. We propose in this paper an alternative approach when the constraints are inequalities and the feasible space has a non-null volume. First, we extract an inner region, i.e., an entirely feasible convex polyhedron or box in which all points satisfy the constraints. Second, we select a point inside the extracted inner region and update the upper bound with its cost. We describe in this paper two original inner region extraction algorithms implemented in our interval B&B called IbexOpt (AAAI, pp 99–104, 2011). They apply to nonconvex constraints involving mathematical operators like , \( +\; \bullet ,\; /,\; power,\; sqrt,\; exp,\; log,\; sin\). This upper bounding shows very good performance obtained on medium-sized systems proposed in the COCONUT suite.








Similar content being viewed by others
Notes
We consider minimization in this paper without loss of generality.
An interval \([x_i]=[\underline{x_i},\overline{x_i}]\) defines the set of reals \(x_i\) s.t. \(\underline{x_i} \le x_i \le \overline{x_i}\). A box \([x]\) is the Cartesian product of intervals \([x_1] \times \cdots \times [x_i] \times \cdots \times [x_n]\).
\(\epsilon \)-minimize \(f(x)\) means minimize \(f(x)\) with a precision \(\epsilon \), i.e., we have \(f(y) \ge f(x)-\epsilon \), for all (feasible) \(y\).
In addition, Chabert and Beldiceanu handled a dual problem consisting in finding a box with no solution (i.e., all points in this box violate the constraints) and required an initial point to be “inflated” to a box...
With floating-point numbers, an interval evaluation is conservative (i.e., contains all the real-valued images) if the lower bound of the interval image is rounded towards \(-\infty \) while the upper bound is rounded to \(+\infty \). Both rounding operations constitute a so-called outward rounding. With inward rounding, the lower bound is rounded towards \(+\infty \) and the upper bound towards \(-\infty \). The property enforced by outward (resp. inward) rounding for an operator \(op\) is (1), resp. (2):
-
1.
\(\forall x \in [x] ~~ \exists z \in op([x]) ~~ z=op(x)\)
-
2.
\(\forall z\in op([x]) ~~ \exists x \in [x] ~~ z=op(x)\)
-
1.
In the case 2, only one inner interval is considered among the different ones in the union. In the case 3, only one maximal inner box is computed (using a random choice on \(x_1\)) among an infinite number of possibles boxes. The last case gathers both drawbacks (from cases 2 and 3). Consider for instance the case of the multiplication \(x_1 \cdot x_2 \in [z]\) where \(z\) is positive (see left side of Fig. 6).
The difficulty is only related to our implementation. The maximality can be more easily checked with a direct implementation.
References
Araya, I., Trombettoni, G., Neveu, B.: Exploiting monotonicity in interval constraint propagation. In: Proceedings of AAAI, pp. 9–14 (2010)
Araya, I., Trombettoni, G., Neveu, B.: A contractor based on convex interval Taylor. In: CPAIOR, pp. 1–16. LNCS 7298 (2012)
Belotti, P.: Couenne, a user’s manual (2013). http://www.coin-or.org/Couenne/
Benhamou, F., Goualard, F.: Universally quantified interval constraints. In: Proceedings of CP, Constraint Programming, LNCS 1894, pp. 67–82 (2004)
Benhamou, F., Goualard, F., Granvilliers, L., Puget, J.F.: Revising hull and box consistency. In: Proceedings of ICLP, pp. 230–244 (1999)
Bliek, C.: Computer methods for design automation. Ph.D. thesis, MIT (1992)
Chabert, G., Beldiceanu, N.: Sweeping with continuous domains. In: Proceedings of CP, LNCS 6308, pp. 137–151 (2010)
Chabert, G., Jaulin, L.: Contractor programming. Artif. Intell. 173, 1079–1100 (2009)
Collavizza, H., Delobel, F., Rueher, M.: Extending consistent domains of numeric CSP. In: Proceedings of IJCAI, pp. 406–413 (1999)
Goldsztejn, A.: Définition et applications des extensions des fonctions réelles aux intervalles généralisés: nouvelle formulation de la théorie des intervalles modaux et nouveaux résultats. Ph.D. thesis, University of Nice Sophia Antipolis (2005)
Hansen, E.: Global Optimization Using Interval Analysis. Marcel Dekker, New York (1992)
Kearfott, R.B.: Rigorous Global Search: Continuous Problems. Kluwer Academic, Dordrecht (1996)
Kreinovich, V., Lakeyev, A., Rohn, J., Kahl, P.: Computational Complexity and Feasibility of Data Processing and Interval Computations. Kluwer, Dordrecht (1997)
Lebbah, Y., Michel, C., Rueher, M., Daney, D., Merlet, J.: Efficient and safe global constraints for handling numerical constraint systems. SIAM J. Numer. Anal. 42(5), 2076–2097 (2005)
Lin, Y., Stadtherr, M.: LP strategy for the interval-Newton method in deterministic global optimization. Ind. Eng. Chem. Res. 43, 3741–3749 (2004)
McAllester, D., Van Hentenryck, P., Kapur, D.: Three cuts for accelerated interval propagation. tech. rep. AI Memo 1542, Massachusetts Institute of Technology (1995)
Messine, F., Laganouelle, J.L.: Enclosure methods for multivariate differentiable functions and application to global optimization. J. Univ. Comput. Sci. 4(6), 589–603 (1998)
Messine, F.: Méthodes d’optimisation globale basées sur l’analyse d’intervalle pour la résolution des problèmes avec contraintes. Ph.D. thesis, LIMA-IRIT-ENSEEIHT-INPT, Toulouse (1997)
Moore, R., Kearfott, R.B., Cloud, M.: Introduction to Interval Analysis. SIAM, Philadelphia (2009)
Moore, R.E.: Interval Analysis. Prentice-Hall, Englewood Cliffs (1966)
Neumaier, A.: Interval Methods for Systems of Equations. Cambridge University Press, Cambridge (1990)
Ninin, J., Messine, F., Hansen, P.: A reliable affine relaxation method for global optimization. tech. rep. RT-APO-10-05, IRIT (2010)
Oettli, W.: On the solution set of a linear system with inaccurate coefficients. SIAM J. Numer. Anal. 2(1), 115–118 (1965)
Rohn, J.: Inner solutions of linear interval systems. In: Proceedings of Interval Mathematics 1985, LNCS 212, pp. 157–158 (1986)
Shary, S.: Solving the linear interval tolerance problem. Math. Comput. Simul. 39, 53–85 (1995)
Tawarmalani, M., Sahinidis, N.V.: A polyhedral branch-and-cut approach to global optimization. Math. Program. 103(2), 225–249 (2005)
Trombettoni, G., Araya, I., Neveu, B., Chabert, G.: Inner regions and interval linearizations for global optimization. In: AAAI, pp. 99–104 (2011)
Trombettoni, G., Chabert, G.: Constructive interval disjunction. In: Proceedings of CP, LNCS 4741, pp. 635–650 (2007)
Author information
Authors and Affiliations
Corresponding author
Additional information
Ignacio Araya is supported by the Fondecyt Project 11121366 and the UTFSM Researcher Associated Program.
Rights and permissions
About this article
Cite this article
Araya, I., Trombettoni, G., Neveu, B. et al. Upper bounding in inner regions for global optimization under inequality constraints. J Glob Optim 60, 145–164 (2014). https://doi.org/10.1007/s10898-014-0145-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-014-0145-7