Effect of Dust Grains on Dust-Ion-Acoustic KdV Solitons in Magnetized Complex Plasma with Superthermal Electrons

Abstract

In this paper, the propagation of dust-ion-acoustic (DIA) waves in a magnetized collisionless complex (dusty) plasma consisting of superthermal electrons are investigated. In the discharge plasma, the electron temperature is usually much greater than ion temperature. Thus, the electron distribution function DF), is generally nonmaxwellian, has to be modeled. For this purpose, the generalized Lorentzian ($\kappa$)-DF is used to simulate the electron DF. Two types of modes (fast and slow DIA modes) exist in this plasma. By deriving Korteweg-de Vries (KdV) equation, using reductive perturbation method, both regions of solitary waves, rarefactive (dark) and compressive (bright) solitary waves, are allowed to be propagated in this plasma. Properties of DIA solitary waves are investigated numerically. How dust grains and superthermal electrons affect the sign and the magnitude of nonlinear coefficient of KdV equation is also discussed in detail. It is noted that the velocity, amplitude, and width of a DIA soliton is studied as well.

Introduction

In last years, complex (dusty) plasmas have achieved a large interest because of their importance in astrophysical and upper atmosphere (planetary rings, comets and magnetosphere) as well as in the lower part of the Earth’s ionosphere [1–5].

Dusts are micron-sized particles and become electrically charged through interaction with the background plasma, causing them to act as a third charged plasma species.

However, when an electron–ion plasma contains extremely massive, micrometer-size charged dust grains, there are appeared the possibility of new normal modes. Such as dust-acoustic (DA) waves [2, 6, 7], dust-ion-acoustic (DIA) waves [6, 7], dust-lattice (DL) waves [7–9], etc.

Dusty plasma is also an important issue for the industrial community [10]. Since plasmas are used to produce microchips, thin film coatings and hardened metals which in all of these cases, dust might produced from materials in the plasma reactor. Accordingly, the study of dusty plasma has been advanced regarding to these two reasons.

Solitons are nonlinear and localized structures that propagate when the nonlinearity and dispersion are balanced. They are a subject of continuing interest because of their practical importance. A comprehensive nonlinear theory for arbitrary amplitude ion-acoustic solitary (IAS) waves was suggested by Sagdeev [11] for an unmagnetized plasma. The theory has been extended to cover oblique soliton propagation with respect to a constant magnetic field [12–15]. Recently, some works have been done on the propagation of dust acoustic solitary (DAS) waves in different views. Several investigations [13, 16–19] have shown that the dust charge variation plays an important role in the nonlinear properties of solitary waves structure. Also, the propagation of DAS in cylindrical and spherical geometry has been studied [20, 21] which show different behavior of DAS in cylindrical and spherical geometry rather than planar geometry.

In this paper, we focus our attention on the nonlinear properties of DIA solitary waves in the presence of superthermal electrons in magnetized complex plasma in planar geometry.

Although, the electron DF in the Q-machine is almost Maxwellian. In the RF discharge, it is non-Maxwellian [22]. There are a numerous researches based on non-Maxwellian DF for the plasma particles [23–25]. Among the most popular non-Maxwellian DF is the generalized Lorentzian ($\kappa$) DF.

The kappa DF applications include, for instance, an interpolation of observations in the Earth’s foreshock ($3 < \kappa < 6$) [23, 26] and solarwind models with coronal electrons satisfying ($2 < \kappa < 6$) [23, 27, 28]. In laser matter interactions or plasma turbulence, a superthermal DF was also observed [23, 29]. Therefore, we use it to simulate the electron DF.

The manuscript is organized as follows: the basic equation, describing the dusty plasma system under consideration and incorporating the variable dust charge, is given in “Basic Equation”. “Linear Dispersion Relation” is devoted to linear approximation by which linear dispersion relation is given. In “Derivation of the Nonlinear KdV Equation”, we drive a KdV equation for small amplitude nonlinear DIA soliton wave. In fifth section the “Results” are discussed. The “Conclusion” is given in the Last section.

Basic Equation

We consider a tree-component complex plasma consisting of cold positively charged ions, negatively charged dust grains and hot electrons, in the presence of an external magnetic field $\vec{B} = B\hat{z}$ where B is the strength of the magnetic field and $\hat{z}$ is a unit vector along the z direction. Thus, the set of equations in this case are as follows:

$$ \frac{{\partial n_{i} }}{\partial t} + \nabla \cdot \left( {n_{i} \vec{v}_{i} } \right) = 0, $$

(1)

$$ \frac{{\partial \vec{v}_{i} }}{\partial t} + \left( {\vec{v}_{i} \cdot \nabla } \right) \cdot \vec{v}_{i} = \frac{{z_{i} e}}{{m_{i} }}\left( { - \nabla \varphi + \frac{{\vec{v}_{i} \times B\hat{z}}}{c}} \right), $$

(2)

$$ \frac{{\partial n_{d} }}{\partial t} + \nabla \cdot \left( {n_{d} \vec{v}_{d} } \right) = 0, $$

(3)

$$ \frac{{\partial \vec{v}_{d} }}{\partial t} + \left( {\vec{v}_{d} \cdot \nabla } \right) \cdot \vec{v}_{d} = \frac{{ - z_{d} e}}{{m_{d} }}\left( { - \nabla \varphi + \frac{{\vec{v}_{d} \times B\hat{z}}}{c}} \right). $$

(4)

The dust grains, positive ions and electrons are coupled through Poisson’s equation

$$ \nabla^{2} \varphi = 4\pi e\left( {n_{e} + z_{d} n_{d} - z_{i} n_{i} } \right). $$

(5)

And in equilibrium, the following charge neutrality condition

$$ n_{0e} + z_{d} n_{0d} - z_{i} n_{0i} = 0, $$

(6)

is fulfilled. The variables $n_{d} ,n_{i}$ and $n_{e}$ refer to dust grain density, ion density and electron density respectively which $n_{0d} ,\,\,n_{0i}$ and $n_{0e}$ being their equilibrium values. $\vec{v}_{i} (\vec{v}_{d} )$ is the ion (dust) fluid velocity vector, $\varphi$ is the self-consistent electric potential, $z_{i} (z_{d} )$ is the charge state of an ion (dust grain), e is the magnitude of the electrocharge, c is the speed of light, and $m_{i} (m_{d} )$ is the mass of an ion (a dust grain) in the plasma.

The electron DF is considered to be non-Maxwellian. The $\kappa$ DF is a convenient option for this purpose. As was mentioned, the following $\kappa$ DF that is modified by the presence of an electrostatic potential is introduced.

$$ f\left( {v_{e\parallel } ,v_{e \bot } } \right) = \frac{{n_{0} \Upgamma (\kappa + 1)}}{{\sqrt \pi v_{Te,\kappa } \kappa^{3/2} \Upgamma (\kappa - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2})}}\left[ {1 + \frac{{m_{e} v_{{_{e\parallel } }}^{2} - 2e\varphi }}{{m_{e} \kappa v_{{_{Te,\kappa } }}^{2} }}} \right]^{ - \kappa } \frac{{\delta (v_{e \bot } )}}{{2\pi v_{e \bot } }}, $$

(7)

where f is the velocity DF, $\bot (\parallel )$ is the sign denotes the perpendicular (parallel) direction to the B, n ₀ $n_{0}$ is the equilibrium electron density, m _e is the electron mass, $\Upgamma$ is the gamma function, $\delta$ is the Dirac delta function and is used to model the electron temperature anisotropy, $T_{e\parallel } \gg T_{e \bot } ,$ by this choice, $T_{e \bot }$ does not appear in the formalism, $v_{Te}$ is the electron thermal velocity $\left( {\sqrt {\frac{{T_{e\parallel } }}{{m_{e} }}} } \right),$ $\kappa$ is the spectral index $\left( {\kappa > 3/2} \right)$ and $v_{Te,\kappa }$ is the modified thermal speed $\left( {v_{Te,\kappa } = v_{Te} \left( {\frac{2\kappa - 3}{\kappa }} \right)^{1/2} } \right).$

The electron density is then obtained by integrating the DF over the whole velocity range,

$$ n_{e} = \int\limits_{0}^{\infty } {2\pi v_{e \bot } {\text{d}}v_{e \bot } } \int\limits_{ - \infty }^{\infty } {f\left( {v_{e\parallel } ,v_{e \bot } } \right){\text{d}}v_{e\parallel } } . $$

The electron density, in the weak nonlinear regime $\left( {e\varphi /T_{e\parallel } < 1} \right),$ has the following expression,

$$ \frac{{n_{e} }}{{n_{0e} }} = 1 + a_{\kappa } \frac{e\varphi }{{T_{e\parallel } }} + b_{\kappa } \left( {\frac{e\varphi }{{T_{e\parallel } }}} \right)^{2} , $$

(8)

where

$$ a_{\kappa } = \frac{2\kappa - 1}{2\kappa - 3},\,\,\,\,\,\,\,\,\,\,\,\,\,\, $$

(9)

$$ b_{\kappa } = \frac{{4\kappa^{2} - 1}}{{2\left( {2\kappa - 3} \right)^{2} }}. $$

(10)

Linear Dispersion Relation

Let us first study the linear dispersion relation. To do that, assume a DIA wave whose propagation vector $\vec{k},$ is in the x–z plane and the angle between $\vec{k}$ and $\vec{B}$ is $\theta .$ Thus, for positive ions the model equations in this case are as,

$$ \frac{{\partial n_{i} }}{\partial t} + \frac{{\partial \left( {n_{i} v_{ix} } \right)}}{\partial x} + \frac{{\partial \left( {n_{i} v_{iz} } \right)}}{\partial z} = 0, $$

(11)

$$ \frac{{\partial v_{ix} }}{\partial t} + \left( {v_{ix} \frac{\partial }{\partial x} + v_{iz} \frac{\partial }{\partial z}} \right)v_{ix} = \frac{{ - z_{i} e}}{{m_{i} }}\frac{\partial \varphi }{\partial x} + \frac{{z_{i} e}}{{m_{i} c}}Bv_{iy} , $$

(12)

$$ \frac{{\partial v_{iy} }}{\partial t} + \left( {v_{ix} \frac{\partial }{\partial x} + v_{iz} \frac{\partial }{\partial z}} \right)v_{iy} = - \frac{{z_{i} e}}{{m_{i} c}}Bv_{ix} , $$

(13)

$$ \frac{{\partial v_{iz} }}{\partial t} + \left( {v_{ix} \frac{\partial }{\partial x} + v_{iz} \frac{\partial }{\partial z}} \right)v_{iz} = \frac{{ - z_{i} e}}{{m_{i} }}\frac{\partial \varphi }{\partial z}, $$

(14)

for dust grains are,

$$ \frac{{\partial n_{d} }}{\partial t} + \frac{{\partial \left( {n_{d} v_{dx} } \right)}}{\partial x} + \frac{{\partial \left( {n_{d} v_{dz} } \right)}}{\partial z} = 0, $$

(15)

$$ \frac{{\partial v_{dx} }}{\partial t} + \left( {v_{dx} \frac{\partial }{\partial x} + v_{dz} \frac{\partial }{\partial z}} \right)v_{dx} = \frac{{z_{d} e}}{{m_{d} }}\frac{\partial \varphi }{\partial x} - \frac{{z_{d} e}}{{m_{d} c}}Bv_{dy} , $$

(16)

$$ \frac{{\partial v_{dy} }}{\partial t} + \left( {v_{dx} \frac{\partial }{\partial x} + v_{dz} \frac{\partial }{\partial z}} \right)v_{dy} = \frac{{z_{d} e}}{{m_{d} c}}Bv_{dx} , $$

(17)

$$ \frac{{\partial v_{dz} }}{\partial t} + \left( {v_{dx} \frac{\partial }{\partial x} + v_{dz} \frac{\partial }{\partial z}} \right)v_{dz} = \frac{{z_{d} e}}{{m_{d} }}\frac{\partial \varphi }{\partial z}, $$

(18)

and passion equation is,

$$ \nabla^{2} \varphi = 4\pi e\left( {n_{e} + z_{d} n_{d} - z_{i} n_{i} } \right), $$

(19)

where $v_{j} (j = x,y,z)$ is the j component of the ion (dust) hydrodynamic velocity.

To linearize (8) and (11–19), the following dispersion relation is obtained.

$$ 1 + a_{\kappa } (k\lambda_{De} )^{ - 2} - \sin^{2} \theta \left( {\frac{{\omega_{pd}^{2} }}{{\omega^{2} \left( {1 - {{\omega_{Bd}^{2} } \mathord{\left/ {\vphantom {{\omega_{Bd}^{2} } {\omega^{2} }}} \right. \kern-\nulldelimiterspace} {\omega^{2} }}} \right)}} + \frac{{\omega_{pi}^{2} }}{{\omega^{2} \left( {1 - {{\omega_{Bi}^{2} } \mathord{\left/ {\vphantom {{\omega_{Bi}^{2} } {\omega^{2} }}} \right. \kern-\nulldelimiterspace} {\omega^{2} }}} \right)}}} \right) - \cos^{2} \theta \left( {\frac{{\omega_{pd}^{2} }}{{\omega^{2} }} + \frac{{\omega_{pi}^{2} }}{{\omega^{2} }}} \right) = 0, $$

(20)

where $\lambda_{De} = \left( {\frac{{T_{e} }}{{4\pi e^{2} n_{0e} }}} \right)^{1/2}$is the electron Debye length, $\omega_{pd}^{{}} = \left( {\frac{{4\pi z_{d}^{2} e^{2} n_{0d} }}{{m_{d} }}} \right)^{1/2}$is the dust plasma period, $\omega_{pi}^{{}} = \left( {\frac{{4\pi z_{i}^{2} e^{2} n_{0i} }}{{m_{i} }}} \right)^{1/2}$ is the ion plasma period, $\omega_{Bd}^{{}} = \frac{{z_{d}^{{}} eB}}{{m_{d} }}$ is the dust-cyclotron frequency and $\omega_{Bi}^{{}} = \frac{{z_{i}^{{}} eB}}{{m_{i} }}$ is the ion-cyclotron frequency.

Because of the large mass of the dust grains $\omega_{pd} \ll \omega_{pi}$ and $\omega_{Bd} \ll \omega_{Bi} ,$ therefore (20) can be rewritten in the following form:

$$ 1 + a_{\kappa } (k\lambda_{De} )^{ - 2} - \frac{{\omega_{pi}^{2} \sin^{2} \theta }}{{\omega^{2} \left( {1 - {{\omega_{Bi}^{2} } \mathord{\left/ {\vphantom {{\omega_{Bi}^{2} } {\omega^{2} }}} \right. \kern-\nulldelimiterspace} {\omega^{2} }}} \right)}} - \frac{{\omega_{pi}^{2} \cos^{2} \theta }}{{\omega^{2} }} = 0. $$

(21)

And with some straightforward manipulations, the spectrum of the DIA waves is obtained as follows:

$$ \omega^{2} = \frac{1}{2}\left[ {\omega_{Bi}^{2} + \frac{{\rho k^{2} c_{s}^{2} }}{{k^{2} \lambda_{{_{De} }}^{2} + a_{\kappa } }} \pm \left[ {\left( {\omega_{Bi}^{2} + \frac{{\rho k^{2} c_{s}^{2} }}{{k^{2} \lambda_{{_{De} }}^{2} + a_{\kappa } }}} \right)^{2} - \frac{{4\rho k^{2} c_{s}^{2} \cos^{2} \theta }}{{k^{2} \lambda_{{_{De} }}^{2} + a_{\kappa } }}} \right]^{1/2} } \right], $$

(22)

where $\rho = \frac{{z_{i}^{2} n_{0i} }}{{n_{0e} }}$ and $c_{s} = \left( {\frac{{T_{e} }}{{m_{i} }}} \right)^{1/2}$ is the ion-acoustic velocity.

If $k^{2} c_{s}^{2} \gg \omega_{Bi}^{2}$ and $k^{2} \lambda_{De}^{2} \ll \,\,1$ (22) gives the dispersion relation of the fast DIA wave

$$ \omega = \sqrt {\frac{\rho }{{a_{\kappa } }}} kc_{s}^{{}} \left[ {1 + \frac{{a_{\kappa } \mu^{2} \sin^{2} \theta }}{{2k^{2} \lambda_{{_{De} }}^{2} }} - \frac{{k^{2} \lambda_{{_{De} }}^{2} }}{{2a_{\kappa } }}} \right], $$

(23)

where $\mu = \omega_{Bi} /\omega_{pi}$. The effect of the magnetic field thus is small, since $k^{2} \mu^{2} \ll 1.$ The plasma must be dense and the magnetic field weak to support this mode because $\omega_{pi} \gg \omega_{Bi} .$

If $k^{2} c_{s}^{2} \ll \,\,\omega_{Bi}^{2}$ and $k^{2} \lambda_{De}^{2} \ll \,\,1$ (22) yields the dispersion relation of the slow DIA mode

$$ \omega = \sqrt {\frac{\rho }{{a_{\kappa } }}} kc_{s}^{{}} \cos \theta \left[ {1 - \frac{{k^{2} \lambda_{{_{De} }}^{2} \sin^{2} \theta }}{{2a_{\kappa } \mu^{2} }} - \frac{{k^{2} \lambda_{{_{De} }}^{2} }}{{2a_{\kappa } }}} \right]. $$

(24)

This mode is supported by rare plasma in the presence of a strong magnetic field. The effect of magnetic field is strong as in the slow mode because in this case $k^{2} \mu^{2} \gg \,\,1$.

Derivation of the Nonlinear KdV Equation

As has been shown, the effects of including the equations of motion of the massive dust component of the dusty plasma introduce a very small correction to the physics of the dispersion relation of the DIA waves (similar to [25]).

We can then safely assume that the dust grains are immobile. Then we introduce the normalizations $c_{s} /\lambda_{De} t \equiv t,$ $x/\lambda_{De} \equiv x,$ $v/c_{s} \equiv v,$ $n_{i} /n_{0i} \equiv n_{i}$ and $ez_{i} \varphi /T_{e} \equiv \varphi .$

After these normalizations (8) can be expanded to obtain

$$ \frac{{n_{e} }}{{n_{0e} }} = 1 + \frac{{a_{\kappa } }}{{z_{i} }}\varphi + \frac{{b_{\kappa } }}{{z_{i}^{2} }}\varphi^{2} . $$

(25)

Substituting (25) into (19), (11–19) can be rewritten in the following forms,

$$ \frac{{\partial n_{i} }}{\partial t} + \frac{{\partial \left( {n_{i} v_{ix} } \right)}}{\partial x} + \frac{{\partial \left( {n_{i} v_{iz} } \right)}}{\partial z} = 0, $$

(26)

$$ \frac{{\partial v_{ix} }}{\partial t} + \left( {v_{ix} \frac{\partial }{\partial x} + v_{iz} \frac{\partial }{\partial z}} \right)v_{ix} = - \frac{\partial \varphi }{\partial x} + \rho^{1/2} \mu v_{iy} , $$

(27)

$$ \frac{{\partial v_{iy} }}{\partial t} + \left( {v_{ix} \frac{\partial }{\partial x} + v_{iz} \frac{\partial }{\partial z}} \right)v_{iy} = - \rho^{1/2} \mu v_{ix} , $$

(28)

$$ \frac{{\partial v_{iz} }}{\partial t} + \left( {v_{ix} \frac{\partial }{\partial x} + v_{iz} \frac{\partial }{\partial z}} \right)v_{iz} = - \frac{\partial \varphi }{\partial z}, $$

(29)

$$ \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + \frac{{\partial^{2} \varphi }}{{\partial z^{2} }} = a_{\kappa } \varphi + \frac{{b_{\kappa } }}{{z_{i}^{{}} }}\varphi^{2} + \rho \left( {1 - n_{i} } \right). $$

(30)

For simplicity, a new axis $\eta$ is defined in the x–z plane which has angle θ with the z-axis. Then the 1-D wave propagating is considered along the η-axis. Therefore, the complete set equations are:

$$ \frac{{\partial n_{i} }}{\partial t} + \sin \theta \frac{{\partial \left( {n_{i} v_{ix} } \right)}}{\partial \eta } + \cos \theta \frac{{\partial \left( {n_{i} v_{iz} } \right)}}{\partial \eta } = 0, $$

(31)

$$ \frac{{\partial v_{ix} }}{\partial t} + v_{ix} \sin \theta \frac{{\partial v_{ix} }}{\partial \eta } + v_{iz} \cos \theta \frac{{\partial v_{ix} }}{\partial \eta } = - \sin \theta \frac{\partial \varphi }{\partial \eta } + \rho^{1/2} \mu v_{iy} , $$

(32)

$$ \frac{{\partial v_{iy} }}{\partial t} + \sin \theta v_{ix} \frac{{\partial v_{iy} }}{\partial \eta } + \cos \theta v_{iz} \frac{{\partial v_{iy} }}{\partial \eta } = - \rho^{1/2} \mu v_{ix} , $$

(33)

$$ \frac{{\partial v_{iz} }}{\partial t} + \sin \theta v_{ix} \frac{{\partial v_{iz} }}{\partial \eta } + \cos \theta v_{iz} \frac{{\partial v_{iz} }}{\partial \eta } = - \cos \theta \frac{\partial \varphi }{\partial \eta }, $$

(34)

$$ \frac{{\partial^{2} \varphi }}{{\partial \eta^{2} }} = a_{\kappa } \varphi + \frac{{b_{\kappa } }}{{z_{i}^{{}} }}\varphi^{2} + \rho \left( {1 - n_{i} } \right). $$

(35)

To study DIA solitary waves in this dusty plasma system, we employ a reductive perturbation theory and construct a weakly nonlinear theory for DIA solitary waves with small but finite amplitude.

According to this method we introduce the stretched time–space coordinates:

$$ \zeta = \varepsilon^{1/2} \left( {\eta - v_{\nu } t} \right),\quad \tau = \varepsilon^{3/2} t, $$

(36)

where the velocity $v_{\nu } \left( {\upsilon = f,s} \right)$ is determined later. Also we expand $n_{i} ,v_{i}$ and $\varphi$ in power series in ε, as follows:

$$ n_{i} = 1 + \varepsilon n^{(1)} + \varepsilon^{2} n^{(2)} , $$

(37)

$$ v_{i} = \varepsilon v_{i}^{(1)} + \varepsilon^{2} v_{i}^{(2)} , $$

(38)

$$ \varphi = \varepsilon \varphi^{(1)} + \varepsilon^{2} \varphi^{(2)} , $$

(39)

where ε is a smallness parameter.

From the dispersion relation, it is obvious that $\mu \ll 1$ (weak magnetic field) for fast mode and $\mu \gg 1$(strong magnetic field) for the slow mode, therefore $O\left( \mu \right) = \varepsilon^{3/2}$ for fast mode and with straightforward manipulation we obtain a KdV equation as follows:

$$ \frac{\partial \varphi }{\partial \tau } + \alpha \varphi \frac{\partial \varphi }{\partial \zeta } + \beta \frac{{\partial^{3} \varphi }}{{\partial \zeta^{3} }} = 0, $$

(40)

where

$$ \alpha = \frac{{3a_{\kappa } \left( {{1 \mathord{\left/ {\vphantom {1 {\rho^{1/2} }}} \right. \kern-\nulldelimiterspace} {\rho^{1/2} }}} \right) - 2b_{\kappa } \left( {{{\rho^{1/2} } \mathord{\left/ {\vphantom {{\rho^{1/2} } {z_{i} }}} \right. \kern-\nulldelimiterspace} {z_{i} }}} \right)}}{{2a_{{_{\kappa } }}^{3/2} }}, $$

(41)

$$ \beta = \frac{{\rho^{1/2} }}{{2a_{{_{\kappa } }}^{3/2} }}, $$

(42)

$$ \varphi = \varphi^{(1)} . $$

(43)

And $v_{f}$ the phase velocity of the linear fast mode propagation is given as:

$$ v_{f} = \sqrt {\frac{\rho }{{a_{\kappa } }}} , $$

(44)

To obtain the proper order of $\mu$, in the case of the slow mode, we have to consider $O\left( \mu \right) = \varepsilon^{ - 1/2}$ (strong magnetic field) and get the following KdV equation:

$$ \frac{\partial \varphi }{\partial \tau } + \alpha \cos \theta \varphi \frac{\partial \varphi }{\partial \zeta } + \beta \cos \theta \frac{{\partial^{3} \varphi }}{{\partial \zeta^{3} }} = 0, $$

(45)

where $\alpha$ and $\beta$ are the same of (41) and (42) and $\varphi = \varphi^{(1)} .$ Also $v_{s} ,$ the phase velocity of the linear slow mode propagation, is obtained as:

$$ v_{s} = \sqrt {\frac{\rho }{{a_{\kappa } }}} \cos \theta . $$

(46)

To study the nonlinear stage, it is necessary to obtain the soliton solution of (40) and (45). The stationary single soliton of (40) is obtained by assuming $\varphi = \varphi \left( {\eta - u_{f} \tau } \right),$ where u _f is the constant soliton velocity in the moving frame (the frame which moves with $v_{f} .$) Then by imposing the appropriate conditions, namely, $\varphi \to 0,\,\,\partial_{\zeta } \varphi \to 0,$ and $\partial_{\zeta \zeta } \varphi \to 0,$ as $\left| {\eta - u_{f} \tau } \right| \to \infty ,$ one obtains

$$ \varphi = \frac{{3u_{f} }}{\alpha }\sec h^{2} \left[ {\sqrt {\left| {\frac{\alpha }{12\beta }} \right|\varphi_{fm} } \left( {\eta - u_{f} \tau } \right)} \right], $$

(47)

$$ \varphi_{fm} = \frac{{3u_{f} }}{\alpha }, $$

(48)

$$ \Updelta_{f} = 4\sqrt {\left| {\frac{3\beta }{\alpha }} \right|} \varphi_{fm}^{ - 1/2} \cosh^{ - 1} \sqrt 2 , $$

(49)

where $\varphi_{m}$ is the maximum amplitude and Δ _f is the half width at half maximum of the soliton.

In the laboratory frame, the soliton velocity is

$$ u_{f,lab} = u_{f} + \sqrt {\frac{\rho }{{a_{\kappa } }}} . $$

(50)

The nonlinear evolution of the slow DIA wave follows (45). The stationary solution of this equation, in a quite similar manner, is obtained by assuming $\varphi = \varphi \left( {\eta - u_{s} \tau } \right)$, where u _s is the constant soliton velocity in the moving frame (the frame which moves with $v_{s}$). After imposing the proper boundary conditions, that is, $\varphi \to 0,\,\,\partial_{\zeta } \varphi \to 0,$ and $\partial_{\zeta \zeta } \varphi \to 0,$ as $\left| {\eta - u_{s} \tau } \right| \to \infty ,$ the following is obtained:

$$ \varphi = \frac{{3\,u_{s} }}{\alpha \cos \theta }\sec h^{2} \left[ {\sqrt {\left| {\frac{\alpha }{12\beta }} \right|\varphi_{sm} } \left( {\eta - u_{s} \tau } \right)} \right], $$

(51)

$$ \varphi_{sm} = \frac{{3\,u_{s} }}{\alpha \cos \theta }, $$

(52)

$$ \Updelta_{s} = 4\sqrt {\left| {\frac{3\beta }{\alpha }} \right|} \varphi_{sm}^{ - 1/2} \cosh^{ - 1} \sqrt 2 . $$

(53)

In the laboratory frame the soliton velocity is

$$ u_{s,lab} = u_{s} + \sqrt {\frac{\rho }{{a_{\kappa } }}} \cos \theta . $$

(54)

Results

At first, let us to study the effect of the dust grains and superthermal electrons on the linear dispersion relation of fast mode (23) and slow mode (24).

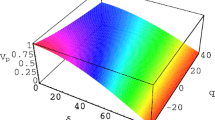
Figures 1 and 2 exhibit the variation of phase velocity for fixed zi = 1 and two different ρ.

Fig. 1

The linear dispersion relation of fast mode with $\theta = 0.7rad\,$ and $\mu = 10^{ - 3}$ for fixed zi = 1 and (a) ρ = zi, (b) ρ = 2zi

Fig. 2

The linear dispersion relation of slow mode with $\theta = 0.7rad$ and $\mu = 10^{3}$ for fixed zi = 1 and (a) ρ = zi, (b) ρ = 2zi

In the absence of dust, ρ = zi while, ρ = 2zi signifies the case that the total negative charge of electrons and dusts are equal. Precisely, in agreement with the physical prediction [based on (23) and (24)], for larger ρ, both the fast mode (Fig. 1b) and the slow mode (Fig. 2b), the phase velocity has been larger in comparison to ρ = zi (Figs. 1a, 2a).

It is also observed from Figs. 1 and 2 that by increasing the population of the superthermal electrons (smaller $\kappa$), both of modes propagate with smaller phase velocity in comparison with the Maxwellian plasma (similar to the results of [30]).

Figure 3 shows the changes of coefficients $\alpha ,\beta$ with $\kappa$ for different ρ. It appears that the dust grains can have a signification influence on the behavior of DIA solitary waves and deeply modify its nonlinear feature.

Fig. 3

The changes of coefficients $\alpha ,\beta$ with $\kappa$ for fixed $zi = 1$ when (a) ρ = zi, (b) ρ = 2zi

It is found from our numerical analysis with appearances of dust grains (Fig. 3b), the coefficient $\alpha$ of nonlinearity increases for larger $\kappa$ (the smaller population of superthermal electrons). This means, DIA solitons should move faster in moving frame which moves with $v_{f} (v_{s} ).$ Also for $2 \le \kappa < 3,$ the coefficient $\alpha$ becomes negative (it has been proved the KdV equation with a negative coefficient for the nonlinear term governs the propagation of dark (rarefactive) solitons) [12, 31].

Nevertheless, in the absence of dusts (Fig. 3a), ρ = zi, for larger $\kappa ,$ nonlinear term in the KdV equation is smaller and therefore IA solitons should move slower in moving frame which moves with $v_{f} (v_{s} ).$

In both of figures, for the larger population of superthermal electrons (smaller $\kappa$), the coefficient of the dispersive term of the KdV equation, $\beta ,$ becomes smaller and consequently the solitons have to be much slimmer [30].

Figure 4 depicts the influence of the charge state of ions, zi, on the coefficients $\alpha ,\beta$ for fixed ρ = 2zi.

Fig. 4

The coefficients $\alpha ,\beta$ versus $\kappa$ for fixed ρ = 2z and (a) zi = 1, (b) zi = 2

It is clear from the Fig. 4 that for larger number of charge on ions, the coefficients $\alpha ,\beta$ become larger therefore DIA solitons have to be faster and wider.

It is obvious from this investigation that dusts and superthermal electrons, affect on the properties of DIA solitary waves in dusty plasma. In order to obtain a better insight into the role of the dusts and superthermal electrons on the nature of DIA solitary waves, we perform a numerical simulation of the velocity, u, of DIA solitary waves and their width.

Figure 5 depicts the normalized soliton velocity versus $\kappa$ for $\varphi_{fm} = \varphi_{sm} = 0.1$ and $\theta = 0.7\,rad.$ As seen from this figure, the presence of superthermal electrons, for both modes, is that for a larger population of superthermal electrons (smaller $\kappa$) the soliton velocity significantly decreases [30]. Also for larger ρ, (Fig. 5b, c), the DIA waves have been faster [32, 33] and the velocity of DIA soliton in the Maxwellian limit ($\kappa > 15$) is supersonic for both modes, but the soliton velocity of the slow mode is always subsonic when the dust grains are absent (i.e. ρ = zi) [30].

Fig. 5

The normalized soliton velocity in the laboratory frame versus $\kappa$ for $\varphi_{fm} = \varphi_{sm} = 0.1$ and $\theta = 0.7rad.$ The dashed line shows the border of the subsonic and supersonic regime (for $2 < \kappa < 3,$ dark solitons and for $\kappa \ge 3$ bright solitons are propagated)

It is clear from the Fig. 5c that the soliton velocity from zi = 2 is larger in comparison to zi = 1 (Fig. 5b) and the soliton velocity of the fast mode, is always supersonic.

The last figure is about the effect of $\kappa ,\rho$ and zi on the width of DIA solitons.

The width of both modes does not depended on $\theta$ (49), (53) therefore, if we choose equal maximum amplitude for the slow and fast DIA solitons, their width would be the same.

Figure 6a exhibits, in the absence of dusts, ρ = zi, for larger population of superthermal electrons (smaller $\kappa$) the soliton width is smaller [30, 32] but Fig. 6b and c indicate for $2 < \kappa < 3$ (that dark solitons are propagated), for larger $\kappa ,$ the soliton width becomes larger but for $\kappa \succ 3$ (that bright solitons are propagated) for larger $\kappa ,$ the solitons become slimmer and on approaching the Maxwellian limit the width becomes near its minimum. The meaningful dependence of soliton width on the ρ variation shows the important role of dust grains.

Fig. 6

The normalized soliton width versus $\kappa$ for $\varphi_{fm} = \varphi_{sm} = 0.1$and $\theta = 0.7 {\rm rad}$ for fast mode and slow mode (for $2 < \kappa < 3,$ dark solitons and for $\kappa \ge 3$ bright solitons are propagated)

Also, it is clear from that the Fig. 6c for larger zi, the soliton width becomes wider [32].

Conclusions

We have derived a nonlinear KdV equation for the nonlinear propagation of DIA waves in a magnetized complex (dusty) plasma with superthermal electrons by applying the standard reductive perturbation theory.

For this purpose, we considered plasma composed of the cold positively charged ions, negatively charged dusts and hot electrons. We have then derived a linear dispersion relation. The linear dispersion relation predicts that two types of modes (fast and slow DIA modes) are allowed to propagate in the plasma. We have found a narrow domain in $\kappa$ where the nonlinear coefficient of KdV equation takes the negative sign. So DIA waves can propagate either an envelope hole sometimes called a dark soliton or rarefactive soliton. We investigated influence of $\kappa ,$ dust grains (ρ) and charge of ions (zi) on the velocity and width of solitons. Also it is found, that with increasing $\kappa ,zi$ and ρ the soliton velocity increase and they can be propagated in supersonic form.

We have also found, in appearance of dust grains with increasing $\kappa ,$ dark solitons become wider but bright solitons become slimmer.

Finally, it is stressed the results of our investigations should be useful to understand the feature of DIA waves in magnetized dusty plasma with superthermal electrons.