Skip to main content
SpringerLink
Log in

Developing plant fibre composites for structural applications by optimising composite parameters: a critical review

  • Review
  • Published:
Journal of Materials Science Aims and scope Submit manuscript

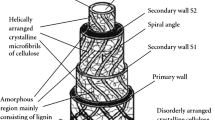
Abstract

Plant fibres, perceived as environmentally sustainable substitutes to E-glass, are increasingly being employed as reinforcements in polymer matrix composites. However, despite the promising technical properties of cellulose-based fibres and the historic use of plant fibre reinforced plastics (PFRPs) in load-bearing components, the industrial uptake of PFRPs in structural applications has been limited. Through an up-to-date critical review of the literature, this manuscript presents an overview on key aspects that need consideration when developing PFRPs for structural applications, including the selection of (I) the fibre type, fibre extraction process and fibre surface modification technique, (II) fibre volume fraction, (III) reinforcement geometry and interfacial properties, (IV) reinforcement packing arrangement and orientation and (V) matrix type and composite manufacturing technique. A comprehensive materials selection chart (Ashby plot) is also produced to facilitate the design of a PFRP component, based on the (absolute and specific) tensile properties.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Reux F (2012). Worldwide composites market: main trends of the composites industry, in 5th Innovative Composites Summit—JEC ASIA, 26–28 June 2012

  2. Joshi S, Drzal LT, Mohanty AK, Arora S (2004) Compos A 35:371

    Article  CAS  Google Scholar 

  3. Steger J (2010) J Biobased Mater Bioenergy 4(2):181

    Article  CAS  Google Scholar 

  4. Pickering S (2006) Compos A 37:1206

    Article  CAS  Google Scholar 

  5. Yang Y, Boom R, Irion B, van Heerden D, Kuiper P, de Wita H (2012) Chem Eng Process 51:53

    Article  CAS  Google Scholar 

  6. John M, Thomas S (2008) Carbohydr Polym 71:343

    Article  CAS  Google Scholar 

  7. Bledzki A, Gassan J (1999) Prog Polym Sci 24:221

    Article  CAS  Google Scholar 

  8. Faruk O, Bledzki AK, Fink HP, Sain M (2012) Prog Polym Sci 37(11):1552

    Article  CAS  Google Scholar 

  9. Mohanty A, Misra M, Drzal LT (eds) (2005) Natural fibers, biopolymers and biocomposites. Taylor and Francis, New York

    Google Scholar 

  10. Riedel U (2012) Polym Sci 10(18):295

    Google Scholar 

  11. Pickering K (ed) (2008) Properties and performance of natural-fibre composites. CRC Press LLC, Boca Raton

    Google Scholar 

  12. Khot S, Lascala JJ, Can E, Morye SS, Williams GI, Palmese GR, Kusefoglu SH, Wool RP (2000) J Appl Polym Sci 82(3):702

    Google Scholar 

  13. Wool R, Khot SN (2001) ASM handbook: composites. ASM International, Ohio, p 184

    Google Scholar 

  14. Bledzki A, Sperber VE, Faruk O (2002) Natural wood and fibre reinforcement in polymers. Rapra Technology Ltd, Shrewsbury

    Google Scholar 

  15. Franck R (ed) (2005) Bast and other plant fibres. CRC Press LLC, Boca Raton

    Google Scholar 

  16. Chand N, Fahim M (2008) Tribology of natural fiber polymer composites. Woodhead Publishing Ltd, Cambridge

    Book  Google Scholar 

  17. Wool R, Sun XS (2005) Bio-based polymers and composites. Elsevier Science & Technology Books, New York

    Google Scholar 

  18. Wambua P, Ivens J, Verpoest I (2003) Compos Sci Technol 63:1259

    Article  CAS  Google Scholar 

  19. Zini E, Scandola M (2011) Polym Compos 32(12):1905

    Article  CAS  Google Scholar 

  20. Summerscales J, Dissanayake N, Virk AS, Hall W (2010) Compos A 41(10):1336

    Article  CAS  Google Scholar 

  21. Shahzad A (2012) J Compos Mater 46(8):973

    Article  CAS  Google Scholar 

  22. Dhanasekaran S, Balachandran G (2008). Structural behavior of jute fiber composites—a review. SAE technical paper Vol 1, p 2653

  23. Li Y, Mai Y, Ye L (2000) Compos Sci Technol 60(11):2037

    Article  CAS  Google Scholar 

  24. Kalia S, Kaith BS, Kaur I (2009) Polym Eng Sci 49(7):1253

    Article  CAS  Google Scholar 

  25. Miao M, Finn N (2008) J Text Eng 54(6):165

    Article  Google Scholar 

  26. Ku H, Wang H, Pattarachaiyakoop N, Trada M (2011) Compos B Eng 42:856

    Article  CAS  Google Scholar 

  27. Dittenber D, Gangarao HVS (2012) Compos A 43:1419

    Article  Google Scholar 

  28. Kalia S, Dufresne A, Cherian BM, Kaith BS, Avérous L, Njuguna J, Nassiopoulos A (2011) Int J Polym Sci. doi:10.1155/2011/837875

    Google Scholar 

  29. Shah D, Schubel PJ, Licence P (2012) J Mater Sci. doi:10.1007/s10853-011-6096-1

    Google Scholar 

  30. Lewin M (2007) Handbook of fiber chemistry, 3rd edn. CRC Press LLC, Boca Raton

    Google Scholar 

  31. Vuure A (2008) Innovation for sustainable production (i-SUP). Bruges, Belgium

    Google Scholar 

  32. Witten E, Schuster A (2010). Composites market report: market developments, challenges, and chances. Industrievereinigung verstärkte kunststoffe and carbon composites

  33. Carus M (2011). Bio-composites: technologies, applications and markets, in 4th international conference on sustainable materials, polymers and composites. Birmingham, UK 6–7 July 2011

  34. FAOSTAT- Food and Agriculture Organization of the United Nations (2012). http://faostat.fao.org/site/567/DesktopDefault.aspx?PageID=567#ancor. Accessed 5 May 2013

  35. Carus M, Gahle C (2008) Natural fibre reinforced plastics—material with future. nova-Institut GmbH, Huerth

    Google Scholar 

  36. Dumanli A, Windle AH (2012) J Mater Sci. doi:10.1007/s10853-011-6081-8

    Google Scholar 

  37. Bos H (2004). The potential of flax fibres as reinforcement for composite materials. PhD, 2004. Technische Universiteit Eindhoven, Eindhoven

  38. Bledzki A, Faruk O, Sperber VE (2006) Macromol Mater Eng 291:449

    Article  CAS  Google Scholar 

  39. Almaguer R (2011) Opportunities in natural fiber composites. Las Colinas, Lucintel

  40. Ticoalu A, Aravinthan T, Cardona F (2010). A review of current development in natural fiber composites for structural and infrastructure applications, in southern region engineering conference, Toowoomba, 11–12 November 2010

  41. van Rijswijk K, Brouwer WD, Beukers A (2001) Application of natural fibre composites in the development of rural societies. Delft University of Technology, Delft

    Google Scholar 

  42. Fowler P, Hughes JM, Elias RM (2006) J Sci Food Agric 86:1781

    Article  CAS  Google Scholar 

  43. Sharma R, Raghupathy VP, Rao SS, Shubhanga P (2007). Review of recent trends and developments in biocomposites, in international conference on recent developments in structural engineering, Manipal, Aug 30–Sep 1 2007

  44. Riedel U, Nickel J (1999) Die Angewandte Makromolekulare Chemie 272:34

    Article  CAS  Google Scholar 

  45. Yu H, Kim SS, Hwang IU, Lee DG (2008) Compos Struct 86:285

    Article  Google Scholar 

  46. Frohnapfel P, Muggenhamer M, Schlögl C, Drechsler K (2010). Natural fibre composites for innovative small scale wind turbine blades, in international workshop on small scale wind energy for developing countries, Pokhara, Nepal, 15–17 November 2010

  47. Shah D, Schubel PJ, Clifford MJ, Licence P (2012). Fatigue characterisation of plant fibre composites for small-scale wind turbine blade applications, in 5th innovative composites summit—JEC Asia, Singapore, 26–28 June 2012

  48. Shah D, Schubel PJ, Clifford MJ, Licence P (2012). JEC composites magazine, No. 73: special JEC Asia, JEC composites, Paris June 2012 p 51–54

  49. Shah D, Schubel PJ (2013). JEC composites magazine, no. 78: feature wind energy, JEC Composites, Paris, Jan–Feb 2013 p 29–33

  50. Brøndsted P, Holmes JW, Sørensen BF, Jiang Z, Sun Z, Chen X (2008) Evaluation of a bamboo/epoxy composite as a potential material for hybrid wind turbine blades. Chinese Wind Energy Association, Beijing, China

  51. Shah D, Schubel PJ, Clifford MJ (2013) Compos B Eng 52:172

    Article  CAS  Google Scholar 

  52. Auto body made of plastics resists denting under hard blows, in popular mechanics magazine (1941). vol 76 no. 6 p 12

  53. Aero Research Limited (1945) A fighter fuselage in synthetic material, vol 34. Aero Research Limited, Cambridge

    Google Scholar 

  54. Sakurada I, Nukushina Y, Ito T (1962) J Polym Sci 57(165):651

    Article  CAS  Google Scholar 

  55. Eichhorn S, Dufresne A, Aranguren M et al (2010) J Mater Sci. doi:10.1007/s10853-009-3874-0

    Google Scholar 

  56. Summerscales J, Dissanayake N, Virk AS, Hall W (2010) Compos A 41(10):1329

    Article  CAS  Google Scholar 

  57. John M, Anandjiwala RD (2008) Polym Compos 29:187

    Article  CAS  Google Scholar 

  58. Kabir M, Wang H, Lau KT, Cardona F (2012) Compos B 43:2883

    Article  CAS  Google Scholar 

  59. Nunna S, Chandra PR, Shrivastava S, Jalan AK (2012) J Reinf Plast Compos 31:759

    Article  CAS  Google Scholar 

  60. Summerscales J, Virk AS, Hall W (2013) Compos A 44:32

    Article  CAS  Google Scholar 

  61. Virk A, Hall W, Summerscales J (2012) Mater Sci Technol 28(7):864

    Article  CAS  Google Scholar 

  62. Facca A, Kortschot MT, Yan N (2006) Compos A 37:1660

    Article  CAS  Google Scholar 

  63. Joseph K, Filho RDT, James B, Thomas S, de Carvalho LH (1999) Revista Brasileira de Engenharia Agrícola e Ambiental 3(3):367

    Google Scholar 

  64. Mishra S, Mohanty AK, Drzal LT, Misra M, Hinrichsen G (2004) Macromol Mater Eng 289:955

    Article  CAS  Google Scholar 

  65. Harish S, Michael DP, Bensely A, Lal DM, Rajadurai A (2009) Mater Charact 60:44

    Article  CAS  Google Scholar 

  66. Hassan A, Salema AA, Ani FN, Bakar AA (2010) Polym Compos 31(12):2079

    Article  CAS  Google Scholar 

  67. La Mantia F, Morreale M (2011) Compos A 42:579

    Article  CAS  Google Scholar 

  68. Koronis G, Silva A, Fontul M (2013) Compos B 44(1):120

    Article  CAS  Google Scholar 

  69. Ashby M (1992) Materials selection in mechanical design. Pergamon, Oxford

    Google Scholar 

  70. Ashby M (2007) The CES EduPack database of natural and man-made materials (MFA, 20/12/2007). Cambridge University and Granta Design, Cambridge

    Google Scholar 

  71. Shah D, Schubel PJ, Clifford MJ, Licence P (2011). Mechanical characterization of vacuum infused thermoset matrix composites reinforced with aligned hydroxyethyl cellulose sized plant bast fibre yarns, in 4th international conference on sustainable materials, polymers and composites, Birmingham, UK, 6–7 July 2011

  72. Goutianos S, Peijs T, Nystrom B, Skrifvars M (2006) Appl Compos Mater 13(4):199

    Article  CAS  Google Scholar 

  73. Madsen B, Lilholt H (2003) Compos Sci Technol 63:1265

    Article  CAS  Google Scholar 

  74. Madsen B, Thygesen A, Liholt H (2009) Compos Sci Technol 69:1057

    Article  CAS  Google Scholar 

  75. Madsen B (2004). Properties of plant fibre yarn polymer composites—an experimental study. PhD, 2004. Technical University of Denmark, Lyngby

  76. Lamy B, Baley C (2000) J Mater Sci Lett 19:979

    Article  CAS  Google Scholar 

  77. Summerscales J, Hall W, Virk AS (2011) J Mater Sci. doi:10.1007/s10853-011-5569-6

    Google Scholar 

  78. Thomason J, Gentles F, Brennan A (2012). Natural fibre cross sectional area effects on the determination of fibre mechanical properties, in 15th European conference on composite materials (ECCM-15), Venice, Italy

  79. Shah D, Schubel PJ, Clifford MJ (2013) J Compos Mater 47(4):425

    Article  Google Scholar 

  80. Cox H (1952) Br J Appl Phys 3:72

    Article  Google Scholar 

  81. Kelly A, Tyson WR (1965) J Mech Phys Solids 13(6):329

    Article  CAS  Google Scholar 

  82. Harris B (1999) Engineering composite materials. The Institute of Materials, London

    Google Scholar 

  83. Krenchel H (1964) Fibre reinforcement. Akademisk Forlag, Denmark, p 16

    Google Scholar 

  84. Thomason J, Carruthers J, Kelly J, Johnson G (2011) Compos Sci Technol 71:1008

    Article  CAS  Google Scholar 

  85. d’Almeida J, Mauricio MHP, Paciornik S (2012) J Compos Mater 46(24):3057

    Article  Google Scholar 

  86. Virk A (2010). Numerical models for natural fibre composites with stochastic properties. PhD, 2010, University of Plymouth, Plymouth

  87. Kadam K, Forrest LH, Jacobson WA (2000) Biomass Bioenergy 18:369

    Article  CAS  Google Scholar 

  88. Putun A, Apaydin E, Putun E (2004) Energy 29:2171

    Article  CAS  Google Scholar 

  89. Steele P, El-Hissewy A, Badawi AEE (2009). Agro-industrial use of rice straw—exploring opportunities for making better use of rice residues in Egypt, 2009. Food and Agriculture Organization of the United Nations Regional Office for the Near East (Cairo, Egypt) and Ministry of Agriculture and Land Reclamation (Cairo, Egypt): Egypt

  90. Wolcott M, Englund K (1999). A technology review of wood-plastic composites, in 33rd international particleboard/composite materials symposium, Washington State University, Pullman

  91. Ismail M, Yassen AAM, Afify MS (2011) Fibers Polym 12(5):648

    Article  CAS  Google Scholar 

  92. Buzarovska A, Bogoeva-Gaceva G, Grozdanov A, Avella M, Gentile G, Errico M (2008) Aust J Crop Sci 1(2):37

    CAS  Google Scholar 

  93. Venkateshwaran N, Elayaperumal A (2010) J Reinf Plast Compos 29:2387

    Article  CAS  Google Scholar 

  94. Kamath M, Bhat GS, Parikh DV, Mueller D (2005) Int Nonwovens J 14(1):34

    CAS  Google Scholar 

  95. Fu S, Lauke B, Mader E, Yue CY, Hu X (2007) Compos A 31:1117

    Article  Google Scholar 

  96. van den Oever M, Bos HL, van Kemenade MJJM (2000) Appl Compos Mater 7:387

    Article  Google Scholar 

  97. Arib R, Sapuan SM, Ahmad MMHM, Paridah MT, Zaman HMDK (2006) Mater Des 27:391

    Article  CAS  Google Scholar 

  98. Paul S, Joseph K, Mathew GDG, Pothen LA, Thomas S (2010) Compos A 41:1380

    Article  CAS  Google Scholar 

  99. Rukmini K, Ramaraj B, Shetty SK, Taraiya A, Bandyopadhyay S (2013) Adv Polym Technol 32(1):1

    Article  CAS  Google Scholar 

  100. Rozman H, Tay GS, Kumar RN, Abusamah A, Ismail H, Ishak ZAM (2001) Eur Polymer J 37(6):1283

    Article  CAS  Google Scholar 

  101. Okuba K, Fujii T, Yamamoto Y (2004) Compos A 35:377

    Article  CAS  Google Scholar 

  102. Lee N, Jang J (1999) Compos A 30:815

    Article  Google Scholar 

  103. Placet V, Trivaudey F, Cisse O, Gucheret-Retel V, Boubakar ML (2012) Compos A 43(2):275

    Article  CAS  Google Scholar 

  104. Mwaikambo L, Ansell MP (2001) J Mater Sci Lett 20(23):2095

    Article  CAS  Google Scholar 

  105. Thygesen A (2006). Properties of hemp fibre polymer composites—an optimisation of fibre properties using novel defibration methods and fibre characterisation. PhD, 2006. The Royal Agricultural and Veterinary University of Denmark, Roskilde

  106. McLaughlin E, Tait RA (1980) J Mater Sci. doi:10.1007/BF00552431

    Google Scholar 

  107. Mukherjee P, Satyanarayana KG (1986) J Mater Sci. doi:10.1007/BF01106524

    Google Scholar 

  108. Satyanarayana K, Pillai CKS, Sukumaran K, Pillai SGK, Rohatgi PK, Vijayan K (1982) J Mater Sci. doi:10.1007/BF00543759

    Google Scholar 

  109. Baley C (2002) Compos A 33:939

    Article  Google Scholar 

  110. Gassan J, Chate A, Bledzki AK (2001) J Mater Sci. doi:10.1023/A1017969615925

    Google Scholar 

  111. Karine C, Jean-Paul J, Moussa G, Baley C, Laurent B, Joel B (2007). Morphology and mechanical behaviour of a natural composite: the flax fiber, in 16th international conference on composite materials (ICCM-16), Kyoto, Japan

  112. Thygesen A, Oddershede J, Liholt H, Thomsen AB, Stahl K (2005) Cellulose 12:563

    Article  CAS  Google Scholar 

  113. Parikh D, Thibodeaux DP, Condon B (2007) Text Res J 77(8):612

    Article  CAS  Google Scholar 

  114. Sheng-zuo F, Wen-zhong Y, Xiang-xiang FU (2004) J For Res 15(4):261

    Article  Google Scholar 

  115. Bodros E, Baley C (2008) Mater Lett 62(14):2143

    Article  CAS  Google Scholar 

  116. Porter D, Guan J, Vollrath F (2013) Adv Mater 25(9):1275

    Article  CAS  Google Scholar 

  117. Charlet K, Baley C, Morvan C, Jernot JP, Gomina M, Bréard J (2007) Compos A 28:1912

    Article  CAS  Google Scholar 

  118. Hanninen T, Thygesen A, Mehmood S, Madsen B, Hughes M (2012) Ind Crops Prod 39:7

    Article  CAS  Google Scholar 

  119. Weyenberg I, Ivens J, Coster A, Kino B, Baetens E, Verpoest I (2003) Compos Sci Technol 63:1241

    Article  CAS  Google Scholar 

  120. Baets J, Plastria D, Ivens J, Verpoest I (2011). Determination of the optimal flax fibre preparation for use in UD-epoxy composites, in 4th international conference on sustainable materials, polymers and composites, 6–7 July 2011 Birmingham

  121. Hughes M (2012) J Mater Sci. doi:10.1007/s10853-011-6025-3

    Google Scholar 

  122. Aslan M, Chinga-Carrasco G, Sørensen BF, Madsen B (2011) J Mater Sci. doi:10.1007/s10853-011-5581

    Google Scholar 

  123. Madsen B, Mehmood S, Aslan M (2012). Variability in properties of natural fibres, in NATEX workshop, Chesterfield, UK

  124. Goutianos S, Peijs T (2003) Adv Compos Lett 12(6):237

    Google Scholar 

  125. Dissanayake N (2011). Life cycle assessment of flax fibres for the reinforcement of polymer matrix composites. PhD, 2011. University of Plymouth, Plymouth

  126. Dissanayake N, Summerscales J, Grove SM, Singh MM (2009) J Biobased Mater Bioenergy 3(3):1

    Article  CAS  Google Scholar 

  127. Dissanayake N, Summerscales J, Grove SM, Singh MM (2009) J Nat Fibers 6(4):331

    Article  CAS  Google Scholar 

  128. Le Duigou A, Davies P, Baley C (2011) J Biobased Mater Bioenergy 5(1):153

    Article  CAS  Google Scholar 

  129. Garkhail S, Heijenrath RWH, Peijs T (2000) Appl Compos Mater 7:351

    Article  CAS  Google Scholar 

  130. Bos H, Mussig J, van den Oever MJA (2006) Compos A 37:1591

    Article  CAS  Google Scholar 

  131. Awal A, Cescutti G, Ghosh SB, Mussig J (2011) Compos A 42:50

    Article  CAS  Google Scholar 

  132. Oksman K (2001) J Reinf Plast Compos 20(7):621

    Article  CAS  Google Scholar 

  133. Weyenberg I, Chitruong T, Vangrimde B, Verpoest I (2006) Compos A 37:1368

    Article  CAS  Google Scholar 

  134. Roe P, Ansell MP (1985) J Mater Sci. doi:10.1007/BF00552393

    Google Scholar 

  135. Shah D, Schubel PJ, Licence P, Clifford MJ (2012) Compos Sci Technol 72:1909

    Article  CAS  Google Scholar 

  136. Madsen B, Hoffmeyer P, Lilholt H (2007) Compos A 38:2204

    Article  CAS  Google Scholar 

  137. Pan N (1993) Polym Compos 14(2):85

    Article  CAS  Google Scholar 

  138. Petrulis D (2003) Mater Sci 9:116

    Google Scholar 

  139. Hearle J, Grosberg P, Backer S (1969) Structural mechanics of yarns and fabrics. Vol. 1. Wiley-Interscience, New York, p 180

    Google Scholar 

  140. Petrulis D, Petrulyte S (2003) Fibres Text East Eur 11(1):16

    Google Scholar 

  141. Zarate C, Aranguren MI, Reboredo MM (2003) J Appl Polym Sci 89:2714

    Article  CAS  Google Scholar 

  142. Lee B, Kim HJ, Yu WR (2009) Fibers Polym 10(1):83

    Article  CAS  Google Scholar 

  143. Williams G, Wool RP (2000) Appl Compos Mater 7:421

    Article  CAS  Google Scholar 

  144. Devi L, Bhagawan SS, Thomas S (1997) J Appl Polym Sci 64(9):1739

    Article  CAS  Google Scholar 

  145. Hepworth D, Bruce DM, Vincent JFV, Jeronimidis G (2000) J Mater Sci. doi:10.1023/A1004784931875

    Google Scholar 

  146. Charlet K, Jernot JP, Gomina M, Bizet L, Bréard J (2010) J Compos Mater 44(24):2887

    Article  CAS  Google Scholar 

  147. Gassan J, Bledzki AK (1999) Compos Sci Technol 59:1303

    Article  CAS  Google Scholar 

  148. Arbelaiz A, Fernandez B, Cantero G, Llano-Ponte R, Valea A, Mondragon I (2005) Compos A 36:1637

    Article  CAS  Google Scholar 

  149. Mutje P, Girones J, Lopez A, Llop MF, Vilaseca F (2006) J Reinf Plast Compos 25:313

    Article  CAS  Google Scholar 

  150. Beckwith S (2003). Natural fiber reinforcement materials: lower cost technology for composites applications, in composites fabrication, November/December 2003 p 12–16

  151. Shahzad A (2012) Polym Compos 33(7):1129

    Article  CAS  Google Scholar 

  152. Rodríguez E, Petrucci R, Puglia D, Kenny JM, Vazquez A (2005) J Compos Mater 39(5):265

    Article  CAS  Google Scholar 

  153. George J, Ivens J, Verpoest I (1999) Die Angewandte Makromolekulare Chemie 272(1):41

    Article  CAS  Google Scholar 

  154. Gil R (2003). Forming and consolidation of textile composites. PhD, 2003. The University of Nottingham, Nottingham

  155. Hughes M, Carpenter J, Hill C (2007) J Mater Sci. doi:10.1007/s10853-006-1027-2

    Google Scholar 

  156. Daniel M, Ishai O (1994) Engineering mechanics of composite materials. Oxford University Press, Oxford

    Google Scholar 

  157. Liang S, Gning PB, Guillaumat L (2012) Compos Sci Technol 72(5):535

    Article  CAS  Google Scholar 

  158. Phillips S, Baets J, Lessard L, Hubert P, Verpoest I (2013) Characterization of flax/epoxy prepregs before and after cure. J Reinf Plast Compos. doi:10.1177/0731684412473359

    Google Scholar 

  159. Meredith J, Coles SR, Powe R, Collings E, Cozien-Cazuc S, Weager B, Müssig J, Kirwan K (2013) Compos Sci Technol 80:31

    Article  CAS  Google Scholar 

  160. Sawpan M, Pickering KL, Fernyhough A (2012) J Compos Mater. doi:10.1177/0021998312449028

    Google Scholar 

  161. Mwaikambo L, Tucker N, Clark AJ (2007) Macromol Mater Eng 292:993

    Article  CAS  Google Scholar 

  162. Shah D (2013). Characterisation and optimisation of the mechanical performance of plant fibre composites for structural applications. PhD, 2013. University of Nottingham, Nottingham

  163. Vallejos M, Espinach FX, Julián F, Torres LI, Vilaseca F, Mutjé P (2012) Compos Sci Technol 72:1209

    Article  CAS  Google Scholar 

  164. Serrano A, Espinach FX, Julian F, del Rey R, Mendez JA, Mutje P (2013) Compos B 50:232

    Article  CAS  Google Scholar 

  165. Cabral H, Cisneros M, Kenny JM, Vazquez A, Bernal CR (2005) J Compos Mater 39:51

    Article  CAS  Google Scholar 

  166. Cichocki JF, Thomason JL (2002) Compos Sci Technol 62:669

    Article  CAS  Google Scholar 

  167. Rao Y, Farris RJ (2000) J Appl Polym Sci 77:1938

    Article  CAS  Google Scholar 

  168. Naik N, Madhavan V (2000) J Strain Anal 35(2):83

    Article  Google Scholar 

  169. Zhang L, Miao M (2010) Compos Sci Technol 70:130

    Article  CAS  Google Scholar 

  170. Reussman T, Mieck P, Grützner R, Bayer R (1999) Kunststoffe Plast Europe 89:80

    Google Scholar 

  171. Boey F, Lye SW (1992) Composites 23(4):261

    Article  CAS  Google Scholar 

  172. Anderson J, Altan MC (2012) J Eng Mater Technol 134:1

    Article  CAS  Google Scholar 

  173. Ghiorse S (1993). Effect of void content on the mechanical properties of carbon/epoxy laminates, in SAMPE Quarterly, p 54

  174. Madsen B, Thygesen A, Lilholt H (2007) Compos Sci Technol 67:1584

    Article  CAS  Google Scholar 

  175. Oksman K, Wallstrom L, Berglund LA, Filho RDT (2002) J Appl Polym Sci 84:2358

    Article  CAS  Google Scholar 

Download references

Acknowledgement

The author would like to thank Dr Peter Schubel (the University of Nottingham), Dr Mike Clifford (the University of Nottingham), Dr Peter Licence (the University of Nottingham) and Prof Ton Peijs (Queen Mary, University of London) for their insightful discussions. The author also thanks the anonymous referees for suggesting valuable improvements to this study. For funding, the author thanks the University of Nottingham, the Nottingham Innovative Manufacturing Research Centre (EPSRC, Project title ‘Sustainable manufacture of wind turbine blades using natural fibre composites and optimal design tools’) and the University of Oxford (Oxford Silk Group).

Author information

Authors and Affiliations

  1. Oxford Silk Group, Department of Zoology, University of Oxford, Oxford, OX1 3PS, UK

    Darshil U. Shah

Authors
  1. Darshil U. Shah
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Darshil U. Shah.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shah, D.U. Developing plant fibre composites for structural applications by optimising composite parameters: a critical review. J Mater Sci 48, 6083–6107 (2013). https://doi.org/10.1007/s10853-013-7458-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10853-013-7458-7

Keywords

Search

Navigation