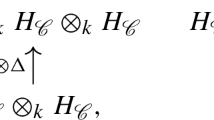Abstract
In this paper, we use subword complexes to provide a uniform approach to finite-type cluster complexes and multi-associahedra. We introduce, for any finite Coxeter group and any nonnegative integer k, a spherical subword complex called multi-cluster complex. For k=1, we show that this subword complex is isomorphic to the cluster complex of the given type. We show that multi-cluster complexes of types A and B coincide with known simplicial complexes, namely with the simplicial complexes of multi-triangulations and centrally symmetric multi-triangulations, respectively. Furthermore, we show that the multi-cluster complex is universal in the sense that every spherical subword complex can be realized as a link of a face of the multi-cluster complex.
Similar content being viewed by others
1 Introduction
Cluster complexes were introduced by S. Fomin and A. Zelevinsky to encode exchange graphs of cluster algebras [20]. N. Reading then showed that the definition of cluster complexes can be extended to all finite Coxeter groups [48, 49]. In this article, we present a new combinatorial description of cluster complexes using subword complexes. These were introduced by A. Knutson and E. Miller, first in type A to study the combinatorics of determinantal ideals and Schubert polynomials [35], and then for all Coxeter groups in [34]. We provide, for any finite Coxeter group W and any Coxeter element c∈W, a subword complex which is isomorphic to the c-cluster complex of the corresponding type, and we thus obtain an explicit type-free characterization of c-clusters. This characterization generalizes a description for crystallographic types obtained by K. Igusa and R. Schiffler in the context of cluster categories [29]. The present approach allows us to define a new family of simplicial complexes by introducing an additional parameter k, such that one obtains c-cluster complexes for k=1. In type A, this simplicial complex turns out to be isomorphic to the simplicial complex of multi-triangulations of a convex polygon which was described by C. Stump in [62] (see also [60]), and, in a similar manner, by V. Pilaud and M. Pocchiola in the framework of sorting networks [43]. In type B, we obtain that this simplicial complex is isomorphic to the simplicial complex of centrally symmetric multi-triangulations of a regular convex polygon. Therefore, we call them multi-cluster complexes. Besides, there is a “naive” way of generalizing the cluster complex by considering the simplicial complex of sets of almost positive roots that do not contain any k+1 pairwise not compatible roots. In fact, this alternative definition lacks basic properties of the cluster complex, see Remark 2.9. The multi-cluster complexes introduced in this paper are different from generalized cluster complexes as defined by S. Fomin and N. Reading [18]. In the generalized cluster complex, the vertices are given by the simple negative roots together with several distinguished copies of the positive roots, while the vertices of the multi-cluster complex correspond to the positive roots together with several distinguished copies of the simple negative roots. Multi-cluster complexes turn out to be intimately related to Auslander–Reiten quivers and repetition quivers [24]. In particular, the Auslander–Reiten translate on facets of multi-cluster complexes in types A and B corresponds to cyclic rotation of (centrally symmetric) multi-triangulations. Furthermore, multi-cluster complexes uniformize questions about multi-triangulations, subword complexes, and cluster complexes. One important example concerns the open problem of realizing the simplicial complexes of (centrally symmetric) multi-triangulations and spherical subword complexes as boundary complexes of convex polytopes.
In Sect. 2, we recall the various objects in question, namely multi-triangulations, subword complexes, and cluster complexes. Moreover, the main results are presented, and the multi-cluster complex is defined (Definition 2.5). In Sect. 3, we study flips on spherical subword complexes and present two natural isomorphisms between subword complexes whose words differ by commutation or by rotation of letters. In Sect. 4, we prove that the multi-cluster complex is independent of the choice of the Coxeter element (Theorem 2.6). Section 5 contains a proof that the multi-cluster complex is isomorphic to the cluster complex for k=1 (Theorem 2.2). In Sect. 6, we discuss possible generalizations of associahedra using subword complexes; we review known results about polytopal realizations, prove polytopality of multi-cluster cluster complexes of rank 2 (Theorem 6.1), and prove that the multi-cluster complex is universal in the sense that every spherical subword complex is the link of a face of a multi-cluster complex (Theorem 2.15). Section 7 contains a combinatorial description of the sorting words of the longest element of finite Coxeter groups (Theorem 7.2) and an alternative definition of multi-cluster complexes in terms of the strong intervening neighbors property (Theorem 2.7). In Sect. 8, we connect multi-cluster complexes to Auslander–Reiten quivers and repetition quivers, and use this connection to introduce an action on vertices and facets of multi-cluster complexes generalizing the natural rotation action on multi-triangulations in type A. Finally, in Sect. 9, we discuss open problems and questions arising in the context of multi-cluster complexes.
In a subsequent paper, C. Stump and V. Pilaud study the geometry of subword complexes and use the theory developed in the present paper to describe the connections to Coxeter-sortable elements, and how to recover Cambrian fans, Cambrian lattices, and the generalized associahedra purely in terms of subword complexes [45].
2 Definitions and main results
In this section, we review the essential notions concerning multi-triangulations, subword complexes, and cluster complexes of finite type and present the main results. Throughout the paper, (W,S) denotes a finite Coxeter system of rank n, and c denotes a Coxeter element, i.e., the product of the generators in S in some order. The smallest integer h for which c h=1∈W is called a Coxeter number. Coxeter elements of W are in bijection with (acyclic) orientations of the Coxeter graph of W: a noncommuting pair s,t∈S has the orientation s→t if and only if s comes before t in c, i.e., s comes before t in any reduced expression for c [57]. In the simply laced types A, D, and E, this procedure yields a quiver Ω c associated to a given Coxeter element c, where by quiver we mean a directed graph without loops or two-cycles. For two examples, see Fig. 1 on p. 26. The length function on W is given by ℓ(w)=min{r:w=a 1⋯a r , a i ∈S}. An expression for w of minimal length is called reduced. The unique longest element in W is denoted by w ∘, and its length is given by ℓ(w ∘)=N:=nh/2. We refer the reader to [28] for further definitions and a detailed introduction to finite Coxeter groups. Next, we adopt some writing conventions: in order to emphasize the distinction between words and group elements, we write words in the alphabet S as a sequence between brackets (a 1,a 2,…,a r ) and use square letters such as w to denote them, and we write group elements as a concatenation of letters a 1 a 2⋯a r using normal script such as w to denote them.
2.1 Multi-triangulations
Let Δ m be the simplicial complex with vertices being diagonals of a convex m-gon and faces being subsets of noncrossing diagonals. Its facets correspond to triangulations (i.e., maximal subsets of diagonals which are mutually noncrossing). This simplicial complex is the boundary complex of the dual associahedron [13, 22, 25, 26, 37, 38], we refer to the recent book [39] for a detailed treatment of the history of associahedra. The complex Δ m can be generalized using a positive integer k with 2k+1≤m: define a (k+1)-crossing to be a set of k+1 diagonals which are pairwise crossing. A diagonal is called k-relevant if it is contained in some (k+1)-crossing, that is, if there are at least k vertices of the m-gon on each side of the diagonal. The complex Δ m,k is the simplicial complex of (k+1)-crossing free sets of k-relevant diagonals. Its facets are given by k-triangulations (i.e., maximal subsets of diagonals which do not contain a (k+1)-crossing), without considering k-irrelevant diagonals. The reason for restricting the set of diagonals is that including all diagonals that are not k-relevant would yield the join of Δ m,k and an mk-simplex. This simplicial complex has been studied by several authors, see, e.g., [14, 31, 32, 36, 41, 55, 62]; an interesting recent treatment of k-triangulations using complexes of star polygons can be found in [44]. We refer to this simplicial complex as the simplicial complex of multi-triangulations.
In [62], the following description of Δ m,k is exhibited: let \(\mathcal{S}_{n+1}\) be the symmetric group generated by the n simple transpositions s i =(i i+1) for 1≤i≤n, where n=m−2k−1. The k-relevant diagonals of a convex m-gon are in bijection with (positions of) letters in the word
of length \(kn+\binom{n+1}{2} = \binom{m}{2}-mk\). If the vertices of the m-gon are cyclically labeled by the integers from 0 to m−1, the bijection sends the ith letter of Q to the ith k-relevant diagonal in lexicographic order. Under this bijection, a collection of k-relevant diagonals forms a facet of Δ m,k if and only if the complement of the corresponding subword in Q forms a reduced expression for the permutation \([n+1,\ldots,2,1]\in \mathcal{S}_{n+1}\). A similar approach, which admits various possibilities for the word Q, was described in [43] in the context of sorting networks. We present these general bijections in the context of this paper in Sect. 2.4.
Example 2.1
For m=5 and k=1, we get Q=(q 1,q 2,q 3,q 4,q 5)=(s 2,s 1,s 2,s 1,s 2). By cyclically labeling the vertices of the pentagon with the integers {0,…,4}, the bijection sends the (position of the) letter q i to the ith entry of the list of ordered diagonals [0,2],[0,3],[1,3],[1,4],[2,4]. On one hand, two cyclically consecutive diagonals in the list form a triangulation of the pentagon. On the other hand, the complement of two cyclically consecutive letters of Q form a reduced expression for \([3,2,1] = s_{1} s_{2} s_{1} = s_{2} s_{1} s_{2} \in \mathcal{S}_{3}\).
The main objective of this paper is to describe and study a natural generalization of multi-triangulations to finite Coxeter groups.
2.2 Subword complexes
Let Q=(q 1,…,q r ) be a word in the generators S of W, and let π∈W. The subword complex Δ(Q,π) was introduced by A. Knutson and E. Miller in order to study Gröbner geometry of Schubert varieties, see [35, Definition 1.8.1], and was further studied in [34]. It is defined as the simplicial complex whose faces are given by subwords P of Q for which the complement Q∖P contains a reduced expression of π. Note that subwords come with their embedding into Q; two subwords P and P′ representing the same word are considered to be different if they involve generators at different positions within Q. In Example 2.1, we have seen an instance of a subword complex with Q=(q 1,q 2,q 3,q 4,q 5)=(s 2,s 1,s 2,s 1,s 2) and π=s 1 s 2 s 1=s 2 s 1 s 2. In this case, Δ(Q,π) has vertices {q 1,…,q 5} and facets
Subword complexes are known to be vertex-decomposable and hence shellable [34, Theorem 2.5]. Moreover, they are topologically spheres or balls depending on the Demazure product of Q. Let Q′ be the word obtained by adding s∈S at the end of a word Q. The Demazure product δ(Q′) is recursively defined by
where μ=δ(Q) is the Demazure product of Q, and where the Demazure product of the empty word is defined to be the identity element in W. A subword complex Δ(Q,π) is a sphere if and only if δ(Q)=π, and a ball otherwise [34, Corollary 3.8].
2.3 Cluster complexes
In [20], S. Fomin and A. Zelevinsky introduced cluster complexes associated to finite crystallographic root systems. This simplicial complex along with the generalized associahedron has become the object of intensive studies and generalizations in various contexts in mathematics, see, for instance, [12, 27, 40, 48]. A generator s∈S is called initial or final in a Coxeter element c if ℓ(sc)<ℓ(c) or ℓ(cs)<ℓ(c), respectively. The group W acts naturally on the real vector space V with basis Δ={α s :s∈S} whose elements are called simple roots. Let Φ denote a root system for W, and let Φ +⊆Φ be the set of positive roots for the simple system Δ. Furthermore, let Φ ≥−1=Φ +∪−Δ be the set of almost positive roots. We denote by W 〈s〉 the maximal standard parabolic subgroup generated by S∖{s} and by Φ 〈s〉 the associated subroot system. For s∈S, the involution σ s :Φ ≥−1→Φ ≥−1 is given by
N. Reading showed that the definition of cluster complexes can be extended to all finite root systems and enriched with a parameter c being a Coxeter element [48]. These c-cluster complexes are defined using a family ∥ c of c-compatibility relations on Φ ≥−1, see [52, Sect. 5]. This family is characterized by the following two properties:
-
(i)
for s∈S and β∈Φ ≥−1,
$$-\alpha_s \parallel_c \beta\quad \Longleftrightarrow \quad \beta\in(\varPhi _{\langle s \rangle})_{\geq-1}; $$ -
(ii)
for β 1,β 2∈Φ ≥−1 and s being initial in c,
$$\beta_1 \parallel_c \beta_2 \quad \Longleftrightarrow \quad \sigma_s(\beta_1) \parallel_{\mathit{scs}} \sigma_s(\beta_2). $$
A maximal subset of pairwise c-compatible almost positive roots is called c-cluster. The c-cluster complex is the simplicial complex whose vertices are the almost positive roots and whose facets are c-clusters. It turns out that all c-cluster complexes for the various Coxeter elements are isomorphic, see [40, Proposition 4.10] and [48, Proposition 7.2]. In crystallographic types, they are moreover isomorphic to the cluster complex as defined in [20].
2.4 Main results
We are now in the position to state the main results of this paper and to define the central object, the multi-cluster complex. Let c=(c 1,…,c n ) be a reduced expression for a Coxeter element c∈W, and let w ∘(c)=(w 1,…,w N ) be the lexicographically first subword of c ∞ that represents a reduced expression for the longest element w ∘∈W. The word w ∘(c) is called c-sorting word for w ∘, see [48]. The first theorem (proved in Sect. 5) gives a description of the cluster complex as a subword complex.
Theorem 2.2
The subword complex Δ(cw ∘(c),w ∘) is isomorphic to the c-cluster complex. The isomorphism is given by sending the letter c i of c to the negative root \(-\alpha_{c_{i}}\) and the letter w i of w ∘(c) to the positive root \(w_{1} \cdots w_{i-1}(\alpha_{w_{i}})\).
As an equivalent statement, we obtain the following explicit description of the c-compatibility relation.
Corollary 2.3
A subset C of Φ ≥−1 is a c-cluster if and only if the complement of the corresponding subword in cw ∘(c)=(c 1,…,c n ,w 1,…,w N ) represents a reduced expression for w ∘.
This description was obtained independently by K. Igusa and R. Schiffler [29] for finite crystallographic root systems in the context of cluster categories [29, Theorem 2.5]. They use results of W. Crawley-Beovey and C.M. Ringel saying that the braid group acts transitively on isomorphism classes of exceptional sequences of modules over a hereditary algebra, see [29, Sect. 2]. K. Igusa and R. Schiffler then show combinatorially that the braid group acting on sequences of elements in any Coxeter group W of rank n acts as well transitively on all sequences of n reflections whose product is a given Coxeter element [29, Theorem 1.4]. They then deduce Corollary 2.3 in crystallographic types from these two results, see [29, Theorem 2.5]. The present approach holds uniformly for all finite Coxeter groups and is developed purely in the context of Coxeter group theory. We study the connections to the work of K. Igusa and R. Schiffler more closely in Sect. 8. In the particular case of bipartite Coxeter elements, as defined in Sect. 8.3 below, a similar description as in Corollary 2.3 was as well obtained by T. Brady and C. Watt in [11] in the context of the geometry of noncrossing partitions.Footnote 1
Example 2.4
Let W be the Coxeter group of type B 2 generated by S={s 1,s 2}, and let c=c 1 c 2=s 1 s 2. Then the word cw ∘(c) is (c 1,c 2,w 1,w 2,w 3,w 4)=(s 1,s 2,s 1,s 2,s 1,s 2). The corresponding list of almost positive roots is
The subword complex Δ(cw ∘(c),w ∘) is a hexagon with facets being any two cyclically consecutive letters. The corresponding c-clusters are
Inspired by results in [62] and [43], we generalize the subword complex in Theorem 2.2 by considering the concatenation of k copies of the word c. In type A, this generalization coincides with the description of the complex Δ m,k given in [43] in a different language.
Definition 2.5
The multi-cluster complex \(\varDelta ^{k}_{c}(W)\) is the subword complex Δ(c k w ∘(c),w ∘).
Multi-cluster complexes are in fact independent of the Coxeter element c. In particular, we reobtain that all c-cluster complexes are isomorphic (see Sect. 4 for the proof).
Theorem 2.6
All multi-cluster complexes \(\varDelta ^{k}_{c}(W)\) for the various Coxeter elements are isomorphic.
The following two results give alternative descriptions of multi-cluster complexes. A word Q=(q 1,…,q r ) in S has the intervening neighbors property, if all noncommuting pairs s,t∈S alternate within Q, see [15, Sect. 3] and [59, Proposition 2.1]. Let ψ:S→S be the involution given by \(\psi(s)=w_{\circ}^{-1} s w_{\circ}\), and extend ψ to words as ψ(Q)=(ψ(q 1),…,ψ(q r )). We say that Q has the strong intervening neighbors property (SIN-property) if Qψ(Q)=(q 1,…,q r ,ψ(q 1),…,ψ(q r )) has the intervening neighbors property and if in addition the Demazure product δ(Q) is w ∘. Two words coincide up to commutations if they can be obtained from each other by a sequence of interchanges of consecutive commuting letters. The next theorem (proved in Sect. 7) characterizes all words that are equal to c k w ∘(c) up to commutations.
Theorem 2.7
A word in S has the SIN-property if and only if it is equal to c k w ∘(c), up to commutations, for some Coxeter element c and some nonnegative integer k.
The following proposition gives a different description of the facets of the multi-cluster complex. It generalizes results in [11, Sect. 8] (see also [1, Sect. 2.6]) and in [29, Lemma 3.2]. In [11], the authors consider the case k=1 with bipartite Coxeter elements (see Sect. 8.3 for the definition). In [29], the authors consider the case k=1 for crystallographic types with arbitrary Coxeter elements. Set c k w ∘(c)=(q 1,q 2,…,q kn+N ). For an index 1≤i≤kn+N, set the reflection t i to be q 1 q 2⋯q i−1 q i q i−1⋯q 2 q 1. For example, in Example 2.4, we obtain the sequence
Proposition 2.8
A collection \(\{q_{\ell_{1}},\ldots,q_{\ell_{kn}}\}\) of letters in c k w ∘(c) forms a facet of \(\varDelta ^{k}_{c}(W)\) if and only if
Proof
The proof follows the lines of the proof of [29, Lemma 3.2]. A direct calculation shows that \(t_{\ell_{1}}\cdots t_{\ell_{kn}} q_{1}q_{2}\cdots q_{kn+N}\) equals the product of all letters in cw ∘(c) not in \(\{q_{\ell_{1}},\ldots ,q_{\ell_{kn}}\}\). We get that \(\{q_{\ell_{1}},\ldots,q_{\ell_{kn}}\} \) is a facet of \(\varDelta ^{k}_{c}(W)\) if and only if \(t_{\ell_{1}}\cdots t_{\ell _{kn}} q_{1}q_{2}\cdots q_{kn+N} = w_{\circ}\). As q 1 q 2⋯q kn+N =c k w ∘, the statement follows. □
We have seen in Sect. 2.1 that the multi-cluster complex of type A m−2k−1 is isomorphic to the simplicial complex whose facets correspond to k-triangulations of a convex m-gon,
Thus, the multi-cluster complex extends the concept of multi-triangulations to finite Coxeter groups and provides a unifying approach to multi-triangulations and cluster complexes.
Remark 2.9
Note that there is as well a “naive” way of extending the notion of cluster complexes. Consider the simplicial complex on the set of almost positive roots whose faces are given by the sets that do not contain any subset of k+1 pairwise not compatible roots. In type A, this complex gives rise to the simplicial complex of multi-triangulations of a convex polygon as desired. However, this simplicial complex lacks basic properties of cluster complexes in general; in type B 3, it is not pure. In this case, the maximal faces have cardinality 6 or 7. A similar phenomenon was observed in [43, Remark 29], where the authors suggest that subword complexes of type A (viewed as pseudoline arrangements) are the right objects to define “multi-pseudotriangulations” and explain that the approach using pairwise crossings does not work.
The dictionary for type A is presented in Table 1. The general bijection between k-relevant diagonals of the m-gon and (positions of) letters of the word Q=c k w ∘(c) of type A m−2k−1 is given as follows. Label the vertices of the m-gon from 0 to m−1 in clockwise direction, and let n=m−2k−1 for simplicity. For i∈{1,2,…,n}, denote by p i the position of the generator s i in c, and let

The bijection sends the ℓth copy of a generator s i in Q to the k-relevant diagonal obtained by rotating ℓ−1 times the diagonal [a i ,b i ] in clockwise direction. Under this bijection, a collection of k-relevant diagonals is a facet of Δ m,k if and only if the corresponding subword in Q is a facet of \(\varDelta ^{k}_{c}(A_{m-2k-1})\).
Also in type B, we obtain a previously known object, namely the simplicial complex \(\varDelta _{m,k}^{\mathrm{sym}}\) of centrally symmetric k-triangulations of a regular convex 2m-gon. The vertices of this complex are pairs of centrally symmetric k-relevant diagonals, and a collection of vertices form a face if and only if the corresponding diagonals do not contain a (k+1)-crossing. This simplicial complex was studied in algebraic and combinatorial contexts in [51, 63]. We refer to Sect. 6.3 for a proof of Theorem 2.10.
Theorem 2.10
The multi-cluster complex \(\varDelta ^{k}_{c}(B_{m-k})\) is isomorphic to the simplicial complex of centrally symmetric k-triangulations of a regular convex 2m-gon.
The description of the simplicial complex of centrally symmetric multi-triangulations as a subword complex provides straightforward proofs of nontrivial results about centrally symmetric multi-triangulations.
Corollary 2.11
The following properties of centrally symmetric multi-triangulations of a regular convex 2m-gon hold.
-
(i)
All centrally symmetric k-triangulations of a regular convex 2m-gon contain exactly mk relevant (centrally) symmetric pairs of diagonals, of which k are diameters.
-
(ii)
For any centrally symmetric k-triangulation T and any k-relevant symmetric pair of diagonals d∈T, there exists a unique k-relevant symmetric pair of diagonals d′ not in T such that T′=(T∖{d})∪{d′} is again a centrally symmetric k-triangulation. The operation of interchanging a symmetric pair of diagonals between T and T′ is called symmetric flip.
-
(iii)
All centrally symmetric k-triangulations of a 2m-gon are connected by symmetric flips.
The dictionary between the type B multi-cluster complex and the simplicial complex of centrally symmetric k-triangulations of a regular convex 2m-gon is presented in Table 2.
The bijection between k-relevant symmetric pairs of diagonals of a regular convex 2m-gon and (positions of) letters of the word Q=c k w ∘(c)=c m of type B n , where n=m−k and \((s_{1}s_{2})^{4}=(s_{i}s_{i+1})^{3}={\bf1}\) for 1<i<n, is given as follows. Label the vertices of the 2m-gon from 0 to 2m−1 in clockwise direction. For i∈[n], denote by p i the position of the generator s i in c, and let

The bijection sends the ℓth copy of a generator s i in Q to the k-relevant symmetric pair of diagonals obtained by rotating ℓ−1 times the symmetric pair [a i ,b i ]sym:={[a i ,b i ],[a i +m,b i +m]} in clockwise direction (observe that both diagonals coincide for i=1). Under this bijection, a collection of k-relevant symmetric pairs of diagonals is a facet of \(\varDelta _{m,k}^{\mathrm{sym}}\) if and only if the corresponding subword in Q is a facet of \(\varDelta ^{k}_{c}(B_{m-k})\).
Example 2.12
Let m=5 and k=2, and let W be the Coxeter group of type B 3 generated by S={s 1,s 2,s 3} where (s 1 s 2)4=(s 2 s 3)3=(s 1 s 3)2=1. The multi-cluster complex \(\varDelta _{c}^{2}(B_{3})\) is isomorphic to the simplicial complex of centrally symmetric 2-triangulations of a regular convex 10-gon. In the particular case where the Coxeter element c=c 1 c 2 c 3=s 1 s 2 s 3, the bijection between 2-relevant symmetric pairs and the letters of the word Q=c 2 w ∘(c)=(s 1,s 2,s 3)5 is given by
For instance, the first appearance of the letter s 3 is mapped to the symmetric pair of diagonals [2,5]sym={[2,5],[7,0]}, while the third appearance of s 1 is mapped to the symmetric pair of diagonals [2,7]sym={[2,7]}. The centrally symmetric k-triangulations can be easily described using the subword complex approach. For example, the symmetric pairs of diagonals at positions {3,5,7,9,13,15} form a facet of \(\varDelta _{m,k}^{\mathrm{sym}}\), and the symmetric flips are interpreted using Lemma 3.3.
Using algebraic techniques, D. Soll and V. Welker proved that \(\varDelta _{m,k}^{\mathrm{sym}}\) is a (mod 2)-homology-sphere [63, Theorem 10]. The subword complex description in Theorem 2.10 and the results by A. Knutson and E. Miller [34, Theorem 2.5 and Corollary 3.8] imply the following stronger result.
Corollary 2.13
The simplicial complex of centrally symmetric k-triangulations of a regular convex 2m-gon is a vertex-decomposable simplicial sphere.
This result, together with the proof of [63, Conjecture 13] given in [51],Footnote 2 implies the following conjecture by D. Soll and V. Welker.
Corollary 2.14
[63, Conjecture 17]
For the term-order ⪯ defined in [63, Sect. 7], the initial ideal \(\operatorname{in}_{\preceq}(I_{n,k})\) of the determinantal ideal I n,k defined in [63, Sect. 3] is spherical.
We finish this section by describing all spherical subword complexes in terms of faces of multi-cluster complexes (see Sect. 6.5 for the proofs). This generalizes the universality of the multi-associahedron presented in [46, Proposition 5.6] to finite Coxeter groups.
Theorem 2.15
A simplicial sphere can be realized as a subword complex of a given finite type W if and only if it is the link of a face of a multi-cluster complex \(\varDelta ^{k}_{c}(W)\).
The previous theorem can be obtained for any family of subword complexes for which arbitrary large powers of c appear as subwords. However, computations seem to indicate that the multi-cluster complex maximizes the number of facets among subword complexes Δ(Q,w ∘) with word Q of the same size. We conjecture that this is true in general, see Conjecture 9.8. We also obtain the following corollary.
Corollary 2.16
The following two statements are equivalent.
-
(i)
Every spherical subword complex of type W is polytopal.
-
(ii)
Every multi-cluster complex of type W is polytopal.
3 General results on spherical subword complexes
Before proving the main results, we discuss several properties of spherical subword complexes in general which are not specific to multi-cluster complexes. Throughout this section, we let Q=(q 1,…,q r ) be a word in S and π=δ(Q).
3.1 Flips in spherical subword complexes
Lemma 3.1
(Knutson–Miller)
Let F be a facet of Δ(Q,δ(Q)). For any vertex q∈F, there exists a unique vertex q′∈Q∖F such that (F∖{q})∪{q′} is again a facet.
Proof
This follows from the fact that Δ(Q,δ(Q)) is a simplicial sphere [34, Corollary 3.8]. See [34, Lemma 3.5] for an analogous reformulation. □
Such a move between two adjacent facets is called flip. Next, we describe how to find the unique vertex q′∉F corresponding to q∈F. For this, we introduce the notion of root functions.
Definition 3.2
The root function r F :Q→Φ associated to a facet F of Δ(Q,π) sends a letter q∈Q to the root r F (q):=w q (α q )∈Φ, where w q ∈W is given by the product of the letters in the prefix of \(Q\setminus F=(q_{i_{1}}, \dots, q_{i_{\ell}})\) that appears on the left of q in Q, and where α q is the simple root associated to q.
Lemma 3.3
Let F, q, and q′ be as in Lemma 3.1. The vertex q′ is the unique vertex not in F for which r F (q′)∈{±r F (q)}.
Proof
Since \(q_{i_{1}}\dots q_{i_{\ell}}\) is a reduced expression for π=δ(Q), the set \(\{\mathsf{r}_{F}({q_{i_{1}}}), \dots, \mathsf{r}_{F}({q_{i_{\ell}}})\}\) is equal to the inversion set \(\operatorname{inv}(\pi) = \{ \alpha_{i_{1}}, q_{i_{1}}(\alpha_{i_{2}}), \ldots, q_{i_{1}}\cdots q_{i_{\ell-1}}(\alpha _{i_{\ell}}) \}\) of π, which only depends on π and not on the chosen reduced expression. In particular, any two elements in this set are distinct. Notice that the root r F (q) for q∈F is, up to sign, also contained in \(\operatorname{inv}(\pi)\); otherwise it would contradict the fact that the Demazure product of Q is π. If we insert q into the reduced expression of π, the exchange property in Coxeter groups implies that we have to delete the unique letter q′ that corresponds to the same root, with a positive sign if it appears on the right of q in Q, or with a negative sign otherwise. The resulting word is again a reduced expression for π. □
Remark 3.4
In the case of cluster complexes, this description can be found in [29, Lemma 2.7].
Example 3.5
As in Example 2.4, consider the Coxeter group of type B 2 generated by S={s 1,s 2} with c=c 1 c 2=s 1 s 2 and cw ∘(c)=(c 1,c 2,w 1,w 2,w 3,w 4)=(s 1,s 2,s 1,s 2,s 1,s 2). Considering the facet F={c 2,w 1}, we obtain

Since r F (c 2)=r F (w 2), the letter c 2 in F flips to w 2. As w 2 appears on the right of c 2, both roots have the same sign. Similarly, the letter w 1 flips to c 1 because r F (c 1)=−r F (w 1). In this case, the roots have different signs because c 1 appears on the left of w 1.
The following lemma describes the relation between the root functions of two facets connected by a flip.
Lemma 3.6
Let F and F′=(F∖{q})∪{q′} be two adjacent facets of the subword complex Δ(Q,δ(Q)), and assume that q appears on the left of q′ in Q. Then, for every letter p∈Q,
Here, \(t_{q}=w_{q}qw_{q}^{-1}\) where w q is the product of the letters in the prefix of Q∖F that appears on the left of q in Q. By construction, t q is the reflection in W orthogonal to the root r F (q)=w q (α q ).
Proof
Let p be a letter in Q, and \(w_{p} ,w_{p} '\) be the products of the letters in the prefixes of Q∖F and Q∖F′ that appear on the left of p. Then, by definition r F (p)=w p (α p ) and \(r_{F'}(p)=w_{p} '(\alpha_{p})\). We consider the following three cases:
-
If p is on the left of q or p=q, then \(w_{p} =w_{p} '\) and r F (p)=r F′(p).
-
If p is between q and q′ or p=q′, then \(w_{p} '\) can be obtained from w p by adding the letter q at its corresponding position. This addition is the result of multiplying w p by \(t_{q}=w_{q}qw_{q}^{-1}\) on the left, i.e., \(w_{p} '=t_{q}w_{p} \). Therefore, r F (p)=t q (r F′(p)).
-
If p is on the right of q′, consider the reflection \(t_{q'}=w_{q'}q'w_{q'}^{-1}\) where w q′ is the product of the letters in the prefix of Q∖F that appears on the left of q′. By the same argument, one obtains that \(w_{p} '=t_{q}t_{q'}w_{p} \). In addition, t q =t q′ because they correspond to the unique reflection orthogonal to the roots r F (q) and r F (q′), which are up to sign equal by Lemma 3.3. Therefore, \(w_{p} '=w_{p} \) and r F′(p)=r F (p).
□
3.2 Isomorphic spherical subword complexes
We now reduce the study of spherical subword complexes in general to the case where δ(Q)=π=w ∘ and give two operations on the word Q giving isomorphic subword complexes.
Theorem 3.7
Every spherical subword complex Δ(Q,π) is isomorphic to Δ(Q′,w ∘) for some word Q′ such that δ(Q′)=w ∘.
Proof
Let r be a reduced word for π −1 w ∘=δ(Q)−1 w ∘∈W. Moreover, define the word Q′ as the concatenation of Q and r. By construction, the Demazure product of Q′ is w ∘, and every reduced expression of w ∘ in Q′ must contain all the letters in r. The reduced expressions of w ∘ in Q′ are given by reduced expressions of π in Q together with all the letters in r. Therefore, the subword complexes Δ(Q,π) and Δ(Q′,w ∘) are isomorphic. □
Recall the involution ψ:S→S given by \(\psi(s)=w_{\circ}^{-1} s w_{\circ}\). This involution was used in [8] to characterize isometry classes of the c-generalized associahedra. Define the rotated word \(Q_{\stackrel {\circlearrowleft }{s}}\) or the rotation of Q=(s,q 2,…,q r ) along the letter s as (q 2,…,q r ,ψ(s)). The following two propositions are direct consequences of the definition of subword complexes.
Proposition 3.8
If two words Q and Q′ coincide up to commutations, then Δ(Q,π)≅Δ(Q′,π).
Proof
The isomorphism between Δ(Q,π) and Δ(Q′,π) is induced by reordering the letters of Q to obtain Q′. □
Proposition 3.9
Let Q=(s,q 2,…,q r ). Then \(\varDelta (Q,w_{\circ})\cong \varDelta (Q_{\stackrel {\circlearrowleft }{s}}, w_{\circ})\).
Proof
The isomorphism between Δ(Q,w ∘) and \(\varDelta (Q_{\stackrel {\circlearrowleft }{s}},w_{\circ})\) is induced by sending q i to q i for 2≤i≤r and the initial s to the final ψ(s). The results follows using the fact that sw ∘=w ∘ ψ(s). □
Theorem 3.7 and Proposition 3.9 give an alternative viewpoint on spherical subword complexes. First, we can consider π to be the longest element w ∘∈W. Second, Δ(Q,w ∘) does not depend on the word Q but on the bi-infinite word

Taking any connected subword in \(\widetilde{Q}\) of length r gives rise to an isomorphic spherical subword complex.
4 Proof of Theorem 2.6
In this section, we prove that all multi-cluster complexes for the various Coxeter elements are isomorphic. This result relies on the theory of sorting words and sortable elements introduced by N. Reading in [48]. The c-sorting word for w∈W is the lexicographically first (as a sequence of positions) subword of c ∞=ccc… which is a reduced word for w. We use the following result of D. Speyer.
Lemma 4.1
[59, Corollary 4.1]
The longest element w ∘∈W can be expressed as a reduced prefix of c ∞ up to commutations.
The next lemma unifies previously known results; the first statement it trivial, the second statement can be found in [59, Sect. 4], and the third statement is equivalent to [27, Lemma 1.6].
Lemma 4.2
Let s be initial in c, and let \({\bf p}=(s,p_{2},\dots, p_{r})\) be a prefix of c ∞ up to commutations. Then,
-
(i)
(p 2,…,p r ) is a prefix of (c′)∞ up to commutations, where c′ denotes a word for the Coxeter element c′=scs,
-
(ii)
if p=sp 2⋯p r is reduced, then \(\bf p\) is the c-sorting word for p up to commutations,
-
(iii)
if sp 2⋯p r s′ is reduced for some s′∈S, then p is a prefix of the c-sorting word for ps′ up to commutations.
Proposition 4.3
Let s be initial in c, and let w ∘(c)=(s,w 2,…,w N ) be the c-sorting word of w ∘ up to commutations. Then, (w 2,…,w N ,ψ(s)) is the scs-sorting word of w ∘ up to commutations.
Proof
By Lemma 4.1, the element w ∘ can be written as a prefix of c ∞. By Lemma 4.2, this prefix is equal to the c-sorting of w ∘, which we denote by w ∘(c). Let scs denote the word for the Coxeter element scs. By Lemma 4.2 (i), the word (w 2,…,w N ) is a prefix of (scs)∞, and by (ii) it is the scs-sorting word for w 2⋯w N . By the definition of ψ, the word (w 2,…,w N ,ψ(s)) is a reduced expression for w ∘. Lemma 4.2 (iii) with the word (w 2,…,w N ) and ψ(s) implies that (w 2,…,w N ,ψ(s)) is the scs-sorting word for w ∘ up to commutations. □
Remark 4.4
In [52], N. Reading and D. Speyer present a uniform approach to the theory of sorting words and sortable elements. This approach uses an antisymmetric bilinear form, which is used to extend many results to infinite Coxeter groups. In particular, the previous proposition can be easily deduced from [52, Lemma 3.8].
We are now in the position to prove that all multi-cluster complexes for the various Coxeter elements are isomorphic.
Proof of Theorem 2.6
Let c and c′ be two Coxeter elements such that c′=scs for some initial letter s of c, and let c and \(\mathbf{c'}\) denote reduced words for c and c′, respectively. Moreover, let Q c =c k w ∘(c), and Q c′=(c′)k w ∘(c′). By Proposition 3.8, we can assume that Q c =(s,c 2,…,c n )k⋅(s,w 2,…,w N ), and by Proposition 4.3, we can also assume that Q c′=(c 2,…,c n ,s)k⋅(w 2,…,w N ,ψ(s)). Therefore, \(Q_{c'} = (Q_{c})_{\stackrel {\circlearrowleft }{s}}\), and Proposition 3.9 implies that the subword complexes Δ(Q c ,w ∘) and Δ(Q c′,w ∘) are isomorphic. Since any two Coxeter elements can be obtained from each other by conjugation of initial letters (see [23, Theorem 3.1.4]), the result follows. □
5 Proof of Theorem 2.2
In this section, we prove that the subword complex Δ(cw ∘(c),w ∘) is isomorphic to the c-cluster complex. As in Theorem 2.2, we identify letters in cw ∘(c)=(c 1,…,c n ,w 1,…,w N ) with almost positive roots using the bijection \(\mathsf{Lr}_{c}: { \mathbf{c}{\mathbf {w} _{\circ}(\mathbf{c})}}\ \tilde{\rightarrow}\ \varPhi_{\geq-1}\) given by
In [48], this map was used to establish a bijection between c-sortable elements and c-clusters. Note that under this bijection, letters of cw ∘(c) correspond to almost positive roots and subwords of cw ∘(c) correspond to subsets of almost positive roots. We use this identification to simplify several statements in this section. Observe, that for the particular facet F 0 of Δ(cw ∘(c),w ∘) corresponding to the prefix c of cw ∘(c), we have that
where \(\mathsf{r}_{F_{0}}(q)\) is the root function as defined in Definition 3.2. We interpret the two parts (i) and (ii) in the definition of c-compatibility (see Sect. 2.3), in Theorem 5.1 and Theorem 5.7. Proving these two conditions yields a proof of Theorem 2.2. The majority of this section is devoted to the proof of the initial condition. The proof of the recursive condition follows afterwards.
5.1 Proof of condition (i)
The following theorem implies that Δ(cw ∘(c),w ∘) satisfies the initial condition.
Theorem 5.1
{−α s ,β} is a face of the subword complex Δ(cw ∘(c),w ∘) if and only if β∈(Φ 〈s〉)≥−1.
We prove this theorem in several steps.
Lemma 5.2
Let F be a facet of the subword complex Δ(cw ∘(c),w ∘) such that c i ∈F. Then
-
(i)
for every q∈F with q≠c i , \(r_{F}(q)\in\varPhi_{\langle c_{i} \rangle}\),
-
(ii)
for every q∈cw ∘(c), \(r_{F}(q)\in\varPhi_{\langle c_{i} \rangle }\) if and only if \(\mathsf{Lr}_{c}(q)\in(\varPhi_{\langle c_{i} \rangle})_{\geq-1}\).
Proof
For the proof of (i), notice that if F=c, then the result is clear. Now suppose that the result is true for a given facet F with c i ∈F, and consider the facet F′=(F∖{p})∪{p′} obtained by flipping a letter p≠c i in F. Since all the facets containing c i are connected by flips which do not involve the letter c i , it is enough to prove the result for the facet F′. By hypothesis, since p∈F and p≠c i , we have \(r_{F}(p)\in\varPhi _{\langle c_{i} \rangle}\). Then, the reflection t p orthogonal to r F (p) defined in Lemma 3.6 satisfies \(t_{p}\in W_{\langle c_{i} \rangle}\). Using Lemma 3.6, we obtain that for every q∈cw ∘(c),
If q∈F′ and q≠c i , then (q∈F and q≠c i ) or q=p′. In the first case, r F (q) is contained in \(\varPhi_{\langle c_{i} \rangle}\) by hypothesis, and consequently \(r_{F'}(q) \in\varPhi _{\langle c_{i} \rangle}\). By Lemma 3.3, the second case q=p′ implies that r F (q)=±r F (p). Again since r F (p) belongs to \(\varPhi_{\langle c_{i} \rangle}\) by hypothesis, the root r F′(q) belongs to \(\varPhi_{\langle c_{i} \rangle}\).
For the second part of the lemma, notice that the set \(\{ q \in { \mathbf{c}{\mathbf {w} _{\circ}(\mathbf{c})}}: r_{F}(q) \in\varPhi_{\langle c_{i} \rangle} \}\) is invariant for every facet F containing c i . In particular, if F=c, this set is equal to \(\{q \in { \mathbf{c}{\mathbf {w} _{\circ}(\mathbf{c})}}: \mathsf{Lr}_{c}(q) \in(\varPhi_{\langle c_{i} \rangle })_{\geq-1} \}\). Therefore, \(r_{F}(q)\in\varPhi_{\langle c_{i} \rangle}\) if and only if \(\mathsf{Lr}_{c}(q) \in(\varPhi_{\langle c_{i} \rangle})_{\geq-1}\). □
Proposition 5.3
If a facet F of Δ(cw ∘(c),w ∘) contains c i and q≠c i , then \(\mathsf{Lr}_{c}(q)\in(\varPhi_{\langle c_{i} \rangle})_{\geq-1}\).
Proof
This proposition is a direct consequence of Lemma 5.2. □
Next, we consider the parabolic subgroup \(W_{\langle c_{i} \rangle}\) obtained by removing the generator c i from S.
Lemma 5.4
Let c′ be the Coxeter element of the parabolic subgroup \(W_{\langle c_{i} \rangle}\) obtained from c by removing the generator c i . Consider the word \(\widehat{Q} = {\mathbf{c}' w_{\circ}}(\mathbf{c})\) obtained by deleting the letter c i from Q=cw ∘(c), and let Q′=c′w ∘(c′). Then, the subword complexes \(\varDelta (\widehat{Q},w_{\circ})\) and \(\varDelta (Q',w'_{\circ})\) are isomorphic.
Proof
Since every facet F of \(\varDelta (\widehat{Q}, w_{\circ})\) can be seen as a facet F∪{c i } of Δ(cw ∘(c),w ∘) which contains c i , for every q∈F, we have that \(\mathsf{Lr}_{c}(q)\in(\varPhi_{\langle c_{i} \rangle})_{\geq-1}\) by Proposition 5.3. This means that only the letters of \(\widehat{Q}\) that correspond to roots in \((\varPhi _{\langle c_{i} \rangle})_{\ge-1}\) appear in the subword complex \(\varDelta (\widehat{Q},w_{\circ})\). The letters in Q′ are in bijection, under the map Lr c′, with the almost positive roots \((\varPhi_{\langle c_{i} \rangle})_{\ge-1}\). Let φ be the map that sends a letter \(q\in\widehat{Q}\) corresponding to a root in \((\varPhi_{\langle c_{i} \rangle})_{\ge-1}\) to the letter in Q′ corresponding to the same root. We will prove that φ induces an isomorphism between the subword complexes \(\varDelta (\widehat{Q},w_{\circ})\) and \(\varDelta (Q',w'_{\circ})\). In other words, we show that F is a facet of \(\varDelta (\widehat{Q}, w_{\circ})\) if and only if φ(F) is a facet of \(\varDelta (Q',w_{\circ}')\). Let \(\widetilde{\mathsf{r}}_{F}\) and \(\mathsf{r}'_{\varphi(F)}\) be the root functions associated to F and φ(F) in \(\widehat{Q}\) and Q′, respectively. Then, for every \(q\in\widehat{Q}\) such that \(\mathsf{Lr}_{c}(q)\in (\varPhi_{\langle c_{i} \rangle})_{\ge-1}\), we have

If F=c′, then φ(F)=c′, and the equality (⋆) holds by the definition of φ. Moreover, if (⋆) holds for a facet F, then it is true for a facet F′ obtained by flipping a letter in F. This follows by applying Lemma 3.6 and using the fact that the positive roots \((\varPhi _{\langle c_{i} \rangle})_{\ge-1}\) in \(\widehat{Q}\) and Q′ appear in the same order, see [48, Proposition 3.2]. Finally, Lemma 3.3 and (⋆) imply that the map φ sends flips to flips. Since c′ and φ(c′) are facets of \(\varDelta (\widehat {Q}, w_{\circ})\) and \(\varDelta (Q',w_{\circ}')\), respectively, and all facets are connected by flips, F is a facet of \(\varDelta (\widehat{Q}, w_{\circ})\) if and only if φ(F) is a facet of \(\varDelta (Q',w_{\circ}')\). □
The next lemma states that every letter in cw ∘(c) is indeed a vertex of Δ(cw ∘(c),w ∘).
Lemma 5.5
Every letter in cw ∘(c) is contained in some facet of Δ(cw ∘(c),w ∘).
Proof
Write the word Q=cw ∘(c) as the concatenation of c and the c-factorization of w ∘, i.e., \(Q= \mathbf{c}\mathbf{c}_{K_{1}} \mathbf{c}_{K_{2}} \cdots \mathbf{c}_{K_{r}}\), where K i ⊆S for 1≤i≤r and c I , with I⊆S, is the Coxeter element of W I obtained from c by keeping only letters in I. Since w ∘ is c-sortable, see [48, Corollary 4.4], the sets K i form a decreasing chain of subsets of S, i.e., K r ⊆K r−1⊆⋯⊆K 1⊆S. This implies that the word \(\mathbf{c}\mathbf{c}_{K_{1}} \cdots \widehat{\mathbf{c}}_{K_{i}} \cdots \mathbf{c}_{K_{r}}\) contains a reduced expression for w ∘ for any 1≤i≤r. Thus, all letters in \(\mathbf{c}_{K_{i}}\) are indeed vertices. □
Proposition 5.6
For every q∈cw ∘(c) satisfying \(\mathsf{Lr}_{c}(q) \in(\varPhi_{\langle c_{i} \rangle})_{\geq-1}\), there exists a facet of Δ(cw ∘(c),w ∘) that contains both c i and q.
Proof
Consider the parabolic subgroup \(W_{\langle c_{i} \rangle}\) obtained by removing the letter c i from S, and let \(\widehat{Q}\) and Q′ be the words as defined in Lemma 5.4. Since \(\varDelta (\widehat{Q},w_{\circ})\) and \(\varDelta (Q',w'_{\circ})\) are isomorphic, applying Lemma 5.5 to \(\varDelta (Q',w_{\circ}')\) completes the proof. □
Proof of Theorem 5.1
Taking c i =s, −α s =Lr c (c i ), and β=Lr c (q), the two directions of the equivalence follow from Propositions 5.3 and 5.6. □
5.2 Proof of condition (ii)
The following theorem proves condition (ii).
Theorem 5.7
Let β 1,β 2∈Φ ≥−1, and let s be an initial letter of a Coxeter element c. Then, {β 1,β 2} is a face of the subword complex Δ(cw ∘(c),w ∘) if and only if {σ s (β 1),σ s (β 2)} is a face of the subword complex Δ(c′w ∘(c′),w ∘) with c′=scs.
Proof
Let Q=cw ∘(c), s be initial in c, and \(Q_{\stackrel {\circlearrowleft }{s}}\) be the rotated word of Q, as defined in Sect. 3.2. By Proposition 4.3 the word \(Q_{\stackrel {\circlearrowleft }{s}}\) is equal to \(\mathbf{c'}\mathbf {w} _{\circ}(\mathbf{c}')\) up to commutations, and by Proposition 3.9 the subword complexes Δ(cw ∘(c),w ∘) and Δ(c′w ∘(c′),w ∘) are isomorphic. For every letter q∈cw ∘(c), we denote by q′ the corresponding letter in \(\mathbf{c'}\mathbf {w} _{\circ}(\mathbf{c}')\) obtained from the previous isomorphism. We write q 1∼ c q 2 if and only if {q 1,q 2} is a face of Δ(cw ∘(c),w ∘). In terms of almost positive roots, this is written as
Note that the bijection Lr scs can be described using Lr c . Indeed, it is not hard to check that Lr scs (q′)=σ s (Lr c (q)) for all q∈Q. Therefore,
Taking β 1=Lr c (q 1) and β 2=Lr c (q 2), we get the desired result. □
6 Generalized multi-associahedra and polytopality of spherical subword complexes
In this section, we discuss the polytopality of spherical subword complexes and present what is known in the particular cases of cluster complexes, simplicial complexes of multi-triangulations, and simplicial complexes of centrally symmetric multi-triangulations. We then prove polytopality of multi-cluster complexes of rank 2. Finally, we show that every spherical subword complex is the link of a face of a multi-cluster complex, and consequently reduce the question of realizing spherical subword complexes to the question of realizing multi-cluster complexes. We use the term generalized multi-associahedron for the dual of a polytopal realization of a multi-cluster complex—but the existence of such realizations remains open in general, see Table 3. The subword complex approach provides new perspectives and methods for finding polytopal realizations. In a subsequent paper, C. Stump and V. Pilaud obtain a geometric construction of a class of subword complexes containing generalized associahedra purely in terms of subword complexes [45].
6.1 Generalized associahedra
We have seen that for k=1, the multi-cluster complex \(\varDelta _{c}^{1}(W)\) is isomorphic to the c-cluster complex. S. Fomin and A. Zelevinsky conjectured the existence of polytopal realizations of the cluster complex in [20, Conjecture 1.12]. F. Chapoton, S. Fomin, and A. Zelevinsky then proved this conjecture by providing explicit inequalities for the defining hyperplanes of generalized associahedra [12]. N. Reading constructed c-Cambrian fans, which are complete simplicial fans coarsening the Coxeter fan, see [47]. In [50], N. Reading and D. Speyer prove that these fans are combinatorially isomorphic to the normal fan of the polytopal realization in [12]. C. Hohlweg, C. Lange, and H. Thomas then provided a family of c-generalized associahedra having c-Cambrian fans as normal fans by removing certain hyperplanes from the permutahedron [27]. V. Pilaud and C. Stump recovered c-generalized associahedra by giving explicit vertex and hyperplane descriptions purely in terms of the subword complex approach introduced in the present paper [45].
6.2 Multi-associahedra of type A
In type A n for n=m−2k−1, the multi-cluster complex \(\varDelta ^{k}_{c}(A_{n})\) is isomorphic to the simplicial complex Δ m,k of k-triangulations of a convex m-gon. This simplicial complex is conjectured to be realizable as the boundary complex of a polytope.Footnote 3 It was studied in many different contexts, see [44, Sect. 1] for a detailed description of previous work on multi-triangulations. Apart from the most simple cases, very little is known about its polytopality. Nevertheless, this simplicial complex possesses very nice properties which makes this conjecture plausible. Indeed, the subword complex approach provides a simple description of the 1-skeleton of a possible multi-associahedron (see Lemma 3.3) and gives a new and very simple proof that it is a vertex-decomposable triangulated sphere [62, Theorem 2.1], see also [30]. Below, we survey the known polytopal realizations of Δ m,k as boundary complexes of convex polytopes. The simplicial complex Δ m,k , or equivalently the multi-cluster complex \(\varDelta ^{k}_{c}(A_{n})\) for n=m−2k−1, is the boundary complex of
-
a point, if k=0,
-
an n-dimensional dual associahedron if k=1,
-
a k-dimensional simplex if n=1,
-
a 2k-dimensional cyclic polytope on 2k+3 vertices if n=2, see [44, Sect. 8],
-
a 6-dimensional simplicial polytope if n=3 and k=2, see [10].
The case n=2 is also a direct consequence of the rank 2 description in Sect. 6.4. Further unsuccessful attempts to realize Δ m,k come from various directions in discrete geometry.
-
(a)
A generalized construction of the polytope of pseudo-triangulations [53] using rigidity of pseudo-triangulations [42, Sect. 4.2 and Remark 4.82].
-
(b)
A generalized construction of the secondary polytope. As presented in [22], the secondary polytope of a point configuration can be generalized using star polygons [42, Sect. 4.3].
-
(c)
The brick polytope of a sorting network [46]. This new approach brought up a large family of spherical subword complexes that are realizable as the boundary of a polytope. In particular, it provides a new perspective on generalized associahedra [45]. Unfortunately, this polytope fails to realize the multi-associahedron.
6.3 Multi-associahedra of type B
We start by proving Theorem 2.10, which says that the multi-cluster complex \(\varDelta ^{k}_{c}(B_{m-k})\) is isomorphic to the simplicial complex of centrally symmetric k-triangulations of a regular convex 2m-gon. This simplicial complex was studied in [51, 63]. We then present what is known about its polytopality. The new approach using subword complexes provides in particular very simple proofs of Corollaries 2.11, 2.13, and 2.14.
Proof of Theorem 2.10
Let S={s 0,s 1,…,s m−k−1} be the generators of B m−k , where s 0 is the generator such that (s 0 s 1)4=1∈W, and the other generators satisfy the same relations as in type A m−k−1. Then, embed the group B m−k in the group A 2(m−k)−1 by the standard folding technique: replace s 0 by \(s'_{m-k}\) and s i by \(s'_{m-k+i} s'_{m-k-i}\) for 1≤i≤m−k−1, where the set \(S'=\{s_{1}',\dots, s_{2(m-k)-1}'\}\) generates the group A 2(m−k)−1. The multi-cluster complex \(\varDelta ^{k}_{c}(B_{m-k})\) now has an embedding into the multi-cluster complex \(\varDelta ^{k}_{c'}(A_{2(m-k)-1})\), where c′ is the Coxeter element of type A 2(m−k)−1 corresponding to c in B m−k ; the corresponding subcomplex has the property that 2(m−k) generators (all of them except \(s'_{m-k}\)) always come in pairs. Using the correspondence between k-triangulations and facets of the multi-cluster complex described in Sect. 2.4, the facets of \(\varDelta ^{k}_{c}(B_{m-k})\) considered in \(\varDelta ^{k}_{c'}(A_{2(m-k)-1})\) correspond to centrally symmetric multi-triangulations. □
Here, we present the few cases for which this simplicial complex is known to be polytopal. The multi-cluster complex \(\varDelta ^{k}_{c}(B_{m-k})\) is the boundary complex of
-
an (m−1)-dimensional dual cyclohedron (or type B associahedron) if k=1, see [26, 58],
-
an (m−1)-dimensional simplex if k=m−1,
-
a (2m−4)-dimensional cyclic polytope on 2m vertices if k=m−2, see [63].
The case k=m−2 also follows from the rank 2 description in Sect. 6.4.
6.4 Generalized multi-associahedra of rank 2
We now prove that multi-cluster complexes of rank 2 can be realized as boundary complexes of cyclic polytopes. In other words, we show the existence of rank 2 multi-associahedra. This particular case was known independently by D. Armstrong.Footnote 4
Theorem 6.1
(Type I 2(m) multi-associahedra)
The multi-cluster complex \(\varDelta ^{k}_{c}(I_{2}(m))\) is isomorphic to the boundary complex of a 2k-dimensional cyclic polytope on 2k+m vertices. The multi-associahedron of type I 2(m) is the simple polytope given by the dual of a 2k-dimensional cyclic polytope on 2k+m vertices.
Proof
This is obtained by Gale’s evenness criterion on the word Q=(a,b,a,b,a,…) of length 2k+m: Let F be a facet of \(\varDelta ^{k}_{c}(I_{2}(m))\), and take two consecutive letters x and y in the complement of F. Since the complement of F is a reduced expression of w ∘, x and y must represent different generators. Since the letters in Q are alternating, this implies that the number of letters between x and y is even. □
6.5 Generalized multi-associahedra
Recall from Sect. 2.2 that a subword complex Δ(Q,π) is homeomorphic to a sphere if and only if the Demazure product δ(Q)=π, and to a ball otherwise. This motivates the question whether spherical subword complexes can be realized as boundary complexes of polytopes [34, Question 6.4.]. We show that it is enough to consider multi-cluster complexes to prove polytopality for all spherical subword complexes, and we characterize simplicial spheres that can be realized as subword complexes in terms of faces of multi-cluster complexes.
Lemma 6.2
Every spherical subword complex Δ(Q,w ∘) is the link of a face of a multi-cluster complex Δ(c k w ∘(c),w ∘).
Proof
Observe that any word Q in S can be embedded as a subword of Q′=c k w ∘(c) for k less than or equal to the size of Q, by assigning the ith letter of Q within the ith copy of c. Since the Demazure product δ(Q) is equal to w ∘, the word Q contains a reduced expression for w ∘. In other words, the set Q′∖Q is a face of Δ(Q′,w ∘). The link of this face in Δ(Q′,w ∘) consists of subwords of Q—viewed as a subword of Q′—whose complements contain a reduced expression of w ∘. This corresponds exactly to the subword complex Δ(Q,w ∘). □
We now prove that simplicial spheres realizable as subword complexes are links of faces of multi-cluster complexes.
Proof of Theorem 2.15
For any spherical subword complex Δ(Q,π), we have that the Demazure product δ(Q) equals π. By Theorem 3.7, Δ(Q,π) is isomorphic to a subword complex of the form Δ(Q′,w ∘). Using the previous lemma, we obtain that Δ(Q,π) is the link of a face of a multi-cluster complex. The other direction follows since the link of a subword (i.e., a face) of a multi-cluster complex is itself a subword complex, corresponding to the complement of this subword. □
Finally, we prove that the question of polytopality of spherical subword complexes is equivalent to the question of polytopality of multi-cluster complexes.
Proof of Corollary 2.16
On one hand, if every spherical subword complex is polytopal, then clearly every multi-cluster complex is polytopal. On the other hand, suppose that every spherical subword complex is polytopal. Every spherical subword complex is the link of a face of a multi-cluster complex. Since the link of a face of a polytope is also polytopal, Theorem 2.15 implies that every spherical subword complex is polytopal. □
7 Sorting words of the longest element and the SIN-property
In this section, we give a simple combinatorial description of the c-sorting words of w ∘ and prove that a word Q coincides up to commutations with c k w ∘(c) for some nonnegative integer k if and only if Q has the SIN-property as defined in Sect. 2.4. This gives us an alternative way of defining multi-cluster complexes in terms of words having the SIN-property. Recall the involution ψ:S→S from Sect. 4 defined by \(\psi(s) = w_{\circ}^{-1} s w_{\circ}\). The sorting word of w ∘ has the following important property.
Proposition 7.1
The sorting word w ∘(c) is, up to commutations, equal to a word with suffix (ψ(c 1),…,ψ(c n )), where c=c 1⋯c n .
Proof
As w ∘ has a c-sorting word having c=(c 1,…,c n ) as a prefix, the corollary is obtained by applying Proposition 4.3 n times. □
Given a word w in S, define the function \(\phi_{\mathbf{w}}: S \rightarrow\mathbb{N}\) given by ϕ w (s) being the number of occurrences of the letter s in w.
Theorem 7.2
Let w ∘(c) be the c-sorting word of w ∘, and let s,t be neighbors in the Coxeter graph such that s comes before t in c. Then
Proof
Sorting words of w ∘ have intervening neighbors, see [59, Proposition 2.1] for an equivalent formulation. Therefore, s and t alternate in w ∘(c), with s coming first. Thus, \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s) = \phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(t)\) if and only if the last t comes after the last s. Using Proposition 7.1, this means that s appears before t in ψ(c) or equivalently ψ(s) appear before ψ(t) in c. Otherwise, the last s will appear after the last t. □
It is known that if ψ is the identity on S, or equivalently if w ∘=−1, then the c-sorting word of w ∘ is given by \({ \mathbf {w} _{\circ}(\mathbf{c})}=\mathbf{c}^{\frac{h}{2}}\), where h denotes the Coxeter number given by the order of any Coxeter element. In the case where ψ is not the identity on S (that is, when W is of types A n (n≥2), D n (n odd), E 6 and I 2(m) (m odd), see [6, Exercise 10 of Chap. 4]), the previous theorem gives a simple way to obtain the sorting words of w ∘.
Algorithm 7.3
Let W be an irreducible finite Coxeter group, and let c=c 1 c 2⋯c n be a Coxeter element.
-
(i)
Since the Coxeter diagram is connected, one can use Theorem 7.2 to compute \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s)\) for all s depending on \(m := \phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(c_{1})\).
-
(ii)
Using that the number of positive roots equals nh/2, one obtains m and thus all \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s)\) using
$$2 \cdot\sum_{s \in S} \phi_{{ \mathbf {w} _\circ (\mathbf{c})}}(s) = nh. $$ -
(iii)
Using that \({ \mathbf {w} _{\circ}(\mathbf{c})}= \mathbf{c}_{K_{1}} \mathbf{c}_{K_{2}} \cdots \mathbf{c}_{K_{r}}\) where K i ⊆S for 1≤i≤r and c I , with I⊆S, is the Coxeter element of W I obtained from c by keeping only letters in I, we obtain that \(\mathbf{c}_{K_{i}}\) is the product of all s for which \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s) \geq i\).
This algorithm provides an explicit description of the sorting words of the longest element w ∘ of any finite Coxeter group using nothing else than Coxeter group theory. This answers a question raised in [27, Remark 2.3] and simplifies a step in the construction of the c-generalized associahedron. We now give two examples of how to use this algorithm.
Example 7.4
Let W=A 4 and S={s 1,s 2,s 3,s 4} with the labeling of the graph shown in Fig. 1 on page 26. Moreover, let c=s 1 s 3 s 2 s 4. Fix \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{1})=m\). Since s 1 comes before s 2 in c and ψ(s 1)=s 4 comes after ψ(s 2)=s 3, the letter s 1 appears one more time than the letter s 2 in w ∘(c), i.e., \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{2})=m-1\). Repeating the same argument gives \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{3}) = m \text{ and } \phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{4}) = m-1\). Summing up these values gives the equality \(4m-2=\frac{n\cdot h}{2}=\frac{4\cdot5}{2}=10\), and thus m=3. Finally, the c-sorting word is w ∘(c)=(s 1,s 3,s 2,s 4|s 1,s 3,s 2,s 4|s 1,s 3).
Example 7.5
Let W=E 6 and S={s 1,s 2,…,s 6} with the labeling of the graph shown in Fig. 1 on page 26. Moreover, let c=s 3 s 5 s 4 s 6 s 2 s 1. Fix \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{6})=m\). Repeating the same procedure from the previous example and using that ψ(s 6)=s 6, ψ(s 3)=s 3, ψ(s 2)=s 5, ψ(s 1)=s 4, we get \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{1}) = \phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{2}) = {m-1}\), \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{3}) = \phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{6}) = m\), \(\phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{4}) = \phi_{{ \mathbf {w} _{\circ}(\mathbf{c})}}(s_{5}) = m+1\). As the sum equals \(\frac{nh}{2} = \frac{6\cdot12}{2} = 36\), we obtain m=6. Finally, the c-sorting word is (c 5|s 3,s 5,s 4,s 6|s 5,s 4).
Remark 7.6
Propositions 4.3 and 7.1 have the following computational consequences. Denote by \(\operatorname{rev}(\mathbf{w})\) the reverse of a word w. First, up to commutations, we have
Second, we also have, up to commutation,
Third, for all s∈S,
We are now in the position to prove Theorem 2.7.
Proof of Theorem 2.7
Suppose that a word Q has the SIN-property; then it has complete support by definition, and it contains, up to commutations, some word c=(c 1,…,c n ) for a Coxeter element c as a prefix. Moreover, the word (ψ(c 1),…,ψ(c n )) is a suffix of Q, up to commutations. Observe that a word has intervening neighbors if and only if it is a prefix of c ∞ up to commutations, see [15, Sect. 3]. In view of Lemma 4.1 and the equality δ(Q)=w ∘, the word Q has, up to commutations, w ∘(c) as a prefix. If the length of Q equals w ∘, the proof ends here with k=0. Otherwise, the analogous argument for \(\operatorname{rev}(Q)\) gives that the word \(\operatorname{rev}(Q)\) has, up to commutations, \(\mathbf {w} _{\circ}(\psi(\operatorname{rev}(\mathbf{c})))\) as a prefix. By Remark 7.6, the word \(\mathbf {w} _{\circ}(\psi (\operatorname{rev}(\mathbf{c})))\) is, up commutations, equal to the reverse of w ∘(c). Therefore, Q has the word w ∘(c) also as a suffix. Since c=(c 1,…,c n ) is a prefix of Q and of w ∘(c), and Q has intervening neighbors, Q coincides with c k w ∘(c) up to commutations. Moreover, if Q is equal to c k w ∘(c) up to commutations, it has intervening neighbors, and a suffix (ψ(c 1),…,ψ(c n )), up to commutations, by Proposition 7.1. This implies that the word Q has the SIN-property. □
Remark 7.7
In light of Theorem 2.7 and Sect. 3.2, starting with a word Q having the SIN-property suffices to construct a multi-cluster complex, and choosing a particular connected subword in the bi-infinite word \(\widetilde {Q}\), defined in Sect. 3.2, corresponds to choosing a particular Coxeter element.
We finish this section with a simple observation on the bi-infinite word \(\widetilde{Q}\). For any letter q in the word Qψ(Q), let β q be the root obtained by applying the prefix w q of Qψ(Q) before q to the simple root α q . To obtain roots for all letters in \(\widetilde {Q}\), repeat this association periodically.
Proposition 7.8
Let Q be a word in S having the SIN-property, and let q,q′ be two consecutive occurrences of the same letter s in \(\widetilde {Q}\). Then
where the sum ranges over the collection of letters p in \(\widetilde{Q}\) between q and q′ corresponding to neighbors of s in the Coxeter graph, and where (a st ) s,t∈S is the corresponding Cartan matrix.
Proof
Without loss of generality, we can assume that q is the first letter in some occurrence of Q, as otherwise, we can shift Q accordingly. Let w 〈s〉 be the product of all neighbors of s in the Coxeter graph (in any order, as they all commute). The result follows from a direct calculation

where the first equality comes from the fact that Q has the SIN-property, the second comes from the facts that p(α s )=α s −a sp α p and that any two neighbors of s in the Coxeter graph commute, while the last two are trivial calculations. □
8 Multi-cluster complexes, Auslander–Reiten quivers, and repetition quivers
In this section, we connect multi-cluster complexes to Auslander–Reiten quivers and repetition quivers. This approach emphasizes that the multi-cluster complex can be seen as a cyclic object that does not depend on a particular choice of a Coxeter element. In type A, this approach corresponds to considering subword complexes on a Möbius strip, see [43]. We use this connection to introduce an action on vertices and facets of multi-cluster complexes generalizing the natural rotation action on multi-triangulations in type A.
Auslander–Reiten and repetition quivers play a crucial role in Auslander–Reiten theory, which studies the representation theory of Artinian rings and quivers. The Auslander–Reiten quiver Γ Ω of a quiver Ω encodes the irreducible morphisms between isomorphism classes of indecomposable representations of right modules over k Ω. These were introduced by M. Auslander and I. Reiten in [2, 3]. We also refer to [5, 21] for further background. We use these connections to describe a natural cyclic action on multi-cluster complexes generalizing the rotation of the polygon in types A and B, see Theorems 8.8 and 8.10.
8.1 The Auslander–Reiten quiver
In types A, D and E, sorting words of w ∘ are intimately related to Auslander-Reiten quivers. Starting with a quiver Ω c associated to a Coxeter element c (as described in Sect. 2), one can construct combinatorially the Auslander–Reiten quiver \(\varGamma_{\varOmega_{c}}\), see [7, Sect. 2.6]. R. Bédard then shows how to obtain all reduced expressions for w ∘ adapted to Ω c (i.e., the words equal to w ∘(c) up to commutations) using the Auslander–Reiten quiver and a certain tableau. K. Igusa and R. Schiffler use these connections in order to obtain their description of cw ∘(c), see [29, Sects. 2.1–2.3]. Conversely, given the c-sorting word w ∘(c), one can recover the Auslander–Reiten quiver \(\varGamma_{\varOmega_{c}}\), see [64, Proposition 1.2] and the discussion preceding it. Algorithm 7.3 thus provides a way to construct the Auslander–Reiten quiver in finite types using only Coxeter group theory; it uses results on admissible sequences [59] and words with intervening neighbors [16].
Algorithm 8.1
The following fourth step added to Algorithm 7.3 yields the Auslander–Reiten quiver \(\varGamma _{\varOmega_{c}}\) of Ω c .
-
(iv)
The vertices of \(\varGamma_{\varOmega_{c}}\) are the letters of w ∘(c) and two letters q,q′ of w ∘(c) are linked by an arrow q→q′ in \(\varGamma_{\varOmega_{c}}\) if and only if q and q′ are neighbors in the Coxeter graph and q comes directly before q′ in w ∘(c) when restricted to the letters q and q′.
Figure 1 shows two examples of Auslander–Reiten quivers and how to obtain it using this algorithm.
8.2 The repetition quiver
Next, we define the repetition quiver.
Definition 8.2
[33, Sect. 2.2]
The repetition quiver \(\mathbb{Z}\varOmega\) of a quiver Ω consists of vertices (i,v) for a vertex v of Ω and \(i \in \mathbb{Z}\). The arrows of \(\mathbb{Z}\varOmega\) are given by (i,v)→(i,v′) and (i,v′)→(i+1,v) for any arrow v→v′ in Ω.
For a Coxeter element c, the repetition quiver \(\mathbb{Z}\varOmega_{c}\) turns out to be a bi-infinite sequence of Auslander–Reiten quivers \(\varGamma _{\varOmega_{c}}\) and \(\varGamma_{\varOmega_{\psi(\mathbf{c})}}\) linked at the initial c and the final ψ(c). More precisely, the repetition quiver \(\mathbb{Z}\varOmega_{c}\) can be obtained applying the procedure described in Algorithm 8.1 to the bi-infinite word
As discussed in Remark 7.7, the word \(\widetilde{{ \mathbf {w} _{\circ}(\mathbf{c})}}\) does not depend on the choice of a Coxeter element. Therefore, the repetition quiver is independent of the choice of Coxeter element, as expected. The repetition quiver comes equipped with the Auslander–Reiten translate τ given by τ(i,v)=(i−1,v). A second natural map acts on the vertices of the repetition quiver: the shift operation \([1]: \mathbb{Z}\varOmega_{c} \rightarrow \mathbb{Z}\varOmega _{c}\) that sends a vertex in w ∘(c) or ψ(w ∘(c)) to the corresponding vertex in the next (to the right) copy of ψ(w ∘(c)) or of w ∘(c) respectively. In Fig. 2, we present an example of a repetition quiver of type A 4. Copies of the Auslander–Reiten quivers \(\varGamma_{\varOmega_{c}}\) and \(\varGamma_{\varOmega _{\psi(\mathbf{c})}}\) are separated by dashed arrows. The Auslander–Reiten translate τ sends a vertex to the one located directly to its left. One orbit of the shift operation shown in bold, we have (4,s 1)=[1](1,s 4)=[2](−1,s 1).
Remark 8.3
Vertices in the Auslander–Reiten quiver correspond to (isomorphism classes of) indecomposable representations of Ω c and thus have a dimension vector attached. By the knitting algorithm, the dimension vector at a vertex V=(i,v) of \(\varGamma_{\varOmega_{c}}\) plus the dimension vector at the vertex τ(V) equals the sum of all dimension vectors at vertices V′ for which τ(V)→V′→V are arrows in \(\varGamma_{\varOmega _{c}}\), see [24, Sect. 10.2]. This procedure is intimately related to the SIN-property, which ensures that this sum is indeed over all neighbors of v. Moreover, Proposition 7.8 implies that this property holds as well for the root β q attached to a letter q in the bi-infinite sequence \(\widetilde {Q}\). This yields the well-known property that the dimension vector and the corresponding root coincide.
The following proposition describes words for the multi-cluster complex using the repetition quiver, the Auslander–Reiten translate, and the shift operation.
Proposition 8.4
Let Ω c be a quiver corresponding to a Coxeter element c. Words for the multi-cluster complex are obtained from the bi-infinite word \(\widetilde{{ \mathbf {w} _{\circ}(\mathbf{c})}}\) by setting τ k=[1]. Choosing a particular fundamental domain for this identification corresponds to choosing a particular Coxeter element. In other words, words for multi-cluster complexes are obtained by a choice of linear extension of a fundamental domain of the identification τ k=[1] in the repetition quiver.
Proof
With the identification [1]V=τ k V in the repetition quiver, a fundamental domain will consist of k copies of Ω c and one copy of the Auslander–Reiten quiver \(\varGamma_{\varOmega_{c}}\). This fundamental domain is exactly the quiver formed from the word c k w ∘(c) using Algorithm 8.1. As linear extensions of this quiver correspond to words equal to c k w ∘(c) up to commutations, the result follows. □
The two boxes in Fig. 2 mark two particular choices of a fundamental domain for the multi-cluster complex of type A 4 with k=1 corresponding to the Coxeter elements s 1 s 2 s 3 s 4 and s 1 s 3 s 2 s 4, respectively.
8.3 The Auslander–Reiten translate on multi-cluster complexes
The Auslander–Reiten translate gives a cyclic action on the vertices and facets of a multi-cluster complex. This action corresponds to natural actions on multi-triangulations in types A and B, and is well studied in the case of cluster complexes.
Definition 8.5
Let Q=c k w ∘(c). The permutation \(\varTheta: Q\ \tilde {\rightarrow}\ Q\) is given by sending a letter q i =s to the next occurrence of s in Q, if possible, and to the first occurrence of ψ(s) in Q otherwise.
Observe that in types ADE, the operation Θ corresponds to the inverse of the Auslander–Reiten translate, Θ=τ −1 when considered within the repetition quiver.
Proposition 8.6
The permutation Θ induces a cyclic action on the facets of Δ(Q,w ∘).
Proof
By Proposition 3.9, the subword complexes Δ(Q,w ∘) and \(\varDelta (Q_{\stackrel {\circlearrowleft }{s}},w_{\circ})\) are isomorphic for an initial letter s in Q. Proposition 4.3 asserts that c k w ∘(c) and the rotated word obtained from c k w ∘(c) by rotating n times are equal up to commutations. By construction, Θ is the automorphism of Δ(Q,w ∘) given by inverse rotation of c. □
Example 8.7
As in Example 7.4, consider c=s 1 s 3 s 2 s 4 and Q=cw ∘(c)=(q i :1≤i≤14)=(c 2|s 1 s 3 s 2 s 4|s 1,s 3). After rotating along all letters in c from the right, we obtain the word (s 3 s 1 s 4 s 2|c 2|s 1,s 3), so we have to reorder the initial 4 letters using commutations to obtain again (c 3|s 1,s 3). Therefore, Θ permutes the letter of Q along the permutation of the indices given by

Here is an example of an orbit of Θ:

To relate the permutation Θ to clusters, we recall the definition of bipartite Coxeter elements. Consider a bipartition of the set S=S −⊔S + such that any two generators in S ϵ commute (this is possible since the graph of the Coxeter group is a tree), then form the Coxeter element c ∗=c − c +, where \(c_{\epsilon}=\prod_{s\in S_{\epsilon}}s\). Using the bijection \(\mathsf{Lr}_{c^{*}}\) between letters in c ∗ w ∘(c ∗) and almost positive roots, the cyclic action induced by Θ is equal to the action induced by the tropical Coxeter element
on almost positive roots, see Sect. 2.3 for the definition of σ s and [4, Sect. 5.2] for more details about tropical Coxeter elements. In the case of cluster complexes, S. Fomin and N. Reading computed the order of Θ [19, Theorem 4.14]. Since the words cw ∘(c) are all connected via rotation along initial letters, the order of Θ does not depend on a specific choice of Coxeter element.
Theorem 8.8
For Q=c k w ∘(c), the order of Θ is given by
Proof
To obtain the order of this action, we consider the length of Q divided by the length of c if \(w_{\circ}\equiv-{\bf1}\) and twice the length of Q divided by the length of c otherwise. We have already seen in Algorithm 7.3 that the length of Q is given by kn+nh/2. As the length of c is given by n, the result follows. □
Remark 8.9
The action induced by the tropical Coxeter element on facets of the cluster complex was shown by S.-P. Eu and T.-S. Fu to exhibit a cyclic sieving phenomenon [17]. Therefore, the cyclic action induced by Θ exhibits a cyclic sieving phenomenon for facets of the cluster complex Δ(cw ∘(c),w ∘) and any Coxeter element c.
Finally, for types A and B, the cyclic action \(\varTheta: Q \tilde {\rightarrow} Q\) corresponds to the cyclic action induced by rotation of the associated polygons.
Theorem 8.10
Let Q=c k w ∘(c). In type A m−2k−1, the cyclic action Θ on letters in Q corresponds to the cyclic action induced by rotation on the set of k-relevant diagonals of a convex m-gon. In type B m−k , the cyclic action Θ corresponds to the cyclic action induced by rotation on the set of k-relevant centrally symmetric diagonals of a regular convex 2m-gon.
Proof
The simplicial complex of k-triangulations of a convex m-gon is isomorphic to the multi-cluster complex of type A m−2k−1, so the order of Θ is given by 2k+h=2k+m−2k=m as expected. The simplicial complex of centrally symmetric k-triangulations of a regular convex 2m-gon is isomorphic to the multi-cluster complex of type B m−k , so the order of Θ equals k+h/2=k+m−k=m as well. In type A, the result follows from the correspondence between letters in Q and k-relevant diagonals in the m-gon as described in Sect. 2.4. In type B, the result follows from the correspondence between letters in Q and k-relevant centrally symmetric diagonals in the 2m-gon as described in Sect. 2.4. □
9 Open problems
We discuss open problems and present several conjectures. We start with two open problems concerning counting formulas for multi-cluster complexes.
Open Problem 9.1
Find multi-Catalan numbers counting the number of facets in the multi-cluster complex.
Although a formula in terms of invariants of the group for the number of facets of the generalized cluster complex defined by S. Fomin and N. Reading is known [18, Proposition 8.4], a general formula in terms of invariants of the group for the multi-cluster complex is yet to be found. An explicit formula for type A can be found in [31, Corollary 17]. In type B, a formula was conjectured in [63, Conjecture 13] and proved in [51].Footnote 5 In the dihedral type I 2(m), the number of facets of the multi-cluster complex is equal to the number of facets of a 2k-dimensional cyclic polytope on 2k+m vertices. These three formulas can be reformulated in terms of invariants of the Coxeter groups of type A, B and I 2 as follows:
where d 1≤…≤d n are the degrees of the corresponding group, and h is its Coxeter number. In general, this product is not an integer. The smallest example we are aware of is type D 6 with k=5. Therefore, this product cannot count facets of the multi-cluster complex in general. The cyclic action Θ (see Definition 8.5) on multi-cluster complexes might be useful to solve Open Problem 9.1, and it gives rise to the following generalization.
Open Problem 9.2
Find multi-Catalan polynomials f(q) such that the triple
exhibits the cyclic sieving phenomenon as defined by V. Reiner, D. Stanton, and D. White in [54].
In types A, B, and I 2, there is actually a natural candidate for f(q), namely
where [m] q =1+q+⋯+q m−1 is a q-analogue of the integer m. In the case of multi-triangulations and centrally symmetric multi-triangulations, this triple is conjectured to exhibit the cyclic sieving phenomenon.Footnote 6 The counting formula in types A, B, and I 2 can be enriched with a parameter m such that it reduces for k=1 to the Fuss–Catalan numbers counting the number of facets in the generalized cluster complexes. The next open problem raises the question of finding a family of simplicial complexes that includes the generalized cluster complexes of S. Fomin and N. Reading and the multi-cluster complexes.
Open Problem 9.3
Construct a family of simplicial complexes which simultaneously contains generalized cluster complexes and multi-cluster complexes.
The next open problem concerns a possible representation theoretic description of the multi-cluster complex in types ADE. For k=1, one can describe the compatibility by saying that V∥ c V′ if and only \(\dim(\operatorname{Ext}^{1}(V,V')) = 0\), see [9].
Open Problem 9.4
Describe the multi-cluster complex within the repetition quiver using similar methods.
The following problem extends the diameter problem of the associahedron to the family of multi-cluster complexes, see [42, Sect. 2.3.2] for further discussions in the case of multi-triangulations.
Open Problem 9.5
Find the diameter of the facet-adjacency graph of the multi-cluster complex \(\varDelta ^{k}_{c}(W)\).
Finally, we present several combinatorial conjectures on the multi-cluster complexes. We start with a conjecture concerning minimal non-faces.
Conjecture 9.6
Minimal nonfaces of the multi-cluster complex \(\varDelta ^{k}_{c}(W)\) have cardinality k+1.
Since w ∘ is c-sortable, we have \(\mathbf{c}^{k}{ \mathbf {w} _{\circ}(\mathbf{c})}= \mathbf{c}^{k}\mathbf{c}_{K_{1}}\mathbf{c}_{K_{2}}\cdots \mathbf{c}_{K_{r}}\) with K r ⊆⋯⊆K 2⊆K 1. This implies that the complement of any k letters still contains a reduced expression for w ∘. In other words, minimal nonfaces have at least cardinality k+1. Moreover, using the connection to multi-triangulations and centrally symmetric triangulations, we see that the conjecture holds in types A and B. It also holds in the case of dihedral groups: it is not hard to see that the faces of the multi-cluster complex are given by subwords of c k w ∘(c)=(a,b,a,b,…) that do not contain k+1 pairwise nonconsecutive letters (considered cyclically). The conjecture was moreover tested for all multi-cluster complexes of rank 3 and 4 with k=2.
In types A and I 2(m), there is a binary compatibility relation on the letters of c k w ∘(c) such that the faces of the multi-cluster complex can be described as subsets avoiding k+1 pairwise incompatible elements. We remark that this is not possible in general: in type B 3 with k=2, as in Example 2.12, \(\varDelta _{c}^{2}(B_{3})\) is isomorphic to the simplicial complex of centrally symmetric 2-triangulations of a regular convex 10-gon. Every pair of elements in the set \(\mathcal{A}=\{ [1,4]_{\mathrm{sym}}, [4,7]_{\mathrm{sym}}, [7,10]_{\mathrm{sym}} \}\) is contained in a minimal nonface. But since \(\mathcal{A}\) does not contain a 3-crossing, it forms a face of \(\varDelta _{c}^{2}(B_{3})\).
Theorem 2.7 gives an alternative way of defining multi-cluster complexes as subword complexes Δ(Q,w ∘) where the word Q has the SIN-property. It seems that this definition covers indeed all subword complexes isomorphic to multi-cluster complexes.
Conjecture 9.7
Let Q be a word in S with complete support, and π∈W. The subword complex Δ(Q,π) is isomorphic to a multi-cluster complex of type W if and only if Q has the SIN-property and π=δ(Q)=w ∘.
The fact that π=δ(Q) is indeed necessary so that the subword complex is a sphere. It remains to show that π=w ∘ and that Q has the SIN-property. One reason for this conjecture is that if Q does not have the SIN-property, then it seems that the subword complex Δ(Q,w ∘) has fewer facets than required. Indeed, we conjecture that multi-cluster complexes maximize the number of facets among all subword complexes with a word Q of a given size.
Conjecture 9.8
Let Q be any word in S with kn+N letters (where N denotes the length of w ∘), and Δ(Q,w ∘) be the corresponding subword complex. The number of facets of Δ(Q,w ∘) is less than or equal to the number of facets of the multi-cluster complex \(\varDelta ^{k}_{c}(W)\). Moreover, if both numbers are equal, then the word Q has the SIN-property.
We remark that the previous two conjectures hold for the dihedral types I 2(m). In this case, the multi-cluster complex is isomorphic to the boundary complex of a cyclic polytope, which is a polytope that maximizes the number of facets among all polytopes in fixed dimension on a given number of vertices, see, e.g., [65]. Moreover, we present below a simple polytope theory argument in order to show that if a word does not satisfy the SIN-property, then the corresponding subword complex has strictly less facets than the multi-cluster complex. First note that Corollary 2.16 and Theorem 6.1 imply that all spherical subword complexes of type I 2(m) are polytopal. By the upper bound theorem, a polytope has as many facets as a cyclic polytope if and only if it is neighborly, see, e.g., [65]. Therefore, it is enough to prove that if Q=(q 1,…,q r ) with r=2k+m is a word in S={a,b} containing two consecutive letters that are equal, then the subword complex Δ(Q,w ∘) is not neighborly. Since this is a 2k-dimensional complex, this is equivalent to show that there is a set of k letters of Q that do not form a face. By applying rotation of letters and Proposition 3.9, we can assume without loss of generality that the last two letters of Q are equal. Among the first 2k+1 letters of Q, one of the generators a or b appears no more than k times. The set of these no more than k letters is not a face of the subword complex. The reason is that the reduced expressions in the complement of this set in Q have length at most m−1, which is one less than the length of w ∘.
In view of Corollary 2.16, the following conjecture restricts the study of [34, Question 6.4].
Conjecture 9.9
The multi-cluster complex is the boundary complex of a simplicial polytope.
In types A and B, this conjecture coincides with the conjecture on the existence of the corresponding multi-associahedra, see [31, 63], and Theorem 6.1 shows that this conjecture is true for dihedral groups.
Notes
We thank an anonymous referee for pointing us to this result.
The proof appeared in Sect. 7 in the arxiv version, see http://arxiv.org/abs/0904.1097v2.
As far as we know, the first reference to this conjecture appears in [31, Sect. 1].
Personal communication.
The proof appeared in Sect. 7 in the arxiv version, see http://arxiv.org/abs/0904.1097v2.
Personal communication with V. Reiner.
References
Athanasiadis, C.A., Brady, T., McCammond, J., Watt, C.: h-vectors of generalized associahedra and noncrossing partitions. Int. Math. Res. Not. 2006 (2006), 28 pp.
Auslander, M., Reiten, I.: Almost split sequences. II. In: Proceedings of the International Conference on Representations of Algebras, Carleton Univ., Ottawa, Ont., 1974. Carleton Math. Lecture Notes, vol. 9, p. 13 (1974). Paper No. 2
Auslander, M., Reiten, I.: Representation theory of Artin algebras. III. Almost split sequences. Commun. Algebra 3, 239–294 (1975)
Armstrong, D.: Generalized noncrossing partitions and combinatorics of Coxeter groups. In: Mem. Amer. Math. Soc., vol. 202 (2009). No. 949, x+159
Auslander, M., Reiten, I., Smalø, S.O.: Representation Theory of Artin Algebras. Cambridge Studies in Advanced Mathematics, vol. 36. Cambridge University Press, Cambridge (1995)
Björner, A., Brenti, F.: Combinatorics of Coxeter Groups, vol. 231. Springer, Berlin (2005)
Bédard, R.: On commutation classes of reduced words in Weyl groups. Eur. J. Comb. 20(6), 483–505 (1999)
Bergeron, N., Hohlweg, C., Lange, C.E.M.C., Thomas, H.: Isometry classes of generalized associahedra. Sém. Lothar. Combin. 61A (2009), Art. B61Aa, 13 pp.
Bakke Buan, A., Marsh, R., Reineke, M., Reiten, I., Todorov, G.: Tilting theory and cluster combinatorics. Adv. Math. 204(2), 572–618 (2006)
Bokowski, J., Pilaud, V.: On symmetric realizations of the simplicial complex of 3-crossing-free sets of diagonals of the octagon. In: Proc. 21th Canadian Conference on Comput. Geom., pp. 41–44 (2009)
Brady, T., Watt, C.: Lattices in finite real reflection groups. Trans. Am. Math. Soc. 360, 1983–2005 (2008)
Chapoton, F., Fomin, S., Zelevinsky, A.: Polytopal realizations of generalized associahedra. Can. Math. Bull. 45(4), 537–566 (2002)
Ceballos, C., Santos, F., Ziegler, G.M.: Many non-equivalent realizations of the associahedron (2011), 28 pp. arXiv:1109.5544
Dress, A., Koolen, J.H., Moulton, V.: On line arrangements in the hyperbolic plane. Eur. J. Comb. 23(5), 549–557 (2002)
Eriksson, H., Eriksson, K.: Conjugacy of Coxeter elements. Electron. J. Comb. 16(2), R4 (2009), 7 pp.
Eriksson, H., Eriksson, K.: Words with intervening neighbours in infinite Coxeter groups are reduced. Electron. J. Comb. 17(1), N9 (2010), 7 pp.
Eu, S.-P., Fu, T.-S.: The cyclic sieving phenomenon for faces of generalized cluster complexes. Adv. Appl. Math. 40(3), 350–376 (2008)
Fomin, S., Reading, N.: Generalized cluster complexes and Coxeter combinatorics. Int. Math. Res. Not. 2005(44), 2709–2757 (2005)
Fomin, S., Reading, N.: Root Systems and Generalized Associahedra. Geometric Combinatorics, IAS/Park City Math. Ser., vol. 13, pp. 63–131. Amer. Math. Soc., Providence (2007)
Fomin, S., Zelevinsky, A.: Y-systems and generalized associahedra. Ann. Math. 158(3), 977–1018 (2003)
Gabriel, P.: Auslander–Reiten sequences and representation-finite algebras. In: Representation Theory I, vol. 831, pp. 1–71. Springer, Berlin/Heidelberg (1980)
Gelfand, I.M., Kapranov, M.M., Zelevinsky, A.V.: Discriminants, Resultants and Multidimensional Determinants (2008). Modern Birkhäuser Classics, Birkhäuser Boston Inc.
Geck, M., Pfeiffer, G.: Characters of Finite Coxeter Groups and Iwahori–Hecke Algebras. Oxford University Press, London (2000)
Gabriel, P., Roiter, A.V.: Representations of Finite-Dimensional Algebras. Springer, Berlin (1997)
Haiman, M.: Constructing the associahedron (1984, unpublished)
Hohlweg, C., Lange, C.E.M.C.: Realizations of the associahedron and cyclohedron. Discrete Comput. Geom. 37(4), 517–543 (2007)
Hohlweg, C., Lange, C.E.M.C., Thomas, H.: Permutahedra and generalized associahedra. Adv. Math. 226(1), 608–640 (2011)
Humphreys, J.E.: Reflection Groups and Coxeter Groups. Cambridge Studies in Advanced Mathematics, vol. 29. Cambridge University Press, Cambridge (1992)
Igusa, K., Schiffler, R.: Exceptional sequences and clusters. J. Algebra 323(8), 2183–2202 (2010)
Jonsson, J.: Generalized triangulations of the n-gon. Unpublished manuscript, abstract in Mathematisches Forschungsinstitut Oberwolfach. Report No. 16/2003 (2003)
Jonsson, J.: Generalized triangulations and diagonal-free subsets of stack polyominoes. J. Comb. Theory, Ser. A 112(1), 117–142 (2005)
Jonsson, J., Welker, V.: A spherical initial ideal for Pfaffians. Ill. J. Math. 51(4), 1397–1407 (2007)
Keller, B.: Cluster algebras, quiver representations and triangulated categories. In: London Math. Soc. Lecture Note Ser., vol. 375, pp. 76–160. Cambridge University Press, Cambridge (2010)
Knutson, A., Miller, E.: Subword complexes in Coxeter groups. Adv. Math. 184(1), 161–176 (2004)
Knutson, A., Miller, E.: Gröbner geometry of Schubert polynomials. Ann. Math. (2) 161(3), 1245–1318 (2005)
Krattenthaler, C.: Growth diagrams, and increasing and decreasing chains in fillings of Ferrers shapes. Adv. Appl. Math. 37(3), 404–431 (2006)
Lee, C.W.: The associahedron and triangulations of the n-gon. Eur. J. Comb. 10(6), 551–560 (1989)
Loday, J.-L.: Realization of the Stasheff polytope. Arch. Math. 83(3), 267–278 (2004)
Müller-Hoissen, F., Pallo, J.M., Stasheff, J. (eds.): Associahedra, Tamari Lattices and Related Structures. Progress in Mathematics, vol. 299 (2012). Birkhäuser Boston Inc., Boston, MA
Marsh, R., Reineke, M., Zelevinsky, A.: Generalized associahedra via quiver representations. Trans. Am. Math. Soc. 355(10), 4171–4186 (2003)
Nakamigawa, T.: A generalization of diagonal flips in a convex polygon. Theor. Comput. Sci. 235(2), 271–282 (2000)
Pilaud, V.: Multitriangulations, pseudotriangulations and some problems of realization of polytopes. Ph.D. thesis, Université Paris 7 and Universidad de Cantabria, p. 312 (2010). Available at http://www.lix.polytechnique.fr/~pilaud/documents/reports/theseVPilaud.pdf
Pilaud, V., Pocchiola, M.: Multitriangulations, pseudotriangulations and primitive sorting networks. Discrete Comput. Geom. 48(1), 142–191 (2012)
Pilaud, V., Santos, F.: Multitriangulations as complexes of star polygons. Discrete Comput. Geom. 41(2), 284–317 (2009)
Pilaud, V., Stump, C.: Brick polytopes of spherical subword complexes: A new approach to generalized associahedra. Preprint (2011). Available at arXiv:1111.3349
Pilaud, V., Santos, F.: The brick polytope of a sorting network. Eur. J. Comb. 33, 632–662 (2012)
Reading, N.: Cambrian lattices. Adv. Math. 205(2), 313–353 (2006)
Reading, N.: Coxeter-sortable elements and noncrossing partitions. Trans. Am. Math. Soc. 359(12), 5931–5958 (2007)
Reading, N.: Sortable elements and Cambrian lattices. Algebra Univers. 56(3–4), 411–437 (2007)
Reading, N., Speyer, D.E.: Cambrian fans. J. Eur. Math. Soc. 11(2), 407–447 (2009)
Rubey, M., Stump, C.: Crossings and nestings in set partitions of classical types. Electron. J. Comb. 17(1), R120 (2010)
Reading, N., Speyer, D.E.: Sortable elements in infinite Coxeter groups. Trans. Am. Math. Soc. 363(2), 699–761 (2011)
Rote, G., Santos, F., Streinu, I.: Expansive motions and the polytope of pointed pseudo-triangulations. In: Discrete and Computational Geometry, Algorithms Combin, vol. 25, pp. 699–736. Springer, Berlin (2003)
Reiner, V., Stanton, D., White, D.: The cyclic sieving phenomenon. J. Comb. Theory, Ser. A 108, 17–50 (2004)
Rubey, M.: Increasing and decreasing sequences in fillings of moon polyominoes. Adv. Appl. Math. 47(1), 57–87 (2011)
Stein, W.A., et al.: In: Sage Mathematics Software (Version 4.8) (2012). The Sage Development Team. http://www.sagemath.org
Shi, J.-Y.: The enumeration of Coxeter elements. J. Algebr. Comb. 6(2), 161–171 (1997)
Simion, R.: A type-B associahedron. Adv. Appl. Math. 30(1–2), 2–25 (2003)
Speyer, D.E.: Powers of Coxeter elements in infinite groups are reduced. Proc. Am. Math. Soc. 137(4), 1295–1302 (2009)
Serrano, L., Stump, C.: Maximal fillings of moon polyominoes, simplicial complexes, and Schubert polynomials. Electron. J. Combin. 19 (2012). MR2880647
Stella, S.: Polyhedral models for generalized associahedra via Coxeter elements. J. Algebr. Comb., 1–38 (2012). doi:10.1007/s10801-012-0396-7
Stump, C.: A new perspective on k-triangulations. J. Comb. Theory, Ser. A 118(6), 1794–1800 (2011)
Soll, D., Welker, V.: Type-B generalized triangulations and determinantal ideals. Discrete Math. 309(9), 2782–2797 (2009)
Zelikson, S.: Auslander–Reiten quivers and the Coxeter complex. Algebr. Represent. Theory 8(1), 35–55 (2005)
Ziegler, G.M.: Lectures on Polytopes, Graduate Texts in Mathematics, vol. 152. Springer, New York (1995). Revised edition (1998), seventh updated printing (2007)
Acknowledgements
The authors would like to thank Hugh Thomas for pointing them to the results in [29], and Christophe Hohlweg, Carsten Lange, Vincent Pilaud, Hugh Thomas, and Günter M. Ziegler for important comments and remarks on preliminary versions of this article. The first two authors are thankful to Drew Armstrong, Carsten Lange, Emerson Leon, Ezra Miller, Vincent Pilaud, and Luis Serrano for useful discussions that took place during the 23rd FPSAC Conference in Reykjavik. They are particularly grateful to Carsten Lange and Emerson Leon for numerous fruitful discussions that took place in the Arnimallee 2 Villa in Berlin.
We used the computer algebra system Sage [56] for implementing the discussed objects, and to test the conjectures.
C. Ceballo was supported by DFG via the Research Training Group “Methods for Discrete Structures” and the Berlin Mathematical School.
J.-P. Labbé was supported by an FQRNT Doctoral scholarship.
C. Stump was partially supported by a CRM-ISM postdoctoral fellowship and the DFG via the Research Group “Methods for Discrete Structures”.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ceballos, C., Labbé, JP. & Stump, C. Subword complexes, cluster complexes, and generalized multi-associahedra. J Algebr Comb 39, 17–51 (2014). https://doi.org/10.1007/s10801-013-0437-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10801-013-0437-x