Abstract
Asymptotic multi-layer (AML) analyses and computation of solutions for turbulent flows over steady and unsteady monochromatic surface waves are reviewed in the limits of low-turbulence stresses and small wave amplitude. The structure of the flow is defined in terms of asymptotically matched thin layers, namely the surface layer and a critical layer (CL), whether it is ‘elevated’ or ‘immersed’, corresponding to its location above or within the surface layer. The results particularly demonstrate the physical importance of the singular flow features and physical implications of the elevated CL in the limit of the unsteadiness tending to zero. These agree with the variational mathematical solution of Miles (J Fluid Mech, 3:185–204, 1957) for a small but finite growth rate, but they are not consistent physically or mathematically with his analysis in the limit of a growth rate tending to zero. As this and other studies conclude, in the limit of zero growth rate, the effect of the elevated CL is eliminated by finite turbulent diffusivity, so that the perturbed flow and the drag force are determined by the asymmetric or sheltering flow in the surface shear layer and its matched interaction with the upper region. But for groups of waves, in which the individual waves grow and decay, there is a net contribution of the elevated CL to the wave growth. CLs, whether elevated or immersed, affect this asymmetric sheltering mechanism, but in quite a different way from their effect on growing waves. These AML methods lead to physical insights and suggest approximate methods for analysing higher-amplitude and more complex flows, such as flow over wave groups.





Similar content being viewed by others
Notes
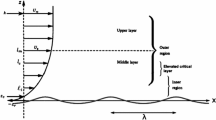
This assumes that in the middle layer the advection term is negligible compared with the curvature term, and thus (1) reduces to \({\fancyscript{W}}''-U''/(\fancyscript{U}-\hbox {i}c_\mathrm{i}){\fancyscript{W}}\sim 0.\)
The turbulence model adopted here is the high-Reynolds-number extension of that given by Sajjadi et al. [25].
Miles and Sajjadi arrived at the same equation independently, but they invoked different turbulence closure schemes for turbulent flow above surface waves.
The detailed evaluations may be obtained from the authors upon request.
References
Hunt JCR (2002) Wind over waves. In: Proceedings of the IMA conference and INI programme. Mathematics Today, April Issue, pp 46–48
Hunt JCR, Belcher SE, Stretch DD, Sajjadi SG, Clegg JR (2010) Turbulence and wave dynamics across gas–liquid interfaces. In: Komori S, Kurose R (eds) Proceedings of the symposium on gas transfer at water surfaces, Kyoto, Japan
Van Dyke M (1964) Perturbation methods in fluid mechanics. Academic Press, New York
Stewartson K (1974) Boundary layers on flat plates and related bodies. Adv Appl Mech 14:145–239
Belcher SL, Hunt JCR (1998) Turbulent flow over hills and waves. Annu Rev Fluid Mech 30:507–538
Phillips OM (1977) Dynamics of the upper ocean. Cambridge University Press, Cambridge
Tsai YS, Grass AJ, Simons RR (2005) On the spatial linear growth of gravity-capillary waves sheared by a laminar flow. Phys Fluids 17:95–101
Jeffreys H (1925) On the formation of water waves by wind. Proc R Soc Lond A 107:189–206
Benjamin TB (1959) Shearing flow over a wavy boundary. J Fluid Mech 6:161–205
Mastenbroek C, Makin VK, Garat MH, Giovanangeli JP (1996) Experimental evidence of the rapid distortion of turbulence in air flow over waves. J Fluid Mech 318:273–302
Townsend AA (1972) Flow in a deep turbulent boundary layer over a surface distorted by water waves. J Fluid Mech 55:719–735
Belcher SL, Hunt JCR (1993) Turbulent shear flow over slowly moving waves. J Fluid Mech 251:109–148
Sullivan PP, McWilliams JC (2010) Dynamics of wind and currents coupled to surface waves. Annu Rev Fluid Mech 42:19–42
Hristov TS, Miller SD, Friehe CA (2003) Dynamical coupling of wind and ocean waves through wave-induced air flow. Nature 422:55–58
Miles JW (1957) On the generation of surface waves by shear flows. J Fluid Mech 3:185–204
Lighthill MJ (1962) Physical interpretation of the theory of wind generated waves. J Fluid Mech 14:385–397
Komen GJ, Cavaleri L, Donelan MA, Hasselmann K, Hasselmann S, Janssen PAEM (1994) Dynamics and modelling of ocean waves. Cambridge University Press, Cambridge
Janssen PAEM (1991) Quasi-linear theory of wind-wave generation applied to wave forecasting. J Phys Oceanogr 21:1631–1642
Benjamin TB (1964) Fluid flow with flexible boundaries. In: Görtler H (ed) 11th Proceedings of international congress in applied mechanics. Springer, Berlin, pp 109–128
McIntyre ME (1993) On the role of wave propagation and wave breaking in atmosphere–ocean dynamics. In: Proceedings of the 18th international congress theoretical and applied mechanics, Haifa. Elsevier, Amsterdam, pp 281–304
Belcher SE, Hunt JCR, Cohen JE (1999) Turbulent flow over growing waves. In: Sajjadi SG, Thomas NH, Hunt JCR (eds) Proceedings of IMA conference on wind over waves. Oxford University Press, Oxford, pp 19–30
Hunt JCR, Leibovich S, Richards KJ (1988) Turbulent shear flows over low hills. Q J R Meteorol Soc 114:1435–1470
Kharif C, Giovanangeli JP, Touboul J, Grare L, Pelinovsky E (2008) Influence of wind on extreme wave events: experimental and numerical approaches. J Fluid Mech 594:209–247
Sajjadi SG, Drullion F (2013) Influence of grouping on growth of surface gravity waves by turbulent shear flow. Int J Numer Methods Fluids (to be submitted)
Sajjadi SG, Craft TJ, Feng Y (2001) A numerical study of turbulent flow over a two-dimensional hill. Int J Numer Methods Fluids 35:1–23
Banner ML, Melville WK (1976) On separation of air flow over water waves. J Fluid Mech 77:825–842
Banner ML, Peregrine DH (1993) Wave breaking in deep water. Annu Rev Fluid Mech 25:373–397
Li L, Kareem A, Xiao Y, Hunt JCR (2012) Turbulence spectra in typhoon boundary layer winds—a conceptual framework and field measurements at coastlines. Boundary-Layer Meteorol (submitted)
Sajjadi SG (2007) Interaction of turbulence due to tropical cyclones with surface waves. Adv Appl Fluid Mech 1:101–145
Miles JW (1996) Surface-wave generation: a viscoelastic model. J Fluid Mech 322:131–145
Sajjadi SG (1998) On the growth of a fully nonlinear Stokes wave by turbulent shear flow. Part 2: Rapid distortion theory. Math Eng Ind 6:247–260
Sajjadi SG (1988) Shearing flows over Stokes waves. Department of Mathematics Internal Report, Coventry Polytechnic, UK
Charnock H (1955) Wind stress on a water surface. Q J R Meteorol Soc 81:639–640
Launder BE, Reece GJ, Rodi W (1975) Progress in the development of a Reynolds-stress turbulence closure. J Fluid Mech 68:537–566
Cohen JE (1997) Theory of turbulent wind over fast and slow waves. PhD dissertation, University of Cambridge
Fitzpatrick P, Mostovoi G, Li Y, Bettencourt M, Sajjadi SG (2002) Coupling of COAMPS and WAVEWATCH with improved wave physics. DoD High Performance Computing Modernization Program Programming Environment and Training, Report No 0005
Sajjadi SG, Bettencourt MT, Fitzpatrick PJ, Mostovoi G, Li Y (2002) Sensitivity of a coupled tropical cyclone/ocean wave simulation to different energy transfer schemes. In: Proceeding of 25th conference on hurricanes and tropical meteorology, p 15D.5
Conte SD, Miles JW (1959) On the numerical integration of the Orr–Sommerfeld equation. J Soc Ind Appl Math 7:361–366
Acknowledgments
We would like to thank the referees for the their critical review and useful comments, which have substantially improved the manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendix: Effect of the inertial critical layer
Appendix: Effect of the inertial critical layer
In a frame of reference moving with waves, the vertical perturbation to the air flow, \(\Delta w=\fancyscript{W}(z)\hbox {e}^{\mathrm{i}k(x-c_\mathrm{r}t)+kc_\mathrm{i}t}\), satisfies the Orr–Sommerfeld-like equation [30, 31]Footnote 3
where \(\nu _\mathrm{e}\) is the eddy viscosity.
In the outer region, turbulence is negligible, and thus the left-hand side of (9) can be neglected compared to the right-hand side, and hence we obtain the Rayleigh equation
As shown by Sajjadi [32], the leading-order solution to (10) is
where \(A\) is constant, which can be determined by matching the solutions to the outer and inner regions.
For slowly growing waves \(c_\mathrm{i}>0\), the CL lies within the inner region close to the surface wave and the integral in (11) is regular since \(\fancyscript{U}>0\) there. Let us now suppose that
then the integral in (11) can be evaluated approximately. Hence, indenting the path of integration in (11) under the singularity \(z=z_\mathrm{c}\) we obtain
where
If we expand \(\fancyscript{U}\!(z)\) as a Taylor expansion in the vicinity of the critical point, i.e.
and set \(z=z_\mathrm{c}\varpi \hbox {e}^{\mathrm{i}\theta }\), where \(\varpi \equiv c_\mathrm{i}/U_*\ll 1\), and \(\tan \theta =-c_\mathrm{i}/U_\mathrm{c}'\eta \), then (13) becomes
which is in agreement with the result obtained by Belcher et al. [21].
As also pointed out by Belcher et al. [21], for a logarithmic mean velocity profile \(\tan \theta =\varpi z_\mathrm{c}/(z-z_\mathrm{c})\). Hence \(\theta \) varies between \(0\) and \(\pi \) as \((z-z_\mathrm{c})/l_\mathrm{c}\) tends to \(\pm \infty \), respectively. Note that the transition between these limiting values occurs across the layer of thickness \(l_\mathrm{c}=\varpi z_\mathrm{c}\). Note also that the significance of the term \(\hbox {i}U_\mathrm{c}''/U_\mathrm{c}^{\prime 3}\) in the solution for \(I\) is that it leads to an out-of-phase contribution to the wave-induced vertical velocity. This gives rise to the same wave growth rate as that of Miles’ [15] CL model.
The result of the present analysis confirms the earlier finding [21] in that Miles’ [15] solution is only valid when waves grow significantly slowly such that
Our analysis also shows that when inertial effects control the behaviour around the CL, there is a smooth behaviour around the CL of thickness [21]
Hence, this proves the effects of a CL [15] are only valid in the limit \(c_\mathrm{i}/U_*\downarrow 0\).
To calculate the energy-transfer parameter due to the CL, \(\beta _\mathrm{c}\), we let \(\fancyscript{W}=-\fancyscript{VM}\), where \(\fancyscript{V}=\fancyscript{U}-\hbox {i}c_\mathrm{i}\). Thus, (9) becomes
In the quasi-laminar limit the left-hand side of (17) is negligible, and thus we have
Multiplying (18) by \({\fancyscript{M}}\), integrating by parts over \(0<z<\infty \), and invoking the inner limits \({\fancyscript{M}}\rightarrow a\) and \({\fancyscript{V}}^2{\fancyscript{M}}'\rightarrow {\fancyscript{P}}_0\) (the complex amplitude of the surface pressure) and a null condition at \(z=\infty \), we obtain
The simplest admissible trial function for the variational integral (19), may be taken as
where \(\varsigma \) is a free parameter. Substituting (20) into (19) together with the approximation \({\fancyscript{V}}\approx U_1\ln (z/z_\mathrm{c})-\hbox {i}c_\mathrm{i}\) we obtain
where
and \(\hat{c}_\mathrm{i}=c_\mathrm{i}/U_1\). Evaluating the integral we obtain
where \(\xi _\mathrm{c}\equiv kz_\mathrm{c}\) (cf. [15]; see also the caption of Fig. 1), \(\gamma =0.5772\) is Euler’s constant, \(U_1=U_*/\kappa \), and \(\kappa =0.41\) is von Kármán’s constant. It then follows from the variational condition \(\partial \hat{{\fancyscript{P}}}_0/\partial \varsigma =0\) that
where \(L_\varsigma =-(L_0+\ln \varsigma )\) and \(L_0=\gamma -\ln (2\xi _\mathrm{c})=\Lambda ^{-1}\).
The corresponding CL approximation to the energy-transfer parameter \(\beta \) may then be calculated from (12), which implies \(\fancyscript{W}_\mathrm{c}={\fancyscript{P}}_\mathrm{c}/U_\mathrm{c}'\approx {\fancyscript{P}}_0/U_\mathrm{c}'\), and (14), which yields
To obtain the corresponding expression for the component of the energy-transfer parameter, \(\beta _T\), due to turbulence, we multiply (9) by \(-{\fancyscript{M}}\), integrating over \(0<z<\infty \), invoking the conditions
on \(z=0\) and the null condition for \(z\rightarrow 0\), and we obtain
where \({\fancyscript{T}}_0\) is the complex amplitude of the surface shear stress and \(c=c_\mathrm{r}+\hbox {i}c_\mathrm{i}\). In the limit as \(s\equiv \rho _\mathrm{a}/\rho _\mathrm{w}\downarrow 0\), where \(\rho _\mathrm{a}\) and \(\rho _\mathrm{w}\) are densities of the air and water, respectively, we obtain
In (25) \(c\) is the complex wave speed,
is the speed of water waves in the absence of the airflow above it, \(\nu _\mathrm{w}\) is the kinematic viscosity of water, and the suffix zero denotes evaluation at \(z=0\). Then it follows from (24) and (21) that
The preceding integral can be evaluated asymptotically,Footnote 4 and its imaginary part yields
In Fig. 6, we show a comparison of the energy-transfer rate, \(\beta \), between the present result for a monochromatic unsteady (growing) wave, both analytically and numerically, and those calculated by Miles [15] and Janssen [18] for the steady wave counterpart. Miles and Janssen both assumed that the drag \(C_D\), and thence \(\beta \), was dominated by the limiting inviscid wave growth mechanism, and thus their formulation is independent of \(c_\mathrm{i}\). In contrast, the present calculation is for a viscous unsteady (growing) wave, where \(c_\mathrm{i}/U_*=0.01\) and \(kz_0=10^{-4}\).
Total energy-transfer parameter, \(\beta \), due to combined effect of sheltering and inertial critical layer for growing waves (where \(c_\mathrm{i}\ll U_*\)) as a function of wave age \(c_\mathrm{r}/U_1\). Plus symbol Miles’ [15] calculation (\(c_\mathrm{i}=0, \nu _\mathrm{e}=0\)) from his formula \(\beta =\pi \xi _\mathrm{c}\big \{\textstyle \frac{1}{6}\pi ^2+\log ^2(\gamma \xi _\mathrm{c})+2\sum _{n=1}^{\infty }\textstyle \frac{(-1)^n\xi _\mathrm{c}^n}{n!n^2}\big \}^2\), where \(\xi _\mathrm{c}=kz_\mathrm{c}\) is the critical height \(\xi _\mathrm{c}=\Omega (U_1/c_\mathrm{r})^2\hbox {e}^{c_\mathrm{r}/U_1}\) and \(\Omega =gz_0/U_1^2\) is Charnock’s constant [33]. Thick solid line: parameterisation of Miles’ formula [18] for \(c_\mathrm{i}=0, \nu _\mathrm{e}=0\): \(\beta =1.2\kappa ^{-2}\xi _\mathrm{c}\log ^4\xi _\mathrm{c}\), where \(\xi _\mathrm{c}=\min \left\{ 1,kz_0\hbox {e}^{[\kappa /(U_*/c+0.011)]}\right\} \). Thin solid line: present formulation: (\(\beta _\mathrm{T}+\beta _\mathrm{c}\)) for \(c_\mathrm{i}\ne 0, \nu _\mathrm{e}\ne 0\). \(\circ \), Numerical simulation using Reynolds-stress closure model [34] for \(c_\mathrm{i}\ne 0, \nu _\mathrm{e}\ne 0\). Note that \(\beta \) given in [15, 18] is equivalent to \(\beta _\mathrm{c}\) in our notation
We emphasize that the various models [10, 12, 35] all generally agree with our numerical simulations performed using the Reynolds-stress closure scheme [34] for the energy transfer parameter, \(\beta \), shown in Fig. 6. This shows the consistency between these models and the unimportance of very small \(c_\mathrm{i}\) for which viscous processes are significant.
These parameterisations have been incorporated into and tested in spectral the wave models WaveWatch and WindWave, which yields superior results compared with field data [36, 37].
Figure 7 shows a comparison of \(\beta _\mathrm{c}\) as a function of wave age \(c_\mathrm{r}/U_1\), calculated from the numerical solution of the inviscid Orr–Sommerfeld equation [38], against the numerical solution of Eq. (1) for \(c_\mathrm{i}/U_*=0.01, kz_0=10^{-4}\) and \(\nu _\mathrm{e}\ne 0\). Increasing \(c_\mathrm{i}/U_*\) from 0.01 to 0.1 (not shown here) makes no significant difference in the magnitude of \(\beta _\mathrm{c}\). We conclude, therefore, for a finite value of \(\nu _\mathrm{e}\), the right-hand side of Eq. (1) is dominant, and therefore the magnitude of \(\beta _\mathrm{c}\), calculated from the solution of (1), is practically zero over a wide range of the wave age, in particular for a ‘young’ wave, where \(c_\mathrm{r}/U_1<2.\) We thus conclude that the CL mechanism plays an insignificant role for \(c_\mathrm{r}/U_1<9\) and has very little effect for \(9\le c_\mathrm{r}/U_1\le 10.5\).
Component of energy-transfer parameter, \(\beta _\mathrm{c}\), due to inertial CL for growing waves (where \(c_\mathrm{i}\ll U_*\)) as a function of wave age \(c_\mathrm{r}/U_1\). Filled circle: numerical solution of inviscid Orr–Sommerfeld equation [38] for \(c_\mathrm{i}=0\) and \(\nu _\mathrm{e}=0\) using singular CL approach; open circle: numerical solution of Eq. (1) for \(c_\mathrm{i}\ne 0\) and \(\nu _\mathrm{e}\ne 0\)
Rights and permissions
About this article
Cite this article
Sajjadi, S.G., Hunt, J.C.R. & Drullion, F. Asymptotic multi-layer analysis of wind over unsteady monochromatic surface waves. J Eng Math 84, 73–85 (2014). https://doi.org/10.1007/s10665-013-9663-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10665-013-9663-4