Abstract
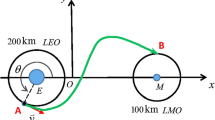
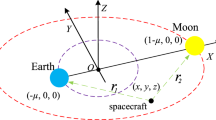
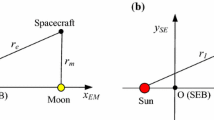
Of the three collinear libration points of the Sun–Earth Circular Restricted Three-Body Problem (CR3BP), L3 is that located opposite to the Earth with respect to the Sun and approximately at the same heliocentric distance. Whereas several space missions have been launched to the other two collinear equilibrium points, i.e., L1 and L2, taking advantage of their dynamical and geometrical characteristics, the region around L3 is so far unexploited. This is essentially due to the severe communication limitations caused by the distant and permanent opposition to the Earth, and by the gravitational perturbations mainly induced by Jupiter and the close passages of Venus, whose effects are more important than those due to the Earth. However, the adoption of a suitable periodic orbit around L3 to ensure the necessary communication links with the Earth, or the connection with one or more relay satellites located at L4 or L5, and the simultaneous design of an appropriate station keeping-strategy, would make it possible to perform valuable fundamental physics and astrophysics investigations from this location. Such an opportunity leads to the need of studying the ways to transfer a spacecraft (s/c) from the Earth’s vicinity to L3. In this contribution, we investigate several trajectory design methods to accomplish such a transfer, i.e., various types of two-burn impulsive trajectories in a Sun-s/c two-body model, a patched conics strategy exploiting the gravity assist of the nearby planets, an approach based on traveling on invariant manifolds of periodic orbits in the Sun–Earth CR3BP, and finally a low-thrust transfer. We examine advantages and drawbacks, and we estimate the propellant budget and time of flight requirements of each.
Similar content being viewed by others
References
Barrabés E., Ollé M.: Invariant Manifolds of L3 and horseshoe motion in the restricted three-body problem. Nonlinearity 9, 2065–2090 (2006)
Brison A.E., Ho Y.-C.: Applied Optimal Control. Blaisdell Publishing Company, Waltham (1969)
Font, J.: The Role of Homoclinic and Heteroclinic Orbits in Two-Degrees of Freedom Hamiltonian Systems. Ph.D. Dissertation, Departament de Matematica. Aplicada i Analisi, Universitat de Barcelona (1990)
Gill P.E., Murray W., Saunders M.A.: Snopt: an sqp algorithm for large-scale constrained optimization. SIAM J. Optim. 12, 979–1006 (2002)
Gómez G., Koon W.S., Lo M.W., Marsden J., Masdemont J., Ross S.D.: Connecting orbits and invariant manifolds in the spatial three-body problem. Nonlinearity 17, 1571 (2004)
Hechler, M., Yanez, A.: Herschel/Planck Consolidated Report on Mission Analysis FP-MA-RP-0010-TOS/GMA (3.1) (2006)
Hou, X., Tang, J., Liu, L.: Transfer to the Collinear Libration Point L3 in the Sun–Earth + Moon System. Nasa Technical Report 20080012700 (2007)
Koon W.S., Lo M.W., Marsden J.E., Ross S.D.: Heteroclinic connections between periodic orbits and resonance transitions in celestial mechanics. Chaos 10(2), 427–469 (2000)
Lo, M.W., Williams, B.G., Bollman, W.E., Han, D., Hahn, Y., et al.: Genesis Mission Design. AIAA Space Flight Mechanics, Paper No. AIAA 98–4468 (1998)
Senent J., Ocampo C., Capella A.: Low-thrust variable-specific-impulse transfers and guidance to unstable periodic orbits. J. Guid. Control Dyn. 28, 280–290 (2005)
Szebehely V.: Theory of Orbits. Academic Press, Massachusetts (1967)
Tantardini, M.: Transfer Strategies to the L3 Libration Point of the Sun–Earth System. MS Thesis, Aerospace Engineering, Delft University of Technology, Delft (2009)
Vallado D.A.: Fundamentals of Astrodynamics and Applications. Microcosm Press, Hawthorne (2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Tantardini, M., Fantino, E., Ren, Y. et al. Spacecraft trajectories to the L3 point of the Sun–Earth three-body problem. Celest Mech Dyn Astr 108, 215–232 (2010). https://doi.org/10.1007/s10569-010-9299-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10569-010-9299-x