1 Introduction

In the business environment enterprises are forced to develop and implement enterprise-wide integrated risk management systems. Risks have to be limited and managed from an enterprise-wide portfolio perspective. The increasing amount of risks in today’s market has increased the demand for risk measurement models and risk management tools. This paper presents an analytic (quantitative) model for the optimization of a portfolio of risks based on prudent and complete stochastic information.

The portfolio optimization problem considered in this paper relates to the original Markowitz (1952) formulation. The original Markowitz portfolio optimization problem is modeled as a mean-risk bicriteria optimization problem where the portfolio mean rate of return is maximized and the risk measured by standard deviation or variance is minimized. Several other risk measures have been later considered thus creating the entire family of mean-risk models (Mitra et al. 2003 and references therein). It is often argued that the variability of the rate of return above the mean should not be penalized, since the investors are concerned with the underperformance rather than the overperformance of a portfolio. This led Markowitz (1959) to propose downside risk measures such as (downside) semivariance to replace variance as the risk measure. Consequently, one observes growing popularity of downside risk models for portfolio selection (Bawa 1978; Fishburn 1977; Sortino and Forsey 1996).

This paper presents copula-based conditional value-at-risk (CCVaR) as a downside risk measure. The measure is intended for multidimensional risk measurement, where the risk is defined as a multivariate random vector whose elements (coordinates) represent risk components. It is assumed that the risk components depend on each other in a stochastic sense and their dependence structure is given by a copula function. It is also assumed that the risk components are perfect substitutes, i.e., they are expressed in the same units (e.g. monetary).

In order to define the measure, the concept of multivariate quantile is introduced. The multivariate quantile is defined as a cone covering the worst (smallest) realizations of a multivariate random variable with a total probability equaling the level of a quantile (throughout the paper it is assumed that larger outcomes are preferred). CCVaR is a scalar risk measure defined as the worst expectation within multivariate quantile of a given level. The measure can be viewed as a prudent variant of multivariate conditional value at risk (MCVaR) introduced by Prékopa (2012), where the conditional expectation of a scalarized random vector is taken over the entire set of multivariate quantiles.

CCVaR allows one to parameterize prudent attitudes toward risk ranging from the extreme risk aversion (worst case) to the risk neutrality (expectation) by changing the level of a quantile. CCVaR is a pessimistic risk measure and it defines almost the same kind of risk as popular and well-researched conditional value-at-risk (CVaR) (Rockafellar and Uryasev 2000). Specifically, in the univariate case both measures coincide, but in the multivariate setting they differ due to the different definitions of quantiles. CCVaR uses cones as opposed to CVaR which uses half-hiperplanes.

An important advantage of CCVaR is its portfolio optimization model which permits one to efficiently solve real life problems based on the full information carried by a multivariate random variable. For a discrete multivariate random vector, the CCVaR portfolio optimization model is a linear program with an infinite number of constraints. However, the dual formulation of this model can be efficiently solved by column generation algorithm based on the Dantzig and Wolfe (1961) decomposition.

The paper is organized as follows. Section 2 presents the definition of CCVaR. Section 3 describes how the measure relates to Conditional Value-at-Risk. Section 4 shows some properties of the measure in terms of coherent risk measures (Artzner et al. 1997, 1999). Section 5 presents the portfolio optimization model of the measure. Section 6 describes the approximate portfolio optimization algorithm. Section 7 presents the results of the computational analysis. Finally, some concluding remarks are given.

2 The definition of copula-based conditional value-at-risk

Let us consider an \(n\)-dimensional random vector \(\mathbf {R}= (R_1,\ldots ,R_n)^T\) whose each element represents a risk component. We restrict the space of risks to \(\mathbb {R}^n\)-valued random vectors \(\mathbf {R}\in L_n^1(\Omega ,\mathcal {F},\mathbb {P})\) and assume that the risk components are perfect substitutes, i.e., they are expressed in the same units. Let \(F_i\) be the cumulative distribution function of \(R_i\), \(i=1,\ldots ,n\), i.e., \(F_{R_i}(\eta ) = \mathbb {P}(R_i \le \eta )\). The random variables \(R_i\) depend on each other in a stochastic sense and their dependence structure is given by a copula function \(C\). Specifically, \(H(\xi ,\ldots ,\zeta ) = C(F_{R_1}(\xi ), \ldots , F_{R_n}(\zeta ))\), where \(H\) is the joint cumulative distribution function of \(\mathbf {R}\). Further, let \(F_{R_i}^{(-1)}\) be the left-continuous inverse of \(F_{R_i}\) (usually termed as a quantile function), i.e., \(F_{R_i}^{(-1)}(p) = \inf \{\eta : F_{R_i}(\eta ) \ge p\}\) for \(0 < p \le 1\). In order to define CCVaR, let us introduce the \(\beta \)-set of univariate quantile levels for \(\beta \in (0, 1]\):

$$\begin{aligned} \mathcal {U}_\beta = \{\mathbf {u}= (u_1,\ldots ,u_n)^T\ : \ C(u_1,\ldots ,u_n) = \beta \}. \end{aligned}$$

Definition 1

For a fixed tolerance level \(\beta \in (0, 1]\), we define CCVaR (\(\hbox {CCVaR}_\beta \)) as

$$\begin{aligned} \hbox {CCVaR}_\beta (\mathbf {R})&= \frac{1}{\beta } \min _{\mathbf {u}\in \mathcal {U}_\beta } \int _0^{u_1} \cdots \int _0^{u_n} \sum _{i=1}^n F_{R_i}^{(-1)}(p_i)\ d C(p_1,\ldots ,p_n). \end{aligned}$$

Let us associate with any \(\mathbf {u}\in \mathcal {U}_\beta \) a multivariate \(\beta \)-quantile of \(\mathbf {R}\):

$$\begin{aligned} \mathbf {Q}(\mathbf {u}) = \Bigl \{(q_1,\ldots ,q_n)^T\ :\ q_i = F_{R_i}^{(-1)}(u_i)\ \hbox {for} \ i =1,\ldots ,n\Bigr \}. \end{aligned}$$

If there is no jump at the optimal multivariate \(\beta \)-quantile, CCVaR equals the minimum expectation of the sum of risk components provided that \(\mathbf {R}\le \mathbf {Q}(\mathbf {u})\) for all \(\mathbf {u}\in \mathcal {U}_\beta \), i.e.,

$$\begin{aligned} \hbox {CCVaR}_\beta (\mathbf {R}) = \min _{\mathbf {u}\in \mathcal {U}_\beta } \mathbb {E}(\mathbf {1}^T \mathbf {R}| \mathbf {R}\le \mathbf {Q}(\mathbf {u})). \end{aligned}$$

Note that \(\hbox {CCVaR}_\beta \) tends to \(\inf (\mathbf {1}^T \mathbf {R})\) for \(\beta \) approaching 0 and \(\mathbf {R}\) bounded from below, and equals \(\mathbb {E}(\mathbf {1}^T \mathbf {R})\) when \(\beta =1\). Hence, the measure covers the whole spectrum of prudent attitudes toward risk ranging from the extreme risk aversion to the complete risk neutrality.

3 A relation to conditional value-at-risk

CVaR (Rockafellar and Uryasev 2000) is a univariate risk measure. For a fixed level \(\beta \in (0, 1]\), we define \(\hbox {CVaR}_\beta \) as the mean within \(\beta \)-quantile, i.e.,

$$\begin{aligned} \hbox {CVaR}_\beta (R) = \frac{1}{\beta } \int _0^\beta F_R^{(-1)}(p)\ dp. \end{aligned}$$
(1)

CVaR has been proved to be coherent (see, e.g., Pflug 2000), and several empirical analyses (see, e.g., Andersson et al. 2001; Rockafellar and Uryasev 2002; Mansini et al. 2003) have confirmed its applicability to various financial optimization problems.

In a multivarite setting, typically we take the sum of risks as an input random variable passed to CVaR, i.e.,

$$\begin{aligned} \hbox {CVaR}_\beta (\mathbf {1}^T \mathbf {R}) = \frac{1}{\beta } \int _0^\beta F_{\mathbf {1}^T \mathbf {R}}^{(-1)}(p)\ dp. \end{aligned}$$
(2)

Note that although both measures compute the means within specified multivariate quantiles, CVaR is more prudent than CCVaR. From the formulation (2) it follows that CVaR uses the half-hiperplane as a quantile and therefore it collects all the worst cases within a given tolerance level of \(\beta \). This is not true in the case of CCVaR which collects only some portion of the worst cases within a given tolerance level of \(\beta \), since according to the definition (1) it uses the cone as a quantile. Therefore, the following assertion is valid.

Proposition 1

For any random vector \(\mathbf {R}\) and \(\beta \in (0,1]\)

$$\begin{aligned} \hbox {CCVaR}_\beta (\mathbf {R}) \ge \hbox {CVaR}_\beta (\mathbf {1}^T \mathbf {R}). \end{aligned}$$

Note that in the univariate case both measures coincide, i.e., for any random variable \(R\) and \(\beta \in (0,1]\)

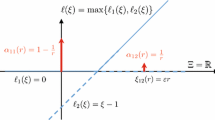
$$\begin{aligned} \hbox {CCVaR}_\beta (R) = \hbox {CVaR}_\beta (R). \end{aligned}$$
(3)

Figure 1 presents the graphical comparison of \(\hbox {CVaR}_\beta \) and \(\hbox {CCVaR}_\beta \) for a bivariate random vector \(\mathbf {R}\) bounded from above and below.

Fig. 1
figure 1

\(\hbox {CVaR}_\beta \) and \(\hbox {CCVaR}_\beta \) for the bounded bivariate random vector

Full size image

Note that it is possible to represent CCVaR in terms of CVaR:

$$\begin{aligned} \hbox {CCVaR}_\beta (\mathbf {R})&= \frac{1}{\beta } \min _{\mathbf {u}\in \mathcal {U}_\beta } \int _0^{u_1} \cdots \int _0^{u_n} \sum _{i=1}^n F_{R_i}^{(-1)}(p_i)\ d C(p_1,\ldots ,p_n) \nonumber \\&= \min _{\mathbf {u}\in \mathcal {U}_\beta } \left( \frac{1}{\beta } \int _0^{u_1} F_{R_1}^{(-1)}(p_1)\ d C(p_1,\ldots ,u_n) + \cdots \right. \nonumber \\&\left. +\, \frac{1}{\beta } \int _0^{u_n} F_{R_n}^{(-1)}(p_n)\ d C(u_1,\ldots ,p_n) \right) \nonumber \\&= \min _{\mathbf {u}\in \mathcal {U}_\beta } \sum _{i=1}^n \hbox {CVaR}_\beta (R_i, \mathbf {u}). \end{aligned}$$
(4)

In the above equation \(\hbox {CVaR}_\beta (R_i, \mathbf {u})\) corresponds to \(\hbox {CVaR}_\beta (R_i)\) calculated over some joint probability depending on \(\mathbf {u}\) and equaling \(\beta \).

4 The properties of copula-based conditional value-at-risk

In this section we state and prove some properties of CCVaR.

Proposition 2

\(\hbox {CCVaR}_\beta \) exhibits the following properties:

  1. (i)

    \(\hbox {CCVaR}_\beta \) is translation-equivariant, i.e.,

    $$\begin{aligned} \hbox {CCVaR}_\beta (\mathbf {R}+ \mathbf {c}) = \hbox {CCVaR}_\beta (\mathbf {R}) + \mathbf {1}^T \mathbf {c}. \end{aligned}$$
  2. (ii)

    \(\hbox {CCVaR}_\beta \) is positively homogenous, i.e.,

    $$\begin{aligned} \hbox {CCVaR}_\beta (\lambda \mathbf {R}) = \lambda \,\hbox {CCVaR}_\beta (\mathbf {R}), \end{aligned}$$

    if \(\lambda > 0\).

  3. (iii)

    \(\hbox {CCVaR}_\beta \) in general is not monotonic, i.e., if

    $$\begin{aligned} \mathbf {R}_1(\omega ) \ge \mathbf {R}_2(\omega ) \hbox { for all } \omega \in \Omega \end{aligned}$$

    then not always

    $$\begin{aligned} \hbox {CCVaR}_\beta (\mathbf {R}_1) \ge \hbox {CCVaR}_\beta (\mathbf {R}_2). \end{aligned}$$
  4. (iv)

    \(\hbox {CCVaR}_\beta \) is superadditive in the following sense:

    $$\begin{aligned} \hbox {CCVaR}_\beta (\mathbf {R}) \ge \sum _{i=1}^n \hbox {CCVaR}_\beta (R_i). \end{aligned}$$

Proof

The properties (i) and (ii) are obvious from the definition of \(\hbox {CCVaR}_\beta \). Let us show the counterexample for (iii). Let us consider two random vectors \(\mathbf {R}_1\) and \(\mathbf {R}_2\) with the following distributions:

\(i\)

\(\mathbf {R}_1(\omega _i)\)

\(\mathbf {R}_2(\omega _i)\)

\(\mathbb {P}(\omega _i)\)

1

\((1,0)^T\)

\((1,0)^T\)

0.1

2

\((0,1)^T\)

\((0,1)^T\)

0.1

3

\((2,2)^T\)

\((1,1)^T\)

0.8

One sees that \(\mathbf {R}_1(\omega ) \ge \mathbf {R}_2(\omega )\) for all \(\omega \in \Omega \). Let us compute the value of \(\hbox {CCVaR}_{0.2}(\mathbf {R}_1)\):

$$\begin{aligned} \hbox {CCVaR}_{0.2}(\mathbf {R}_1) = \frac{1}{0.2} \Bigl ((1+0)\cdot 0.1 + (0+1)\cdot 0.1\Bigr ) = 1. \end{aligned}$$

In the case of \(\hbox {CCVaR}_{0.2}(\mathbf {R}_2)\), the probability atoms will split due to the fact that the points (1,0), (0,1), and (1,1) lie along the perimeter of the cone (multivariate quantile). Therefore \(\hbox {CCVaR}_{0.2}(\mathbf {R}_2)\) can be obtained as the solution of the following optimization problem:

$$\begin{aligned} \min _{w_1,w_2}&\frac{1}{0.2}\Bigl ( (1+0)\cdot 0.1 w_1 + (0+1) \cdot 0.1 w_2 + (1+1) \cdot 0.8w_1 w_2 \Bigr ) \\ \hbox {s.t.}&0.1 w_1 + 0.1 w_2 + 0.8 w_1 w_2 = 0.2, \\&0 \le w_i \le 1 \quad \hbox {for}\ \, i=1,2. \end{aligned}$$

After solving we get \(\hbox {CCVaR}_{0.2}(\mathbf {R}_2) = 13/9 > 1 = \hbox {CCVaR}_{0.2}(\mathbf {R}_1)\) for either \(w_1 = 1/9\) and \(w_2 = 1\), or \(w_1 = 1\) and \(w_2 = 1/9\). Thus CCVaR is not monotonic. In order to prove the property (iv) we use Proposition 1, the relation (3), and the fact that CVaR is supperadditive when larger outcomes are preferred (see, e.g., Pflug 2000). Therefore we have

$$\begin{aligned} \hbox {CCVaR}_\beta (\mathbf {R}) \ge \hbox {CVaR}_\beta (\mathbf {1}^T \mathbf {R}) \ge \sum _{i=1}^n \hbox {CVaR}_\beta (R_i) = \sum _{i=1}^n \hbox {CCVaR}_\beta (R_i). \end{aligned}$$

\(\square \)

Artzner et al. (1997, 1999) call a risk measure coherent, if it is translation-equivariant, positively homogenous, superadditive, and monotonic. One sees that \(\hbox {CCVaR}_\beta \) is not coherent in this sense, since it is not monotonic.

Let us consider the following special case related to portfolio optimization further discussed in Sect. 5. We are interested in selecting the optimal portfolio of risk components \(R_i\) scaled by portfolio weights \(x_i\), i.e., in maximizing \(\hbox {CCVaR}_\beta (\mathbf {x}\circ \mathbf {R})\), where \(\circ \) is the Hadamard product operator. Under the above assumption the following assertion is valid.

Proposition 3

\(\hbox {CCVaR}_\beta \) is monotonic for linearly scaled random variables, i.e., if

$$\begin{aligned} \mathbf {x}\circ \mathbf {R}(\omega ) \ge \mathbf {R}(\omega ) \hbox { for all } \omega \in \Omega \end{aligned}$$

then

$$\begin{aligned} \hbox {CCVaR}_\beta (\mathbf {x}\circ \mathbf {R}) \ge \hbox {CCVaR}_\beta (\mathbf {R}). \end{aligned}$$

Proof

Note that the assumption can hold only for \(\mathbf {x}=(\mathbf {x}_P,\mathbf {x}_N)^T\), \(\mathbf {x}_P \ge \mathbf {1}\), \(\mathbf {x}_N \le \mathbf {1}\), and \(\mathbf {R}=(\mathbf {R}_P,\mathbf {R}_N)^T\), where \(P\) and \(N\) are index sets defined as follows: \(P = \{i : R_i(\omega ) \ge 0 \hbox {for all } \omega \in \Omega \}\), \(N = \{i : R_i(\omega ) \le 0 \hbox { for all } \omega \in \Omega \}\). It follows from the definition of \(\hbox {CCVaR}_\beta \) that

$$\begin{aligned}&\hbox {CCVaR}_\beta \Bigl ((\mathbf {x}_P,\mathbf {x}_N)^T \circ (\mathbf {R}_P,\mathbf {R}_N)^T\Bigr ) \ge \hbox {CCVaR}_\beta \Bigl ((\mathbf {R}_P,\mathbf {R}_N)^T\Bigr )\\&\qquad \hbox {for any } \mathbf {x}_P \ge \mathbf {1}\hbox { and } \mathbf {x}_N \le \mathbf {1}. \end{aligned}$$

\(\square \)

Hence CCVaR preserves coherency in problems where linear combinations of risk components are considered.

Finally, let us address the issue of accuracy of the measure determined in the computational process for risk components \(R_i\) initially modeled by continuous random variables. We will consider the following approximations of continuous marginal distributions. Let \([a_i, b_i] \supset R_i\), \(i=1,\ldots ,n\) be the closed subsets partitioned with finite sequences \(a_i = t^{(1)}_i < t^{(2)}_i < \cdots < t^{(k)}_i = b_i\) for some \(k \in \mathbb {N}\). We will assume that \(\mathbb {P}[a_i, t^{(j)}_i]= F_{R_i}(t^{(j)}_i)\) for \(1 \le j \le k\). The approximate random variables will be further denoted by \(R^{(k)}\) and random vectors by \(\mathbf {R}^{(k)}\), respectively.

Proposition 4

For approximate random vectors we have the following relations:

$$\begin{aligned}&\hbox {CCVaR}_\beta (\mathbf {R}^{(k)}) \ge \hbox {CCVaR}_\beta (\mathbf {R}) \hbox { for any } k \in \mathbb {N},\\&\hbox {CCVaR}_\beta (\mathbf {R}^{(k)}) \rightarrow \hbox {CCVaR}_\beta (\mathbf {R}) \hbox { when } k \rightarrow +\infty . \end{aligned}$$

Proof

According to the formula (4) we have:

$$\begin{aligned} \hbox {CCVaR}_\beta (\mathbf {R}) = \min _{\mathbf {u}\in \mathcal {U}_\beta } \sum _{i=1}^n \hbox {CVaR}_\beta (R_i, \mathbf {u}). \end{aligned}$$

Note that \(\hbox {CVaR}_\beta (R^{(k)}_i, \mathbf {u}) \ge \hbox {CVaR}_\beta (R_i, \mathbf {u})\) for any \(k \in \mathbb {N}\) due to the fact that \(F_{R^{(k)}_i}^{(-1)}(p) \ge F_{R_i}^{(-1)}(p)\) for all \(p \in (0, 1]\). These two functions coincide when \(k \rightarrow +\infty \). \(\square \)

5 The portfolio optimization model

The portfolio optimization problem considered in this paper is based on a single period model of investment. Let \(\mathbf {x}= (x_1,\ldots ,x_n)^T\) denote a portfolio of assets with \(x_i\) being the position in an asset \(i\). The portfolio \(\mathbf {x}\) belongs to the feasible set \(\mathcal {P}\) which in the simplest form is defined as:

$$\begin{aligned} \mathcal {P}= \biggl \{\mathbf {x}: \ \sum _{i=1}^n x_i = 1, \ x_i \ge 0 \ \hbox {for}\ i=1,\ldots ,n \biggr \}. \end{aligned}$$
(5)

A decision maker usually needs to consider some other requirements expressed as a set of additional side constraints. It is hereafter assumed that \(\mathcal {P}\) is a general polyhedral set given in a linear programming (LP) canonical form as a system of linear equations with nonnegative variables:

$$\begin{aligned} \mathcal {P}= \{\mathbf {x}: \ \mathbf {A}\mathbf {x}= \mathbf {b}, \ \mathbf {x}\ge \mathbf {0}\}, \end{aligned}$$

where \(\mathbf {A}\) is a given \(k \times n\) matrix, and \(\mathbf {b}= (b_1,\ldots ,b_k)^T\) is a given right-hand side vector. The rate of return of each asset is given by a random variable \(R_i\). Let \(\mathbf {R}\) denote a vector of risk components represented by \(R_i\).

Following the seminal work by Markowitz (1952), the portfolio optimization problem is modeled as a mean-risk bicriteria optimization problem. Below we present the most prudent approach to portfolio optimization involving optimization of a risk measure only, which allows one to determine the maximum safety portfolios. Thus, the following portfolio optimization problem will be considered:

$$\begin{aligned} \max \{\hbox {CCVaR}_\beta (\mathbf {x}\circ \mathbf {R}) \ : \ \mathbf {x}\in \mathcal {P}\}. \end{aligned}$$
(6)

Based on the representation (4) and the fact that CVaR is positively homogenous (see, e.g., Pflug 2000), the problem (6) can be rewritten as:

$$\begin{aligned} \max \biggl \{\min _{\mathbf {u}\in \mathcal {U}_\beta } \sum _{i=1}^n x_i \hbox {CVaR}_\beta (R_i, \mathbf {u}) \ : \ \mathbf {x}\in \mathcal {P}\biggr \}. \end{aligned}$$

The above problem for the simplest feasible set (5) leads to the following LP:

$$\begin{aligned} \max _{z,x_i}&z \nonumber \\ \hbox {s.t.}&z \le \sum _{i=1}^n x_i \hbox {CVaR}_\beta (R_i, \mathbf {u}_j) \quad \hbox {for all}\ j:\mathbf {u}_j \in \mathcal {U}_\beta ,\\&\sum _{i=1}^n x_i = 1, \nonumber \\&x_i \ge 0 \quad \hbox {for}\ i=1,\ldots ,n. \nonumber \end{aligned}$$
(7)

This representation is not well defined due to the fact that it uses an infinite number of constraints to model \(\hbox {CCVaR}_\beta \), since \(|\mathcal {U}_\beta | = +\infty \). At the optimum, the variable \(z\) takes the maximum value of \(\hbox {CCVaR}_\beta \). Let us consider the following dual problem associated with the LP (7):

$$\begin{aligned} \min _{v,s_j}&v \nonumber \\ \hbox {s.t.}&v \ge \sum _{j:\mathbf {u}_j \in \mathcal {U}_\beta } s_j \hbox {CVaR}_\beta (R_i, \mathbf {u}_j) \quad \hbox {for}\ i=1,\ldots ,n,\\&\sum _{j:\mathbf {u}_j \in \mathcal {U}_\beta } s_j = 1, \nonumber \\&s_j \ge 0 \quad \hbox {for all}\ j:\mathbf {u}_j \in \mathcal {U}_\beta . \nonumber \end{aligned}$$
(8)

The model (8) consists of an infinite number of variables and \(n+1\) constraints. This structure allows us to solve the problem (8) by column generation algorithm. The pricing subproblem associated with the problem (8) can be stated as:

$$\begin{aligned} \min _{u_i}&\sum _{i=1}^n \pi _i \hbox {CVaR}_\beta (R_i, (u_1,\ldots ,u_n)^T) - \pi _{n+1} \nonumber \\ \hbox {s.t.}&C(u_1, \ldots , u_n) = \beta ,\\&\beta \le u_i \le 1 \quad \hbox {for}\ i=1,\ldots ,n, \nonumber \end{aligned}$$
(9)

where \(\pi _i\) are dual prices determined by (8).

Before we continue with (9), let us recall the CVaR optimization model. The CVaR definition (1) translates into the following optimization problem (Ogryczak and Ruszczyński 2002):

$$\begin{aligned} \hbox {CVaR}_\beta (R) = \max _{\eta \in \mathbb {R}} \Bigl \{ \eta - \frac{1}{\beta } \mathbb {E}(\eta -R)_+ \Bigr \}, \end{aligned}$$

where \((\cdot )_+ = \max \{\cdot ,0\}\). The above problem for a discrete random variable \(R\) represented by its realizations \(r_t\) with probabilities \(p_t\), \(t=1,\ldots ,m\), can be stated as:

$$\begin{aligned} \hbox {CVaR}_\beta (R) = \max _{\eta \in \mathbb {R}} \biggl \{ \eta - \frac{1}{\beta } \sum _{t=1}^{m} \max \{ \eta - r_t, 0 \} p_t \biggr \}. \end{aligned}$$

It corresponds to the following LP:

$$\begin{aligned} \max _{\eta ,d_t}&\eta - \frac{1}{\beta } \sum _{t=1}^{m} d_t p_t \\ \hbox {s.t.}&d_t \ge \eta - r_t,\ d_t \ge 0 \quad \hbox {for}\ t=1,\ldots ,m, \end{aligned}$$

where \(\eta \) is an auxiliary (unbounded) variable. The optimal value of \(\eta \) represents the value of \(\beta \)-quantile of \(R\). This representation uses \(m + 1\) variables and \(m\) constraints to model CVaR.

Coming back to the formulation (9), let us assume that random variables \(R_i\) are represented by the following discrete distributions:

$$\begin{aligned} \mathbb {P}(R_i = \xi ) = \left\{ \begin{array}{ll} p_{i1}, &{} \xi =r_{i1} \\ \ldots , &{} \ldots \\ p_{it}, &{} \xi =r_{it} \\ \ldots , &{} \ldots \\ p_{im}, &{} \xi =r_{im}, \end{array} \right. \end{aligned}$$
(10)

where \(r_{i1} \le \cdots \le r_{it} \le \cdots \le r_{im}\). Let us initially assume that the conditional joint probabilities associated with realizations \(r_{it}\) are correctly given by the values \(q_{it}\). In this case, the constraints in (9) are satisfied and do not need to be taken into account. The problem (9) can be expressed then as the following LP:

$$\begin{aligned} \max _{\eta _i,d_{it}}&\sum _{i=1}^n \pi _i \biggl (\eta _i - \frac{1}{\beta } \sum _{t=1}^{m} d_{it} q_{it} \biggr ) - \pi _{n+1} \nonumber \\ \hbox {s.t.}&d_{it} \ge \eta _i - r_{it},\ d_{it} \ge 0 \quad \hbox {for}\ \;i=1,\ldots ,n \,\hbox { and }\, t=1,\ldots ,m. \end{aligned}$$
(11)

Note that the problem (11) is maximization one as opposed to (9) and the probabilities \(q_{it}\) need to be determined automatically by optimization. Moreover, the above problem is an LP for given probabilities \(q_{it}\), whereas it becomes nonlinear for variable \(q_{it}\). All these difficulties can be overcome by taking advantages of the LP dual to (11):

$$\begin{aligned} \min _{y_{it}}&\sum _{i=1}^n \sum _{t=1}^{m} r_{it} y_{it} - \pi _{n+1} \nonumber \\ \hbox {s.t.}&\sum _{t=1}^{m} y_{it} = \pi _i \quad \hbox {for}\ \, i=1,\ldots ,n, \\&0 \le y_{it} \le \frac{\pi _i q_{it}}{\beta } \quad \hbox {for}\ \;i=1,\ldots ,n\, \hbox { and }\, t=1,\ldots ,m. \nonumber \end{aligned}$$
(12)

We can extend the problem (12) with the set of constraints that allow us to determine the probabilities \(q_{it}\):

$$\begin{aligned} \min _{y_{it}, q_{it}, u_i}&\sum _{i=1}^n \sum _{t=1}^{m} r_{it} y_{it} - \pi _{n+1} \nonumber \\ \hbox {s.t.}&\sum _{t=1}^{m} y_{it} = \pi _i \quad \hbox {for}\ \;i=1,\ldots ,n, \nonumber \\&0 \le y_{it} \le \frac{\pi _i q_{it}}{\beta } \quad \hbox {for}\ i=1,\ldots ,n\, \hbox { and }\, t=1,\ldots ,m,\\&C(u_1, \ldots , \sum _{j=1}^t p_{ij}, \ldots , u_n) - \sum _{j=2}^t q_{i,j-1} = q_{it} \nonumber \\& \quad \hbox {for}\ \; i=1,\ldots ,n \,\hbox { and }\, t=1,\ldots ,m, \nonumber \\&C(u_1, \ldots , u_n) = \beta , \nonumber \\&\beta \le u_i \le 1 \quad \hbox {for}\ \; i=1,\ldots ,n. \nonumber \end{aligned}$$
(13)

Now the problem (13) corresponds to the pricing subproblem (9) for random variables \(R_i\) represented by the discrete distributions (10). At the optimum, the variables \(u_i\) take the values of cumulative distribution functions \(F_{R_i}\). Note that the above model is no longer LP due to the nonlinearity and non-convexity of a copula function \(C\). If the value of the objective function is less than 0, then the optimal values of \(\frac{1}{\pi _i}\sum _{t=1}^{m} r_{it} y_{it}\) represent the coefficients \(\hbox {CVaR}_\beta (R_i,\mathbf {u}_j)\) of the \(j\)-th column to be inserted to the restricted master problem (8) of column generation algorithm. Otherwise the initial optimization problem (7) is solved. In the latter case the optimal portfolio weights are represented by the coefficients \(\pi _i\), whereas the optimal value of \(\hbox {CCVaR}_\beta \) is represented by the coefficient \(\pi _{n+1}\).

6 The approximate portfolio optimization algorithm

Column generation algorithm requires a solution of the pricing subproblem (13) which is difficult to solve due to the nonlinearity and non-convexity of a copula function \(C\). We need a heuristic that will allow us to efficiently solve the CCVaR portfolio optimization problem (8). Let us rewrite the initial pricing subproblem (9):

$$\begin{aligned} \min _{u_i}&\sum _{i=1}^n \pi _i \hbox {CVaR}_\beta (R_i, (u_1,\ldots ,u_n)^T) - \pi _{n+1} \nonumber \\ \hbox {s.t.}&C(u_1, \ldots , u_n) = \beta ,\\&\beta \le u_{\tau (i)} \le 1 \quad \hbox {for}\ i=1,\ldots ,n. \nonumber \end{aligned}$$
(14)

The last \(n\) constraints are ordered by \(\pi _i\) in non-ascending order represented by a permutation \(\tau \) of the index set \(\{i: 1,\ldots ,n\}\). The constraints of the problem (14) have to be satisfied.

Let us consider the following auxiliary optimization problem:

$$\begin{aligned} \min _{u_i}&(C(u_1,\ldots ,u_n) - \beta )^2 \nonumber \\ \hbox {s.t.}&\beta \le u_{\tau (i)} \le \min \{b(i),1\} \quad \hbox {for}\ \; i=1,\ldots ,n. \end{aligned}$$
(15)

When the objective function of the problem (15) attains the value of zero, the level of a quantile is equal to \(\beta \). Our goal is to find a vector \(\mathbf {u}^\star = (u_1,\ldots ,u_n)^{T}\) for which the value of the objective function of the problem (14) is negative and as small as possible. The vector \(\mathbf {u}^\star \) can be found through the iterative solution of the problem (15) with the values of \(b(i)\) given by the heuristic formula:

$$\begin{aligned} b(i)=\beta +shift+slope\frac{(bulge^{i-1}-1)(1-\beta )}{bulge^{n-1}-1}, \end{aligned}$$
(16)

where \(\textit{shift}\), \(\textit{slope}\), and \(\textit{bulge}\) are random parameters. For given sets of parameters \(\textit{shift} \ge 0\), \(slope \ge 0\), and \(\textit{bulge} > 0\), \(\textit{bulge} \ne 1\), we obtain various values of \(b(i) \ge \beta \), as presented in Fig. 2, and different vectors \(\mathbf {u}\) at the optimum.

Note that the upper bounds in (15) defined by the function (16) ensure that the largest \(\pi _i\)-s in (14) representing nonnegative portfolio shares receive the smallest weights given by \(\hbox {CVaR}_\beta (R_i, \mathbf {u})\). For \(\mathbf {u}^\star \) the value of the objective function of the problem (14) approximates the minimum.

In order to determine the value of the objective function of the problem (14) we need to calculate the values of \(\hbox {CVaR}_\beta (R_i, \mathbf {u})\). The procedure that calculates the single value of \(\hbox {CVaR}_\beta (R_i, \mathbf {u})\) for a random variable \(R_i\) represented by the discrete distribution (10) is summarized in Algorithm 1.

Fig. 2
figure 2

Values of \(b(i)\) for \(\beta = 0.1\) and three different sets of parameters shift, slope, and bulge

Full size image
figure a

The above way of solving the initial pricing subproblem (9) does not guarantee achieving the optimal result of the problem (7). But surely the calculated value is the upper bound of the optimal value of the problem (7), which follows from the fact that we solve its dual formulation (8). Below is the complete approximate algorithm for CCVaR portfolio optimization.

The approximate algorithm for CCVaR portfolio optimization

  • Step 1 Create \(i=1,\ldots ,n\) initial vectors \(\mathbf {u}_i=(1,\ldots ,\beta ,\ldots 1)^T\) with \(\beta \) placed on the \(i\)-th position. Compute values of \(\hbox {CVaR}_\beta (R_i, \mathbf {u}_i)\) using Algorithm 1 and set up the restricted master problem (8).

  • Step 2 Solve the restricted master problem (8) in order to determine the dual prices \(\pi _i\).

  • Step 3 Determine the values of the objective function of the problem (14) for several different vectors \(\mathbf {u}\). Retain the smallest value of the objective function along with the corresponding values of \(\hbox {CVaR}_\beta (R_i, \mathbf {u})\) to be further inserted to the restricted master problem (8) as a new column. In order to solve the problem (14), perform the following steps:

    1. 1.

      Get a vector of \(\mathbf {u}\) by solving the auxiliary optimization problem (15) for assumed values of shift, slope, and bulge.

    2. 2.

      Determine the value of the objective function of the problem (14) using Algorithm 1.

  • Step 4 If the smallest value of the objective function of the problem (14) obtained in Step 3 is negative, insert a new column to the restricted master problem (8) and go to Step 2. Otherwise the optimal value of \(\hbox {CCVaR}_\beta \) is represented by the coefficient \(\pi _{n+1}\), wheras the optimal portfolio weights are represented by the coefficients \(\pi _i\).

7 Computational results

The computational analysis has been conducted using the approximate algorithm for CCVaR portfolio optimization, as described in the previous section, and the CVaR dual LP portfolio optimization model developed by Ogryczak and Śliwiński (2011). Both approaches correspond to each other, since they allow one to determine the maximum safety portfolios. The CVaR dual portfolio optimization model for a random vector \(\mathbf {R}\) represented by the discrete distribution

$$\begin{aligned} \mathbb {P}(\mathbf {R}= \mathbf {r}) = \left\{ \begin{array}{ll} p_1, &{} \mathbf {r}=(r_{11},\ldots , r_{i1} ,\ldots ,r_{n1})^T \\ \ldots , &{} \ldots \\ p_t, &{} \mathbf {r}=(r_{1t},\ldots , r_{it} ,\ldots ,r_{nt})^T \\ \ldots , &{} \ldots \\ p_m, &{} \mathbf {r}=(r_{1m},\ldots , r_{im} ,\ldots ,r_{nm})^T \end{array} \right. \end{aligned}$$

takes the following form:

$$\begin{aligned} \min _{v,s_t}&v \nonumber \\ \hbox {s.t.}&v - \sum _{t=1}^m r_{it} s_t \ge 0 \quad \hbox {for}\ \; i=1,\ldots ,n,\\&\sum _{t=1}^m s_t = 1, \nonumber \\&0 \le s_t \le p_t/\beta \quad \hbox {for}\ \; t=1,\ldots ,m. \nonumber \end{aligned}$$
(17)

In the above formulation \(r_{it}\) denotes the rate of return of the \(i\)-th asset for the realization \(t\) of the random vector \(\mathbf {R}\), \(p_t\) denotes the probability of the realization \(t\), \(\beta \) denotes the tolerance level of CVaR. The dual prices associated with the constraints (17) correspond to optimal portfolio shares. Note that the above model contains \(m\) constraints that take the form of simple upper bounds (SUB) on \(s_t\) thus not affecting the problem complexity. Actually, the number of constraints in (17) is proportional to the total number of assets \(n\), thus it is independent from the number of realizations \(m\) of the random vector \(\mathbf {R}\). Exactly, there are \(m+1\) variables and \(n+1\) constraints. This guarantees a high computational efficiency of the model even for a very large number of realizations of the random vector \(\mathbf {R}\).

A PC with a 2 GHz Intel Core Duo processor and 2 GB RAM has been used to run an application written in Matlab by using the Global Optimization Toolbox and the IBM ILOG CPLEX optimizer version 12.2. The computations have been conducted for the following marginal distributions: log-normal, Gaussian, and Student’s \(t\) with 4 degrees of freedom. The values of realizations have been limited to the range \([-1, 3]\) so as to cover the typical asset returns. The distributions had different expectations and standard deviations.

CCVaR has been calculated for the parameter \(\beta \in \{0.01,\,0.1\}\) and the following copula functions: Clayton, Frank, and Gumbel. The marginal distributions have been approximated by discrete distributions with 100 and 500 realizations. The pricing subproblem has been evaluated 15 times in each iteration of column generation algorithm. In turn CVaR has been calculated for identical betas and 100,000 random variates drawn from the considered discrete multivariate distributions. Both measures have been used to determine optimal portfolios for 10 and 100 assets.

The results of CCVaR optimization for log-normal marginal distributions are shown in Table 1. Table 1 consists of ten columns showing: the name and the parameter \(\theta \) of a copula function, the parameter \(\beta \) of a risk measure, the number of assets (\(n\)), the number of realizations of a marginal distribution (\(m\)), the value of CCVaR, the portfolio diversification (div.), the maximum and minimum share within the portfolio, and the computation time in seconds. Similar results are presented in Table 2 for CVaR. The results for CVaR are averages computed over 50 estimations. The results for Gaussian and Student’s \(t\) distribution for both measures are reported in Appendix.

Table 1 CCVaR optimization results for log-normal marginal distributions
Full size table
Table 2 CVaR optimization results for log-normal marginal distributions
Full size table

Analyzing the results one may observe that they are not consistent with Proposition 1. We have got an opposite relation, i.e.,

$$\begin{aligned} \text {CCVaR}_{\beta }(\mathbf {R}) < \text {CVaR}_{\beta }(\mathbf {1}^{T}\mathbf {R}). \end{aligned}$$

Note that the approximate algorithm for CCVaR portfolio optimization computes the upper bound of \(\hbox {CCVaR}_\beta \). Thus, the actual values of \(\hbox {CCVaR}_\beta \) could have been even lower than those reported. Moreover, according to Proposition 4 the above relation is not caused by the discretization of continuous marginal distributions. Sparse discretization would increase the value of \(\hbox {CCVaR}_\beta \) as one can observe for \(n=100\) and \(m \in \{100,\,500\}\). The above relation follows from the fact the CVaR underestimates risk, since its calculation is based on an insignificant amount of information. Due to the computational limitations of the CVaR dual portfolio optimization model, only 100,000 discrete realizations have been taken from multivariate distributions consisting of \(m^n\) realizations, where \(m\in \{100,\,500\}\) and \(n \in \{10,\,100\}\). In order to experimentally show the validity of Proposition 1, additional tests have been carried out for smaller problems with \(n = 5\) and \(m = 10\) covering all the discrete realizations of a multivariate random variable. The results presented in Table 3 show that in this case the relation between measures is consistent with Proposition 1.

Table 3 CVaR and CCVaR optimization results for \(n = 5\) and \(m = 10\)
Full size table

Another observation is an excessive diversification of CVaR portfolios, which is not the case for CCVaR. For each multivariate distribution the mean diversification of CVaR portfolios is almost 100 %.

The computation time has also been taken into account as an important performance criterion. The CCVaR optimal portfolios for the largest tested multivariate distributions (\(n=100\) and \(m=500\)) have been determined in 3.5 min on average. The computation time for all the tested CCVaR models never exceeded 12 min.

8 Concluding remarks

In this paper, we presented an analytic model for the optimization of a portfolio of risks based on prudent and complete stochastic information. The model uses a copula-based extension of CVaR. CVaR gained popularity in many practical applications, because it is coherent and, as a downside risk measure, allows one to emphasize the consequences of more pessimistic scenarios. In portfolio selection problems, CVaR leads to linear programming optimization models. In typical real life problems, the high computationally efficient formulations of these models can account only for a small amount of information upon which decisions are made, and consequently, they may be far from being optimal. CCVaR solves this problem as it allows one to efficiently determine the optimal portfolio of risks based on the full information carried by a multivariate random variable.