1 Introduction

Adequate representation of land-surface heterogeneity effects in numerical models is of vital relevance for the quantification of land-surface processes and their interaction with the atmospheric boundary layer (ABL). The air-surface exchange is characterized by the turbulent fluxes of energy, momentum, and water vapour. Heterogeneities associated with surface parameters like albedo, soil moisture, roughness length, and vegetation cover have great influence on near-surface values of temperature, humidity and wind as well as on ABL structure and cloud formation (Giorgi and Avissar 1997). While the coupling between atmosphere and underlying surface is well known for homogeneous surface conditions (e.g. Stull 1988), the situation is more complicated for heterogeneous terrain. Several field experiments have been carried out over heterogeneous land surfaces on different scales and climate regions (e.g., HAPEX Andre et al. 1986, FIFE Sellers et al. 1988, EFEDA Bolle 1993, LITFASS Beyrich et al. 2002). A main task of the experiments was the estimation of area-averaged surface parameters and fluxes from measurements.

Ground-based measurements are a common method for the determination of surface fluxes. However, for heterogeneous conditions the construction of area-averages would require flux data for all relevant vegetation, terrain, and soil characteristics in the study area, which are difficult to obtain. Airborne measurements provide the opportunity to measure area-representative fluxes directly, but flight campaigns are very expensive and have the disadvantage of being available only for limited time periods. While some studies report the underestimation of airborne fluxes compared to ground-based fluxes (e.g. Betts et al. 1990; Grunwald et al. 1996), other authors do not find systematic discrepancies (Desjardins et al. 1992; Bange et al. 2002).

Mesoscale modelling with high spatial resolution can be used as an additional method to study the air-surface exchange. The main advantage is the continuous calculation of variables with high temporal and spatial resolution, thus enabling the area-integrated estimation of parameters and energy fluxes. On the other hand, processes at sub-grid scale have to be parameterized. This may yield some uncertainties e.g., regarding the arithmetic averaging of parameters in contrast to the non-linear character of microscale processes (i.e., aggregation effect). In addition, it is difficult to obtain a detailed and adequate initial-state description of various soil properties (e.g., soil moisture, albedo, and leaf area index) for large complex areas. Thus, a validation of models against measurements is essential. Several studies show the influence of the resolution of surface heterogeneity on energy fluxes (e.g., Mölders and Raabe 1996; Shao et al. 2001). They concluded that the use of a high model resolution is important to reduce aggregation effects. Furthermore, this enables a better comparison to e.g., airborne measurements. There are different methods to validate models against measurements, ranging from the direct comparison of single-grid points to the calculation of energy budgets. The latter method has the main advantage of not being restricted to the ground level, thus integrating the energy processes for the whole ABL. Energy budgets from airborne measurements have been calculated by a number of authors and feature satisfying results (Kerschgens and Hacker 1985; Betts et al. 1990; Grunwald et al. 1996; Maurer and Heinemann 2006).

In the present study, we perform a model validation based on energy budgets with special focus on model resolution aspects. For that purpose, we compare the moisture and heat budgets from high-resolution simulations with the mesoscale model FOOT3DK against corresponding aircraft budgets. The airborne measurements were performed over heterogeneous terrain in Western Germany for 5 days in April and August 2009 under convective synoptic conditions. The “FLUXPAT” flight campaigns have been carried out in the framework of the project TR32 (Transregional Collaborative Research Centre 32), which investigates the influence of heterogeneous surface characteristics on air-surface exchange processes for different temporal and spatial scales.

The model validation via energy budgets has two main objectives. The first is to study the moisture and heat budgets from model simulations and airborne measurements. In particular, we aim at identifying which terms agree well and for which processes the model may exhibit discrepancies. Secondly, we consider simulations with different horizontal grid sizes to assess the effects of model resolution on the individual budget terms.

2 Model and measurement data

2.1 FOOT3DK model

The mesoscale non-hydrostatic model FOOT3DK (flow over orographically structured terrain 3-dimensional, Kölner version) is a prognostic flow model developed at the Institute of Geophysics and Meteorology, University of Cologne. Originally designed for simulations in the atmospheric boundary layer, the current version is able to simulate the entire troposphere. The model is suitable for simulations over complex terrain in a range from mesoscale γ (~10 km) down to microscale α (~100 m). It has been used for applications in different climatic regions (tropics, mid-latitudes, Arctic) for simulation of atmospheric flow, dispersion, and air-surface exchange (e.g., Brücher et al. 2001; Shao et al. 2001; Heinemann and Kerschgens 2005; Maurer and Heinemann 2006; Pinto et al. 2009; Reyers et al. 2011).

An overview of the basic model characteristics and parameterizations is presented in Table 1, further details of the model can be found in e.g., Brücher et al. (2001) and Shao et al. (2001). The primitive equations are solved on terrain-following η-coordinates for an Arakawa-C grid. For the advection of scalar quantities and momentum a quasi-monotone semi-Lagrange scheme is used (Bermejo and Staniforth 1992).

Table 1 Basic features of the model FOOT3DK as used for the budget simulations
Full size table

The land-surface scheme is based on the interface soil-biosphere atmosphere (ISBA) scheme by Noilhan and Planton (1989), which includes the treatment of soil moisture content for two soil layers. Calculation of soil temperature is done via the extended force restore method following Jacobsen and Heise (1982). The empirical soil hydraulic properties are described by Clapp and Hornberger (1978). Turbulent fluxes in the atmospheric layers are calculated by a 1½ closure following the level 2.5 formulation of Mellor and Yamada (1982). At the surface the energy budget is given by

$$ G - Q - H - LE = 0 $$
(1)

The ground flux G is calculated as residual of the net radiation Q, sensible heat flux H, and latent heat flux LE, and thus contains the storage of energy. The sensible heat flux is given by

$$ H = \rho_{a} c_{p} C_{H} V_{a} (\theta_{s} - \theta_{a} ), $$
(2)

where ρ a is the density of air, c p the specific heat of air at constant pressure, C H the drag coefficient for heat, V a the wind speed of the lowest atmospheric layer, and θ s and θ a the surface and air potential temperatures. The drag coefficient C H is expressed from Monin–Obukhov similarity theory, using an analytic approximation function according to Louis (1979). The latent heat flux LE includes the direct evaporation from fractional open water surfaces and from bare ground E g, the evaporation from intercepted leaf water E r and the transpiration of the plants E tr:

$$ E_{\text{g}} = (1 - \sigma_{\text{f}} )\rho_{\text{a}} \frac{{(h_{\text{u}} q_{\text{sat}} (T_{\text{s}} ) - q_{\text{a}} )}}{{r_{\text{a}} }}, $$
(3)
$$ E_{\text{r}} = \sigma_{\text{f}} \rho_{\text{a}} \frac{\delta }{{r_{\text{a}} }}(q_{\text{sat}} (T_{\text{s}} ) - q_{\text{a}} ), $$
(4)
$$ E_{\text{tr}} = \sigma_{\text{f}} \rho_{\text{a}} \frac{1 - \delta }{{r_{\text{a}} + r_{\text{s}} }}\left( {q_{\text{sat}} (T_{\text{s}} ) - q_{\text{a}} } \right). $$
(5)

These three fluxes are dependent on the potential evaporation q sat(T s) − q a, where q sat(T s) is the saturation specific humidity at surface temperature T s and q a the specific humidity in the lowest atmospheric layer, and the aerodynamic resistance r a = C −1H V −1a . The factors h u and δ describe the influence of soil and plant water content, and σ f denotes the fraction of vegetation cover. The transpiration rate E tr is additionally dependent on the bulk stomatal resistance r s.

The initial and boundary atmospheric conditions for the FOOT3DK simulations are obtained from COSMO-DE analyses with a horizontal resolution of 2.8 km (Baldauf et al. 2011). COSMO-DE is a non-hydrostatic operational weather prediction model, originally developed by the German Weather Service (Steppeler et al. 2003). Using a triple one-way nesting procedure, FOOT3DK resolutions of 1,000, 250, and 100 m are realized. While the general atmospheric conditions are prescribed by the COSMO-DE simulations, the high-resolution FOOT3DK simulations are used to improve the estimation of turbulent surface fluxes over heterogeneous underground.

Surface properties are determined according to soil types and land-use classes. The dominating soil type in the investigation area is loam and we use a land-use classification based on ASTER satellite data of 2009 with a horizontal resolution of 15 m (Waldhoff 2010). For the purposes of our study we integrated the originally 22 classes to eight classes. The orography was taken from the global digital Shuttle Radar Topography Mission (SRTM) atlas, which contains remote sensing information of the earth surface of the year 2000 and features a resolution of 90 m (van Zyl 2001).

Considering sub-grid scale land-surface heterogeneities, an “effective parameter” approach is used (e.g., Arain et al. 1996): for each model grid cell, the surface parameters are averaged according to the fractional coverage of the land-use types. While for coarse resolutions this approach may feature some inaccuracies due to the non-linear character of microscale processes, for high resolutions it is suitable, since large parts of the heterogeneity are resolved directly.

In general, model grid size has an important influence on the parts of the atmospheric fluxes that are parameterized or explicitly resolved. This means that increased resolutions (smaller grid meshes) lead to reduced sub-grid fluxes and enhanced resolved fluxes. On the other hand, no fluxes are resolved in the surface layer (zero wind speeds in the lowest model layer). Due to the Monin–Obukhov similarity approach in the lowest model layer, the surface fluxes show no such dependence on model resolution, thus containing motions of all scales. Therefore, we will here use only fluxes from the lowest model layer for comparison with measured/observed fluxes, as well as for comparison between simulations with different resolutions.

2.2 Measurements

Airborne measurements were performed by the Swiss MetAir atmospheric research aircraft Dimona, which is instrumented with state-of-the-art sensors for the determination of numerous atmospheric variables and parameters. Derived data used in this study include the 3D wind vector (post-processed from attitude and velocity reference system, Oxford technical solutions, OXS RT3102, Great Britain), air temperature (Meteolabor thermocouple, Switzerland), pressure (Keller, capacitive sensors, Switzerland), humidity (LICOR, LI-7500, USA), and height above ground (RIEGL, Laser altimeter LD90-3300HR, Austria). All meteorological data were stored together with the position, speed, and acceleration of the aircraft with a rate of 10 Hz. Taking into account an average aircraft speed of 50 m s−1, this corresponds to a horizontal measurement scale of 5 m. Further information regarding the aircraft equipment can be found in Neininger et al. (2001).

At the beginning and the end of the flights vertical ascents were flown to provide profiles of potential temperature and specific humidity to determine the height of the boundary layer. In addition, radiosonde soundings (GRAW radiosondes DFM-06, Germany) were carried out in the investigation area in order to monitor the temporal development.

3 Methods

3.1 Investigation area and experimental set-up

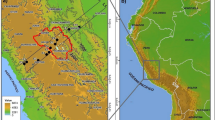
The investigation area is located in the Rur catchment in Western Germany, about 40 km west of Cologne. The area is characterized by heterogeneous terrain with predominantly agricultural land use and the river Rur crossing the domain from south to northwest (Fig. 1). The FLUXPAT 2009 campaign comprises two flight periods (April 20–24, August 5–6/18–19), which cover the main growing season of the prevailing land-use types, winter wheat, and sugar beet. From all field experiment days, 5 days with suitable weather conditions, i.e., undisturbed synoptic conditions without high cloud cover or strong external forcing, were selected (Table 2). While in April the wheat fields exhibit active growing characteristics, the sugar beet fields consist of nearly bare soil (vice versa in August).

Fig. 1
figure 1

Investigation area with land-use types (shaded, see colour bar), flight pattern (blue line) and starting point of radiosonde soundings (FZ Juelich)

Full size image
Table 2 Flight data for FLUXPAT experiments
Full size table

The typical flight pattern was a hexagon with an extent of about 7 × 7 km². This pattern was repeated several times on each day at approximately 130 m AGL (above ground level), and the runs were made between morning and noon. Since the investigation area is situated between two open-cast mines (grey shaded in Fig. 1), the execution of a larger flight pattern was not possible. On approach and departure of the measurement area the airplane performed vertical ascents to heights of up to 3.5 km well above the boundary layer. In addition, hourly radiosonde soundings were started near the northern boundary of the study area at station “FZ Juelich”.

The FOOT3DK model simulations are run with horizontal resolutions of 1,000, 250, and 100 m (F1000, F250, F100) and a vertical resolution of 21 layers within 5,000 m. The model domains are 24 × 23, 50 × 48, and 95 × 90 grid points, respectively, with each domain covering the flight pattern. Due to the model spin-up time of 1 hour, the simulations are started 1 hour later per model nesting (F1000, F250, F100 at 01, 02, 03 UTC, respectively). Therefore, the output values are used for all simulation starting 04 UTC. All model results in chapter 4 are based on F100 simulations. In chapter 5, F1000 and F250 simulations are taken into account additionally to assess the effects of different horizontal resolution.

3.2 Energy budgets

According to thermodynamic theory, the overall energy of a system can be changed only by energy transitions through the boundaries of the system. Therefore, the budget equation for a conserved scalar S can be written as follows (e.g., Betts et al. 1990):

$$ \frac{{\partial \overline{S} }}{\partial t} + \overline{u} \frac{{\partial \overline{S} }}{\partial x} + \overline{v} \frac{{\partial \overline{S} }}{\partial y} + \overline{w} \frac{{\partial \overline{S} }}{\partial z} + \frac{{\partial (\overline{{u^{ '} S^{ '} }} )}}{\partial x} + \frac{{\partial (\overline{{v^{ '} S^{ '} }} )}}{\partial y} + \frac{{\partial (\overline{{w^{ '} S^{'} }} )}}{\partial z} = 0 $$
(6)

Here u, v, and w are the horizontal and vertical wind speeds along the corresponding x, y, and z directions. Equation (6) consists of a local temporal change term, advection terms, and divergence terms of eddy transports. Since the horizontal divergences of the turbulent fluxes are small compared with the vertical ones, they can be neglected. Similar findings are valid for the vertical advection (Desjardins et al. 1988). Thus, (6) may be written for specific humidity q and potential temperature θ as follows:

$$ \frac{{\partial \overline{q} }}{\partial t} + \overline{u} \frac{{\partial \overline{q} }}{\partial x} + \overline{v} \frac{{\partial \overline{q} }}{\partial y} + \frac{{\partial (\overline{{w^{ '} q^{ '} }} )}}{\partial z} = 0 $$
(7)
$$ \frac{{\partial \overline{\theta } }}{\partial t} + \overline{u} \frac{{\partial \overline{\theta } }}{\partial x} + \overline{v} \frac{{\partial \overline{\theta } }}{\partial y} + \frac{{\partial (\overline{{w^{ '} \theta^{ '} }} )}}{\partial z} = 0 $$
(8)

Following (7) and (8), the local moistening rate is controlled by the divergence of latent heat flux and the horizontal advection of moisture, and the local heating is determined by the divergence of sensible heat flux and the horizontal advection of heat (note that for the θ budget the divergence of net radiation was also neglected).

3.3 Estimation of budget terms

Turbulent fluxes derived from the airborne measurements are solely available for one flight level. To determine the surface fluxes and the vertical divergence of fluxes, we require flux estimates for at least one more vertical level. Therefore, we additionally assess the fluxes at the inversion height, which means that we calculate energy budgets for the entire depth of the boundary layer. Furthermore, the general assumption is made that time trends and advection terms of the flight level are representative for the whole ABL.

The individual budget terms are estimated from airborne measurements as follows: regarding the temporal change terms, the averages of specific humidity and potential temperature are calculated for each complete round of the flight pattern (Fig. 1), thus enabling the assessment of a linear time trend. Turbulent fluxes at flight level were calculated with the eddy-covariance method for each round of the flight pattern separately. Average round length was about 23 km, but only detrended data from the straight flight parts (summing up to 21 km) have been used to derive the fluxes. All signals are sampled at 10 Hz and high-pass filtered at 0.007 Hz. This sampling corresponds to spatial scales from about 5 m to 7 km at an average aircraft speed of 50 m s−l. The cut-off filter length L of 7 km was chosen to minimize the variability from run to run and in order to obtain representative fluxes for the study area, which has a diameter of 7 km. An additional reason for applying this filter length is the comparison with modelled surface fluxes. These fluxes show a good agreement with surface fluxes from ground-based eddy-covariance station data (Reyers et al. 2011), which also use a cut-off filter length of about 7 km (fluxes calculated from 30 min time intervals with an average wind speed of 3.6 m s−1).

Obviously, the resulting airborne fluxes contain not only turbulent motions (<1 km), but also large eddy and mesoscale motions (for a classification see e.g., Sun et al. 1996). The comparison of fluxes calculated with different values of L (Table 3) shows that the fluxes decrease if the filter lengths are reduced, because only smaller scale motions are taken into account (see also Sect. 2.1). For e.g., a filter length of 1 km only considers turbulent motions and leads to fluxes reduced by 26 % if compared to the 21 km filter of the complete flight round. Nevertheless, applying the 7 km filter results only in a minimal reduction of the fluxes (3 %), so we feel confident to use this value of L for calculation of airborne fluxes. Finally, even though the fluxes calculated with the 7 km filter contain also mesoscale and large eddy motions, they are dominated by turbulent motions and therefore will be called turbulent fluxes, which is in line with the nomenclature used by other authors (e.g., Desjardins et al. 1986; Maurer and Heinemann 2006).

Table 3 Mean values of airborne latent and sensible heat flight level fluxes (average of five investigation days) for different cut-off filter lengths L of 21, 7, 3.5, 2, and 1 km. The values in brackets denote the deviation of the individual fluxes from the L = 21 km flux value in percentage
Full size table

For the turbulent divergence term three quantities are required: the surface fluxes, the inversion level fluxes, and the depth of the ABL. The ABL depth is estimated from flight profiles and hourly radiosonde soundings. For the simultaneous determination of surface and inversion level fluxes we use an iterative procedure. Given the flight level fluxes in a first step the surface fluxes are assessed via extrapolation of the flight level fluxes to the ground (first guess: vanishing inversion level fluxes). Furthermore, a linear gradient of the turbulent fluxes within the ABL is assumed for well-mixed boundary layer conditions (e.g., Garratt 1992; Kaimal and Finnigan 1994). Assuming that the virtual heat flux at inversion top is proportional to the surface virtual heat flux, the turbulent sensible and latent heat fluxes at the inversion level H i and LE i are derived by a dry mixed-layer model approach according to Betts et al. (1990) using the Bowen ratios at the surface (β sfc) and inversion height (β i):

$$ {{H}}_{\text i} = - k\;H_{\text{sfc}} \frac{{1 + 0.073/\beta_{\text {sfc}} }}{{1 + 0.073/\beta_{\text i} }} $$
(9)
$${LE}_{\text i} = H_{\text i} /\beta_{\text i} $$
(10)

Following (9) and (10), we require the ratio k of surface and inversion height virtual heat flux, and the surface fluxes H sfc and LE sfc. As suggested by experimental data (e.g., Stull 1976) and LES simulations (e.g., Ament and Simmer 2006), the proportional factor is chosen as k = 0.2. The Bowen ratio at the inversion height was estimated from radiosonde soundings by calculating the slope of ∂θ/∂q across the capping inversion. Subsequently, we can use the obtained inversion level fluxes to renew the extrapolation of the surface fluxes and so on. Finally, the iteratively obtained fluxes for the individual flight runs are averaged to a daily mean. However, this correction did not alter the extrapolated surface fluxes substantially because the flight level fluxes were measured close to the surface in comparison to the boundary layer height.

Regarding the calculation of horizontal advection, a large dimension of the flight pattern would be favourable. For e.g., Betts et al. (1990) used a 15 × 11 km2 box, but stated high advection uncertainties and recommended the application of larger patterns. As an extended flight pattern was not possible (see Sect. 3.1), we determine the advection terms indirectly as residua of the budget equations.

To enable a precise comparison between FOOT3DK simulations and measurements, we compute the budget terms in the same way as for the airborne data, restricting the data base to the flight pattern and level. Hence, we estimate the temporal rates of change from the fifth model level (136 m above ground). Furthermore, we use only model grid meshes covered by the flight pattern. Solely the assessment of vertical divergence undergoes a slight change (compared with the flight data approach): the turbulent fluxes are taken directly from the surface instead of extrapolating the atmospheric values to the ground.

The estimation of errors is an important task, since it gives evidence regarding the reliability of results. In the present study, the uncertainty of the local time trend is determined as statistical slope error (e.g., Wilks 1995). The uncertainties of the surface fluxes and flux divergences are estimated as standard deviation of the detrended values of the individual flight runs and the advection residua errors are calculated using Gaussian error propagation. Even though the errors are estimated in a simple way, they provide an opportunity to assess which terms of the budget are well known and which terms show a high uncertainty.

4 Results

4.1 General synoptic characteristics

An overview of the basic synoptic conditions from Dimona airborne measurements and F100 simulations is given in Table 4. Specific humidity, potential temperature, wind direction, and wind speed are averaged over the flight period of each day to obtain a mean value. Regarding specific humidity and potential temperature, the simulations deviate less than 1 g kg−1 and 1 K from the measurements. The mean wind matches well: while maximum wind direction differences are about 10°, the corresponding wind speed deviations are 1 m s−1 (with the exception of April 24, where the wind speed is underestimated by 2 m s−1). The latter can be attributed to the mesoscale COSMO-DE forcing, which has strong influence on the FOOT3DK simulations. Nevertheless, the general synoptic conditions obtained by model simulations and airborne observations agree well, thus indicating that the model is able to reproduce the general features of the boundary layer adequately.

Table 4 Mean values of specific humidity, potential temperature, wind direction, and wind speed on April 20, 21, 24 and August 5, 18 (2009) from Dimona airborne measurements (first value) and F100 model simulations (second value)
Full size table

Furthermore, vertical profiles of specific humidity and potential temperature are considered to assess the depth of the boundary layer. As an e.g., the profiles of atmospheric moisture and potential temperature from radiosonde sounding, airborne flight and F100 simulation are shown for April 20 noon (Fig. 2). Even though the simulation is able to reflect the general characteristics of the profiles, the upper limit of the ABL and the inversion level are not displayed as sharply as in the measured profiles, making the determination of ABL depth from the simulation profile difficult. Furthermore, the inversion level fluxes are independent from the magnitude of the surface fluxes and are always very small (not shown). Such behaviour is typical for mesoscale models and may be attributed to the coarse vertical resolution at the top of the ABL (Ament 2006). Therefore, we use the measured ABL depths and inversion level fluxes for the calculation of the vertical divergence term for both measurements and model simulations.

Fig. 2
figure 2

Vertical profiles of specific humidity (left) and potential temperature (right) on April 20, 2009 noon from three different sources: airborne measurements (red), radiosonde observations (black) and F100 simulation (blue diamonds)

Full size image

4.2 Temporal rate of change

The temporal rates of change are calculated from the individual flight run averages and the corresponding F100 simulation time periods (same atmospheric level as the measurements). Figure 3 shows the temporal development for specific humidity and potential temperature on April 20. The atmospheric moisture is slightly underestimated by the model at the beginning of the flight, but later it matches the observed value, leading to a reduced negative time trend of specific humidity. Regarding potential temperature, results are slightly heterogeneous: while the simulation exhibits a persistent overestimation of the absolute θ values by about 0.8 K, the time trend is matched accurately.

Fig. 3
figure 3

Temporal development of specific humidity (upper panel) and potential temperature (lower panel) on April 20, 2009 from two different sources: airborne measurements (red squares) and F100 simulation (blue diamonds). Red and blue lines reflect the linear fits to the data

Full size image

An overview of the temporal rates of change for specific humidity and potential temperature is given in Table 5. For all investigation days in April and August 2009, the presumption of linear time trends proved to be realistic. As can be seen, a reduction of atmospheric moisture during the flight times is observed for all dates (except for August 5, where the moisture remains nearly constant). Unfortunately, the agreement between airborne measurements and model simulations is relatively poor for the moisture trend. The general reduction of moisture is reproduced, but there is a wide disparity of the simulated trends compared to the measured trends. However, since the moisture trends are both overestimated and underestimated for different dates, no systematic model bias can be detected.

Table 5 Temporal development of specific humidity and potential temperature on April 20, 21, 24 and August 5, 18 (2009) for Dimona airborne measurements (first value) and F100 model simulations (second value)
Full size table

Regarding potential temperature, large positive heating rates are observed, which reflect the fair and nearly cloudless synoptic conditions with strong irradiation. The agreement between measured and simulated trends is considerably better: for all investigated days the temperature trends are matched closely. Even though the heating rates vary for the different dates (for e.g., strong heating on April 24), accurate temperature trends were reproduced by the simulations.

In summary, FOOT3DK is able to reproduce the mean atmospheric heat and moisture characteristics in a realistic way. Results for the temporal rates of change are inconsistent for the two parameters: while the corresponding temperature trends agree closely, the moisture trends exhibit some inaccuracies. It should be mentioned that the non-near-surface atmospheric layers are strongly influenced by mesoscale forcing (see also Sect. 5.1). Thus, especially the advection of moist/dry air from outside into the study area may contribute considerably to the development of atmospheric humidity.

4.3 Turbulent surface fluxes

Turbulent latent and sensible heat fluxes LE and H are calculated from the airborne measurements via eddy-covariance method and are subsequently extrapolated to the surface. As an e.g., flux profiles for April 20 are shown in Fig. 4. Flight level fluxes are 235 W m−2 (LE) and 107 W m−2 (H), and the ABL depth is 950 m. Assuming a linear flux gradient within the boundary layer, the inversion level fluxes (74 and −36 W m−2, respectively) and surface fluxes (265 and 135 W m−2, respectively) are estimated. While the sensible heat flux errors are relatively small, the latent heat flux shows increased uncertainties due to larger fluctuations between the individual aircraft runs. F100 simulation fluxes are taken directly from the surface level and averaged for the domain of the flight pattern. Results show that the simulated surface fluxes are in good agreement to the measured fluxes on April 20. While LE matches almost exactly, H is underestimated by the model, but still lies within the variability range of the measurements.

Fig. 4
figure 4

Turbulent surface fluxes on April 20, 2009 from two different sources: estimated from low-level airborne measurements (red squares), F100 simulations (blue diamonds)

Full size image

Turbulent surface fluxes for the complete investigation period are shown in Fig. 5. Regarding the airborne measurements, on average the latent heat fluxes feature higher values than the corresponding sensible heat fluxes (221 and 171 W m−2, respectively). While in April, LE is considerably higher than H, the differences vanish in August and sensible heat fluxes become larger than latent heat fluxes due to decreased soil moisture and a higher fraction of harvested fields (bare surfaces). For all days, the uncertainty range is higher for LE than for H.

Fig. 5
figure 5

Turbulent surface fluxes LE (upper panel), H (central panel), and sum LE + H (lower panel) on April 20, 21, 24 and August 05, 18 (2009) from two different sources: airborne measurements with error estimates (red) and F100 simulations (blue squares)

Full size image

The simulated fluxes are comparable to the measured ones. While the latent heat flux is moderately overestimated for the five investigation days (+35 W m−2 and +16 %, respectively), the opposite is observed for the sensible heat flux (−33 W m−2 and −19 %, respectively). Even though the partition of turbulent energy into LE and H differs between the individual days, the simulated fluxes match the airborne fluxes within the uncertainty range of the measurements for most cases (an exception are the sensible heat fluxes in August). Furthermore, the total available energy for the turbulent fluxes, i.e., the sum of LE + H, agrees well (Fig. 5, lower panel): the measurements show an average value of 391 W m−2 and the corresponding simulated flux is 394 W m−2.

The encouraging agreement between measured and modelled surface fluxes is supported by the work of Reyers et al. (2011), who found a close relationship between turbulent fluxes from FOOT3DK simulations and ground-based measurements for the same investigation period and area. Thus, the high-resolution model proved to be able reproducing appropriate surface fluxes for a heterogeneous terrain.

4.4 Budgets

Heat and moisture budgets as obtained from airborne measurements and F100 simulations are summarized in Table 6. All terms, namely time rate of change, vertical divergence of turbulent fluxes, and horizontal advection, are converted to units of W m−3. While the first term is derived from the linear trend for the flight period of each day, the second term is obtained by surface fluxes, inversion level fluxes, and ABL depth, and the advection term is assessed as residuum.

Table 6 Heat and moisture budgets on April 20, 21, 24 and August 05, 18 (2009) from Dimona airborne measurements (left column) and F100 model simulations (right column). All values are converted to units of watts per cubic meter (W m−3)
Full size table

For the aircraft moisture budgets, the divergence terms of latent heat flux give a negative contribution, since the surface fluxes are positive for each flight period. This means that there is a transport of humidity from the surface into the investigated volume of air. However, a decrease of atmospheric moisture is observed for most of the days (slight increase for August 5). As our flight pattern represents an area with diameter of about 7 km (see Sect. 3.1), our residual budget term contains only energy fluxes which are representative for mesoscale effects (>5 km, cf., Sun et al. 1996). Therefore, these patterns can be attributed to a strong advection of dry air from outside the study area. For the aircraft θ budgets, the divergences of sensible heat give a negative contribution as well, i.e., there is a transport of heat from the surface into the atmospheric column. However, the increase of atmospheric temperature is larger than it was expected from the divergence term. Thus, an additional advection of warm air from outside into the volume must be assumed. It should be mentioned that two large open-cast coal mines are located near the western and north-eastern boundary of the flight pattern. Due to the dry and un-vegetated character of these areas, they may contribute to the advection of warm and dry air.

If we consider the F100 budgets, the general characteristics are comparable. The simulated flux divergences reflect the slight over- and underestimation of the turbulent surface fluxes, but match the measured divergences mostly within the range of variability. Regarding the temporal change terms, some deviations are found for moisture, while for heat the terms agree closely. Again, the advection terms are relatively large. Overall, the model heat and moisture budgets show reasonable results. The general energetic characteristics of the ABL are simulated adequately for the individual days, which give confidence in the model’s capability to reproduce realistic atmospheric conditions.

Error estimates for the airborne measurements show that uncertainties are larger for moisture than for heat. Furthermore, variability is higher for flux divergences than for the time rate of change. Error estimates for the model results are much smaller, in particular for the vertical flux divergences, as it could be expected from the smoothing influence of model parameterizations, compared to the fluctuating character of field measurements.

5 Effects of different model resolutions

It has been shown that the high-resolution F100 simulations are able to capture the synoptic conditions for the investigated days and to reproduce reasonable budget terms. However, there remains one question worth to be studied in more detail: the influence of different horizontal model resolutions on the individual budget terms. Thus, we assessed which terms are resolved adequately with relatively coarse resolution and which processes need a higher resolution to obtain a realistic simulation. Therefore, in this chapter we additionally consider the forcing COSMO-DE simulation (2,800 m) and FOOT3DK simulations with horizontal resolutions of 1,000 and 250 m.

5.1 Temporal rate of change

The temporal development terms of specific humidity and potential temperature for all five investigated days are displayed in Fig. 6. In terms of moisture trends, a wide scatter is found between measurements and the individual simulations. The time trends of different model runs are somewhat inconsistent: while for some dates, e.g., April 21 or August 5, a clear improvement with increased resolution is found, for other days (e.g., April 20) the opposite is observed. On average, the differences between simulated and measured moisture trends are slightly smaller if model resolution is enhanced, but the observed changes appear rather by chance.

Fig. 6
figure 6

Temporal development term (W m−3) of specific humidity (upper panel) and potential temperature (lower panel) on April 20, 21, 24 and August 05, 18 (2009) from three different sources: airborne measurements (red squares), COSMO-DE simulation (black triangles) and F1000 (light blue), F250 (medium blue), and F100 simulations (dark blue)

Full size image

If we consider the potential temperature trends, measurements and model simulations agree much better compared with the moisture results. Furthermore, for all five studied cases the modelled values become more similar to the measured ones if model resolution increases. This observation is valid for days where COSMO-DE overestimates the temperature trend (April 20, 21 and August 5) as well as for days where the trend is underestimated (April 24 and August 18). Summarizing, the use of higher model resolutions reduces systematically the discrepancy between simulated and measured temperature trends.

Overall, the enhancement of resolution leads to inconsistent results for the rate of change contributions to the moisture and heat budgets. While for potential temperature a general improvement is found, the observed humidity changes exhibit a more random nature. This may be attributed to the role of transport processes for variables in non-near-surface atmospheric layers. Since moisture advection is three times as large as temperature advection (cf. Sect. 4.4), the influence of mesoscale processes from outside the area may play a more important role for humidity than for heat. Therefore, uncertainties in the assessment of humidity advection can lead to inaccuracies in the prediction of humidity time trends inside the model area.

5.2 Turbulent surface fluxes

Turbulent latent and sensible heat fluxes are calculated for the F1000 and F250 simulations using the same method and averaging domain as for the F100 simulation. Unfortunately, turbulent fluxes are not available for COSMO-DE. Therefore, we compare surface fluxes solely estimated from airborne measurements and three FOOT3DK simulations (Fig. 7). All simulations reveal an overestimation of LE compared with the airborne data. However, we do observe an effect of different model resolutions: while the average deviations are largest for the F1000 simulations (+53 W m−2), they are smaller for the F250 simulations (+44 W m−2) and minimal for the F100 simulations (+35 W m−2). Similar observations are made for H, which is underestimated by all simulations. Again, an influence of model resolution is noticed: the average underestimation is highest for F1000 (−45 W m−2), reduces for F250 (−40 W m−2), and is minimal for F100 (−33 W m−2). The resolution effects for LE and H are valid for all investigated cases, but the magnitude of the effect varies.

Fig. 7
figure 7

Turbulent surface fluxes LE and H on April 20, 21, 24 and August 05, 18 (2009) from airborne measurements (red) and FOOT3DK simulations with different horizontal resolution: F1000 (light blue), F250 (medium blue), F100 (dark blue)

Full size image

One could ask whether the detected resolution impacts are associated with surface properties of specific land-use classes. To answer this question, we averaged the F100 and F250 fluxes for grid meshes of 1,000 m and constructed horizontal maps of flux differences F250–F1000 and F100–F1000. As we observe decreased LE and increased H values for all grid meshes in the investigated domain (Fig. 8), these effects are present for all land-use types and not due to specific characteristics of one or two individual classes. Therefore, the changes of LE and H are attributed to a reduction of the aggregation effect. This explanation is supported by the observation that more than 50 % of the F100 grid meshes are dominated by one single land-use class (i.e., fractional coverage >80 %). Since large parts of the heterogeneity are resolved directly for the high-resolution simulations, inaccuracies due to inadequate averaging of surface properties are reduced, leading to a more realistic representation of microscale processes at the surface.

Fig. 8
figure 8

Difference between FOOT3DK simulations F100–F1000 for turbulent surface fluxes LE (upper panel) and H (lower panel) on August 18, 2009

Full size image

6 Summary and conclusions

The objective of this study was to estimate energy budgets both from airborne measurements and model simulations, and to investigate the influence of different model resolutions. With this aim, heat, and moisture budgets of a slightly convective boundary layer for 5 days in April and August 2009 over heterogeneous terrain were calculated. Main findings are as follows:

  • The aircraft energy budgets are comparable with results obtained by other budget studies, in particular in terms of the time trends of moisture and temperature, and the vertical divergence of fluxes (e.g., Betts et al. 1990; Grunwald et al. 1996; Maurer and Heinemann 2006). The advection terms are relatively large, as it is often the case for heterogeneous surfaces (e.g., Grunwald et al. 1996). Error estimates show higher uncertainties for latent heat than for sensible heat fluxes, which is also in agreement with results by other authors (e.g., Bange et al. 2002; Maurer and Heinemann 2006).

  • Regarding mean quantities of humidity, temperature, wind speed, and wind direction, the high-resolution FOOT3DK simulations proved to be able to capture the general structure and characteristics of the ABL for the presented case studies.

  • Simulated turbulent surface fluxes match the airborne fluxes within the range of variability in most cases, if an adequate filter length for the airborne fluxes is used, which has to correspond with the fetch of the ground measurements. While the sum of LE and H shows a very close agreement, the latent heat flux is overestimated by 16 % and the sensible heat flux is underestimated by 19 %. Due to the generally adequate representation of surface fluxes, the terms of vertical divergence also show a reasonable agreement.

  • The temporal rates of change are simulated accurately for the potential temperature. However, larger discrepancies are found for specific humidity. The latter is attributed to COSMO-DE forcing and the corresponding advection of moist/dry air from outside the study area.

  • The comparison between different model resolutions shows inconsistent effects for the local time trends: while the modelled potential temperature trends agree better with the measured values if resolution increases, only random changes are found for specific humidity (due to advection processes). Furthermore, a systematic improvement of simulated surface fluxes LE and H is observed for enhanced resolutions, which can be attributed to a reduction of the aggregation effect.

Even though aircraft-based measurements are a common method for the calculation of energy budgets, they may feature relatively high statistical uncertainties, in particular, regarding the turbulent fluxes (e.g., Maurer and Heinemann 2006). In the present study, several assumptions had to be made before calculating the budgets (due to the restricted aircraft data). However, we have to keep in mind that these assumptions may not be valid for all situations. Therefore, future flight campaigns should consider some changes concerning the measurement design in order to strengthen the reliability of results: first, the execution of a larger flight pattern would be advantageous to enable an explicit calculation of the advection term; second, the flights should be performed in more than one level of the ABL to allow a better estimation of the vertical flux profiles; and third, area-averaged fluxes from ground-based measurements or remote sensing could provide a supplemental source of validation data.

Regarding high-resolution modelling, some requirements have to be fulfilled to obtain an accurate simulation of atmospheric properties. In particular, realistic input data are of crucial importance, since initial and boundary conditions have strong impact on ABL development and mesoscale advection. For e.g., we used the COSMO-DE soil moisture at 2.8 km resolution to initialize FOOT3DK. A more detailed description of the initial soil moisture content would help to improve the partition of turbulent energy into LE and H. Furthermore, the use of a high-resolution is important to achieve an appropriate representation of surface processes. Model results are highly dependent on adequate parameterization of sub-grid processes. For the current version of FOOT3DK, a sun/shade scheme (following de Pury and Farquhar 1997) was used coupled to the land-surface model ISBA instead of a big-leaf scheme. The application of this sun/shade approach within FOOT3DK showed to be able to improve the air-surface exchange and in particular the turbulent surface fluxes considerably, when compared to eddy-covariance stations (Reyers et al. 2011).

The presented results underline the relevance of numerical models for the investigation of boundary layer characteristics and air-surface exchange. We demonstrated the ability of mesoscale models to calculate energy budgets for the ABL with some confidence. Further, we showed that the budget approach is a suitable tool for the evaluation of energy exchange between surface and atmosphere. By comparing measurements and modelling approaches, effects of scale interaction could be identified. This gives evidence to the assumption that advection and time trends are strongly influenced by mesoscale forcing, while the turbulent surface fluxes and the corresponding flux divergences are mainly controlled by microscale processes.