Skip to main content
SpringerLink
Log in

A quantum-inspired version of the nearest mean classifier

  • Foundations
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

We introduce a framework suitable for describing standard classification problems using the mathematical language of quantum states. In particular, we provide a one-to-one correspondence between real objects and pure density operators. This correspondence enables us: (1) to represent the nearest mean classifier (NMC) in terms of quantum objects, (2) to introduce a quantum-inspired version of the NMC called quantum classifier (QC). By comparing the QC with the NMC on different datasets, we show how the first classifier is able to provide additional information that can be beneficial on a classical computer with respect to the second classifier.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. Hence, as a pattern is an object characterized by the knowledge of its features, analogously, in quantum mechanics a state of a physical system is represented by a density operator, characterized by the knowledge of its observables.

  2. In the standard pattern recognition theory, the symbol y is generally used to identify the label of the pattern. In this paper, for the sake of simplicity, we agree with a different notation.

  3. Let us remark that, in general, \(a^*\) and \(b^*\) do not represent true centroids, but centroids estimated on the training set.

  4. For the sake of the simplicity, from now on, we indicate \(\sum _{j=1}^C \mathrm{TP}_j\) with TP. Similarly for TN, FP, and FN.

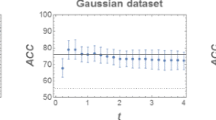
  5. This make sense because it can be seen that for all the datasets we deal with, the classification error is very similar both with and without splitting training and test sets.

  6. Let us remark that there are some patterns correctly classified by the NMC which are neglected by the QC. On this basis, exploiting their complementarity, in principle it also makes sense to consider a combination of both classifiers.

  7. In this case, by combining QC and NMC together, the mean error decreases up to about \(0.247\ (\pm 4.280)\).

  8. Similarly to the Gaussian case, also for the Banana dataset, the NMC is able to correctly classify some points unclassified by the QC. Indeed, by considering the combination of both classifiers, the mean error can decrease up to 10%.

References

  • Aerts D, D’Hooghe B (2009) Classical logical versus quantum conceptual thought: examples in economics, decision theory and concept theory. Quantum interaction (Lecture Notes in Computer Science), vol 5494. Springer, Berlin, pp 128–142

  • Aerts D, Gabora L, Sozzo S (2013) Concepts and their dynamics: a quantum-theoretic modeling of human thought. Top Cogn Sci 5(4):737–772

    Google Scholar 

  • Aharonov D, Kitaev A, Nisan N (1998) Quantum circuits with mixed states. In: Proceedings of the 30th annual ACM symposium on theory of computing, pp 20–30. ACM

  • Barnett SM (2009) Quantum information, 16, Oxford Master Series in Physics. Oxford University Press, Oxford. Oxford Master Series in Atomic, Optical, and Laser Physics

  • Beltrametti E, Chiara ML Dalla, Giuntini R, Leporini R, Sergioli G (2014a) A quantum computational semantics for epistemic logical operators. Part II: semantics. Int J Theor Phys 53(10):3293–3307

    Article  MathSciNet  MATH  Google Scholar 

  • Beltrametti E, Chiara ML Dalla, Giuntini R, Leporini R, Sergioli G (2014b) A quantum computational semantics for epistemic logical operators. Part I: epistemic structures. Int J Theor Phys 53(10):3279–3292

    Article  MathSciNet  MATH  Google Scholar 

  • Bennett CH, Shor PW (1998) Quantum information theory. IEEE Trans Inf Theory 44(6):2724–2724

    Article  MathSciNet  MATH  Google Scholar 

  • Bertlmann RA, Krammer P (2008) Bloch vectors for qudits. J Phys A 41(23):235303

    Article  MathSciNet  MATH  Google Scholar 

  • Caraiman S, Manta V (2012) Image processing using quantum computing. In: IEEE 16th international conference on system theory, control and computing (ICSTCC), 2012, pp 1–6

  • Chefles A (2000) Quantum state discrimination. Contemp Phys 41(6):401–424. arXiv:quant-ph/0010114

  • Chiang H-P, Chou Y-H, Chiu C-H, Kuo S-Y, Huang Y-M (2013) A quantum-inspired Tabu search algorithm for solving combinatorial optimization problems. Soft Comput 18(9):1771–1781

    Article  Google Scholar 

  • Coxeter HSM (1969) Introduction to geometry, 2nd edn. Wiley, New York

    MATH  Google Scholar 

  • Chiara ML Dalla, Giuntini R, Greechie R (2004) Reasoning in quantum theory: sharp and unsharp quantum logics, vol 22. Springer Science and Business Media, Berlin

    Book  MATH  Google Scholar 

  • Duda RO, Hart PE, Stork DG (2000) Pattern classification, 2nd edn. Wiley Interscience, Hoboken

    MATH  Google Scholar 

  • Eisert J, Wilkens M, Lewenstein M (1999) Quantum games and quantum strategies. Phys Rev Lett 83(15):3077

    Article  MathSciNet  MATH  Google Scholar 

  • Eldar YC, Oppenheim AV (2002) Quantum signal processing. IEEE Sig Process Mag 19(6):12–32

    Article  Google Scholar 

  • Fawcet T (2006) An introduction to ROC analysis. Pattern Recogn Lett 27(8):861–874

    Article  Google Scholar 

  • Freytes H, Sergioli G, Aricò A (2010) Representing continuous \(t\)-norms in quantum computation with mixed states. J Phys A 43(46):465306 12

    Article  MathSciNet  MATH  Google Scholar 

  • Giovannetti V, Lloyd S, Maccone L (2008) Quantum random access memory. Phys Rev Lett 100(16):160501

    Article  MathSciNet  MATH  Google Scholar 

  • Hastie T, Tibshirani R, Friedman J (2001) The elements of statistical learning. Springer, Berlin

    Book  MATH  Google Scholar 

  • Hayashi A, Horibe M, Hashimoto T (2005) Quantum pure-state identification. Phys Rev A 72(5):052306

    Article  Google Scholar 

  • Helstrom CW (1976) Quantum detection and estimation theory. Academic Press, Cambridge

    MATH  Google Scholar 

  • Jaeger G (2007) Quantum information. Springer, New York (An overview, With a foreword by Tommaso Toffoli)

  • Jaeger G (2009) Entanglement, information, and the interpretation of quantum mechanics. Frontiers Collection. Springer, Berlin

    Book  Google Scholar 

  • Jakóbczyk L, Siennicki M (2001) Geometry of Bloch vectors in two-qubit system. Phys Lett A 286(6):383–390

    Article  MathSciNet  MATH  Google Scholar 

  • Karlıǧa B (1996) On the generalized stereographic projection. Beiträge Algebra Geom 37(2):329–336

    MathSciNet  Google Scholar 

  • Kimura G (2003) The Bloch vector for N-level systems. Phys Lett A 314(56):339–349

    Article  MathSciNet  MATH  Google Scholar 

  • Kimura G, Kossakowski A (2005) The Bloch-vector space for N-level systems: the spherical-coordinate point of view. Open Syst Inf Dyn 12(03):207–229. arXiv:quant-ph/0408014

  • Kolossa D, Haeb-Umbach R (2011) Robust speech recognition of uncertain or missing data: theory and applications. Springer Science and Business Media, Berlin

    Book  MATH  Google Scholar 

  • Lloyd S, Mohseni M, Rebentrost P (2013) Quantum algorithms for supervised and unsupervised machine learning. arXiv:1307.0411

  • Lloyd S, Mohseni M, Rebentrost P (2014) Quantum principal component analysis. Nat Phys 10(9):631–633

    Article  Google Scholar 

  • Lu S, Braunstein SL (2014) Quantum decision tree classifier. Quantum Inf Process 13(3):757–770

    Article  MathSciNet  MATH  Google Scholar 

  • Manju A, Nigam MJ (2014) Applications of quantum inspired computational intelligence: a survey. Artif Intell Rev 42(1):79–156

    Article  Google Scholar 

  • Manning CD, Raghavan P, Schütze H (2008) Introduction to information retrieval, vol 1. Cambridge university press, Cambridge

    Book  MATH  Google Scholar 

  • Miszczak JA (2012) High-level structures for quantum computing, 6 synthesis (Lectures on Quantum Computing). Morgan and Claypool Publishers, San Rafael

  • Nagel E (1963) Assumptions in economic theory. Am Econ Rev 53(2):211–219

    Google Scholar 

  • Nagy M, Nagy N (2016) Quantum-based secure communications with no prior key distribution. Soft Comput 20(1):87–101

    Article  Google Scholar 

  • Nielsen MA, Chuang IL (2000) Quantum computation and quantum information. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  • Ohya M, Volovich I (2011) Mathematical foundations of quantum information and computation and its applications to nano- and bio-systems. Theoretical and Mathematical Physics. Springer, Dordrecht

    MATH  Google Scholar 

  • Ostaszewski M, Sadowski P, Gawron P (2015) Quantum image classification using principal component analysis. Theor Appl Inf 27:3. arXiv:1504.00580

  • Rebentrost P, Mohseni M, Lloyd S (2014) Quantum support vector machine for big feature and big data classification. Phys Rev Lett 113:130503

    Article  Google Scholar 

  • Sause MGR, Horn S (2013) Quantification of the uncertainty of pattern recognition approaches applied to acoustic emission signals. J Nondestruct Eval 32(3):242–255

    Article  Google Scholar 

  • Schuld M, Sinayskiy I, Petruccione F (2014a) An introduction to quantum machine learning. Contemp Phys 56(2). arXiv:1409.3097

  • Schuld M, Sinayskiy I, Petruccione F(2014b) Quantum computing for pattern classification. In: PRICAI 2014: trends in artificial intelligence, pp 208–220. Springer

  • Schuld M, Sinayskiy I, Petruccione F (2014c) The quest for a quantum neural network. Quantum Inf Process 13(11):2567–2586

    Article  MathSciNet  MATH  Google Scholar 

  • Schwartz JM, Stapp HP, Beauregard M (2005) Quantum physics in neuroscience and psychology: a neurophysical model of mind-brain interaction. Philos Trans R Soc B Biol Sci 360(1458):1309–1327

    Article  Google Scholar 

  • Shannon CE (1948) A mathematical theory of communication. Bell Syst Tech J 27(379–423):623–656

    Article  MathSciNet  MATH  Google Scholar 

  • Sozzo S (2015) Effectiveness of the quantum-mechanical formalism in cognitive modeling. Soft Comput. doi:10.1007/s00500-015-1834-y

  • Stapp HP (1993) Mind, matter, and quantum mechanics. Springer, Berlin

    Book  MATH  Google Scholar 

  • Tanaka K, Tsuda K (2008) A quantum-statistical-mechanical extension of gaussian mixture model. J Phys Conf Ser 95(1):012023

    Article  Google Scholar 

  • Trugenberger CA (2002) Quantum pattern recognition. Quantum Inf Process 1(6):471–493

    Article  MathSciNet  Google Scholar 

  • Webb AR, Copsey KD (2011) Statistical pattern recognition, 3rd edn. Wiley, New York

    Book  MATH  Google Scholar 

  • Wiebe N, Kapoor A, Svore KM (2015) Quantum nearest-neighbor algorithms for machine learning. Quantum Inf Comput 15(34):0318–0358

    Google Scholar 

  • Wilde MM (2013) Quantum Inf Theory. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Wittek P (2014) Quantum machine learning: what quantum computing means to data mining. Academic Press, Cambridge

    MATH  Google Scholar 

Download references

Acknowledgements

This work has been partly supported by the project “Computational quantum structures at the service of pattern recognition: modeling uncertainty” (CRP-59872) funded by Regione Autonoma della Sardegna, L.R. 7/2007 (2012) and the FIRB project “Structures and Dynamics of Knowledge and Cognition” (F21J12000140001).

Funding This study was funded by Regione Autonoma della Sardegna, L.R. 7/2007, CRP-59872 (2012).

Author information

Authors and Affiliations

  1. Università di Cagliari, Via Is Mirrionis 1, 09123, Cagliari, Italy

    Giuseppe Sergioli, Enrica Santucci, Luca Didaci & Roberto Giuntini

  2. Institute of Theoretical and Applied Informatics, Polish Academy of Sciences, Bałtycka 5, 44-100, Gliwice, Poland

    Jarosław A. Miszczak

Authors
  1. Giuseppe Sergioli
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Enrica Santucci
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Luca Didaci
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jarosław A. Miszczak
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Roberto Giuntini
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Giuseppe Sergioli.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Communicated by A. Di Nola.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sergioli, G., Santucci, E., Didaci, L. et al. A quantum-inspired version of the nearest mean classifier. Soft Comput 22, 691–705 (2018). https://doi.org/10.1007/s00500-016-2478-2

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-016-2478-2

Keywords

Search

Navigation