Duality Properties of Strong Isoperimetric Inequalities on a Planar Graph and Combinatorial Curvatures

Abstract

This paper is about hyperbolic properties on planar graphs. First, we study the relations among various kinds of strong isoperimetric inequalities on planar graphs and their duals. In particular, we show that a planar graph satisfies a strong isoperimetric inequality if and only if its dual has the same property, if the graph satisfies some minor regularity conditions and we choose an appropriate notion of strong isoperimetric inequalities. Second, we consider planar graphs where negative combinatorial curvatures dominate, and use the outcomes of the first part to strengthen the results of Higuchi, Żuk, and, especially, Woess. Finally, we study the relations between Gromov hyperbolicity and strong isoperimetric inequalities on planar graphs, and give a proof that a planar graph satisfying a proper kind of a strong isoperimetric inequality must be Gromov hyperbolic if face degrees of the graph are bounded. We also provide some examples to support our results.

1 Introduction

The main topic of this paper is strong isoperimetric inequalities on planar graphs, as one can guess from the title. In fact, we have studied the relations of three kinds of strong isoperimetric inequalities on planar graphs and their dual graphs, and as an application we have strengthened the results of [22, 37, 39]. We believe that some of our works can be considered a ‘similar effort’ for showing that a planar graph satisfies a strong isoperimetric inequality if and only of its dual has the same property, as suggested in [37].

To describe our results precisely, let $G$ be a connected simple planar graph embedded into $\mathbb {R}^2$ locally finitely such that its dual graph $G^*$ is also simple. See Sect. 2 for details of the terminologies. We denote by $V(G), E(G)$, and $F(G)$ the vertex set, the edge set, and the face set, respectively, of $G$. For each $v \in V(G)$, $\deg (v)$ is the number of edges with one end at $v$. Similarly for each $f \in F(G)$, $\deg (f)$ is the number of edges surrounding $f$. In this paper we assume that $3 \le \deg (v), \deg (f) < \infty$ for every $v \in V(G)$ and $f \in F(G)$, unless otherwise stated.

Next suppose $S$ is a finite subgraph of $G$, and we consider three types of boundaries of $S$. The first one is $\partial S$, the set of edges in $E(G)$ such that each element of $\partial S$ has one end on $V(S)$ and the other end on $V(G) \setminus V(S)$. The second one is $\partial _v S \subset V(S)$, each of whose element is an end vertex of some edges in $\partial S$. The last boundary $\partial _e S$ is the set of edges surrounding $S$; i.e., $e \in \partial _e S$ if and only if $e \in E(S)$ and $e$ belongs to $E(f)$ for some $f \in F(G) \setminus F(S)$. Now we define three different strong isoperimetric constants by

$$\begin{aligned} \imath (G) := \inf _S \frac{|\partial S|}{\text{ Vol }(S)}, \quad \jmath (G) := \inf _S \frac{|\partial _v S|}{|V(S)|}, \quad \kappa (G) := \inf _S \frac{|\partial _e S|}{|F(S)|}, \end{aligned}$$

where $|\cdot |$ denotes the cardinality, $\text{ Vol }(S) = \sum _{v \in V(S)} \deg (v)$, and $S$ runs over all the nonempty finite subgraphs of $G$.

The above constants $\imath (G), \jmath (G), \kappa (G)$ characterize some properties of the edge set, the vertex set, and the face set, respectively, of $G$, and are discrete analogues of Cheeger’s constant [9]. The condition $\imath (G)>0$ is of particular interest in spectral theory on graphs, since this condition is equivalent to the positivity of the smallest eigenvalue of the negative Laplacian [14, 15], implying the simple random walk on $G$ is transient. For more about this subject, see for instance [6, 16, 17, 25, 29, 33, 38] and the references therein. The constant $\kappa (G)$ is essentially dealt with in the geometric(combinatorial) group theory [18, 20], and it was also investigated in [23, 28]. The constant $\jmath (G)$ appears in the geometric group theory as well [12, 18, 20], and early versions of spectral theory on graphs [14, 34]. Note that $\jmath (G)$ is quantitatively equivalent to $\imath (G)$ if vertex degrees of $G$ are bounded, and to $\kappa (G)$ if face degrees of $G$ are bounded (cf. Theorem 1 below).

We will call a simple planar graph proper if every face of the graph is a topological closed disk. Now we are ready to describe our main result.

Theorem 1

Suppose $G$ is a proper planar graph as described above, and $G^*$ is its dual graph. Then

• (a) $\imath (G) > 0$ if and only if $\kappa (G^*) >0$, and $\kappa (G) > 0$ if and only if $\imath (G^*) >0$;

• (b) $\jmath (G) >0$ if and only if $\jmath (G^*) >0$;

• (c) if $\jmath (G) >0$, then $\imath (G) > 0$, $\imath (G^*) >0$, $\kappa (G) > 0$, and $\kappa (G^*) >0$.

Of course the main part of the above theorem is (b). We believe that the part (a) is well known to experts, but we have decided to contain a proof of it for the sake of completeness. Moreover, it is not long. For (c), one can easily deduce it from (a) and (b) as explained in Sect. 4. The reason why we state our results as above, instead of emphasizing (b) alone, is because this way could help one seeing the whole picture easily.

In Theorem 1 we did not require any upper bound for vertex degrees or face degrees of $G$, which makes the theorem useful. All the statements in Theorem 1 become trivial if both vertex and face degrees of $G$ are bounded, since in this case $G$ is roughly isometric(quasi-isometric) to its dual $G^*$, hence (b) follows from Theorem (7.34) of [34]. (For rough isometries, see Sect. 6.)

In the course of proving Theorem 1(b) we obtained the following result as a byproduct, which might be interesting by itself (compare it with [37, Reduction Lemma 2]).

Theorem 2

Suppose $G$ is a proper planar graph such that $|V(S)| \le C|\partial _v S|$ for every polygon $S \subset G$, where $C$ is a constant not depending on $S$. If either $G$ is normal or face degrees of $G$ are bounded, then $\jmath (G) > 0$.

We call a planar graph normal if it is proper and the intersection of every two different faces is exactly one of the following: the empty set, a vertex, or an edge. We chose the terminology ‘normal’ since we adopted the first two properties of normal tilings defined in [21]. For polygons, they are basically finite unions of faces in $F(G)$ with simply connected interiors; for the precise definition, see Sect. 2.

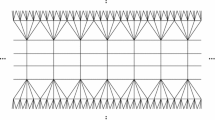
One cannot omit the properness condition in Theorem 1, because without it the statement (b) is no longer true. For example, let $\Gamma$ be a triangulation of the plane such that $\deg v \ge 7$ for every $v \in V(\Gamma )$. Then it is well known that $\jmath (\Gamma )>0$ and $\jmath (\Gamma ^*)>0$. (Also see Corollary 4 below for this fact.) Furthermore, let us assume that there exists a sequence of vertices $v_k \in V(\Gamma )$ such that $n_k := \deg v_k \rightarrow \infty$ as $k \rightarrow \infty$. The essential property of $\Gamma$ is that face degrees of $\Gamma$ are bounded since it is a triangulation of the plane, while vertex degrees are not bounded. Now for each $k$, we attach $n_k$ copies of the graph $\Lambda$ in Fig. 1a to $v_k$ so that a degree 3 vertex of each copy is identified with $v_k$ and each face $f \in F(\Gamma )$ with $V(f) \ni v_k$ contains exactly one copy of $\Lambda$ in it (Fig. 1b). Let $G$ denote this new graph, which is definitely not proper but satisfies all the other properties we require; that is, $3 \le \deg v, \deg f < \infty$ for every $v \in V(G)$ and $f \in F(G)$, and both $G$ and $G^*$ are simple.

Fig. 1

Constructing the graph $G$ from $\Gamma$

It is not difficult to see $\jmath (G) =0$ since if we denote by $S_k$ the union of $n_k$ copies of $\Lambda$ sharing the vertex $v_k$, then we have $\partial _v (S_k) = \{ v_k \}$ and $|V(S_k)| = 4 n_k +1$. To see that $\jmath (G^*)>0$, first note that $G^*$ and $\Gamma ^*$ are roughly isometric. Moreover, face degrees of $G$ and $\Gamma$, or vertex degrees of $G^*$ and $\Gamma ^*$, are both bounded and we chose $\Gamma$ so that $\jmath (\Gamma ^*) >0$. Thus the inequality $\jmath (G^*) > 0$ follows from Theorem (7.34) of [34].

To obtain an application of Theorem 1, let us introduce so-called combinatorial curvatures defined on planar graphs. Suppose $G$ is a proper planar graph as before. For each $e \in E(G)$, $v \in V(G)$, and $f \in F(G)$ we define edge curvature $\phi$, vertex curvature $\psi$, and face curvature $\chi$ by

$$\begin{aligned} \phi (e)&= \sum _{w \in V(e)} \frac{1}{\deg (w)} + \sum _{g: e \in E(g)} \frac{1}{\deg (g)} -1,\\ \psi (v)&= 1 - \frac{\deg (v)}{2} + \sum _{g: v \in V(g)} \frac{1}{\deg (g)}, \quad \text{ and }\\ \chi (f)&= 1 - \frac{\deg (f)}{2} + \sum _{w \in V(f)} \frac{1}{\deg (w)}. \end{aligned}$$

In the above $w$ and $g$ stand for a vertex and a face, respectively. Remark that the notations $\phi , \psi ,$ and $\chi$ are those used in [37], but we have changed the signs. Other than the above combinatorial curvatures for planar graphs, there is another one called corner curvature [26, 27].

Recently combinatorial curvatures have been extensively studied by various researchers [2, 3, 6, 11, 13, 22, 25–27, 35, 37, 39], but this concept was introduced more than seven decades ago. In [30, Chap.XII], Nevanlinna introduced a characteristic number called excess, which is essentially equal to the vertex curvature. Moreover, there might be older literature in this line than [30], since in [30] Nevanlinna mentioned a work of Teichmüller [36] related to excess. In fact, excess was defined for a special type of bipartite regular planar graphs, called Speiser graphs, which capture the combinatorial properties of meromorphic functions defined on some simply connected Riemann surfaces and ramified only over finitely many points in the extended complex plane $\mathbb {\overline{C}}$. For more about Speiser graphs and excess, see for example [5, 30, 32].

For finite subsets $E \subset E(G)$, let $\overline{\phi }(E) = (1/|E|)\sum _{e\in E} \phi (e)$ and define the upper average of $\phi$ on $G$ by

$$\begin{aligned} \overline{\phi }(G) = \limsup _{|E(S)| \rightarrow \infty } \overline{\phi }(E(S)), \end{aligned}$$

where limit superior is taken over all simply connected finite subgraphs $S$ of $G$. Similarly, for finite subsets $V \subset V(G)$ and $F \subset F(G)$, let $\overline{\psi }(V) = (1/|V|)\sum _{v\in V} \psi (v)$ and $\overline{\chi }(F) = (1/|F|)\sum _{f\in F} \chi (f)$, and define the upper averages of $\psi$ and $\chi$ on $G$, respectively, by

$$\begin{aligned} \overline{\psi }(G) = \limsup _{|V(S)| \rightarrow \infty } \overline{\psi }(V(S)), \quad \overline{\chi }(G) = \limsup _{|F(S)| \rightarrow \infty } \overline{\chi }(F(S)), \end{aligned}$$

where the limit superiors are also taken over all simply connected finite subgraphs $S$ of $G$. Our second main result is the following.

Theorem 3

Suppose $G$ is a proper planar graph.

• (a) If $\overline{\phi }(G) < 0$ or $\overline{\chi }(G) < 0$, then $\jmath (G) >0$.

• (b) If $\overline{\psi }(G) < 0$, and if either $G$ is normal or the vertex degrees of $G$ are bounded, then $\jmath (G)>0$.

• (c) It is possible to have $\overline{\psi }(G) < 0$ and $\jmath (G)=\kappa (G) = 0$.

The most surprising part in Theorem 3 might be (c), because it is very tempting to believe that $\overline{\psi }(G) < 0$ if and only if $\overline{\chi }(G^*) < 0$. However, (a) and (c) of Theorem 3, when combined with Theorem 1(b), show that it cannot be true. This discrepancy comes from the fact that the definition of $\overline{\chi }(G^*)$ requires some subgraphs of $G^*$ whose corresponding subgraphs of $G$ are disconnected. This will be explained in the subsequent sections in detail. For Theorem 3(a) and the second part (the case when vertex degrees are bounded) of Theorem 3(b), their credits should be addressed to Woess [37]. In fact, Woess showed that $\imath (G) > 0$ if one of the following conditions holds: $\overline{\phi }(G) < 0$, or $\overline{\psi }(G) < 0$, or $\overline{\chi }(G) < 0$. Note that this result is already enough for the second part of Theorem 3(b), because $\imath (G)$ is quantitatively equivalent to $\jmath (G)$ when vertex degrees of $G$ are bounded. Also one can check that Woess’s arguments are enough to show (a) only with some minor modifications. This will be explained in Sect. 5.

It was observed independently in [22, 39] that the condition $\psi (v)<0$ actually implies $\psi (v) \le -\varepsilon _0$ for some positive constant $\varepsilon _0$. Higuchi also showed in [22] that one can choose $\varepsilon _0 = 1/1806$. Thus we obtain the following immediate corollary of Theorems 1 and 3.

Corollary 4

Suppose $G$ is a proper planar graph. If $\psi (v)<0$ for all $v \in V(G)$, or $\chi (f)<0$ for all $f \in F(G)$, then $\jmath (G)>0$. Consequently, in either case we have $\imath (G)>0$, $\kappa (G)>0$, $\imath (G^*)>0$, $\jmath (G^*)>0$, and $\kappa (G^*)>0$.

Compare this corollary with [22, Theorem B and Corollary 2.3] and [39, Proposition 4]. Another corollary of Theorem 3 is the following.

Corollary 5

Suppose $G$ is a graph satisfying the assumptions in (a) or (b) of Theorem 3. Then $G$ contains a tree $T$ such that $\jmath (T) > 0$.

Proof

This corollary is an immediate consequence of Theorem 3 above, and Theorem 1.1 of [4]. For a given locally finite graph $\Gamma$ and its subgraph $S \subset \Gamma$, let $\tilde{\partial }_v S$ be the set of all vertices in $V(\Gamma ) \setminus V(S)$ that have a neighbor in $S$. Define

$$\begin{aligned} \tilde{\jmath } (\Gamma ) := \inf _S \frac{|\tilde{\partial }_v S|}{|V(S)|}, \end{aligned}$$

where $S$ runs over all the nonempty finite subgraphs of $\Gamma$ as before. Then Benjamini and Schramm showed in [4] that every graph $G$ with $\tilde{\jmath }(G)>0$ contains a tree $T$ with $\tilde{\jmath }(T)>0$. But one can check that $\jmath (\Gamma ) = \tilde{\jmath }(\Gamma ) /(1+ \tilde{\jmath }(\Gamma ))$ for every planar graph $\Gamma$, so we have the corollary. The details are left to the readers. $\square$

Our last topic is about the relation between strong isoperimetric inequalities and Gromov hyperbolicity on planar graphs. For the definition of Gromov hyperbolic spaces, see Sect. 6.

Theorem 6

Suppose $G$ is a planar graph whose face degrees are bounded.

• (a) If $\kappa (G)>0$, then $G$ is hyperbolic in the sense of Gromov.

• (b) The converse of (a) is not true. That is, $G$ could be Gromov hyperbolic (and normal), but $\kappa (G) = 0$.

• (c) The right isoperimetric constant for Gromov hyperbolicity is $\kappa (G)$. That is, it is possible that $G$ is (normal and) not Gromov hyperbolic, but $\imath (G)>0$.

Theorem 6(a) is widely believed and even considered trivial to some experts, but surprisingly we could not find its proof in the literature. Of course, however, it deserves to be written somewhere since it can save some works like [3, Corollary 5] or [39, Corollary 1]. Also note that the condition $\kappa (G)>0$ is equivalent to $\jmath (G)>0$ in the above theorem, since face degrees of $G$ are bounded.

2 Planar Graphs

Let $G = \bigl ( V(G), E(G) \bigr )$ be a graph, where $V(G)$ is the vertex set and $E(G)$ is the (undirected) edge set of $G$. Every edge $e \in E(G)$ is associated with two vertices $v, w \in V(G)$, saying that $e$ is incident to $v$ and $w$, or $e$ connects $v$ and $w$. In this case we write $e= [v,w]$, and the vertices $v$ and $w$ are called the endpoints of $e$. Also we say that $v$ and $w$ are neighbors of each other. A graph $G$ is called simple if there is no self-loop nor multiple edges; that is, for every edge $[v,w]\in E(G)$ we have $v\ne w$, and for every two vertices $v, w \in V(G)$ there is at most one edge connecting these two vertices. A graph $G$ is called connected if it is connected as a one-dimensional simplicial complex, and planar if there is a continuous injective map $h: G \rightarrow \mathbb {R}^2$. The image $h(G)$ is called an embedded graph, but we will not distinguish $G$ from $h(G)$ when the embedding is fixed, and the embedded graph will be denoted by $G$ instead of $h(G)$. We say that $G$ is embedded into $\mathbb {R}^2$ locally finitely if every compact set in $\mathbb {R}^2$ intersects only finite number of vertices and edges of $G$. From now on, $G$ will always be a connected simple planar graph embedded into $\mathbb {R}^2$ locally finitely.

The closure of each component of $\mathbb {R}^2 \setminus G$ is called a face of $G$, and we denote by $F(G)$ the face set of $G$. The dual graph $G^*$ of $G$ is the planar graph such that the vertex set of $G^*$ is just $V(G^*)=F(G)$, and for the edge set we have $[f_1, f_2] \in E(G^*)$ if and only if $f_1$ and $f_2$ share an edge in $G$. The degree of a vertex $v\in V(G)$, denoted by $\deg v$, is the number of neighbors of $v$, and the degree of a face $f \in F(G)$, denoted by $\deg f$, is the number of edges in $E(G)$ surrounding $f$. In this paper, one essential assumption about $G$ is that $G^*$ is simple, and that $3 \le \deg v, \deg f < \infty$ for every $v \in V(G)$ and $f \in F(G)$. Under this assumption, $\deg f$ is just the degree of $f$ as a vertex in $G^*$.

A graph $S$ is called a subgraph of $G$, denoted by $S \subset G$, if $V(S) \subset V(G)$ and $E(S) \subset E(G)$. A subgraph will be always assumed to be an induced subgraph; that is, if $v, w \in V(S)$ and $[v,w] \in E(G)$, then $[v,w] \in E(S)$. A subgraph is called finite if $|V(S)|$ is finite, and a finite subgraph $S \subset G$ is called simply connected if it is connected as a one-dimensional simplicial complex and $G\setminus S$ has only one component. Here we remark that our definition of simply connectedness might be different from the one in some other literature, since a subgraph $S \subset G$ could be simply connected as a subset of $\mathbb {R}^2$, but not as a subgraph of $G$ (Fig. 2a). However, this usually makes no difference when studying strong isoperimetric inequalities, because in the proof we can always add to $S$ all the finite components of $G \setminus S$ (cf. proofs of Lemma 8, Theorem 2, etc.).

Fig. 2

A face graph $S$ (right) and its dual part $S^*$ (left)

For $S \subset G$, we define $F(S)$ as the subset of $F(G)$ such that $f \in F(S)$ if and only if $f \in F(G)$ and it is the closure of a component of $\mathbb {R}^2 \setminus S$. This notation is a little bit confusing, since $F(S)$ in fact means the intersection of $F(G)$ and the face set of $S$. By abuse of the notation, we will treat a face $f \in F(G)$ as a subgraph of $G$ consisting of all the edges and vertices on the topological boundary of $f$. Thus we have $|E(f)|= \deg f$. Edges are also treated as subgraphs in a similar way. A subgraph $S \subset G$ is called a face graph if it is a union of faces; i.e., $V(S) = \bigcup _{f \in F(S)} V(f)$. A finite subgraph is called a polygon if it is a simply connected face graph and the interior of $S$,

$$\begin{aligned} D(S) := \Bigg ( \bigcup _{f \in F(S)} f \Bigg )^\circ , \end{aligned}$$

(2.1)

is simply connected as a subset of $\mathbb {R}^2$, where $(\cdot )^\circ$ denotes the interior of the considered set with respect to the Euclidean topology. Note that even though a face graph has simply connected interior, the graph itself may not be simply connected (Fig. 2b). Thus in the definition we require a polygon to be simply connected.

Now suppose $S \subset G$ is a face subgraph, and define $S^*$ as the subgraph of $G^*$ such that $V(S^*)=F(S)$ (Fig. 2). Then it is easy to check that for a given face graph $S\subset G$, the interior $D(S)$ is connected if and only if $S^*$ is connected, and such $S$ is a polygon if and only if $S^*$ is simply connected. In particular this suggests that even though $S$ is connected, $S^*$ may not be connected. For example, suppose $f_1, f_2$ are faces of $G$ such that $f_1 \cap f_2$ is a vertex. Then the face graph $S\subset G$ with $F(S) = \{ f_1, f_2 \}$ is simply connected, but $S^*$ is definitely disconnected. Thus if we define

$$\begin{aligned} \overline{\chi }_1 (G) = \limsup _{|F(S)|\rightarrow \infty } \overline{\chi }(F(S)), \end{aligned}$$

(2.2)

where at this time the limit superior is taken over all the polygons $S \subset G$, then we have $\overline{\psi }(G^*) =\overline{\chi }_1 (G) \le \overline{\chi }(G)$. Therefore the condition $\overline{\chi }(G) < 0$ is stronger than the condition $\overline{\psi }(G^*)<0$, and this observation has delivered us to Theorem 3.

For a face subgraph of $S \subset G$, there is a bijection between $\partial S^*$ and $\partial _e S$. However, there is no set defined in $S$ which corresponds to $\partial _v S^*$. Thus if $S$ is a subgraph of $G$, which may or may not be a face graph, let us define the face boundary of $S$ by

$$\begin{aligned} \partial _f S := \{ f \in F(S) : E(f) \cap \partial _e S \ne \emptyset \}. \end{aligned}$$

That is, $\partial _f S$ is the set of faces in $F(S)$, each of which shares an edge with a face in $F(G) \setminus F(S)$.

We finish this section with the following lemma. Recall that a planar graph $G$ is called proper if every face of $G$ is a topological closed disk, and normal if it is proper and any two different faces of $G$ share at most a vertex or an edge.

Lemma 7

Suppose $G$ is a proper planar graph. Then for every finite and connected subgraph $S \subset G$ with $|V(S)| \ge 2$, we have $|\partial _v S| \ge 2$. Moreover, if $G$ is normal and $S \subset G$ has the property $|V(S)| \ge 3$, then $|\partial _v S| \ge 3$.

Proof

Suppose $S \subset G$ is a finite and connected subgraph of $G$. Then we cannot have $\partial _v S = \emptyset$ since $G$ is connected. If $|\partial _v S| = 1$, there must be a unique face $f \in F(G)$ surrounding $S$; i.e., there is only one face $f \in F(G) \setminus F(S)$ such that $E(f) \cap E(S) \ne \emptyset$. Then $f$ cannot be a topological closed disk because $S$ contains an edge, contradicting the properness condition of $G$.

Now suppose $G$ is normal, $S \subset G$, $\partial _v S = \{ v_1, v_2 \}$, and $|V(S)| \ge 3$. In this case there are exactly two faces, say $f_1$ and $f_2$, whose union surrounds $S$. Then we must have $v_1, v_2 \in V(f_1) \cap V(f_2)$, so the normality condition of $G$ implies that $f_1 \cap f_2 = [v_1, v_2]$. This means that $S$ is just an edge because both $f_1$ and $f_2$ are topological closed disks, which is definitely a contradiction since $|V(S)|\ge 3$. $\square$

3 Proof of Theorem 1(a)

First, let us derive a useful formula which will be used frequently. Let $S$ be a finite simply connected subgraph of $G$. Then every vertex $v \in V(S) \setminus \partial _v S$ corresponds to at least three edges in $E(S)$ and each vertex $v \in \partial _v S$ corresponds to at least one edge in $E(S)$, while every edge in $E(S)$ corresponds to exactly two vertices in $V(S)$. Therefore we have

$$\begin{aligned} 2 |E(S)| \ge 3(|V(S)| - |\partial _v S|) + |\partial _v S| = 3|V(S)| - 2|\partial _v S|. \end{aligned}$$

Thus by Euler’s formula we obtain

$$\begin{aligned} |E(S)| +1 = |V(S)| + |F(S)| \le \frac{2}{3} \cdot |E(S)| + \frac{2}{3} \cdot |\partial _v S| + |F(S)|, \end{aligned}$$

or

$$\begin{aligned} |E(S)| \le 2 |\partial _v S| + 3|F(S)| - 3. \end{aligned}$$

(3.1)

Lemma 8

For a given planar graph $G$, the following two conditions are equivalent:

• (a) for every finite $S \subset G$, there is a constant $C_1$ such that $|F(S)| \le C_1 |\partial _e S|$;

• (b) for every finite $S \subset G$, there is a constant $C_2$ such that $\sum _{f \in F(S)} \deg (f) \le C_2 |\partial _e S|$.

Furthermore, the constants $C_i$ are quantitative to each other.

Proof

We only need to show the implication (a) $\rightarrow$ (b), since the other direction is trivial. In this case, we can assume without loss of generality that $S$ is a polygon, since otherwise we can add to $S$ all the finite components of $G \setminus S$ and cut from $S$ all the edges not surrounding a face in $F(S)$. Note that these operations make either the set $\partial _e S$ smaller, or the set $F(S)$ bigger, or both. If $D(S)$ consists of several components, we can consider them separately.

Then since $S$ is a polygon we have $|\partial _v S| \le |\partial _e S|$ and

$$\begin{aligned} 2 |E(S)| = \sum _{f \in F(S)} \deg (f) + |\partial _e S|. \end{aligned}$$

(3.2)

Now Eqs. (3.1) and (3.2) imply that

$$\begin{aligned} \sum _{f \in F(S)} \deg (f) = 2|E(S)| - |\partial _e S| \le 4|\partial _v S| + 6|F(S)| - |\partial _e S| \le 3 |\partial _e S| + 6|F(S)|, \end{aligned}$$

(3.3)

and we obtain the implication (a) $\rightarrow$ (b) with $C_2 = 6C_1 +3$. In fact one can check, by modifying (3.1), that a better estimate $C_2 \le 6 C_1 +1$ holds since $S$ is a polygon hence every vertex in $\partial _v S$ corresponds at least two edges in $E(S)$. This completes the proof.$\square$

Note that the condition (a) of the previous lemma is equivalent to the condition $\kappa (G) >0$ and, considering the duality property, one can check that (b) is equivalent to $\imath (G^*)>0$. Thus Lemma 8 implies the equivalence between $\imath (G^*)>0$ and $\kappa (G)>0$. The equivalence between $\imath (G)>0$ and $\kappa (G^*)>0$ comes from the duality. This completes the proof of Theorem 1(a).

4 Partitioning a Finite Subgraph

In this section we will prove Theorem 2 and the rest of Theorem 1. Our main strategy is partitioning a given finite subgraph into ‘nice’ subgraphs, and passing strong isoperimetric inequalities of ‘nice’ subgraphs to the given one.

In the lemma below, the notation $S_1 \cup S_2$, where $S_1, S_2$ are subgraphs of $G$, means the subgraph $S \subset G$ with $V(S) = V(S_1) \cup V(S_2)$ and $E(S)=E(S_1)\cup E(S_2)$. A priori, therefore, $S_1 \cup S_2$ does not have to be an induced subgraph, but we will only consider the case when it is induced. The graph $S_1 \cap S_2$ is defined similarly.

Lemma 9

Suppose $S$ is a finite subgraph of $G$. If $S = S_1 \cup S_2 \cup \cdots \cup S_n$, where $S_1, S_2, \ldots , S_n$ are subgraphs of $G$ such that

• (a) $|V(S_i)| \le C |\partial _v S_i|$ for each $i =1,2, \ldots , n$,

• (b) $S_1 \cup S_2 \cup \cdots \cup S_{i}$ is an induced subgraph for each $i =1,2, \ldots , n$,

• (c) $|V\bigl ( (S_1 \cup S_2 \cup \cdots \cup S_{i-1} ) \cap S_i\bigr ) | = 1$ for each $i =2,3, \ldots , n$, and

• (d) $|\partial _v S| \ge n / \tau$ for some $\tau > 0$,

then we have $|V(S)| \le (1+2\tau )C|\partial _v S|$.

Proof

From (b) and (c), it is easy to see that

$$\begin{aligned} |\partial _v (S_1 \cup \cdots \cup S_{i})| \ge |\partial _v (S_1 \cup \cdots \cup S_{i-1})| + |\partial _v S_i| -2. \end{aligned}$$

(4.1)

Therefore,

$$\begin{aligned} |V(S)|&= |V(S_1 \cup \cdots \cup S_n)| \le |V(S_1)| + |V(S_2)| + \cdots + |V(S_n)|\\&\le C (|\partial _v S_1| + |\partial _v S_2| + \cdots + |\partial _v S_n|)\\&\le C( |\partial _v (S_1 \cup S_2)| + |\partial _v S_3| + \cdots + |\partial _v S_n| +2) \\&\le \cdots \le C(|\partial _v (S_1 \cup \cdots \cup S_n)| + 2n-2) \le (1+2 \tau ) C |\partial _v S|, \end{aligned}$$

as desired. $\square$

Suppose $S$ is a finite simply connected subgraph of $G$. If $T \subset S$ is a polygon such that no $T'$ with $T \subsetneq T' \subset S$ is a polygon, we call $T$ a leaf of $S$. If $T \subset S$ is finite tree such that $E(T) \cap E(f) = \emptyset$ for every $f \in F(S)$, and no $T'$ with $T \subsetneq T' \subset S$ is a tree satisfying the same property, we call such $T$ a branch of $S$. If $T \subset S$ is either a leaf or a branch, we call $T$ a part of $S$ (see Fig. 3).

Fig. 3

A subgraph composed of ten parts (seven leaves and three branches) is shown on the left, and it is divided into leaves and branches on the right. The largest part in the center of each figure should be called a trunk, but we accidently call it a leaf

Proof of Theorem 2

(the normal case) Let $G$ be a normal planar graph satisfying the assumptions in Theorem 2, and suppose a finite subgraph $S \subset G$ is given. To prove Theorem 2, we may assume that $S$ is simply connected. Otherwise we can add to $S$ all the finite components of $G \setminus S$ and consider each component of $S$ separately.

Choose an edge $e_1 \in E(S)$, and note that there exists a unique leaf or branch $S_1$ of $S$ such that $e \in E(S_1)$, depending on whether $e \in E(f)$ for some $f \in F(S)$ or not, respectively. If $S_1 \ne S$, choose $e_2 \in E(S) \setminus E(S_1)$ with only one end in $V(S_1)$, and let $S_2$ be the part of $S$ such that $e_2 \in E(S_2)$. Then because $S_1$ and $S_2$ are maximal polygons or trees of the simply connected subgraph $S$, one can see that $S_1 \cap S_2$ is a single vertex that is an end of $e_2$, and $S_1 \cup S_2$ is an induced subgraph of $S$. If $S_1 \cup S_2 \ne S$, choose $e_3 \in E(S) \setminus E(S_1 \cup S_2)$ with only one end in $V(S_1 \cup S_2)$, and repeat the same process. This process cannot run forever, since $S$ is a finite graph. Thus we just have enumerated the parts $S_1, S_2, \ldots , S_n$ of $S$ so that $S = S_1 \cup S_2 \cup \cdots \cup S_n$ and they satisfy the conditions (b) and (c) of Lemma 9.

Each $S_i$ is either a branch or a leaf, i.e., a finite tree or a polygon. If $S_i$ is a leaf, the inequality $|V(S_i)| \le C|\partial _v S_i|$ holds by our assumption. If $S_i$ is a branch, then since $F(S_i) = \emptyset$ and $|V(S_i)| = |E(S_i)| +1$, we have $|V(S_i)| \le 2 |\partial _v S_i|$ by (3.1). Thus the condition (a) of Lemma 9 is also satisfied for the sequence $S_1, \ldots , S_n$.

It remains to show that $|\partial _v S| \ge n/3$. To see this, let $k$ be the number of $S_i$ such that $|\partial _v S_i| = 2$ and $\partial _v S \cap V(S_i) \ne \emptyset$. If $k \ge n/3$, there is nothing more to prove since such $S_i$ must be an edge by Lemma 7, hence such $S_i$’s are disjoint by our definition of a branch. Now suppose that $k < n/3$. Then a part $S_i$ satisfying $|\partial _v S_i| = 2$ and $\partial _v S \cap V(S_i) = \emptyset$ must be an edge whose both ends are connected to leaves. Thus the number of such $S_i$’s cannot exceed $(n-k)/2$. This means that there are at least $(n-k)/2$ parts with $|\partial _v S_i| \ge 3$. Since such $S_i$ makes the left hand side of (4.1) increase at least by one, we conclude that

$$\begin{aligned} |\partial _v S| = |\partial _v (S_1 \cup \cdots \cup S_n)| \ge \frac{n-k}{2} \ge \frac{n}{3} \end{aligned}$$

since $k < n/3$. This completes the proof. $\square$

The approach used in the previous proof, that is, partitioning $S$ into parts and using Lemma 9, has some problems when $G$ is not normal. Let $\Lambda$ be the graph of Fig. 1a given in the introduction, and for each $i =1,2,\ldots ,n$, let $S_i$ be a copy of $\Lambda$. We next connect them back to back as in Fig. 4 and obtain a new graph $S := S_1 \cup S_2 \cup \cdots \cup S_n$. Also suppose $S$ is enclosed by the union of two faces with huge face degrees. Then even though each $S_i$ satisfies the inequality $|V(S_i)| \le 3 |\partial _v S_i|$, we cannot pass this inequality to $S$; i.e., we have $|\partial _v S|/|V(S)| \rightarrow 0$ as $n \rightarrow \infty$. As we saw in the previous proof, however, this problem cannot occur when $G$ is normal. The next lemma says that it cannot happen either if $\jmath (G^*)>0$.

Fig. 4

A problem when partitioning into polygons

Lemma 10

Suppose $\jmath (G^*)>0$, and let $S$ be a finite simply connected subgraph of $G$ satisfying the following two properties:

• (a) every branch of $S$ is a path; i.e., a finite union of consecutive edges without self-intersections;

• (b) $P \cap P' \cap P'' = \emptyset$ for every three distinct parts $P, P', P''$ of $S$.

Then there is an absolute constant $C$ such that $|V(S)| \le C |\partial _v S|$.

Note that the subgraph $S$ in Lemma 10 has the following property: for any vertex $v \in V(S)$ and every sufficiently small neighborhood $U \ni v$ in $\mathbb {R}^2$, $U \setminus (S \cup D(S))$ has at most two components.

Proof

Let $\{ v_1, v_2, \ldots , v_m \}$ be an enumeration of $\partial _v S$ along the boundary of $S$. In other words, when walking along the topological boundary of $S \cup D(S)$ either clockwise or counterclockwise, we enumerate the vertices in $\partial _v S$ in the order we encounter them, allowing some multiple counts. However, any vertex in $\partial _v S$ will not be counted more than twice by the assumptions (a) and (b). Consequently we have $2|\partial _v S| \ge m$.

Note that $S$ is a simply connected graph with no outbound edge in $E(G) \setminus E(S)$ between $v_i$ and $v_{i+1}$, where $i$ is in mod $m$. Thus for each $i \in \{1, 2, \ldots , m\}$, there is the face $f_i$ attached to $S$ between $v_i$ and $v_{i+1}$. To be precise, $f_i$ is the face in $F(G) \setminus F(S)$ such that $E(f_i)$ contains all the edges in $\partial _e S$ between $v_i$ and $v_{i+1}$ (Fig. 5).

Fig. 5

A sketch of a subgraph satisfying the assumptions in Lemma 10; this graph consists of 6 polygons and 5 edges, and dotted lines indicate the faces attached to $S$; the section that does not belong to $T$ would be some union of faces in $F(G) \setminus F(T)$

Let $T$ be the subgraph of $G$ such that $V(T) = V(S) \cup \bigcup _{i=1}^m V(f_i)$. Definitely $T$ is a face graph with $\partial _f T \subset \{ f_1, f_2, \ldots , f_m \}$, hence our assumption $\jmath (G^*)>0$ implies that $|V(T^*)| \le C_1 |\partial _v T^*|$ for $C_1 = \jmath (G^*)^{-1}$, or

$$\begin{aligned} |F(T)| \le C_1 |\partial _f T| \le C_1 \cdot m \le 2C_1 |\partial _v S|. \end{aligned}$$

Thus by (3.1) we have

$$\begin{aligned} |V(S)|&= |E(S)| - |F(S)| + 1 \le 2 |\partial _v S| + 2|F(S)| \\&\le 2 |\partial _v S| + 2|F(T)| \le (2+ 4C_1) |\partial _v S|, \end{aligned}$$

as desired. $\square$

Corollary 11

Suppose $G$ is a proper planar graph with bounded face degrees such that $|V(T)|\le C|\partial _v T|$ for every polygon $T \subset G$. If $S$ is a simply connected subgraph of $G$ satisfying the conditions (a) and (b) in Lemma 10, then $|V(S)| \le C_1 |\partial _v S|$ for some constant $C_1$ not depending on $S$.

Proof

We follow the proof of Theorem 2, the normal case, and enumerate the parts $S_1, S_2, \ldots , S_n$ of $S$ so that they satisfy the conditions (a), (b), and (c) of Lemma 9. Then as in Lemma 10, we enumerate $\partial _v S$ by $v_1, v_2, \ldots , v_m$, where some vertices are counted twice, and let $f_1, f_2, \ldots , f_m$ be the faces attached to $S$ between $v_i$ and $v_{i+1}$, where $i$ is in mod $m$.

By the definition of a part, we have $\partial _e S \cap E(S_i) \ne \emptyset$ for each $i=1,2,\ldots , n$, so we must have $|\partial _e S| \ge n$. On the other hand, face degrees of $G$ are bounded above, say by $M$, so the number of edges in $E(f_i) \cap \partial _e S$ cannot exceed $M$. Thus the inequality $m M \ge |\partial _e S|$ holds. Since $m \le 2|\partial _v S|$, we have $|\partial _v S| \ge n/(2M)$. The corollary follows from Lemma 9. $\square$

The problem in Fig. 4 is caused by the fact that face degrees of $G$ are not bounded, and we have seen so far that this phenomenon does not occur under the assumptions of either Theorem 1 or Theorem 2. However, there is still a problem in partitioning a subgraph into leaves and branches, since we still have to worry about the unboundedness of vertex degrees. For example the proof in Lemma 10 does not work for a general subgraph $S \subset G$ since when one walks along the topological boundary of $S \cup D(S)$, there may be a vertex in $\partial _v S$ which appears too many times. So to overcome this obstacle, one may need a different kind of partition.

Lemma 12

Suppose $G$ is a proper planar graph and $S$ is a finite simply connected subgraph of $G$. Then there exists a partition $S_1 \cup S_2 \cup \cdots \cup S_n = S$ which satisfies the conditions (b), (c), and (d) of Lemma 9. Furthermore, we can make the partition so that each $S_i$ satisfies the conditions (a) and (b) of Lemma 10.

Proof

Suppose $S \subset G$ is given, and let $V_1 := \{L_1, L_2, \ldots , L_k \}$ be the set of all the leaves of $S$. Define $V^i$, $i=1,2, \ldots , k$, such that

$$\begin{aligned} V^i := \{ v \in \partial _v L_i : \text{ there } \text{ exists } \text{ an } \text{ edge } e \in E(S) \setminus E(L_i) \text{ with } \text{ one } \text{ end } \text{ at } v \}. \end{aligned}$$

Then by reducing each $L_i$ to a vertex, connecting it to the vertices in $V^i$, and keeping the rest of $S$ unchanged, we get a new finite tree $T$ (Fig. 6). The reason we add to $T$ the vertices in $V^i$ is because we do not want to change the combinatorial pattern of $S$. Formally, $T$ is the graph with $V(T) := V_1 \cup V_2 \cup V_3$, where $V_1$ is as above, $V_2 := V(S) \setminus V(L_1 \cup L_2 \cup \cdots \cup L_k)$, and $V_3 := \bigcup _{i=1}^k V^i$, and we define the edge set $E(T)$ so that $[v, w] \in E(T)$ if one of the following holds: (1) $v, w \in V_2 \cup V_3$ and $[v, w] \in E(S)$, or (2) $v \in V_1, w \in V_3$, and $w \in V(v)$, or (3) $v \in V_3, w \in V_1$, and $v \in V(w)$. Such $T$ must be a tree since $S$ is simply connected.

Fig. 6

A sketch of a simply connected graph $S$ (left) and the tree $T$ obtained from $S$ (right); on the tree $T$, the symbols filled circles, open circles and multiplication signs indicate the vertices in $V_1$, $V_2$, and $V_3$, respectively

In $T$, let $A = \{ v \in V(T) : \deg _T v \ge 3 \}$. Here $\deg _T v$ denotes the number of edges in $T$ with one end at $v$. Then we consider $T$ a simplicial complex, and let $\{ T_1, T_2, \ldots , T_m \}$ be the set of the closures of each components of $T \setminus A$ (Fig. 7). Note that each $T_j$ is isomorphic to a finite path. Moreover for $i \ne j$, $T_i \cap T_j$ is either empty or a vertex in $A$, hence we can enumerate $\{T_j\}$ so that $T_1 \cup T_2 \cup \cdots \cup T_{j}$ is connected for $j =1,2, \ldots , m$ and $(T_1 \cup T_2 \cup \cdots \cup T_{j-1}) \cap T_j$ is a single vertex for $j =2,3, \ldots , m$.

Fig. 7

$T$ is partitioned so that each $T_j$ is a path (top), and $S$ is partitioned associated with the partition of $T$ (bottom)

For each $j$ we assign a subgraph $S_j \subset S$ in an obvious way, but some modification is needed. For $S_1$, we define it so that

$$\begin{aligned} V(S_1) = \bigl ( V(T_1) \cap (V_2 \cup V_3) \bigr ) \cup \bigcup _{v \in V(T_1) \cap V_1} V(v), \end{aligned}$$

and for $j =2,3, \ldots , m$ we define $S_j$ so that

$$\begin{aligned} V(S_j) = \bigl ( V(T_j) \cap (V_2 \cup V_3) \bigr ) \cup \bigcup _{v \in V(T_j \setminus (T_1 \cup \dots \cup T_{j-1})) \cap V_1} V(v). \end{aligned}$$

In other words, $S_j$ is the graph consisting of the vertices in $T_j \cap (V_2 \cup V_3)$ and the leaves in $T_j \cap V_1$, but from $S_j$ we remove the leaf in $T_1 \cup \cdots \cup T_{j-1}$, if any. But if a leaf is removed from $S_j$, it must correspond to a vertex $v = L_i \in V(T)$ such that $\{ L_i \} =(T_1 \cup T_2 \cup \cdots \cup T_{j-1}) \cap T_j$. Then since $T_j$ contains a vertex in $V^i$, $(S_1 \cup \cdots \cup S_{j-1}) \cap S_j$ must be a single vertex. Clearly $(S_1 \cup \cdots \cup S_{j-1}) \cap S_j$ is also a single vertex when no leaf is removed from $S_j$.

Some of $S_j$ could be just a vertex in $V_3$, so we eliminate all such $S_j$’s from the list. Now we have just obtained a sequence of subgraphs $\{ S_{n_1}, S_{n_2}, \ldots , S_{n_s} \}$ which satisfies the condition (c) of Lemma 9. The condition (b) of Lemma 9 easily follows from the construction. Moreover, since each $T_{n_i}$ is a path, each $S_{n_i}$ satisfies the conditions (a) and (b) of Lemma 10.

Now it remains to verify the condition (d) of Lemma 9. Let $B := \{ v \in V(T) : \deg _T v =1\}$. If $v \in B$, then $v \notin V_3$ by the definition of $V^i$. Thus $v \in V_1 \cup V_2$. If $v \in V_2$, then $v$ is in fact a vertex in $\partial _v S$. If $v \in V_1$, it corresponds to a leaf $L_i$ with $|V^i| =1$. Then since $|\partial _v L_i| \ge 2$ by Lemma 7, we can assign $v$ to a vertex $w \in \partial _v S \setminus V_3$. Thus there exists an injection map from $B$ into $\partial _v S$, so the inequality $|B| \le |\partial _v S|$ holds.

Now in $T$, we replace each $T_j$ by an edge and get another tree $T'$. Then the number of edges in $T'$ is exactly $m$, and every vertex in $T'$ has degree either 1 or $\ge 3$. Also the number of vertices $v \in V(T')$ with $\deg _{T'} v =1$ is exactly $|B|$. Therefore by a computation similar to (3.1) we obtain

$$\begin{aligned} m = |E(T')| \le 2|B| \le 2 |\partial _v S|. \end{aligned}$$

Since $s \le m$, we conclude that the sequence $\{ S_{n_1}, S_{n_2}, \ldots , S_{n_s} \}$ also satisfies the condition (d) of Lemma 9. Since $S = S_{n_1} \cup S_{n_2} \cup \cdots \cup S_{n_s}$, this finishes the proof. $\square$

Proof of Theorems 1 and 2

Theorem 1(a) was already proved. For (b) of Theorem 1, the implication $\jmath (G^*)>0 \rightarrow \jmath (G)>0$ is a consequence of Lemmas 9, 10, and 12, and the converse comes from the duality. Theorem 1(c) is an easy consequence of Theorem 1(a) and (b). In fact, for a simply connected subgraph $S \subset G$ we have

$$\begin{aligned} \text{ Vol }(S)=\sum _{v \in V(S)} \deg v \le 3 |\partial S| + 6|V(S)|, \end{aligned}$$

which comes from the dual property of (3.3). Thus the inequality $\jmath (G)>0$ implies $\imath (G)>0$, because we always have $|\partial _v S| \le |\partial S|$. Now the other inequalities in Theorem 1(c) follow from Theorem 1(a) and (b), and a computation similar to the above. We leave the details to the readers.

The normal case of Theorem 2 was already proved, and the case when face degrees of $G$ are bounded comes from Lemmas 9, 12, and Corollary 11. This completes the proof of Theorems 1 and 2. $\square$

5 Combinatorial Curvatures and Strong Isoperimetric Inequalities

In this section we deal with combinatorial curvatures and prove Theorem 3. But as explained in the introduction, Theorem 3(a) was essentially proved in [37]. To see it, and to prove Theorem 3(b), suppose $S$ is a subgraph of a proper graph $G$. As before, we can assume that $S$ is simply connected without loss of generality.

When $\overline{\phi }(G) < 0$, Woess showed the inequality $|E(S)| \le C |\partial _v S|$, where $C$ is an absolute constant, in the proof of Theorem 1 of [37]. But since $|V(S)| \le |E(S)|+1 \le 2|E(S)|$ by Euler’s formula, the conclusion $\jmath (G)>0$ follows immediately. When $\overline{\chi }(G) < 0$, the inequality $|F(S)| \le C |\partial _v S|$ was obtained in the proof of Theorem 2(b) of [37], where $C$ is an absolute constant. Then by (3.1) and Euler’s formula we have

$$\begin{aligned} |V(S)| = |E(S)|-|F(S)|+1 \le 2|\partial _v S| + 2|F(S)| - 2 \le (2+2C)|\partial _v S|, \end{aligned}$$

(5.1)

showing that $\jmath (G)>0$.

We next consider Theorem 3(b). When vertex degrees of $G$ are bounded, Theorem 3(b) follows from Theorem 2(a) of [37] as explained in the introduction, but let us prove it in a different way. Since $\overline{\psi }(G) = \overline{\chi }_1(G^*)$, where $\overline{\chi }_1(G)$ is defined in (2.2), the assumption $\overline{\psi }(G) < 0$ implies the inequality $\overline{\chi }_1(G^*) <0$. Then we follow the proof of Theorem 2(b) of [37] and use (5.1), and confirm that there exists an absolute constant $C$ such that $|V(S)| \le C |\partial _v S|$ for every polygon $S \subset G^*$. Thus we have $\jmath (G^*) >0$ by Theorem 2 if either $G^*$ is normal or face degrees of $G^*$ are bounded. Since $G$ is normal if and only if $G^*$ is normal, and face degrees of $G^*$ are bounded if and only if vertex degrees of $G$ are bounded, Theorem 3(b) follows from Theorem 1(b).

For Theorem 3(c), we construct a planar graph $G$ such that $\overline{\psi }(G) < 0$ but $\jmath (G) =0$. Note that such graph cannot be normal.

For $n \in \mathbb {Z}$, let $S_n$ be the finite graph such that

$$\begin{aligned} V(S_n) = \big \{ o_n, o_{n+1}, b_1^n, b_2^n, v_1^n, v_2^n, \ldots , v_{2|n|-1}^n, v_{2|n|}^n \big \} \end{aligned}$$

with edges $[o_{n+i}, b_j^n], [o_{n+i}, v_{2k-1}^n], [o_{n+i}, v_{2k}^n],$ and $[v_{2k-1}^n, v_{2k}^n]$, where $0 \le i \le 1$, $1 \le j \le 2$, and $1 \le k \le |n|$. Then for each $n \in \mathbb {Z}$, $S_n$ and $S_{n+1}$ share the vertex $o_{n+1}$, so $S := \bigcup _{n=-\infty }^\infty S_n$ is a connected planar graph. Furthermore, we can embed it into $\mathbb {R}^2$ in such a way that each $v_k^n$ is enclosed by the cycle $[o_n, b_1^n] \cup [b_1^n, o_{n+1}] \cup [o_{n+1}, b_2^n] \cup [b_2^n, o_{n}]$ (see Fig. 8).

Fig. 8

The graph $S$

On the unbounded faces of $S$, we add vertices and edges so that the resulting graph $G$ satisfies the following properties: $G$ is a simple proper planar graph with $3 \le \deg v, \deg f < \infty$ for every $v \in V(G)$ and $f \in F(G)$, $\deg v \ge 7$ for every added vertex $v \in V(G) \setminus V(S)$, $\deg b_j^n \ge 7$ for $j=1,2$ and $n \in \mathbb {Z}$, and $\deg o_n \ge 14 |n| + 14$ for all $n \in \mathbb {Z}$. In other words, we for example triangulate both of the unbounded faces of $S$ so that every added vertices and $b_j^n$’s are of degree at least 7 and the degrees of $o_n$ are huge enough. Note that this can be done by mathematical induction.

It is easy to see that $\kappa (G)=\jmath (G)=0$ since $|\partial _v S_n| = |\partial _e S_n|=4$ but $|F(S_n)| = 3|n| +1$ and $|V(S_n)|=2|n| +4$. On the other hand, we have $\psi (v) \le -1/6$ if $v \in V(G) \setminus V(S)$ or $v = b_j^n$ for some $j=1,2$ and $n \in \mathbb {Z}$. Also direct computation shows that

$$\begin{aligned} \psi (v_k^n)&= 1 - \frac{3}{2} + \frac{2}{3} + \frac{1}{4} = \frac{5}{12} \quad \text{ for } \text{ all } n \in \mathbb {Z} \quad \text{ and } \quad 1 \le k \le 2|n|;\\ \psi (o_n)&\le 1 - \frac{\deg o_n}{2} + \frac{\deg o_n}{3} \le - \frac{ 7 |n| +4}{3} \quad \text{ for } \text{ all } n \in \mathbb {Z}. \end{aligned}$$

Thus the vertex curvature function $\psi$ assumes a positive value only at $v_k^n$, but they are dominated by the negative vertex curvature at $o_n$. In fact, for each $o_n$ there are at most $4|n|+2$ neighboring vertices $v_k^n$ and $v_k^{n-1}$, so

$$\begin{aligned} \psi (o_n) + \sum _{k=1}^{2|n|} \psi (v_k^n) + \sum _{k=1}^{2|n-1|} \psi (v_k^{n-1}) \le - \frac{ 7 |n| +4}{3} + \frac{5(4|n|+2)}{12} = -\frac{4|n| +3}{6}. \end{aligned}$$

This means that if $T$ is a finite connected subgraph of $G$ with $|V(T)| \ge 3$, then $\sum _{v \in V(T)} \psi (v) \le -|V(T)|/6$. Consequently we have $\overline{\psi }(G) \le -1/6 < 0$, and this completes the proof of Theorem 3. Note that the face graph $U_n \subset G^*$ with $F(U_n)= V(U_n^*)=\{ v_k^n : 1 \le k \le 2|n| \}$ is a connected graph which looks similar to the one in Fig. 4, while $U_n^*$ is a disconnected graph in $G$ (Fig. 9).

Fig. 9

The dual graph of $G$; the subgraph $U_2$ corresponds to the disconnected graph $U_2^* = \big [v_1^2, v_2^2\big ] \cup \big [v_3^2, v_4^2\big ]$

6 Gromov Hyperbolicity and Strong Isoperimetric Inequalities

Let $X$ be a geodesic metric space; that is, $X$ is a metric space such that for every $a, b \in X$ there is a geodesic line segment $\gamma$ from $a$ to $b$ such that $\text{ dist }(a,b)= \text{ length }(\gamma )$. Then $X$ is called $\delta$-hyperbolic if every geodesic triangle $\triangle \subset X$ is $\delta$-thin; i.e., any side of $\triangle$ is contained in the $\delta$-neighborhood of the union of the other two sides. If $X$ is $\delta$-hyperbolic for some $\delta \ge 0$, we just say that $X$ is hyperbolic in the sense of Gromov, or Gromov hyperbolic. For other equivalent definitions and general theory about Gromov hyperbolic spaces, we refer [10, 18, 20]. Note that every connected graph can be realized as a geodesic metric space, where the metric is the simplicial metric such that every edge is of length 1.

Now suppose $\varphi : [\alpha , \beta ] \subset \mathbb {R} \rightarrow X$ is a path; i.e., a continuous function. We say that $\varphi$ is $t$-detour if there exists a geodesic segment $\gamma$ from $\varphi (\alpha )$ to $\varphi (\beta )$ and a point $z \in \gamma$ such that $\text{ Im } (\varphi ) \cap B(z, t) = \emptyset$. Here $B(z,t)$ denotes the open ball with center $z$ and radius $t$. The detour growth function $g_X : (0, \infty ) \rightarrow [0, \infty ]$ is defined by

$$\begin{aligned} g_X (t) := \inf \{ \text{ length }(\text{ Im }\varphi ) : \varphi \text{ is } \text{ a } t \text{-detour } \text{ map } \} \end{aligned}$$

with the convention $g_X (t) = \infty$ when there is no rectifiable $t$-detour map. Then it is known [7] that a geodesic metric space $X$ is Gromov hyperbolic if and only if $\lim _{t \rightarrow \infty } g_X (t) /t = \infty$, which is what we will use for a proof of Theorem 6.

Suppose $X_1$ and $X_2$ are metric spaces. A function $f: X_1 \rightarrow X_2$ is called a rough isometry, or quasi-isometry, if there exist constants $A \ge 1$, $B \ge 0$, and $C \ge 0$ such that for all $x, y \in X_1$ we have

$$\begin{aligned} \frac{1}{A} \, \text{ dist }(x,y) - B \le \text{ dist }\bigl ( f(x), f(y) \bigr ) \le A \, \text{ dist }(x,y) + B, \end{aligned}$$

and for every $w \in X_2$ there exists $x \in X_1$ such that $\text{ dist }(f(x), w) \le C$. The notion of rough isometries was introduced by Kanai [24] and Gromov [19]. We say that $X_1$ is roughly isometric to $X_2$ if there exists a rough isometry from $X_1$ to $X_2$, and it is not difficult to see that rough isometries define an equivalence relation on the space of metric spaces. Moreover, it is well known that if $X_1$ is roughly isometric to $X_2$, then $X_1$ is Gromov hyperbolic if and only if $X_2$ is Gromov hyperbolic (cf. [10, p. 35] or [8, p. 6]), and if $G_1$ and $G_2$ are roughly isometric graphs of bounded vertex degree, then $\jmath (G_1)>0$ if and only if $\jmath (G_2) >0$ [34, Theorem (7.34)]. Note that we already used the latter fact in the introduction.

It is well known that if $G$ is a planar graph with $\jmath (G)>0$, then the growth rate of the volume of combinatorial balls in $G$ is exponential. To be precise, let us fix $v \in V(G)$, and suppose $B_{n}$ is the combinatorial ball of radius $n$ and centered at $v$; i.e., $B_n$ is the subgraph of $G$ such that $w \in V(B_n)$ if and only if the distance between $v$ and $w$ is less than or equal to $n$. We also let $B_0 = \{v\}$. Then because $\partial _v B_{n} \subset V(B_n) \setminus V(B_{n-1})$, we deduce from the definition of $\jmath (G)$ that

$$\begin{aligned} |V(B_n)|&= |V(B_{n-1})| + |V(B_n) \setminus V(B_{n-1})| \ge |V(B_{n-1})| + |\partial _v B_{n}|\\&\ge |V(B_{n-1})| + \jmath (G) |V(B_{n})| \ge \bigl ( 1 + \jmath (G) \bigr ) |V(B_{n-1})|. \end{aligned}$$

Since $|V(B_0)|=1$, this inequality implies that

$$\begin{aligned} |V(B_n)| \ge \bigl (1 + \jmath (G) \bigr )^n \end{aligned}$$

(6.1)

for all $n \in \mathbb {N}$.

One more ingredient we need for the proof of Theorem 6 is Sperner’s Lemma applied to the two-dimensional case. Let $T$ be a triangulation of a topological triangle with vertices $A_1$, $A_2$, and $A_3$. We also assume that a function $h: V(T) \rightarrow \{1,2,3\}$ satisfies the following properties: $h(A_i) =i$ for $i=1,2,3$, and if $v \in V(T)$ lies on the side $A_iA_j$, $i \ne j$, then $h(v) \in \{i, j\}$. Such $h$ is called a Sperner Labeling of $T$, and Sperner’s Lemma [8, p. 124] says that there exists a face (triangle) $f \in F(T)$ such that $h(V(f)) = \{1,2,3\}$; i.e., if $v, w \in V(f)$ and $v \ne w$, then $h(v) \ne h(w)$ (see Fig. 10).

Fig. 10

A Sperner labeled triangulation of a triangle

Now we are ready to prove Theorem 6. For (a), the following proof is suggested by Mario Bonk. Suppose $G$ is a planar graph of bounded face degree such that $\kappa (G) > 0$, or equivalently, $\jmath (G) > 0$. We assume without loss of generality that $G$ is a triangulation graph of the plane, since otherwise we can add bounded number of vertices and edges on every face of $G$ to obtain a triangulation graph $G'$. This is possible because face degrees of $G$ are bounded. Then obviously $G'$ is roughly isometric to $G$, so we have $G$ is Gromov hyperbolic if and only if $G'$ is Gromov hyperbolic. Moreover, in this case $(G')^*$ is also roughly isometric to $G^*$, so Theorem 1(b) and Theorem (7.34) of [34] imply that $\jmath (G') > 0$ since vertex degrees of $(G')^*$ and $G^*$ are bounded. (Alternatively, it is not difficult to show that $\kappa (G') > 0$ directly.)

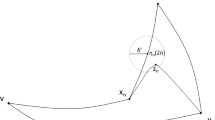
Let $\varphi$ be a $t$-detour map from $a \in G$ to $b \in G$. By the definition there exist a geodesic segment $\gamma$ from $a$ to $b$, and a point $z \in \gamma$ such that $\varphi \cap B(z, t) = \emptyset$, where we denoted $\text{ Im }(\varphi )$ by $\varphi$ for simplicity. Furthermore by shrinking $\gamma$ and $\varphi$ if necessary, we can assume that $\gamma$ meets $\varphi$ only at $a$ and $b$. Thus we can treat $\gamma \cup \varphi$ as a topological triangle with vertices $a, b$, and $z$ (see Fig. 11).

Fig. 11

A detour map $\varphi$

Let $\Gamma$ be the subgraph of $G$ whose vertices are those on $\gamma$, $\varphi$, and the bounded component of $G \setminus (\gamma \cup \varphi )$. Then since $G$ is a triangulation graph, $\Gamma$ becomes a triangulation of the 2-dimensional simplex $\triangle$ with $\partial \triangle = \gamma \cup \varphi$. Let $\gamma _0 = \gamma \cap B(z, t/4)$, $\gamma _a$ be the component of $\gamma \setminus \gamma _0$ containing $a$, and $\gamma _b$ be the component of $\gamma \setminus \gamma _0$ containing $b$.

Define

$$\begin{aligned} A_1&:= \{ v \in V(\Gamma ) : \text{ dist }(v, \gamma _0) \le t/4 \text{ and } \text{ dist }(v, \gamma _0) \le \text{ dist }(v, \gamma _a \cup \gamma _b) \},\\ A_2&:= \{ v \in V(\Gamma ) \setminus A_1 : \text{ dist }(v, \gamma _a) < \text{ dist }(v, \gamma _b) \}, \\ A_3&:= \{ v \in V(\Gamma ) \setminus A_1 : \text{ dist }(v, \gamma _b) \le \text{ dist }(v, \gamma _a) \}. \end{aligned}$$

It is clear that $\varphi \cap A_1 = \emptyset$. Otherwise there exists $v \in \varphi$ and $w \in \gamma _0$ such that $\text{ dist }(v, w) \le t/4$, so we must have $\text{ dist }(v, z) \le \text{ dist }(v, w) + \text{ dist }(w, z) \le t/2$, contradicting the assumption $\varphi \cap B(z, t) = \emptyset$. Moreover if $v \in \gamma$ lies between $a$ and $z$, that is, if $v$ lies on the side opposite the vertex $b$ of $\gamma \cup \varphi$, then $v$ is definitely in either $A_1$ or $A_2$. Similarly if $v \in \gamma$ lies between $b$ and $z$, then $v$ belongs to $A_1 \cup A_3$. Thus if we label every vertex $v \in A_i$ by $i \in \{ 1,2,3 \}$, it becomes a Sperner labeling. Hence there exists a triangle in $\Gamma$ with vertices $v_i \in A_i$, $i=1,2,3$, by Sperner’s lemma.

Let $B:=B(v_1, t/8)$ and we claim that $B \cap (\varphi \cup \gamma ) = \emptyset$ for $t \ge 12$. First, note that $B \cap \varphi = \emptyset$ since otherwise there exists $v \in \varphi$ such that $\text{ dist }(v,z) \le 5t/8$. If $\text{ dist }(v_1, \gamma ) \le t/8$, then because $v_1 \in A_1$ we have $\text{ dist }(v_1, \gamma _0) \le t/8$. But because $v_2 \in A_2$ and

$$\begin{aligned} \text{ dist }(v_2, \gamma _0) \le 1 + \text{ dist }(v_1, \gamma _0) \le 1 + t/8 \le t/4 \end{aligned}$$

for $t \ge 8$, there exists $x \in \gamma _a$ such that

$$\begin{aligned} \text{ dist }(v_2, x) = \text{ dist }(v_2, \gamma _a) < \text{ dist }(v_2, \gamma _0) \le 1 + t/8. \end{aligned}$$

Similarly there exists $y \in \gamma _b$ such that $\text{ dist }(v_3, y) \le 1 + t/8$, so we have

$$\begin{aligned} \text{ dist }(x,y) \le \text{ dist }(x,v_2) + \text{ dist }(v_2,v_3) + \text{ dist }(v_3,y) < 3 + t/4. \end{aligned}$$

(6.2)

On the other hand, $\gamma$ is a geodesic segment and $B(z, t/4)$ separates $\gamma _a$ and $\gamma _b$. Then because $x \in \gamma _a$ and $y \in \gamma _b$, we must have $\text{ dist }(x,y) \ge t/2$. This contradicts (6.2) for $t \ge 12$, so the claim follows.

Note that

$$\begin{aligned} |\partial _e \Gamma | = \text{ length }(\varphi ) + \text{ length }(\gamma ) \le 2 \cdot \text{ length }(\varphi ). \end{aligned}$$

Moreover because $v_1 \in V(\Gamma )$ and $B \cap (\varphi \cup \gamma ) = \emptyset$ for $t \ge 12$, we must have $B \subset \Gamma$ in this case. Thus if $t \ge 12$ and $8n \le t < 8(n+1)$ for some $n \in \mathbb {N}$, the inequality (6.1) implies

$$\begin{aligned} |V(\Gamma )| \ge |V(B)| \ge \bigl ( 1+\jmath (G) \bigr )^n \ge \bigl ( 1+\jmath (G) \bigr )^{t/8-1}. \end{aligned}$$

Now because $|\partial _e \Gamma | \ge |\partial _v \Gamma |$, we have

$$\begin{aligned} \text{ length }(\varphi ) \ge \frac{1}{2} |\partial _e \Gamma | \ge \frac{1}{2} |\partial _v \Gamma | \ge \frac{1}{2}\jmath (G) |V(\Gamma )| \ge \frac{1}{2}\jmath (G)\bigl ( 1+\jmath (G) \bigr )^{t/8-1}. \end{aligned}$$

This proves that $g_G (t) / t \rightarrow \infty$ as $t \rightarrow \infty$, where $g_G$ is the detour growth function introduced at the beginning of this section. We conclude that $G$ is Gromov hyperbolic by Ref. [7].

We remark here that the above argument can be considered an alternative proof of (a part of) Theorem 2.1 in [10, Chap. 6], where it is proved that every reasonable complete simply connected Riemannian manifold satisfying a linear isoperimetric inequality must be Gromov hyperbolic. In fact, one only needs to modify some terminologies in the above proof so that they are adequate to the continuous case, and use the continuous version of Sperner’s lemma [1, p. 378] instead of the combinatorial version. Since it is irrelevant to our subject, we omit the details here.

To prove Theorem 6(b), let us construct a normal planar graph $G_1$ which is Gromov hyperbolic but $\jmath (G_1)=\kappa (G_1)=0$ . Let $\Gamma _1$ be a triangulation of the plane such that $\deg v \ge 7$ for all $v \in V(\Gamma _1)$. Then obviously $\Gamma _1$ is Gromov hyperbolic. Choose a sequence of edges $e_n =[a_n, b_n] \in E(\Gamma _1)$ which are far away from each other, for instance $\text{ dist }(a_n, a_m) \ge 10$ for $n \ne m$, and let $f_n$ and $g_n$ be the triangular faces of $\Gamma _1$ sharing $e_n$. Also let $c_n$ and $d_n$ be the vertices of $f_n$ and $g_n$, respectively, which are not lying on $e_n$.

We obtain a new graph from $\Gamma _1$ by replacing $e_n$ by $n$-multiple edges and drawing a line from $c_n$ to $d_n$ (Fig. 12). We do this operation for all $n \in \mathbb {N}$, and let $G_1$ denote the resulting graph. $G_1$ is obviously normal. Moreover, $G_1$ is Gromov hyperbolic because it is roughly isometric to $\Gamma _1$. It is also easy to see that $\jmath (G_1)=\kappa (G_1)=0$, since if we let $S_n$ be the subgraph of $G_1$ such that $V(S_n)$ consists of $a_n, b_n, c_n, d_n$, and all the added vertices in $f_n \cup g_n$, then we have $|F(S_n)| = 2n+2$ and $|\partial _e S_n| =4$. This completes the proof of Theorem 6(b).

Fig. 12

Replacing $e_3$ with triple edges and drawing a diagonal line

The graph $G$ constructed in Sect. 5 also satisfies the properties in Theorem 6(b) except being normal. To explain this, first note that we could construct $G$ so that every face is of degree at most 4. Now if we let $S$ be the infinite subgraph of $G$ such that

$$\begin{aligned} V(S) = V(G) \setminus \{ v_k^n : n \in \mathbb {Z} \text{ and } 1 \le k \le 2|n| \}, \end{aligned}$$

then one can check that $S$ is a planar graph of bounded face degree such that every vertex has degree at least 7. Thus $S$ is Gromov hyperbolic by Corollary 4 and Theorem 6, so $G$ is also Gromov hyperbolic since it is roughly isometric to $S$.

For the last, we prove Theorem 6(c); i.e., construct a normal planar graph $G_2$ of bounded face degree such that $\imath (G_2)>0$ but not Gromov hyperbolic. The main idea here is to construct a graph with a structure far from being hyperbolic, but the simple random walk on it is transient.

We start with the square lattice graph $\Gamma _2$; i.e., $V(\Gamma _2) = \mathbb {Z} \times \mathbb {Z}$, and $\Gamma _2$ has an edge between $(n_1, m_1)$ and $(n_2, m_2)$ if and only if $|n_1 - n_2| + |m_1 - m_2| =1$. Let $O=(0,0)$ be the origin, and for each $n \in \mathbb {N}\cup \{0\}$ define $V_n$ as the set of vertices of $\Gamma _2$ whose combinatorial distance from $O$ is equal to $n$. Also for each $n \in \mathbb {N}$, let $E_n$ be the set of edges of $\Gamma _2$ connecting a vertex in $V_{n-1}$ to another one in $V_n$. Then as in Theorem 6(b) we replace each edge in $E_n$ by $\ell _n$-multiple edges, where the sequence $\{ \ell _n \}$ increases to infinity very fast but will be determined later. Finally we draw the lines $x=m + 1/2$ and $y = m+1/2$ for all $m \in \mathbb {Z}$. We can do this operation so that each vertical line $x=m+1/2$ meets no vertical edges, and meets every horizontal edge at most once. Of course we can draw the horizontal lines $y= m+1/2$ in a similar way, and let $G_2$ denote the obtained graph (Fig. 13).

Fig. 13

The graph $G_2$; it is drawn with $\ell _n =2n-1$ for aesthetic reasons, but $\ell _n$ should increase faster

It is clear that $G_2$ is not Gromov hyperbolic, since it is roughly isometric to $\Gamma _2$. Also one can immediately see that $G_2$ is normal, face degrees of $G_2$ are bounded above by 4, and $\jmath (G_2) = \kappa (G_2) =0$. So we only need to show that $\imath (G_2)>0$. Define $h:V(\Gamma _2) \rightarrow V(G_2)$ as the natural injection which maps each integer lattice point to itself, and suppose that $S$ is a finite subgraph of $G_2$. Let $N$ be the largest natural number such that $h(V_N) \cap V(S) \ne \emptyset$, and $W_1$ be the set of vertices of $S$ which lies in the region $\{(x,y): |x| + |y|<N+1/10\}$. If no such $N$ exists, we set $W_1 = \emptyset$. We also define $W_2$ as the set of vertices in $V(S) \setminus W_1$ lying on the intersection of two lines $x= k_1+1/2$ and $y=k_2+1/2$ for some $k_1, k_2 \in \mathbb {Z}$, and let $W_3 = V(S) \setminus (W_1 \cup W_2)$.

The vertices in $W_3$ must be on the ‘middle’ of some multiple edges, so each of them has a neighbor in $V_{l}$ for some $l \ge N+1$. Consequently $W_3 \subset \partial _v S$ and $|W_3| \le |\partial _v S| \le |\partial S|$. For $W_2$, the only neighbors of a vertex $v \in W_2$ are those at the ‘middle’ of some multiple edges. Then since $(k_1 + 1/2)+(k_2+1/2) \ge N+1/10$ implies $k_1 + k_2 + 1/2 \ge N+1/10$ for $k_1, k_2 \in \mathbb {N}$, every $v \in W_2$ is either in $\partial _v S$ or has a neighbor in $W_3$. Thus $|W_2| \le |W_3| + |\partial _v S| \le 2 |\partial S|$.

Suppose $W_1 \ne \emptyset$, and let $v \in h(V_N) \cap V(S)$. Also let us assume that there are $k$ edges in $\partial S$ with one end at $v$. Then by our construction $v$ must have at least $\ell _{N+1} - k$ neighbors in $W_3$, all of which are in $\partial _v S$. So we must have $|\partial S| \ge \ell _{N+1}$. On the other hand, if we denote by $C_n$ the number of vertices in $G_2$ lying in the region $\{(x,y): |x| + |y|<n+1/10\}$, then definitely $C_n$ depends only on $\ell _1, \ldots , \ell _n$ and $n$. Thus we can choose the sequence $\{ \ell _n \}$ so that $\ell _{n+1} \ge C_n$ for all $n \in \mathbb {N}$. This in particular implies that $|W_1| \le C_N \le \ell _{N+1} \le |\partial S|$, and note that the inequality $|W_1| \le |\partial S|$ is obviously true when $W_1 = \emptyset$.

So far we have shown that $|V(S)|=|W_1|+|W_2|+|W_3| \le 4 |\partial S|$, but this is enough to conclude $\imath (G_2) >0$ by considering the duality property of Lemma 8. This completes the proof of Theorem 6.

7 Further Remarks

One of the main assumptions of Theorem 1(b) is that $G$ is embedded into the plane locally finitely, so it must be a planar graph with only one end. Recently we have extended this result to the case when $G$ has finitely many ends [31]. Furthermore, if $G$ is normal, Theorem 1(b) remains valid even when $G$ has infinitely many ends.