1 Introduction

In combinatorial topology, the principal objects of study are combinatorial manifolds, which are abstract simplicial complexes together with additional local constraints. In this way, topological information is encoded purely combinatorially making the field of topology accessible to algorithmic methods. As a consequence, one topological manifold has a large number of combinatorially distinct presentations and attention has to be paid to the choice of a suitable combinatorial manifold. One way to find combinatorial manifolds which are easy to handle and easy to analyze is to reduce a given combinatorial manifold in the number of its simplices using bistellar moves (see [6]), another method is to construct highly symmetric combinatorial manifolds which can be described efficiently just by the generators of its symmetry and a system of orbit representatives of the simplices.

Here we will focus on the latter technique. More precisely, we will look at n-vertex combinatorial manifolds which do not change under a vertex-shift of type v↦v+1modn. Such combinatorial manifolds will be called cyclic. These objects are interesting to investigate for several reasons. They account for the largest group of so-called transitive combinatorial manifolds, i.e. combinatorial manifolds which are globally defined by a local neighborhood of a single vertex. Cyclic combinatorial manifolds can be described using so-called difference cycles (cf. Definition 2.1), they are especially easy to analyze and easy to work with. Because of their easy combinatorial structure they allow theoretical proofs on a scale where non-symmetric combinatorial manifolds need complicated computer proofs or cannot be handled at all and other highly symmetric combinatorial manifolds fail to be easy to investigate because of the complicated structure of their symmetry.

As a consequence, cyclic combinatorial manifolds have been used to establish upper and lower bounds for combinatorial properties of simplicial complexes (see [22] for small triangulations of the d-torus and [23] for a set of several infinite families of combinatorial manifolds due to Kühnel and Lassmann), to prove tightness of existing upper and lower bounds (see [17, Theorem 5.5] for an infinite family of tight and minimal sphere bundles over the circle), and to provide example complexes that are easy to describe, efficient to store and easy to work with (see [1, Theorem 4] for the infinite family of the so-called Altshuler tori with dihedral automorphism group, [21] for a 2-neighborlyFootnote 1 infinite family of the 3-dimensional Klein bottle, and [7] for a 2-neighborly infinite family of the 3-torus). Altogether, cyclic combinatorial manifolds are a natural choice when looking for a combinatorial version of a topological manifold to work with.

In addition, most of the applications mentioned not only need single cyclic combinatorial manifolds but infinite families of such complexes to prove their respective results. Thus, providing construction principles for such families is of particular interest. In Sect. 3, we will present a simple combinatorial criterion to decide if a cyclic d-dimensional combinatorial manifold can be modified in its description to give rise to an infinite number of cyclic d-dimensional combinatorial manifolds. In dimension d=3, we explain a similar condition which detects all cyclic combinatorial 3-manifolds that can be generalized in this way.

Furthermore, in Sect. 4 we classify all cyclic combinatorial 3-manifolds with up to 22 vertices. Thus, we significantly extend the number of triangulations where the findings from Sect. 3 can be applied in order to obtain further insights into the world of combinatorial 3-manifolds. The classification provides small and easy-to-handle combinatorial manifolds of 67 distinct topological 3-manifolds which can be used as a canonical choice to work with these particular topological manifolds on a combinatorial basis.

The classification itself is only the latest one in a line of other classifications dating back almost 30 years. Neighborly combinatorial 3-manifolds with dihedral automorphism group with up to 19 vertices as well as cyclic neighborly combinatorial 3-manifolds with up to 15 vertices have already been classified by Kühnel and Lassmann in 1985, see [21]. In 1999, a more general classification of all transitive combinatorial manifolds with up to 13 vertices was presented by Lutz in [29] (which also contains a classification of all transitive combinatorial d-manifolds up to 15 vertices in the cases d≤3 and d≥9). More recently, Lutz extended the classification of transitive combinatorial 2-manifolds up to 21 vertices (cf. [30]) and the classification of transitive combinatorial 3-manifolds up to 17 vertices (cf. [28]). These classification results have been proved to be useful as an extended set of small example triangulations with interesting properties [27], to obtain additional insights into upper bounds on minimal triangulations of 3-manifolds [31] and as a starting point to find infinite families of combinatorial manifolds [21].

Finally, the classification together with the results from Sect. 3 sets the ground work for many more results of similar nature. Most of this work is still in progress and will be presented separately in [10]. As a preview of this work we present an infinite family of cyclic combinatorial 3-manifolds of pairwise topologically distinct lens spaces in Sect. 5.

Remark 1.1

At this point it is important to stress that there is no canonical notion of an infinite family of cyclic combinatorial manifolds: any infinite set of cyclic combinatorial manifolds defines such a family. However, in order to be useful for applications such a family should be (i) easy to describe and (ii) easy to generate, i.e. given in precise terms of its combinatorial structure. In order to meet these requirements, we will focus on generalizations of cyclic combinatorial manifolds via arithmetic progressions for the entries of the orbit representatives of the respective complexes and will refer to the resulting infinite sets of cyclic combinatorial manifolds as infinite families.

2 Preliminaries

An abstract simplicial complex, C, can be seen as a combinatorial structure consisting of tuples 〈a 0,a 1,…,a d 〉, \(a_{i} \in\mathbb{Z}_{n}\), 0≤i≤d, where the n elements of \(\mathbb{Z}_{n}\) are referred to as the vertices of the complex (cf. [23]). The automorphism group, \(\operatorname{Aut}(C)\), of C is the group of all permutations σ∈S n of the vertices of C which do not change C as a whole. If \(\operatorname{Aut}(C)\) acts transitively on the vertices, C is called a transitive simplicial complex. If a transitive simplicial complex is invariant under the cyclic \(\mathbb {Z}_{n}\)-action v↦v+1modn, i.e. if for a complex C, possibly after a relabeling of the vertices, \(\mathbb{Z}_{n} = \langle( 0, 1, \ldots, n-1 ) \rangle\) is a subgroup of \(\operatorname{Aut}(C)\) then C is called a cyclic simplicial complex or a complex with transitive cyclic symmetry.

For cyclic simplicial complexes we have the following situation: Since the whole complex does not change under a vertex-shift of type v↦v+1modn, two tuples are in one orbit of the cyclic group action if and only if the differences modulo n of its vertices are equal. Hence, we can compute a system of orbit representatives by just looking at the differences modulo n of the vertices of all tuples of the simplicial complex. This motivates the following definition.

Definition 2.1

(Difference Cycle)

Let a i , 0≤i≤d, be positive integers such that \(n := \sum_{i=0}^{d} a_{i}\). The simplicial complex

$$ ( a_0 : \ldots: a_{d} ) := \mathbb{Z}_n \biggl\langle 0 , a_0 , \ldots, \sum_{i=0}^{d-1} a_i \biggr\rangle $$

is called difference cycle of dimension d on n vertices where G〈⋅〉 denotes the G-orbit of 〈⋅〉. The number of elements of (a 0:…:a d ) is referred to as the length of the difference cycle and a difference cycle of length n is said to be of full length.

If a simplicial complex C is a union of difference cycles of dimension d on n vertices and λ is a unit of \(\mathbb{Z}_{n}\) such that the complex λC (obtained by multiplying all vertex labels by λ modulo n) equals C, then λ is called a multiplier of C.

Note that for any unit \(\lambda\in\mathbb{Z}_{n}^{\times}\), the complex λC is combinatorially isomorphic to C. In particular, all \(\lambda\in\mathbb{Z}_{n}^{\times}\) are multipliers of the complex \(\bigcup_{\lambda\in\mathbb{Z}_{n}^{\times}} \lambda C\) by construction. The definition of a difference cycle above is equivalent to the one given in [23].

Difference cycles as well as other cyclic combinatorial structures have been thoroughly investigated under purely combinatorial aspects (see for example [25, Part V] for a work on cyclic Steiner systems in the field of design theory, see [14, Sect. III.4] for the highly symmetric Emch design). However, interpreting these well-known combinatorial structures as simplicial complexes and hence geometric objects is a relatively new development (see [19] for an interpretation of two-fold triple systems as singular surfaces or [41, Sect. 5.4] for an interpretation of Emch’s design as the quotient of a hyperbolic tesselation of 3-space).

A combinatorial manifold is a special kind of simplicial complex which is defined as follows: An abstract simplicial complex M is said to be pure, if all of its tuples are of length d+1, where d is referred to as the dimension of M. If, in addition, any vertex link of M, i.e. the boundary of a simplicial neighborhood of a vertex of M, is a triangulated (d−1)-sphere endowed with the standard piecewise linear structure, M is called a combinatorial d-manifold. Throughout this article, we will describe cyclic combinatorial manifolds as a set of difference cycles. In this way, many problems dealing with cyclic combinatorial manifolds can be solved in an elegant way.

One of the principal tools to analyze combinatorial manifolds is the use of a discrete Morse type theory following Kuiper, Banchoff and Kühnel [3, 4, 17, 24]. In this theory, the discrete analogue of a Morse function is given by a mapping from the set of vertices V of a combinatorial manifold M to the real numbers \(\mathbb{R}\) such that no two vertices have the same image, in this way inducing a total ordering on V. This mapping can then be extended to a function \(f: M \to\mathbb{R} \) by linearly interpolating the values of the vertices of a face of M for all points inside that face. f is called a regular simplexwise linear function or rsl-function on M.

A point x∈M is said to be critical for an rsl-function \(f:M \to\mathbb{R}\) if

$$H_{\star} \bigl(M_x , M_x \backslash\{ x \} , \mathbb{F} \bigr) \neq0 $$

where M x :={y∈M | f(y)≤f(x)} and \(\mathbb{F}\) is a field. Here, H ⋆ denotes an appropriate homology theory. It follows that no point of M can be critical except possibly the vertices. More precisely we call a vertex v critical of index i and multiplicity m if \(\beta_{i} (M_{v} , M_{v} \backslash\{ v \} , \mathbb{F}) = m\).

A result of Kuiper [24] states that the number of critical points of an rsl-function of M counted by multiplicity is an upper bound for the sum of the Betti numbers of M, hence extending the famous Morse relations from the smooth theory to the discrete setting.

The pre-image of a point under an rsl-function which does not meet any vertex of the surrounding combinatorial manifold is called a slicing. By construction, a slicing is an embedded co-dimension 1 submanifold which contains information about the topology of the surrounding manifold (see Figs. 1, 2 and 4 for slicings in the case d=3, and [42] for further details about slicings).

3 Infinite Families of Transitive Cyclic Combinatorial Manifolds

For cyclic combinatorial manifolds, one straightforward generalization of a given complex to an infinite family of cyclic combinatorial manifolds with increasing number of vertices can be constructed by finding a slicing of a cyclic combinatorial manifold which exhibits the symmetry of the surrounding manifold in a cyclic pattern, extending this pattern and then re-constructing a larger version of the original combinatorial manifold (cf. [41, Sect. 4.5]).

However, in this article we want to focus on when a combinatorial d-manifold given by a set of difference cycles can be generalized using arithmetic progressions for the entries of its difference cycles (cf. Remark 1.1). More precisely, for a combinatorial manifold M={d 1,…,d m } with n vertices represented by m difference cycles \(d_{i} = ( a_{i}^{0} : \ldots: a_{i}^{d} )\), 1≤i≤m, we define complexes M k ={d 1,k ,…,d m,k }, \(k > - \min_{1 \leq i \leq m} \{ a_{i}^{d} \}\), with n+k vertices and difference cycles \(d_{i,k} = ( a_{i}^{0} : \ldots: a_{i}^{d-1} : a_{i}^{d} + k )\), 1≤i≤m, and ask for a purely combinatorial condition on M to check whether (and for which range of k) the complexes M k are combinatorial manifolds (see Theorem 3.5 below). We will start with discussing the case d=3, where the “generalizability” of a cyclic combinatorial manifold is even equivalent to the following combinatorial criterion.

Theorem 3.1

Let M={d 1,…,d m } be a combinatorial 3-manifold with n vertices, represented by m difference cycles \(d_{i} = ( a_{i}^{0} : a_{i}^{1} : a_{i}^{2} : a_{i}^{3} )\), 1≤i≤m. Then the complex M k is a combinatorial manifold for all k≥0 if and only if \(a_{i}^{3} > \frac{n}{2}\) for all 1≤i≤m.

In order to prove Theorem 3.1 let us first take a look at a few lemmas.

Lemma 3.2

Let (a 0:…:a d ) be a difference cycle of dimension d on n vertices and 1≤k≤d+1 the smallest integer such that k∣(d+1) and a i =a i+k , 0≤i≤d−k. Then (a 0:…:a d ) has length \(\frac{nk}{d+1}\).

Proof

Since \(\sum_{i=0}^{d} a_{i} = n\) and a i =a i+k , 0≤i≤d−k, we have \(\sum_{i=0}^{d} a_{i} = \frac{d+1}{k} \sum_{i=0}^{k-1} a_{i}\) and hence \(\sum_{i=0}^{k-1} a_{i} = \frac{nk}{d+1}\). Keeping this in mind we have (all entries are computed modulo n)

$$\begin{aligned} &\biggl\langle 0 + \frac{nk}{d+1}, a_0 + \frac{nk}{d+1}, \ldots, \biggl(\sum_{i=0}^{d-1} a_i \biggr) + \frac{nk}{d+1} \biggr\rangle \\ &\quad = \biggl\langle \sum _{i=0}^{k-1} a_i , \sum _{i=0}^{k} a_i, \ldots, \sum _{i=0}^{d-1} a_i , 0 , a_0 , \ldots, \sum_{i=0}^{k-2} a_i \biggr\rangle \\ &\quad = \biggl\langle 0 , a_0, \ldots, \sum_{i=0}^{d-1} a_i \biggr\rangle . \end{aligned}$$

Hence, for the length ℓ of (a 0:…:a d ) we have \(\ell\leq\frac{nk}{d+1}\) and since k is minimal with k∣(d+1) and a i =a i+k , the upper bound is attained. □

Lemma 3.3

Let M k , k≥0, be an infinite family of cyclic combinatorial 3-manifolds with n+k vertices represented by the union of m difference cycles of full length. Then we have for the f-vectors of the vertex links

$$f \bigl(\operatorname{lk}_{M_0} (0) \bigr) = f \bigl(\operatorname {lk}_{M_k} (0) \bigr) = (2m+2, 6m, 4m) $$

for all k≥0. In particular, the number of vertices of \(\operatorname{lk}_{M_{k}} (0)\) does not depend on the value of k.

Proof

Since M k is the union of m difference cycles of full length, we have for the number of tetrahedra f 3(M k )=m(n+k) for all k≥0. Furthermore, as M k is cyclic, all vertices are contained in the same number of tetrahedra which have four vertices. By the fact that any facet of \(\operatorname{lk}_{M_{k}} (0)\) corresponds to a facet in M k containing 0 it follows that for the number of triangles of the link \(f_{2} (\operatorname{lk}_{M_{k}} (0)) = \frac{4m(n+k)}{n+k} = 4m\) holds, which is independent of k. Since for all k≥0 the link \(\operatorname{lk}_{M_{k}} (0)\) is a combinatorial 2-sphere, all edges of \(\operatorname{lk}_{M_{k}} (0)\) lie in exactly two triangles, hence \(f_{1} (\operatorname{lk}_{M_{k}} (0)) = 6m\). Finally, the Euler characteristic of the 2-sphere is 2, and by the Euler–Poincaré formula we have \(f_{0} (\operatorname{lk}_{M_{k}} (0)) = 2m+2\). □

Let us now come to the proof of Theorem 3.1.

Proof

Let M={d 1,…,d m } be a combinatorial 3-manifold with n vertices, represented by m difference cycles \(d_{i} = ( a_{i}^{0} : a_{i}^{1} : a_{i}^{2} : a_{i}^{3} )\), 1≤i≤m, such that \(a_{i}^{3} > \frac{n}{2} > a_{i}^{0} + a_{i}^{1} + a_{i}^{2}\) for all 1≤i≤m. For the link of vertex 0 in M we then have (all entries are computed modulo n)

$$\begin{aligned} &\operatorname{lk}_M (0) = \bigcup _{i=1}^{m} \bigl\{ \bigl\langle a_i^0, a_i^0 + a_i^1, a_i^0 + a_i^1 + a_i^2 \bigr\rangle , \bigl\langle - a_i^0, a_i^1, a_i^1 + a_i^2 \bigr\rangle , \bigl\langle - a_i^0 - a_i^1 , - a_i^1 , a_i^2 \bigr\rangle , \\ &\hphantom{\operatorname{lk}_M (0) = \bigcup _{i=1}^{m} \bigl\{ } \bigl\langle - a_i^0 - a_i^1 - a_i^2 , - a_i^1 - a_i^2 , - a_i^2 \bigr\rangle \bigr\} , \end{aligned}$$
(3.1)

and for the link of vertex 0 in M k (all entries are computed modulo n+k)

$$\begin{aligned} \operatorname{lk}_{M_k} (0) =& \bigcup_{i=1}^{m} \bigl\{ \bigl\langle a_i^0, a_i^0 + a_i^1, a_i^0 + a_i^1 + a_i^2 \bigr\rangle , \bigl\langle - a_i^0, a_i^1, a_i^1 + a_i^2 \bigr\rangle , \bigl\langle - a_i^0 - a_i^1 , - a_i^1 , a_i^2 \bigr\rangle , \\ &\hphantom{\bigcup_{i=1}^{m} \bigl\{ } \bigl\langle - a_i^0 - a_i^1 - a_i^2 , - a_i^1 - a_i^2 , - a_i^2 \bigr\rangle \bigr\} . \end{aligned}$$
(3.2)

Since M is a combinatorial 3-manifold, (3.1) must be a triangulated 2-sphere. Since \(a_{i}^{3} > \frac{n}{2} > a_{i}^{0} + a_{i}^{1} + a_{i}^{2}\) for all 1≤i≤m, the vertices v j of \(\operatorname {lk}_{M} (0)\) can be mapped to the vertices of \(\operatorname{lk}_{M_{k}} (0)\), k≥0, as follows:

$$v_j \mapsto \left \{ \begin{array}{l@{\quad}l} v_j & \textrm{if}\ v_j < \frac{n}{2}, \\ v_j + k & \textrm{if}\ v_j \geq\frac{n}{2} . \end{array} \right . $$

Applying this relabeling to the vertices of M yields a simplicial complex on vertices of M k equal to (3.2) and hence a combinatorial isomorphism between \(\operatorname{lk}_{M} (0)\) and \(\operatorname{lk}_{M_{k}} (0)\). Since M and M k are cyclic, all vertex links are isomorphic. Altogether it follows that M k is a combinatorial manifold for all k≥0.

This part of the proof can be generalized to combinatorial d-manifolds for arbitrary d, see Theorem 3.5.

Conversely, let M={d 1,…,d m } contain a difference cycle \(d_{i} = ( a_{i}^{0} : a_{i}^{1} : a_{i}^{2} : a_{i}^{3})\), 1≤i≤m, such that \(a_{i}^{3} \leq\frac{n}{2}\) and let \(\tilde{k} := \max_{1 \leq j \leq m} ( a_{j}^{0} + a_{j}^{1} + a_{j}^{2} - a_{j}^{3})\). Since by construction \(a_{j}^{3} + \tilde{k} \geq a_{j}^{0} + a_{j}^{1} + a_{j}^{2}\) and \(a_{j}^{l} > 0\) for all 1≤j≤m, 0≤l≤3, it follows by Lemma 3.2 that all difference cycles of \(M_{\tilde{k}}\) and \(M_{\tilde{k}+1}\) have full length. By Lemma 3.3 it now follows that the links of vertex 0 in \(M_{\tilde{k}}\) and \(M_{\tilde{k}+1}\) have the same f-vector. On the other hand, since \(a_{i}^{3} + \tilde{k} = a_{i}^{0} + a_{i}^{1} + a_{i}^{2}\) for at least one 1≤i≤m and \(a_{j}^{3} + \tilde{k} \geq a_{j}^{0} + a_{j}^{1} + a_{j}^{2}\) for all 1≤j≤m, \(\operatorname{lk}_{M_{\tilde {k}+1}}(0)\) has to have strictly more vertices than the link of vertex 0 in \(M_{\tilde{k}}\): Namely, we have \(- \sum_{r=0}^{2} a_{i}^{r} = \sum_{r=0}^{2} a_{i}^{r}\) for at least one 1≤i≤m in \(\operatorname{lk}_{M_{\tilde{k}}}(0)\), and in \(\operatorname {lk}_{M_{\tilde{k}+1}}(0)\) this vertex splits into two distinct vertices. On the other hand, two vertices which are distinct in \(\operatorname{lk}_{M_{\tilde{k}}}(0)\) cannot be equal in \(\operatorname {lk}_{M_{\tilde{k}+1}}(0)\) by \(a_{j}^{3} + \tilde{k} \geq a_{j}^{0} + a_{j}^{1} + a_{j}^{2}\) for all 1≤j≤m. This is a contradiction to Lemma 3.3. □

From now on, we will require an infinite family of cyclic combinatorial manifolds to start with the smallest complex possible, that is, the complex M −1 must not be a combinatorial manifold.

Corollary 3.4

Let M k , k≥0, be an infinite family of cyclic combinatorial 3-manifolds such that M −1 is not a combinatorial manifold, then M 0 has an odd number of vertices.

Proof

This follows immediately from the fact that \(\varDelta _{j} := a_{j}^{3} - a_{j}^{0} - a_{j}^{1} - a_{j}^{2} > 0\) for all 1≤j≤m in M 0. If the minimum over all Δ j , 1≤j≤m, is strictly greater than 1, the vertices of \(\operatorname{lk}_{M_{0}}(0)\) are either strictly smaller than \(\lfloor\frac{n}{2} \rfloor\) or strictly greater than \(\lceil\frac{n}{2}\rceil\). Following the proof of Theorem 3.1, the mapping

$$v_j \mapsto \left \{ \begin{array}{l@{\quad}l} v_j & \textrm{if}\ v_j < \frac{n}{2}, \\ v_j - 1 & \textrm{if}\ v_j \geq\frac{n}{2} + 1 . \end{array} \right . $$

of the vertices of \(\operatorname{lk}_{M_{0}}(0)\) to the vertices of \(\operatorname{lk}_{M_{-1}}(0)\) yields a combinatorial isomorphism between the vertex links of M 0 and M −1 and hence M −1 is a combinatorial 3-manifold. Hence, Δ i =1 for some 1≤i≤m and \(n = 2 a_{i}^{3} - 1\). □

So far, we have only considered one particular type of arithmetic progression which led to infinite families of cyclic combinatorial manifolds that have members for all integers n≥n 0 for n 0 sufficiently large. A more general but closely related approach results in other (weaker) formulations of infinite families of cyclic combinatorial manifolds: Let N={d 1,…,d m } be a combinatorial d-manifold with n vertices, represented by m difference cycles \(d_{i} = ( a_{i}^{0} : \ldots: a_{i}^{d} )\), 1≤i≤m. The simplicial complexes N k ={d 1,k ,…,d m,k }, k≥0, with n+ℓk vertices, ℓ≥1 fixed, given by \(d_{i,k} = ( a_{i}^{0} + \ell_{i}^{0} k : \ldots: a_{i}^{d} + \ell_{i}^{d} k )\), 1≤i≤m, where for each 1≤i≤m we have \(\sum_{j=0}^{d} \ell_{i}^{j} = \ell\), \(\ell_{i}^{j} \geq0\), will be called an infinite family of cyclic combinatorial manifolds of order ℓ if all N k , k≥0, are combinatorial manifolds. The case ℓ=1 coincides with the previously described type of infinite family which from now on will be referred to as a dense family.

There is an analogue of the “if”-part of Theorem 3.1 for infinite families of combinatorial d-manifolds of order ℓ which can be formulated as follows.

Theorem 3.5

Let N={d 1,…,d m } be a combinatorial d-manifold with n vertices, represented by m difference cycles \(d_{i} = ( a_{i}^{0} : \ldots: a_{i}^{d} )\), 1≤i≤m. Then N k , defined by non-negative integers ℓ≥1 and \(\ell _{i}^{j}\), 1≤i≤m, 0≤j≤d with \(\sum_{j=0}^{d} \ell _{i}^{j} = \ell\), 1≤i≤m, is a combinatorial d-manifold with n+ℓk vertices for all k≥0 if

$$ \frac{\ell_i^j n}{\ell+1} < a_i^{j}, $$
(3.3)

holds for all 1≤i≤m, 0≤j≤d.

Note that the case d=3 and ℓ=1 in the following proof corresponds to the “if”-part of Theorem 3.1.

Proof

The proof is completely analogous to the one of the first part of Theorem 3.1. Here, too, we look at a relabeling of the vertices of the link \(\operatorname{lk}_{N} (0)\) in order to transform it to \(\operatorname{lk}_{N_{k}} (0)\) for arbitrary values of k≥0.

First note that from Condition (3.3) we can derive

$$\begin{aligned} a_i^{j} =& n - \sum _{p = 0, p \neq j}^{d} a_i^p < n - \sum _{p = 0, p \neq j}^{d} \frac{\ell_i^p n}{\ell+1} = \frac{n}{\ell +1} \biggl( \ell+1 - \sum _{p = 0, p \neq j}^{d} \ell_i^p \biggr)\\ =& \frac{(\ell_i^j +1)n}{\ell+1}, \end{aligned}$$

and hence we have

$$ \frac{\ell_i^j n}{\ell+1} < a_i^{j} < \frac{(\ell_i^j +1)n}{\ell+1}. $$
(3.4)

Now, consider the collection of disjoint intervals

$$\alpha_r^k := \bigg] \frac{r(n+\ell k)}{\ell+1}, \frac{(r+1)(n+ \ell k)}{\ell+1} \bigg[ \subset \,] 0 , n+ \ell k [ \, \subset \mathbb{R} . $$

By Condition (3.4), each vertex of \(\operatorname {lk}_{N_{k}} (0)\) lies in exactly one of the \(\alpha_{r}^{k}\), 0≤r≤ℓ. Now consider the relabeling

$$\iota: v_j \mapsto v_j + \biggl\lfloor \frac{(\ell+1) v_j}{n} \biggr\rfloor k $$

from the vertices of \(\operatorname{lk}_{N} (0)\) to the vertices of \(\operatorname{lk}_{N_{k}} (0)\). By construction, if \(v_{j} \in\alpha_{r}^{0}\) then \(\iota(v_{j}) \in\alpha_{r}^{k}\) and, following the proof of Theorem 3.1, ι is injective and defines a combinatorial isomorphism between \(\operatorname{lk}_{N} (0)\) and \(\operatorname {lk}_{N_{k}} (0)\). □

Theorem 3.5 defines families of order ℓ by a purely combinatorial criterion. Since all dense families contain families of order ℓ, the following characterization of higher order families is interesting.

Lemma 3.6

Let N k =(d 1,k ,…,d m,k ), k≥0, be an infinite family of combinatorial d-manifolds of order ℓ, 1≤ℓ≤d, with n+ℓk vertices given by non-negative integers \(\ell _{i}^{j}\), 1≤i≤m, 0≤j≤d, \(\sum_{j=0}^{d} \ell_{i}^{j} = \ell\).

If ℓ is a unit in \(\mathbb{Z}_{n}\) then there exists a dense infinite family containing all but finitely many members of N k , k≥0.

Proof

Let ℓ be a unit in \(\mathbb{Z}_{n}\) and let \(a_{i,k}^{j}\) be the jth entry of the ith difference cycle of N k . By multiplying N k by ℓ we get \(\ell N_{k} = \{ (\ell a_{1,k}^{0} : \ldots: \ell a_{1,k}^{d}) , \ldots, (\ell a_{m,k}^{0} : \ldots: \ell a_{m,k}^{d}) \}\) which is isomorphic to N k since if ℓ is a unit in \(\mathbb {Z}_{n}\) then ℓ is a unit in \(\mathbb{Z}_{n + \ell k}\), for all k≥0. Hence, we have

$$\begin{aligned} \ell a_{i,k}^{j} = & \ell \bigl(a_i^{j} + \ell_i^j k \bigr) \\ = & \ell a_i^{j} + \ell\ell_i^j k \\ = & \ell a_i^{j} + \ell_i^j \bigl(\ell k - (n+\ell k) \bigr) \\ = & \ell a_i^{j} - \ell_i^j n \end{aligned}$$

which is independent of k. Now let \(b_{i}^{j} := \varSigma_{r=0}^{j} \ell a_{i}^{r} - \ell_{i}^{r} n\) and for each 1≤i≤m let π i be a permutation such that

$$b_{i}^{\pi_i(0)} \leq b_{i}^{\pi_i(1)} \leq\cdots \leq b_{i}^{\pi _i(d)}. $$

It follows that for \(k > b_{i}^{\pi_{i}(d)} - b_{i}^{\pi_{i}(0)} - n\) the difference cycle \((\tilde{a}_{i}^{0} : \tilde{a}_{i}^{1} : \ldots: \tilde{a}_{i}^{d-1} : \tilde {a}_{i}^{d} + \ell k)\) with \(\tilde{a}_{i}^{j} := b_{i}^{\pi_{i}(j+1)} - b_{i}^{\pi_{i}(j)}\), 0≤j≤d−1, and \(\tilde{a}_{i}^{d} = n - \varSigma_{j=0}^{d-1} \tilde{a}_{i}^{j}\) is isomorphic to \(( a_{i,k}^{0} : \ldots: a_{i,k}^{d})\) for all 1≤i≤m. Note that in particular this means that \(\tilde{a}_{i}^{j} > 0\) for all 1≤i≤m and 0≤j≤d−1. We write

$$\tilde{N}_{\ell k} = \bigl\{ \bigl(\tilde{a}_i^0 : \tilde{a}_i^1 : \ldots: \tilde {a}_i^{d-1} : \tilde{a}_i^{d} + \ell k \bigr) \,|\, 1 \leq i \leq m \bigr\} $$

which by construction is isomorphic to N k and we conclude the proof by the observation that in \(\tilde{N}_{\ell k}\) only the dth entries depend on k and thus for k 0 sufficiently large \(\tilde{N}_{\ell k_{0}}\) satisfies the preconditions of Theorem 3.5. Hence \(\tilde{N}_{\ell k_{0}}\) extends to an infinite dense family containing isomorphic copies of N k for each k>k 0. □

Corollary 3.7

Let N k , k≥0, be an infinite family of cyclic combinatorial d-manifolds of order 2 such that no dense family contains an infinite number of members of N k . Then the number of vertices of N 0 has to be even.

Proof

If no dense family contains an infinite number of members of N k , then in particular for all fixed dense families an infinite number of members of N k is not contained in this family. The statement now follows from Lemma 3.6 since 2 is a unit in \(\mathbb {Z}_{n}\) for all n≡1(2). □

Remark 3.1

Theorem 3.5 gives us an easy-to-check combinatorial criterion for arbitrarily dimensional simplicial complexes to be combinatorial d-manifolds. This is of great use in dimension d≥5: Checking the manifold property of a d-dimensional simplicial complex involves the recognition of a (d−1)-dimensional sphere. While this is easy for d≤3 and there are deterministic algorithms for the case d=4 [39], heuristic methods have to be used in dimensions d≥5.

4 Classification of Cyclic 3-Manifolds

There is a number of classifications containing cyclic combinatorial manifolds described in the literature due to Kühnel and Lassmann [21] and Lutz in [28–30]. These classifications contain 336 cyclic combinatorial 3-manifolds of 13 distinct topological types (cf. Tables 1 and 10 for the number of cyclic combinatorial 3-manifolds and the number of distinct topological types up to 17 vertices).

Table 1 The classification of cyclic combinatorial 3-manifolds with up to 22 vertices
Full size table

The main motivation to extend this classification was to substantially extend the set of example triangulations where the results from Sect. 3 can be applied in order to get new results. Moreover, a larger set of examples gives us a better chance to understand which topological properties are compatible with a cyclic symmetry and which ones are not.

Theorem 4.1

(Classification of Cyclic Combinatorial 3-Manifolds)

There are 6070 combinatorial types of (connected) combinatorial 3-manifolds with transitive cyclic symmetry with up to 22 vertices. These complexes split up into 67 topological types.

The number of combinatorial manifolds, combinatorial types, locally minimal combinatorial manifolds, i.e. complexes which cannot be reduced by bistellar moves without inserting new vertices, and topological types can be found in Table 1. A list of all topological types of 3-manifolds in the classification together with a particular combinatorial manifold of each type sorted by their model geometries is shown in Table 2 to 9. An overview over all topological types of cyclic combinatorial 3-manifolds sorted by vertex number is listed in Table 10.

Table 2 Cyclic combinatorial 3-manifolds of spherical type
Full size table

The calculations were done with the help of the GAP-package simpcomp [11–13] as well as GAP [15]. In addition, the 3-manifold software packages regina by Burton et al. [9], SnapPy by Weeks [47] and the Three-manifold Recognizer developed by the research group of Matveev [32] were used for topological type recognition. All cyclic manifolds are available within simpcomp by calling the function SCCyclic3Mfld(n,k) where n is the number of vertices and k is the number of a specific cyclic combinatorial 3-manifold. The total number of cyclic n-vertex combinatorial 3-manifolds can be obtained using the function SCNrCyclic3Mfld(n).

4.1 Discussion of the Proof

The proof of Theorem 4.1 was mainly done by computer. In the following, we will discuss the methods and software involved in the proof.

The complexes were found using the classification algorithm for transitive combinatorial manifolds due to Kühnel and Lassmann [21] which is integrated into the software package simpcomp as of Version 1.3. The topological distinctions of most of the spherical and flat manifolds, as well as the connected sums of S 2×S 1 and were done via analysis of the fundamental group of the complexes:

  • The manifolds of type (S 2×S 1)#k and were identified by calculating the fundamental group—the free group on k generators—and applying Kneser’s conjecture, proved by Stallings in 1959 (see [43]) together with [16, Theorem 5.2].

  • By the elliptization conjecture (stated by Thurston in [45, Chap. 3], recently proved by Perelman, see [35–37]), the topological type of a spherical 3-manifold distinct from a lens space is already determined by the isomorphism type of its (finite) fundamental group. This allows an identification of all such 3-manifolds using the finite group recognition algorithm of GAP.

  • The fundamental group distinguishes all flat 3-manifolds by a theorem of Bieberbach (see [5] and [33, p. 4]). On the other hand, all other 3-manifolds with a fundamental group containing \(\mathbb{Z}^{3}\) are known to be the connected sum of a flat 3-manifold with some other 3-manifold (cf. [26]). Hence, all 3-manifolds with the fundamental group of a flat manifold have to be prime (as all flat manifolds are prime and the fundamental group of a 3-manifold M determines the length of a prime decomposition of M, cf. [43] and [16, Theorem 5.2]) and thus are flat. Altogether, the topological type of a 3-manifold with the fundamental group of a flat manifold is in fact flat and the manifold is determined by its fundamental group. Hence, it can be identified by determining its fundamental group using simpcomp and GAP.

For more information about the spherical case in the classification of 3-manifolds see [34, 44], for more about flat 3-manifolds see [5, 20, 33].

In the following we will show that only lens spaces of type \(\operatorname{L}(3,1)\), \(\operatorname{L}(5,1)\), \(\operatorname {L}(7,1)\), \(\operatorname{L}(8,3)\) and \(\operatorname{L}(15,4)\) can be represented as a transitive cyclic combinatorial manifold with at most 22 vertices.

First, let us show that the cyclic combinatorial manifold C with 18 vertices given by

$$\begin{aligned} C :=& \bigl\{ (1:1:1:15),(1:2:5:10),(1:5:2:10),(1:5:10:2),(2:5:2:9),\\ &\hphantom{\bigl\{ } (2:6:4:6),(2:7:2:7),(4:4:4:6) \bigr\} \end{aligned}$$

is homeomorphic to the lens space L(5,1).

Fig. 1
figure 1

Slicing of C between the odd labeled and the even labeled vertices together with the boundary of the two solid tori spanned by the even and by the odd vertices

Full size image

Figure 1 shows the slicing of C between the odd labeled vertices and the even labeled vertices. Here, the slicing is a torus. Also, both the span of the odd and the span of the even labeled vertices is a solid torus and hence C is a manifold of Heegaard genus at most 1. For the 1-homology of the two tori \(T_{-} := \partial (\operatorname{span} (0,2, \ldots, 16))\) and \(T_{+} := \partial (\operatorname{span} (1,3, \ldots, 17))\) we choose a basis as follows (here and in the following [v 0,v 1,…,v r ] denotes a path of edges in a simplicial complex starting at vertex v 0 and ending at vertex v r ):

$$\begin{aligned} \alpha_- :=& [ 0, 10, 4, 14, 8, 0 ], \\ \beta_- :=& [ 0, 12, 6, 0 ] \end{aligned}$$

and

$$\begin{aligned} \alpha_+ :=& [ 1, 11, 5, 15, 9, 1 ], \\ \beta_+ :=& [ 1, 13, 7, 1 ] \end{aligned}$$

such that H 1(T ±)=〈α ±,β ±〉, \(H_{1} (\operatorname{span} (0,2, \ldots, 16)) = \langle\beta_{-} \rangle\) and \(H_{1} (\operatorname{span} (1,3, \ldots, 17)) = \langle \beta_{+} \rangle\).

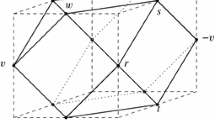
Now, we want to express α − in terms of α + and β +. With the help of the slicing (the thick line in Fig. 1 denotes a path homologous to α − in the slicing) we see that α − can be transported to the path

$$[ 17,15,7,5,3,13,11,3,1,17,9,7,17 ] $$

which entirely lies in T +. This path is homologous to −5 times β + plus 4 times α + and hence the topological type of C must be L(−5,4)≅L(5,1).

The proof that the cyclic combinatorial manifold D with 22 vertices defined by

$$\begin{aligned} D :=& \bigl\{ (1:1:1:19),(1:2:5:14),(1:7:12:2),(2:5:2:13),(2:7:2:11), \\ & \hphantom{\bigl\{ } (2:8:4:8),(2:9:2:9),(2:12:3:5),(4:6:4:8),(4:6:6:6) \bigr\} \end{aligned}$$

is homeomorphic to the lens space L(7,1) is completely analogous to the above.

For the identification of the exact topological type of the lens spaces

$$\begin{aligned} L_0 :=& \bigl\{ (1:1:1:11),(1:2:4:7),(1:4:2:7),(1:4:7:2),(2:4:4:4), \\ &\hphantom{\big\{ } (2:5:2:5) \bigr\} \\ L_1 :=& \bigl\{ (1:1:1:15),(1:2:4:11),(1:4:2:11),(1:4:11:2), \\ &\hphantom{\bigl\{ } (2:4:8:4),(2:5:2:9),(2:7:2:7),(4:4:4:6) \bigr\} \\ L_2 :=& \bigl\{ (1:1:1:19),(1:2:4:15),(1:4:2:15),(1:4:15:2),(2:4:12:4), \\ &\hphantom{\bigl\{ } (2:5:2:13),(2:7:2:11),(2:9:2:9),(4:4:4:10),(4:6:4:8) \bigr\} \end{aligned}$$

with 14, 18, and 22 vertices see Theorem 5.3. Using the 3-manifold software regina [9], we checked that all other lens spaces in the classification are of one of the above types.

Finally, there are 74 homeomorphic cyclic triangulations of a homology 3-sphere with the lexicographically minimal complex being

$$\begin{aligned} \operatorname{HS} :=& \bigl\{ (1:1:1:19),(1:2:4:15),(1:4:8:9),(1:4:15:2),(1:6:6:9), \\ & \hphantom{\bigl\{ } (2:4:10:6),(2:5:6:9),(2:9:2:9),(2:9:5:6),(4:4:4:10) \bigr\} \end{aligned}$$

(cf. Table 9). In order to describe its topological type observe that the slicing between the even and the odd labeled vertices of \(\operatorname{HS}\) (cf. Fig. 2) is a torus decomposing \(\operatorname {HS}\) into two complexes \(\operatorname{HS}^{+}\) (containing the even labeled vertices) and \(\operatorname{HS}^{-}\) (containing the odd labeled vertices) which both are homeomorphic to the knot exterior of the trefoil knot. The recognition step of this result is due to the 3-manifold software SnapPy by Weeks [47] which is well suited to deal with knot complements.

Fig. 2
figure 2

Slicing of \(\operatorname{HS}\) between the odd and the even labeled vertices splitting the complex into two isomorphic knot exteriors of the trefoil knot

Full size image

Such a manifold is determined by how the canonical meridian m + and longitude ℓ + of \(\operatorname{HS}^{+}\) are glued to the boundary of \(\operatorname{HS}^{-}\). Following the conventions of [40] a gluing is given by integers a, b, c, and d with ad−bc=−1 and ℓ + is glued to a⋅ℓ −+c⋅m − and m + is glued to b⋅ℓ −+d⋅m − where c=±1 whenever the resulting manifold is a homology sphere. The canonical meridians of both \(\operatorname{HS}^{+}\) and \(\operatorname{HS}^{-}\) were computed using simpcomp and are given by the thick lines in Fig. 2. It follows that m + is glued to −m −, thus b=0, d=−1, and as a result a=1. This determines the topological type of \(\operatorname{HS}\).

Alternatively, using Matveev’s Three-manifold Recognizer [32] \(\operatorname{HS}\) is identified as the graph manifold

$$\operatorname{SFS} \bigl[D: (2,1) (3,1) \bigr] \cup_{m} \operatorname{SFS} \bigl[D: (2,1) (3,1) \bigr], m = \left ( \begin{array}{c@{\quad}c} -10 & 11 \\ -9 & 10 \end{array} \right ), $$

here given in the notation used by regina.

All complexes with fewer than 18 vertices have already been described in literature. See the indicated sources in Tables 2, 3, 4 and 8. The remaining topological types of cyclic 3-manifolds were identified using regina, the (orientable) graph manifolds were additionally checked using the Three-manifold Recognizer. The notation for the Seifert fibered spaces as well as the graph manifolds is following the one regina is using which in turn is based on work by Burton [8] and Orlik [34, pg. 88] (note that the Three-manifold Recognizer is using a slightly different notation). To make sure that none of the Seifert fibered spaces or graph manifolds equal any other topological type of combinatorial 3-manifold previously described in the classification, we additionally computed the Turaev–Viro invariant of the manifolds [46] whenever necessary. See the documentation of regina or one of the indicated sources for more information.

Table 3 Cyclic combinatorial 3-manifolds of type \(S^{2} \times\mathbb{R}\)
Full size table
Table 4 Cyclic combinatorial 3-manifolds of flat type
Full size table
Table 5 Cyclic combinatorial 3-manifolds of Nil type
Full size table
Table 6 Cyclic combinatorial 3-manifolds of type \(SL(2,\mathbb{R})\)
Full size table
Table 7 Cyclic combinatorial 3-manifolds of type \(\mathbb {H}^{2} \times\mathbb{R}\)
Full size table
Table 8 Cyclic combinatorial 3-manifolds that are connected sums
Full size table
Table 9 Cyclic combinatorial 3-dimensional graph manifolds∗∗ including the homology sphere \(\operatorname{HS}\)
Full size table
Table 10 Topological types of cyclic combinatorial 3-manifolds ordered by number of vertices n
Full size table

It is interesting to see that some of the homological types of the complexes do not occur for certain integers. Especially, if n is a prime number, the number of topologically distinct complexes seems to be limited. In particular, we believe the following to be true.

Conjecture 4.2

Let M be a combinatorial 3-manifold with transitive cyclic symmetry homeomorphic to S 2×S 1. Then M has an even number of vertices.

5 Further Results

A direct consequence from the extension of the classification of transitive cyclic combinatorial manifolds together with Theorem 3.1 is the following result.

Corollary 5.1

There are exactly 396 combinatorially distinct dense infinite families of combinatorial 3-manifolds starting with a triangulation with fewer than 23 vertices.

The results from Sect. 3 allow us to formulate a number of further results similar to Corollary 5.1 using the data of the classification. However, these infinite families typically only contain a few distinct topological types of 3-manifolds: Most of the infinite families have members of type S 2×S 1 or , family number 17 (SCSeriesK(17,k) in simpcomp) has members of type \(\mathbb{T}^{3}\) and \(\mathfrak{B}_{2}\), and families number 30, 42, and 356 (SCSeriesK(30,k), SCSeriesK(42,k) and SCSeriesK(356,k) in simpcomp) contain combinatorial 3-manifolds of three further topological types. This observation is emphasized by the following upper bound on the Betti numbers of the members of a dense infinite family of combinatorial 3-manifolds.

Proposition 5.2

Let M k ={d 1,k ,…,d m,k } with \(d_{i,k} = ( a_{i}^{0} : a_{i}^{1} : a_{i}^{2} : a_{i}^{3} + k )\) be a dense infinite family of transitive cyclic combinatorial 3-manifolds with n+k vertices. Then there exists a constant c such that

$$\sum _{i=0}^{d} \beta_i (M_0) + c \geq\sum _{i=0}^{d} \beta_i (M_k) $$

for all k≥0.

Proof

By Kuiper’s discrete Morse relations (see Sect. 2 or [24]) we know that the number of critical points of any rsl-function on M k is an upper bound for the sum of the Betti numbers of M k . We will prove Proposition 5.2 by giving an upper bound on the number of critical points of the rsl-function f k on M k induced by the natural ordering of the vertices V k :={0,1,…,n+k−1} of M k .

In this setting, the relevant slicings S i of M k with respect to f k are given by the partitions P i =({0,1,…,i−1},{i,…,n+k−1}) of V k . Now, observe that the set of tetrahedra having both vertices in {0,1,…,i−1} and {i,…,n+k−1} must be isomorphic to the set of tetrahedra having vertices in both {0,1,…,i} and {i+1,…,n+k−1} for all μ<i<n+k−1−μ where \(\mu:= \max_{1 \leq i \leq m} (a_{i}^{0} + a_{i}^{1} + a_{i}^{2})\). This follows from the cyclic symmetry and the fact that by construction all tetrahedra of M k for all k≥0 have their vertices within an interval (modulo (n+k)) of length less or equal μ. As a consequence, we have S i =S i+1 and since a vertex of a combinatorial manifold can only be critical if the topological type of the associated slicing changes when the vertex is passed, none of the vertices μ<i<n+k−1−μ can be critical.

Moreover, note that whenever μ<n+k−1−μ the combinatorial types of the remaining slicings S i , 1≤i≤μ+1 and n+k−1−μ≤i≤n+k−1 in M k are independent of k and hence the number of critical points of f k is the same for all k. Now since \(\mu< \frac{n}{2}\) we have μ<n+k−1−μ whenever k≥1 and the number of critical points of f k for any k is bounded above by the maximum of the number of critical points of M 0 and M 1. Hence, for c being the maximum of the number of critical points of M 0 and M 1 the statement follows. □

In order to find infinite families which are richer from the topological point of view, we want to use the classification of transitive cyclic combinatorial 3-manifolds described in Sect. 4 to search for manifolds that look like the start of an infinite family of 2-neighborly combinatorial 3-manifolds (which thus have to contain an increasing number of difference cycles) containing infinitely many members of pairwise distinct topological types.

This is motivated by the situation in dimension 2 where several of such infinite families exist. There is a family of neighborly orientable surfaces of genus \(\frac{1}{6} {12s + 4 \choose2}\) with 12s+7 vertices (cf. [38, Fig. 2.15] and [18, Example 2.7]) starting with the 7-vertex Möbius torus. In addition, many further families of transitive combinatorial 2-manifolds with similar properties can be found in [30] by Lutz.

Note that there are infinite 2-neighborly families of combinatorial 3-manifolds described in the literature. However, these families have members of only a constant number of distinct topological types per family (see the boundary of the cyclic 4-polytopes for a family of neighborly S 3, [21] and [41, Sect. 4.2] for families of sphere bundles over the circle, and [7] and [23] for neighborly 3-dimensional tori).

A detailed analysis of the data provided by the classification led to a general construction principle for infinite families of Seifert Fibered Spaces and in particular Brieskorn homology spheres with transitive cyclic symmetry and an infinite number of distinct topological types per family. However, for the remainder of this article we will focus on an infinite family of topologically distinct lens spaces which was conjectured following a different approach and refer the reader to [10] where the former type of infinite family is described in detail.

Theorem 5.3

The complex

$$\begin{aligned} L_k :=& \bigl\{ (1:1:1:11+4k), (1:2:4:7+4k), (1:4:2:7+4k), (1:4:7+4k:2)\bigr\} \\ & \bigcup_{i=0}^{k} \bigl\{ (2:5+2i:2:5+4k-2i) , (4:2+2i:4:4+4k-2i)\bigr\} \end{aligned}$$
(5.1)

is a combinatorial 3-manifold with n=14+4k, k≥0, vertices. It is homeomorphic to the lens space L(k 2+4k+3,k+2).

Proof

Obviously, L k has n=14+4k vertices. By looking at Fig. 3 we can verify that the link \(\operatorname{lk}_{L_{k}} (0)\) of the vertex 0 in L k is a triangulated 2-sphere. Hence, as L k has transitive symmetry, it follows immediately that L k is in fact a combinatorial 3-manifold for all k≥0. Furthermore, we can see that \(\operatorname{lk}_{L_{k}} (0)\) has 13+4k vertices and thus L k is 2-neighborly.

Fig. 3
figure 3

Link of vertex 0 of L k —a triangulated 2-sphere with 13+4k vertices

Full size image

To determine the exact topological type of L k we will proceed as follows:

  1. 1.

    for all k≥0, determine a Heegaard splitting of L k of genus 1 which will be given by a decomposition of L k into two disjoint solid tori \(T_{k}^{-}\) and \(T_{k}^{+}\) and a center piece of type Cartesian product of a torus with an interval,

  2. 2.

    draw the middle torus S k of the center piece as a slicing (see Fig. 4),

    Fig. 4
    figure 4

    Slicing of L k between the odd labeled and the even labeled vertices—a torus

    Full size image
  3. 3.

    choose a basis \(\{\alpha_{k}^{-}, \beta_{k}^{-}\}\) for the 1-homology of the boundary of the solid torus \(T_{k}^{-}\) such that \(H_{1} (T_{k}^{-}) = \langle\beta_{k}^{-} \rangle\),

  4. 4.

    do the same for the solid torus \(T_{k}^{+}\), that is, choose \(\{ \alpha_{k}^{+}, \beta_{k}^{+} \}\) such that \(H_{1} (\partial T_{k}^{+}) = \langle \alpha_{k}^{+}, \beta_{k}^{+} \rangle\) and \(H_{1} (T_{k}^{+}) = \langle\beta_{k}^{+} \rangle\),

  5. 5.

    with the help of the slicing S k , determine the class of \(\alpha _{k}^{-}\) in \(H_{1} (\partial T_{k}^{+})\)—by construction this will be a torus knot which will determine the topological type of L k .

1. For all k≥0, the span of the even labeled vertices \(T_{k}^{-} := \operatorname{span} (\{ 0, 2, \ldots, n-1 \})\) as well as the span of the odd labeled vertices \(T_{k}^{+} := \operatorname{span} (\{ 1, 3, \ldots, n \})\) (which is combinatorially isomorphic to \(T_{k}^{-}\) by the cyclic symmetry) form a solid torus.

To see this note that \(T_{k}^{-}\) together with \(T_{k}^{+}\) are exactly the difference cycles

$$T_k^- \cup T_k^+ = \bigcup _{i=0}^{k} \bigl\{ (4:2+2i:4:4+4k-2i)\bigr\} \subset L_k. $$

Since the gcd of 4, 2+2i and 4+4k−2i, 0≤i≤k, is 2 for all k≥0, \(T_{k}^{-}\) and \(T_{k}^{+}\) are disjoint but connected and we have

$$T_k^- \cong T_k^+ \cong\bigcup _{i=0}^{k} \bigl\{ (2:1+i:2:2+2k-i) \bigr\} =: T_k . $$

For k=0 we have T 0={(1:1:1:4)}≅B 2×S 1. If k≥1, T k consists of k+1 difference cycles, which we will denote by δ i :=(2:1+i:2:2+2k−i), 0≤i≤k. δ i shares two triangles per tetrahedron with δ 2+i , 0≤i≤k−2, δ k−1 shares two triangles per tetrahedron with δ k , k≥1, δ 1 shares two triangles per tetrahedron with itself and δ 0 shares two triangles per tetrahedron with ∂T k and hence contains the complete boundary of T k . Altogether, we have the following collapsing scheme of T k :

figure a

Thus, T k collapses onto δ 1=(2:2:2:1+2k) and since δ 1 contains an odd number of vertices we have δ 1≅(1:1:1:4+2k)≅B 2×S 1.

Finally \(T_{k}^{-}\) and \(T_{k}^{+}\) span all the vertices of L k and contain all tetrahedra with only even or only odd vertex labels. As a consequence the center piece between the two solid tori is of type Cartesian product of a torus with an interval, \(T_{k}^{-}\) and \(T_{k}^{+}\) define a Heegaard splitting of L k of genus 1 and L k is homeomorphic to the 3-sphere, S 2×S 1 or a lens space L(p,q).

2. As follows from the above, the slicing S k between the odd labeled and the even labeled vertices is a torus and is shown in Fig. 4. It is interesting to see that apart from \(T_{k}^{-}\) and \(T_{k}^{+}\) the difference cycles (1:2:4:7+4k) and (1:4:2:7+4k) are the only ones which do not contain two odd and two even labels per tetrahedron and thus are the only ones which are not sliced by S k in a quadrilateral. Hence, S k consists of only 28+8k triangles but (2+k)(14+4k)+7+2k=4k 2+24k+35 quadrilaterals. Its complete f-vector is

$$f(S_k) = \bigl(4k^2+28k+49,8k^2+60k+112, (8k+28) \varDelta , \bigl(4k^2+24k+35 \bigr) \Box \bigr). $$

3. and 4. In order to find a suitable basis of \(H_{1} (\partial T_{k}^{-})\) as indicated above, let us first take a look at \(\partial T_{k}^{-}\) itself which is shown in Fig. 5. We choose the basis \(\{ \alpha_{k}^{-}, \beta_{k}^{-} \}\) of \(H_{1} (\partial T_{k}^{-})\) to be

$$\begin{aligned} \alpha_k^- =& [ 0, 4, 8, \ldots, n-6, 0 ], \\ \beta_k^- =& [ 0, 6, 12, 18, 22, 26, \ldots, n-4, 0 ] \end{aligned}$$

or in the case that n<26 as indicated in Fig. 5. By construction, \(\alpha_{k}^{-}\) is contractible in \(T_{k}^{-}\) and \(H_{1} (T_{k}^{-}) = \langle\beta_{k}^{-} \rangle\).

Fig. 5
figure 5

Fundamental domain of the boundary of \(T_{k}^{-}\) together with the basis \(\{ \alpha_{k}^{-}, \beta_{k}^{-} \}\) of \(H_{1} (\partial T_{k}^{-})\) for selected values of k and in greater generality

Full size image

For \(\{ \alpha_{k}^{+}, \beta_{k}^{+} \}\) we choose analogously

$$\begin{aligned} \alpha_k^+ =& [ 1, 5, 9, \ldots, n-5, 1 ], \\ \beta_k^+ =& [ 1, 7, 13, 19, 23, 27, \ldots, n-3, 1 ] \end{aligned}$$

and hence \(H_{1} (T_{k}^{+}) = \langle\beta_{k}^{+} \rangle\).

5. To finish the proof we will express \(\alpha_{k}^{-}\) in terms of \(\alpha_{k}^{+}\) and \(\beta_{k}^{+}\). This is done by a map \(\phi: H_{1} (\partial T_{k}^{-}) \to H_{1} (\partial T_{k}^{+})\) which lifts any path in L k passing only even labeled vertices (a path in \(\partial T_{k}^{-}\)) to a homologically equivalent path passing only odd labeled vertices (a path in \(\partial T_{k}^{+}\)). The image of a path under ϕ can be determined with the help of the slicing S k . In the case of \(\alpha _{k}^{-}\) it is the thick line in Fig. 4 and results in the following path:

$$\begin{aligned} \phi(\alpha_k^-) =& [ n-7, n-9, n-11, \ldots, 9, 7, 1, n-1, n-3, \\ & \hphantom{[} n-3, n-5, n-7, \ldots, 13, 11, 5, 3, 1, \\ & \hphantom{[} 1, n-1, n-3 \ldots, 17, 15, 9, 7, 5, \\ &\hphantom{[} \ldots \\ &\hphantom{[} n-13, n-15, n-17, \ldots, 3, 1, n-5, n-7 ] . \end{aligned}$$
(5.2)

By taking a closer look to Fig. 5 we see that all edges of a path of type 〈s,s−2〉 in both \(\partial T_{k}^{-}\) and \(\partial T_{k}^{+}\) go from the left upper corner of a square of the grid to the lower right corner (↘) whereas an edge of type 〈s,s−6〉 is simply going down in the grid (↓). As \(\phi(\alpha_{k}^{-})\) has (k+2)(2k+2)+2k+1 segments of type ↘ and k+3 segments of type ↓, \(\phi(\alpha_{k}^{-})\) results in the vector (2k 2+8k+5,2k 2+9k+8) on the integer grid with basis (→,↓) (cf. Fig. 5 where \(\partial T_{k}^{+}\) is obtained from \(\partial T_{k}^{-}\) by the shift v↦(v+1)modn of all vertex labels).

On the other hand, we know that \(\alpha_{k}^{+}\) corresponds to the vector (k+2,−1) and \(\beta_{k}^{+}\) to (k−1,−3) on the grid for \(\partial T_{k}^{+}\) with basis (→,↓). Thus, to express \(\phi (\alpha_{k}^{-})\) in terms of \(\alpha_{k}^{+}\) and \(\beta_{k}^{+}\) we have to solve the following system of equations:

$$ \begin{array}{l@{\quad}l} \mbox{I.}&(k+2)q + (k-1)p=2k^2+8k+5, \\ \mbox{II.}&(-1)q+(-3)p=2k^2+9k+8 \end{array} $$
(5.3)

which results in the solution

$$q = k^2+3k+1; \qquad p = -k^2-4k-3 $$

and hence

$$\phi \bigl(\alpha_k^- \bigr) = \bigl(k^2+3k+1 \bigr) \alpha_k^+ + \bigl(-k^2-4k-3 \bigr) \beta_k^+. $$

Furthermore, note that L(p,q 1)≅L(p,q 2) if and only if \(q_{1} \equiv\pm q_{2}^{\pm1} \mod p\) from which it follows that

$$L_k \cong L \bigl(k^2 + 4k + 3,k+2 \bigr). $$

 □

The family L k can be modified into a family of 3-spheres which only differs from L k in the part which is disjoint to the slicing S k . Hence, Theorem 5.3 shows that combinatorial surgery of infinitely many essentially different types can be applied in a setting respecting the cyclic symmetry of the underlying combinatorial manifolds. The following corollary, which is a direct implication of Theorem 5.3, summarizes the findings of this section under a more general point of view.

Corollary 5.4

There are infinitely many topologically distinct combinatorial (prime) 3-manifolds with transitive cyclic symmetry.