1 Introduction

Computer methods have proved to be a versatile and effective approach for solving boundary value problems. With the development of such methods, it has become possible to create automated techniques to solve various boundary problems. The most popular and widely used methods for solving these problems are undoubtedly finite difference method [1, 2], finite element method [3, 4] and boundary element method [5–9]. A characteristic feature of all these methods is the need for the discretization of the domain or the boundary into elements. Despite their popularity, these methods have some limitations, which can be identified as:

  • the need to divide the continuous physical domain or the boundary,

  • the necessity to process large amounts of input data (nodes and elements) and solve large system of algebraic equations,

  • the discrete form of the obtained solutions,

  • the stability of the method depending strongly on discretization schemes of input geometries,

  • the modification of the shape of the boundary or the domain (e.g., the problems of shape identification or optimization) requiring a change in the position of a large number of nodes or re-generating element mesh.

For many years, the authors of this paper have been using parametric integral equation system (PIES) to solve boundary value problems. So far, however, PIES has been mainly used to solve 2D potential boundary value problems modeled by partial differential equations such as: Laplace [10, 11], Poisson [12], Helmholtz [13] and Navier–Lame [14]. These equations have been written in the alternative form, with the help of PIES, which takes into account in its mathematical formalism the shape of the boundary modeled by curves known from computer graphics. The shape of the boundary could be defined by such curves as Bézier [15], Hermite [16] and B-spline [17], and its definition is practically reduced to giving a small set of control points. The complexity of modeling the shape of the boundary in PIES depends on the complexity of the shape of the concerned boundary problem. However, this eliminates the need for definition of traditional boundary or finite elements. The results obtained in PIES for problems modeled by these equations were compared with the results obtained by FEM and BEM. High accuracy and effectiveness of PIES for those 2D problems have been encouraging its generalization to the 3D boundary problems.

The purpose of this paper is to propose an alternative approach to boundary shape representation for 3D boundary value problems based on parametric surface patches. Surface patches allow describing a shape of 3D objects using a given set of control points and associated basis functions [18, 19]. Over the years, parametric surfaces as well as curves have become one of the most important modeling tools in computer graphics and the subject of intensive scientific studies and practical development. This development applies to both new ways of defining parametric curves and surfaces [20, 21], as well as practical applications, especially in the case of widespread CAD systems [22, 23]. Recently, there have been several attempts to use the domain or boundary decryptions by parametric patches directly in solving boundary value problems. This trend is seen especially in the context of isogeometric analysis, where functions that are used to describe geometry in CAD software are also used to approximate the unknown fields. Initially, isogeometric analysis had been developed to improve finite element analysis [24, 25], but recently there have been publications with implementation of this idea to BEM [26]. However, we want to emphasize that the concept used in PIES is different from that of isogeometric analysis. In PIES, we want to separate the necessity of performing simultaneous approximation of both boundary shape and boundary functions with the possibility of analytical description of the boundary directly in the mathematical formula of PIES.

In this paper, the boundary representation for 3D boundary problems is created by triangular Bézier surface patches. In this case, the shape of the boundary could be described with a relatively small number of control points of constituent triangular Bézier surface patches. It should be pointed out that the proposed boundary shape representation by triangular Bézier surface patches does not need to be divided into any elements, but directly used in the process of solving boundary value problems. The approach based on PIES is so general and flexible that it is possible to use another type of surface for boundary representation instead of triangular patches.

Analogical to that in 2D problems, the proposed non-element shape representation scheme has been directly integrated in mathematical formalism of PIES, which has been used in this paper to solve boundary value problems in 3D. We focus on the solving of 3D boundary problem modeled by Laplace’s partial differential equation. This equation has been written in the alternative form, with the help of PIES, which takes into account in its mathematical formalism the shape of the boundary modeled by parametric patches. In the introduced PIES, the boundary geometry is directly considered in its mathematical formalism and can be directly defined with the help of parametric patches. The proposed boundary shape representation would lead to a considerable simplification of the modeling process as well as to a reduction of the necessary amount of input data that defines its shape when compared with traditional element methods.

The numerical solution obtained by PIES comes down only to the approximating of boundary functions. In this paper, we extend a pseudo-spectral method [27] previously used in the case of 2D problems to presented 3D problems. Boundary functions are defined on the surface of individual triangular Bézier patches that model the geometry of the boundary directly in PIES and are approximated by the Chebyshev series. Having calculated the coefficients of the Chebyshev approximating series after solving PIES, we can obtain solutions at any chosen point on the 3D boundary. The proposed representation for the solutions on the boundary is particularly effective from the point of view of the possibility of improving the accuracy of the obtained numerical results in PIES. The improvement of solutions is investigated as a result of a change of the number of input data in the program that is responsible for the number of expressions in the Chebyshev approximating series and does not require changing the original geometry created by the Bézier patches. After solving PIES, we obtain the solution of the boundary problem only on its boundary, represented by the Chebyshev series. To find a solution in the domain, we need to obtain an integral identity known for BIE that makes use of the solution on the boundary obtained by PIES.

Based on these considerations, computer software has been developed and practically tested on the potential problems modeled by Laplace’s equation. The analysis is concerned with the compatibility of the obtained results with known analytical and numerical solutions available in the literature.

2 Triangular Bézier patches

A triangular Bézier patch is represented by a smooth parametric surface with a shape described by a set of control points and basic functions. A Bézier surface of the order n can be defined in terms of a set of 0.5(n + 1)(n + 2) control points \( \user2{P}_{ijk} \) for indices, \( i \ge 0,\,j \ge 0,\,k \ge 0, \) and \( i + j + k = n \), and presented as below [18]

$$ \user2{P}(v,w,u) = \sum\limits_{\begin{subarray}{l} i,j,k \ge 0 \\ i + j + k = n \end{subarray} } {\user2{P}_{ijk} B_{ijk}^{n} (v,w,u)} ,\quad {\text{for }}0\leq v + w + u \le 1, \, v + w + u \le 1 $$
(1)

where \( B_{ijk}^{n} (v,w,u) \) are the basis functions described in the following way

$$ B_{ijk}^{n} (v,w,u) = \frac{n!}{i!j!k!}v^{i} w^{j} u^{k} . $$
(2)

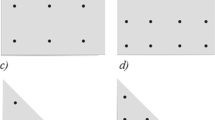
Figure 1 shows the graphical representation of the surface patches of degrees 3 and 4 defined by 10 and 15 control points, respectively.

Fig. 1
figure 1

Triangular Bézier patches of degrees 3 (a) and 4 (b) with control points

Full size image

Formula (1) for the patches of degrees 3 and 4 is written in the form

$$ \begin{aligned} \user2{P}(u,v,w) & = w^{3} \user2{P}_{003} + 3vw^{2} \user2{P}_{012} + 3v^{2} w\user2{P}_{021} + v^{3} \user2{P}_{030} \\ & \quad + 3uw^{2} \user2{P}_{102} + 6uvw\user2{P}_{111} + 3uv^{2} \user2{P}_{120} \\ & \quad + 3u^{2} w\user2{P}_{201} + 3u^{2} v\user2{P}_{210} \\ & \quad + u^{3} \user2{P}_{300} \\ \end{aligned} $$
(3)
$$ \begin{aligned} \user2{P}(u,v,w) & = w^{4} \user2{P}_{004} + 4vw^{3} \user2{P}_{013} + 6v^{2} w^{2} \user2{P}_{022} + 4v^{3} w\user2{P}_{031} + v^{4} \user2{P}_{040} \\ & \quad + 4uw^{3} \user2{P}_{103} + 12uvw^{2} \user2{P}_{112} + 12uv^{2} w\user2{P}_{121} + 4uv^{3} \user2{P}_{130} \\ & \quad + 6u^{2} w^{2} \user2{P}_{202} + 12u^{2} vw\user2{P}_{211} + 6u^{2} v^{2} \user2{P}_{220} \\ & \quad + 4u^{3} w\user2{P}_{301} + 4u^{3} v\user2{P}_{310} \\ & \quad + u^{4} \user2{P}_{400} \\ \end{aligned} $$
(4)

After substituting u = 1 – v − w in (1) and with additional restrictions imposed on \( 0 \le v,w \le 1 \) and \( v + w \le 1 \), the surface of the Bézier patch can be mapped by only two parameters: v, w. In this case, the expressions (1, 2) may be reduced to

$$ \user2{P}(v,w) = \sum\limits_{\begin{subarray}{l} i,j,k \ge 0 \\ i + j + k = n \end{subarray} } {\user2{P}_{ijk} B_{ijk}^{n} (v,w,1 - v - w)} $$
(5)

and

$$ B_{ijk}^{n} (v,w,1 - v - w) = \frac{n!}{i!j!k!}v^{i} w^{j} (1 - v - w)^{k} . $$
(6)

The above formulas for Bézier patches will be used in the rest of the paper.

Triangular Bézier patches are characterized by the simplicity of their creation and modification with the help of a small number of control points. Figure 2 shows the visualization of the patch defined by 15 control points.

Fig. 2
figure 2

Triangular Bézier patch of degree 4: a defined by 15 control points, b and c the updated surfaces after moving the selected control points

Full size image

In this way, it is possible to declare both flat triangular surfaces (Fig. 2a), as well as curvilinear surfaces. Figures 2b, c shows sample modifications of the initial shape of the surface after moving the selected control points.

3 Modification of the traditional boundary integral equation (BIE) for Laplace’s equation in 3D

We consider a 3D boundary value problem modeled by Laplace’s equation defined on domain Ω bounded by boundary Γ as presented in Fig. 3.

Fig. 3
figure 3

Definition of boundary value problem in domain Ω with boundary Γ

Full size image

The solution of such a problem consists in the determination of field function denoted as u, satisfying the given differential equation (Laplace’s), as well as established boundary conditions (Dirichlet, Neumann, or mixed), and may be solved using the traditional integral identity (Green’s formula). A generalized form of the integral identity for 3D problems can be presented by the formula [6]

$$ \bar{u}(\user2{x}) = \int\limits_{\Upgamma } {U^{ * } (\user2{x},\user2{y})p(\user2{y})\;{\text{d}}\Upgamma (\user2{y})} - \int\limits_{\Upgamma } {P^{ * } (\user2{x},\user2{y})u(\user2{y})\;{\text{d}}\Upgamma (\user2{y})} . $$
(7)

In identity (7), integrand \( U^{*} (\user2{x},\user2{y}) \) is the classical fundamental solution, whereas \( P^{*} (\user2{x},\user2{y}) \) is the classical singular solution and \( u(\user2{y}) \) and \( p(\user2{y}) \) are boundary function and its partial derivative, respectively. Additionally, \( \user2{x} \equiv \left\{ {x_{1} ,\,x_{2} ,x_{3} } \right\},\,\user2{y} \equiv \left\{ {y_{1} ,y_{2} ,y_{3} } \right\} \) indicate the source and the field points, respectively. The value of \( \bar{u}(\user2{x}) \) depends on the location of x hence \( \bar{u}(\user2{x}) = u(\user2{x}) \) for \( \user2{x} \in \Upomega , \, \bar{u}(\user2{x}) = 0.5u(\user2{x}) \), \( \user2{x} \in \Upgamma , \, \bar{u}(\user2{x}) = 0 \) and \( \user2{x} \notin \bar{\Upomega } \). If \( \user2{x} \in \Upgamma \), then formula (7) is the classical boundary integral equation (BIE).

Presented briefly, the modification of traditional BIE is considered as a generalization of the modification applied to 2D problems as in [10–17]. In general, it consists in analytically defining curvilinear boundary geometry in traditional BIE with the help of triangular Bézier surface patches.

The modification of generalized integral identity (7) for 3D problems was performed in an analogical way to that for 2D problems. Applying the Fourier transform to Eq. (7), we obtain the following transform:

$$ \hat{\bar{u}}(\varvec{\xi}) = \Updelta^{ - 1} (\varvec{\xi})\left\{ {\tilde{p}(\varvec{\xi}) + i[\xi_{1} \tilde{u}\tilde{n}_{1} (\varvec{\xi}) + \xi_{2} \tilde{u}\tilde{n}_{2} (\varvec{\xi}) + \xi_{3} \tilde{u}\tilde{n}_{3} (\varvec{\xi})]} \right\}, $$
(8)

where \( \xi_{1} ,\xi_{2} ,\xi_{3} \) are variables in the domain of Fourier transform and \( \Updelta^{ - 1} (\varvec{\xi}) = [\xi_{1}^{2} + \xi_{2}^{2} + \xi_{3}^{2} ]^{ - 1} \).

The expression \( \Updelta^{ - 1} (\varvec{\xi}) \) in Eq. (8) is obtained by the use of the Fourier transformation for the boundary fundamental solution (for Laplace’s equation) \( \Updelta (\user2{x})U^{*} (\user2{x},\user2{y}) = - \delta (\user2{x},\user2{y}) \) and by calculating the transform \( \tilde{U}^{*} (\varvec{\xi},\user2{y}) \) that is then substituted into the transform obtained from Green’s formula (7). The boundary in Eq. (8) is defined by means of the following boundary integrals

$$ \tilde{p}(\varvec{\xi}) = \int\limits_{\Upgamma } {e^{{ - i(\xi_{1} y_{1} + \xi_{2} y_{2} + \xi_{3} y_{3} )}} } p(\user2{y})\;{\text{d}}\Upgamma (\user2{y}), $$
(9)
$$ \tilde{u}\tilde{n}_{m} (\varvec{\xi}) = \int\limits_{\Upgamma } {e^{{ - i(\xi_{1} y_{1} + \xi_{2} y_{2} + \xi_{3} y_{3} )}} n_{m} (\user2{y})u(\user2{y})} \;{\text{d}}\Upgamma (\user2{y}),\quad m = 1,2,3, \, \user2{y} \in \Upgamma , $$
(10)

where \( n_{m} \) (\( m = 1,2,3 \)) is a normal vector to the boundary \( \Upgamma \).

In our further considerations, integral (10) is used to describe transform \( \tilde{u}\tilde{n}_{m} (\varvec{\xi}) \) on the boundary. The unknown identity function \( u(\user2{y}) \) in (10) can be presented by

$$ u(\user2{y}) = \frac{1}{{4\pi^{3} }}\int\limits_{{R^{3} }} {e^{{i(\omega_{1} y_{1} + \omega_{2} y_{2} + \omega_{3} y_{3} )}} \hat{u}(\varvec{\omega })\;{\text{d}}\varvec{\omega}} ,\quad\varvec{\omega}\equiv \{ \omega_{1} ,\omega_{2} ,\omega_{3} \} , $$
(11)

where function \( \widehat{u}(\varvec{\omega}) \) is presented by the following formula

$$ \hat{u}(\varvec{\omega}) = 2\Updelta^{ - 1} (\varvec{\omega})\left\{ {\widetilde{p}(\varvec{\omega}) + i[\omega_{1} \widetilde{u}\widetilde{n}_{1} (\varvec{\omega}) + \omega_{2} \widetilde{u}\widetilde{n}_{2} (\varvec{\omega}) + \omega_{3} \widetilde{u}\widetilde{n}_{3} (\varvec{\omega})]} \right\}. $$
(12)

Equation (12) is a particular case of formula (8); after inserting (12) and (11) into (10) we get the convolution integral equation in the domain of Fourier transforms. The final form of the equation is presented below as

$$ \begin{aligned} & \widetilde{u}_{l} \widetilde{n}_{m}^{(l)} (\varvec{\xi}) \\ & \quad = \int\limits_{{R^{3} }} {\overline{{\widetilde{K}}}_{m} (\gamma_{1} ,\gamma_{2} ,\gamma_{3} )} \sum\limits_{j = 1}^{n} {\Updelta^{ - 1} (\varvec{\omega})} \left\{ {\left. {\widetilde{p}_{j} (\varvec{\omega}) + i[\omega_{1} \widetilde{u}_{j} \widetilde{n}_{1} (\varvec{\omega}) + \omega_{2} \widetilde{u}_{j} \widetilde{n}_{2} (\varvec{\omega}) + \omega_{3} \widetilde{u}_{j} \widetilde{n}_{3} (\varvec{\omega})]} \right\}\;{\text{d}}{\varvec\omega} ,} \right. \\ \end{aligned} $$
(13)

where

$$ \overline{{\widetilde{K}}}_{m} (\gamma_{1} ,\gamma_{2} ,\gamma_{3} ) = \frac{1}{{4\pi^{3} }}\int\limits_{{\Upgamma_{l} }} {e^{{i(\gamma_{1} y_{1} + \gamma_{2} y_{2} + \gamma_{3} y_{3} )}} } n_{m}^{(l)} (\user2{y})\;{\text{d}}\Upgamma (\user2{y}),\quad l = 1,2, \ldots ,n, \, \gamma_{i} = \omega_{i} - \xi_{i} , $$
(14)
$$ \tilde{p}_{j} (\varvec{\omega}) = \int\limits_{{\Upgamma_{j} }} {e^{{ - i(\omega_{1} y_{1} + \omega_{2} y_{2} + \omega_{3} y_{3} )}} } p_{j} (\user2{y})\;{\text{d}}\Upgamma (\user2{y}), $$
(15)
$$ \tilde{u}_{p} \tilde{n}_{m}^{(p)} (\varvec{\omega}) = \int\limits_{{\Upgamma_{p} }} {e^{{ - i(\omega_{1} y_{1} + \omega_{2} y_{2} + \omega_{3} y_{3} )}} n_{m}^{(p)} (\user2{y})u_{p} (\user2{y})} \;{\text{d}}\Upgamma (\user2{y}),\quad\varvec{\omega}=\varvec{\xi}, \, p = l,j. $$
(16)

3.1 Triangular Bézier patches in the mathematical definition of boundary surface in BIE

Smooth surfaces of the boundary geometry in both kernel (14) and boundary integrals (15, 16) can be defined by curvilinear triangular Bézier patches of any degree described by formula (5). Having considered the boundary geometry defined by Bézier surface patches in kernel (14), we obtain

$$\bar{\tilde{K}}_{m} (\gamma_{1} ,\gamma_{2} ,\gamma_{3} ) = \frac{1}{{4\pi^{3} }}\int\limits_{{\nu_{j - 1} }}^{{\nu_{j} }} {\int\limits_{{w_{j - 1} }}^{{w_{j} }} {e^{{i[\gamma_{1} P_{j}^{(1)} (v,w) + \gamma_{2} P_{j}^{(2)} (v,w) + \gamma_{3} P_{j}^{(3)} (v,w)]}} } J_{l} (v,w)n_{m} (v,w)\;{\text{d}}\nu \;{\text{d}}w},$$
(17)

where

$$ J_{l} (v,w) = \left[ {\sum\limits_{i = 1}^{3} {A_{i}^{2} (v,w)} } \right]^{0.5} ,n_{m} (v,w) = \frac{{A_{m} (v,w)}}{{J_{l} (v,w)}},m = 1,2,3,\,\nu_{l - 1} \le \nu \le \nu_{l} ,\,w_{l - 1} \le w \le w_{l} $$

and

$$ \begin{aligned} A_{1} (v,w) & = \frac{{\partial P_{l}^{(2)} (v,w)}}{\partial w}\frac{{\partial P_{l}^{(3)} (v,w)}}{\partial v} - \frac{{\partial P_{l}^{(2)} (v,w)}}{\partial v}\frac{{\partial P_{l}^{(3)} (v,w)}}{\partial w}, \\ A_{2} (v,w) & = \frac{{\partial P_{l}^{(3)} (v,w)}}{\partial w}\frac{{\partial P_{l}^{(1)} (v,w)}}{\partial v} - \frac{{\partial P_{l}^{(3)} (v,w)}}{\partial v}\frac{{\partial P_{l}^{(1)} (v,w)}}{\partial w}, \\ A_{3} (v,w) & = \frac{{\partial P_{l}^{(1)} (v,w)}}{\partial w}\frac{{\partial P_{l}^{(2)} (v,w)}}{\partial v} - \frac{{\partial P_{l}^{(1)} (v,w)}}{\partial v}\frac{{\partial P_{l}^{(2)} (v,w)}}{\partial w}. \\ \end{aligned} $$

Boundary transforms \( \widetilde{p}_{j} (\varvec{\omega}),\,\widetilde{u}_{p} \widetilde{n}_{m}^{(p)} (\varvec{\omega}) \) represented by formulas (15, 16) after considering Bézier patches in them take the following form

$$ \begin{aligned} & \widetilde{p}_{j} (\varvec{\omega}) = \int\limits_{{\nu_{j - 1} }}^{{\nu_{j} }} {\int\limits_{{w_{j - 1} }}^{{w_{j} }} {e^{{ - i[\omega_{1} P_{j}^{(1)} (v,w) + \omega_{2} P_{j}^{(2)} (v,w) + \omega_{3} P_{j}^{(3)} (v,w)]}} } p_{j} (\nu ,w)J_{j} (v,w)\;{\text{d}}\nu \;{\text{d}}w,} \quad\varvec{\omega}=\varvec{\xi}, \, p = l,j, \\ & \widetilde{u}_{p} \widetilde{n}_{m}^{(p)} (\varvec{\omega}) = \int\limits_{{\nu_{p - 1} }}^{{\nu_{p} }} {\int\limits_{{w_{p - 1} }}^{{w_{p} }} {e^{{ - i[\omega_{1} P_{j}^{(1)} (v,w) + \omega_{2} P_{j}^{(2)} (v,w) + \omega_{3} P_{j}^{(3)} (v,w)]}} u_{p} (\nu ,w)} n_{m}^{(p)} J_{p} (v,w)\;{\text{d}}\nu \;{\text{d}}w} . \\ \end{aligned} $$
(18)

Bézier surface patches \( \user2{P}_{j} (v,w) = [P_{j}^{(1)} (v,w),P_{j}^{(2)} (v,w),P_{j}^{(3)} (v,w)]^{\text{T}} \) are defined by formula (5).

4 PIES for Laplace’s equation

The PIES for 3D problems is obtained after inversing the Fourier transform from the expression obtained after substituting (17) and (16) into (12). Having calculated some relatively complex integrals resulting from the transform inversion, we obtain an expression that can be written explicitly as

$$ 0.5u_{l} (v_{1} w_{1} ) = \sum\limits_{j = 1}^{n} {\int\limits_{{v_{j - 1} }}^{{v_{j} }} {\int\limits_{{w_{j - 1} }}^{{w_{j} }} {\{ {\bar{U}_{lj}^{*} (v_{1} ,w_{1} ,v,w)p_{j} (v,w) - \overline{P}_{lj}^{*} (v_{1} ,w_{1} ,v,w)u_{j} (v,w)}\}J_{j} (v,w)\;{\text{d}}v\;{\text{d}}w} } } $$
(19)

where \( \nu_{l - 1} < \nu_{1} < \nu_{l} ,w_{l - 1} < w_{1} < w_{l} ,\nu_{j - 1} < \nu < \nu_{j} ,w_{j - 1} < w < w_{j} ,l = 1,2,3, \ldots ,n, \) and n is the number of parametric patches that create the domain boundary in 3D.

The integrands \( \bar{U}_{lj}^{ * } (v_{1} ,w_{1} ,v,w),\,\bar{P}_{lj}^{ * } (v_{1} ,w_{1} ,v,w) \) in Eq. (19) are represented in the following form:

$$ \bar{U}_{lj}^{*} (\nu_{1} ,w_{1} ,\nu ,w) = \frac{1}{4\pi }\frac{1}{{[\eta_{1}^{2} + \eta_{2}^{2} + \eta_{3}^{2} ]^{0.5} }}, $$
(20)
$$ \bar{P}^{*}_{lj} (v_{1} ,w_{1} ,v,w) = \frac{1}{4\pi }\frac{{\eta_{1} n_{1}^{(j)} + \eta_{2} n_{2}^{(j)} + \eta_{3} n_{3}^{(j)} }}{{[\eta_{1}^{2} + \eta_{2}^{2} + \eta_{3}^{2} ]^{1.5} }}. $$
(21)

Function \( J_{j} \left( {v,w} \right) \) is the Jacobian, while \( n_{1}^{(j)} ,\,n_{2}^{(j)} ,\,n_{3}^{(j)} , \) are the components of the normal vector \( \user2{n}_{j} \) to the surface Bézier patch designated by index j. Kernels (20) and (21) include in their mathematical formalism the shape of a closed boundary, created by means of appropriate relationships between surfaces \( (l,j = 1,2,3, \ldots ,n), \) which are defined in Cartesian coordinates using the following relations

$$ \eta_{1} = P_{l}^{(1)} (v_{1} ,w_{1} ) - P_{j}^{(1)} (v,w),\quad \eta_{2} = P_{l}^{(2)} (v_{1} ,w_{1} ) - P_{j}^{(2)} (v,w),\quad \eta_{3} = P_{l}^{(3)} (v_{1} ,w_{1} ) - P_{j}^{(3)} (v,w), $$
(22)

where \( P_{j}^{(1)} (v,w),\,\,P_{j}^{(2)} (v,w),\,\,P_{j}^{(3)} (v,w) \) are the scalar components of the surface patch \( \user2{P}_{j} (v,w) = [P_{j}^{(1)} (v,w),P_{j}^{(2)} (v,w),P_{j}^{(3)} (v,w)]^{\text{T}} \), which depend on the parameters \( v,w \). This notation is also valid for the patch labeled by index l with parameters \( v_{1} \,w_{1} \), i.e., for \( j = l \) and for parameters \( v = v_{1} \) and \( w = w_{1} \).

We have considered functions \( \user2{P}_{j} (v,w) \) in the form presented in Sect. 2 parametric surface patches. The possibility of analytical description of the boundary directly in the formula of PIES is the main advantage of the presented approach in comparison with traditional BIE. In classical BIE, a description of the boundary is not included in the mathematical formalism of the equation, but very generally defined by the integral boundary. This necessitates the discretization of the domain boundary into elements, as is the case in classical BEM.

4.1 Approximation of the boundary functions over the surface patches

The use of PIES for solving 2D and 3D boundary problems made it possible to eliminate the need for discretization of both the above-mentioned boundary geometry and the boundary functions. The boundary functions defined as the boundary conditions as well as obtained after solving PIES are approximated on each triangular Bézier patch j by means of the following Chebyshev series:

$$ p_{j} (v,w) = \sum\limits_{p = 0}^{N} {\sum\limits_{r = 0}^{M} {p_{j}^{(pr)} T_{j}^{(p)} (v)} T_{j}^{(r)} (w)} , $$
(23)
$$ u_{j} (v,w) = \sum\limits_{p = 0}^{N} {\sum\limits_{r = 0}^{M} {u_{j}^{(pr)} T_{j}^{(p)} (v)} T_{j}^{(r)} (w)} , $$
(24)

where \( u_{j}^{(pr)} \), \( \,p_{j}^{(pr)} \) are requested coefficients, \( T_{j}^{(p)} (v) \), \( T_{j}^{(r)} (w) \) are Chebyshev polynomials, and \( \bar{n} = N*M \) is the number of coefficients in the approximating series. After substituting (23) and (24) in PIES (19), we obtain an algebraic equation system with respect to the unknown coefficients \( u_{j}^{(pr)} \) or \( \,\,p_{j}^{(pr)} \)

$$ \begin{aligned} 0.5u_{l} (\nu_{1} ,w_{1} ) & = \sum\limits_{j = 1}^{n} {\sum\limits_{p = 0}^{N} {\sum\limits_{r = 0}^{M} {\left\{ {p_{j}^{(pr)} \int\limits_{{v_{j - 1} }}^{{v_{j} }} {\int\limits_{{w_{j - 1} }}^{{w_{j} }} {\overline{U}_{lj}^{*} (\nu_{1} ,w_{1} ,\nu ,w) - u_{j}^{(pr)} \int\limits_{{v_{j - 1} }}^{{v_{j} }} {\int\limits_{{w_{j - 1} }}^{{w_{j} }} {\overline{P}_{lj}^{*} (\nu_{1} ,w_{1} ,\nu ,w)\,} } } } } \right\}} } } \\ & \quad\times T_{j}^{(p)} (v)T_{j}^{(r)} (w)J_{j} (v,w)\;{\text{d}}v\;{\text{d}}w. \\ \end{aligned} $$
(25)

One of these functions, either \( u_{j}^{(pr)} \) or \( \,\,p_{j}^{(pr)} \), depending on the type of the resolved boundary problem, is posed in the form of boundary conditions, whereas the other is the searched function resulting from the solution of PIES.

Next, writing down expression (25) at the collocation points on individual Bézier patches, we obtain an algebraic equation system with respect to the unknown coefficients \( u_{j}^{(pr)} \) or \( \,p_{j}^{(pr)} \). After its resolution, we obtain the values of the unknown coefficients in one of the approximating series (23) or (24), approximating the unknown function on the boundary.

4.2 Solutions in the domain

After solving PIES, we obtain the solution of the boundary problem only on its boundary, represented by series (23) or (24). To find a solution in the domain, we need to obtain an integral identity known for BIE that makes use of the solution on the boundary obtained by PIES. After using similar modifications as in the case of 2D problems [10, 11], we have had an integral identity which used solutions (23) and (24) at the boundary, previously obtained by the PIES solution. The modified identity takes the following form:

$$ u(\user2{x}) = \sum\limits_{j = 1}^{n} \int\limits_{{\nu_{j - 1}}}^{{\nu_{j} }} \int\limits_{{w_{j - 1} }}^{{w_{j} }} \left\{\left.{\hat{\overline{U}}}_{j}^{*} (\user2{x},\nu ,w)p_{j} (\nu ,w) -{\hat{\overline{P}}}_{j}^{*} (\user2{x},\nu ,w)u_{j} (\nu ,w)\right\}J_{j} \right. (v,w)\;{\text{d}}\nu \;{\text{d}}w. $$
(26)

The integrands appearing in the identity (26) are expressed in the following form:

$$ \hat{\overline{U}}_{j}^{*} (\user2{x},v,w) = \frac{1}{4\pi }\frac{1}{{[\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{1}^{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{2}^{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{3}^{2} ]^{0.5} }}, $$
(27)
$$ \hat{\overline{P}}_{j}^{ * } (\user2{x},\nu ,w) = \frac{1}{4\pi }\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{1} n_{1} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{2} n_{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{3} n_{3} }}{{[\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{1}^{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{2}^{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{3}^{2} ]^{1.5} }}, $$
(28)

where

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{1} = x_{1} - P_{j}^{(1)} (v,w),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{2} = x_{2} - P_{j}^{(2)} (v,w),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {r}_{3} = x_{3} - P_{j}^{(3)} (v,w). $$
(29)

Both integrands in the identity (26) are visually very similar to kernels (20) and (21). The main difference, however, lies in the fact that in kernels (27) and (28), apart from Bézier patches defining boundary geometry, we have the coordinates of the point in domain \( \user2{x} \equiv \left\{ {x_{1} ,x_{2} ,x_{3} } \right\} \). Using coordinates, we can pose any point in the domain in which we look for the solutions.

5 Numerical examples

The discussed algorithm has been successfully applied to solve boundary problems described by Laplace’s equation. Numerical examples are given to compare the results obtained by the proposed PIES method with analytical ones and those obtained by BEM. There are several geometries with smooth boundaries available in the literature for 3D potential problems. In most cases, however, these objects are shaped as spheres, and the sphere models are used in the examples presented below. This does not limit the shapes available.

5.1 Declaration of a sphere by triangular Bézier patches

A single Bézier patch can only capture a small class of shapes. To increase modeling possibilities, triangular patches of higher degree may be introduced. However, they are harder to control and, in practice, the most common solution is to join independent low-degree patches together into a piecewise surface. The surface of the sphere may be simultaneously approximated in PIES by eight symmetrical triangular Bézier patches of degree 4, as shown in Fig. 4a.

Fig. 4
figure 4

A sphere approximated with eight symmetrical triangular Bézier patches of the fourth degree (a); geometry modification by moving control points (b)

Full size image

A triangular patch approximating 1/8 of the sphere of radius 1 with center at the origin is defined by 15 control points with the following coordinates (placed in the first quadrant of Cartesian coordinates \( x_{1} ,x_{2} ,x_{3} \)) [28]

$$ \begin{array}{*{20}c} {\user2{P}_{004} \left\{ {0,1,0} \right\},} & {\user2{P}_{013} \left\{ {\alpha ,1,0} \right\},} & {\user2{P}_{022} \left\{ {\beta ,\beta ,0} \right\},} & {\user2{P}_{031} \left\{ {1,\alpha ,0} \right\},} & {\user2{P}_{040} \left\{ {1,0,0} \right\},} \\ {\user2{P}_{103} \left\{ {0,1,\alpha } \right\},} & {\user2{P}_{112} \left\{ {\gamma ,1,\gamma } \right\},} & {\user2{P}_{121} \left\{ {1,\gamma ,\gamma } \right\},} & {\user2{P}_{130} \left\{ {1,0,\alpha } \right\},} & {} \\ {\user2{P}_{202} \left\{ {0,\beta ,\beta } \right\},} & {\user2{P}_{211} \left\{ {\gamma ,\gamma ,1} \right\},} & {\user2{P}_{220} \left\{ {\beta ,0,\beta } \right\},} & {} & {} \\ {\user2{P}_{301} \left\{ {0,\alpha ,1} \right\},} & {\user2{P}_{310} \left\{ {\alpha ,0,1} \right\},} & {} & {} & {} \\ {\user2{P}_{400} \left\{ {0,0,1} \right\},} & {} & {} & {} & {} \\ \end{array} $$
(30)

where

$$ \alpha = (\sqrt 3 - 1)/\sqrt 3 ,\quad \beta = (\sqrt 3 + 1)/2\sqrt 3 ,\quad \gamma = 1 - (5 - \sqrt 2 )(7 - \sqrt 3 )/46. $$

The outer edges of formed patches are joined together to form a closed sphere. As a result, the patches share the same points along the common edges and the total number of control points used to sphere approximation is reduced to 66.

The created shape representation scheme of the sphere is directly integrated in mathematical formalism of PIES. Therefore, modeling the boundary is only limited to the above-mentioned declaration of surface patches without their further division, for example into boundary or finite elements. This is a big advantage of PIES, which leads to a radical simplification of both the boundary geometry description and numerical calculations.

The accuracy of the fitting process, in terms of the error of Bézier sphere-shaped surface in relation to the radius of ideal sphere, is presented in Fig. 5. The error can be computed as

$$ E(v,w) = { \max }\left| {\sqrt {P^{(1)} (v,w)^{2} + P^{(2)} (v,w)^{2} + P^{(3)} (v,w)^{2} } - 1} \right|, $$
(31)

where \( 0 \le v,w \le 1 \), \( v + w \le 1 \) and \( \user2{P}(v,w) = [P^{(1)} (v,w),P^{(2)} (v,w),P^{(3)} (v,w)]^{\text{T}} \) are the Cartesian components of triangular Bézier patch \( \user2{P}(v,w) \). The maximum of \( E\left( {v,w} \right) \) for the presented model reaches the value of 0.027.

Fig. 5
figure 5

The error between Bézier patch formed by formula (31) and the radius of the 1/8 unit sphere (b) at four cross sections through the patch (a) for spherical polar coordinates

Full size image
Fig. 6
figure 6

The hollow sphere (a) with cross section and boundary conditions (b)

Full size image

Additionally, we can perform easy shape modification by moving individual or group of Bézier control points. The model given in Fig. 4b can be seen as an effective modification of the sphere from Fig. 4a. For this purpose, the sphere model is transformed into an ellipsoidal form, shown in Fig. 4b, after scalar multiplication of the \( x_{1} \)-coordinates of all Bézier control points by 2. This unified approach to boundary shape modification offers two significant advantages. Firstly, the operation is performed with the help of a limited number of data, only control points of Bézier patches, and secondly keeps a continuous smooth structure of modified boundary. The model of the boundary presented here is used in numerical examples given in this section.

5.2 Example 1

In our first example, we consider the problem of a spherical cavity outside a unit sphere. On the surface, a constant radial influx equal to 10 J/m2s (the Neumann boundary condition) is posed. The exact solution of the problem has an asymptotic nature and is given by [7]

$$ u(r) = \frac{10}{r}, $$
(32)

and goes to zero when \( r \to \infty \).

The sphere is approximated by boundary model show in Fig. 4a and directly used in PIES to solve this boundary problem without performing any discretization. The solutions of PIES obtained by integral identity (26) have been compared in Table 1 with formula (32) and with available literature BEM results with flat boundary elements [7].

Table 1 Solutions in the domain outside of the sphere
Full size table

The solutions of PIES in external points (column 5) agree well with the analytical results (32) (column 2) and with BEM solutions (columns 3, 4). To increase the accuracy of solutions in the PIES, we only need to increase the degree of the Chebyshev polynomial series (23, 24) without any modification boundary geometry from Fig. 4a. From the programming point of view, the operation simply involves changing the number \( \bar{n} \) in the program, which makes it possible to quickly verify the convergence. The solutions on the boundary approximated by the polynomials for \( \bar{n} = 15 \) are presented in column 6.

5.3 Example 2

The aim of our second example is to demonstrate the efficiency of the proposed 3D boundary description in PIES by Bézier patches in the case of its shape modification. To validate the proposed approach, inside the boundaries created by Bézier patches from Fig. 4a, b, the Laplace equation with Dirichlet boundary conditions is solved. The prescribed values of Dirichlet boundary conditions depend on the Cartesian coordinates \( \user2{x} \equiv \left\{ {x_{1} ,x_{2} ,x_{3} } \right\} \) that are calculated on the basis of the following four independent functions [29, 30]

$$ u_{1} (\user2{x}) = x_{1} + x_{2} + x_{3} , $$
(33)
$$ u_{2} (\user2{x}) = x_{1} x_{2} + x_{2} x_{3} + x_{3} x_{1} , $$
(34)
$$ u_{3} (\user2{x}) = x_{1}^{3} + x_{2}^{3} + x_{3}^{3} - 3x_{1}^{2} x_{2} - 3x_{2}^{2} x_{3} - 3x_{3}^{2} x_{1} , $$
(35)
$$ u_{4} (\user2{x}) = { \sinh }\left( {\frac{{\pi x_{1} }}{2}} \right){ \sin }\left( {\frac{{\pi x_{2} }}{2\sqrt 2 }} \right){ \sin }\left( {\frac{{\pi x_{3} }}{2\sqrt 2 }} \right), $$
(36)

that satisfy Laplace’s equation.

The normal derivatives of functions (33–36) computed on the surface of the Bézier patches can be identified with exact analytical solutions of the problem on the boundary. The derived normal derivatives for these functions are presented below:

$$ p_{1} (\user2{x}) = \frac{{{\text{d}}u_{1} (\user2{x})}}{{{\text{d}}\user2{n}}} = n_{1} (\user2{x}) + n_{2} (\user2{x}) + n_{3} (\user2{x}), $$
(37)
$$ p_{2} (\user2{x}) = \frac{{{\text{d}}u_{2} (\user2{x})}}{{{\text{d}}\user2{n}}} = (x_{2} + x_{3} )n_{1} (\user2{x}) + (x_{1} + x_{3} )n_{2} (\user2{x}) + (x_{1} + x_{2} )n_{3} (\user2{x}), $$
(38)
$$ \begin{aligned} p_{3} (\user2{x}) & = \frac{{{\text{d}}u_{3} (\user2{x})}}{{{\text{d}}\user2{n}}} = (3x_{1}^{2} - 3x_{3}^{2} - 6x_{1} x_{2} )n_{1} (\user2{x}) + (3x_{2}^{2} - 3x_{1}^{2} - 6x_{2} x_{3} )n_{2} (\user2{x}) \\ & \quad + (3x_{3}^{2} - 3x_{2}^{2} - 6x_{1} x_{3} )n_{3} (\user2{x}), \\ \end{aligned} $$
(39)
$$ \begin{aligned} p_{4} (\user2{x}) & = \frac{{{\text{d}}u_{4} (\user2{x})}}{{{\text{d}}\user2{n}}} = \frac{\pi }{2}\cosh \left( {\frac{{\pi x_{1} }}{2}} \right)\sin \left( {\frac{{\pi x_{2} }}{2\sqrt 2 }} \right)\sin \left( {\frac{{\pi x_{3} }}{2\sqrt 2 }} \right)n_{1} (\user2{x}) \\ & \quad + \frac{\pi }{2\sqrt 2 }\sinh \left( {\frac{{\pi x_{1} }}{2}} \right)\cos \left( {\frac{{\pi x_{2} }}{2\sqrt 2 }} \right)\sin \left( {\frac{{\pi x_{3} }}{2\sqrt 2 }} \right)n_{2} (\user2{x}) \\ & \quad + \frac{\pi }{2\sqrt 2 }\sinh \left( {\frac{{\pi x_{1} }}{2}} \right)\sin \left( {\frac{{\pi x_{2} }}{2\sqrt 2 }} \right)\cos \left( {\frac{{\pi x_{3} }}{2\sqrt 2 }} \right)n_{3} (\user2{x}). \\ \end{aligned} $$
(40)

Both boundary conditions and unknown boundary functions in PIES, due to the lack of conventional discretization, take the form of approximation series \( u_{j} (v,w) \) or \( p_{j} (v,w) \), spread over each declared Bézier patch. To find a solution on the boundary in the PIES, we need to find the coefficients \( u_{j}^{(pr)} \), \( \,p_{j}^{(pr)} \) in the approximation series only. After these coefficients \( u_{j}^{(pr)} \) and \( \,p_{j}^{(pr)} \) have been calculated and multiplied by Chebyshev polynomials \( T_{j}^{\left( p \right)} \left( v \right) \) and \( T_{j}^{\left( r \right)} \left( w \right), \) the solution at any point \( v,w \) on our Bézier patch is obtained.

The stability of solutions is investigated as a result of a change in the number of input data in the program that are responsible for the number \( \bar{n} \) of expressions in the approximating series (23, 24). In Tables 2 and 3, we summarize the error norms in the domain for different values of parameter \( \bar{n} \). The \( L_{2} \) error norms for solutions on the boundary is derived on the basis of the following formula [30]:

$$ ||e|| = \frac{1}{{\left| {\bar{p}^{(k)} } \right|_{ \max } }}\sqrt {\frac{1}{K}\sum\limits_{k = 1}^{K} {\left( {p^{(k)} - \bar{p}^{(k)} } \right)}^{2} } \times 100\;\% , $$
(41)

where \( p^{(k)} \) represents a set of K = 1,568 solutions obtained on the boundary on the basis of series (24), while \( \bar{p}^{(k)} \) are exact solutions given by (37–40).

Table 2 The impact of change in the number of terms \( \bar{n} \) in series \( \,\,p_{j} (v,w) \) on the accuracy of solutions on the boundary from Fig. 4a in PIES
Full size table
Table 3 The impact of change in the number of terms \( \bar{n} \) in the series \( \,\,p_{j} (v,w) \) on the accuracy of solutions on the boundary from Fig. 4b in PIES
Full size table

Approximation of the boundary functions over the surface patches by Chebyshev series (23, 24) introduces an effective approach of the convergence analysis. It is realized by the increase of used approximation forms of series (23, 24). In practice, it is performed by change in values \( \bar{n} \) in the program without any intervention in the previously declared boundary geometry. This is a considerable advantage over the element methods in which the increased accuracy involves the increase in the number of elements.

5.4 Example 3

The domain bounded by the hollow sphere with internal radius \( R_{1} = 1.0 \) and external radius \( R_{2} = 2.0 \), respectively, is considered (Fig. 6).

The inner and outer surfaces of the domain are posed with temperature \( T_{1} = 100\;^\circ {\text{C}} \) and \( T_{2} = 200\;^\circ {\text{C}}, \) respectively. The exact solution may be written in the following way [31]:

$$ T(r) = 300 - 200/r, $$
(42)

where r is the radius of the domain inside the hollow sphere.

Despite significant differences in the surface areas of both sphere areas, expressed by radiuses \( R_{1} \) and \( R_{2} \), each of them is described by eight Bézier patches of degree 4 according to the later scheme discussed in Sect. 5.1. As a result, a complete geometric description of the spherical wall requires 16 patches with 112 control points.

The results obtained in the domain bounded between two spherical boundaries are presented in Table 4 and proved good agreements with analytical ones.

Table 4 The PIES values inside the domain bounded by Bézier patches from Fig. 6
Full size table

Table 4 shows a good agreement of the solutions obtained in PIES with the analytical values. The solutions were obtained after solving only system of 144 and 240 linear equations by a pseudospectral method.

6 Conclusions

Triangular Bézier patches seem to be efficient tools for 3D boundary modeling and in connection with PIES provides an easy way of solving 3D boundary value problems. The patches are applied to analytic modification of traditional BIE and to obtain the PIES formula for 3D Laplace’s problems. This paper generalizes the existing and intensively developed 2D PIES scheme to solve boundary value problems in 3D. The explicit form of PIES for Laplace’s equation has been presented. The PIES solution requires neither the domain nor the boundary discretization and is reduced to approximation of boundary functions. In addition, it has presented the identity for solutions in the domain. The obtained PIES formula has been tested on elementary examples, but with analytical and numerical solutions. The analysis showed the previously existing advantages of PIES for 2D problems also in relation to the 3D problems described by Laplace’s equation. These advantages are related to the simplicity of defining the shape of the boundary by control points. The discussed numerical examples show the good accuracy of the obtained solutions.