Skip to main content
SpringerLink
Log in

Cutoff for the East Process

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

The East process is a 1d kinetically constrained interacting particle system, introduced in the physics literature in the early 1990s to model liquid-glass transitions. Spectral gap estimates of Aldous and Diaconis in 2002 imply that its mixing time on L sites has order L. We complement that result and show cutoff with an \({O(\sqrt{L})}\)-window.

The main ingredient is an analysis of the front of the process (its rightmost zero in the setup where zeros facilitate updates to their right). One expects the front to advance as a biased random walk, whose normal fluctuations would imply cutoff with an \({O(\sqrt{L})}\)-window. The law of the process behind the front plays a crucial role: Blondel showed that it converges to an invariant measure ν, on which very little is known. Here we obtain quantitative bounds on the speed of convergence to ν, finding that it is exponentially fast. We then derive that the increments of the front behave as a stationary mixing sequence of random variables, and a Stein-method based argument of Bolthausen (‘82) implies a CLT for the location of the front, yielding the cutoff result.

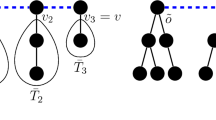
Finally, we supplement these results by a study of analogous kinetically constrained models on trees, again establishing cutoff, yet this time with an O(1)-window.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aldous, D.: Random walks on finite groups and rapidly mixing Markov chains. Seminar on probability, XVII, pp. 243–297 (1983)

  2. Aldous D., Diaconis P.: Shuffling cards and stopping times. Am. Math. Monthly 93, 333–348 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  3. Aldous D., Diaconis P.: The asymmetric one-dimensional constrained Ising model: rigorous results. J. Stat. Phys. 107(5–6), 945–975 (2002)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  4. Aldous, D., Fill, J.: Reversible Markov chains and random walks on graphs. In preparation, http://www.stat.berkeley.edu/~aldous/RWG/book.html

  5. Blondel O.: Front progression for the East model. Stoch. Process. Appl. 123, 3430–3465 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  6. Bolthausen E.: On the central limit theorem for stationary mixing random fields. Ann. Probab. 10(4), 1047 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  7. Bolthausen E., Deuschel J.D., Zeitouni O.: Recursions and tightness for the maximum of the discrete, two dimensional Gaussian free field. Electron. Commun. Probab. 16, 114–119 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  8. Bramson, M., Zeitouni, O.: Tightness for the minimal displacement of branching random walk. J. Stat. Mech. Theory Exp. (7), P07010, 12 (2007)

  9. Bramson M., Zeitouni O.: Tightness for a family of recursion equations. Ann. Probab. 37(2), 615–653 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  10. Cancrini N., Martinelli F., Roberto C., Toninelli C.: Kinetically constrained spin models. Probab. Theory Relat. Fields 140(3–4), 459–504 (2008)

    MATH  MathSciNet  Google Scholar 

  11. Chleboun P., Faggionato A., Martinelli F.: Time scale separation and dynamic heterogeneity in the low temperature East model. Common Math. Phys. 328(3), 955–993 (2014)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  12. Cancrini, N., Martinelli, F., Roberto, C., Toninelli, C.: Mixing time of a kinetically constrained spin model on trees: power law scaling at criticality. Probab. Theory Relat. Fields (to appear)

  13. Cancrini N., Martinelli F., Schonmann R., Toninelli C.: Facilitated oriented spin models: some non equilibrium results. J. Stat. Phys. 138(6), 1109–1123 (2010)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  14. Diaconis P.: The cutoff phenomenon in finite Markov chains. Proc. Nat. Acad. Sci. USA 93(4), 1659–1664 (1996)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  15. Diaconis P., Fill J.A.: Strong stationary times via a new form of duality. Ann. Probab. 18(4), 1483–1522 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  16. Diaconis P., Shahshahani M.: Generating a random permutation with random transpositions. Z. Wahrsch. Verw. Gebiete 57(2), 159–179 (1981)

    Article  MATH  MathSciNet  Google Scholar 

  17. Dekking F.M., Host B.: Limit distributions for minimal displacement of branching random walks. Probab. Theory Relat. Fields 90(3), 403–426 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  18. Faggionato, A., Martinelli, F., Roberto, C., Toninelli, C.: The East model: recent results and new progresses. Markov Process. Relat. Fields (in press)

  19. Fredrickson G.H., Andersen H.C.: Kinetic Ising Model of the Glass Transition. Phys. Rev. Lett. 53(13), 1244–1247 (1984)

    Article  ADS  Google Scholar 

  20. Grimmett, G.: Percolation, 2nd ed. Grundlehren der Mathematischen Wissenschaften (Fundamental Principles of Mathematical Sciences), vol. 321. Springer, Berlin (1999)

  21. Jäckle J., Eisinger S.: A hierarchically constrained kinetic Ising model. Zeitschrift fr Physik B Condensed Matter 84(1), 115–124 (1991)

    Article  ADS  Google Scholar 

  22. Levin D.A., Peres Y., Wilmer E.L.: Markov chains and mixing times, American Mathematical Society, Providence, RI (2009). (With a chapter by James G. Propp and David B. Wilson)

  23. Martinelli F., Toninelli C.: Kinetically constrained spin models on trees. Ann. Appl. Probab. 23(5), 1721–2160 (2013)

    Article  MathSciNet  Google Scholar 

  24. Saloff-Coste, L.: Lectures on finite Markov chains. Lectures on probability theory and statistics (Saint-Flour, 1996), Lecture Notes in Math., vol. 1665, Springer, Berlin, pp. 301–413 (1997)

  25. Stein, C.: A bound for the error in the normal approximation to the distribution of a sum of dependent random variables. Proc. of the Sixth Berkeley Symp. Math. Statist. Prob. Univ. California Press, pp. 583–602 (1972)

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Washington, Seattle, WA, 98195, USA

    S. Ganguly

  2. Courant Institute, New York University, 251 Mercer Street, New York, NY, 10012, USA

    E. Lubetzky

  3. Dip. Matematica & Fisica, Università Roma Tre, Largo S. Murialdo 1, 00146, Roma, Italy

    F. Martinelli

Authors
  1. S. Ganguly
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. Lubetzky
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. F. Martinelli
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. Lubetzky.

Additional information

Communicated by F. Toninelli

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ganguly, S., Lubetzky, E. & Martinelli, F. Cutoff for the East Process. Commun. Math. Phys. 335, 1287–1322 (2015). https://doi.org/10.1007/s00220-015-2316-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-015-2316-x

Keywords

Search

Navigation