Worst-case topology optimization of self-weight loaded structures using semi-definite programming

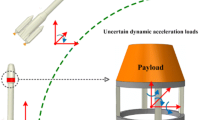
Abstract

The paper concerns worst-case compliance optimization by finding the structural topology with minimum compliance for the loading due to the worst possible acceleration of the structure and attached non-structural masses. A main novelty of the paper is that it is shown how this min-max problem can be formulated as a non-linear semi-definite programming (SDP) problem involving a small-size constraint matrix and how this problem is solved numerically. Our SDP formulation is an extension of an eigenvalue problem seen previously in the literature; however, multiple eigenvalues naturally arise which makes the eigenvalue problem non-smooth, whereas the SDP problem presented in this paper provides a computationally tractable problem. Optimized designs, where the uncertain loading is due to acceleration of applied masses and the weight of the structure itself, are shown in two and three dimensions and we show that these designs satisfy optimality conditions that are also presented.

Appendices

Appendix A: Equivalence between bounded eigenvalue and SDP

Proposition 1

Let $\boldsymbol {H}\in \mathbb {S}^{s}$ and $\lambda _{1}(\boldsymbol {H}) = \max \limits _{i=1,\ldots ,s} \lambda _{i}(\boldsymbol {H})$ . Then

$$\lambda_{1}(\boldsymbol{H}) \leq z,\; \Leftrightarrow \; \boldsymbol{H} - z\boldsymbol{I} \preceq \boldsymbol{0}. $$

Proof

“$\boldsymbol {H} - z\boldsymbol {I} \preceq \boldsymbol {0}$” means that

$$\begin{array}{@{}rcl@{}} \boldsymbol{y}^{\textsf{T}}(\boldsymbol{H} - z\boldsymbol{I})\boldsymbol{y} &\leq& 0 \quad \forall \boldsymbol{y} \in \mathbb{R}^{s} \Leftrightarrow \\ (\alpha\boldsymbol{v})^{\textsf{T}}(\boldsymbol{H} - z\boldsymbol{I})(\alpha\boldsymbol{v}) &\leq& 0 \quad \forall (\alpha , \boldsymbol{v}) \in \mathbb{R}^{s+1} : ||\boldsymbol{v}||=1 \Leftrightarrow \\ \alpha^{2}\boldsymbol{v}^{\textsf{T}}(\boldsymbol{H} - z\boldsymbol{I})\boldsymbol{v} &\leq& 0 \quad \forall (\alpha , \boldsymbol{v}) \in \mathbb{R}^{s+1} : ||\boldsymbol{v}||=1 \Leftrightarrow \\ \boldsymbol{v}^{\textsf{T}}(\boldsymbol{H} - z\boldsymbol{I})\boldsymbol{v} &\leq& 0 \quad \forall \boldsymbol{v} \in \mathbb{R}^{s} : ||\boldsymbol{v}||=1 \Leftrightarrow \\ \boldsymbol{v}^{\textsf{T}}\boldsymbol{H}\boldsymbol{v} &\leq& z \quad \forall \boldsymbol{v} \in \mathbb{R}^{s} : ||\boldsymbol{v}||=1 \Leftrightarrow \\ \lambda_{1}(\boldsymbol{H}) = \max_{||\boldsymbol{v}||=1}\,\boldsymbol{v}^{\textsf{T}}\boldsymbol{H}\boldsymbol{v} &\leq& z , \end{array} $$

where the equality to the left in the last line follows from the Rayleigh-Ritz theorem (Horn and Johnson 1985, Theorem 4.2.2). □

Appendix B: Worst-case compliance and optimization problem for a singular stiffness matrix

For a singular stiffness matrix $\boldsymbol {K}\left (\boldsymbol {x}\right )$ the compliance is still a well-defined function and can be expressed as

$$C(\boldsymbol{x},\boldsymbol{r}) = - \inf_{\boldsymbol{v}\in\mathbb{R}^{n}} {\Pi}(\boldsymbol{v},\boldsymbol{x},\boldsymbol{r}), $$

where

$${\Pi}(\boldsymbol{v},\boldsymbol{x},\boldsymbol{r}) = \frac{1}{2}\boldsymbol{v}^{\textsf{T}}\boldsymbol{K}\left( \boldsymbol{x}\right)\boldsymbol{v} - \boldsymbol{r}^{\textsf{T}}\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v}, $$

is the total potential energy for a general nodal displacement v. (See Klarbring (2015) for a recent general discussion of compliance minimization.)

The worst-case compliance is defined as

$$ P\left( \boldsymbol{x}\right) = \sup_{\boldsymbol{r}\in T}\, C(\boldsymbol{x},\boldsymbol{r}). $$

(19)

By straightforward manipulations we get²

$$\begin{array}{@{}rcl@{}} P\left( \boldsymbol{x}\right) &=& - \inf_{\boldsymbol{r}\in T}\,\left( \inf_{\boldsymbol{v}\in\mathbb{R}^{n}} {\Pi}(\boldsymbol{v},\boldsymbol{x},\boldsymbol{r})\right)\\ &=& - \inf_{\boldsymbol{v}\in\mathbb{R}^{n}} \left( \inf_{\boldsymbol{r}\in T} {\Pi}(\boldsymbol{v},\boldsymbol{x},\boldsymbol{r})\right)\\ &=& - \inf_{\boldsymbol{v}\in\mathbb{R}^{n}} \left( \frac{1}{2}\boldsymbol{v}^{\textsf{T}}\boldsymbol{K}\left( \boldsymbol{x}\right)\boldsymbol{v} + \inf_{\boldsymbol{r}\in T} \left( -\boldsymbol{r}^{\textsf{T}}\boldsymbol{B}\left( \boldsymbol{x}\right) \boldsymbol{v}\right)\right)\\ &=& - \inf_{\boldsymbol{v}\in\mathbb{R}^{n}} \left( \frac{1}{2}\boldsymbol{v}^{\textsf{T}}\boldsymbol{K}\left( \boldsymbol{x}\right)\boldsymbol{v} - \sup_{\boldsymbol{r}\in T}\, \boldsymbol{r}^{\textsf{T}}\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v}\right). \end{array} $$

The inner maximization problem is solved by noting that

$$\boldsymbol{r}^{\textsf{T}}\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v} \leq |\boldsymbol{r}^{\textsf{T}}\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v}| \leq ||\boldsymbol{r}||\,||\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v}|| \leq ||\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v}||, $$

using the Cauchy-Schwarz inequality and the fact that ||r||≤1 for r∈T. Equality holds for $\boldsymbol {r}=\boldsymbol {B}\left (\boldsymbol {x}\right )\boldsymbol {v}/||\boldsymbol {B} \left (\boldsymbol {x}\right )\boldsymbol {v}||$, so we have

$$ \sup_{\boldsymbol{r}\in T}\, \boldsymbol{r}^{\textsf{T}}\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v}=\sup_{||\boldsymbol{r}||=1}\, \boldsymbol{r}^{\textsf{T}}\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v}=||\boldsymbol{B} \left( \boldsymbol{x}\right)\boldsymbol{v}||, $$

(20)

where the first equality follows from Rockafeller (1972, Corollary 32.3.1). Substitution in (19) yields

$$\begin{array}{@{}rcl@{}} P\left( \boldsymbol{x}\right) &=& -\inf_{\boldsymbol{v}\in \mathbb{R}^{n}} \left( \frac{1}{2}\boldsymbol{v}^{\textsf{T}}\boldsymbol{K}\left( \boldsymbol{x}\right)\boldsymbol{v} - ||\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v}||\right)\\ &=&\sup_{\boldsymbol{v}\in \mathbb{R}^{n}} \left( ||\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v}|| - \frac{1}{2}\boldsymbol{v}^{\textsf{T}}\boldsymbol{K}\left( \boldsymbol{x}\right)\boldsymbol{v}\right). \end{array} $$

(21)

We are now interested in essentially the equivalent problem to (9), i.e.,

$$\min\limits_{\boldsymbol{x}\in\mathcal{H}} P\left( \boldsymbol{x}\right), $$

but now without requiring a non-singular stiffness matrix. As for (9) we rephrase it into a bound formulation, which, using (21), leads to the following optimization problem:

$$ \begin{array}{l} \min\limits_{z\in\mathbb{R},\,\boldsymbol{x}\in\mathcal{H}} \quad z \\ \text{subject to} \;\;||\boldsymbol{B}\left( \boldsymbol{x}\right)\boldsymbol{v}|| - \frac{1}{2}\boldsymbol{v}^{\textsf{T}}\boldsymbol{K}\left( \boldsymbol{x}\right)\boldsymbol{v} \leq \frac{1}{2}z, \quad \forall \boldsymbol{v}\in\mathbb{R}^{n}. \end{array} $$

(22)

This is a semi-infinite problem since it has a finite number of variables, but an infinite number of constraints. However, it can be shown by the following theorem that this problem is equivalent to a semi-definite program.

Theorem

$$\left( \begin{array}{cc} z\boldsymbol{I} & \boldsymbol{B} \\ \boldsymbol{B}^{\textsf{T}} & \boldsymbol{K} \end{array} \right) \succeq \boldsymbol{0}\Leftrightarrow -\frac{1}{2}\boldsymbol{v}^{\textsf{T}}\boldsymbol{K}\boldsymbol{v} + ||\boldsymbol{B}\boldsymbol{v}|| \leq \frac{1}{2}z, \; \quad \; \forall \boldsymbol{v}\in\mathbb{R}^{n}. $$

Proof

The proof resembles that of Lemma 2.2 in Ben-Tal and Nemirovski (1997).

Since the matrix is positive semi-definite,

$$\begin{array}{@{}rcl@{}} \left( -\boldsymbol{\tau} \;\boldsymbol{u}\right) \left( \begin{array}{cc}z\boldsymbol{I} & \boldsymbol{B} \\ \boldsymbol{B}^{\textsf{T}} & \boldsymbol{K} \end{array}\right) \left( \begin{array}{c}-\boldsymbol{\tau} \\\boldsymbol{u} \end{array}\right) &\geq& 0 \quad \forall\, (\boldsymbol{\tau}, \boldsymbol{u}) \in \mathbb{R}^{s+n} \Leftrightarrow \\ z\boldsymbol{\tau}^{\textsf{T}}\boldsymbol{\tau} + \boldsymbol{u}^{\textsf{T}}\boldsymbol{K}\boldsymbol{u} - 2\boldsymbol{u}^{\textsf{T}}\boldsymbol{B}^{\textsf{T}}\boldsymbol{\tau} & \geq& 0 \quad \forall\, (\boldsymbol{\tau}, \boldsymbol{u}) \in \mathbb{R}^{s+n} \Leftrightarrow \\ z\lambda^{2} + \boldsymbol{u}^{\textsf{T}}\boldsymbol{K}\boldsymbol{u} - 2\boldsymbol{u}^{\textsf{T}}\boldsymbol{B}^{\textsf{T}}\boldsymbol{\tau} & \geq& 0 \quad \forall (\boldsymbol{\tau}, \boldsymbol{u},\lambda)\\ & \in& \mathbb{R}^{s+n+1} : ||\boldsymbol{\tau}||^{2} = \lambda^{2}. \end{array} $$

Now let u=λ y and τ=λ κ. Then the last inequality is equivalent to

$$\begin{array}{@{}rcl@{}} z\lambda^{2} + \lambda^{2}\boldsymbol{y}^{\textsf{T}}\boldsymbol{K}\boldsymbol{y} - 2\lambda^{2}\boldsymbol{y}^{\textsf{T}}\boldsymbol{B}^{\textsf{T}}\boldsymbol{\kappa} & \geq& 0 \quad \forall\, (\boldsymbol{\kappa}, \boldsymbol{y},\lambda) \\ &\in& \mathbb{R}^{s+n+1} : ||\boldsymbol{\kappa}||^{2} = 1 \Leftrightarrow \\ z + \boldsymbol{y}^{\textsf{T}}\boldsymbol{K}\boldsymbol{y} - 2\boldsymbol{y}^{\textsf{T}}\boldsymbol{B}^{\textsf{T}}\boldsymbol{\kappa} & \geq& 0 \quad \forall\, (\boldsymbol{\kappa},\boldsymbol{y})\\ &\in& \mathbb{R}^{n+s} : ||\boldsymbol{\kappa}||^{2} = 1. \end{array} $$

The latter holds in particular for $\boldsymbol {\kappa } = {\arg \max }_{||\boldsymbol {\kappa }|| = 1} \boldsymbol {y}^{\textsf {T}}\boldsymbol {B}^{\textsf {T}}\boldsymbol {\kappa }$, for which y ^T B ^T κ=||B y||, see (20). The last inequality is thus equivalent to

$$\begin{array}{@{}rcl@{}} z + \boldsymbol{y}^{\textsf{T}}\boldsymbol{K}\boldsymbol{y} - 2||\boldsymbol{B}\boldsymbol{y}|| &\geq& 0~~\forall\boldsymbol{y} \in \mathbb{R}^{n} \Leftrightarrow \\ - \boldsymbol{y}^{\textsf{T}}\boldsymbol{K}\boldsymbol{y} + 2||\boldsymbol{B}\boldsymbol{y}|| &\leq& z~~\forall\boldsymbol{y} \in \mathbb{R}^{n} \Leftrightarrow \\ - \frac{1}{2}\boldsymbol{y}^{\textsf{T}}\boldsymbol{K}\boldsymbol{y} + ||\boldsymbol{B}\boldsymbol{y}|| &\leq& \frac{1}{2}z~~\forall\boldsymbol{y} \in \mathbb{R}^{n}. \end{array} $$

□

Using this theorem, the semi-infinite optimization problem (22) can be formulated as the semi-definite program

$$ \begin{array}{l} \min\limits_{z\in\mathbb{R},\,\boldsymbol{x}\in\mathcal{H}} \quad z \\ \text{subject to} \;\; \left( \begin{array}{cc} z\boldsymbol{I} & \boldsymbol{B}\left( \boldsymbol{x}\right) \\ \boldsymbol{B}\left( \boldsymbol{x}\right)^{\textsf{T}} & \boldsymbol{K}\left( \boldsymbol{x}\right) \end{array}\right) \succeq \boldsymbol{0}. \end{array} $$

(23)

This problem is convex if B and K are linear in x and does not require K to be non-singular. Unfortunately, currently available solvers for semi-definite programs are not suitable for matrix inequalities with large matrices (see however Bogani et al. (2009) and Stingl et al. (2009)).

For the special case of a non-singular stiffness matrix, we note two interesting results obtained from (23):

• 1. We may use the Schur-complement theorem (Boyd and Vandenberghe (2004, p. 560-561), Horn and Johnson (1985, Theorem 7.7.6)) and (6) to rewrite (23) into (10) derived in Section 2.4.

• 2. We may also obtain the generalized eigenvalue formulation proposed by Brittain et al. (2012). To start with, it is straightforward to show that

  $$\left( \begin{array}{cc} z\boldsymbol{I} & \boldsymbol{B}\\ \boldsymbol{B}^{\textsf{T}} & \boldsymbol{K} \end{array} \right) \succeq \boldsymbol{0} \; \Leftrightarrow \; \left( \begin{array}{cc} \boldsymbol{K} & \boldsymbol{B}^{\textsf{T}} \\ \boldsymbol{B} & z\boldsymbol{I} \end{array} \right) \succeq \boldsymbol{0}. $$

  Then assuming z>0 and applying the Schur-complement theorem to the right side of the equivalence one finds that this inequality is equivalent, in turn, to

  $$\begin{array}{@{}rcl@{}} \boldsymbol{K} - z^{-1}\boldsymbol{B}^{\textsf{T}}\boldsymbol{B} \succeq \boldsymbol{0} && \qquad\qquad\qquad\qquad \Leftrightarrow \\ \boldsymbol{x}^{\textsf{T}}\left( \boldsymbol{K} - z^{-1}\boldsymbol{B}^{\textsf{T}}\boldsymbol{B}\right)\boldsymbol{x} \geq 0 && \forall \boldsymbol{x} \in \mathbb{R}^{n}\qquad\qquad \Leftrightarrow \\ z \geq \frac{\boldsymbol{x}^{\textsf{T}}\boldsymbol{B}^{\textsf{T}}\boldsymbol{B}\boldsymbol{x}}{\boldsymbol{x}^{\textsf{T}}\boldsymbol{K}\boldsymbol{x}} && \forall \boldsymbol{x} \in \mathbb{R}^{n}\qquad\qquad \Leftrightarrow \\ z =\max_{||\boldsymbol{x}||=1} \frac{\boldsymbol{x}^{\textsf{T}}\boldsymbol{B}^{\textsf{T}}\boldsymbol{B}\boldsymbol{x}}{\boldsymbol{x}^{\textsf{T}}\boldsymbol{K}\boldsymbol{x}} & =& \mu_{1}(\boldsymbol{K},\boldsymbol{B}^{\textsf{T}}\boldsymbol{B}), \end{array} $$

  where μ ₁(⋅,⋅) is the largest generalized eigenvalue of a given matrix pencil. The last step in the above chain of equivalences follows from Theorem 2.4 in Hestnes(1975, Chapter 2). Problem (23) can now be replaced by

  $$\min_{\boldsymbol{x}\in\mathcal{H}} \mu_{1}(\boldsymbol{K}(\boldsymbol{x}),\boldsymbol{B}(\boldsymbol{x})^{\textsf{T}}\boldsymbol{B}(\boldsymbol{x})), $$

  which is similar to the generalized eigenvalue formulation found in Brittain et al. (2012).