Skip to main content
SpringerLink
Log in

2-D Duffing Oscillator: Elliptic Functions from a Dynamical Systems Point of View

  • Published:
Qualitative Theory of Dynamical Systems Aims and scope Submit manuscript

An Erratum to this article was published on 06 March 2013

Abstract

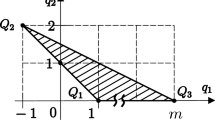
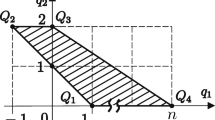
K. Meyer has advocated for the study of elliptic functions and integrals from a dynamical systems point of view. Here, we follow his advice and we propose the bidimensional Hamiltonian Duffing oscillator as a model; it allows us to deal with the elliptic integral of third kind directly. Focusing on bounded trajectories we do a detailed analysis of the solutions in the three regions defined by the parameters. In our opinion, for the study of elliptic functions, the model presented here represents an alternative to the pendulum or the free rigid body systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Armitage, J.V., Eberlein, W.F.: Elliptic Functions. LMS 67, Cambridge (2006)

  2. Arnold, V.I.: On teaching mathematics. Address at the Palais de Découverte, Paris, 7 March 1997

  3. Bates L.: Monodromy in the champagne bottle. Z. Angew Math. Phys. 42(6), 837–847 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bolsinov A.V., Borisov A.V., Mamaev I.S.: Topology and stability of integrable systems. Russ. Math. Surv. 65(2), 259–318 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  5. Born M.: The Mechanics of the Atom. Bell and Sons, London (1927)

    MATH  Google Scholar 

  6. Byrd P.F., Friedman M.D.: Handbook of Elliptic Integrals for Engineers and Scientists. Springer, Berlin (1971)

    Book  MATH  Google Scholar 

  7. Céspedes, F.: El oscilador de Duffing bidimensional. Tesina Máster, Universidad de Murcia (2011)

  8. David D., Holm D.D.: Multiple Lie-Poisson structures, reductions, and geometric phases for the Maxwell-Bloch travelling wave equations. J. Nonlinear Sci. 2, 241–262 (1992)

    Article  MathSciNet  Google Scholar 

  9. Deprit A.: Free rotation of a rigid body studied in the phase plane. Am. J. Phys. 35, 424–428 (1967)

    Article  Google Scholar 

  10. Deprit A.: The Lissajous transformation. I:Basics. Celest. Mech. Dyn. Astron. 51, 201–225 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  11. Fukushima T.: Fast computation of Jacobian elliptic functions and incomplete elliptic integrals for constant values of elliptic parameter and elliptic characteristic. Celest. Mech. Dyn. Astron. 105, 245–260 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Fukushima T.: Fast computation of complete elliptic integrals and Jacobian elliptic functions. Celest. Mech. Dyn. Astron. 105, 305–328 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  13. Garnier R.: Sur une classe de systèmes différentiels abéliens déduits de théorie des équatios linéaires. Rend. Circ. Math. Palermo 43(4), 155–191 (1919)

    Article  MathSciNet  MATH  Google Scholar 

  14. Gradshteyn, I.S., Ryzhik, I.M.: Table of Integrals, Series, and Products, 6th edn, and Errata. Academic Press, San Diego (2000)

  15. Greenhill A.G.: Applications of Elliptic Functions. Macmillan, London (1982)

    Google Scholar 

  16. Gurarie D.: Long-range dynamics of a shallow water triad: renormalization, modulation, and cyclogenesis. J. Atmos. Sci. 60, 693–710 (2003)

    Article  MathSciNet  Google Scholar 

  17. Hille E. : Lectures on Ordinary Differential Equations. Addison-Wesley, Reading (1969)

  18. Holm, D.D. Marsden, J.E.: The rotor and the pendulum. In: Donato, E., et al. (eds.) Symplectic Geometry and Mathematical Physics. Progress in Mathematics, vol. 99, pp. 189–203. Birhäuser, Boston (1991)

  19. Lantoine, G., Russell, R. P.: Complete closed-form solutions of the Stark problem. Celest. Mech. Dyn. Astron. doi:10.1007/s10569-010-9331-1

  20. Lawden D.F.: Elliptic Functions and Applications. Springer, New York (1989)

    Book  MATH  Google Scholar 

  21. MarsdenJ.E. Ratiu T.: Introduction to Mechanics and Symmetry, 2nd edn. Springer, Berlin (1999)

    Book  Google Scholar 

  22. McLachlan N.W.: Ordinary Non-linear Differential Equations in Engineering and Physical Sciences, 2nd edn. Clarendon, Oxford (1958)

    Google Scholar 

  23. McSwiggen P.D., Meyer K.R.: The evolution of invariant manifolds in Hamiltonian-Hopf bifurcations. J. Differ. Equ. 189, 538–555 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  24. Meyer K.R.: Scaling Hamiltonian systems. SIAM J. Math. Anal. 15, 877–889 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  25. Meyer K.R.: Jacobi elliptic functions from a dynamical systems point of view. Am. Math. Mon. 108, 729–737 (2001)

    Article  MATH  Google Scholar 

  26. Meyer K.R., Hall G.R.: Introduction to Hamiltonian Dynamical Systems and the N-Body Problem, vol 90. Springer, New York (1992)

    Google Scholar 

  27. Meyer K.R., Hall G.R., Offin D.: Introduction to Hamiltonian Dynamical Systems and the N-Body Problem, 2nd edn, vol. 90, pp. 243–250. Springer, New York (2009)

    Google Scholar 

  28. Nguyen T.Z.: A note on focus–focus singularities. Differ. Geom. Appl. 7, 123–130 (1997)

    Article  MATH  Google Scholar 

  29. Radulescu, V.: An example with periodic orbits. The Mathematical Association of America, p. 260, Problem # 11073 (2004)

  30. Schaub, H., Junkins, J.L: Analytical Mechanics of Space Systems, 2nd edn. AIAA Education Series, Reston (2009)

  31. Tricomi, F.G.: Equazioni Differenziale. Einaudi, Torino (1965)

  32. Van der Meer, J.C.: The Hamiltonian Hopf Bifurcation. Lectures Notes in Mathematics, vol. 1160. Springer, Berlin (1985)

  33. Van der Meer, J.C.: On nonlinearly coupled Duffing equations. A note on problem 11073. The AMM 111 (2004, unpublished)

  34. Whittaker, E.T., Watson, G.N.: A Course of Modern Analysis. Cambridge University Press, Cambridge (1927)

  35. Wojciechowski S.: On a Lax-type representation and separability of the anisotropic harmonic oscillator in a radial quartic potential.. Lett. Nuovo Cimento 41, 361–369 (1984)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Departamento de Matemática Aplicada, Universidad de Murcia, Campus de Espinardo, 30071, Espinardo, Murcia, Spain

    Francisco Javier Molero, Martín Lara, Sebastián Ferrer & Francisco Céspedes

Authors
  1. Francisco Javier Molero
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Martín Lara
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sebastián Ferrer
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Francisco Céspedes
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Francisco Javier Molero.

Additional information

In Honor of Ken R. Meyer.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Molero, F.J., Lara, M., Ferrer, S. et al. 2-D Duffing Oscillator: Elliptic Functions from a Dynamical Systems Point of View. Qual. Theory Dyn. Syst. 12, 115–139 (2013). https://doi.org/10.1007/s12346-012-0081-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12346-012-0081-1

Keywords

Search

Navigation