Introduction

Direct density dependence in some vital rate is necessary—but not sufficient—for stable population dynamics (Murdoch 1994; Turchin 1995). Our understanding of the mechanisms producing density-dependent population regulation derives in large part from experiments and observations conducted at relatively small spatial and temporal scales (Harrison and Cappuccino 1995) with the expectation that these observations can scale up to predict larger-scale dynamics (Forrester et al. 2002; Melbourne and Chesson 2005, 2006; Steele and Forrester 2005). However, density-dependent processes are often observable only when the study is carried out at a particular spatial scale (Ray and Hastings 1996). Moreover, there is growing evidence that processes observed at different spatial scales in the same system may have opposing effects on population dynamics, such as inverse density dependence at one scale and direct density dependence at another (Mohd Norowi et al. 2000; Veldtman and McGeoch 2004; White and Warner 2007).

Many species exhibit inversely density-dependent (“IDD”) mortality, in which the per capita mortality rate decreases with population density, at the spatial scale of aggregations and social groups (e.g., sessile invertebrates, Gascoigne et al. 2005; shoaling fish, White and Warner 2007; social mammals, Clutton-Brock et al. 1999; aggregating insects, Mohd Norowi et al. 2000). Other demographic processes, such as fecundity, may also exhibit inverse density dependence (Gascoigne et al. 2005; Courchamp et al. 2008), but for simplicity I focus on mortality here. IDD mortality would produce unbounded growth if it were the only density-dependent process operating in a population (Murdoch 1994; Gascoigne and Lipcius 2004b), but that is rarely the case. Directly density-dependent (“DDD”) processes, in which per capita mortality increases with density (or some other fitness component, such as fecundity, decreases with density), are also likely to occur. When mortality is IDD at low densities and DDD at high densities (i.e., survival is a unimodal function of density), the population is said to exhibit an Allee effect. In that well-known scenario, IDD mortality tends to destabilize population dynamics that would otherwise be stably regulated by DDD mortality (Courchamp et al. 1999, 2008). However, stability has not been explored for the scenario in which a population experiences both IDD and DDD processes simultaneously, albeit at different spatial scales, though such patterns have been observed in nature. It has been hypothesized that in such cases DDD processes could offset the destabilizing effects of IDD mortality (Sale and Tolimieri 2000; Gascoigne and Lipcius 2004b), but the dynamical consequences of opposing processes operating at different spatial scales is not well understood.

Invoking terminology from the Allee effect literature (Stephens et al. 1999; Gascoigne and Lipcius 2004b; Courchamp et al. 2008), this paper examines the effects of “component” inverse density dependence in a single vital rate rather than “demographic” inverse density dependence in the overall population growth rate. Specifically, the question at hand is whether component IDD at one spatial scale is sufficient to produce destabilizing demographic IDD in the overall population dynamics. That is, what are the conditions under which IDD mortality at one spatial scale could destabilize population dynamics that would otherwise be regulated by DDD mortality occurring at a different spatial scale?

The relative importance of DDD and IDD mortality is especially relevant to populations of benthic marine organisms with pelagic larvae. The bouts of high mortality experienced by benthic juveniles have provided ample opportunities to study mechanisms of DDD mortality (e.g., Hixon and Webster 2002; Hixon et al. 2002). There is a growing consensus from this body of work that benthic population densities may fluctuate in response to variable larval supply, but that those fluctuations have an upper bound imposed by DDD mortality soon after settlement from the plankton (Menge 2000; Armsworth 2002; Sandin and Pacala 2005a). This paradigm may be difficult to reconcile with recent evidence for IDD mortality in several reef fish species. For example, per capita postsettlement mortality declines with group size in site-attached, socially aggregating damselfishes (Booth 1995; Sandin and Pacala 2005b) and wrasses (White and Warner 2007) and mobile, schooling snappers (Wormald 2007). Similarly, sessile invertebrates such as barnacles and mussels often experience higher survival in large aggregations due to reduced vulnerability to overheating (Bertness and Grosholz 1985; Lively and Raimondi 1987) and possibly wave dislodgement (Gascoigne et al. 2005). It is not surprising to discover that aggregating species find safety in numbers; indeed, such benefits likely provide the selective pressure that drives many fish species to shoal (Pitcher and Parrish 1993; Parrish and Edelstein-Keshet 1999) and many sessile invertebrates to settle gregariously (Bertness and Grosholz 1985). However, given the apparent importance of postsettlement DDD mortality to benthic population regulation, it is unclear whether IDD mortality in these aggregating species could lead to unstable population dynamics.

In benthic reef fishes, IDD mortality is generally observed at the relative small spatial scale of a discrete aggregation of individuals, such as a shoal of fish (Sandin and Pacala 2005b; White and Warner 2007). When a predator attacks such a group, per capita prey mortality decreases with prey density (Gascoigne and Lipcius 2004a). At the same time, reef fish predators commonly produce DDD mortality at larger spatial scales via numeric, functional, developmental, or aggregative responses (Holling 1959; Murdoch 1969, 1971; Hassell and May 1974; Hixon and Carr 1997; Anderson 2001; Webster 2003; Overholtzer-McLeod 2006; White 2007). In the only study to date which has examined reef fish mortality patterns at multiple spatial scales, White and Warner (2007) found IDD mortality of the bluehead wrasse (Thalassoma bifasciatum, Labridae) at the aggregation scale (tens of square centimeter) but DDD mortality at the scale of entire reefs (thousands of square meter). This general pattern is expected when predators exhibit a characteristic spatial scale at which they define a “patch” of prey and choose to stay in that patch or move on (Bernstein et al. 1991; Ritchie 1998). This spatial scale of predator foraging is likely to exceed the spatial scale at which prey aggregate. In such cases, variation in prey density at the scale of individual prey aggregations will not influence predator behavior, i.e., predators will forage indiscriminately among prey aggregations within a foraging patch (e.g., Sandin and Pacala 2005b; Overholtzer-McLeod 2006). Consequently, predation could produce IDD mortality at the aggregation scale (due to numerical dilution of predator attacks among group members) but DDD mortality at the larger scale of predator foraging (due to predator aggregative and functional responses; White et al. 2010). This phenomenon is probably not limited to reef fishes, and similar transitions between IDD and DDD across spatial scales have been observed in insect predator–prey interactions (Mohd Norowi et al. 2000; Veldtman and McGeoch 2004). This type of scale-dependent transition between IDD and DDD mortality may also occur due to nonpredatory mechanisms, such as the transition from small-scale facilitation to large-scale competition for zooplankton prey in soft-sediment mussel beds (Gascoigne et al. 2005). Indeed, a switch between small-scale positive intraspecific interactions and large-scale competition may be a common feature of populations of sessile organisms (Bertness and Leonard 1997; van de Koppel et al. 2008).

In this paper, I employed deterministic population models to determine whether a population exhibiting stabilizing DDD mortality at a large spatial scale can be destabilized by IDD mortality occurring at smaller spatial scales. The models were intended to apply to any relatively site-attached, aggregating species but generally describe a coral reef fish population like those recently shown to experience this type of scale-dependent switch between IDD and DDD (White and Warner 2007). By varying the degree of small-scale spatial aggregation and the strength of DDD mortality, I was able to evaluate a range of possible scenarios, including a baseline scenario with DDD mortality only, scenarios with IDD only, as well scenarios with both DDD and IDD with a range of relative strengths.

Materials and methods

Scale transition theory

The essential problem of describing density-dependent processes at different scales is accounting for the variance in density at the smaller scale. Consider a population in which survivorship, F, is a function of density, X: F = G(X). Specifically, G is a nonlinear, asymptotically decreasing function of density at the scale of a single coral head (e.g., 1 m2). In a population model, it is daunting to keep track of dynamics within each square meter and far more convenient to use the currency of density at a much larger scale, such as an entire reef. It is tempting, then, to assume that \( \overline F = G\left( {\overline X } \right) \), where overbars indicate the mean survivorship and density at the reef scale (this expression is termed the mean-field approximation). However, any spatial variation in density at the smaller scale will impair the accuracy of this approximation. For example, a density of one fish per square meter measured at a 10-m2 scale could be obtained from a uniform distribution of one fish in each of ten 1-m2 quadrats or from a single 1-m2 quadrat with ten fish and nine empty 1-m2 quadrats. The former case (uniform small-scale density) will have much higher average survival (because all fish experience low density at the small scale) than the latter case (highly clumped density), in which all fish occur at high density at the small scale. In general, if survivorship is a nonlinear function of density, survivorship at the mean density is not equal to the mean survivorship across all densities (Melbourne and Chesson 2005). This is due to the general mathematical rule known as Jensen’s inequality, that for a set of values X, the mean value of a nonlinear function of X, \( \overline {G(X)} \), is not equal to the function of the mean of X, \( G\left( {\overline X } \right) \) (Ruel and Ayres 1999).

It is possible to correct for Jensen’s inequality and approximate density-dependent survivorship at a large spatial scale by incorporating a scale transition which accounts for the effects of spatial variation in density at the small scale (Chesson 1998; Melbourne and Chesson 2005). This is done by taking a second-order Taylor expansion of G(X) at \( \overline X \):

$$ F \approx G\left( {\overline X } \right) + G\prime \left( {\overline X } \right)\left( {X - \overline X } \right) + 0.5G\prime \prime \left( {\overline X } \right){\left( {X - \overline X } \right)^2} $$

then averaging over all values X, which yields

$$ \overline F \approx G\left( {\overline X } \right) + 0.5G\prime \prime \left( {\overline X } \right)\operatorname{var} \left( X \right) $$

where var(X) is the spatial variance in density at the small scale (this assumes that G is twice differentiable and that higher-order terms in the Taylor series are negligible). The G' term falls out because the expectation of \( \left( {X - \overline X } \right) \) is zero. Note that this approximation amounts to the mean-field approximation \( G\left( {\overline X } \right) \) plus a correction factor: the scale transition. Including the scale transition causes the large-scale estimate of survivorship to decrease with increasing spatial variance in density (i.e., the degree of aggregation), thus accounting for the effect of DDD mortality at the smaller scale (note that this assumes that G(X) is a decreasing, saturating function, so \( G\prime \prime \left( X \right) \) is negative; the large-scale estimate of \( \overline F \) will increase if \( G\prime \prime \left( X \right) \) is positive).

Population model

The models describe a hypothetical reef fish population that is demographically closed (all larvae are locally retained and there is no immigration) and therefore resembles a population with extremely high self-recruitment such as that found on an isolated or far upstream island. This is obviously a simple model that ignores many aspects of real populations (size structure, metapopulation dynamics, etc.) but it permits straightforward examination of the dynamic role of IDD. It also affords a conservative test of the destabilizing effect of IDD mortality, since including connectivity with other populations will tend to stabilize fluctuations in this type of model (Hastings et al. 1993; Amarasekare 1998).

It was assumed that, like many reef fishes, this species spends a relatively fixed period of time in the planktonic larval stage before settling in discrete pulses. New settlers utilize different habitat than do adults, so that juveniles do not interact with adults for a short period of time prior to recruiting to the adult population, after which they experience low, density-independent mortality. The general dynamics are then given by

$$ {N_{t + 1}} = F\left( {z{N_t}} \right) + s{N_t} $$
(1)

where z is a composite parameter equal to the product of per capita fecundity, z 1, and larval survivorship, z 2. Parameter s is adult survivorship, and F describes the process of most interest here: the form of postsettlement survivorship (i.e., between settlement and recruitment to the adult population). The time step used in this model is intended to correspond to the pelagic larval duration of the species, which is 1–2 months for most reef fishes (47 days for bluehead wrasse; Caselle and Warner 1996). This interval also matches the timescale over which most of the parameters values were estimated.

In the model, juveniles that have recently settled to the benthos are affected by processes occurring at two distinct spatial scales. At the larger, “landscape” scale (approximately hundreds of square meters for the bluehead wrasse), settler mortality is DDD, which could be due to some combination of competition for refuge spaces and/or a predator functional response. At the smaller, “aggregation” scale (approximately tens of square centimeters for the bluehead wrasse), settler mortality takes on one of three forms: (1) density-independent (i.e., the only density-dependent process occurs at the landscape scale); (2) a monotonic decrease with density, representing a dilution of predation risk with increasing group size (Foster and Treherne 1981); or (3) mortality decreases with density to a minimum before rising again, representing a dilution effect tempered by increased detectability of very large groups by foraging predators (Krause and Godin 1995). The first case (“DDD Baseline”) describes a reef fish population regulated by DDD postsettlement mortality. The DDD Baseline scenario is known to have stable population dynamics (Armsworth 2002), so it is used as a point of comparison for subsequent cases in which the introduction of IDD mortality may produce instability. The second case (“IDD Dilution”) approximates the postsettlement dynamics of bluehead wrasse on St. Croix described by White and Warner (2007), while the third case (“IDD Dilution + Detection”) includes the large-group detection effect that was not observed in the relatively small groups described by White and Warner (2007) but which is likely to occur in larger groups (Krause and Godin 1995). The two IDD cases thus describe two types of aggregation-scale IDD mortality that may be typical of reef fishes and other prey species.

Postsettlement survivorship at the landscape scale is described using a Beverton–Holt model (Armsworth 2002; Osenberg et al. 2002). For convenience, settlers, S t , are defined as S t  = zN t ; the subscript t will be dropped hereafter for simplicity. The Beverton–Holt survivorship is then given by

$$ G\left( {\overline S } \right) = \frac{a}{{1 + {{\left( {\frac{a}{b}\overline S } \right)}^d}}} $$
(2)

where a is density-independent survivorship, b is the asymptotic maximum density, and d describes the “strength” of density dependence: no density dependence (d = 0), undercompensation (0 < d < 1), exact compensation (d=1), or overcompensation (d >  1) (Fig. 1a). The Beverton–Holt function can describe intraspecific competition for any resource, including food or refuge space. Here, it is taken to represent DDD predation mortality. The overbars on S indicate that the function depends on the mean density at the landscape scale.

Fig. 1
figure 1

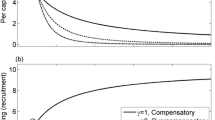
Landscape-scale and aggregation-scale survivorship functions used in the model. a Landscape-scale Beverton–Holt survivorship function, shown for three different values of the strength parameter d. b The three different aggregation-scale survivorship functions. c Spatial variance in settler density as a function of settler density for three levels of aggregation (indicated by negative binomial clumping parameter 1/k). d–f Aggregate survivorship across both scales, calculated using the scale transition. In panels d–f, survivorships are shown for each aggregation-scale function for three different levels of spatial aggregation (indicated with the same line style as in c). Note that the low, medium, and high aggregation curves are completely overlapping for the DDD Baseline case in which there is no effect of group size on aggregation-scale survivorship. The inset windows in panels e–f show details of the curves near the origin and for very high values of S; note the changes in scale on the axes. All curves calculated using the best estimates of each parameter given in Table 1

Full size image

At the smaller spatial scale at which fish aggregate into social groups, survival is a function H(S) of the size of the social group. Overall postsettlement survival measured at this scale is assumed to be the combination of both large- and small-scale processes: \( F\left( {\overline S, S} \right) = G\left( {\overline S } \right)H(S) \), where G is a function of mean density at the larger scale and H is a function of density at the smaller scale. Note that \( G\left( {\overline S } \right) \) is treated as a survivorship (\( 0 \leqslant G\left( {\overline S } \right) \leqslant 1 \)) while the units of \( F\left( {\overline S, S} \right) \) and H(S) are actual numbers of fish, to be consistent with Eq. 1.

In the DDD Baseline scenario, there is no effect of group size on mortality at all, so H(S) = a 2 S, where a 2 is a density-independent constant (Fig. 1b). Alternatively, the IDD Dilution effect might take the form

$$ H(S) = \left[ {1 - \exp \left( { - \left( {f + gS} \right)} \right)} \right]S $$
(3)

where the bracketed term ranges from 0 to 1 and is an increasing function of S (i.e., survivorship increases with density). The parameter g describes the strength of the dilution effect (H(S) increases with g), and f is a density-independent constant (Fig. 1b). In the IDD Dilution + Detection scenario, there is a dilution effect for small groups, but larger groups are easier for predators to detect, so that H is hump-shaped:

$$ H(S) = \left[ {1 - \exp \left( { - \left( {f + gS} \right)} \right)} \right]\left[ {1 - \exp \left( { - h/S} \right)} \right]S. $$
(4)

This equation retains the dilution effect term from Eq. 3 but contains the second bracketed term that also ranges from 0 to 1 but is a decreasing function of S. The parameter h determines the rate of decline with S (smaller values lead to faster declines) and thus indirectly determines the value of S at which H(S) reaches a maximum (Fig. 1b).

Sensibly modeling large-scale population dynamics in this system requires a scale transition to represent the processes occurring at both large and small spatial scales. If postsettlement survivorship F at the aggregation scale is \( F\left( {\overline S, S} \right) = G\left( {\overline S } \right)H(S) \), then as shown by Melbourne and Chesson (2005), the landscape-scale approximation is

$$ \overline {F\left( S \right)} = G\left( {\overline S } \right)\left[ {H\left( {\overline S } \right) + 0.5H\prime \prime \left( {\overline S } \right)\operatorname{var} \left( S \right)} \right] $$
(5)

To calculate the spatial variance in S, I assumed that individuals follow a negative binomial distribution (Fig. 1c).:

$$ {\rm var} (S) = \overline S + {\overline S^2}/k $$
(6)

This distribution is widely used to describe aggregation patterns in natural populations, including grasses (Conlisk et al. 2007), zooplankton (Young et al. 2009), mosquitoes (Nedelman 1983; Alexander et al. 2000), herbivorous insects (Desouhant et al. 1998; Grear and Schmitz 2005), and rabbits (Fernandez 2005). Additionally, Conlisk et al. (2007) showed that the negative binomial distribution can arise from simple behavioral decision rules for joining groups. While Conlisk et al. (2007) found that more complicated decision rules and distributions sometimes fit natural aggregation patterns better than the negative binomial, the latter is more amenable to analysis in the present context because it affords a simple relationship between the degree of aggregation and the spatial variance in S. The parameter 1/k describes the degree to which individuals aggregate, which can range from a purely random, Poisson distribution (1/k ≈ 0) to highly clumped as 1/k approaches infinity (Fig. 2; White and Bennetts 1996). The intensity of aggregation at the smaller spatial scale (i.e., the spatial variance in population density) strongly affects the form of density dependence observed at the larger spatial scale once the scale transition is accounted for (Fig. 1d–f).

Fig. 2
figure 2

Examples of spatial clustering of individuals in two-dimensional space with negative binomial distributions for a representative range of the clustering parameter 1/k. Each panel shows the distribution of approximately 90 points

Full size image

For extreme values of S or var(S), it is possible for the bracketed term in Eq. 5 to fall below 0 or exceed S, both of which are biologically impossible. To constrain the behavior of Eq. 5 and preserve a smoothly differentiable function (which is necessary for the evaluation of Eq. 7, below), I added two corrections to Eq. 5. If \( X = \left[ {H\left( {\overline S } \right) + 0.5H\prime \prime \left( {\overline S } \right)\operatorname{var} \left( S \right)} \right]/S \), then

$$ \mathop {X}\limits^{\frown} = X - \frac{X}{{1 + \exp \left( {{{10}^{10}}X} \right)}} $$

and

$$ \mathop {X}\limits^{\mathop {\frown}\limits^\frown } = \frac{{\mathop {X}\limits^\frown }}{{\exp \left( { - 2\mathop {X}\limits^\frown } \right) + \mathop {X}\limits^\frown }} $$

By substituting \( \mathop {X}\limits^{\mathop {\frown}\limits^\frown } \) for X in Eq. 5, the value of X is essentially unchanged for most values but asymptotically approaches both 0 and 1 without exceeding those bounds. The sensitivity of \( \overline {F(S)} \) to these correction factors is presented in Online Resource 1.

The second derivative in the formula for \( \overline {F(S)} \) yields an expression that is far too lengthy to write out in full, precluding an analytical examination of the effect of aggregation on stability. Instead, a numerical stability analysis was performed. The overall population dynamics (Eq. 1) can be represented as a recursive equation, N t + 1=W(N t ), the stability of which is determined by the Jacobian eigenvalue

$$ \lambda = {\left. {\frac{{{\text{d}}W}}{{{\hbox{d}}N}}} \right|_{N = N * }} $$
(7)

which is the derivative dW/dN evaluated at the steady-state equilibrium N* (Gurney and Nisbet 1998). Population dynamics are unstable with exponentially increasing divergences for λ > 1, stable for 0 < λ < 1, stable with dampened oscillations for −1 < λ < 0, and unstable with increasing oscillations for λ < −1. The value of N*, and thus λ, varies with each of the parameters in the model. Rather than attempt a full exploration of the eight-dimensional parameter space, effort was focused on evaluating the effect of aggregation (1/k) on stability. Therefore, parameter space was explored by sequentially varying each parameter across a range of biologically plausible values (estimated for the reef fish Thalassoma bifasciatum; Table 1), while simultaneously varying 1/k between 1 × 10−3 (approximating a random Poisson distribution) and 1 × 103 (highly clumped) and holding all other parameters constant at their best estimates. The eigenvector λ was calculated for each parameter combination. Thus, for each parameter, I determined the set of λ values possible for different values of that parameter and 1/k, given constant values of the other parameters. This process identified parameters that had an effect on dynamic stability for at least some levels of aggregation. For parameter combinations that produced multiple equilibria, I reported λ for the equilibrium associated with the most stable value of λ, i.e., closest to the interval [0, 1], giving a conservative test of the potential for dynamic instability. The parameter combinations that produced multiple equilibria and the stability properties of those equilibria are reported in Online Resource 2. Because the Beverton–Holt parameter b merely scales the maximum possible recruit density, its value does not affect λ, and it was not included in this analysis. The numerical stability analysis was conducted with the Symbolic Math toolbox using the MuPAD kernel, in Matlab 7.9 (R2009b; The Mathworks, Inc., Natick, MA).

Table 1 Symbols and parameter values used in scale transition population model
Full size table

Results

The exploration of parameter space revealed that variation (within a biologically plausible range) in the values of the dilution effect parameters f and g did not have an effect on dynamic stability, i.e., for a particular value of 1/k, λ was constant across the full range of either f or g (given that the other parameters were held constant at their best estimates). However, depending on the type of density dependence at the aggregation scale, certain values of the aggregation parameter 1/k, the strength of reef-scale density dependence d, fecundity z, adult survivorship s, density-independent settler survivorship a, and the detection effect parameter h did produce changes in dynamic stability. These effects are displayed in Figs. 3 and 4, in which the shading indicates the value of the Jacobian eigenvalue λ for each parameter combination and the contour lines demarcate regions of differing dynamic stability.

Fig. 3
figure 3

Numerical stability analysis of scale transition population model. For each parameter combination, shading indicates the value of the Jacobian eigenvalue, assuming all other parameters take their best estimates. Black contour lines demarcate regions of different dynamic behavior: λ < −1 (unstable with diverging oscillations, UO), −1 < λ < 0 (stable with dampened oscillations, SO), 0 < λ < 1 (stable with no oscillations, S), and λ > 1 (unstable without oscillations, U). White areas indicate parameter combinations that lack a nonzero equilibrium. Models had Beverton–Holt density-dependent settler mortality at the larger spatial scale; the size of social groups at the smaller spatial scale had either no effect on mortality (DDD Baseline, a, c) or caused a monotonic reduction in mortality (IDD Dilution, b, d) The parameters varied were the strength of large-scale density dependence (Beverton–Holt parameter d), per capita fecundity (z), and intensity of spatial aggregation (negative binomial parameter 1/k; larger values indicate greater clumping). The stars in b, d indicate typical parameter values for bluehead wrasse, T. bifasciatum, on St. Croix, US Virgin Islands

Full size image
Fig. 4
figure 4

Numerical stability analysis of scale transition population model. In this figure, models had Beverton–Holt density-dependent settler mortality at the larger spatial scale; mortality at the smaller spatial scale initially decreased then increased with the size of a social group (IDD Dilution + Detection). All symbols and shading as in Fig. 3. The parameters varied were the strength of large-scale density dependence (Beverton–Holt parameter d), fecundity (z), adult survivorship (s), density-independent settler survivorship (a), the strength of the detection effect (h), and intensity of spatial aggregation (negative binomial parameter 1/k; larger values indicate greater clumping). The stars in each panel indicate typical parameter values for bluehead wrasse, T. bifasciatum, on St. Croix, US Virgin Islands

Full size image

In the DDD Baseline scenario (Fig. 3a, c), which lacked IDD at the aggregation scale, there was by definition no effect of the aggregation index on stability. In this scenario, dynamics were unstable and exponentially increasing when d ≤ 0.66 (effectively density-independent dynamics with exponential growth; Fig. 3a), but stable when d >  0.66 for all combinations of 1/k and all other parameters. The population did not have a nonzero equilibrium for values of fecundity, z, less than approximately 1.4 settlers per adult (Fig. 3c).

When groups experienced a dilution effect (IDD Dilution scenario; Fig. 3b, d), dynamics were stable for most combinations of 1/k and other parameter values. However, variation in the strength of reef-scale density dependence, d, and fecundity, z, did produce unstable dynamics at very high levels of settler aggregation (high 1/k). For low and moderate levels of aggregation (approximately 1/k < 20), the dynamics in this scenario were similar to the DDD Baseline scenario, with exponential growth or extinction for low values of d (d < 0.66) or z (z < 1.4), respectively, and stable equilibria elsewhere. The case of d = 0 and very small 1/k is equivalent to a standard model of IDD-only dynamics and had unbounded growth. However, when landscape-scale density dependence was very weak (d ≤ 0.66) but aggregation was quite strong (1/k >  20), the survivorship function \( \overline {F(S)} /S \) became multimodal rather than monotonically increasing, and a stable equilibrium was sometimes present (upper right corner of Fig. 3a). This region of parameter space typically exhibited multiple equilibria, and even parameter combinations that had a stable equilibrium also had a second, unstable (λ < −1 or λ >  1) equilibrium (Online Resource 2). Dynamics also exhibited either stable (−1 < λ < 0) or unstable (λ < −1) oscillations for a band of intermediate values of fecundity (3–10 settlers per recruit) and high levels of aggregation (1/k > 20; Fig. 3d). These regions of instability in the IDD Dilution scenario were a product of the shape of the second derivative, H''(S), of the aggregation-scale survival function. H''(S) is positive for most values of S (i.e., an increase in S produces an even greater increase in the number of surviving recruits, R), but for certain values of S (approximately 10 < S < 30), H''(S) is slightly negative, so that the rate of increase in R slows with increases in S. Consequently, for particular values of S and high values of 1/k, the term including var(S) on the right-hand side of Eq. 5 becomes negative, and aggregation-scale IDD actually reduces survival. The biological interpretation of this is that, at those value of \( \overline S \), the marginal increase in survival experienced by aggregated fish at an effective density higher than \( \overline S \) is less than the marginal decrease in survival experienced by fish with an effective density lower than \( \overline S \) . When the spatial variance in density is quite high, the actual mean survival \( \overline {F(S)} \) is lower than the mean-field estimate. This effect is visible as a slight dip in the combined-scale survivorship function, \( \overline {F(S)} /S \), for moderate levels of aggregation (1/k = 10; Fig. 1e); for higher levels of aggregation (1/k = 100), \( \overline {F(S)} /S \) drops to zero before returning to nonzero values (see right inset in Fig. 1e). The small regions of instability in Fig. 3b, d occurred because those values of d and z produced equilibrium values of S that fell near the region of \( \overline {F(S)} /S = 0 \). Note that, outside of these regions, dynamics were stable despite the increasing IDD limb of the survival function (see left inset in Fig. 1e).

Adding a predator detection effect to the dilution effect (IDD Dilution + Detection scenario; Fig. 4) produced notably different results from the other two cases. In this scenario, the set of best parameter estimates generally produced stable dynamics (0 < λ < 1) but was unstable (λ ≤ −1 or λ > 1) for moderately high levels of aggregation (approximately 10 < 1/k < 50). In some cases, there were also regions of stable oscillatory dynamics (−1 < λ < 0) adjacent to the unstable region. The precise shape of these regions of unstable dynamics varied with the other demographic parameters (Fig. 4), which I describe further below. These instabilities occur when high levels of aggregation (and thus high values of var(S)) cause the postsettlement survivorship function, \( \overline {F(S)} /S \) (Eq. 5), to drop sharply to near-zero values at high settler densities (Fig. 1d). This drop results from large settler aggregations suffering high mortality due to detection effects in this scenario, rather than from a subtle change in the concavity of H(S)/S, as in the IDD Dilution scenario. At extremely high settler densities, the aggregation-scale survival function H(S)/S flattens out (Fig. 1b), so H''(S) ≈ 0 and the scale transition is negligible (as a result, \( \overline {F(S)} /S \) returns to nonzero values for very high S; see right inset in Fig. 1f). For moderate values of 1/k, settler densities often fell within the region of \( \overline {F(S)} /S = 0 \), producing instability. As 1/k increased above 50, equilibrium settler densities also became greater and generally fell within nonzero regions of\( \overline {F(S)} /S \), causing the return to stable dynamics seen in Fig. 4.

Variation in several of the other parameters shifted the positions of the regions of instability relative to the value of 1/k. The minimum value of 1/k producing instability declined with increasing d (Fig. 4a); that is, stronger landscape-scale density dependence led to instability at lower levels of aggregation by decreasing the value of S at which \( \overline {F(S)} /S \) dropped to near zero. Note that the case of d = 0 (no landscape-scale density dependence) bears some similarity to standard Allee effect models, in which survival is a hump-shaped function of density. However, the survivorship function \( \overline {F(S)} /S \) does not have a positive second derivative at the origin, so there was not an unstable equilibrium adjacent to zero, as in typical Allee effect models (e.g., Courchamp et al. 1999). Rather, there was a single stable equilibrium for most values of 1/k when d = 0. Some values of 1/k produced three equilibria for certain values of d and the other parameters shown in Fig. 4; in all cases, this occurred in regions shown in Fig. 4 as having stable (or oscillatory stable) dynamics. The alternative equilibria always consisted of stable, unstable, and stable points, in ascending order of population density. Because the unstable equilibrium was always bracketed in this way, the overall results shown in Fig. 4 are robust (see Online Resource 2 for details on the alternative equilibria).

The fecundity parameter z also affected stability (Fig. 4b). For values of z lower than approximately 3,000 settlers per adult, dynamics were unstable for all levels of aggregation above a minimum threshold in the vicinity of 1/k = 100. However, the level of aggregation associated with instability decreased with z above values of approximately z = 100 settlers per adult.

Unlike the DDD Baseline and IDD Dilution scenarios, several other parameters also affected dynamic stability in the IDD Dilution + Detection scenario. The minimum value of 1/k producing oscillatory instability increased slightly with adult survivorship, s (Fig. 4c). Additionally, for low values of s and 1/k, dynamics were stable but the return tendency exhibited dampened oscillations rather than a monotonic approach to equilibrium (−1 < λ < 0). In general, higher adult survivorships led to more stable dynamics. The same was also generally true for the Beverton–Holt density-independent survivorship term a, for which low values (a < 0.2) made instability possible for slightly lower levels of aggregation (1/k < 20; Fig. 4d). There was also an unusual effect of the detection effect parameter h on stability (Fig. 4e). For 1/k > 10, there was a “chattering” pattern of stable and unstable regions of parameter space across all values of h. This appears to occur because the shape of \( \overline {F(S)} \) and thus the value of λ are very sensitive to h for high values of 1/k, and small changes in h can rapidly switch the sign and magnitude of λ. Given this sensitivity to particular parameter values, it would be unwise to draw conclusions about the specific values of h that produce stability or instability, which may depend on numerical artifacts in calculating λ. Rather, note that instability is generally much more likely for those higher values of 1/k. Indeed, instability generally set in at values of 1/k higher than that observed in the field for Thalassoma bifasciatum, the species used to parameterize the model (star symbols in Figs. 3 and 4).

The general result that instability is likely only for values of 1/k greater than approximately 10 in the IDD Dilution + Detection scenario does not appear to be an artifact of the specific parameterization or shape of the survival function H(S)/S. The range of values considered for parameters g and h leads to a wide variety of shapes H(S)/S (Fig. 5a; compare to the example given for the best estimates of g and h in Fig. 1b). However, when the scale transition is applied to any of the curves shown in Fig. 5a to obtain F(S)/S, the transition between a smooth F(S)/S curve (typical of low spatial variance scenarios) and a F(S)/S curve that drops sharply to zero (typical of unstable, high spatial variance scenarios) always occurs for values of 1/k between 5 and 10 (Fig. 5b,c). That is, spatial variance at the aggregation scale begins to produce survivorship curves typical of instability in the vicinity of 1 < 1/k < 10. This result is not surprising given the form of the negative binomial variance function: the \( {\overline S^2} \) term in Eq. 6 will remain relatively small for 1/k < 1 but will begin to dominate the variance expression once 1/k becomes greater than 1, and the variance can become quite large for values of 1/k not much greater than 1. It was not feasible to confirm this generalization by performing a full stability analysis for the wide range of curves shown in Fig. 5a, but analyses performed using both the upper and lower values of parameter g given in Table 1 (yielding two relatively different shapes for H(S)/S), suggested that the unstable regions of parameter space remained restricted to values of 1/k higher than those observed in the field for T. bifasciatum (see Online Resource 3).

Fig. 5
figure 5

Range of possible survivorship curves for the IDD Dilution + Detection scenario. a Aggregation-scale survivorship functions H(S)/S for a range of values of parameters g and h (all other parameters set to the best estimates from Table 1). Each cluster of curves has the indicated values of h (in units of settlers); within each cluster, values of g were indicated by shading and had values of 0.095, 0.295, or 0.495 per settlers (light to dark, respectively). b, c Aggregate survivorship across both spatial scales for b g = 0.095 per settlers, h = 1 settlers, c g = 0.495 per settlers, h = 20 settlers. The degree of spatial clumping, 1/k, ranges from 0.001 (solid gray curve) to 100 (solid black curve). Intermediate curves have values of 1/k = 1.0, 2.5 (dashed gray curves), 5.0, 7.5, and 10 (dashed black curves). Note that gray curves have a smooth asymptotic approach to zero whereas black curves drop sharply to zero

Full size image

There was also a range of values of 1/k that produced multiple equilibria in the IDD Dilution + Detection scenario, typically in the vicinity of 3 < 1/k < 10. The region of parameter space with multiple equilibria always had one stable equilibrium (these values are those shown in Fig. 4) and two other unstable equilibria. The stability properties of the other equilibria are reported in Online Resource 2.

Discussion

The goal of this analysis was to determine the conditions under which inversely density-dependent (IDD) mortality produced unstable dynamics in a population that would otherwise be stable and regulated by directly density-dependent (DDD) mortality. In general, the results of the model with an IDD Dilution effect (a monotonic increase in survival with aggregation-scale density) demonstrated that IDD mortality is compatible with stable population dynamics for highly aggregated species so long as both fecundity (including larval survival) and the strength of landscape-scale DDD mortality take on moderate or high parameter values. In the IDD Dilution scenario, unstable dynamics were observed only for very high levels of aggregation and either very weak DDD mortality or low levels of fecundity.

In contrast, when both dilution and detection effects acted at the aggregation scale (so that survival is a hump-shaped function of aggregation size), instability was possible for a broader range of biologically plausible parameter values. Compared to the IDD Dilution scenario, instability was possible for much lower levels of aggregation, although the precise level of aggregation at which dynamics became unstable varied subtly with fecundity, the strength of landscape-scale density dependence, density-independent survivorship, and the strength of the detection effect.

In a broad sense, this analysis is consistent with well-known results from the Allee effect literature (e.g., Courchamp et al. 1999; Gascoigne and Lipcius 2004b). In particular, instability was more common with a unimodal survivorship function, in which mortality is IDD at low densities but DDD at higher densities (obtained in the IDD Dilution + Detection scenario), and instability increased with the strength of IDD (in this case, the degree of aggregation). However, my analysis moved beyond this typical result by exploring a range of cases in which IDD and DDD processes occur simultaneously—and at different spatial scales—over a range of densities, which may be common in nature. The importance of considering alternative spatial scales in this analysis is made clear by the observation that dynamics were always stable when IDD and DDD processes occurred at the same spatial scale (i.e., if 1/k was close to zero and aggregation was negligible) but the potential for instability increased with the degree of aggregation.

To put the model results in biological context, parameter values estimated for bluehead wrasse, Thalassoma bifasciatum, in St. Croix (White 2008, White, J.W., unpublished data) place that population within the region of dynamic stability, regardless of the form of aggregation-scale IDD mortality (star symbols in Figs. 3 and 4). Estimates of 1/k for other species are not widely reported, but values in the range of 0.1–10 are typically observed in insects (Nedelman 1983; Desouhant et al. 1998). Shaw et al. (1998) calculated 1/k for the aggregation of parasites to hosts for a range of host species, including fish, birds, and mammals, and found that values were usually >1 and ranged as high as 26. These estimates should be used cautiously, however, as Grear and Schmitz (2005) pointed out that the value of 1/k depends on the total number of individuals in the sample, so comparing values across study systems is problematic. Nonetheless, in the IDD Dilution effect scenario, instability began to become possible at rather high values of 1/k (in the vicinity of 1/k = 30) and either very weak DDD mortality or certain values of adult fecundity. For comparison, see Fig. 2c for an example of this level of aggregation, and note that Osenberg et al. (2002) estimated that d was typically equal to one for most reef fish populations. Instability was possible at values of 1/k = 10 in the IDD Dilution + Detection scenario, and in general instability can be expected to set in for values of 1/k between 1 and 10 (Fig. 5). This is a much more modest degree of aggregation (see Fig. 2b for comparison) that is more commonly observed in nature, so there is much greater potential for instability at biologically reasonable parameter values (note the proximity of the stars in Fig. 4 to the stability boundary). The relative prevalence of these two types of aggregation-scale IDD mortality (dilution vs. dilution + detection) is not known. Surveys of the reef fish literature (Hixon and Webster 2002; White et al. 2010) reveal several cases of mortality declining monotonically with density as in the dilution scenario (Booth 1995; Sandin and Pacala 2005b; White and Warner 2007), but only one example of a hump-shaped relationship between density and survival as in the IDD Dilution + Deletion scenario (Jones 1988), and that paper did not report a value of 1/k.

Increasing the strength, d, of landscape-scale DDD mortality tended to decrease the minimum level of aggregation (1/k) that would produce unstable dynamics, at least in the presence of both dilution and detection effects. This is not surprising, as values of d >  1 imply overcompensation, in which recruitment actually decreases with increasing settler densities. Overcompensation is typically associated with oscillatory dynamic instability, such as in the well-known Ricker and logistic map models (Gurney and Nisbet 1998).

The fecundity parameter z (which incorporated both egg production and larval survival) had a complex effect on stability. When z took on relatively high values (z > 3,000 settlers per adult), stability was possible with relatively high levels of aggregation, but at lower values of z, instability occurred with much lower levels of aggregation. This pattern occurred because spatial variance in settler density, S, is an increasing function of S, so at very low fecundities there is little variance and thus a weaker destabilizing effect of aggregation-scale IDD mortality. At extremely high fecundities, settler density was also high and fell in the asymptotic region of the aggregation-scale survivorship function, so there was relatively little effect of spatial variance in setter density and dynamics were stable. It was only at intermediate fecundity values that spatial variation greatly affected overall settler survival and destabilized population dynamics. Other parameters also had effects on stability in the IDD Dilution + Detection scenario, including adult survival, density-independent postsettlement survival, and the detection effect parameter. While the effect of aggregation on stability varied somewhat over the range of these parameters, the general pattern of unstable dynamics for moderate levels of aggregation (1/k  >  10) was consistent.

The unstable dynamics exhibited by these population models arose in part from the time delay in density dependence imposed by the discrete-time framework: settler mortality in time t + 1 depended on production in time t. It is likely that similar models with inverse density dependence formulated in continuous time would not exhibit this type of instability, as is generally the case for continuous analogs of discrete-time models (Turchin 2003). However, discrete time steps are a natural feature of benthic marine populations with pelagic larvae and are imposed by the time lag between larval production and larval settlement, so the discrete-time formulation is more appropriate. I did not consider the case in which IDD and DDD processes are separated in time (rather than in space), which would introduce an additional lag into the dynamics. I am not aware of empirical evidence for that type of delay, so I leave that scenario for future consideration.

In many models of marine population dynamics, the benthic, adult component of the life history is represented as having directly density-dependent mortality at the time of settlement, followed by density-independent adult growth and survival (e.g., Armsworth 2002; James et al. 2002; White 2008). Such models are generally thought to capture the key regulatory dynamics in these systems (but see Sandin and Pacala 2005a). The results of this paper suggest that benthic marine species that also experience monotonic IDD mortality at the scale of social aggregations will not exhibit population dynamics with fundamentally different stability characteristics except at very high levels of spatial aggregation. However, if IDD survival has a hump-shaped functional form, then unstable dynamics are possible for relatively moderate levels of aggregation. In that type of system, a population model describing only mean-field processes without accounting for small-scale variance in density would not adequately represent the potential for unstable population dynamics.

It is also important to note that the models used here assumed that the population is closed to immigration and emigration. Many benthic marine populations actually exhibit some degree of metapopulation structure (Kritzer and Sale 2006). In a metapopulation, the exchange of individuals across populations is likely to decouple local settlement from local production somewhat, dampening the feedbacks that lead to instability (Hastings et al. 1993; Amarasekare 1998) so long as dispersal of juveniles is obligate or an increasing function of population density (Vance 1984). Similarly, Hassell (1984) found that purely IDD predation could produce stable population dynamics in a coupled predator–prey metapopulation because predator and prey growth rates were decoupled in space and time. Consequently, the results presented here likely represent an extreme condition; in real benthic metapopulations, unstable dynamics should be even less likely than these model results suggest.

The examples used in this study were largely drawn from the reef fish literature, where a large body of work has been devoted to exploring mechanisms of population regulation across a range of spatial scales. However, the models and results developed here may also apply to other systems. Predators of a broad range of taxa appear to respond to prey densities at a particular foraging scale (wading birds: Colwell and Landrum 1993; Cummings et al. 1997; pelagic seabirds: Burger et al. 2004; pelagic fishes: Horne and Schneider 1994; coccinellid insects: Schellhorn and Andow 2005), and in some insect populations this phenomenon produces a pattern of large-scale DDD and small-scale IDD mortality (Mohd Norowi et al. 2000, reviewed by Walde and Murdoch 1988) like that described for reef fishes by White and Warner (2007). Gascoigne et al. (2005) reported a similar scale-dependent switch in the direction of density dependence in soft-sediment mussels, which exhibited facilitation at small spatial scales, apparently representing shared resistance to dislodgement by waves, but competition at large scales, apparently for zooplankton prey. This pattern is not universal, as alternative combinations of DDD, IDD, and density-independent mortality at different spatial scales have also been reported (Stiling et al. 1991; Schellhorn and Andow 2005). Nonetheless, the results presented here suggest that only in extreme circumstances is IDD mortality sufficient to destabilize population dynamics regulated by DDD mortality.