Delay-dependent Robust Stabilization and H∞ Control for Uncertain Stochastic T-S Fuzzy Systems with Discrete Interval and Distributed Time-varying Delays

Abstract

In this paper, delay-dependent robust stabilization and H∞ control for uncertain stochastic Takagi-Sugeno (T-S) fuzzy systems with discrete interval and distributed time-varying delays are discussed. The purpose of the robust stochastic stabilization problem is to design a memoryless state feedback controller such that the closed-loop system is mean-square asymptotically stable for all admissible uncertainties. In the robust H∞ control problem, in addition to the mean-square asymptotic stability requirement, a prescribed H∞ performance is required to be achieved. Sufficient conditions for the solvability of these problems are proposed in terms of a set of linear matrix inequalities (LMIs) and solving these LMIs, a desired controller can be obtained. Finally, two numerical examples are given to illustrate the effectiveness and less conservativeness of our results over the existing ones.

1 Introduction

In modeling of dynamical systems, Takagi-Sugeno (T-S) fuzzy systems[1] provide an alternative approach to the control of plants that are complex, uncertain, and ill-defined. In the last two decades, with wide applications from consumer products to industrial processes, T-S fuzzy model[1–5] is proven to be effective universal approximations over differential geometric and differentiable algebraic methods. By making use of simple fuzzy reasoning rules and fuzzy inference methods, it provides a basis for development of systematic approaches to stability, stabilization, H _∞ control and filtering problems[6–13].

Time delays are often encountered in many industrial and engineering systems such as chemical processes, rolling mill systems, networked control systems, etc. It is well known that time delays can cause poor performance or instability. Therefore, the problem of delay-dependent stability analysis and controller synthesis for T-S fuzzy systems with time delays have received great efforts by many researchers in recent years. Moreover, delay-dependent approaches[6,9,14] are generally less conservative than delay-independent[2] ones when the sizes of time delays are small. Recently, the delay-dependent stabilization and H _∞ control of T-S fuzzy systems with interval time-varying delay are discussed[15,16]. Robust stability, stabilization and H _∞ controller design of discrete and distributed time delays with or without fuzzy systems are considered[17–19].

In the past few years, stochastic nonlinear systems have received much attention since stochastic modeling has come to play an important role in many branches of science and engineering applications. For instance, stabilization, H _∞ control, and H _∞ filtering problems for linear and nonlinear stochastic systems have been considered[20–26]. The control technique based on the so-called T-S fuzzy model has attracted lots of attention. Recently, some attempts have been made to use T-S fuzzy model based control technique for stochastic nonlinear systems[27–30]. Very recently, the delay-dependent robust H _∞ control for uncertain stochastic T-S fuzzy systems with time delays have been discussed in [31,32]. However, to the best of our knowledge, the delay-dependent robust stabilization and H _∞ control for uncertain stochastic T-S fuzzy systems with discrete interval and distributed time-varying delays have not yet been fully investigated and this will be the goal of this paper.

In this paper, we investigate the problem of the delay-dependent robust stabilization and H _∞ control for uncertain stochastic T-S fuzzy systems with discrete interval and distributed time-varying delays. The uncertainties are assumed to be norm bounded and time-varying. For the robust stabilization problem, a state feedback fuzzy controller is designed such that the closed-loop system is mean-square asymptotically stable for all admissible uncertainties, while for the robust H∞ control problem, a state feedback fuzzy controller is designed such that the closed-loop system is not only mean-square asymptotically stable but also guarantees a prescribed H∞ performance level. Sufficient conditions for the solvability of these problems are obtained, and desired state feedback controllers can be constructed by solving certain LMIs. Further, two numerical examples are given to illustrate the effectiveness of the proposed approach.

Throughout this paper, notation X ⩾ Y X > Y) where X and Y are symmetric matrices, means that X − Y is positive semidefinite (respectively, positive definite). I denotes the identity matrix of appropriate dimension. L ₂[0, ∞) is the space of square integrable vector. Moreover, let ($\Omega ,\mathcal{F},{\left\{ {{\mathcal{F}_t}} \right\}_{t0,}}\mathcal{P}$) be a complete probability space with a filtration ${\left\{ {{\mathcal{F}_t}} \right\}_{t \geqslant 0}}$ satisfying the usual conditions (i.e., the filtration contains all $\mathcal{P}$-null sets and is right continuous). The symmetric elements of the symmetric matrix will be denoted by ✽. Matrices, if their dimensions are not explicitly stated, are assumed to have compatible dimensions for algebraic operations.

2 Problem formulation

Consider the following uncertain stochastic T-S fuzzy model with discrete and distributed time-varying delays described by

Plant rule i: If θ ₁(t) is η _{i 1} and θ ₂(t) is η _{i 2} and ⋯ and θp(t) is ηip, then

$$\begin{array}{*{20}{l}} {(\Sigma ):dx(t) = } \\ {\left[ {({A_i} + \Delta {A_i}(t))x(t) + ({A_{di}} + \Delta {A_{di}}(t)) \times x(t - \tau (t)) + } \right.} \\ {({B_{1i}} + \Delta {B_{1i}}(t))u(t) + {B_{{v_{1i}}}}v(t) + {B_{{d_{1i}}}}\int_{t - d(t)}^t {\left. {x(s){\text{d}}t} \right]dt} + } \\ {\left[ {({C_i} + \Delta {C_i}(t))x(t)} \right. + ({C_{di}} + \Delta {C_{di}}(t)) \times x(t - \tau (t)) + } \\ {({B_{2i}} + \Delta {B_{2i}}(t))u(t) + {B_{{v_{2i}}}}v(t) + {B_{{d_{2i}}}}\int_{t - d(t)}^t {\left. {x(s){\text{d}}s} \right]} {\text{d}}w(t)} \end{array}$$

(1)

$$z(t) = {D_i}x(t) + {D_{di}}x(t - \tau (t)) + {B_{3i}}u(t)$$

(2)

$$x(t) = \phi (t),\forall t \in \left[ { - \tau ,0} \right],\quad i = 1,2, \cdots ,r$$

(3)

where η _ij is the fuzzy set, θ ₁ (t), θ ₂ (t), ⋯ ,θ _p(t) are the premise variables, r is the number of IF-THEN rules of T-S fuzzy model, x(t) ∈ Rⁿ is the state, u(t) ∈ R^m is control input, v(t) ∈ R^p is a disturbance input which belongs to L ₂[0, ∞), z(t) ∈ R^q is controlled output vector, and ω(t) ∈ Rⁿ is a one-dimensional Brownian motion defined on the probability space ($\Omega ,\mathcal{F},{\left\{ {{\mathcal{F}_t}} \right\}_{t0,}}\mathcal{P}$) satisfying $\varepsilon \left\{ {{\text{d}}w\left( t \right)} \right\} = 0,{\text{ }}\varepsilon \left\{ {{\text{d}}w{{\left( t \right)}^2}} \right\} = dt$. In the above system (Σ), Ai, A _di , B _{1 i} , B _vii , B _dli , C _i , C _di , B _2i , B _v2i , B _d2i , Di, D _di and B _3i are known real constant matrices with appropriate dimensions. ∆ A _i(t), ∆A _di(t), ∆B _{1 i} (t), ∆C _i(t), ∆Cdi(t) and ∆B _2i(t) are unknown matrices representing time-varying parameter uncertainties, τ(t) and d(t) are bounded continuous time-varying delays satisfying

$$0 \leqslant {\tau _m} \leqslant \tau (t) \leqslant {\tau _M},\quad \dot \tau (t) \leqslant \mu < \infty ,\,\;0 \leqslant d(t) \leqslant {d_M}$$

(4)

where τ _m , τ _M , μ and d _M are real constant scalars. Let τ = max{τ _M, d _M}. φ(t) is real valued continuous initial function on [−τ,0]. In this paper, the parameter uncertainties are assumed to be of the form

$$\begin{array}{*{20}{c}} {\left[ {\Delta {A_i}(t)\,\,\Delta {A_{di}}(t)\,\,\Delta {B_{1i}}(t)\,\,\Delta {C_i}(t)\,\,\Delta {C_{di}}(t)\,\,{B_{2i}}(t)} \right] = } \\ {\quad \quad {E_i}{F_i}(t)\left[ {{H_{1i}}\;{H_{2i}}\;{H_{3i}}\;{H_{4i}}\;{H_{5i}}\;{H_{6i}}} \right]} \end{array}$$

(5)

where E _i , H _1i , H _2i , H _3i , H _4i , H _5i and H _6i are known real constant matrices with appropriate dimensions, and F _i(t) is an unknown real time-varying matrix function satisfying

$$F_i^{\text{T}}(t){F_i}(t) \leqslant I.$$

(6)

It is assumed that all elements of F _i(t) are Lebesgue measurable. ∆Ai(t), ∆Adi(t), ∆B _{1 i} (t), ∆C _i(t), ∆C _di(t) and ∆B _2i(t) are said to be admissible if both (5) and (6) hold.

By using center average defuzzifier, product inference and singleton fuzzifier, the global dynamics of the T-S fuzzy system (Σ) can be inferred as

$$\begin{array}{*{20}{l}} {({\Sigma _1}):{\text{d}}x(t) = } \\ {\sum\limits_{i = 1}^r {{h_i}(\theta (t))\left\{ {\left[ {({A_i} + \Delta {A_i}(t))x(t) + } \right.} \right.} } \\ {({A_{di}} + \Delta {A_{di}}(t))x(t - \tau (t)) + ({B_{1i}}(t))u(t) + } \\ {{B_{{v_{1i}}}}v(t) + {B_{{d_{1i}}}}\int_{t - d(t)}^t {\left. {x(s){\text{d}}s} \right]} {\text{d}}t + } \\ {\left[ {({C_i} + \Delta {C_i}(t))x(t) + ({C_{di}} + \Delta {C_{di}}(t))x(t - \tau (t)) + } \right.} \\ {({B_{2i}} + \Delta {B_{2i}}(t)u(t) + {B_{{v_{2i}}}}v(t) + } \\ {{B_{{d_{2i}}}}\int_{t - d(t)}^t {\left. {\left. {x(s){\text{d}}s} \right]{\text{d}}w(t)} \right\}} } \end{array}$$

(7)

$$z(t) = \sum\limits_{i = 1}^r {{h_i}(\theta (t))\left\{ {{D_i}x(t) + {D_{di}}x(t - \tau (t)) + {B_{3i}}u(t)} \right\}} $$

(8)

$$x(t) = \phi (t),\quad \forall t \in [ - \tau ,0]$$

(9)

where ${h_i}\left( {\theta \left( t \right)} \right) = \frac{{{v_i}\left( {\theta \left( t \right)} \right)}}{{\mathop {\lim }\limits_{x \to \infty } \sum\nolimits_{i = 1}^r {{v_i}\left( {\theta \left( t \right)} \right)} }},{v_i}\left( {\theta \left( t \right)} \right) = {\prod\nolimits_{j = 1}^p \eta _{ij}}\left( {\theta \left( t \right)} \right)$, and η _ij(θ _j(t)) is the _i grade of membership value of θ _j(t) in η _ij. In this paper, we assume that ν _i( θ (t)) ⩾ 0 for i = 1,2, ⋯ ,r and $\sum\nolimits_{i = 1}^r {{v_i}} \left( {\theta \left( t \right)} \right) > 0$ for all t . Therefore, hi( θ (t)) ⩾ 0 (for i = 1'2,••• ,r), and $\sum\nolimits_{i = 1}^r {{h_i}} \left( {\theta \left( t \right)} \right) > 0$ for all t. In the sequel, for simplicity, we use h _i to represent h _i(θ (t)).

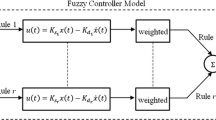
Based on the parallel distributed compensation schemes, a fuzzy model of a state feedback controller for the system (Σ₁) is formulated as follows:

Control rule i: If θ ₁(t) is η _{i 1} and θ ₂(t) is η _{i 2} and ⋯ and θ _p ( t) is η _i p, then

$$u(t) = {K_i}x(t),\quad i = 1,2, \cdots ,r.$$

(10)

The overall state feedback fuzzy control law is represented by

$$u(t) = \sum\limits_{i = 1}^r {{h_i}{K_i}x(t)} $$

(11)

where Ki (i = 1, 2, ⋯ , r) are the local control gains. Under control law (11), the overall closed-loop system is obtained as

$$\begin{array}{*{20}{l}} {({\Sigma _2}):{\text{d}}x(t) = } \\ {\left[ {{A_K}x(t) + {A_d}x(t - \tau (t)) + {B_{{v_1}}}v(t) + {B_{{d_1}}}\int_{t - d(t)}^t {x(s){\text{d}}s} } \right]dt + } \\ {\left[ {{C_K}x(t) + {C_d}x(t - \tau (t)) + {B_{{v_2}}}v(t) + {B_{{d_2}}}\int_{t - d(t)}^t {x(s){\text{d}}s} } \right]dw(t)} \end{array}$$

(12)

$$z(t) = {D_K}x(t) + {D_d}x(t - \tau (t))$$

(13)

$$x(t) = \phi (t),\quad \forall t \in \left[ { - \tau ,0} \right]$$

(14)

where

$$\begin{array}{*{20}{l}} {{A_K} = \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}({A_i} + {B_{1i}}{K_j} + \Delta {A_i}(t) + \Delta {B_{1i}}(t){K_j})} } } \\ {{A_d} = \sum\limits_{i = 1}^r {{h_i}({A_{di}} + \Delta {A_{di}}(t))} } \\ {{B_{{v_1}}} = \sum\limits_{i = 1}^r {{h_i}{B_{{v_{1i}}}}} } \\ {{B_{{d_1}}} = \sum\limits_{i = 1}^r {{h_i}{B_{{d_{1i}}}}} } \\ {{C_K} = \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}({C_i} + {B_{2i}}{K_j} + \Delta {C_i}(t) + \Delta {B_{2i}}(t){K_j})} } } \\ {{C_d} = \sum\limits_{i = 1}^r {{h_i}({C_{di}} + \Delta {C_{di}}(t))} } \\ {{B_{{v_2}}} = \sum\limits_{i = 1}^r {{h_i}{B_{{v_{2i}}}}} } \\ {{B_{{d_2}}} = \sum\limits_{i = 1}^r {{h_i}{B_{{d_{2i}}}}} } \\ {{D_K} = \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}({D_i} + {B_{3i}}{K_j})} } } \\ {{D_d} = \sum\limits_{i = 1}^r {{h_i}{D_{di}}.} } \end{array}$$

Let us introduce the following definition and lemmas that are useful for the development of our results.

Definition 1[25]. The nominal system (7) and (9) with u(t) = 0 and v(t) = 0 is said to be mean-square stable if for any ε > 0, there exists δ(ε) > 0 such that $\varepsilon \left\{ {|x\left( t \right){|^2}} \right\} < \varepsilon$ when

$$\mathop {{\text{sup}}}\limits_{ - \tau \leqslant s \leqslant 0} \mathcal{E}\{ |\phi (s){|^2}\} < \delta (\varepsilon ).$$

In addition,

$$\mathop {{\text{lim}}}\limits_{t \to \infty } \mathcal{E}\{ |x(t){|^2}\} = 0$$

for any initial conditions, then the nominal system (7) and (9) with u(t) = 0 and v(t) = 0 is said to be mean-square asymptotically stable. The uncertain stochastic system (7) and (9) is said to be robustly stochastically stable if the system associated to (7) and (9) with u(t) = 0 and v(t) = 0 is mean-square asymptotically stable for all admissible uncertainties ∆A _i(t), ∆A _di(t), ∆B _1i (t), ∆C _i(t), ∆C _di(t) and ∆B _2i (t).

In this paper, our aim is to develop techniques of robust stochastic stabilization and robust H _∞ control for the stochastic fuzzy system (Σ₂). More specifically, we are concerned with the following two problems:

• 1) Robust stabilization problem: Design a state feedback controller (11) for the system (7) and (9) with v(t) = 0 such that the resulting closed-loop system (12) and (14) with v(t) = 0 is mean-square asymptotically stable for all admissible uncertainties. In this case, the system (12) and (14) with v(t) = 0 is robustly stochastically stablilizable.

• 2) Robust H _∞ control problem: Given a scalar γ > 0, design a state feedback controller in the form of (11) for system (Σ₁) such that, for all admissible uncertainties, the resulting closed-loop system (Σ₂) is mean-square asymptotically stable, and for any non-zero v(t) ∈ L ₂[0, ∞), $||z\left( t \right)||{\varepsilon _2} < \gamma ||v\left( t \right)|{|_2}$ is satisfied under zero initial condition. In this case, the system (Σ₂) is robustly stochastically stabilizable with disturbance attenuation level γ.

Lemma 1[33]. For any vectors x, y ∈ Rⁿ, matrices $P \in {{\text{R}}^{n \times n}},D \in {{\text{R}}^{n \times {n_f}}},E \in {{\text{R}}^{{n_f} \times n}}$ and $F \in {{\text{R}}^{{n_f} \times {n_f}}}$ with $P > 0,||F|| \leqslant 1$, and scalar ε > 0, we have

• 1) 2x ^T y ⩾ x ^T P-¹ x + y ^T Py,

• 2) DFE + E ^T F ^T D ^T⩾ ε-¹ DD ^T + εE ^T E.

Lemma 2[21]. For any constant matrix M > 0, any scalars a and b with a < b, and a vector function x(t) : [a, b] → Rⁿ such that the integrals concerned are well defined, the following holds:

$${\left[ {\int_a^b {x(s){\text{d}}s} } \right]^{\text{T}}}M\left[ {\int_a^b {x(s){\text{d}}s} } \right] \leqslant (b - a)\int_a^b {{x^{\text{T}}}(s)Mx(s){\text{d}}s} .$$

Lemma 3[27]. For any real matrices X _ij for i,j = 1, 2, ⋯ , r and Λ > 0 with appropriate dimensions, we have

$$\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {\sum\limits_{k = 1}^r {\sum\limits_{l = 1}^r {{h_i}{h_j}{h_k}{h_l}X_{ij}^{\text{T}}\Lambda {X_{kl}}} } } } \leqslant \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}X_{ij}^{\text{T}}\Lambda {X_{ij}}} } $$

where hi (1 ⩽ i ⩽ r) are defined as h _i ( θ(t)) ⩾ 0, $\sum\nolimits_{i = 1}^r {{h_i}} \left( {\theta \left( t \right)} \right) = 1$.

3 Robust stochastic stabilization

In this section, we shall present a sufficient condition for the uncertain stochastic fuzzy system (12) and (14) with v(t) = 0 to be robustly stochastically stabilizable in terms of LMIs. The design of the fuzzy controller is to determine the local feedback gains Ki(i = 1, 2, • • • ,r) such that the system (12) and (14) with v(t) = 0 is robustly stochastically stabilizable. When there are no parameter uncertainties in the system (12) and (14) with v(t) = 0, Theorem 1 is specialized as follows.

Theorem 1. For given scalars τ _m , τ _M , d _M and μ, the time-varying delays satisfying (4), the closed-loop stochastic fuzzy system (12) and (14) with v(t) = 0 and ∆ A _i(t) = ∆A _di(t) = ∆B _1i (t) = ∆C _i(t) = ∆Cdi(t) = ∆B _2i(t) = 0 is stochastically stabilizable if there exist matrices X > 0, ${\bar Q_s} > 0$ (s = 1,2,3), ${\tilde R_l} > 0$ (l = 1,2,3,4), $\bar Z > 0$ and real matrices ${\bar N_{lij}},{\bar M_{lij}},{\bar S_{lij}},{Y_j}$(l = 1, 2, 1 ⩽ i ⩽ j ⩽ r) of appropriate dimensions such that the following LMIs hold:

$$\left[ {\begin{array}{*{20}{c}} {\Xi _{11}^{ii}}&{\Xi _{12}^{ii}}&{\Xi _{13}^{ii}} \\ * &{{\Xi _{22}}}&0 \\ * & * &{{\Xi _{33}}} \end{array}} \right] < 0,\quad 1 \leqslant i \leqslant r$$

(15)

(16)

where

$$\begin{array}{*{20}{l}} {\Xi _{11}^{ij} = \left[ {\begin{array}{*{20}{c}} {\phi _{11}^{ij}}&{\phi _{12}^{ij}}&{{{\bar M}_{1ij}}}&{ - {{\bar S}_{1ij}}}&{{B_{{d_{1i}}}}X} \\ * &{\phi _{22}^{ij}}&{{{\bar M}_{2ij}}}&{ - {{\bar S}_{2ij}}}&0 \\ * & * &{ - {{\bar Q}_2}}&0&0 \\ * & * & * &{ - {{\bar Q}_3}}&0 \\ * & * & * & * &{ - \frac{1}{{{d_M}}}\bar Z} \end{array}} \right]} \\ {\Xi _{12}^{ij} = \left[ {\widehat C_{ij}^T\quad {\tau _M}\widehat A_{ij}^{\text{T}}\quad \bar \tau \widehat A_{ij}^{\text{T}}\quad {\tau _M}\widehat C_{ij}^{\text{T}}\quad \bar \tau \widehat C_{ij}^{\text{T}}} \right]} \\ {\Xi _{13}^{ij} = \left[ {{\tau _M}{{\bar N}_{ij}}\quad \bar \tau {{\bar M}_{ij}}\quad \bar \tau {{\bar S}_{ij}}\quad {{\bar N}_{ij}}\quad {{\bar M}_{ij}}\quad {{\bar S}_{ij}}} \right]} \\ {{\Xi _{22}} = {\text{diag}}\left\{ { - X,\quad - {\tau _M}{{\tilde R}_1},\,\; - \bar \tau {{\tilde R}_2},\quad - {\tau _M}{{\tilde R}_3},\quad - \bar \tau {{\tilde R}_4}} \right\}} \\ {{\Xi _{33}} = {\text{diag}}\left\{ { - 2{\tau _M}X + {\tau _M}{{\tilde R}_1},\;\;\; - 2\bar \tau X + \bar \tau {{\tilde R}_2}} \right.,} \\ {\quad \quad - 4\bar \tau X + \bar \tau {{\tilde R}_1} + \bar \tau {{\tilde R}_2},\;\; - 2X + {{\tilde R}_3},\;\;\; - 2X + {{\tilde R}_4},} \\ {\quad \quad \left. { - 4X + {{\tilde R}_3} + {{\tilde R}_4}} \right\}} \end{array}$$

with

$$\begin{array}{*{20}{l}} {\phi _{11}^{ij} = {{\bar Q}_1} + {{\bar Q}_2} + {{\bar Q}_3} + {{\bar N}_{1ij}} + \bar N_{1ij}^{\text{T}} + ({A_i}X + {B_{1i}}{Y_j}) + } \\ {\quad \quad {{({A_i}X + {B_{1i}}{Y_j})}^{\text{T}}} + {d_M}\bar Z} \\ {\phi _{12}^{ij} = {{\bar S}_{1ij}} - {{\bar N}_{1ij}} + \bar N_{2ij}^{\text{T}} - {{\bar M}_{1ij}} + {A_{di}}X} \\ {\phi _{22}^{ij} = - (1 - \mu ){{\bar Q}_1} - {{\bar N}_{2ij}} - \bar N_{2ij}^{\text{T}} + {{\bar S}_{2ij}} + \bar S_{2ij}^{\text{T}} - {{\bar M}_{2ij}} - \bar M_{2ij}^{\text{T}}} \\ {\widehat A_{ij}^{\text{T}} = {{\left[ {{A_i}X + {B_{1i}}{Y_j}\quad {A_{di}}X\quad 0\quad 0\quad {B_{{d_{1i}}}}X} \right]}^{\text{T}}}} \\ {\widehat C_{ij}^{\text{T}} = {{\left[ {{C_i}X + {B_{2i}}{Y_j}\quad {C_{di}}X\quad 0\quad 0\quad {B_{{d_{2i}}}}X} \right]}^{\text{T}}}} \\ {{{\bar N}_{ij}} = {{\left[ {\bar N_{1ij}^{\text{T}}\quad \bar N_{2ij}^{\text{T}}\quad 0\quad 0\quad 0} \right]}^{\text{T}}}} \\ {{{\bar M}_{ij}} = {{\left[ {\bar M_{1ij}^{\text{T}}\quad \bar M_{2ij}^{\text{T}}\quad 0\quad 0\quad 0} \right]}^{\text{T}}}} \\ {{{\bar S}_{ij}} = {{\left[ {\bar S_{1ij}^{\text{T}}\quad \bar S_{2ij}^{\text{T}}\quad 0\quad 0\quad 0} \right]}^{\text{T}}}} \\ {\,\;\bar \tau = {\tau _M} - {\tau _m}.} \end{array}$$

Moreover, the state feedback gain can be constructed as K _j = Y _j X ⁻¹ (j = 1, 2,••• , r).

Proof. Let

$$\begin{array}{*{20}{l}} {{A_K} = \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}({A_i} + {B_{1i}}{K_j})} } } \\ {{A_d} = \sum\limits_{i = 1}^r {{h_i}{A_{di}}} } \\ {{B_{{d_1}}} = \sum\limits_{i = 1}^r {{h_i}{B_{{d_{1i}}}}} } \\ {{C_K} = \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}({C_i} + {B_{2i}}{K_j})} } } \\ {{C_d} = \sum\limits_{i = 1}^r {{h_i}{C_{di}}} } \\ {{B_{{d_2}}} = \sum\limits_{i = 1}^r {{h_i}{B_{{d_{2i}}}}} } \end{array}$$

then the closed-loop nominal system (12) with v(t) = 0 can be represented as

$${\text{d}}x(t) = f(t){\text{d}}t + g(t){\text{d}}w(t)$$

(17)

where

$$\begin{array}{*{20}{l}} {f(t) = {A_K}x(t) + {A_d}x(t - \tau (t)) + {B_{{d_1}}}\int_{t - d(t)}^t {x(s)} {\text{d}}s} \\ {g(t) = {C_K}x(t) + {C_d}x(t - \tau (t)) + {B_{{d_1}}}\int_{t - d(t)}^t {x(s)} {\text{d}}s.} \end{array}$$

Choose a Lyapunov-Krasovskii functional candidate as

$$\begin{array}{*{20}{c}} {V({x_t},t) = {V_1}({x_t},t) + {V_2}({x_t},t) + {V_3}({x_t},t) + } \\ {{V_4}({x_t},t) + {V_5}({x_t},t)} \end{array}$$

(18)

where

$$\begin{array}{*{20}{l}} {{V_1}({x_t},t) = {x^{\text{T}}}(t)Px(t)} \\ {{V_2}({x_t},t) = \int_{t - \tau (t)}^t {{x^{\text{T}}}(s){Q_1}x(s){\text{d}}s} + \int_{t - {\tau _m}}^t {{x^{\text{T}}}(s){Q_2}x(s){\text{d}}s} + } \\ {\quad \quad \quad \quad \int_{t - {\tau _M}}^t {{x^{\text{T}}}(s){Q_3}x(s){\text{d}}s} } \\ {{V_3}({x_t},t) = \int_{ - {\tau _M}}^0 {\int_{t + \theta }^t {{f^{\text{T}}}(s){R_1}f(s){\text{d}}s{\text{d}}\theta {\text{ + }}} } } \\ {\quad \quad \quad \quad \int_{ - {\tau _M}}^{ - {\tau _M}} {\int_{t + \theta }^t {{f^{\text{T}}}(s){R_2}f(s){\text{d}}s{\text{d}}\theta } } } \\ {{V_4}({x_t},t) = \int_{ - {\tau _M}}^0 {\int_{t + \theta }^t {{g^{\text{T}}}(s){R_3}g(s){\text{d}}s{\text{d}}\theta {\text{ + }}} } } \\ {\quad \quad \quad \quad \int_{ - {\tau _M}}^{ - {\tau _m}} {\int_{t + \theta }^t {{g^{\text{T}}}(s){R_{4g}}(s){\text{d}}s{\text{d}}\theta } } } \\ {{V_5}({x_t},t) = \int_{ - {\tau _M}}^{ - {\tau _m}} {\int_{t + \theta }^t {{x^{\text{T}}}(s)Zx(s){\text{d}}s\theta } } } \end{array}$$

where P, Q _s (s = 1,2,3), R _l (l = 1,2,3,4) and Z are symmetric positive definite matrices with appropriate dimensions.

By using Itô′s formula[34], we have

$${\text{dV(}}{x_t},t) = \mathcal{L}V({x_t},t){\text{d}}t + 2{x^{\text{T}}}(t)Pg(t){\text{d}}w(t)$$

(19)

where

$$\mathcal{L}V({x_t},t) = \sum\limits_{i = 1}^5 {\mathcal{L}{V_i}({x_t},t)} .$$

(20)

It is easy to know

$$\begin{array}{*{20}{l}} {\mathcal{L}{V_1}({x_t},t) = 2{x^{\text{T}}}(t)Pf(t) + {g^{\text{T}}}(t)Pg(t) = } \\ {\quad \quad \quad \quad \quad 2{x^{\text{T}}}P\left( {{A_K}x(t) + {A_d}x(t - \tau (t)) + } \right.} \\ {\quad \quad \quad \quad \quad {B_{{d_1}}}\int_{t - d(t)}^t {\left. {x(s){\text{d}}s} \right)} + {g^{\text{T}}}(t)Pg(t)} \\ {\mathcal{L}{V_2}({x_t},t) \leqslant {x^{\text{T}}}(t){Q_1}x(t) - (1 - \mu ){x^{\text{T}}}(t - \tau (t)){Q_1}x(t - \tau (t)) + } \\ {\quad \quad \quad \quad \quad {x^{\text{T}}}(t){Q_2}x(t) - {x^{\text{T}}}(t - {\tau _m}){Q_2}x(t - {\tau _m}) + } \\ {\quad \quad \quad \quad \quad {x^{\text{T}}}(t){Q_3}x(t) - {x^{\text{T}}}(t - {\tau _M}){Q_3}x(t - {\tau _M})} \\ {\mathcal{L}{V_3}({x_t},t) = {\tau _M}{f^{\text{T}}}(t){R_1}f(t) - \int_{t - {\tau _M}}^t {{f^{\text{T}}}(s){R_1}f(s){\text{d}}s} + } \\ {\quad \quad \quad \quad \quad ({\tau _M} - {\tau _m}){f^{\text{T}}}(t){R_2}f(t) - \int_{t - {\tau _M}}^{t - {\tau _m}} {{f^{\text{T}}}(s){R_2}f(s){\text{d}}s} } \\ {\mathcal{L}{V_4}({x_t},t) = {\tau _M}{g^{\text{T}}}(t){R_3}g(t) - \int_{t - {\tau _M}}^t {{g^{\text{T}}}(s){R_3}g(s){\text{d}}s + } } \\ {\quad \quad \quad \quad \quad ({\tau _M} - {\tau _m}){g^{\text{T}}}(t){R_4}g(t) - \int_{t - {\tau _M}}^{t - {\tau _m}} {{g^{\text{T}}}(s){R_4}g(s){\text{d}}s} } \\ {\mathcal{L}{V_5}({x_t},t) \leqslant {d_M}{x^{\text{T}}}(t)Zx(t) - \int_{t - d(t)}^t {{x^{\text{T}}}(s)Zx(s){\text{d}}s} .} \end{array}$$

From the Newton-Leibnitz formula, the following equalities are true for matrices N _lij , M _lij , S _lij (l = 1,2) with appropriate dimensions:

$$\begin{array}{*{20}{l}} {0 = 2\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}\left[ {{x^{\text{T}}}(t){N_{1ij}} + {x^{\text{T}}}(t - \tau (t)){N_{2ij}}} \right]} } \times } \\ {\quad \left[ {x(t) - x(t - \tau (t)) - \int_{t - r(t)}^t {f(s){\text{d}}s} - \int_{t - r(t)}^t {g(s){\text{d}}w(s)} } \right]} \end{array}$$

(21)

$$\begin{array}{*{20}{l}} {0 = 2\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}\left[ {{x^{\text{T}}}(t){M_{1ij}} + {x^{\text{T}}}(t - \tau (t)){M_{2ij}}} \right]} } \times } \\ {\left[ {x(t - {\tau _m}) - x(t - \tau (t)) - \int_{t - \tau (t)}^{t - {\tau _m}} {f(s){\text{d}}s} - \int_{t - \tau (t)}^{t - {\tau _m}} {g(s){\text{d}}w(s)} } \right]} \end{array}$$

(22)

$$\begin{array}{*{20}{l}} {0 = 2\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}\left[ {{x^{\text{T}}}(t){S_{1ij}} + {x^{\text{T}}}(t - \tau (t)){S_{2ij}}} \right]} } \times } \\ {\left[ {x(t - \tau (t)) - x(t - {\tau _M}) - \int_{t - {\tau _M}}^{t - \tau (t)} {f(s){\text{d}}s} - \int_{t - {\tau _M}}^{t - \tau (t)} {g(s){\text{d}}w(s)} } \right].} \end{array}$$

(23)

By Lemma 1 1), for matrices R_t ⩾ 0 (l=1,2,3,4), the following inequalities hold:

$$\begin{array}{*{20}{l}} { - 2\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){N_{ij}}} } \int_{t - \tau (t)}^t {f(s){\text{d}}s} \leqslant } \\ {{\tau _M}\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){N_{ij}}R_1^{ - 1}N_{ij}^{\text{T}}\xi (t)} } + \int_{t - \tau (t)}^t {{f^{\text{T}}}(s){R_1}f(s){\text{d}}s} } \end{array}$$

(24)

$$\begin{array}{*{20}{l}} { - 2\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){M_{ij}}} } \int_{t - \tau (t)}^{t - {\tau _m}} {f(s){\text{d}}s} \leqslant } \\ {\bar \tau \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){M_{ij}}R_2^{ - 1}M_{ij}^{\text{T}}\xi (t)} } + \int_{t - \tau (t)}^{t - {\tau _m}} {{f^{\text{T}}}(s){R_2}f(s){\text{d}}s} } \end{array}$$

(25)

$$\begin{array}{*{20}{l}} { - 2\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){S_{ij}}} } \int_{t - {\tau _M}}^{t - \tau (t)} {f(s){\text{d}}s} \leqslant } \\ {\bar \tau \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){S_{ij}}{{\left( {{R_1} + {R_2}} \right)}^{ - 1}}S_{ij}^{\text{T}}\xi (t) + } } } \\ {\int_{t - {\tau _M}}^{t - \tau (t)} {{f^{\text{T}}}(s)\left( {{R_1} + {R_2}} \right)f(s){\text{d}}s} } \end{array}$$

(26)

$$\begin{array}{*{20}{l}} { - 2\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){N_{ij}}} } \int_{t - \tau (t)}^t {g(s){\text{d}}w(s)} \leqslant } \\ {\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){N_{ij}}R_3^{ - 1}N_{ij}^{\text{T}}\xi (t)} } + } \\ {{{\left( {\int_{t - \tau (t)}^t {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}{R_3}\left( {\int_{t - \tau (t)}^t {g(s){\text{d}}w(s)} } \right)} \end{array}$$

(27)

$$\begin{array}{*{20}{l}} { - 2\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){M_{ij}}} } \int_{t - \tau (t)}^{t - {\tau _m}} {g(s){\text{d}}w(s) \leqslant } } \\ {\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){M_{ij}}R_4^{ - 1}M_{ij}^{\text{T}}\xi (t) + } } } \\ {{{\left( {\int_{t - \tau (t)}^{t - {\tau _m}} {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}{R_4}\left( {\int_{t - \tau (t)}^{t - {\tau _m}} {g(s){\text{d}}w(s)} } \right)} \end{array}$$

(28)

$$\begin{array}{*{20}{l}} { - 2\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){S_{ij}}} } \int_{t - {\tau _M}}^{t - \tau (t)} {g(s){\text{d}}w(s) \leqslant } } \\ {\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){S_{ij}}{{\left( {{R_3} + {R_4}} \right)}^{ - 1}}S_{ij}^{\text{T}}\xi (t) + } } } \\ {{{\left( {\int_{t - {\tau _M}}^{t - \tau (t)} {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}\left( {{R_3} + {R_4}} \right)\left( {\int_{t - {\tau _M}}^{t - \tau (t)} {g(s){\text{d}}w(s)} } \right)} \end{array}$$

(29)

where

Using Lemma 3, one can derive that

$$\begin{array}{*{20}{l}} {{f^{\text{T}}}(t)\left( {{\tau _M}{R_1} + \bar \tau {R_2}} \right)f(t) = \left[ {{A_K}x(t) + {A_d}x(t - \tau (t)) + } \right.} \\ {{B_{{d_1}}}{{\int_{t - d(t)}^t {\left. {x(s){\text{d}}s} \right]} }^{\text{T}}}\left( {{\tau _M}{R_1} + \bar \tau {R_2}} \right) \times } \\ {\left[ {{A_K}x(t) + {A_d}x(t - \tau (t)) + {B_{{d_1}}}\int_{t - d(t)}^t {x(s){\text{d}}s} } \right] = } \\ {\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {\sum\limits_{k = 1}^r {\sum\limits_{l = 1}^r {{h_i}{h_j}{h_k}{h_l}{\xi ^{\text{T}}}(t)\bar A_{ij}^{\text{T}}\left( {{\tau _M}{R_1} + \bar \tau {R_2}} \right){{\bar A}_{kl}}\xi (t) \leqslant } } } } } \\ {\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t)\bar A_{ij}^{\text{T}}\left( {{\tau _M}{R_1} + \bar \tau {R_2}} \right){{\tilde A}_{ij}}\xi (t)} } } \end{array}$$

(30)

where

$$\tilde A_{ij}^{\text{T}} = {\left[ {{A_i} + {B_{1i}}{K_j}\quad {A_{di}}\quad 0\quad 0\quad {B_{{d_{1i}}}}} \right]^{\text{T}}}.$$

Similarly

$$\begin{array}{*{20}{l}} {{g^{\text{T}}}(t)\left( {P + {\tau _M}{R_3} + \bar \tau {R_4}} \right)g(t) \leqslant } \\ {\quad \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t)\tilde C_{ij}^{\text{T}}\left( {P + {\tau _M}{R_3} + \bar \tau {R_4}} \right){{\tilde C}_{ij}}\xi (t)} } } \end{array}$$

(31)

where

Then, it follows from Lemma 2, that

$$\begin{array}{*{20}{l}} { - \int_{t - d(t)}^t {{x^{\text{T}}}(s)Zx(s){\text{d}}s \leqslant } } \\ {\quad \quad \quad - \frac{1}{{{d_M}}}{{\left( {\int_{t - d(t)}^t {x(s){\text{d}}s} } \right)}^{\text{T}}}Z\left( {\int_{t - d(t)}^t {x(s){\text{d}}s} } \right).} \end{array}$$

(32)

Combining (20) to (32), we get

$$\begin{array}{*{20}{l}} {\mathcal{L}V({x_t},t) \leqslant \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){\Xi ^{\iota j}}\xi (t) + } } } \\ {\quad \quad \quad \quad \quad {{\left( {\int_{t - \tau (t)}^t {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}{R_3}\left( {\int_{t - \tau (t)}^t {g(s){\text{d}}w(s)} } \right) + } \\ {\quad \quad \quad \quad \quad {{\left( {\int_{t - \tau (t)}^{t - {\tau _m}} {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}{R_4}\left( {\int_{t - \tau (t)}^{t - {\tau _m}} {g(s){\text{d}}w(s)} } \right) + } \\ {\quad \quad \quad \quad \quad {{\left( {\int_{t - {\tau _M}}^{t - \tau (t)} {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}\left( {{R_3} + {R_4}} \right) \times } \\ {\quad \quad \quad \quad \quad \left( {\int_{t - {\tau _M}}^{t - \tau (t)} {g(s){\text{d}}w(s)} } \right) - \int_{t - \tau (t)}^t {{g^{\text{T}}}(s){R_3}g(s){\text{d}}s} - } \\ {\quad \quad \quad \quad \quad \int_{t - \tau (t)}^{t - {\tau _m}} {{g^{\text{T}}}(s){R_4}g(s){\text{d}}s} - } \\ {\quad \quad \quad \quad \quad \int_{t - {\tau _M}}^{t - \tau (t)} {{g^{\text{T}}}(s)\left( {{R_3} + {R_4}} \right)g(s){\text{d}}s} } \end{array}$$

(33)

where

$$\begin{array}{*{20}{l}} {{\Xi ^{ij}} = \Psi _{11}^{ij} + \tilde C_{ij}^{\text{T}}P{{\tilde C}_{ij}} + {\tau _M}\tilde A_{ij}^{\text{T}}{R_1}{{\tilde A}_{ij}} + \bar \tau \tilde A_{ij}^{\text{T}}{R_2}{{\tilde A}_{ij}} + } \\ {\quad \quad {\tau _M}\tilde C_{ij}^{\text{T}}{R_3}{{\tilde C}_{ij}} + \bar \tau \tilde C_{ij}^{\text{T}}{R_4}{{\tilde C}_{ij}} + {\tau _M}{N_{ij}}R_1^{ - 1}N_{ij}^{\text{T}} + } \\ {\quad \quad \bar \tau {M_{ij}}R_2^{ - 1}M_{ij}^{\text{T}} + \bar \tau {S_{ij}}{{({R_1} + {R_2})}^{ - 1}}S_{ij}^{\text{T}} + } \\ {\quad \quad {N_{ij}}R_3^{ - 1}N_{ij}^{\text{T}} + {M_{ij}}R_4^{ - 1}M_{ij}^{\text{T}} + {S_{ij}}{{({R_3} + {R_4})}^{ - 1}}S_{ij}^T} \\ {\Psi _{11}^{ij} = \left[ {\begin{array}{*{20}{c}} {\psi _{11}^{ij}}&{\psi _{12}^{ij}}&{{M_{1ij}}}&{ - {S_{{\kern 1pt} 1ij}}}&{P{B_{{d_{1i}}}}} \\ * &{\psi _{22}^{ij}}&{{M_{2ij}}}&{ - {S_{2ij}}}&0 \\ * & * &{ - {Q_2}}&0&0 \\ * & * & * &{ - {Q_3}}&0 \\ *& * & * & * &{ - \frac{1}{{{d_M}}}Z} \end{array}} \right]} \end{array}$$

with

$$\begin{array}{*{20}{l}} {\psi _{11}^{ij} = {Q_1} + {Q_2} + {Q_3} + {N_{1ij}} + N_{1ij}^{\text{T}} + P({A_i} + {B_{1i}}{K_j}) + } \\ {\quad \quad {{\left( {{A_i} + {B_{1i}}{K_j}} \right)}^{\text{T}}}P + {d_M}Z} \\ {\psi _{12}^{ij} = {S_{1ij}} - {N_{1ij}} + N_{2ij}^{\text{T}} - {M_{1ij}} + P{A_{di}}} \\ {\psi _{22}^{ij} = - (1 - \mu ){Q_1} - {N_{2ij}} - N_{2ij}^{\text{T}} + {S_{2ij}} + } \\ {\quad \quad S_{2ij}^{\text{T}} - {M_{2ij}} - M_{2ij}^{\text{T}}.} \end{array}$$

It can be known that

$$\begin{array}{*{20}{l}} {\mathcal{E}\left\{ {{{\left( {\int_{t - \tau (t)}^t {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}{R_3}\left( {\int_{t - \tau (t)}^t {g(s){\text{d}}w(s)} } \right)} \right\} = } \\ {\mathcal{E}\left\{ {\int_{t - \tau (t)}^t {{g^{\text{T}}}(s){R_3}g(s){\text{d}}s} } \right\}} \end{array}$$

(34)

$$\begin{array}{*{20}{l}} {\mathcal{E}\left\{ {{{\left( {\int_{t - \tau (t)}^{t - {\tau _m}} {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}{R_4}\left( {\int_{t - \tau (t)}^{t - {\tau _m}} {g(s){\text{d}}w(s)} } \right)} \right\} = } \\ {\mathcal{E}\left\{ {\int_{t - \tau (t)}^{t - {\tau _m}} {{g^{\text{T}}}(s){R_4}g(s){\text{d}}s} } \right\}} \end{array}$$

(35)

and

$$\begin{array}{*{20}{l}} {\mathcal{E}\left\{ {{{\left( {\int_{t - {\tau _M}}^{t - \tau (t)} {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}\left( {{R_3} + {R_4}} \right)\left( {\int_{t - {\tau _M}}^{t - \tau (t)} {g(s){\text{d}}w(s)} } \right)} \right\} = } \\ {\mathcal{E}\left\{ {\int_{t - {\tau _M}}^{t - \tau (t)} {{g^{\text{T}}}(s)\left( {{R_3} + {R_4}} \right)g(s){\text{d}}s} } \right\}.} \end{array}$$

(36)

Taking the mathematical expectation on both sides of (33) and using (34)−(36), we get

$$\mathcal{E}\left\{ {\mathcal{L}V({x_t},t)} \right\} \leqslant \mathcal{E}\left\{ {\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\xi ^{\text{T}}}(t){\Xi ^{ij}}\xi (t)} } } \right\}.$$

(37)

If Ξⁱⁱ < 0 for 1 ⩽ i ⩽ r and Ξ^ij + Ξ^ji < 0 for any 1 ⩽ i < j ⩽ r, it yields $\varepsilon \left\{ {LV({x_t},t} \right\} < 0$. Employing the Schur complement, Ξⁱⁱ < 0 and Ξ ^ij + Ξ ^ji < 0 are equivalent to

$${\tilde \Xi ^{ij}} + {\tilde \Xi ^{ji}} < 0$$

(38)

for any 1 ⩽ i ⩽ j ⩽ r, where

$${\tilde \Xi ^{ij}} = \left[ {\begin{array}{*{20}{c}} {\Psi _{11}^{ij}}&{\Psi _{12}^{ij}}&{\Psi _{13}^{ij}} \\ * &{{\Psi _{22}}}&0 \\ * & * &{{\Psi _{33}}} \end{array}} \right]$$

with

$$\begin{array}{*{20}{l}} {\Psi _{12}^{ij} = \left[ {\tilde C_{ij}^{\text{T}}P\quad {\tau _M}\tilde A_{ij}^{\text{T}}\quad \bar \tau \tilde A_{ij}^{\text{T}}\quad {\tau _M}\tilde C_{ij}^{\text{T}}\quad \bar \tau \tilde C_{ij}^{\text{T}}} \right]} \\ {\Psi _{13}^{ij} = \left[ {{\tau _M}{N_{ij}}\;\;\bar \tau {M_{ij}}\;\;\bar \tau {S_{ij}}\;\;{N_{ij}}\;{M_{ij}}\;\;{S_{ij}}} \right]} \\ {{\Psi _{22}} = - {\text{diag}}\left\{ {P,\,\;{\tau _M}R_1^{ - 1},\;\;\bar \tau R_2^{ - 1},\;\;{\tau _M}R_3^{ - 1},\;\;\bar \tau R_4^{ - 1}} \right\}} \\ {{\Psi _{33}} = - {\text{diag}}\left\{ {{\tau _M}{R_1},\;\bar \tau {R_2},\;\;\bar \tau ({R_1} + {R_2}),\,\,{R_3},{R_4},\,\,({R_3} + {R_4})} \right\}} \end{array}$$

and $\Psi _{11}^{ij}$ is defined previously.

Pre- and post-multiply (38) by diag{X,X, X, X, X, X, I,I,I,I,X,X,X,X,X,X} and its transpose, respectively, and applying the change of variables such that $P = {X^{ - 1}},Z{Q_s}X = {\bar Q_s}(s = 1,2,3),XYZ = \bar Z,X{N_{lij}}X = {\bar N_{lij}},X{M_{lij}}X = {\bar M_{lij}},X{S_{lij}} = {\bar S_{lij}}(l = 1,2)$, then it gives

$${\widehat \Xi ^{ij}} + {\widehat \Xi ^{ji}} < 0$$

(39)

for 1 ⩽ i ⩽ j ⩽ r, where

and $\Xi _{11}^{ij},\Xi _{12}^{ij},\Xi _{13}^{ij}$ are defined in statement of Theorem 1. It follows from inequalities

$$X{R_l}X - 2X + R_l^{ - 1} = (X - R_l^{ - 1}){R_l}(X - R_l^{ - 1}) \geqslant 0$$

that

$$ - 2X + R_l^{ - 1} \geqslant - X{R_l}X,\;\;l = 1,2,3,4.$$

Let us assume that $R_l^{ - 1} = \tilde Rl(l = = 1,2,3,4)$. Then, LMI (39) is equivalent to the LMIs defined in (15) and (16). Therefore, by Definition 1 and [35], the closed-loop nominal stochastic fuzzy system (12) and (14) is stochastically stable with v(t) =0.

In the following part, using Lemma 1 2), we extend the above result to the uncertain stochastic fuzzy system (12) and (14) with v(t) = 0 to obtain a delay-dependent criterion as stated in the following theorem by means of the feasibility of LMIs.

Theorem 2. For given scalars τ _m , τ _M , d _M and μ, the time-varying delays satisfying (4), and the closed-loop uncertain stochastic fuzzy system (12) and (14) with v(t) = 0 is robustly stochastically stabilizable, if there exist matrices $X > 0,{\bar Q_s} > 0(s = 1,2,3),{\tilde R_l} > 0(l = 1,2,3,4),\tilde Z > 0,$, and real matrices ${\bar N_{lij}},{\bar M_{lij}}{\bar S_{lij}}{Y_j}(l = 1,2)$ of appropriate dimensions and scalars ε _{1 ij} > 0, ε _2ij > 0 (1 ⩽ i ⩽ j ⩽ r) such that the following LMIs hold:

$$\left[ {\begin{array}{*{20}{c}} {\Xi _{11}^{ii}}&{\Xi _{12}^{ii}}&{\Xi _{13}^{ii}}&{\Xi _{14}^{ii}} \\ * &{{\Xi _{22}}}&0&{\Xi _{24}^{ii}} \\ * & * &{{\Xi _{33}}}&0 \\ * & * & * &{\Xi _{44}^{ii}} \end{array}} \right] < 0,\quad 1 \leqslant i \leqslant r$$

(40)

$$\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {\Xi _{11}^{ij}}&{\Xi _{12}^{ij}}&{\Xi _{13}^{ij}}&{\Xi _{14}^{ij}} \\ * &{{\Xi _{22}}}&0&{\Xi _{24}^{ij}} \\ * & * &{{\Xi _{33}}}&0 \\ * & * & * &{\Xi _{44}^{ij}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\Xi _{11}^{ji}}&{\Xi _{12}^{ji}}&{\Xi _{13}^{ji}}&{\Xi _{14}^{ji}} \\ * &{{\Xi _{22}}}&0&{\Xi _{24}^{ji}} \\ * & * &{{\Xi _{33}}}&0 \\ * & * & * &{\Xi _{44}^{ji}} \end{array}} \right]} \\ {1 \leqslant i \leqslant j \leqslant r} \end{array}$$

(41)

where

$$\begin{array}{*{20}{l}} {\Xi _{14}^{ij} = \left[ {\begin{array}{*{20}{c}} {{\varepsilon _{1ij}}{E_i}}&0&{XH_{1i}^{\text{T}} + Y_j^{\text{T}}H_{3i}^{\text{T}}}&{XH_{4i}^{\text{T}} + Y_j^{\text{T}}H_{6i}^{\text{T}}} \\ 0&0&{XH_{2i}^{\text{T}}}&{XH_{5i}^{\text{T}}} \\ 0&0&0&0 \\ 0&0&0&0 \end{array}} \right]} \\ {\Xi _{24}^{ij} = \left[ {\begin{array}{*{20}{c}} 0&{{\varepsilon _{2ij}}{E_i}}&0&0 \\ {{\varepsilon _{1ij}}{\tau _M}{E_i}}&0&0&0 \\ {{\varepsilon _{1ij}}\bar \tau {E_i}}&0&0&0 \\ 0&{{\varepsilon _{2ij}}{\tau _M}{E_i}}&0&0 \\ 0&{{\varepsilon _{2ij}}\bar \tau {E_i}}&0&0 \end{array}} \right]} \\ {\Xi _{44}^{ij} = {\text{diag}}\left\{ { - {\varepsilon _{1ij}}I,\quad - {\varepsilon _{2ij}}I,\quad - {\varepsilon _{1ij}}I,\quad - {\varepsilon _{2ij}}I} \right\}} \end{array}$$

$\Xi _{11}^{ij},\Xi _{12}^{ij},\Xi _{13}^{ij},{\Xi _{22}}\,and\,{\Xi _{33}}$ are defined in Theorem 1. Moreover, the state feedback gain can be constructed as K _j = Y _j X ⁻¹ (j = 1, 2, ⋯,r).

Proof. For the sake of presentation and simplicity, denote

$$\begin{array}{*{20}{l}} {{\Omega _{1i}} = {{\left[ {E_i^T\quad 0\quad 0\quad 0\quad 0\quad 0\quad {\tau _M}E_i^{\text{T}}\quad \bar \tau E_i^{\text{T}}\quad {0_{1 \times 8}}} \right]}^{\text{T}}}} \\ {{\Omega _{2i}} = {{\left[ {{0_{1 \times 5}}\quad E_i^{\text{T}}\quad 0\quad 0\quad {\tau _M}E_i^{\text{T}}\quad \bar \tau E_i^T\quad {0_{1 \times 6}}} \right]}^{\text{T}}}} \\ {{\Omega _{3ij}} = \left[ {{H_{1i}}X + {H_{3i}}{Y_j}\quad {H_{2i}}X\quad {0_{1 \times 14}}} \right]} \\ {{\Omega _{4ij}} = \left[ {{H_{4i}}X + {H_{6i}}{Y_j}\quad {H_{5i}}X\quad {0_{1 \times 14}}} \right].} \end{array}$$

Replacing Ai, A _di , B _{1 i} , Ci, C _di , and B _2i in Theorem 1 with Ai + ∆Ai(t), A _di + ∆A _di(t), B _{1 i} + ∆B_1i (t), C _i + ∆C _i(t), C _di + ∆Cdi( t), and B _2i + ∆B_2i(t) respectively, we obtain the following corresponding uncertain stochastic fuzzy system (12) and (14) with v(t) = 0

$$\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {\Xi _{11}^{ij}}&{\Xi _{12}^{ij}}&{\Xi _{13}^{ij}} \\ * &{{\Xi _{22}}}&0 \\ * & * &{{\Xi _{33}}} \end{array}} \right] + {\Omega _{1i}}{F_i}(t){\Omega _{3ij}} + \Omega _{3ij}^{\text{T}}F_i^{\text{T}}(t)\Omega _{1i}^{\text{T}} + } \\ {{\Omega _{2i}}{F_i}(t){\Omega _{4ij}} + \Omega _{4ij}^{\text{T}}F_i^{\text{T}}(t)\Omega _{2i}^{\text{T}} < 0.} \end{array}$$

(42)

By Lemma 1 2), we have

$$\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {\Xi _{11}^{ij}}&{\Xi _{12}^{ij}}&{\Xi _{13}^{ij}} \\ * &{{\Xi _{22}}}&0 \\ * & * &{{\Xi _{33}}} \end{array}} \right] + {\varepsilon _{1ij}}{\Omega _{1i}}\Omega _{1i}^{\text{T}} + \varepsilon _{1ij}^{ - 1}\Omega _{3ij}^{\text{T}}{\Omega _{3ij}} + } \\ {{\varepsilon _{2ij}}{\Omega _{2i}}\Omega _{2i}^{\text{T}} + \varepsilon _{2ij}^{ - 1}\Omega _{4ij}^{\text{T}}{\Omega _{4ij}} < 0.} \end{array}$$

(43)

By Schur complement, we obtain (40) and (41). Then, by Theorem 1, the closed-loop uncertain stochastic fuzzy system (12) and (14) is robustly stochastically stable with v(t) =0.

In the case of u(t) = 0, v(t) = 0, B _{d 1z} = B _d2z = 0, ∆C _i(t) = 0 and ∆C _di(t) = 0, the system (7) is reduced to the following model

$$\begin{array}{*{20}{l}} {{\text{d}}x(t) = } \\ {\sum\limits_{i = 1}^r {{h_i}(\theta (t))\left\{ {\left[ {({A_i} + \Delta {A_i}(t))x(t) + ({A_{di}} + \Delta {A_{di}}(t)) \times } \right.} \right.} } \\ {x(t - \tau (t\left. {))} \right]{\text{d}}t + \left. {\left[ {{C_i}x(t) + {C_{di}}x(t - \tau (t))} \right]{\text{d}}w(t)} \right\}} \end{array}$$

(44)

$$x(t) = \phi (t),\quad \forall t \in [ - {\tau _M},0]$$

(45)

where the time-varying delay τ(t) satisfies

$$0 \leqslant \tau (t) \leqslant {\tau _M} < \infty,\quad \dot \tau (t) \leqslant \mu < \infty $$

(46)

with τ _M and μ are real constant scalars. In the system (44), the parameter uncertainties are assumed to be of the form

$$\begin{array}{*{20}{l}} {\Delta {A_i}(t) = {E_{1i}}{F_{1i}}(t){H_{1i}}} \\ {\Delta {A_{di}}(t) = {E_{2i}}{F_{2i}}(t){H_{2i}}} \end{array}$$

(47)

where E _1i , E _2i , H _1i and H _2i are known real constant matrices with appropriate dimensions, F _1i (t) and F _2i (t) are unknown real time-varying matrix function satisfying

$$\begin{array}{*{20}{l}} {F_{1i}^{\text{T}}(t){F_{1i}}(t) \leqslant I} \\ {F_{2i}^{\text{T}}(t){F_{2i}}(t) \leqslant I.} \end{array}$$

(48)

When there are no parameter uncertainties in the system (44), the following corollary can be obtained by using Theorem 1.

Corollary 1. For given scalars τ _M and μ, the time-varying delays satisfying (46), the nominal stochastic fuzzy system (44) is asymptotically stable in the mean square sense if there exist matrices P > 0, Q1 > 0, Q ₃ > 0, R1 > 0, R ₃ > 0, and real matrices N _li and S _li (l = 1, 2) of appropriate dimensions such that the following LMI holds:

$$\left[ {\begin{array}{*{20}{c}} {\Phi _{11}^i}&{\Phi _{12}^i}&{\Phi _{13}^i} \\ * &{{\Phi _{22}}}&0 \\ * & * &{{\Phi _{33}}} \end{array}} \right] < 0,\quad i = 1,2, \cdots,r$$

(49)

where

$$\begin{array}{*{20}{l}} {\Phi _{11}^i = \left[ {\begin{array}{*{20}{c}} {\phi _{11}^i}&{\phi _{12}^i}&{ - {S_{1i}}} \\ * &{\phi _{22}^i}&{ - {S_{2i}}} \\ * & * &{ - {Q_3}} \end{array}} \right]} \\ {\Phi _{12}^i = \left[ {\begin{array}{*{20}{c}} {C_i^{\text{T}}P}&{{\tau _M}A_i^{\text{T}}{R_1}}&{{\tau _M}C_i^{\text{T}}{R_3}} \\ {C_{di}^{\text{T}}P}&{{\tau _M}A_{di}^{\text{T}}{R_1}}&{{\tau _M}C_{di}^{\text{T}}{R_3}} \\ 0&0&0 \end{array}} \right]} \\ {\Phi _{13}^i = \left[ {\begin{array}{*{20}{c}} {{\tau _M}{N_{1i}}}&{{\tau _M}{S_{1i}}}&{{N_{1i}}}&{{S_{1i}}} \\ {{\tau _M}{N_{2i}}}&{{\tau _M}{S_{2i}}}&{{N_{1i}}}&{{S_{2i}}} \\ 0&0&0&0 \end{array}} \right]} \\ {{\Phi _{22}} = {\text{diag}}\left\{ { - P, - {\tau _M}{R_1},\,\, - {\tau _M}{R_3}} \right\}} \\ {{\Phi _{33}} = {\text{diag}}\left\{ { - {\tau _M}{R_1}, - {\tau _M}{R_1}, - {R_3}, - {R_3}} \right\}} \end{array}$$

with

$$\begin{array}{*{20}{l}} {\phi _{11}^i = P{A_i} + A_i^{\text{T}}P + {Q_1} + {Q_3} + {N_{1i}} + N_{1i}^{\text{T}}} \\ {\phi _{12}^i = P{A_{di}} - {N_{1i}} + N_{2i}^{\text{T}} + {S_{1i}}} \\ {\phi _{22}^i = - (1 - \mu ){Q_1} - {N_{2i}} - N_{2i}^{\text{T}} + {S_{2i}} + S_{2i}^{\text{T}}.} \end{array}$$

Remark 1. Choose the following Lyapunov-Krasovskii functional candidate as in (18) with Q ₂ = 0, R ₂ = 0, R ₄ = 0, Z = 0, replacing N _lij and S _lij (l = 1,2) with N _li and S _li (l = 1,2) in (21) and (23) respectively, and taking M _lij as zero in (22), the proof of Corollary 1 is easily obtained from Theorem 1.

For the system (44), the robust stability conditions can be obtained as stated in the following Corollary 2 by extending the proof of Corollary 1.

Corollary 2. For given scalars τ _M and μ, the time-varying delays satisfying (46), the uncertain stochastic fuzzy system (44) is robustly asymptotically stable in the mean square if there exist matrices P > 0, Q1 > 0, Q ₃ > 0, R1 > 0, R ₃ > 0, real matrices N _li and S _li (l = 1, 2) of appropriate dimensions, and scalars ε _{1 i} > 0 and ε _2i > 0 such that the following LMI holds:

$$\left[ {\begin{array}{*{20}{c}} {\Phi _{11}^i}&{\Phi _{12}^i}&{\Phi _{13}^i}&{\Phi _{14}^i} \\ * &{{\Phi _{22}}}&0&{\Phi _{24}^i} \\ * & * &{{\Phi _{33}}}&0 \\ * & * & * &{\Phi _{44}^i} \end{array}} \right] < 0,\quad i = 1,2, \cdots,r$$

(50)

where

$$\begin{array}{*{20}{l}} {\Phi _{11}^i = \left[ {\begin{array}{*{20}{c}} {\tilde \phi _{11}^i}&{\phi _{12}^i}&{ - {S_{1i}}} \\ * &{\tilde \phi _{22}^i}&{ - {S_{2i}}} \\ * & * &{ - {Q_3}} \end{array}} \right]} \\ {\Phi _{14}^i = \left[ {\begin{array}{*{20}{c}} {P{E_{1i}}}&{P{E_{2i}}} \\ 0&0 \\ 0&0 \end{array}} \right]} \\ {\Phi _{24}^i = \left[ {\begin{array}{*{20}{c}} 0&0 \\ {{\tau _M}{R_1}{E_{1i}}}&{{\tau _M}{R_1}{E_{2i}}} \\ 0&0 \end{array}} \right]} \\ {\Phi _{44}^i = \left[ {\begin{array}{*{20}{c}} { - {\varepsilon _{1i}}I}&0 \\ * &{ - {\varepsilon _{2i}}I} \end{array}} \right]} \end{array}$$

with

$$\begin{array}{*{20}{l}} {\tilde \phi _{11}^i = P{A_i} + A_i^{\text{T}}P + {Q_1} + {Q_3} + {N_{1i}} + N_{1i}^{\text{T}} + {\varepsilon _{1i}}H_{1i}^{\text{T}}{H_{1i}}} \\ {\tilde \phi _{22}^i = - (1 - \mu ){Q_1} - {N_{2i}} - N_{2i}^{\text{T}} + {S_{2i}} + S_{2i}^{\text{T}} + {\varepsilon _{2i}}H_{2i}^{\text{T}}{H_{2i}}.} \end{array}$$

Further, $\phi _{12}^i,\phi _{13}^i$, Φ ₂₂, Φ33 and $\phi _{12}^i$ are defined in Corollary 1.

4 Robust stochastic H _∞ control

In this section, a delay-dependent sufficient condition for the solvability of robust H _∞ control problem is proposed, and an LMI approach for designing a desired state feedback fuzzy controller is developed. The second main result is stated as follows.

Theorem 3. For a prescribed γ > 0, given scalars τ _m , τ _M , d _M and μ, the time-varying delays satisfying (4), there exists a fuzzy control law (11) such that the closed-loop uncertain stochastic fuzzy system (Σ₂) is robustly stochastically stabilizable with attenuation γ if there exist matrices X > 0, ${\bar Q_s} > 0$ (s = 1,2, 3), ${\tilde R_l} > 0$ (l = 1,2,3,4), $\bar Z > 0$, real matrices ${\bar N_{lij}},\;{\bar M_{lij}},{\bar S_{lij}}$, Yj (l = 1,2) of appropriate dimensions, and scalars ε _{1 ij} > 0, ε _2ij > 0 (1 ⩽ i ⩽ j ⩽ r) such that the following LMIs hold:

$$\left[ {\begin{array}{*{20}{c}} {\Upsilon _{11}^{ii}}&{\Upsilon _{12}^{ii}}&{\Upsilon _{13}^{ii}}&{\Upsilon _{14}^{ii}} \\ * &{{\Upsilon _{22}}}&0&{\Upsilon _{24}^{ii}} \\ * & * &{{\Upsilon _{33}}}&0 \\ * & * & * &{\Upsilon _{44}^{ii}} \end{array}} \right] < 0,\quad 1 \leqslant i \leqslant r$$

(51)

$$\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {\Upsilon _{11}^{ij}}&{\Upsilon _{12}^{ij}}&{\Upsilon _{13}^{ij}}&{\Upsilon _{14}^{ij}} \\ * &{{\Upsilon _{22}}}&0&{\Upsilon _{24}^{ij}} \\ * & * &{{\Upsilon _{33}}}&0 \\ * & * & * &{\Upsilon _{44}^{ij}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\Upsilon _{11}^{ji}}&{\Upsilon _{12}^{ji}}&{\Upsilon _{13}^{ji}}&{\Upsilon _{14}^{ji}} \\ * &{{\Upsilon _{22}}}&0&{\Upsilon _{24}^{ji}} \\ * & * &{{\Upsilon _{33}}}&0 \\ * & * & * &{\Upsilon _{44}^{ji}} \end{array}} \right] < 0,} \\ {1\; \leqslant \;i\; < j\; \leqslant \;r} \end{array}$$

(52)

where

with

Further, $\Xi _{14}^{ij}$, Ξ₂₂, $\Xi _{24}^{ij}$, Ξ₃₃, $\Xi _{44}^{ij},\;\phi _{11}^{ij},\;\phi _{12}^{ij},\;\phi _{22}^{ij}$ and $\bar \tau$ are defined as in Theorem 2. Moreover, the state feedback gain can be constructed as K _j = Y _j X ⁻¹ (j = 1, 2, ⋯,r).

Proof. For convenience, we set

$$\begin{array}{*{20}{l}} {f(t) = {A_K}x(t) + {A_d}x(t - \tau (t)) + {B_{{v_1}}}v(t) + {B_{{d_1}}}\int_{t - d(t)}^t {x(s){\text{d}}s} } \\ {g(t) = {C_K}x(t) + {C_d}x(t - \tau (t)) + {B_{{v_2}}}v(t) + {B_{{d_2}}}\int_{t - d(t)}^t {x(s)} {\text{d}}s.} \end{array}$$

By (51) and (52), it is easy to see that the LMIs in (40) and (41) hold. Therefore, it follows from Theorem 2 that the closed-loop system (Σ₂) is robustly stochastically stable. Now, we show that under the zero initial condition, system (Σ₂) satisfies $||z(t)||{\varepsilon _2} < \gamma ||v(t)|{|_2}$ for all non-zero v(t) ∈ L ₂[0,oo). Choose a Lyapunov-Krasovskii functional candidate as defined in (18) and utilizing Itˆô′s formula, we have

$$\begin{array}{*{20}{l}} {\mathcal{L}V({x_t},t) \leqslant \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\zeta ^{\text{T}}}(t){\Upsilon ^{ij}}\zeta (t) + } } } \\ {\quad {{\left( {\int_{t - \tau (t)}^t {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}{R_3}\left( {\int_{t - \tau (t)}^t {g(s){\text{d}}w(s)} } \right) + } \\ {\quad {{\left( {\int_{t - \tau (t)}^{t - {\tau _m}} {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}{R_4}\left( {\int_{t - \tau (t)}^{t - {\tau _m}} {g(s){\text{d}}w(s)} } \right) + } \\ {\quad {{\left( {\int_{t - {\tau _M}}^{t - \tau (t)} {g(s){\text{d}}w(s)} } \right)}^{\text{T}}}\left( {{R_3} + {R_4}} \right) \times } \\ {\quad \left( {\int_{t - {\tau _M}}^{t - \tau (t)} {g(s){\text{d}}w(s)} } \right) - \int_{t - \tau (t)}^t {g{{(s)}^{\text{T}}}{R_3}g(s){\text{d}}s} - } \\ {\quad \int_{t - \tau (t)}^{t - {\tau _m}} {g{{(s)}^{\text{T}}}{R_4}g(s){\text{d}}s} - } \\ {\quad \int_{t - {\tau _M}}^{t - \tau (t)} {g{{(s)}^{\text{T}}}({R_3} + {R_4})g(s){\text{d}}s} } \end{array}$$

(53)

where

with

It can be known that

$$\begin{array}{*{20}{l}} {{z^{\text{T}}}(t)z(t) = \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {\sum\limits_{k = 1}^r {\sum\limits_{l = 1}^r {{h_i}{h_j}{h_k}{h_l}{\zeta ^{\text{T}}}(t)\tilde D_{ij}^{\text{T}}{{\tilde D}_{kl}}\zeta (t) \leqslant } } } } } \\ {\quad \quad \quad \quad \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^r {{h_i}{h_j}{\zeta ^{\text{T}}}(t)\tilde D_{ij}^{\text{T}}{{\tilde D}_{ij}}\zeta (t)} } } \end{array}$$

(54)

where

$$\tilde D_{ij}^{\text{T}} = {\left[ {{D_i} + {B_{3i}}{K_j}\quad {D_{di}}\quad 0\quad 0\quad 0\quad 0} \right]^{\text{T}}}.$$

Now, we set

$$J(t) = \mathcal{E}\left\{ {\int_0^t {[{z^{\text{T}}}(s)z(s) - {\gamma ^2}{v^{\text{T}}}(s)v(s)]{\text{d}}s} } \right\}$$

(55)

where t > 0. Because V(φ(t),0) = 0 under the zero initial condition, i.e., φ(t) = 0 for t e [−τ, 0], then by Itˆo’s formula, it follows that

$$\begin{array}{*{20}{l}} {J(t) = } \\ {\quad \quad \mathcal{E}\left\{ {\int_{}^{} {[{z^{\text{T}}}(s)z(s) - {\gamma ^2}{v^{\text{T}}}(s)v(s) + \mathcal{L}V({x_s},s)]{\text{d}}s} } \right\} - } \\ {\quad \quad \mathcal{E}\left\{ {V({x_t},t)} \right\} \leqslant } \\ {\quad \quad \mathcal{E}\left\{ {\int_0^t {[{z^{\text{T}}}(s)z(s) - {\gamma ^2}{v^{\text{T}}}(s)v(s)} + \mathcal{L}V({x_s},s)]{\text{d}}s} \right\} \leqslant } \\ {\quad \quad \mathcal{E}\left\{ {\int_0^t {{\zeta ^{\text{T}}}(s){{\tilde \Upsilon }^{ij}}\zeta (s){\text{d}}s} } \right\}} \end{array}$$

(56)

where

$${\tilde \Upsilon ^{ij}} = {\Upsilon ^{ij}} + \tilde D_{ij}^{\text{T}}{\tilde D_{ij}} + {\text{diag}}\left\{ {0,\;0,\;0,\;0,\; - {\gamma ^2}I,\;0} \right\}.$$

Then, considering LMIs (51) and (52), following similar line as in the proof of Theorem 2, we have ${\tilde \Upsilon ^{ii}} < 0$ and ${\tilde \Upsilon ^{ij}} + {\tilde \Upsilon ^{ji}} < 0$, which imply that J(t) < 0 for t > 0. Therefore, we have $||z(t)||{\varepsilon _2} < \gamma ||v(t)|{|_2}$.

Remark 2. We mention that Theorem 3 provides a delay-dependent H _∞ control problem for a class of uncertain stochastic fuzzy systems with discrete interval and distributed time-varying delays. Note that, by Theorem 3, the problems of finding the maximum allowable upper bound of the delays are τ _M , d _M , for given γ, μ and τ _m or the smallest γ for given τ _m , τ _M , μ and d _M can be easily solved. For instance, the smallest γ for given τ _m , τ _M , μ and d _M obtainable from Theorem 3 can be determined by solving the following convex optimization problem:

$$\begin{array}{*{20}{l}} {\min \,\,\,\chi } \\ {s.t\,\,X > 0,{{\bar Q}_s} > 0(s = 1,2,3),} \\ {{{\tilde R}_l} > 0(l = 1,2,3,4),\bar Z > 0,} \\ {{\varepsilon _{1ij}} > 0,{\varepsilon _{2ij}} > 0(1 \leqslant i \leqslant j \leqslant r)} \\ {{\text{and}}\,\,{\text{LMIs}}\,\,\,\,{\text{(51)}} - (52)\,\,\,\,with\,\,\chi = {\gamma ^2}.} \end{array}$$

Remark 3. By setting ${B_{{d_1}}} = 0,\;\;{B_{{d_2}}} = 0$ in Theorems 2 and 3, the delay-dependent robust stabilization and H _∞, control for uncertain stochastic fuzzy system with interval time-varying delay criteria can be obtained, corresponding proof is similar to Theorems 2 and 3 and hence omitted.

In the case when there is no parameter uncertainties in the system (Σ₂), Theorem 3 is specialized as follows.

Corollary 3. For a prescribed γ > 0, given scalars τ _m , τ _M , d _M and μ, the time-varying delays satisfying (4), there exists a fuzzy control law (11) such that the closed-loop stochastic fuzzy system (Σ₂) with ∆A _i (t) = ∆A _di(t) = ∆B _{1 i} (t) = ∆Ci(t) = ∆C _di(t) = ∆B _2i(t) = 0 is stochastically stabilizable with a disturbance attenuation γ, if there exist matrices $X > 0,{\bar Q_s} > 0(s = 1,2,3),{\tilde R_l} > 0(l = 1,2,3,4),\tilde Z > 0,$ and real matrices ${\bar N_{lij}},{\bar M_{lij}},{\bar S_{lij}},{Y_j}(l = 1,2)$ of appropriate dimensions such that the following LMIs hold:

$$\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{l}} {\Upsilon _{11}^{ii}}&{\Upsilon _{12}^{ii}}&{\Upsilon _{13}^{ii}} \\ *&{{\Upsilon _{22}}}&0 \\ *&*&{{\Upsilon _{33}}} \end{array}} \right] < 0,\,\,\,\,1 \leqslant i \leqslant r} \\ {\left[ {\begin{array}{*{20}{l}} {\Upsilon _{11}^{ii}}&{\Upsilon _{12}^{ii}}&{\Upsilon _{13}^{ii}} \\ *&{{\Upsilon _{22}}}&0 \\ *&*&{{\Upsilon _{33}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {\Upsilon _{11}^{ii}}&{\Upsilon _{12}^{ii}}&{\Upsilon _{13}^{ii}} \\ *&{{\Upsilon _{22}}}&0 \\ *&*&{{\Upsilon _{33}}} \end{array}} \right] < 0,} \end{array}$$

(57)

(58)

where $\Upsilon _{11}^{ij},\Upsilon _{12}^{ij},\Upsilon _{13}^{ij}$ Υ₂₂ and Υ₃₃ are defined in Theorem 3. Moreover, the state feedback gain can be constructed as K _j = Y _jX^{- 1} (j = 1, 2, • • • ,r).

5 Numerical examples

In this section, we provide illustrative examples to demonstrate the effectiveness of the method proposed in the previous section.

Example 1. Consider the uncertain stochastic T-S fuzzy system (44) with parameters as follows

$$\begin{array}{*{20}{c}} {{A_1} = \left[ {\begin{array}{*{20}{c}} { - 2.3}&0 \\ 0&{ - 5.7} \end{array}} \right],{A_2} = \left[ {\begin{array}{*{20}{c}} { - 10}&{0.1} \\ {0.1}&{ - 12.9} \end{array}} \right],} \\ {{A_{d1}} = \left[ {\begin{array}{*{20}{c}} {0.5}&{ - 0.1} \\ {0.7}&{ - 0.6} \end{array}} \right],{A_{d2}}\left[ {\begin{array}{*{20}{c}} {0.2}&{0.5} \\ 2&{0.7} \end{array}} \right],} \\ {{C_1} = \left[ {\begin{array}{*{20}{c}} { - 0.2}&0 \\ { - 0.1}&{0.1} \end{array}} \right],{C_2}\left[ {\begin{array}{*{20}{c}} { - 1}&{0.7} \\ {0.3}&{0.5} \end{array}} \right],} \\ {{C_{d1}} = \left[ {\begin{array}{*{20}{c}} {0.5}&{0.3} \\ {0.2}&{0.4} \end{array}} \right],{C_{d2}} = \left[ {\begin{array}{*{20}{c}} 2&{0.2} \\ { - 0.1}&{0.1} \end{array}} \right],} \\ {{E_{1i}} = 0.1I,{E_{2i}} = 0.2I,{H_{li}} = 0.1I,} \\ {{F_{li}}(t) = diag\left\{ {sin(t),cos(t)} \right\}(l = 1,2,i = 1,2).} \end{array} $$

For this example, according to Corollary 2, system (44) is robustly asymptotically stable in the mean square. The maximal allowable upper bound of the time delay τ _M for various μ are shown in Table 1. Obviously, our result is less conservative than the method in [27]. Assuming τM = 0.1328 and μ = 0.3, solving LMI (50) in Corollary 2 by the Matlab LMI toolbox, we have the following feasible solutions:

$$\begin{array}{*{20}{c}} {P = \left[ {\begin{array}{*{20}{c}} {4.5595}&{07706} \\ {0.7706}&{6.3112} \end{array}} \right]} \\ {{Q_1} = \left[ {\begin{array}{*{20}{c}} {19.7757}&{4.0450} \\ {4.0450}&{680995} \end{array}} \right]} \\ {{Q_3} = \left[ {\begin{array}{*{20}{c}} {2.4992}&{ - 0.1721} \\ { - 0.1421}&{0.3803} \end{array}} \right]} \\ {{R_1} = \left[ {\begin{array}{*{20}{c}} {4.7269}&{ - 0.3315} \\ { - 0.3315}&{0.0349} \end{array}} \right]} \\ {{R_3} = \left[ {\begin{array}{*{20}{c}} {19.9805}&{ - 1.3832} \\ { - 1.3832}&{0.4812} \end{array}} \right].} \end{array} $$

The time varying delay is assumed as τ(t) = 0.13 + 0.0028 sin(t). For a membership function ${h_1}({x_1}(t)) = \frac{1}{{1 + {e^{({x_1}(t) + 0.5)}}}},{h_2}({x_1}(t)) = 1 - {h_1}({x_1}(t))$, and an initial function φ(t) = [−3, 3]^T, the simulation results of the state response of the system are plotted in Fig. 1.

Fig. 1

State response of the system

Table 1 Maximal allowable delay τ _M for various μ

Example 2. Consider the uncertain stochastic T-S fuzzy system (Σ₂) with parameters as

$$\begin{array}{*{20}{c}} {{A_1} = \left[ {\begin{array}{*{20}{c}} { - 2}&1 \\ {0.1}&{ - 3} \end{array}} \right],\,{A_2} = \left[ {\begin{array}{*{20}{c}} { - 1.5}&0 \\ 0&{ - 2} \end{array}} \right],} \\ {{A_{d1}} = \left[ {\begin{array}{*{20}{c}} {0.1}&0 \\ { - 0.1}&{ - 0.3} \end{array}} \right],\,{A_{d2}} = \left[ {\begin{array}{*{20}{c}} {0.5}&0 \\ {0.4}&{ - 0.3} \end{array}} \right],} \\ {{B_{11}} = \left[ {\begin{array}{*{20}{c}} { - 0.2}&0 \\ { - 0.1}&{0.1} \end{array}} \right],\,{B_{12}} = \left[ {\begin{array}{*{20}{c}} {0.2}&0 \\ 0&{ - 0.2} \end{array}} \right],} \\ {{B_{v11}} = \left[ {\begin{array}{*{20}{c}} { - 0.4}&{0.1} \\ 0&{ - 0.8} \end{array}} \right],\,B{v_{12}} = \left[ {\begin{array}{*{20}{c}} { - 0.1}&0 \\ { - 0.5}&{0.2} \end{array}} \right],} \\ {{B_{d11}} = \left[ {\begin{array}{*{20}{c}} { - 0.2}&0 \\ 0&{0.2} \end{array}} \right],{B_{d12}} = \left[ {\begin{array}{*{20}{c}} 0&{0.5} \\ {0.2}&{ - 0.3} \end{array}} \right],} \\ {{C_1} = \left[ {\begin{array}{*{20}{c}} { - 0.2}&0 \\ 0&{0.2} \end{array}} \right],\,{C_2} = \left[ {\begin{array}{*{20}{c}} { - 0.2}&0 \\ 0&{ - 0.2} \end{array}} \right],} \\ {{C_{d1}} = \left[ {\begin{array}{*{20}{c}} { - 0.1}&0 \\ 0&{ - 0.1} \end{array}} \right],\,{C_{d2}} = \left[ {\begin{array}{*{20}{c}} { - 0.1}&{0.5} \\ {0.2}&{ - 0.5} \end{array}} \right],} \\ {{B_{21}} = \left[ {\begin{array}{*{20}{c}} { - 0.2}&0 \\ {0.1}&{0.1} \end{array}} \right],\,{B_{22}} = \left[ {\begin{array}{*{20}{c}} {0.3}&0 \\ 0&{ - 0.6} \end{array}} \right],} \\ {{B_{v21}} = \left[ {\begin{array}{*{20}{c}} {0.2}&{0.1} \\ 0&{ - 0.2} \end{array}} \right],\,{B_{v22}} = \left[ {\begin{array}{*{20}{c}} { - 0.2}&{0.1} \\ {0.2}&{0.1} \end{array}} \right],} \\ {{B_{d21}} = \left[ {\begin{array}{*{20}{c}} {0.3}&{0.2} \\ 0&{ - 0.3} \end{array}} \right],\,{B_{d22}} = \left[ {\begin{array}{*{20}{c}} { - 0.4}&{0.3} \\ {0.2}&{0.3} \end{array}} \right],} \\ {{D_1} = \left[ {\begin{array}{*{20}{c}} { - 0.03}&0 \\ 0&{0.03} \end{array}} \right],\,{D_2} = \left[ {\begin{array}{*{20}{c}} { - 0.03}&0 \\ 0&{0.03} \end{array}} \right],} \\ {{D_{d1}} = \left[ {\begin{array}{*{20}{c}} { - 0.03}&0 \\ 0&{0.003} \end{array}} \right],\,{D_{d2}} = \left[ {\begin{array}{*{20}{c}} { - 0.13}&{0.2} \\ 0&{0.4} \end{array}} \right],} \\ {{B_{31}} = \left[ {\begin{array}{*{20}{c}} {0.1}&{ - 0.2} \\ { - 0.4}&{0.2} \end{array}} \right],\,{B_{32}} = \left[ {\begin{array}{*{20}{c}} { - 0.3}&{0.3} \\ {0.2}&{ - 0.2} \end{array}} \right],} \\ {{E_1} = \left[ {\begin{array}{*{20}{c}} {0.03}&0 \\ 0&{ - 0.03} \end{array}} \right],\,{E_2} = \left[ {\begin{array}{*{20}{c}} {0.03}&0 \\ 0&{ - 0.03} \end{array}} \right],} \\ {{H_{11}} = \left[ {\begin{array}{*{20}{c}} { - 0.15}&{0.2} \\ 0&{0.3} \end{array}} \right],\,{H_{12}} = \left[ {\begin{array}{*{20}{c}} { - 0.15}&{0.2} \\ 0&{0.3} \end{array}} \right],} \\ {{H_{21}} = \left[ {\begin{array}{*{20}{c}} {0.05}&{ - 0.35} \\ {0.7}&{0.45} \end{array}} \right],\,{H_{22}} = \left[ {\begin{array}{*{20}{c}} {0.05}&{ - 0.5} \\ {0.7}&{0.45} \end{array}} \right],} \\ {{H_{31}} = \left[ {\begin{array}{*{20}{c}} { - 0.11}&{0.2} \\ 0&{0.01} \end{array}} \right],\,{H_{32}} = \left[ {\begin{array}{*{20}{c}} { - 0.1}&{0.1} \\ 0&{0.15} \end{array}} \right],} \\ {{H_{41}} = \left[ {\begin{array}{*{20}{c}} { - 0.15}&{0.2} \\ 0&{0.3} \end{array}} \right],{H_{42}} = \left[ {\begin{array}{*{20}{c}} { - 0.15}&{0.2} \\ 0&{0.3} \end{array}} \right],} \\ {{H_{51}} = \left[ {\begin{array}{*{20}{c}} {0.05}&{ - 0.35} \\ {0.7}&{0.45} \end{array}} \right],\,{H_{52}} = \left[ {\begin{array}{*{20}{c}} { - 0.1}&{0.2} \\ 0&{0.01} \end{array}} \right]} \\ \begin{gathered} {H_{61}} = \left[ {\begin{array}{*{20}{c}} { - 0.21}&{0.3} \\ 0&{0.31} \end{array}} \right],\,{H_{62}} = \left[ {\begin{array}{*{20}{c}} { - 0.05}&{0.35} \\ {0.7}&{0.45} \end{array}} \right], \hfill \\ {F_1}(t) = {F_2}(t) = diag\left\{ {sin(t),cos(t)} \right\}. \hfill \\ \end{gathered} \end{array} $$

In this example, our aim is to design a state feedback fuzzy controller such that, for all admissible uncertainties, the closed-loop system is robustly stochastically stable with disturbance attenuation γ = 0.2. The maximum allowable upper bounds of the time delay τ (for τ _M = d _M) are obtained for different τ _m and various μ from Theorem 3 which are shown in the Table 2. For τ _m = 0.1, μ = 0.2, the time delay τ _M = 0.3432, and d _M = 0.3432, solving the LMIs (51) and (52) through Matlab LMI control toolbox, the feasible solutions are given by:

$$\begin{array}{*{20}{l}} {X = \left[ {\begin{array}{*{20}{c}} {29.4343}&{1.7272} \\ {1.7272}&{7.8654} \end{array}} \right],\;\;{{\bar Q}_1} = \left[ {\begin{array}{*{20}{c}} {22.4363}&{ - 8.5634} \\ { - 8.5634}&{16.7466} \end{array}} \right],} \\ {{{\bar Q}_2} = \left[ {\begin{array}{*{20}{c}} {0.0678}&{0.0114} \\ {0.0114}&{0.0027} \end{array}} \right],\;\;{{\bar Q}_3} = \left[ {\begin{array}{*{20}{c}} {2.0366}&{0.0603} \\ {0.0603}&{0.5159} \end{array}} \right],} \\ {{{\tilde R}_1} = \left[ {\begin{array}{*{20}{c}} {50.0733}&{4.1912} \\ {4.1912}&{12.9957} \end{array}} \right],\;\;{{\tilde R}_2} = \left[ {\begin{array}{*{20}{c}} {58.7164}&{3.4330} \\ {3.4330}&{15.7265} \end{array}} \right],} \\ {{{\tilde R}_3} = \left[ {\begin{array}{*{20}{c}} {29.2726}&{1.0348} \\ {1.0348}&{8.4426} \end{array}} \right],\;\;{{\tilde R}_4} = \left[ {\begin{array}{*{20}{c}} {55.3893}&{2.6179} \\ {2.6179}&{15.5254} \end{array}} \right],} \\ {\bar Z = \left[ {\begin{array}{*{20}{c}} {80.7522}&{11.6452} \\ {11.6452}&{5.4140} \end{array}} \right].} \end{array}$$

Table 2 Maximal allowable delay of τ with given τ _m and for various μ

By Theorem 3, we can obtain the desired state-feedback fuzzy controller as

$$\begin{array}{*{20}{l}} {{K_1} = \left[ {\begin{array}{*{20}{c}} { - 0.3980}&{ - 0.9984} \\ { - 0.0288}&{ - 0.3490} \end{array}} \right]} \\ {{K_2} = \left[ {\begin{array}{*{20}{c}} { - 0.4021}&{0.5118} \\ { - 0.2922}&{ - 0.8733} \end{array}} \right].} \end{array}$$

Define the membership functions as ${h_1}({x_1}(t)) = \frac{{1 - \sin ({x_1}(t))}}{2}\,and\,{h_2}({x_1}(t)) = \frac{{1 + \sin ({x_1}(t))}}{2}$. The time-varying delays are assumed as τ(t) = 0.34 + 0.0032 sin(t) and d(t) = 0.34 + 0.0032sin(t), with an initial condition φ(t) = [−3, 2.5]^T. The disturbance input is assumed to be ${v_1}(t) = \frac{1}{{0.2 + {t^2}}}$ and ${v_2}(t) = \frac{1}{{1 + {t^2}}}$. Fig. 2 shows the state response of the closed-loop system. Figs. 3 and 4 show the graphical representation of the control input and controlled output respectively. From the above, it can be seen that the designed H _∞ controller satisfies the specified requirements.

Fig. 2

State response of the closed-loop system

Fig.3

Control input

Fig. 4

Controlled output

6 Conclusions

In this paper, some sufficient conditions have been derived for the solvability of problems of delay-dependent robust stabilization and H _∞ controller design for uncertain stochastic T-S fuzzy systems with discrete interval and distributed time-varying delays. These conditions are expressed in terms of LMIs, which can be easily tested by using Matlab control toolbox. It has been shown that a desired state feedback controller can be constructed when the LMIs are feasible. Finally, two numerical examples have been given to illustrate the effectiveness of the developed techniques.