The shuffling of mathematics problems improves learning

Abstract

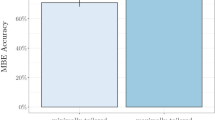
In most mathematics textbooks, each set of practice problems is comprised almost entirely of problems corresponding to the immediately previous lesson. By contrast, in a small number of textbooks, the practice problems are systematically shuffled so that each practice set includes a variety of problems drawn from many previous lessons. The standard and shuffled formats differ in two critical ways, and each was the focus of an experiment reported here. In Experiment 1, college students learned to solve one kind of problem, and subsequent practice problems were either massed in a single session (as in the standard format) or spaced across multiple sessions (as in the shuffled format). When tested 1 week later, performance was much greater after spaced practice. In Experiment 2, students first learned to solve multiple types of problems, and practice problems were either blocked by type (as in the standard format) or randomly mixed (as in the shuffled format). When tested 1 week later, performance was vastly superior after mixed practice. Thus, the results of both experiments favored the shuffled format over the standard format.

Appendix

Permutations

If a sequence of items includes n items and k unique items, the number of permutations of the sequence equals n!/(n ₁! n ₂! ... n _k !), where n _i equals the number of occurrences of item i. Thus, for the sequence abbccc, the number of permutations equals 6!/(1! 2! 3!), or 60.

Wedge

A wedge is obtained by the truncation of a cylinder by two planes if exactly one of the planes is perpendicular to the cylinder and if the linear intersection of the two planes includes exactly one point on the cylindrical surface. If the latter constraint is relaxed so that the linear intersection may intersect the cylindrical surface at either one or two points, the solid is a cylindrical wedge. This is the shape shown in Fig. 3a. We chose the term wedge for this specific case because we do not know of an accepted term. Its volume equals r ² hπ/2, where r equals the radius of its circular base and h equals its maximum height

Spherical cone

A spherical cone is obtained by removing a conical section of a sphere provided that the vertex of the cone is at the sphere’s center and the base of the cone is on the sphere’s surface, as shown in Fig. 3a. Its volume is given by 2r ² hπ/3, where r equals the radius of the sphere and h equals the difference of the sphere’s radius and the cone’s height

Spheroid

A spheroid is obtained by the rotation of an ellipse about one of its axes. The spheroid in Fig. 3a, for example, is rotated about its vertical axis. Its volume equals 4r ² hπ/3, where r equals the “equatorial radius” and h equals the “polar radius.” The values of r and h also equal one-half of the major and minor lengths of the rotated ellipse.

Half cone

A half cone is a cone truncated by a plane parallel to its base so that the truncation reduces the cone’s height by half. Its volume equals 7r ² hπ/3, where r equals the radius of the upper base and h equals the height of the truncated cone, as illustrated in Fig. 3a. The half cone is a specific instance of a conical frustum, which has a height equal to any proportion of the cone’s height. We chose the term “half cone” to describe a conical frustrum with height equal to exactly half of the cone’s height.