Evaluating hospital readmission rates in dialysis facilities; adjusting for hospital effects

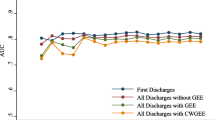
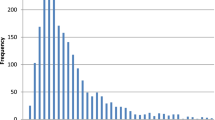
Abstract

Motivated by the national evaluation of readmission rates among kidney dialysis facilities in the United States, we evaluate the impact of including discharging hospitals on the estimation of facility-level standardized readmission ratios (SRRs). The estimation of SRRs consists of two steps. First, we model the dependence of readmission events on facilities and patient-level characteristics, with or without an adjustment for discharging hospitals. Second, using results from the models, standardization is achieved by computing the ratio of the number of observed events to the number of expected events assuming a population norm and given the case-mix in that facility. A challenging aspect of our motivating example is that the number of parameters is very large and estimation of high-dimensional parameters is troublesome. To solve this problem, we propose a structured Newton-Raphson algorithm for a logistic fixed effects model and an approximate EM algorithm for the logistic mixed effects model. We consider a re-sampling and simulation technique to obtain p-values for the proposed measures. Finally, our method of identifying outlier facilities involves converting the observed p-values to Z-statistics and using the empirical null distribution, which accounts for overdispersion in the data. The finite-sample properties of proposed measures are examined through simulation studies. The methods developed are applied to national dialysis data. It is our great pleasure to present this paper in honor of Ross Prentice, who has been instrumental in the development of modern methods of modeling and analyzing life history and failure time data, and in the inventive applications of these methods to important national data problem.

Appendices

Appendices

1.1 Appendix 1: model fitting algorithm of the fixed-effects model

• (i) Set initial values for ${\varvec{\beta }^{(0)}}$ and $\gamma _i^{(0)}$ and $\ell =0$

• (ii) For fixed $\varvec{\beta }={\varvec{\beta }}^{(\ell )}$, update $\gamma _i$ using a one-step Newton-Raphson iteration as

  $$\begin{aligned} \gamma _i^{(\ell +1)} = \gamma _i^{(\ell )} + {I_{i}^{(\ell )}}^{-1} U_{i}^{(\ell )}, \end{aligned}$$

  where

  $$\begin{aligned} U_{i}^{(\ell )}&:= \frac{\partial }{\partial \gamma _i} \log L(\gamma _i,\varvec{\beta }^{(\ell )})\bigg |_{\gamma _i = \gamma _i^{(\ell )}} =\sum _{k=1}^{n_i} [ Y_{ik} - p_{ik}^{(\ell )}], \\ I_{i}^{(\ell )}&:= -\frac{\partial ^2}{\partial \gamma _i^2} \log L(\gamma _i,\varvec{\beta }^{(\ell )})\bigg |_{\gamma _i = \gamma _i^{(\ell )}}=\sum _{k=1}^{n_i} p_{ik}^{(\ell )} [1-p_{ik}^{(\ell )}], \end{aligned}$$

  with

  $$\begin{aligned} p_{ik}^{(\ell )} := p_{ik}(\gamma _i^{(\ell )},\varvec{\beta }^{(\ell )}). \end{aligned}$$

• (iii) Now update $\varvec{\beta }$ by carrying out one step of the Newton-Raphson iteration

  $$\begin{aligned} \varvec{\beta }^{(\ell +1)} := \varvec{\beta }^{(\ell )} + {I_{\varvec{\beta }}^{(\ell )}}^{-1} U_{\varvec{\beta }}^{(\ell )}, \end{aligned}$$

  where

  $$\begin{aligned} U_{\varvec{\beta }}^{(\ell )}&:= \frac{\partial }{\partial \varvec{\beta }} \log L(\gamma ^{(\ell +1)},\varvec{\beta })\bigg |_{\varvec{\beta }= \varvec{\beta }^{(\ell )}} \\&= \sum _{i=1}^{F} \sum _{k=1}^{n_i} \{Y_{ik} - p_{ik}^{(\ell )*} \} \mathbf Z _{ik}, \\ I_{\varvec{\beta }}^{(\ell )}&:= -\frac{\partial ^2}{\partial \beta \partial \beta ^T} \log L(\gamma ^{(\ell +1)},\varvec{\beta })\bigg |_{\varvec{\beta }= \varvec{\beta }^{(\ell )}} \\&= \sum _{i=1}^{F} \sum _{k=1}^{n_i} p_{ij}^{(\ell )*} \{1-p_{ik}^{(\ell )*}\} \mathbf Z _{ik}\mathbf Z _{ik}^T, \end{aligned}$$

  with

  $$\begin{aligned} p_{ik}^{(\ell )*} := p_{ik}(\gamma _i^{(\ell +1)},\varvec{\beta }^{(\ell )}). \end{aligned}$$

• (iv) If $\max \Vert p_{ik}^{(\ell +1)*} - p_{ik}^{(\ell )*} \Vert > 10^{-6}$, set $\ell =\ell +1$ and go back to step (i).

1.2 Appendix 2: Newton-Raphson algorithm for the mixed-effects model

The $\gamma _i$ is updated as

$$\begin{aligned} \gamma _i^{(\ell +1)} = \gamma _i^{(\ell )} {-\mathcal{L ^{\prime \prime }_i}^{(\ell )}}^{-1} \mathcal{L ^{\prime }_i}^{(\ell )}, \end{aligned}$$

where

$$\begin{aligned} \mathcal{L ^{\prime }_i}^{(\ell )}&:= \frac{\partial }{\partial \gamma _i} \mathcal L _i^{(\ell )} \bigg |_{\gamma _i = \gamma _i^{(\ell )}} =\sum _{j=1}^{H} \sum _{k=1}^{n_{ij}} \{ Y_{ijk} - p^{(\ell )}_{ijk} +\frac{\nu ^{(\ell )}_{j0}}{2} ({p^{(\ell )}_{ijk}}{{q^{(\ell )}_{ijk}}}^2-{{p^{(\ell )}_{ijk}}}^2{q^{(\ell )}_{ijk}})\}\\&= \sum _{j=1}^{H} \sum _{k=1}^{n_{ij}} a_{ijk}^{(\ell )}, \\ -\mathcal{L ^{\prime \prime }_j}^{(\ell )}&:= -\frac{\partial ^2}{ \partial \gamma _i^2} \mathcal L _i^{(\ell )} \bigg |_{\gamma _i = \gamma _i^{(\ell )}} =\sum _{j=1}^{H} \sum _{k=1}^{n_{ij}}\{p^{(\ell )}_{ijk}q^{(\ell )}_{ijk}+ \frac{\nu ^{(\ell )}_{j0}}{2}p^{(\ell )}_{ijk}q^{(\ell )}_{ijk} ({q^{(\ell )}_{ijk}}^2+{p^{(\ell )}_{ijk}}^2-4 p^{(\ell )}_ {ijk}q^{(\ell )}_{ijk})\}\\&= \sum _{j=1}^{H} \sum _{k=1}^{n_{ij}} b_{ijk}^{(\ell )} . \end{aligned}$$

Similarly, $\varvec{\beta }$ is updated as

$$\begin{aligned} \varvec{\beta }^{(\ell +1)} = \varvec{\beta }^{(\ell )} {-\mathcal{L ^{\prime \prime }_{\varvec{\beta }} } ^{(\ell )}}^{-1} \mathcal{L ^{\prime }_{\varvec{\beta }}}^{(\ell )}, \end{aligned}$$

where

$$\begin{aligned} \mathcal{L ^{\prime }_{\varvec{\beta }}}^{(\ell )}&:= \frac{\partial }{\partial \varvec{\beta }} \sum _{i=1}^F \mathcal L _i^{(\ell )}\bigg |_{\varvec{\beta }= \varvec{\beta }^{(\ell )}} =\sum _{i=1}^F \sum _{j=1}^{H} \sum _{k=1}^{n_{ij}} \mathbf Z _{ijk}a^{(\ell )}_{ijk}, \\ {-\mathcal L ^{\prime \prime }_{\varvec{\beta }}}^{(\ell )}&:= -\frac{\partial ^2}{\partial \varvec{\beta }^T \partial \varvec{\beta }} \sum _{i=1}^F \mathcal L _i^{(\ell )} =\sum _{i=1}^F \sum _{j=1}^{H} \sum _{k=1}^{n_{ij}}b^{(\ell )}_{ijk}\mathbf Z _{ijk}^T \mathbf Z _{ijk}. \end{aligned}$$

The $\varvec{\gamma }$ and $\varvec{\beta }$ are then repeatedly updated until they converge.