Episodic activity in a heterogeneous excitatory network, from spiking neurons to mean field

Abstract

Many developing neural systems exhibit spontaneous activity (O’Donovan, Curr Opin Neurobiol 9:94–104, 1999; Feller, Neuron 22:653–656, 1999) characterized by episodes of discharge (active phases) when many cells are firing, separated by silent phases during which few cells fire. Various models exhibit features of episodic behavior by means of recurrent excitation for supporting an episode and slow activity-dependent depression for terminating one. The basic mechanism has been analyzed using mean-field, firing-rate models. Firing-rate models are typically formulated ad hoc, not derived from a spiking network description, and the effects of substantial heterogeneity amongst the units are not usually considered. Here we develop an excitatory network of spiking neurons (N-cell model) with slow synaptic depression to model episodic rhythmogenesis. This N-cell model displays episodic behavior over a range of heterogeneity in bias currents. Important features of the episodic behavior include orderly recruitment of individual cells during silent phases and existence of a dynamical process whereby a small critical subpopulation of intermediate excitability conveys synaptic drive from active to silent cells. We also derive a general self-consistency equation for synaptic drive that includes cell heterogeneity explicitly. We use this mean-field description to expose the dynamical bistability that underlies episodic behavior in the heterogeneous network. In a systematic numerical study we find that the robustness of the episodic behavior improves with increasing heterogeneity. Furthermore, the heterogeneity of depression variables (imparted by the heterogeneity in cellular firing thresholds) plays an important role in this improvement: it renders the network episodic behavior more robust to variations in excitability than if depression is uniformized. We also investigate the effects of noise vs. heterogeneity on the robustness of episodic behavior, especially important for the developing nervous system. We demonstrate that noise-induced episodes are very fragile, whereas heterogeneity-produced episodic rhythm is robust.

Appendix

1.1 Details of the mean-field description derivation

To obtain the expression for $\hat{q}(g_{syn},\:I)$ given in (11), we perform the following steps.

• 1. We solve Eq. (6) analytically assuming that synapses are activated for a short period of time relative to the interspike interval, i.e., ε _q  ≤ T(g _syn , I). Using the integrating factor method, we obtain

  $$q_i(t)\!=\!\!\left\{ \begin{array}{ll} {\frac{\alpha_q}{\alpha_q+\beta_q}}\!+\!\left(\! q_i(0)\!-\!{\frac{\alpha_q}{\alpha_q+\beta_q}} \!\right)\! e^{-(\alpha_q+\beta_q)t} & \ 0 \!\leq \!t \!\leq \!\epsilon_q \\ e^{-\beta_q(t-\epsilon_q)}q_i(\epsilon_q) & \ \epsilon_q \!<\! t\! \leq\! T_i \!\equiv \!T(g_{syn},\:I_i) \end{array} \right.$$

  (19)

  Since T _i is the period of neuron i, we must have

  $$\begin{array}{ll} q_i(T_i) & = q_i(0) \\ q_i(0) & = {\frac{\alpha_q}{\alpha_q+\beta_q}}\frac{e^{\beta_q\epsilon_q}-e^{-\alpha_q\epsilon_q}}{e^{\beta_q T_i}-e^{-\alpha_q\epsilon_q}} \end{array}$$

• 2. Find the temporal average of the analytical solution:

  $$\hat{q}(g_{syn},\:I_i)=\!\!\left\{ \begin{array}{ll} \!0, \mbox{ } T_i\!=\!+\infty \mbox{; otherwise:} & \ \nonumber\\ \!1/T_i \int_{0}^{T_i}q_i(t)dt \!=\!1/T_i \!\left( \int_{0}^{\epsilon_q} q_i(t)dt\!+\!\int_{\epsilon_q}^{T_i} \!q_i(t)dt \right) & \ \end{array} \right.$$

  For T _i finite,

  $$\int_{0}^{\epsilon_q} q_i(t)dt = {\frac{\alpha_q}{\alpha_q+\beta_q}}\epsilon_q +\!\left(\! q_i(0)\!-\!{\frac{\alpha_q}{\alpha_q+\beta_q}} \right)\!\frac{1}{\alpha_q+\beta_q}\left(1\!-\!e^{-(\alpha_q+\beta_q)\epsilon_q}\right)$$

  (20)
  $$\begin{array}{*{20}ll}\int_{\epsilon_q}^{T_i} q_i(t)dt &= \left[{\frac{\alpha_q}{\alpha_q+\beta_q}}+\left( q_i(0)-{\frac{\alpha_q}{\alpha_q+\beta_q}} \right)e^{-(\alpha_q+\beta_q)\epsilon_q}\right] \frac{1}{\beta_q}\left(1-e^{-\beta_q(T_i-\epsilon_q)}\right) \\&= \frac{1}{\beta_q}\left({\frac{\alpha_q}{\alpha_q+\beta_q}}\left(1-e^{-(\alpha_q+\beta_q)\epsilon_q}\right) -\left(1-e^{-(\alpha_q+\beta_q)\epsilon_q}\right)q_i(0)\right)\end{array}$$

  (21)

  Hence, combining the similar terms in (20) and (21), we obtain:

  $$\hat{q}_i=r_i\left(c-\frac{d}{e^{\beta_q/r_i}-w}\right)$$

  (22)

  where

  $$\begin{array}{ll} c & = \frac{\alpha_q\epsilon_q}{\alpha_q+\beta_q}+\frac{\alpha_q^2}{(\alpha_q+\beta_q)^2\beta_q}\left(1-e^{-(\alpha_q+\beta_q)\epsilon_q}\right) \\ d & = \frac{\alpha_q^2}{(\alpha_q+\beta_q)^2\beta_q}\left(e^{\beta_q\epsilon_q}-e^{-\alpha_q\epsilon_q}\right)\left(1-e^{-(\alpha_q+\beta_q)\epsilon_q}\right) \\ w & = e^{-\alpha_q\epsilon_q} \end{array}$$

  In general,

  $$\hat{q}(g_{syn},\:I)=r(g_{syn},\: I) \left(c-\frac{d}{e^{\beta_q/r(g_{syn},\: I)}-w}\right)$$

  (23)

  Both (22) and (23) are valid for any firing rate. In particular, for low firing rates, we deduce from (11) that

  $$\hat{q}(g_{syn},\:I) \approx c r(g_{syn},\: I)$$

  (24)

  For high firing rates, by using Taylor’s Formula in powers of $\beta_q/r(g_{syn},\: I)$ and keeping the linear part only, we obtain:

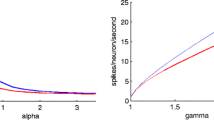
  $$\hat{q}(g_{syn},\:I) \approx \left(c\! - \!\frac{d}{1\!-\!w} \right)\! r(g_{syn},\: I)\! + \frac{b \beta_q}{(1\!-\!c)(1\!-\!c\!+\!\beta_q \tau_{ref})}$$

  (25)

  The β _q τ _ref term in the denominator is the minimum possible value of $\beta_q/r(g_{syn},\: I)$. Thus, the temporally averaged synaptic activation is approximately linear in both cases, with the slope being shallower in the latter. The graph of $\hat{q}(g_{syn},\:I)$ is shown in Fig. 11(b).

Fig. 11

Panel (a): firing rate of the single leaky integrate-and-fire neuron without noise. Transition to repetitive firing occurs when Θ _eff (g _syn , I) = 1, i.e., along the straight line I = 1 + g _syn (1 − V _syn ). If either g _syn or I is fixed at some level, the firing-rate as a function of the other variable possesses the characteristic logarithmic shape. Superimposed are also shown three firing-rate population profiles, corresponding to the three marked steady-state values of g _syn on the lower, middle, and upper branches of the bifurcation diagram in Fig. 7(a). Panel (b): single-cell synaptic activation averaged over one interspike interval as a function of the cell’s firing rate. Note the linear parts for low and high firing rates, consistent with (24) and (25)

We also provide some additional details here. In this work, we use uniform distributions of bias currents on a finite interval (I _min ; I _max ). Then, (14) simplifies to

$$g_{\mathit{syn}}={\overline{g}}_{syn}\frac{1}{I_{max}-I_{min}}\int_{I_{min}}^{I_{max}} s(t, \: \ensuremath{I}) \hat{q}(g_{syn},\:I) dI$$

(26)

For general description purposes (e.g., this is how the bifurcation diagrams in Fig. 7 were generated), we can interpret (14) in terms of ${\overline{g}}_{syn}$ as a function of the self-consistent value of g _syn . This allows us to avoid the numerical solution of (14) altogether, but is not applicable if the self-consistent value of g _syn corresponding to a specific value of ${\overline{g}}_{syn}$ is required. The corresponding expression is

$${\overline{g}}_{syn}=\frac{g_{\mathit{syn}}}{\int_{-\infty}^{\infty}f(\ensuremath{I}) s(t, \: \ensuremath{I}) \hat{q}(g_{syn},\:I) dI}$$

(27)