1 Introduction

Queueing models are a well-established tool for the analysis of stochastic systems from areas as divers as manufacturing, telecommunication, transport and the service industry. Typically, a queueing model is a simplified representation of the real-world system under consideration. In addition, often there is not sufficient statistical data to determine the service and interarrival time distribution, or, in case the type of distribution is known, there is statical uncertainty on the exact values of the parameters of the distribution. For these reasons, perturbation analysis of queueing systems (PAQS) has been developed. PAQS studies the dependence of the performance of a given queueing system on the underlying distributional assumptions. This paper is concerned with PAQS for the finite capacity single server queue, where we assume that the arrival stream is of Poisson type, an assumption which is often justified in applications, see Chen and Xia (2011).

In this paper we present a new approach to PAQS. We develop the performance of the system under consideration into a Taylor series with respect to the parameter of interest, where we make use of a fundamental result on Taylor series for Markov chains, see Heidergott and Hordijk (2003). The usefulness of any Taylor series based approach relies on two factors:

  1. 1.

    Fast convergence of the series (a Taylor polynomial of small order yields already a satisfying approximation).

  2. 2.

    The ability of computing the remainder term of the Taylor series in an efficient way so that the order of the Taylor polynomial that is sufficient to achieve a desired precision of the approximation can be decided a priori.

The contribution of the paper is as follows. We investigate the use of Taylor polynomials for the numerical evaluation of the M/G/1/N queue. Specifically, our numerical studies show that already a Taylor series of small order yields good approximations (this addresses topic (1) above); and that a simplified and easily computable expression bounding the remainder of the Taylor series can be established (this addresses topic (2) above).

The paper is organized as follows. The embedded Markov chain of the M/G/1/N model is presented in Section 2. Our series expansions approach is detailed in Section 3. Numerical examples are provided in Section 4 for the case of the M/D/1/N queue. A more detailed version of this paper is available as technical report (Abbas et al. 2011), which contains more numerical material on the M/D/1 queue, and, as an additional example, a perturbation analysis of the M/W/1/N queue, with W denoting the Weibull distribution is presented.

We conclude the introduction with a brief discussion of implications of our approach to the numerical approximation of the M/G/1/∞ queue. Numerical approximations for the M/G/1/N queue have a long tradition, and we refer to the excellent survey in Smith (2004). The approach presented in this paper is different from the standard approaches as it is also feasible for traffic loads larger than one. In addition, our approach yields an approximation of a performance functional on an entire interval and allows for an error bound of the approximation that holds uniformly on an interval.

2 The M/G/1/N queue

Consider the M/G/1/N queue, where customers arrive according to a Poisson process with rate λ and demand an independent and identically distributed service time with common distribution function B(t) with mean 1/μ. There can at most be N customers be present at the queue (including the one in service), and customers attempting to enter the queue when there are already N customers present are lost. The service discipline is FCFS.

Let X (t) denote the number of customers in the M/G/1/N queue at time t, for t ≥ 0 . Note that the queue-length processes { X(t) : t ≥ 0 } of the M/G/1/N system fails to be a Markov process because the service time distribution does not have the memoryless property. Since we have assumed that customers that do not find an empty buffer place upon their arrival are lost, the stationary distribution of { X (t) : t ≥ 0 } , denoted by π  ∗ , exists (independent of the traffic rate). Let { X n : n ∈ ℕ } denote the queue–length process embedded right after the departure of the nth customer, see Gross and Harris (1985) and Kendall (1953). Note that X n has state-space { 0 , ..., N − 1 } as after the departure of a customer the system cannot be full. Then {X n : n ∈ ℕ } is a Markov chain with transition matrix

$$\label{eq:p} P = \left( \begin{array}{ccccccc} a_{0} & a_{1} & a_{2} & a_{3} & \cdots & a_{N-2} & 1-\sum\limits_{k=0}^{N-2} a_k \\ a_{0} & a_{1} & a_{2} & a_{3} & \cdots & a_{N-2} & 1-\sum\limits_{k=0}^{N-2}a_k \\ 0 & a_{0} & a_{1} & a_{2} & \cdots & a_{N-3} & 1-\sum\limits_{k=0}^{N-3} a_k \\ 0 & 0 & a_{0} & a_{1} & \cdots & a_{N-4} & 1-\sum\limits_{k=0}^{N-4}a_k \\ & & \ddots & & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & a_{0} & 1-a_{0} \\ \end{array} \right) , $$
(1)

where

$$ a_{k} = \int_{0}^{\infty} \frac{(\lambda t)^{k}}{k!} e^{-\lambda t} dB(t) , \quad k = 0 , \ldots , N-2 . $$
(2)

In words, a k is the probability of k Poisson arrivals during an B ( ·) distributed service time.

It is well known that π  ∗  can be expressed via the stationary distribution of the Markov chain embedded at departure points of customers, denoted by π. Specifically, let ρ denote the traffic rate, then it holds that

$$\label{eq:1} \pi^\ast(i) = \frac{\pi (i)}{\pi(0) + \rho} , i = 0 , \ldots N-1, $$
(3)

and

$$ \pi^\ast(N) = \frac{1}{\rho } \left ( \rho - 1 + \frac{\pi(0)}{\pi(0)+\rho} \right ) = \frac{\pi(0) + \rho -1}{\pi(0) +\rho} , $$
(4)

see Gross and Harris (1985) for details.

For the PAQS presented in this paper we consider π  ∗  as a mapping of some real-valued parameter θ, in notation \( \pi^\ast_\theta \). For example, θ may denote the mean service time of the queue. We are interested in obtaining the functional dependence of π  ∗ ( θ) on θ in a simplified form. For our approach we will compute \( \pi_\theta^\ast \) for some parameter value θ numerically. However, then we will approximate the function π  ∗ ( θ + Δ) on some Δ-interval. More specifically, we will approximate π  ∗ ( θ + Δ) by a polynomial in Δ. To achieve this we will use the Taylor series expansion approach established in Heidergott and Hordijk (2003). More specifically, let π θ denote the stationary distribution of the queue-length process embedded at departure epoches in the M/G/1/N queue, where θ ∈ ℝ denotes a control parameter. Under quite general conditions it holds that π θ + Δ can be developed into a Taylor series of the following from

$$ \pi_{\theta + \Delta } = \sum\limits_{n=0}^\infty \frac{\Delta^n}{n!} \pi _{\theta }^{(n) } , $$

where \( \pi_{ \theta }^{ (n)}\) denotes the n-th order derivative of π θ with respect to θ. We call

$$\label{eq:hkhk} H_{\theta} ( k , \Delta ) = \sum\limits_{n=0}^k \frac{\Delta^n}{n!} \pi _{\theta }^{(n) } $$
(5)

the k-th order Taylor approximation of π θ + Δ at θ, and

$$ r_{\theta} ( k , \Delta ) = \pi_{\theta + \Delta } - H_{\theta} ( k, \Delta ) $$

the k-th order remainder term at θ.

3 The Taylor series expansion approach

In this section, we present the Taylor series approximation for the M/G/1/N queue. Let B ( ·) have density mapping b ( ·) . Let Θ = ( a , b ) ⊂ ℝ , for 0 < a < b < ∞.

(A) :

For 0 ≤ k ≤ N − 2 it holds that a k is n-times differentiable with respect to θ on Θ.

Under (A) it holds that the first n derivatives of P exists. Let P (k) denote the kth order derivative of P with respect to θ, then it holds that

$$ P^{(k)} ( i , j ) = \frac{ d^{ ( k ) }}{ d \theta^{ (k ) } } P ( i , j ) , \quad 0 \leq i , j \leq N-1 , $$

or, more specifically,

$$\label{eq:c} P^{(k) } = \left( \begin{array}{ccccccc} a_{0} (k)& a_{1} (k)& a_{2} (k)& a_{3} (k)& \cdots & a_{N-2}(k) & \: - \! \! \! \sum\limits_{j=0}^{N-2} a_j (k)\\ a_{0} (k)& a_{1} (k)& a_{2}(k) & a_{3} (k)& \cdots & a_{N-2} (k)& \:- \! \! \! \sum\limits_{j=0}^{N-2}a_j (k) \\ 0 & a_{0}(k) & a_{1} (k)& a_{2} (k)& \cdots & a_{N-3} (k)& \: - \! \! \! \sum\limits_{j=0}^{N-3} a_j (k)\\ 0 & 0 & a_{0}(k) & a_{1}(k) & \cdots & a_{N-4} (k)& \: - \! \! \! \sum\limits_{j=0}^{N-4}a_j (k) \\ & & \ddots & & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & a_{0}(k) & \: -\, a_{0}(k) \\ \end{array} \right) $$
(6)

where

$$ a_j (k ) = \frac{ d^{k }}{ d \theta^{k } } a_j , \quad 0 \leq j \leq N-2 . $$

Example 1

Consider the M/D/1 queue with arrival rate λ and deterministic service rate c . Then, a k is given by the probability to see k arrivals in an time interval of length c:

$$ a_{k} = \frac{(\lambda c)^{k}}{k!} e^{-\lambda c} . $$

Let π θ denote the stationary distribution of the embedded chain, where θ denotes the parameter of interest, and denote the deviation matrix by D θ defined by

$$ D_\theta = \sum\limits_{n=0}^\infty \left( P^n_\theta - \Pi_\theta \right) , $$

where Π θ is a square matrix with rows equal to \( \pi_\theta^\top \), with \( x^\top \) denoting the transposed of vector x. As shown in Heidergott et al. (2007), for any finite-state aperiodic Markov chain the deviation matrix exists.

Theorem 1

(Theorem 4 in Heidergott and Hordijk (2003)) Let θ ∈ Θ and let Θ0 ⊂ Θ a closed interval with θ be an interior point such that the queue is stable on Θ0 . Provided that the entries of P are n -times differentiable with respect to θ, let

$$ K_\theta ( n ) = \sum\limits_{ \substack{ 1 \leq m \leq n \\ 1 \leq l_k \leq n \\ l_1 + \cdots + l_m = n }} \frac{n!}{l_1! \cdots l_m!} \: \prod\limits_{k=1}^m \left ( P_\theta^{ (l_k ) } \, D_\theta \right ) . $$

Then it holds that

$$ \pi _{\theta }^{(n) } \,=\, \pi _{\theta } \, K_\theta ( n ) \: . $$

Proof

We prove the theorem by induction. For n = 1 , we have to show that π θ ′ = π θ P θ ′ D θ . By simple algebra, it holds that for Δ such that θ + Δ ∈ Θ that

$$ \pi_{\theta+\Delta} - \pi_{\theta} = \pi_{\theta+\Delta} \left( P_{\theta + \Delta } - P_\theta \right)D_\theta , $$

see, e.g., Heidergott et al. (2007) for a proof, which yields

$$\label{eq:th1} \frac{1}{\Delta} \left(\pi_{\theta+\Delta} - \pi_{\theta} \right) = \pi_{\theta} \frac{1}{\Delta}\left( P_{\theta + \Delta } - P_\theta \right)D_\theta + (\pi_{\theta+\Delta} - \pi_{\theta} ) \frac{1}{\Delta}( P_{\theta + \Delta } - P_\theta )D_\theta . $$
(7)

Element-wise differentiability of P implies that

$$\label{eq:th2} \lim\limits_{\Delta \rightarrow 0 } \pi_{\theta} \frac{1}{\Delta}( P_{\theta + \Delta } - P_\theta )D_\theta = \pi_{\theta} P_\theta ' D_\theta . $$
(8)

Since Θ0 is a compact neighborhood of θ, and π θ is finite for any θ ∈ Θ0, it holds that \( \sup_{ \theta \in \Theta_0 } | \pi_\theta | \) is finite. Moreover,

$$ 0 \leq | (\pi_{\theta+\Delta} - \pi_{\theta} ) | \left | \frac{1}{\Delta}( P_{\theta + \Delta } - P_\theta ) D_\theta \right | \leq \sup_{ \theta \in \Theta_0 } | \pi_\theta | \left | \frac{1}{\Delta}( P_{\theta + \Delta } - P_\theta ) D_\theta \right | . $$

Element-wise differentiability of P then yields

$$ \lim\limits_{\Delta \rightarrow 0 } \left | \frac {1}{\Delta}( P_{\theta + \Delta } - P_\theta ) D_\theta \right | = 0 , $$

which implies that the term on the righthand side of Eq. 7 tends to zero as Δ tends to zero. Hence, taking the limit for Δ to zero in Eq. 7 reduces to Eq. 8, which proves the claim for n = 1.

The proof for the general case follows by induction with respect to n like in conventional analysis. □

Example 2

For ease of reference we will provide in the following an explicit representation of the first derivatives of π θ , where have simplified the expression by simple algebra:

$$ \pi_\theta^{(1)} = \pi_\theta P_\theta^{(1)} D_\theta \: , \quad \pi_\theta^{(2)} = \pi_\theta P_\theta^{(2)} D_\theta + 2 \pi_\theta^{(1)} P_\theta^{(1)} D_\theta$$

and

$$\pi_\theta^{(3)} = \pi_\theta P_\theta^{(3)} D_\theta +3 \pi_\theta^{(2)} P_\theta^{(1)} D_\theta + 3 \pi_\theta^{(1)} P_\theta^{(2)} D_\theta . $$

A Taylor polynomial yields an approximation and the error introduced by this approximation can be expressed by the Lagrange form of the remainder as follows

$$\label{eq:remm} r_\theta ( k , \Delta ) = \int_{0}^{ \Delta} \frac{x^k} { k!} \pi_{ \theta + x }^{(k+1)} \, d x . $$
(9)

From a numerical point of view the above expression is rather pointless as, by Theorem 1, it holds that

$$ \pi_{ \theta + x }^{(k+1)} = \pi_{ \theta + x } K_{ \theta + x } ( k +1 ) $$

which implies that for computing the remainder we already have to know the very entity we want to approximate, namely, π η for η ∈ [ θ, θ + η] . To overcome this drawback we will present an alternative form for the remainder term.

The basic idea is that analyticity of π θ implies that of \( \pi_\theta^{(k)} \) for all k and we can again use a Taylor series to approximate \( \pi_{ \theta + x }^{(k+1)} \) in Eq. 9. By doing so we initiate the Taylor series in the tail of original Taylor series, and we expect that the error of this second Taylor approximation step is negligibly small. We explain this approach in the following in more details.

Let

$$ G_\theta ( k , m , \delta ) = \sum\limits_{n=0}^m \frac{\delta^n}{n!} \pi_{\theta}^{(k+1+n)} $$

denote the Taylor polynomial of order m for \( \pi_{\theta}^{(k+1)} \), i.e.,

$$ \pi_{\theta + \delta }^{(k+1)} \approx G_\theta ( k , m , \delta ) $$

for m sufficiently large. Inserting the above approximation into Eq. 9 yields

$$\begin{array}{rll} r_\theta ( k , \Delta ) & \approx & \int_{0}^{ \Delta} \frac{x^k} { k!} G_\theta ( k , m , x ) \, d x \nonumber \\ & = & \int_{ 0 }^{ \Delta} \frac{x^k} { k!} \sum\limits_{n=0}^m \frac{x^n}{n!} \pi_{\theta}^{(k+1+n)} \, d x \nonumber \\ & = & \sum\limits_{n=0}^m \frac{1}{k! \, n!} \pi_{\theta}^{(k+1+n)} \int_{0}^{\Delta} x^{k+n} \, d x \nonumber \\ & = & \sum\limits_{n=0}^m \frac{ \Delta^{k+n+1}}{k! \, n! \, ( k + n +1 ) } \pi_{\theta}^{(k+1+n)} \, . \end{array}$$
(10)

We denote by

$$\label{eq:gg} g_\theta ( k , m , \Delta ) = \sum\limits_{n=0}^m \frac{ \Delta^{k+n+1}}{k! \, n! \, ( k + n +1 ) } \pi_{\theta}^{(k+1+n)} $$
(11)

the expression for the approximation of the remainder term obtained from Eq. 10. Provided that | g θ ( k , m , Δ) − r θ ( k , Δ) | is small for m small, we will use g θ ( k , m , Δ) in our Taylor series approach to determine the order of the polynomial that is sufficient for achieving the desired precision of the approximation. As the following theorem shows, g θ ( k , m , Δ) is of order \(c \Delta^m r_\theta ( k , \Delta ) \) for some small constant c. In other words, letting, for example, Δ = 0.1 and choosing m = 3 , the error introduced by our approximation of the remainder term at k is typically smaller than 10 − (5 + k) .

In order to state the precise statement, we introduce the norm \( || x || = \sum_{i=1}^n | x_i| \) on ℝn .

Theorem 2

Let θ ∈ Θ be an interior point of Θ and let Δ > 0 be such that θ + Δ ∈ Θ. Assume that the entries of P are (k + m + 2)-times continuously differentiable with respect to θ on Θ. Suppose that a finite constant d exists such that

$$ d \geq \sup\limits_{x \in [ \theta , \theta + \Delta ]} \left|\left| \pi_{ x }^{(k+2+m)} \right|\right| , $$

then

$$ \left| g_\theta ( k , m , \Delta ) - r_\theta ( k , \Delta ) \right| \leq d \frac{\Delta^{(m+k+2}} {m! \, k! \, (m+k+2)} . $$

Proof

Note that the Lagrange form of the remainder for G θ ( k , m, δ) reads

$$ \int_{0}^{\delta} \frac{u^{m}} {m!} \pi_{ \theta + u }^{(k+m+2)} \, d u . $$

Applying the norm || ·|| and using the bound d , yields

$$\begin{array}{rll} | g_{\theta }( k , m, \Delta ) - r_\theta ( k , \Delta ) | & \leq & \left | \int_{0}^{\Delta} \frac{x^{k}} {k!} \left ( \int_0^x \frac{u^m}{m!} \pi_{ \theta + u }^{(k+m+2)} \, d u \right ) d x \right | \\ & \leq & d \int_{0}^{\Delta} \frac{x^{k}} {k!} \left ( \int_0^x \frac{u^m}{m!} du \right ) \, d x \\ & = & d \frac{\Delta^{m+k+2}} {m! \, k! \, (m+k+2)} , \end{array}$$

which proves the claim. □

In the numerical examples presented in the following sections, we will show that choosing m = 2 already yields a sufficient precision for approximating the remainder term.

Remark 1

Taylor series approaches for performance approximation have been studied in the literature before, see, e.g. Girish and Hu (1996, 1997) and Gong and Hu (1992). However, no a priori knowledge on the quality of the approximation of these approach could be established.

The Taylor series approximation developed above applies to differentiable Markov kernels. This extends the case of linear θ dependence that has been studied in the literature so far; see, for example, Cao (1998), Heidergott et al. (2010), Kirkland et al. (1998), Leder et al. (2010) and Schweitzer (1968). An interesting property of the linear-dependence case is that the remainder term can be bounded in an efficient way, see Heidergott et al. (2007).

4 Applications to the M/D/1/N queue

In this section we present numerical examples. Let the distribution of the service times be deterministic, with θ denoting the deterministic service time. As performance measure we focus on the blocking probability \( \pi^\ast_\theta ( N ) \), which is due the fact that customers arrive according to a Poisson arrival stream, equal to the probability that an arriving customer is lost due to no available free waiting space. Let E [ B ( θ) ] denote the mean service time depending on θ and assume that the arrival rate λ is independent of θ. Then, the traffic rate is given by

$$ \rho (\theta ) = \lambda \, E [ B ( \theta ) ] . $$

Recall, that by Eq. 4, it holds that

$$\label{eq:tt} \pi^\ast_{\theta +\Delta } ( N ) = \frac{\pi_{\theta +\Delta }(0) + \rho(\theta + \Delta) -1}{\pi_{\theta +\Delta }(0) + \rho(\theta + \Delta)} . $$
(12)

Inserting our Taylor series expansion for π θ + Δ(0) provided in Eq. 5 into the above expression yields a functional representation of \( \pi^\ast_{\theta +\Delta } ( N ) \) as function in Δ. Elaborating on Eq. 4, a similar procedure leads to a functional representation of the mean queue length and via Little’s law to one of the stationary waiting time.

Consider the M/D/1/5 queue with arrival rate λ and deterministic service time c = θ. The elements of P are provided in Example 1.

Lemma 1

The transition probability matrix P of the embedded chain of the M/D/1/N queue is infinitely often differentiable with respect to c .

Proof

By Eq. 6 differentiability properties of P can be deduced from that of the α j entries. By Example 1, all higher-order derivatives exist for a j , which proves the claim. □

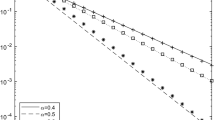
We now turn to the blocking probability. Starting point is the expression for the loss probability in Eq. 12. The traffic rate is given by ρ( θ + Δ) = λ( θ + Δ) and π θ + Δ ( 0 ) is approximated via a Taylor series polynomial of degree k, i.e., we replace π θ + Δ ( 0 ) by H θ ( k , Δ) (0); see Eq. 5. As can be seen from the Table 1, the approximation yields a satisfying precision in predicting the loss probability \( \pi_{\theta +\Delta}^\ast ( N ) \) as a mapping of Δ in a range of Δ being 10% of θ.

Table 1 The relative absolute error in predicting the loss probability for various traffic rates
Full size table

We conclude the discussion of the M/D/1/N queue by providing a bound on the error of the Taylor series approximation for \( \pi_{\theta + \Delta }^\ast ( N) \).

Lemma 2

Consider the M/D/1/N queue with arrival rate λ and deterministic service time θ. Suppose that for k it holds for | Δ| ≤ δ that

$$ | \pi_{\theta + \Delta } ( 0 ) - H_\theta ( k , \Delta ) | \leq R_\theta ( k , \delta ), $$

then

$$ \sup\limits_{ | \Delta | \leq \delta } \left |\pi_{\theta + \Delta }^\ast ( N ) - \frac{ H_\theta ( k , \Delta )+ \lambda ( \theta + \Delta )-1}{H_\theta ( k , \Delta ) + \lambda ( \theta + \Delta )} \right | \nonumber \leq \frac{ 2 R_\theta ( k , \delta ) }{ \lambda^2 ( \theta - \delta )^2 - ( R_\theta ( k , \delta ) )^2} . $$

Proof

Replacing π θ + Δ ( 0 ) in Eq. 4 or Eq. 12 by H θ ( k , Δ) and noting that ρ( θ + Δ) = λθ + Δλ, implies thus that the true value for \( \pi_{\theta + \Delta }^\ast ( N ) \) is bounded by

$$ \frac{H_\theta ( k , \Delta )-R + \lambda \theta + \Delta \lambda -1}{H_\theta ( k , \Delta ) - R + \lambda \theta + \Delta \lambda} \leq \pi_{\theta + \Delta }^\ast ( N ) \leq \frac{H_\theta ( k , \Delta ) +R + \lambda \theta + \Delta \lambda -1}{H_\theta ( k , \Delta ) + R + \lambda \theta + \Delta \lambda} $$

The numerical error can thus be bounded by

$$\begin{array}{lll} \left | \frac{H_\theta ( k , \Delta ) +R + \lambda \theta + \Delta \lambda -1}{H_\theta ( k , \Delta )+ R + \lambda \theta + \Delta \lambda} - \frac{H_\theta ( k , \Delta )-R + \lambda \theta + \Delta \lambda -1}{H_\theta ( k , \Delta ) - R + \lambda \theta + \Delta \lambda} \right | \nonumber \\ \quad=\frac{ 2 R }{(H_\theta ( k , \Delta )+R + \lambda \theta + \Delta \lambda ) (H_\theta ( k , \Delta )-R + \lambda \theta + \Delta \lambda ) } \nonumber \end{array}$$

noting that H θ ( k , Δ) ≥ 0 for all Δ, yields

$$ \leq \frac{ 2 R }{(R + \lambda \theta + \Delta \lambda ) (-R + \lambda \theta + \Delta \lambda ) } = \frac{2 R }{ \lambda^2 ( \theta - \Delta )^2 - R^2} \nonumber $$

and from | Δ| ≤ δ it follows

$$ \leq \frac{2 R }{ \lambda^2 ( \theta - \delta )^2 - R^2} . $$

□

We conclude this section with a discussion of the numerical bound on the error provided in Lemma 2 and Theorem 2. To this end we consider the Taylor series approximation of degree k = 2 for the blocking probability. Table 2 compares the true remainder term with the approximation of the remainder term obtained from replacing R θ (k , δ) in the bound put forward in Theorem 2 by g θ ( k , m , δ) defined in Eq. 11, where we have chosen m = 2. As can be seen from Table 2, the approximation of the remainder term yields good results for small values of Δ. For example, the approximative remainder term indicates that a Taylor series of degree 2 for Δ = 0.1 yields a maximal error of 5 ×10 − 4 in predicting the blocking probability, whereas the true error is no greater than 3 ×10 − 4 .

Table 2 The remainder term vs. the bound for the remainder at ρ = 1 for k = 2 and m = 2
Full size table

5 Conclusion

We have presented a new approach to the functional approximation of finite queues. As illustrated by the numerical examples for the M/D/1/N queue, the convergence rate of the Taylor series is such that already a Taylor polynomial of degree 2 or 3 yields good numerical results. We established an approximation for the remainder term of the Taylor series that provides an efficient way of computing (approximately) the remainder term and thereby provides an algorithmic way of deciding which order of the Taylor polynomial is sufficient to achieve a desired precision of the approximation. This implies that the proposed Taylor series approximation can be of practical value. Future research will be on investigating the behavior of the series expansion for multi-server queues.